Many Exact Solutions of the Nonlinear KPP Equation Using the Bäcklund Transformation of the Riccati Equation
Elsayed ME Zayed1 , Khaled AE Alurrfi2 and Abdul Ghani Al Nowehy3
1Department of Mathematics, Faculty of Sciences, Zagazig University, Zagazig, Egypt
2Department of Mathematics, Faculty of Arts & Science, Mergib University, Msallata, Libya
3Department of Mathematics, Faculty of Education and Science, Taiz University, Taiz, Yemen
*Corresponding author
Elsayed ME Zayed, Department of Mathematics, Faculty of Sciences, Zagazig University, Zagazig, Egypt, E-mail: [email protected]
Int J Opt Photonic Eng, IJOPE-2-006, (Volume 2, Issue 1), Research Article
Received: May 12, 2017
Accepted: August 21, 2017
Published: August 24, 2017
Citation: Zayed EME, Alurrfi KAE, Al Nowehy AG (2017) Many Exact Solutions of the Nonlinear KPP Equation Using the Bäcklund Transformation of the Riccati Equation. Int J Opt Photonic Eng 2:006.
Copyright: © Zayed EME, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The Bäcklund transformation of the Riccati equation is applied in this article to construct traveling wave solutions for the nonlinear Kolmogorov-Petrovskii-Piskunov (KPP) equation. Solitons, trigonometric and rational solutions of this equation are obtained. This transformation is straightforward and concise. It gives much more general results than the well-known results obtaining by other methods. With the aid of Maple, some graphical representations for some results are presented by choosing suitable values of parameters.
Keywords
Exact traveling wave solutions, Bäcklund transformation of the Riccati equation, Kolmogorov-Petrovskii-Piskunov equation, Soliton solutions, Trigonometric solutions, Rational solutions
Mathematics Subject Classification: 35K99, 35P05, 35P99, 35C05.
Introduction
The investigation of exact traveling wave solutions to nonlinear PDEs plays an important role in the study of nonlinear physical phenomena. Nonlinear wave phenomena appears in various scientific and engineering fields, such as fluid mechanics, plasma physics, optical fibers, biology, solid state physics, chemical kinematics, chemical physics and geochemistry. Nonlinear wave phenomena of dispersion, dissipation, diffusion, reaction and convection are very important in nonlinear wave equations. In recent decades, many effective methods have been established to obtain exact solutions of nonlinear PDEs, such as the inverse scattering transform [1], the Hirota method [2], the truncated Painlevé expansion method [3], the Bäcklund transform method [1,4-8], the simplest equation method [9,10], the Weierstrass elliptic function method [11], the Jacobi elliptic function method [12-14], the tanh-function method [15,16], the (G'/G)-expansion method [17-22], the modified simple equation method [23-26], the Kudryashov method [27-29], the multiple exp-function algorithm method [30,31], the transformed rational function method [32], the Frobenius decomposition technique [33], the local fractional variation iteration method [34], the local fractional series expansion method [35], the (G'/G, 1/G)-expansion method [36-40], the generalized Riccati equation mapping method [41-43], the test function method [44,45] and so on.
The objective of this article is to use the Bäcklund transformation of the Riccati equation to construct new exact traveling wave solutions of the following nonlinear Kolmogorov-Petrovskii-Piskunov (KPP) equation [22,26,46].
Where µ,γ,δ are real constants? Eq. (1.1) includes the Fisher equation, Huxley equation, Burgers-Huxley equation, Chaffee-Infanfe equation and Fitzhugh-Nagumo equation as special cases. Recently, Feng, et al. [22] have discussed Eq. (1.1) using the (G'/G)-expansion method and found its exact solutions, while Zayed, et al. [26,46] have applied two methods via the modified simple equation method and the Riccati equation method combined with the (G'/G)-expansion method respectively, to Eq. (1.1) and determined the exact traveling wave solutions of it.
This paper is organized as follows: In Sec. 2, the description of the Bäcklund transformation of the Riccati equation is given. In Sec. 3, we use the given method described in Sec. 2, to find traveling wave solutions of the nonlinear KPP equation. In Sec. 4, physical explanations of some results are presented. In Sec. 5, some conclusions are obtained.
Description of the Bäcklund Transformation of the Riccati Equation
Suppose that we have the following nonlinear PDE:
Where F is a polynomial in u(x,t) and its partial derivatives, in which the highest order derivatives and the nonlinear terms are involved. In the following, we give the main steps of this method [5,47]:
Step 1
Using the wave transformation.
Where k,ω are constants, to reduce Eq. (2.1) to the following ODE:
Where P is a polynomial in u(ξ) and its total derivatives while .
Step 2
Assume that Eq. (2.3) has the formal solution.
Where ai are constants to be determined, such that aN ≠ 0 or a-N ≠ 0, while Ψ(ξ) comes from the following Bäcklund transformation
Where b,A,B are constants with B ≠ 0, while φ(ξ) satisfies the Riccati equation:
It is well-known [16] that Eq. (2.6) has the following solutions:
(i) If b < 0, then
(ii) If b > 0, then
(iii) If b = 0, then
Step 3
We determine the positive integer N in (2.4) by using the homogeneous balance between the highest-order derivatives and the nonlinear terms in Eq. (2.3). More precisely we define the degree of u(ξ) as D[u(ξ)] = N which gives rise to the degree of other expressions as follows:
Therefore, we can get the value of in (2.4). In some nonlinear equations the balance number N is not a positive integer. In this case, we make the following transformations [47]:
(a) When where is a fraction in the lowest terms, we let
Then substituting (2.8) into (2.3) to get a new equation in the new function v(ξ) with a positive integer balance number.
(b) When N is a negative number, we let
and substituting (2.9) into (2.3) to get a new equation in the new function v(ξ) with a positive integer balance number.
Step 4
We substitute (2.4) along with Eq. (2.6) into Eq. (2.3), collect all the terms with the same powers of φI(ξ) and set them to zero, we obtain a system of algebraic equations, which can be solved by Maple to get the values of ai and k,ω. Consequently, we obtain the exact traveling wave solutions of Eq. (2.1).
Finally if B = 0, then the above method reduces to the well-known modified extended tanh-function method [16].
An Application
In this section, we will apply the method described in Sec. 2 to find the exact traveling wave solutions of the nonlinear KPP equation (1.1). To this end, we use the wave transformation (2.2) to reduce Eq. (1.1) to the following ODE:
By balancing u" with u3 in Eq. (3.1), we get N = 1. Consequently, we have the formal solution
Where a0, a1, a-1 are constants to be determined, such that a1 ≠ 0 or a-1 ≠ 0 while Ψ(ξ) is given by (2.5).
Now, substituting (3.2) along with Eqs. (2.5) and (2.6) into (3.1), collecting the coefficients of φi(ξ), (i = 0,1,…,6) and setting them to zero, we get a system of algebraic equations. Solving this system of algebraic equations with aid of Maple, we have the following results:
Result 1
Provided that δ > 0.
From (3.1), (3.2) and (3.3), we deduce the exact traveling solutions of Eq. (1.1) as follows:
If b < 0, then we have the solutions
or
Provided that 4µδ-γ2 < 0.
If b > 0 then we have the solutions
Or
Provided that 4µδ-γ2 > 0.
If b = 0, then we get and we have the rational solution
Where .
Result 2
Provided that δ > 0.
From (3.1), (3.2) and (3.9), we deduce the exact traveling solutions of Eq. (1.1) as follows: If b < 0, then we have the solutions
or
If b > 0 then we have the solutions
or
Where .
Result 3
Provided that 4µδ-γ2 > 0 and δ > 0.
From (3.1), (3.2) and (3.14), we deduce the exact traveling solutions of Eq. (1.1) as follows:
If b < 0 then we have the solutions
or
under the constraint condition .
If b > 0 then we have the solutions
or
under the constraint condition , where .
Result 4
Provided that δ > 0.
From (3.1), (3.2) and (3.19), we deduce the exact traveling solutions of Eq. (1.1) as follows: If b < 0 then we have the solutions
or
If b > 0 then we have the solutions
or
where .
Result 5
provided that µ+2γa0 < 0.
Then from (3.1), (3.2) and (3.24), we have the exact traveling solutions:
or
where .
Result 6
Provided that δ > 0, µ > 0 and .
From (3.1), (3.2) and (3.27), we deduce the exact traveling solutions of Eq. (1.1) as follows: If b < 0 then we have the solutions
or
If b > 0, then we have the solutions
Or
Where .
Result 7
Provided that A2-3bB2 ≠ 0 and 3A2-bB2 ≠ 0.
From (3.1), (3.2) and (3.32), we deduce the exact traveling solutions of Eq. (1.1) as follows:
If b < 0 then we have the solutions
or
If b > 0 then we have the solutions
or
Where .
Physical Explanations of Our Obtained Solutions
The obtained exact traveling wave solutions for the nonlinear KPP equation (1.1) are hyperbolic, trigonometric and rational. In this section, we have presented some graphs of the exact solutions constructed by taking suitable values Figure 1, Figure 2, Figure 3 and Figure 4 as it illustrates some of our results obtained in this article. To this end, we select some special values of the obtained parameters, for example, in some of the hyperbolic solutions (3.4), (3.5) and the trigonometric solutions (3.12), (3.13) of the nonlinear KPP equation (1.1) with B = k = δ = γ =1, -10 < x,t < 1, respectively.
Conclusions
In this article, we have employed the Bäcklund transformation of the Riccati equation to obtain exact traveling wave solutions of the nonlinear Kolmogorov- Petrovskii-Piskunov (KPP) equation (1.1). On comparing our results in this paper with the well-known results obtained in [22,26,46] we deduce that our results in this article are new and are not published elsewhere. Further, all solutions obtained in this article have been checked with the Maple by putting them back into the original equations. Finally, the proposed method in this article can be applied to many other nonlinear PDEs in mathematical physics, which will be done in forthcoming papers.
Acknowledgement
The authors wish to thank the referees for their comments on this paper.
Figures
Figure 1 : Plot solution (3.4) with A = 1, µ = -1.
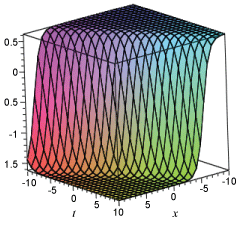
Figure 2: Plot solution (3.5) with A = 1, µ = -1.
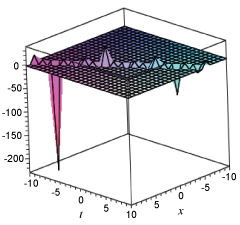
Figure 3: Plot solution (3.12) with A = 2, B = 1.
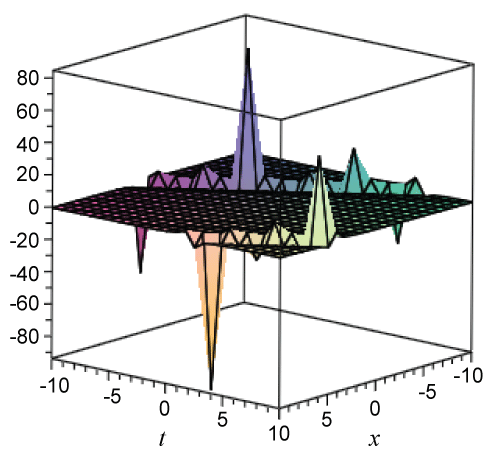
Figure 4: Plot solution (3.13) with A = 2, B = 1.
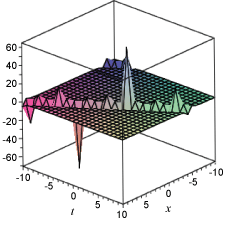
References
-
MJ Ablowitz, PA Clarkson (1991) Solitons nonlinear evolution equation and inverse scattering. Cambridge University Press, New York.
-
R Hirota (1971) Exact solutions of KdV equation for multiple collisions of solitons. Phys Rev Lett 27: 1192-1194.
-
NA Kudryashov (1991) On types of nonlinear non-integrable equations with exact solutions. Phys Lett A 155: 269-275.
-
MR Miura (1978) Bäcklund transformation. Berlin, Springer.
-
B Lu (2012) Bäcklund transformation of fractional Riccati equation and its applications to nonlinear fractional partial differential equations. Phys Lett A 376: 2045-2048.
-
M Singh (2015) Multi soliton solutions, bilinear Bäcklund transformation and Lax pair of nonlinear evolution equation in (2+ 1)-dimension. Comput Methods Diff Eqs 3: 134-146.
-
M Singh, RK Gupta (2016) Bäcklund transformations, Lax system, conservation laws and multisoliton solutions for Jimbo-Miwa equation with Bell-polynomials. Commun Nonlinear Sci Numer Simula 37: 362-373.
-
M Singh (2017) Bilinear Bäcklund transformations and explicit solutions of equation in (3+1)-dimension. Int J Computing Sci Math 8: 82-90.
-
NA Kudryashov, NB Loguinova (2008) Extended simplest equation method for nonlinear differential equations. Appl Math Comput 205: 396-402.
-
YM Zhao (2014) New exact solutions for a higher-order wave equation of KdV type using the multiple simplest equation method. J Appl Math 2014: 848069.
-
NA Kudryashov (1990) Exact solutions of generalized Kuramoto-Sivashinsky equation. Phys Lett A 147: 287-291.
-
S Liu, Z Fu, S Liu, Q Zhao (2001) Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys Lett A 289: 69-74.
-
D Lu, Q Shi (2010) New Jacobi elliptic functions solutions for the combined KdV-mKdV equation. Int J Nonlinear Sci 10: 320-325.
-
EME Zayed, YA Amer, RMA Shohib (2014) The Jacobi elliptic function expansion method and its applications for solving the higher order dispersive nonlinear Schrö dinger equation. Sci J Math Res 4: 53-72.
-
EJ Parkes, BR Duffy (1996) An automated tanh-function method for finding solitary wave solutions to nonlinear evolution equations. Comput Phys Commun 98: 288-300.
-
EME Zayed, KAE Alurrfi (2013) The modified extended tanh-function method and its applications to the generalized KdV-mKdV equation with any-order nonlinear terms. Int J Environ Eng Sci Tech Res 1: 165-170.
-
M Wang, X Li, J Zhang (2008) The (G'/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys Lett A 372: 417-423.
-
EME Zayed (2009) The (G'/G)-expansion method and its applications to some nonlinear evolution equations in the mathematical physics. J Appl Math Comput 30: 89-103.
-
EME Zayed, KA Gepreel (2009) The (G'/G)-expansion method for finding traveling wave solutions of nonlinear partial differential equations in mathematical physics. J Math Phys 50: 12.
-
ZL Li (2017) Constructing of new exact solutions to the GKdV-mKdV equation with any-order nonlinear terms by (G'/G) -expansion method. Appl Math Comput 217: 1398-1403.
-
B Ayhan, A Bekir (2012) The (G'/G)-expansion method for the nonlinear lattice equations. Commun Nonlinear Sci Numer Simula 17: 3490-3498.
-
J Feng, W Li, Q Wan (2011) Using (G'/G)-expansion method to seek the traveling wave solution of Kolmogorov-Petrovskii-Piskunov equation. Appl Math Comput 217: 5860-5865.
-
JM Jawad, MD Petkovic, A Biswas (2011) Modified simple equation method for nonlinear evolution equations. Appl Math Comput 217: 869-877.
-
EME Zayed (2011) A note on the modified simple equation method applied to Sharma-Tasso-Olver equation. Appl Math Comput 218: 3962-3964.
-
EME Zayed, YA Amer (2015) The modified simple equation method for solving nonlinear diffusive predator-prey system and Bogoyavlenskii equations. Int J Phys Sci 10: 133-141.
-
EME Zayed, SA Hoda Ibrahim (2014) Exact solutions of Kolmogorov-Petrovskii-Piskunov equation using the modified simple equation method. Acta Math Appl Sinica English Series 30: 749-754.
-
NA Kudryashov (2012) On one of methods for finding exact solutions of nonlinear differential equations. Commun Nonlinear Sci Numer Simula 17: 2248-2253.
-
PN Ryabov, DI Sinelshchikov, MB Kochanov (2011) Application of the Kudryashov method for finding exact solutions of the high order nonlinear evolution equations. Appl Math Comput 218: 3965-3972.
-
EME Zayed, KAE Alurrfi (2014) The homogeneous balance method and its applications for finding the exact solutions for nonlinear evolution equations. Italian J Pure Appl Math 33: 307-318.
-
WX Ma, Z Zhu (2012) Solving the (3+1)-dimensional generalized KP and BKP equations by the multiple exp-function algorithm. Appl Math Comput 218: 11871-11879.
-
WX Ma, T Huang, Y Zhang (2010) A multiple exp-function method for nonlinear differential equations and its application. Phys Script 82.
-
WX Ma, JH Lee (2009) A transformed rational function method and exact solutions to the (3+1)-dimensional Jimbo-Miwa equation. Chaos Solitons Frac 42: 1356-1363.
-
WX Ma, HY Wu, JS He (2007) Partial differential equations possessing Frobenius integrable decomposition technique. Phys Lett A 364: 29-32.
-
YJ Yang, D Baleanu, XJ Yang (2013) A Local fractional variational iteration method for Laplace equation within local fractional operators. Abst Appl Anal 2013.
-
M Yang, XJ Yang, ZB Li (2013) Local fractional series expansion method for solving wave and diffusion equations on cantor sets. Abst Appl Anal 2013: 202650.
-
EME Zayed, MAM Abdelaziz (2012) The two variables (G'/G, 1/G)-expansion method for solving the nonlinear KdV-mKdV equation. Math Prob Eng 2012: 725061.
-
EME Zayed, SA Hoda Ibrahim (2015) The (G'/G, 1/G)-expansion method and its applications for constructing the exact solutions of the nonlinear Zoomeron equation. World J Modelling and Simulation 11.
-
EME Zayed, KAE Alurrfi (2014) The (G'/G, 1/G)-expansion method and its applications to find the exact solutions of nonlinear PDEs for nanobiosciences. Math Prob Eng 2014.
-
EME Zayed, KAE Alurrfi (2014) The (G'/G, 1/G)-expansion method and its applications for solving two higher order nonlinear evolution equations. Math Prob Eng 2014: 746538.
-
EME Zayed, KAE Alurrfi (2015) On solving two higher-order nonlinear PDEs describing the propagation of optical pulses in optic fibers using the (G'/G, 1/G)-expansion method. Ricerche Mat 64: 167-194.
-
SD Zhu (2008) The generalized Riccati equation mapping method in nonlinear evolution equation: application to (2+1)-dimensional Boiti-leon-Pempinelle equation. Chaos Solitons Frac 37: 1335-1342.
-
EME Zayed, AH Arnous (2013) Many exact solutions for nonlinear dynamics of DNA model using the generalized Riccati equation mapping method. Sci Res Essays 8: 340-346.
-
M Singh, RK Gupta (2015) Explicit exact solutions for variable coefficient Broer-Kaup equations. Comput Methods Diff Eqs 3: 192-199.
-
M Singh (2016) New exact solutions for (3+1)-dimensional Jimbo-Miwa equation. Nonlinear Dyn 84: 875-880.
-
M Singh, RK Gupta (2016) Exact solutions for nonlinear evolution equations using novel test function. Nonlinear Dyn 86: 1171-1182.
-
EME Zayed, YA Amer (2015) Exact solutions for the nonlinear KPP equation by using the Riccati equation method combined with the (G'/G)-expansion method. Sci Res Essays 10: 86-96.
-
EME Zayed, KAE Alurrfi (2016) The Bäcklund transformation of the Riccati equation and its applications to the generalized KdV-mKdV equation with any-order nonlinear terms. Pan-American Math J 26: 50-62.
