International Journal of Industrial and Operations Research
(ISSN: 2633-8947)
Volume 3, Issue 1
Research Article
DOI: 10.35840/2633-8947/6506
A Statistical Comparison between Different Multicriteria Scaling and Weighting Combinations
Sean Harris 1, Luisa Nino2* and David Claudio2
Table of Content
Figures
Tables
Table 1: Summary of weighting-scaling combinations.
Table 2: Numeric value example for single clear winner, Problem 5 IV + Rating.
Table 3: Summary of combination scores.
Table 4: Average score by scaling method.
Table 5: Results breakdown by problem.
References
- Cho KT (2003) Multicriteria decision methods: An attempt to evaluate and unify. Mathematical and Computer Modelling 37: 1099-1119.
- Velazquez MA, Claudio D, Ravindran AR (2010) Experiments in multiple criteria selection problems with multiple decision makers. International Journal of Operational Research 7: 413-428.
- Gershon M, Duckstein L (1983) Multiobjective approaches to river basin planning. Journal of Water Resources Planning and Management 109: 13-28.
- Goicoechea A, Stakhiv EZ, Li F (1992) Experimental evaluation of multiple criteria decision models for application to water resources planning1. JAWRA 28: 89-102.
- Hobbs BF, Chankong V, Hamadeh W (1992) Does choice of multicriteria method matter? An experiment in water resources planning. Water Resources Research 28: 1767-1779.
- Hodgett RE (2015) Comparison of multi-criteria decision-making methods for equipment selection. The International Journal of Advanced Manufacturing Technology 85: 1145-1157.
- Salminen P, Hokkanen J, Lahdelma R (1998) Comparing multicriteria methods in the context of environmental problems. European Journal of Operational Research 104: 485-496.
- Jelassi MT, Ozernoy VM (1989) A framework for building an expert system for MCDM models selection. Improving Decision Making in Organisations 553-562.
- Gershon M (1984) The role of weights and scales in the application of multiobjective decision making. European Journal of Operational Research 15: 244-250.
- Nutt PC (1980) Comparing methods for weighting decision criteria. Omega 8: 163-172.
- Chung-Hsing Yeh, Robert J Willis, Hepu Deng, Hongqi Pan (1999) Task oriented weighting in multi-criteria analysis. European Journal of Operational Research 119: 130-146.
- Pierre DA (1987) An optimal scaling method. IEEE Transactions on Systems, Man, and Cybernetics 17: 2-6.
- Kumar FP, Claudio D (2016) Implications of estimating confidence intervals on group fuzzy decision making scores. Expert Systems with Applications 65: 152-163.
- Eom SB, Min H (1999) The contributions of multi-criteria decision making to the development of decision support systems subspecialties: An empirical investigation. Journal of Multicriteria Decision Analysis 8: 239-255.
- Buchanan JT, Daellenbach HG (1987) A comparative evaluation of interactive solution methods for multiple objective decision models. European Journal of Operational Research 29: 353-359.
- Butler J, Jia J, Dyer J (1997) Simulation techniques for the sensitivity analysis of multi-criteria decision models. European Journal of Operational Research 103: 531-546.
- Karni R, Sanchez P, Tummala VR (1990) A comparative study of multiattribute decision making methodologies. Theory and Decision 29: 203-222.
- Triantaphyllou E (2013) Multi-criteria decision making methods: A comparative study. Springer Science & Business Media 44.
- Ozernoy VM (1992) Choosing The "Best" Multiple Criterlv Decision-Making Method. INFOR: Information Systems and Operational Research 30: 159-171.
- Jurgita Antucheviciene, Zdeněk Kala, Mohamed Marzouk, Egidijus Rytas Vaidogas (2015) Solving civil engineering problems by means of fuzzy and stochastic MCDM methods: Current state and future research. Mathematical Problems in Engineering 2015.
- Athanasios Kolios, Varvara Mytilinou, Estivaliz Lozano-Minguez, Konstantinos Salonitis (2016) A comparative study of multiple-criteria decision-making methods under stochastic inputs. Energies 9: 1-21.
- Saaty TL (2008) Decision making with the analytic hierarchy process. Int J Services Sciences 1: 83-98.
- Triantaphyllou E, Mann SH (1989) An examination of the effectiveness of multi-dimensional decision-making methods: A decision-making paradox. Decision Support Systems 5: 303-312.
- Stelios HnZanakis, Anthony Solomon, Nicole Wishart, Sandipa Dublish (1998) Multi-attribute decision making: A simulation comparison of select methods. European Journal of Operational Research 107: 507-529.
Author Details
Sean Harris 1, Luisa Nino2* and David Claudio2
1Jake Jabs College of Business and Entrepreneurship at Montana State University, USA
2Department of Mechanical and Industrial Engineering, Montana State University, Bozeman, USA
Corresponding author
Luisa Nino, Department of Mechanical and Industrial Engineering, Montana State University, 420 Roberts Hall, Bozeman, MT 59717-3800, USA, Tel: 406-994-7144, Fax: 406-994-6292.
Accepted: May 16, 2020 | Published Online: May 18, 2020
Citation: Harris S, Nino L, Claudio D (2020) A Statistical Comparison between Different Multicriteria Scaling and Weighting Combinations. Int J Ind Operations Res 3:006.
Copyright: © 2020 Harris S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Multicriteria decision making presents several challenges for researchers. These include selecting a technique that will produce accurate results but not require too much time or resources. Researchers have been comparing different techniques for several years, though a comprehensive study of using many different techniques for the same set of problems is relatively new. Additionally, knowing if the difference in scores between alternatives is significant or not presents another challenge. The use of confidence intervals has recently been employed by researchers to examine whether results are actually statistically different from one another. This study uses 21 different scaling-weighting combinations and confidence intervals on six different decision-making problems to measure their ability to produce unambiguous results. Linear normalization as a scaling technique tends to be the best at identifying one or two clear winners while avoiding complete ambiguity. Despite the variety of combinations used, several common themes emerge across the decision problems.
Keywords
Multicriteria decision making, Confidence intervals, Scaling-weighting techniques
Introduction
Multicriteria Decision Making (MCDM) involves deciding on the best alternative from a set of potential candidates. These alternatives often contain multiple and conflicting criteria that can be qualitative or quantitative [1,2]. MCDM methods have been used to aid in decision making for a variety of contexts, such as river basin planning, water resource planning, equipment selection, environmental problems, and other problems involving resource management [3-7]. Evaluating tradeoffs between alternatives can be quite difficult, but MCDM can aid decision-makers in their quest to choose the best alternative [2].
Numerous MCDM techniques exist for solving decision problems. However, these methods often represent radically different approaches and the selection of which technique to use depends on multiple factors such as the specific problem, the decision maker's familiarity with the technique, and computational efficiency, among others. In fact, selecting the most appropriate MCDM method for a given problem could actually be considered a MCDM problem on its own [8].
Most MCDM methods involve determining the importance of each criterion and assigning weights based on the Decision Maker's (DM) preferences [2]. There are many different techniques for weighting criteria [9-11]. The scaling of criteria presents another challenge because different criteria are rarely measured with the same units. Consequently, a number of different scaling techniques exist to address the best way to convert the criteria into like units [12]. Recently, researchers have been to experiment with different weighting and scaling combinations in an attempt to gain insights into which combinations tend to produce the best results [2].
A major concern with decision making is that different MCDM methods can provide different results for the same problem. In fact, the best alternative according to one method may be the worst alternative according to another [1,9]. It can be difficult to discern if there really is a significant difference between the highest scoring and second-highest scoring alternatives. Recent research has explored this concept of looking at how different weighting and scaling combinations produce different results for the same problem [2]. Another important consideration is what method yields results that are closest to the DM's naturalistic choice [2]. In looking at how different MCDM methods yield different results in both orders of alternatives and magnitude of difference between those alternatives, an interesting research question presents itself: Do certain weighting and scaling combination in MCDM tend to produce statistically similar results? This would be of great use to DM's because if two different MCDM techniques produce statistically similar results, then the DM can select the technique that is easiest for them to use, whether it is because of available data, computational complexity, or time needed, among others.
Until recently, little research has been done to address this question. However, the use of confidence intervals can help since they give the range in which a result is valid [13]. The idea of using confidence intervals in decision-making techniques is relatively new. Statistical tests can then be used to verify if the mean scores are significantly different from each other, which in this case means that the alternatives can be ranked based on the value of the mean score. Otherwise, if the difference between the mean scores of the alternatives is not significantly different, then the ranking of the alternatives overlap [13].
Combining the ideas from [2] and [13] can then provide an answer to the proposed question. We conduct a comprehensive study where 21 different scaling-weighting combinations are applied to six different problems and then confidence intervals of the mean scores are calculated for those results. Tukey's HSD test is then used to test whether the alternatives are statistically different from one another. The combination of weighting and scaling methods is one of the unique aspects of our research because, to our knowledge, only [2] have studied this in the past. The other unique aspect is the use of confidence intervals to evaluate and compare the outcomes of the different methods, which, to our knowledge, only [13] have also done.
We use the data from [2] that has the results for six participants giving criteria preferences for six different MCDM problems, where each problem was composed of 6 different criteria. The scaling methods used are ideal values, linear normalization and vector scaling (IV, LN, L1 Norm, L2 Norm, L3 Norm, and L∞ Norm). These scaling methods were paired with the following weighting methods: rating, ranking, analytic hierarchy process (AHP), L1 Metric, L2 Metric, L3 Metric, and L∞ Metric when applicable. Then, we calculate 95% confidence intervals of the mean score of the alternatives and analyze how often the results are actually statistically different as was proposed for [13]. We could then see if certain combinations tend to produce the same results and what these combination families look like. We evaluate these combinations according to their ability to clearly distinguish the best alternative and to avoid complete ambiguity.
Theory
MCDM helps identify and assess a set of conflicting criteria and alternatives in decision making. In classic multicriteria decision environments, there is no universal agreement as to what constitutes the most preferred or satisfying solution [14]. The general objective of MCDM methods is to provide a framework and technique to order the set of possible alternatives in accordance with the DM's preferences. The specific objectives to be reached by several MCDM methods need to be identified; in addition to what degree the attributes meet these objectives [8].
Numerous studies have been carried out to compare various MCDM methodologies [13,15-18]. However, the main question that emerges is why outcomes differ when different techniques are applied to solve the same decision-making problem, even under the same assumptions [1,9,18]. These differences have appeared in the literature, but should not be viewed as inconsistencies [9,18]. Rather, the results of these studies indicate that different algorithms, scaling methods, and uses of weights lead to different outcomes. These differences illustrate the need to know how weights, scales, and other factors are used before applying a technique [9,18]. Therefore, it is vital that users of such techniques be aware of the manner in which results are reached and how their weightings and scaling factors influence these outcomes [17]. Though it is known that different MCDM methods can yield different results, the analyst must still decide which one to use. Often, the method is one that was developed by the DM, one the DM has the most faith in or a method that the DM has used in the past [19].
In addition to not knowing what MCDM method is best for a particular problem, there is also a stochastic element to the criteria and alternatives that further complicates the matter. Researchers have studied the uncertainly surrounding MCDM through simulation [20]. For instance, by using a Monte Carlo simulation, [16] studied the flexibility to vary all of the weights of MCDM method while at the same time changing the functional form of aggregation. The authors analyzed the changes using statistical parameters such as mean, mode, standard deviation, and quartiles to provide recommendations about the correct procedure to assign and assess the weights of the criteria. Also, they worked with the weights of the criteria and used statistic distributions to analyze and compare the data. [16] demonstrated that the functional form of aggregation (multiplicative or additive) had no effect on the outcome of the model. [21] Worked with six deterministic MCDM methods doing a comparative analysis to develop a new methodology that allows the use of those methods in decision-making problems with stochastic inputs. The main objective was to assign confidence levels on the use of certain methods based on the resulting outputs.
Regardless of the MCDM method selected or the uncertainty surrounding the problem, most methods require the establishment of criteria weights that capture the DM's preferences for how important each criterion is relative to the others [9]. Though there are numerous weighting methods, this paper uses the same as [2]. The first method is the rating method. Here, the DM rates from 1 to 10 each criterion independently, usually with 1 being the least important and 10 the most important. The second method is the ranking method, in which pair wise comparisons of criteria are performed and the weights are obtained using Borda Count [2]. The third method is the Analytic Hierarchic Process (AHP). AHP assigns a magnitude of the preference of one criterion over another. AHP uses a standard scale number from 1 to 9, where 1 means no preference and 9 means that criterion is extremely preferred over another [22]. Then, ratio scale priorities are established based on the sets of pair wise comparisons performed between the criteria and alternatives.
Another aspect that plays a role in MCDM problems is the type of decision problem. In single-dimensional MCDM problems where all the units are the same, calculating scores for the alternatives is relatively straightforward. However, difficulties arise in multi-dimensional cases where the additivity utility assumption is violated because it combines different dimensions and thus different units so the result is comparable to adding apples and oranges [23]. Therefore, scaling methods are needed to preserve the additivity utility assumption to solve multi-dimensional MCDM cases.
Several methods exist for scaling. These include ideal values, linear normalization, and vector scaling. Ideal values use the best criteria values among the alternatives. Ideal values denote the best criteria values that are possible to obtain among the alternatives. In linear normalization, the maximum and minimum criteria values are used to scale the data [2]. Vector scaling uses LP Norm to scale the data. LP Norms quantify the lengths of vectors and LP metrics calculate the distance between points. The LP metric can be used as a method to obtain the best alternative once the data is normalized by using the vector scaling method. Velazquez, Claudio [2] presented the LP metric between two vectors x, y as follows:
Where x, y ε Rn
If one of these points is the ideal solution, then the distance denotes how close each alternative is respect to the ideal solution. Therefore, the smaller the distance, an alternative will be closer to the ideal solution [2].
Once the weights of the criteria have been established the next step to solve a MCDM problem is to find a way to process the numerical values to compare and determine the ranking of the different alternatives. One of the most commonly used approaches is the Weighted Sum Model (WSM), which is governed by the addition utility assumption [23]. The WSM is presented by [2] as follows:
In a MCDM problem with m alternatives and P criteria. Let the matrix represent the criteria values to be maximized where fij is the value of criterion j for alternative i. If wj is the normalized weight of criterion j assessed subjectively such that wj ≥ 0 and ∑wj = 1, then the weighted sum model computes a score Si for each alternative i, as follows:
Then, the ranking of the alternatives is created based on the Si scores and the DM selects the best alternative.
Researchers have evaluated the accuracy and efficiency of weighting and scaling methods independently [9,11,12,16,24]. However, little research has been conducted to identify the combination of scaling-weighting methods that will better match the real preferences of the DMs [2]. [2] Experimented with various weighting and scaling combinations for six participants conducting six different decision-making problems. The results were compared to the DM's naturalistic choice in addition to the majority of the combination methods.
[2] Compared different weighting-scaling combinations, however, no testing was done to determine if the methods were significantly different from a statistical perspective. In fact, using confidence intervals to compare different MCDM techniques is relatively new. [13] Applied confidence intervals to the fuzzy AHP and fuzzy Analytical Network Process (ANP) methods by using the mean obtained to calculate the arithmetic standard deviation. Then, the mean and standard deviation were used to calculate the 95% confidence interval [13]. The confidence intervals help to identify any overlaps between the alternatives and therefore provide insight as to whether they are statistically different, which allows for a more informed ranking of the alternatives. Observing if there is a statistical difference between alternatives is the main advantage of confidence intervals because conversations can be initiated regarding tradeoff among the available alternatives. This also helps guarantee the selection of the best alternative since its performance presents a statistically significant difference against the other alternatives.
This paper combines the primary ideas from [2] and [13] to statistically compare different MCDM weighting and scaling combinations. While previous researchers have used stochastic inputs or simulation to examine the uncertainly surrounding MCDM problems, this paper uses confidence intervals calculated directly from DM preferences. While [2] compared different MCDM weighting and scaling techniques, it was hard to draw meaningful conclusions from the results because there was no statistical testing to determine if two different techniques truly were different from one another. Similarly, [13] provides the framework to compare different MCDM techniques, but this paper will use a more comprehensive set of MCDM techniques.
Material and Methods
This paper used the data from [2], in which six participants, half female and half male all between ages 24-27, were independently given six different MCDM problems. The problems included buying a sport utility vehicle (SUV), buying a house, selecting a restaurant, buying a laptop computer, buying airplane tickets for a trip to Italy, and selecting a job. Each problem had five different alternatives and six different criteria within each problem. See Appendix A for more details on these problems.
Seven different weighting techniques and six different scaling techniques were used in different combinations to determine the optimal alternative(s) for each problem. The weighting techniques were rating, ranking, AHP, L1-L3 metric, and the L∞ metric. The scaling techniques were ideal values, linear normalization, L1-L3 norms, and L∞ norm. These techniques were calculated as previously described in the literature review. This paper used the same 18 combinations as [2]. In addition, three other combinations were examined for a total of 21 combinations. These additional combinations were included after an initial analysis of the data suggested that linear normalization was the best scaling method since it yielded the highest total scores regardless of the weighting method used. Table 1 summarizes the combinations used in the study. New combinations, or those that were not used in [2], are denoted with an asterisk.
For each problem, the total score using the weighted sum technique was estimated for each alternative for each participant. It was decided to use the weighted sum technique since, as it was proved by [16], the form of aggregation (multiplicative or additive) had no effect on the outcome of the model. Anderson-Darling tests were conducted for each of the 21 scaling-weighting combinations, per MCDM problem, per alternative to determine whether the six participants' scores had a normal distribution. The tests yielded p-values greater than 0.05. Therefore, normality was assumed to calculate confidence intervals. Then, a 95% confidence interval of the mean score of the alternatives was calculated using the arithmetic mean and standard deviation of the six individual participant scores. The ranked order of alternatives according to the weighted sum calculations was done for each participant for each problem, with the highest scoring alternative being one and the lowest being five. The same methodology was applied to the mean of the ranked order of alternatives. The corresponding 95% confidence interval using the geometric mean was then calculated for each alternative, for each problem, and each of the weighting-scaling methods.
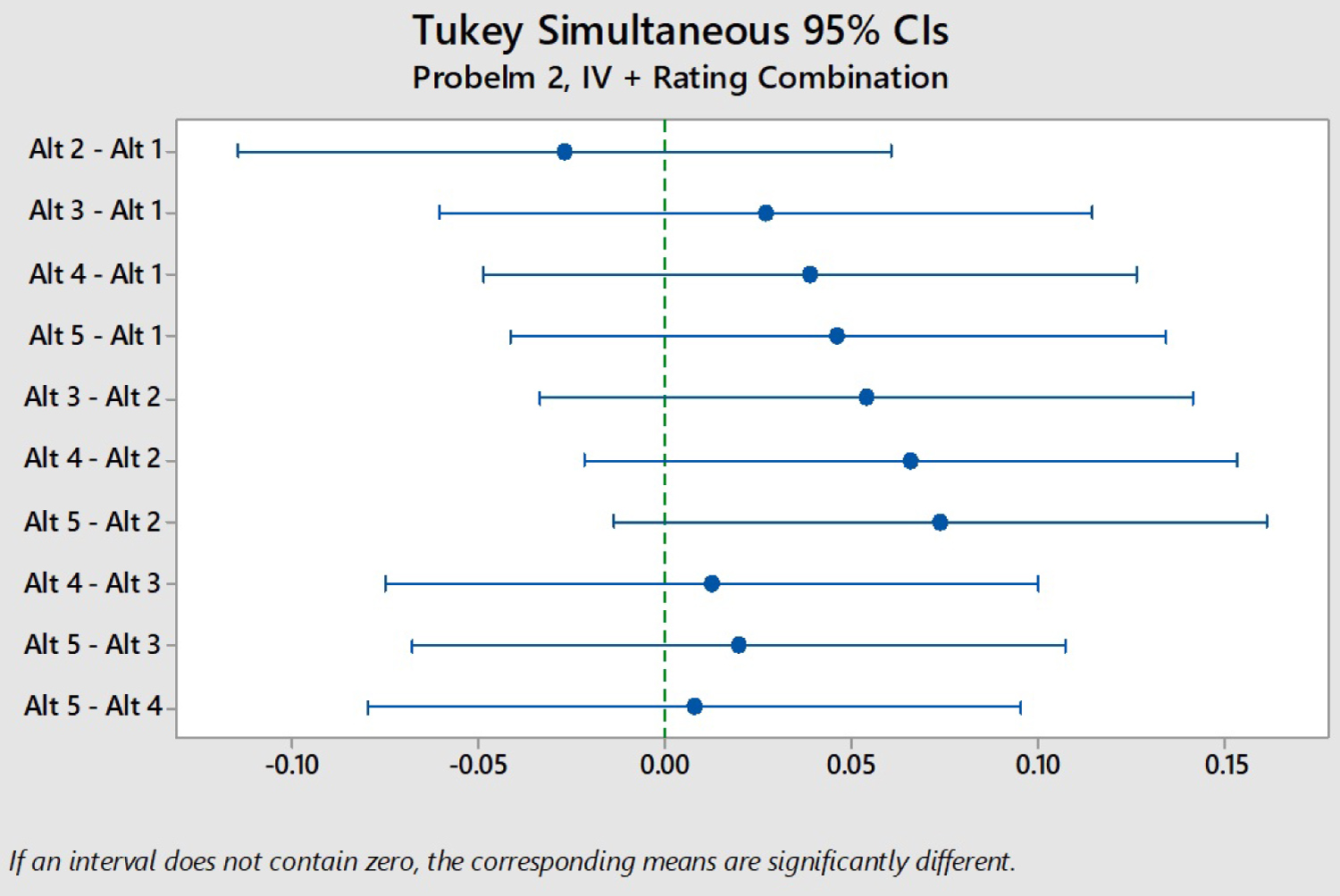
As [13] noted in their paper, the confidence intervals of the differences between alternatives for a given problem often included zero. This was the same case for our study. Therefore, a particular weighting-scaling combination's efficacy was measured by its ability to distinguish a clear winner(s) among the alternatives. Ideally, a MCDM technique yields one clear winner that is statistically significantly better than all other alternatives, an example is shown visually in Figure 1 and then by the corresponding t and p values in Table 2. Conversely, a MCDM technique where the highest scoring alternative is not statistically significantly different than the lowest-scoring alternative (complete ambiguity) is the least preferred result because no alternatives can be eliminated from consideration. Figure 2 shows an example of this complete ambiguity.
The particular weighting-scaling combination's efficacy measure was obtained through the following procedure: Once each weighting-scaling combination produced the results for the six different problems. Three metrics were recorded. The first was the number of times the combination produced a single winning alternative that was significantly different from the other four alternatives (for example, Figure 1). The second metric was the number of times the combination produced two winning alternatives that were significantly different than the other three alternatives (but the two winners were not significantly different from each other). The third and final metric was the number of times a combination produced a completely ambiguous result where the highest scoring alternative was not significantly different than the lowest-scoring alternative (for example, Figure 2). A clear winner was awarded three points, two clear winners were awarded 1 point, and a completely ambiguous result was given negative three points. These point totals reflect how effective each result is because a single clear winner is much preferred to two clear winners, where additional analysis is required to select among the two remaining alternatives. Similarly, a completely ambiguous result is fairly useless and requires the DM to redo the entire process. The total number of points or total score for each weighting-scaling combination were then calculated and compared to one another.
Three other scoring methodologies were considered to determine the robustness of the proposed 3, 1, -3 system. First, a binary system of one point for one clear winner, zero points for two clear winners, and negative one point for complete ambiguity. Second, a quadratic system rewarding clear winners where four points were given for one clear winner, two points for two clear winners, and negative one points for complete ambiguity. Finally, a reverse quadratic system penalizing complete ambiguity with two points for one clear winner, one point for two clear winners, and negative four points for complete ambiguity.
Results and Discussion
Table 3 summarizes the results of the combinations scores. When looking at the weighted sum scores, the linear normalization with L1 metric achieved the highest score, followed by linear normalization with L2 metric and linear normalization with rating. L3 Norm with ranking, L2 Norm with ranking, L∞ Norm with ranking, and L1 Norm with ranking all tied for the lowest score. These results contrast with the results from [2], where L∞ Norm with ranking was found to be the best method. For the mean of the alternative rankings, the linear normalization with L1 metric and linear normalization with L2 metric were first and second, respectively, while L1 norm with L1 metric had the lowest score. [2] Did not have as clearly defined results when evaluating the combinations in a group context, where 7, 12, and 13 of the methods tied for first according to their three performance metrics.
Table 3 also illustrates that the scaling trends are relatively robust to the scoring system. Linear normalization remains the best scaling method in five of the six other scenarios, with it being second best to L∞ norm for the mean of alternative rankings with the reverse quadratic scoring methodology. This suggests that the chosen scoring methodology does not have much effect on determining the best scaling method.
When looking at the combinations by scaling method, a few trends emerge. Table 4 summarizes these results. Linear normalization clearly performs the best among the six scaling methods used with the proposed evaluation method for both weighted sum and ranked alternatives. The L1, L2, and L3 norms all perform in a similar manner. These three norms all have values between -3.67 and -4.67 for the calculated score. The L∞ norm follows a similar trend, but with slightly higher numbers. Linear normalization having the highest scores makes intuitive sense because the method assigns values between zero and one, with the lowest alternative having zero and the highest having one for each criterion. Therefore, this method would better separate alternatives than ideal values, where the alternatives may have very similar scaled values if the raw data is close to one another.
Trends by problem also appear in the data. Table 5 summarizes the result breakdown by problem. Certain problems tended to have similar themes throughout the different combination methods. For example, problem 1 (buying a house) and problem 3 (selecting a job) rarely had a single or two clear winners. Problem 1, however, had complete ambiguity more than twice as often as problem 3 for weighted sum scores. Conversely, problems 5 and 6 had a single or two clear winners the vast majority of the time, with problem 6 having a single or two clear winners 21/21 times for ranked alternatives. Interestingly, the same two alternatives (1 and 6) were always chosen for problems 5 and 6, whether it was one of those alternatives being a single clear winner or the two alternatives being the two clear winners. For problem 4, on all six occasions that the weighted sum produced a single clear winner, it was the same alternative (alternative 2).
These results suggest that the type of problem, or particular details of the problem, do play a role in whether MCDM methods will be able to clearly distinguish the top alternatives for group decisions. Furthermore, there was never a single instance in which one alternative was the statistically worst choice under one method and the statistically best choice according to another method. This is somewhat encouraging, as previous research has sometimes found this dynamic to occur. This previous research, however, did not include whether the choice reversals were statistically significant or not.
There are some differences when considering the weighted sum score or a ranking of the alternatives by the mean. The weighted sum score tends to produce complete statistical ambiguity more often than when the alternatives are ranked and aggregated according to the mean. This finding aligns with the previously mentioned finding that the different methods tend to select the same alternatives. This produces similar rankings across the board, which then makes it less likely to have ambiguity because there is a bigger distinction among the alternatives. For example, the weighted sum score will often only have a difference of a few tenths between all the alternatives. Therefore, even if the methods tend to find similar results, the small numerical differences can result in ambiguity. Conversely, when using the rankings of alternatives, the top alternatives tends to have a value closer to one and the worst alternative close to four or five, making ambiguity less likely.
Conclusions
Researchers have been comparing different MCDM techniques with one another for many years. Comparing techniques' results against a statistical backdrop to determine if the results are significantly different is relatively new. This study used 21 different scaling-weighting combinations of common MCDM techniques and applied them to six different MCDM problems with six participants. Both the weighted sum scores and the rankings of the alternatives were aggregated into a group score and the corresponding confidence intervals were calculated to test if the results were statistically significantly different. The scaling-weighting combinations' ability to distinguish a clear winner or two clear winners and to avoid complete ambiguity in the results were measured.
Among scaling techniques, linear normalization performed best at distinguishing clear winners. This is most likely because of how the technique spreads out the values all the way from zero to one amongst alternatives, whereas other techniques do not. Trends emerged from the results by both problem and the type of aggregation, where the weighted sum scores had much more ambiguity than the ranking of alternatives with mean.
There are some opportunities for future research surrounding this issue. Several of the most common MCDM techniques were used; however, others such as TOPSIS, Delphi, and SPECTRE were omitted and could be included. The experiment could be replicated with a larger sample size to see if any trends by participant demographic emerge. Likewise, the type of problem could be examined in more depth. For example, the topic (purchasing a product, selecting a type of service, life decision such as moving to a new city) or structure (number of alternatives and criterion) could be systematically varied to determine if any trends emerge. Finally, the results of the study provided information that helps to evaluate the positive and negative characteristics of different MCDM techniques. This information could also be useful to face the challenges that are emerging in areas such as automation, social sciences, environmental sciences, modern construction management, and software packages, modeling and recent advances in intelligent decision making.
Acknowledgments
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.