Excitation of the 21S, 21P and n = 3, 4, 5 (n1P) of Helium by Positron Impact

International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 7, Issue 1
Research Article
DOI: 10.35840/2631-5017/2528
Excitation of the 21S, 21P and n = 3, 4, 5 (n1P) of Helium by Positron Impact
JLS Lino
Table of Content
Figures
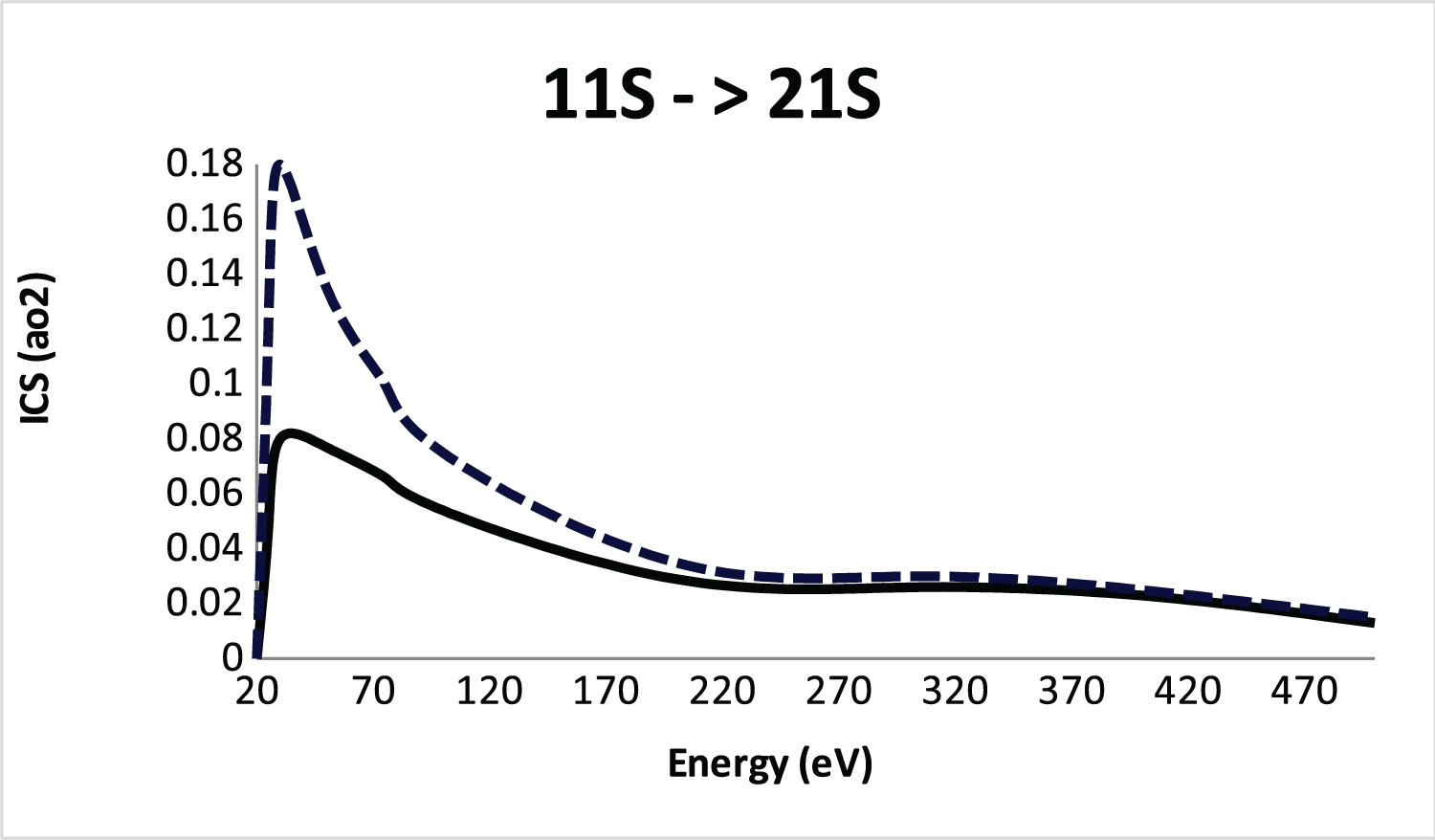
Figure 1: Integral cross section (ICS) for....
Integral cross section (ICS) for 11S-21S excitation of He atom by positron impact. Solid line, SBP approach; Dashed line, FBA.
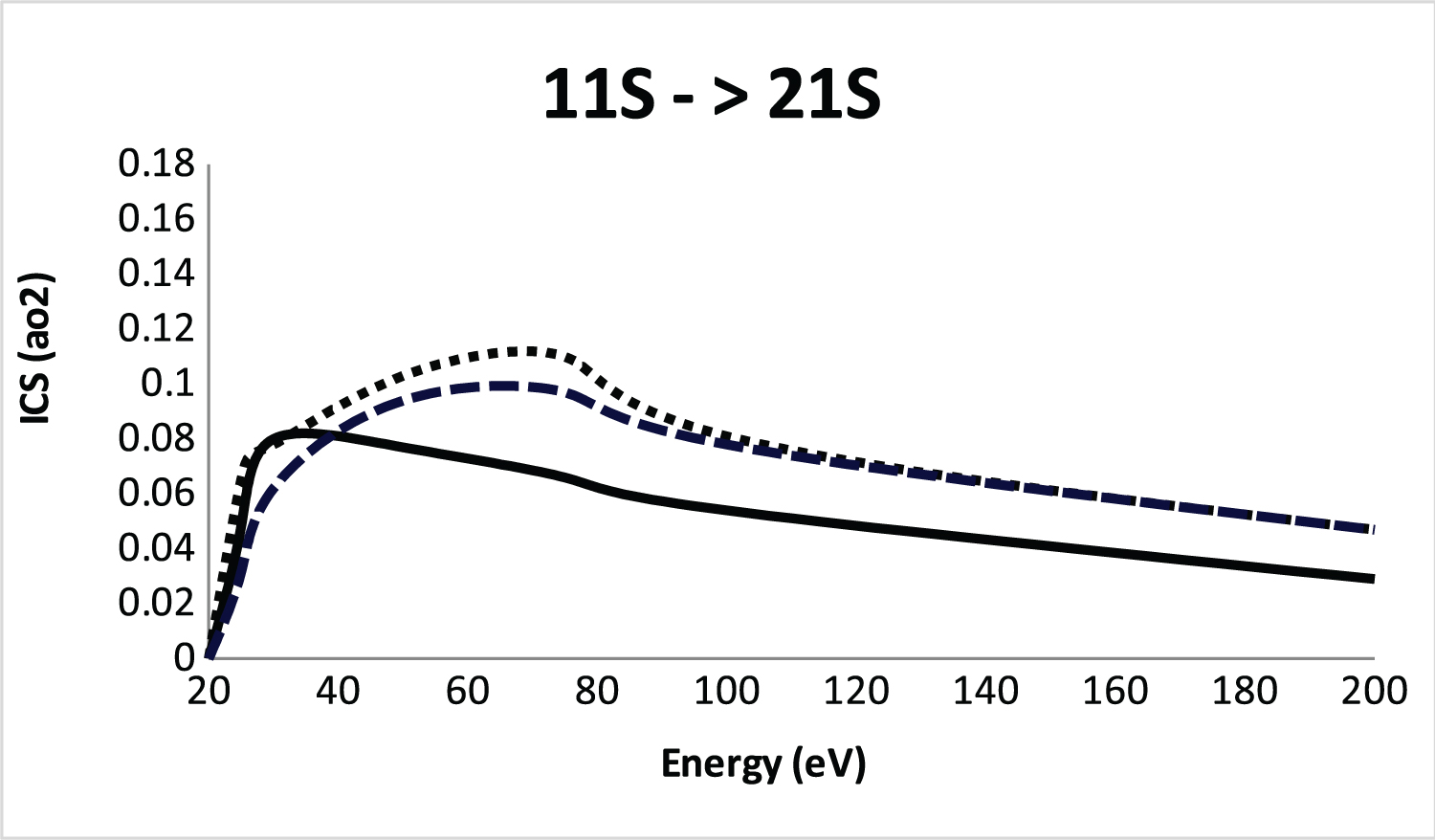
Figure 2: Integral cross section (ICS) for.....
Integral cross section (ICS) for 11S-21S excitation of He atom by positron impact. Solid line, SBP approach; Dashed line, CCC method (without ionization and Ps formation) [15]; Dot line, CCC method (with ionization and Ps formation) [15].
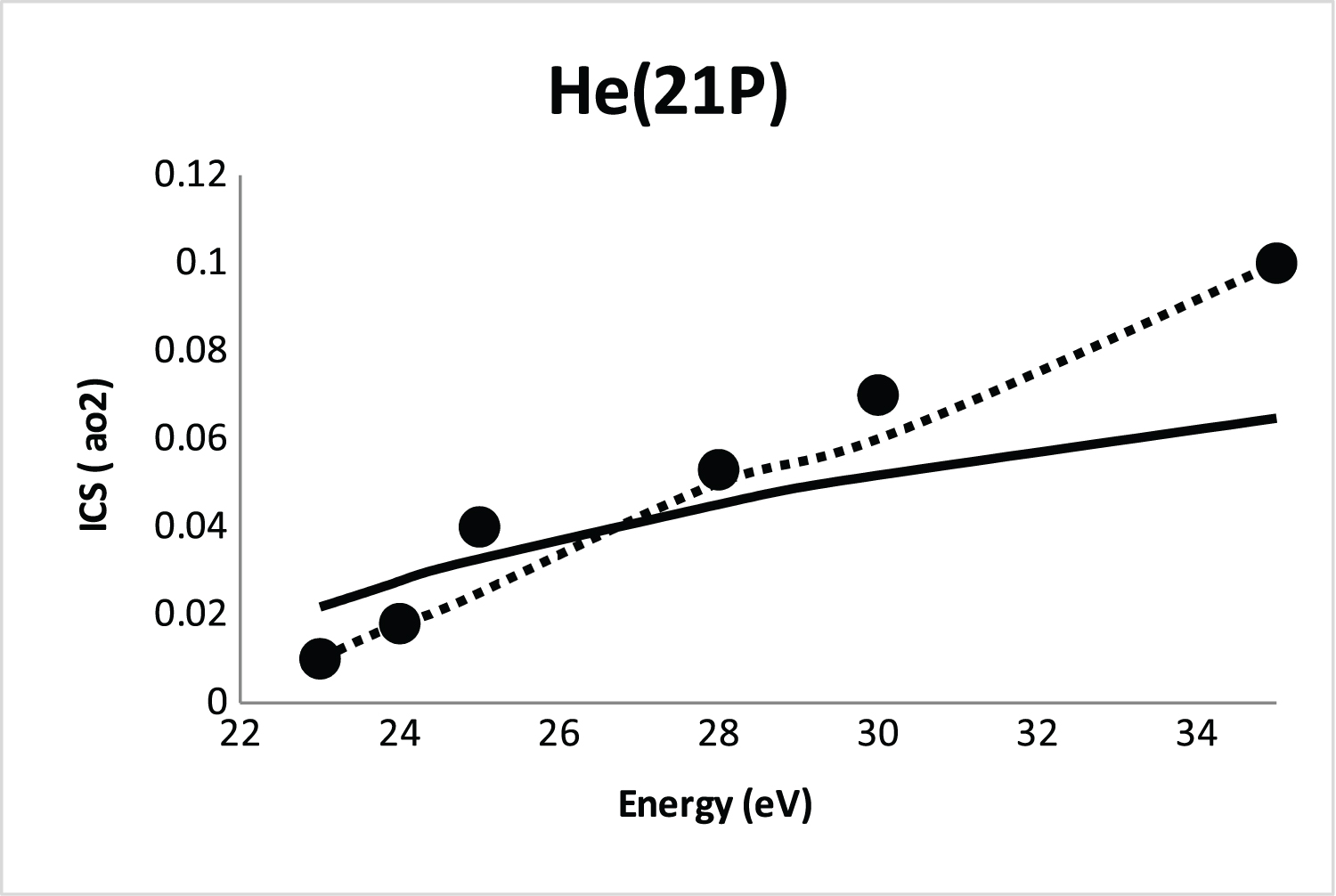
Figure 3: Integral cross section (ICS)....
Integral cross section (ICS) for 11S-21P excitation of He atom by positron impact. Solid line, SBP approach; Dot line, CCC method (with ionization and Ps formation) [15]; Black circle, experimental data [15].
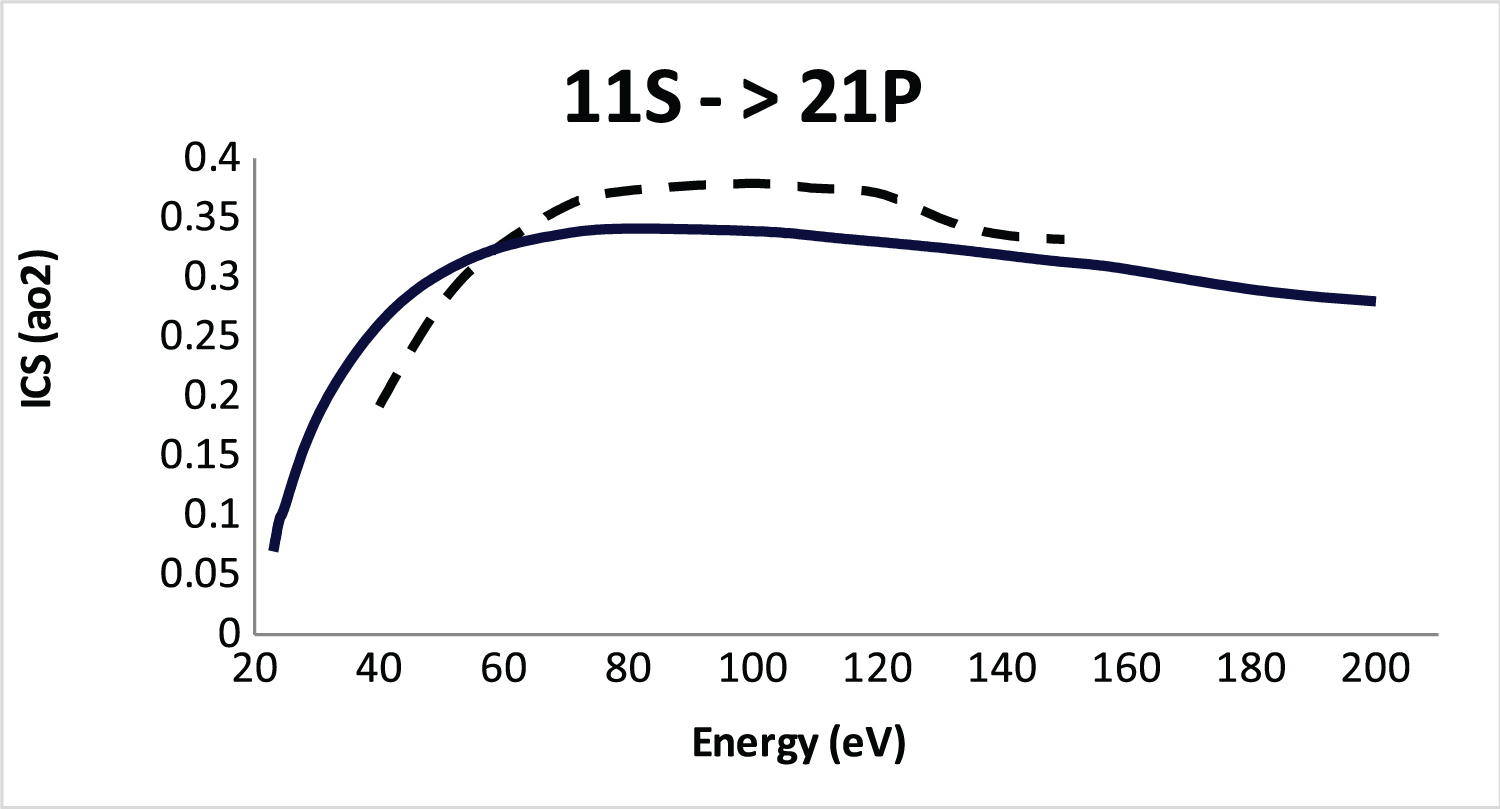
Figure 4: Integral cross section (ICS)....
Integral cross section (ICS) for 11S-21P excitation of He atom by positron impact. Solid line, SBP approach; dashed line, DWA [16].
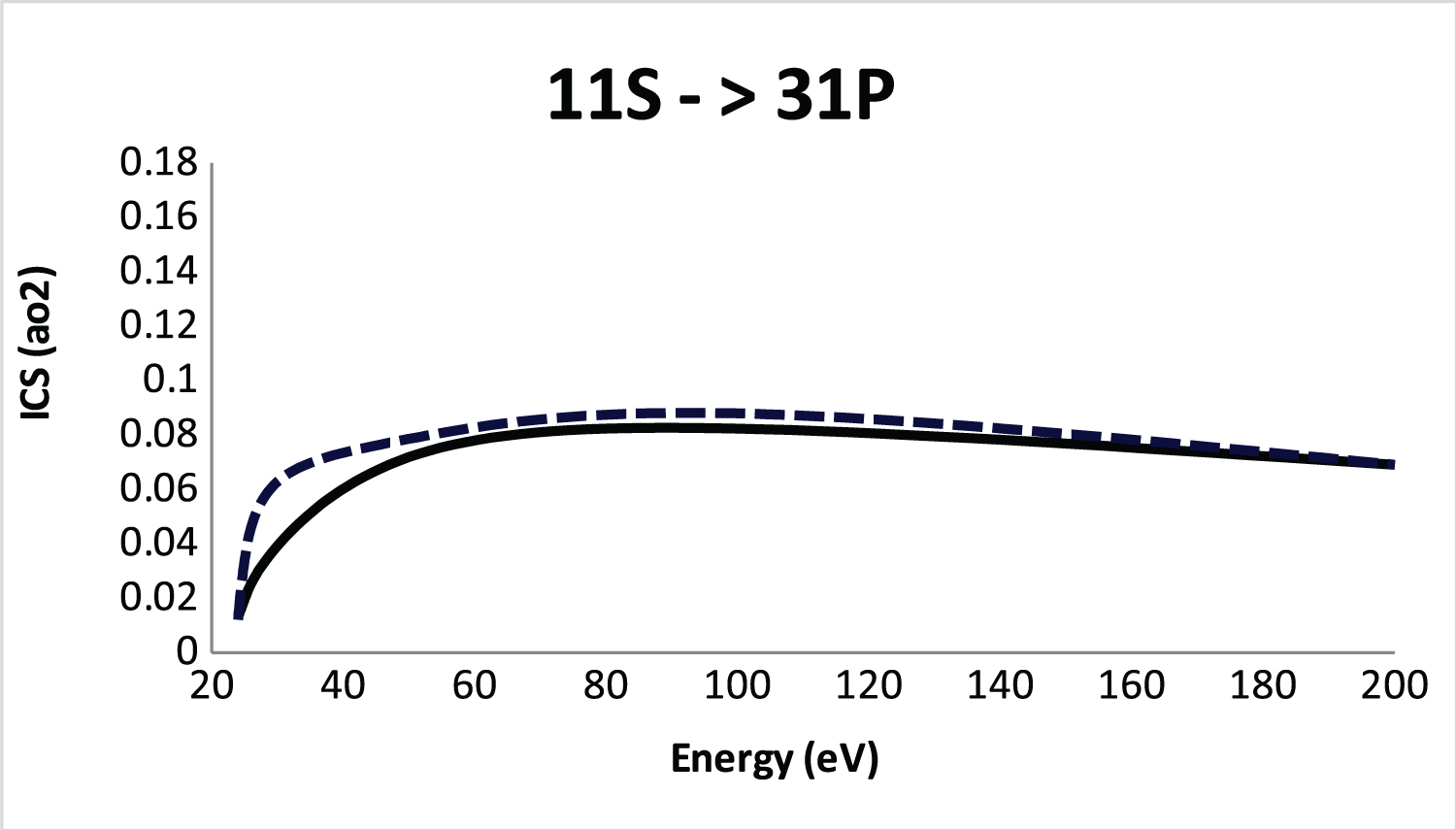
Figure 5: Integral cross section (ICS) for....
Integral cross section (ICS) for 11S-31P excitation of He atom by positron impact. Solid line, SBP approach; Dashed line, CCO method [17].
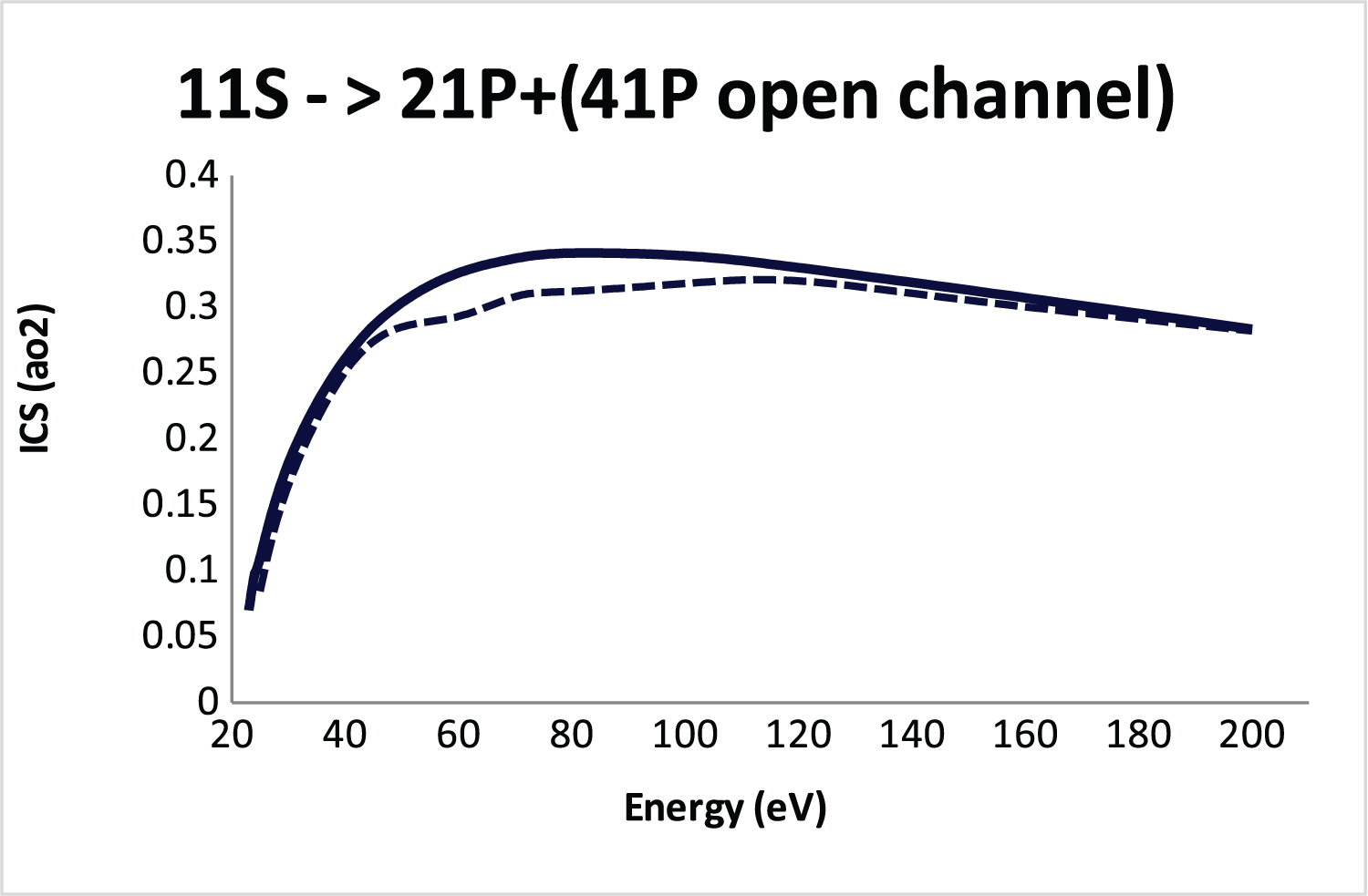
Figure 6: Integral cross section (ICS)....
Integral cross section (ICS) for 11S-21P + 41P (open channel) excitation of He atom by positron impact using SBP approach. Solid line, 21P state; Dashed line, 21P + 41P (open channel).
Tables
Table 1: Excitation energy for n1P states (n = 3, 4, 5).
Table 2: Electronic excitation energy and faccur dipole value from accurate wavefunctions, and fBorn dipole value from FBA.
References
- Surko CM, Gribakin GF, Buckman SJ (2005) Low-energy positron interactions with atoms and molecules. J Phys B 38: R57.
- Varella MTN, Carvalho CRC, Lima MAP, et al. (2001) New directions in antimatter chemistry and physics. Kluwer, Amsterdam, 493.
- Chaudhuri P, Adhikari SK (1999) Close-coupling calculations of elastic and inelastic positron-helium scattering. J Phys B 32: 129-136.
- Van Reeth P, Humberston JW (1999) A significant feature in the total cross section for positron-helium scattering at the positronium formation threshold. J Phys B 32: L103.
- Suvam S, Rahla N, Jaspreet K, Bobby A (2018) Study of elastic and inelastic cross sections by positron impact on inert gases. Eur Phys J D 72.
- Caradonna P, Sullivan JP, Jones A, Makochekanwa C, Slaughter D, et al. (2009) Excitation of the n=2 states of helium by positron impact. Phys Rev A80: 060701R.
- Stein TS, Harte M, Jiang J, Kauppila WE, Kwan CK, et al. (1998) Measurements of positron scattering by hydrogen, alkali metal, and other atoms. Nucl Instr Meth Phys Res B 143: 68-80.
- Lino JLS (unpublished) Positron scattering by He atom at high energies.
- Lino JLS (2016) Scaling of plane-wave born cross sections for positron-impact excitations of H 2 . Rev Mex Física 62: 596-599.
- Karwasz GP (2005) Positrons - An alternative probe to electron scattering. Eur Phy J D 35: 267-278.
- Joachain CJ (1975) Quantum collision theory. North-Holland, Amsterdam.
- Lino JLS (2006) Scaling of plane-wave born cross sections for positron-impact excitations of He and H 2 . Chin J Phy 54: 223-228.
- Lino JLS (2021) Electronic excitation of C 6 H 6 by positron impact. Rev Mex de Fis 67: 188-192.
- Miller TM (1996) CRC handbook of chemistry and physics. DR Lide, (77 th edn), CRC Press, New York.
- Kadyrov AS, Bray I (2016) Recent progress in the description of positron scattering from atoms using the convergent close-coupling theory. J Phys B: At Mol Opt Phys 49: 222002.
- Yong-Jun C, Ya-Jun Z (2010) Elastic and inelastic positron helium scattering. Chin Phys B 19: 063405.
Author Details
JLS Lino*
Assessoria e Orientação Estudantil - Núcleo de Pesquisas São José dos Campos, São Paulo, Brazil
Corresponding author
JLS Lino, Assessoria e Orientação Estudantil - Núcleo de Pesquisas São José dos Campos, São Paulo, Brazil.
Accepted: July 01, 2023 | Published Online: July 03, 2023
Citation: Lino JLS (2023) Excitation of the 21S, 21P and n = 3, 4, 5 (n1P) of Helium by Positron Impact. Int J At Nucl Phys 7:028.
Copyright: © 2023 Lion JLS. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We report cross-sections for excitations of 2 1 S, and 2 1 P state of helium atom by positron impact using the scaled Born positron (SBP) approach. Particular attention is paid to the n 1 P ( n = 3, 4, 5) states which for the first time, integral cross sections are investigated using the SBP method. The possibility of using the SBP approach to estimate the contribution of open channels effects is discussed. An investigation on the determination of Z eff classical (Z eff = Z) in the context of SBP method illustrate the good convergence characteristics of the procedure.
Keywords
Born, Positron, Scaling
PACS: 34.80.Dp
Introduction
Positron-atom scattering has been an important area of research in the last years. For astrophysicists, the knowledge of elastic, ionization and inelastic cross sections would be very welcome as a important information about the interstellar medium [1]. Important area using positron as incident particle is the scans of the human brain in high-resolution positron emission of radiation by positron annihilation [1]. Also well known that material science researchers would like to have a better notion about electronic excitation using positron as incident particle (models to identify vacancies) [1,2]. Also a series of experiments involving positron impact with targets in general has been done recently [2] so that the theoretical calculations are extremely important for a adequate comparison. A suitable theoretical method should be capable of dealing with several important aspects of the positron-target scattering, i.e., electronic excitation, polarization of the target, ionization, multichannel effects, and positronium (Ps) formation. Some important theoretical works in the field of positron-atom collision was made by Chaudhuri, et al. [3] using the close-coupling approximation (CC), Reeth and Humberston [4] using the Kohn variational method (KVM), Singh, et al. [5] using optical-model potential, and several others studies can be obtained in the literature [6-8]. Specifically the positron-He atom scattering represent a good test for several theoretical developments, the helium atom as a stable target, has been the workhorse for many of the recent advances in low energy positron physics (see Refs. [8,9]).
The motivation of this work is to study the inelastic positron-helium scattering to He atom for the 2 1 S, and 2 1 P states using the SBP approach. We report also cross sections for the n 1 P ( n = 3, 4, and 5) states and we include a preliminary study on the open channels (estimative) to see the effect these channels on the inelastic scattering of helium (2 1 P state).
The first Born approximation (FBA) is traditionally used as a first study on cross sections of atoms and molecules by electron or positron impact as incident particle. First calculations of positron-He scattering have been performed by Massey and Mousa using the FBA [10]. They used only the ground state for He and positronium (Ps) formation and obtained reasonable cross sections. Another extensive and important study based on the Born approximation was presented also by Joachain [11]. From the FBA studies it became clear that more sophisticate approaches to the problem were required. In particular the SBP approach has as point start the FBA and we will see that the SBP approach is able to describe positron-atom scattering (subsequent papers using the SBP approach show equally good results for H 2 [12], and C 6 H 6 [13] targets).
In Sec.2 we will identify the SBP method for investigated the 2 1 S (2 1 P) state and in particular the n 1 P states ( n = 3, 4, 5) of He atom by positron impact. In Sec.3 computational procedures and results are discussed. Conclusions are presented in Sec.4.
Theory
The FBA is used here as the starting point, i.e., the plane wave is the correct function at infinity for an positron-atom scattering. The scaling method proposed here applies only to integrated excitation cross sections, not to angular distributions. In a generic form the FBA can be written as
The scaling Born positron (SBP) approach replaces the E (energy) that appears in the denominator of Eq. (1) by E + E exc + E Ps and Eq. (1) is rewritten as
Where
E ps is the positronium energy, E exc is the excitation energy, E is the energy incident of positron particle, f accur is an accurate dipole value from experiments or from accurate wavefunctions, and f Born is the dipole value from first Born approximation (FBA). As observed in Eq. (3), E is increased by a constant (E Ps + E ex ) and this modification has some consequences practical to the performance of the SBP method [9,12,13]. The constant is related with energy of the incident positron in the field of the nucleus and the bound electrons of the target and the Eq. (3) can be seen as the scaling factor to represent the correlation between the positron and electrons of the target. It may be mentioned that cross sections obtained using the FBA are identical for electron and positron as projectiles but the f (E) factor identify the incident positron. The positronium (Ps) energy used in the eq. (3) is written as
Where B is the binding energy of the electron of target represent the positron particle. The f (E) factor reduces the FBA at low energies while keeping the validity of the Born approximation at high energies and the SBP approach has the effect of correcting the FBA. When dealing with dipole transitions the long-range character of the dipolar coupling requires a larger number of partial waves and because of it, higher partial waves are not well described for several sophisticates ab initio methods (furthermore can add considerably to the computational effort [4)]. This consideration is especially important, i.e., in the practical such an effort can be avoided if above a certain angular momentum the remaining partial waves, which are weakly scattered, are obtained from a weak collision theory such as the FBA . As we will see, in principle, the SBP approach can generate cross sections reliably and quickly when compared with sophisticates methods and experimental data. The SBP approach can provide realistic excitation cross sections for many targets, which are not only difficult to measure but also cannot easily be calculated with existing theories. The propose of the present work consist in the study of two cases; first, as cited before, cross sections for the excitation of the 2 1 S, and 2 1 P state of He atom using the SBP approach. The results are important to note that, from the point of view of the theoretical formulation, the SBP method offers results very similar with sophisticate theories. Second, investigate as the open channel can interfere on the cross sections. A study using open channels represent a effort manageable and with the problem in mind, let us define an alternative mechanism, i.e., “pseudo coupling” and we will verify as this procedure alternative can produces similarity or difference with sophisticates methods. In the Eq. (3) we define the term
and Eq. (2) can be rewritten as
It is important to point out that in the Eq. (5) the term can be constructed for “ n states” and the influence of open channel on the compared 2 1 P state can be observed (this type of indirect study is not common but can be opportune). Evidently, in this context we will see that results using Eq. (5) are not refined (multichannel coupling represent a flux competition among all possible electronic transitions, positronium formation, including ionization, with all being due to the positron impact) more can be extremely relevant when compared with sophisticate methods and experimental data.
Computational Procedures and Results
5.1. Excitation to the 2 1 S, and n 1 P states
We have used Hartree-Fock calculations to represent the ground state of the target with the same basis set used (Cartesian Gaussian) in Ref. [14]. With this basis set we have obtained a excitation energy of 19.48 eV for 2 1 S, and 21.21 eV for 2 1 P state. The n 1 P states ( n = 3, 4, 5) are listed in Table 1. The positronium energy (E ps ) is 6.1 eV.
In Figure 1 we show the SBP integral cross section for the 1 1 S → 2 1 S electronic transition compared with the FBA only. As observed the SBP approach not only reduces the cross sections magnitude at low energies, but also shifts the peak to a higher “E” vality of the FBA intact. As expected the SBP converge to the FBA at high energies.
In Figure 2 we show again the SBP integral cross section for the 1 1 S → 2 1 S electronic transition compared with the convergent close-coupling (CCC) method [15] (with and without ionization and Ps formation). The CCC method [15] is an able method and the target states are obtained in the square-integrable orthogonal Laguerre basis. As observed in Figure 2 the SBP approach exhibit a similar shape with the CCC method [15] but with significantly different in magnitude at low energies. The obvious difference between the methods is mainly due to the different treatments, i.e., the SBP approach not include ionization and Ps-formation. Although ionization and Ps-formation channels are expected to play an important role in this energy region our cross sections are very similar with CCC method [15]. At high energies the SBP approach and CCC method [15] exhibit a good level of agreement. This agree is very important, i.e., the CCC method [15], as cited before is able to perform calculations for positron-atom scattering but the method [15] can be considerably enlarge the computational effort. This same computational effort is obviously not found in the SBP approach.
In Figure 3 we show the SBP integral cross section for the 1 1 S → 2 1 P electronic transition compared with the convergent close-coupling (CCC) method (with ionization and Ps formation) [15] and experimental data [15]. As observed in Figure 3 again the SBP approach exhibits a similar shape with the CCC method [15]. It is obvious that the largest effect of ionization and Ps-formation channels occurs at lower energies and the cross sections using SBP approach are in principle valid at low energies.
In Figure 4 we show the SBP integral cross section for the 1 1 S → 2 1 P electronic transition compared now with the DWA (electronic excitation only) [16] at intermediate and high energies. In Figure 4 a good agree between the SBP approach and the DWA [16] can be observed at intermediate and high energies and this is evidently encouraging.
In Figure 5 we show the SBP integral cross section for the 1 1 S → 3 1 P electronic transition compared with the coupled-channel optical method (CCO) [16]. The two methods without Ps-formation. A good agree between the SBP approach and the CCO model [16] can be observed. The results are consistently good, giving confidences that the SBP approach is adequate when compared with the sophisticate CCO model [16].
To test the stability of the 2 1 P cross section, we have performed calculations using other open channel, i.e., the influence of 4 1 P as open channel on the 2 1 P transition. This preliminary study represents only a indicative on the level of influence of a possible open channel. Figure 6 shows the 2 1 P state with the presence of the 4 1 P state as open channel (Eq. 5). As observed the presence of the 4 1 P state as a open channel does not disturb the 1 1 S-2 1 P cross section in the SBP context. Evidently a multichannel convergence process in order to obtain reliable cross sections can be necessary.
Alternatively, the SBP approach can be used as a representation of the Z eff classical “Z”, i.e., when positrons annihilate on many-electron atoms, the annihilation cross sections is traditionally written as [1]
Where
Z eff is the effective number of electrons that contribute to the annihilation process, and ψ(r 1 ,...,r z ,r) is the total wavefunction of the Z electron and one positron coordenates. If substitutes the asymptotic, plane wave function into equation (8), one obtains Z eff = Z (classical). We have noted that the SBP approach can determine the Z eff classical based on the Born approximation (Z eff represent also an important criteria to check the quality of SBP approach using the FBA). The accuracy of the Z eff Born approximation can be given by
and in this sense the present SBP approach retains information on the Z eff classical.
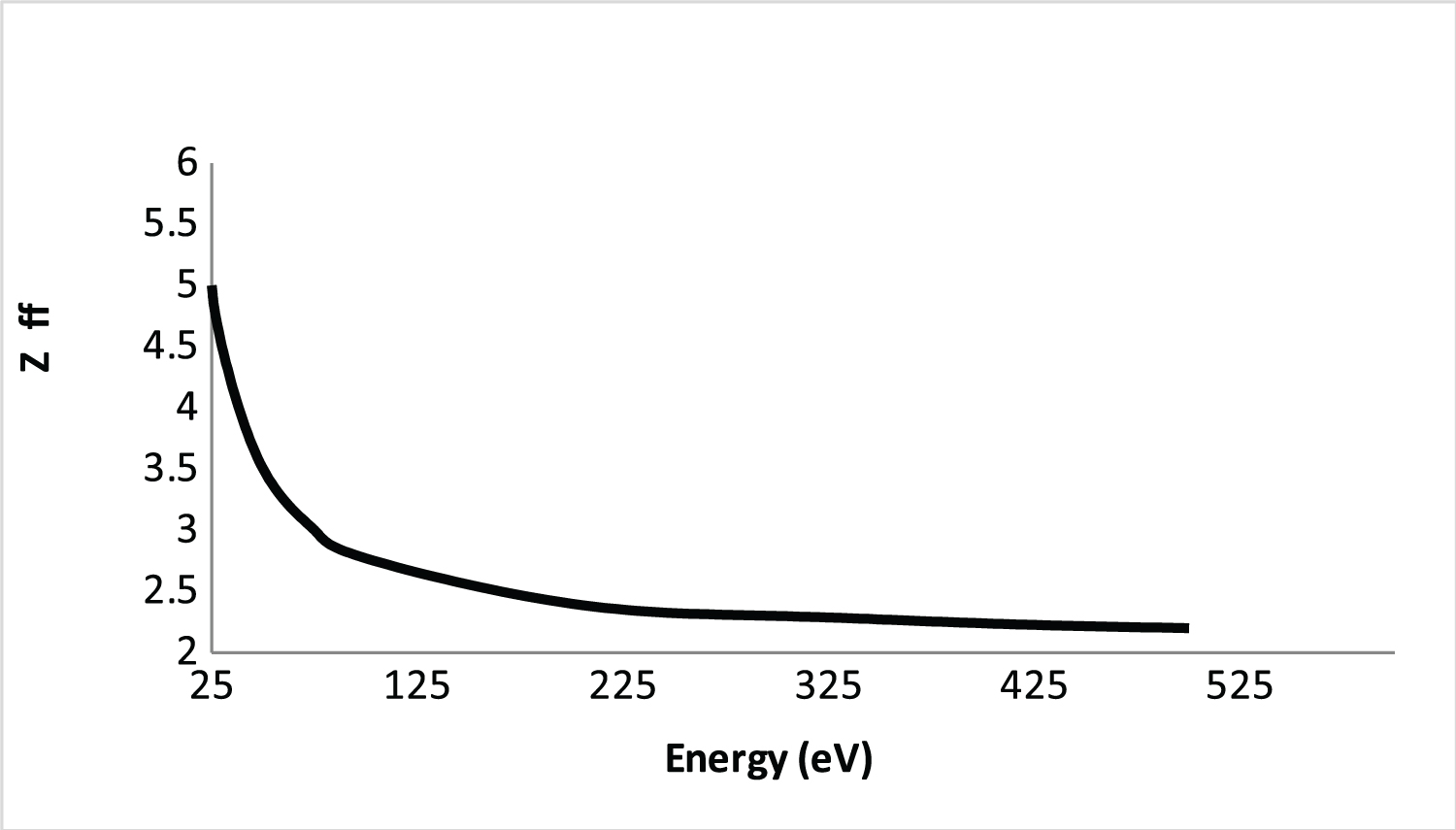
Finally, in Figure 7 we present Z eff (SBP) for the He atom. As observed the Z eff shows aspects of convergence with Z classical (Z = 2) using the 2 1 S state. Figure 6 indicate that the SBP approach is significant and suggested that Eq.(8) can be used as a strategies to treat convergence characteristic of the SBP approach. The numerical data in Table 2 are obtained using the SBP approach and are listed for future reference (units a o 2 ).
Conclusion
We have discussed a recently developed scaling method called scaled Born positron (SBP) for positron-He atom collision. The present paper has examined the validity of the SBP approach to calculating integral cross sections for 2 1 S, and 2 1 P states of He atom by positron impact. Analysis of the results indicated that the SBP is significant, with good convergence characteristics when compared with sophisticates methods at low energies. In particular the calculation for the 2 1 P state using the SBP approach shown cross sections with great similarity with sophisticate methods and the SBP approach is economical in the sense that relatively small basis set (FBA) are capable of providing reliable cross sections with small effort computational. We also conclude that Z eff classical parameter is consistently good which emphasized the importance of the SBP approach.