Unsteady Natural Convection Flow in a Vertical Tube Inspired by Ramped Surface Temperature of the Tube

International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068 )
Volume 10, Issue 1
Research Article
DOI: 10.35840/2631-5068/6543
Unsteady Natural Convection Flow in a Vertical Tube Inspired by Ramped Surface Temperature of the Tube
Basant K. Jha, Michael O. Oni, Junaid M. Abba and Baba I. Mundi
Table of Content
Figures
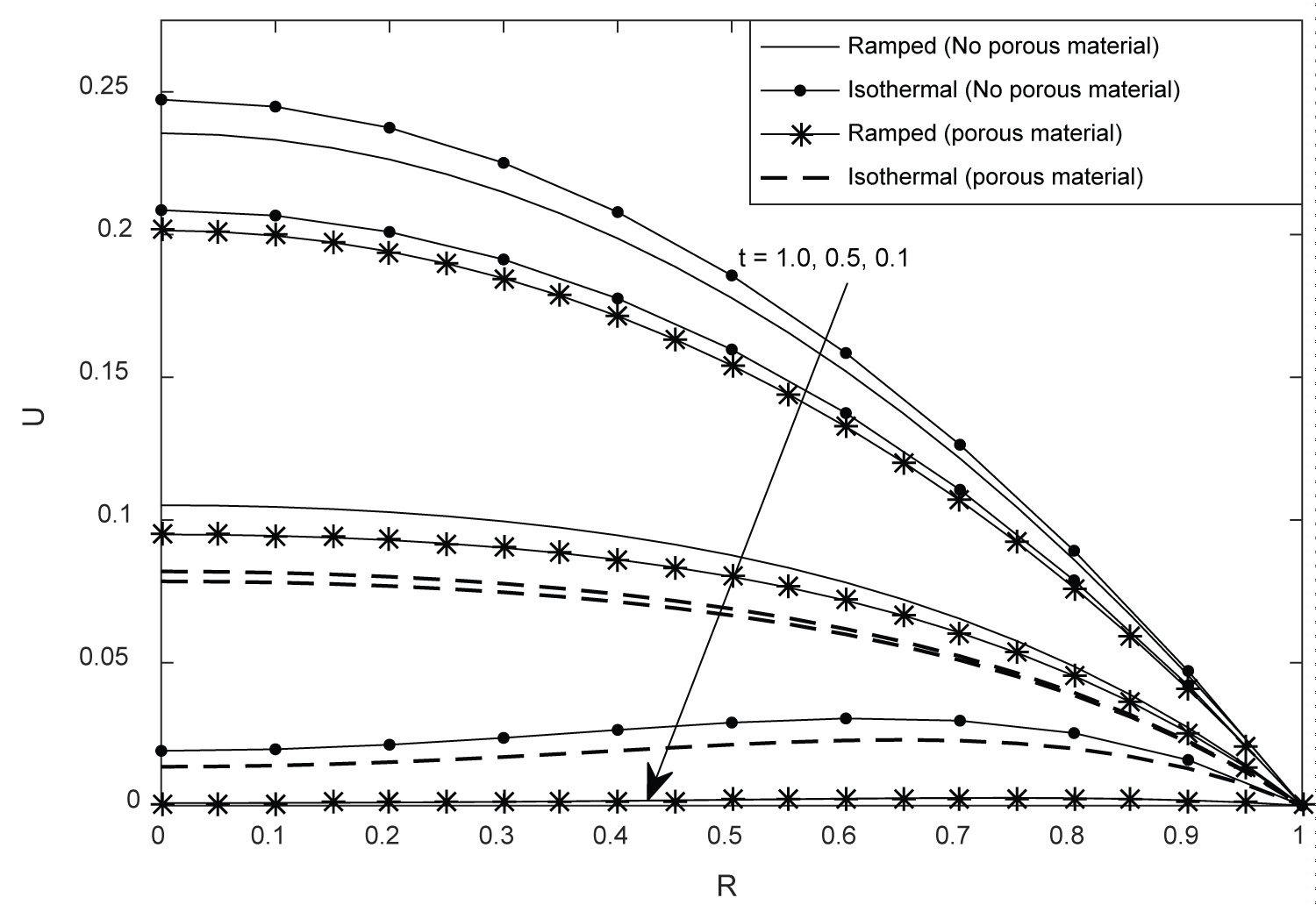
Figure 3: Velocity profiles for different....
Velocity profiles for different physical situations and time at Pr = 0.71, Da = 0.1 and t0 = 0.5.

Figure 4: Velocity profiles for different....
Velocity profiles for different physical situations and time at Pr = 7.0, Da = 0.1 and t0 = 0.5.

Figure 5: Velocity profiles for porous....
Velocity profiles for porous case with different values of at t0 = 1.0, t = 0.5, Pr = 0.7, Da = 0.1.

Figure 6: Velocity profiles for porous....
Velocity profiles for porous case with different values of Da at t0 = 1.0, t = 0.5, Pr = 0.71, = 1.0.

Figure 7: Nusselt number for different...
Nusselt number for different values of t and Pr for t0 = 0.5 (R= 1).

Figure 8: Alignment sequence. 1) He-Ne laser; 2) Optical...
Skin-friction for different Pr and t at t0 = 0.5, Da = 1.0, γ = 1.0 (R = 1.0).
Tables
Table 1: Material parameters .
Table 2: Numerical computation of temperature and velocity for different values of t at
References
- Schetz JA (1963) On the approximate solution of viscous flow problems. J Appl Mech 30: 263-268.
- Schetz JA, Eichhorn R (1964) Natural convection with discontinuous wall-temperature variations. J Fluid Mech 18: 167-176.
- Hayday AA, Bowlus DA, McGraw RA (1967) Free convection from a vertical plate with step discontinuities in surface temperature. J Heat Transf 89: 244-249.
- Kelleher M (1971) Free convection from a vertical plate with discontinuous wall temperature. J Heat Transf 93: 349-356.
- Kao TT (1975) Laminar free convective heat transfer response along a vertical flat plate with step jump in surface temperature. Lett Heat Mass Transf 2: 419-428.
- Lee S, Yovanovich MM (1991) Laminar natural convection from a vertical plate with a step change in wall temperature. J Heat Transf 113: 501-504.
- Jha BK, Prasad R, Rai S (1991) Mass transfer effects on the flow past an exponentially accelerated vertical plate with constant heat flux. Astrophys Space Sci 181: 125-134.
- Singh AK, Chandran P, Sacheti NC (2008) Developing flow near a semi-infinite vertical wall with ramped temperature. Int J Appllied Mathematics and Statistics 13: 34-45.
- Singh RK, Singh AK (2010) Transient MHD free convective near a semi infinite vertical wall having ramped temperature. Int J Appl Math Mech 6: 69-79.
- Saha SC, Patterson JC, Lei C (2010) Natural convection boundary-layer adjacent to an inclined flat plate subject to sudden and ramp heating. Int J Therm Sci 49: 1600-1612.
- Chandran P, Sacheti NC, Singh AK (2004) Natural convection near a vertical plate with ramped wall temperature. Heat Mass Transf 41: 459-464.
- Jha BK, Oni MO (2016) Natural convection flow in a vertical tube inspired by time-periodic heating. Alexandria Eng J 55: 3145-3151.
- Jha BK, Oni MO (2018) Transient natural convection flow between vertical concentric cylinders heated/cooled asymmetrically. Proc IMechE Part A: J Power and Energy. 232.
- Kumar VA (2016) Effect of radial magnetic field on natural convection flow in alternate conducting vertical concentric annuli with ramped temperature. Engineering Science and Technology, an International Journal 19: 1436-1451.
- Kumar VA (2017) Effect of velocity of applied magnetic field on natural convection over ramped type moving inner cylinder with ramped type temperature. International Journal of Mechanical Sciences 131-132: 625-632.
- Khalid A, Khan I, Shafie S (2015) Exact solutions for free convection flow of nanofluids with ramped wall temperature. Eur Phys J Plus 130: 57.
- Khalid A, Khan I, Shafie S (2016) Heat transfer in ferrofluid with cylindrical shape nanoparticles past a vertical plate with ramped wall temperature embedded in a porous medium. J Molecular Liquids 221: 1175-1183.
- Kumar A, Singh AK (2011) Transient MHD natural convection past a vertical cone having ramped temperature on the curved surface. Int J Energy Tech 3: 16.
- Jha BK, Yusuf TS (2016) Transient free convective flow in an annular porous medium: A semi-analytical approach. Eng Sci Tech Int J 19: 1936-1948.
- Oni MO (2017) Combined effect of heat source, porosity and thermal radiation on mixed convection flow in a vertical annulus: An exact solution. Engineering Science and Technology, an International Journal 20: 518-527.
- Jha BK, Chia RA, Aina B (2015) Natural Convection Flow in a Vertical Concentric Annuli filled with Porous Material having variable porosity under Radial Magnetic Field: An Exact Solution. Journal of Applied Physical Science International 4: 8-17.
- Jha BK, Apere CA (2010) Unsteady MHD Couette flow in Annuli: The Riemann-sum approximation Approach. J Phy Soc Jpn 79: 124403.
- Jha BK, Oni MO (2017) An analytical solution for temperature field around a cylindrical surface subjected to a time dependent heat flux: An alternative approach. Alexandria Engineering Journal 57: 927-929.
- Khadrawi AF, Al-Nimr MA (2007) Unsteady natural convection fluid flow in a vertical microchannel under the effect of the Dual-phase-Lag heat conduction model. Int J Thermophys 28: 1387-1400.
- Tzou DY (1997) Macro to Microscale Heat Transfer: The Lagging Behaviour. Washington: Taylor and Francis.
Author Details
Basant K. Jha1, Michael O. Oni1*, Junaid M. Abba1 and Baba I. Mundi2
1Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria
2Nigerian Institute of Transport Technology, NITT, Zaria, Nigeria
Corresponding author
Michael O. Oni, Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria.
Accepted: February 21, 2024 | Published Online: February 23, 2024
Citation: Jha BK, Oni MO, Abba JM, Mundi BI (2024) Unsteady Natural Convection Flow in a Vertical Tube Inspired by Ramped Surface Temperature of the Tube. Int J Magnetics Electromagnetism 10:043.
Copyright: © 2024 Jha BK, et al. This This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
This article is devoted to investigate the unsteady natural convection flow in a tube inspired by ramped surface heating. The governing momentum and energy equations are presented under relevant boundary conditions. Using the Laplace transform technique, exact solutions are obtained for both the clear fluid and the fluid filled with a porous material in Laplace domain. The Riemann-sum approximation procedure is used to invert numerically from Laplace domain to time domain. During the course of numerical computations, it is found that the role of ramped surface heating is to decrease fluid temperature, velocity and skin-friction. In addition, the presence of porous material eliminates the occurrence of discontinuity of flow formation for unity Prandtl number.
Keywords
Vertical tube, Laplace transform, Ramped temperature, Isothermal heating, Porous material
Nomenclature
a: Radius of the tube (m); Da: Darcy Number; g: Gravitational Acceleration (m/s 2 ); I n : Modified Bessel function of the first kind of order n; K: Permeability; Pr: Prandtl Number; r: Dimensional Radial Coordinate (m); R: Dimensionless radial coordinate; RSA: Riemann-Sum Approximation; SS: Steady State; : Dimensionaltime(s); : Dimensional ramped time(s); t: Dimensionless time; T: Dimensional temperature (K); T 0 : Fluid ambient temperature (K); T a : Temperature of the surface of the tube (K); u : Dimensional axial velocity (m/s); U: Dimensionless axial velocity
Greek Letters
: Density; : Skin-friction; : Dimensionless temperature; : Thermal diffusivity (m 2 /s); β : Coefficient of thermal expansion ( K -1 ); k: Thermal conductivity ; γ : Ratio of radiuses; : Fluid density (Kg/m 3 ); : kinematic viscosity (m 2 /s); : Effective kinematic viscosity (m 2 /s); : Skin-friction (dimensionless)
Introduction
Over the years, in an attempt to strike the balance between theoretical studies and real-life situations, several mathematical models have been developed to reduce this imbalance. The study of natural convection flow in different geometries continue to gain pronounced attention due to its daily cooling applications, heat exchanger and need for innovations in radiators. In many physical situations, there exists situations which may require non-uniform or arbitrary thermal conditions at a wall. Practical problems most times require non-similar conditions at the wall. When a fluid is heating, temperature gradually increases, but after boiling point, temperature becomes constant. This phenomena is commonly seen in thermostats, refrigerators and air-conditioners. In view of this fact, several researchers examined free convection flow in a vertical plate with ramped wall temperature. One of the earliest study is the work of Schetz [1], who developed an approximate analytical model for problems with discontinuous wall temperature conditions. Later, experimental justification was carried out by Schetz and Eichhorn [2]. Since then, different articles have been devoted to the study of flow formation and temperature distribution in vertical plate subject to ramped temperature [3-11].
Few articles have been dedicated to understanding flow formation and heat transfer with non-similar wall thermal conditions in cylindrical geometries. Jha and Oni [12] theoretically analysed natural convection flow in a vertical tube inspired by time-periodic heating. They found that flow formation, heat transfer and mass flow rate are appreciably influenced by Prandtl number and Strouhal number. In other work [13], they investigated the transient natural convection flow between vertical concentric cylinders heated/cooled asymmetrically. Other related literature in cylindrical geometric are [14-18].
The applications of flow in porous medium cannot be over-emphasized, as it ranges from oil exploration to bio-mechanical devices. Different studies in the recent time have considered role of porous material on natural convection flow in vertical annuli [19-21].
The aim of this present work is to study the unsteady natural convection flow in a vertical tube, inspired by ramped surface temperature. This work can be seen as a redefinition of [11] when the flow formation and heat transfer is in a vertical tube. In addition, the role of porous material on natural convection flow formation which has significant application in heat transfer and heat exchanger is also investigated.
Mathematical Analysis
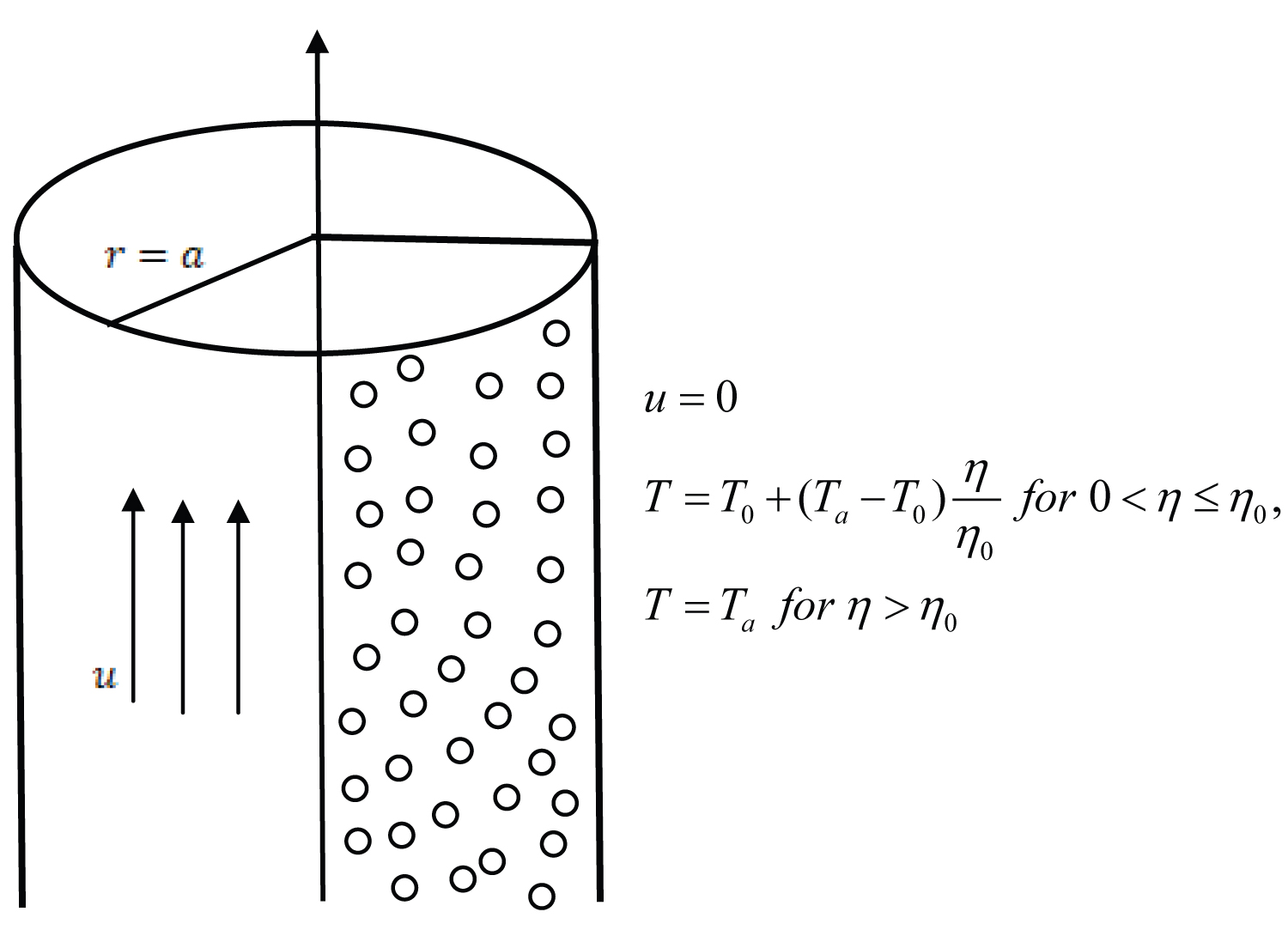
Consider an unsteady incompressible natural convection flow formation in a vertical tube of radius a as shown in Figure 1. The flow is assumed to be fully developed both thermally and hydrodynamically and the viscous dissipation term in the energy equation is also assumed to be negligible. Two different physical situations are considered:
Flow in a vertical pipe with ramped surface temperature
In this case, initially , the temperature of the surface of the tube and the fluid assumes ambient temperature of T 0 . At time , the temperature of the surface of the tube is raised/lowered to when and thereafter maintained a constant temperature T a for . This unequal temperature distribution at the surface of the tube leads to density difference and as such, natural convection is setup. Using the usual Boussinesq approximation, the momentum and energy equations in dimensional form are given as:
Subject to the following boundary conditions:
: ; for
Using the following dimensionless parameters, equations (1-3) become:
, , , , , , , (4)
Subject to the following boundary conditions:
: ; for
where
where is the Heaviside step function defined by:
(10)
Using the Laplace transform technique defined in equation (9) on equations (5-7), the governing partial momentum and energy equations are transformed to ordinary different equations as:
(12)
Subject to the following boundary conditions:
where
Equations (11-12) are then solved exactly with boundary conditions (13) in Laplace domain as:
Using equations (15) and (16) respectively, the rate of heat transfer represented by Nusselt number as well as the skin-friction at the surface of the tube are defined as:
Special Cases
Unity Prandtl number
From equation (16), a discontinuity is observed when the magnitude of fluid kinematic viscosity equals its thermal diffusivity i.e. (unity Prandtl number). A closed form expression in Laplace domain is obtained for fluid velocity to overcome this discontinuity as:
Clearly, equation (19) satisfies boundary condition (13), hence, the skin-friction for unity Prandtl number can be obtained from equation (19) as:
Isothermal case
To clearly understand the role of ramped surface temperature of the tube, it is significant to present exact solution for the case of constant (isothermal) surface heating of the tube. Hence, setting T = T a for all values of t, and solving equations (1 and 2) using the Laplace transform technique, we have the following closed form expressions for temperature, velocity, Nusselt number and skin-friction in Laplace domain:
where and are the modified Bessel’s function of first kind of order zero and one respectively and are defined as:
The solutions obtained are in Laplace domain and need to be transform to time domain. Due to the complexity of the expressions obtained in Laplace domain, we employed a numerical technique used in [22-24] which is based on the Riemann-sum approximation (RSA). In this method, any function in the Laplace domain can be inverted to the time domain as follows:
where Re denotes to the real part of the imaginary number. M is the number of terms used in the Riemann-sum approximation and is the real part of the Bromwich contour that is used in inverting Laplace transforms. The Riemann-sum approximation for the Laplace inversion involves a single summation for the numerical process. Its correctness depends on the value of and the truncation error dictated by M. According to Tzou [25], the value of that best satisfied the result is 4.7.
Steady state solution
Another important solution to the current analysis is the steady state (time independent) solution, due to the fact that it helps to checkmate the accuracy of the solution method of the transient state. This is obtained by taking in equations (1) and (2) which on solving gives the following exact solutions:
Flow in a vertical pipe filled with porous material with ramped surface temperature
This part is concern with studying the role of porous material on unsteady natural convection flow formation in a vertical tube. It has been shown that fluid flowing in a vertical tube subject to either ramped temperature or constant surface heating has a discontinuous point for unity Prandtl number. To solve this problem, we tend to consider a more physical scenario where the fluid flows in vertical tubes filled with homogeneous porous materials. Considering the fully developed natural convection flow in a vertical pipe filled with homogeneous porous material, the governing equations (1 and 2) on adding the porosity term in dimensionless form become:
Clearly, the energy equation (31) is exactly as those presented in equation (6) and hence will not be discussed. Solving equation (30) with boundary conditions (7), the following closed form expressions for fluid velocity as well as skin-friction in Laplace domain are obtained:
Isothermal case
Considering the situation where t = t 0 consequently yields T = T W for all values of t. Since the energy equation is independent on porous material, hence the temperature profile for this case is exactly the same with equation (21). Hence the solution to equation (30) for constant surface heating of the tube is:
Steady state
The steady state solution for flow formation in the vertical tube is also obtained in similar way as those of previous section as:
Results and Discussion
A semi-analytical solution is carried out to investigate the unsteady natural convection flow in a vertical tube inspired by surface ramped temperature. The case when the fluid is filled with homogeneous porous material is also considered for different physical situations. The solutions obtained both for non-porous case and porous case are depicted graphically in order to achieve a deeper understanding on flow formation and rate of heat transfer. The basic dimensionless parameters governing the flow are Prandtl number (Pr), Darcy number (Da), ratio of viscosities and time (t). Throughout this article, we have considered 0.5 ≤ Pr ≤ 100 to capture from gases to higher hydrocarbons, 0.01 ≤ Da ≤ 1.0 and 0.5 ≤ γ ≤ 1.5.
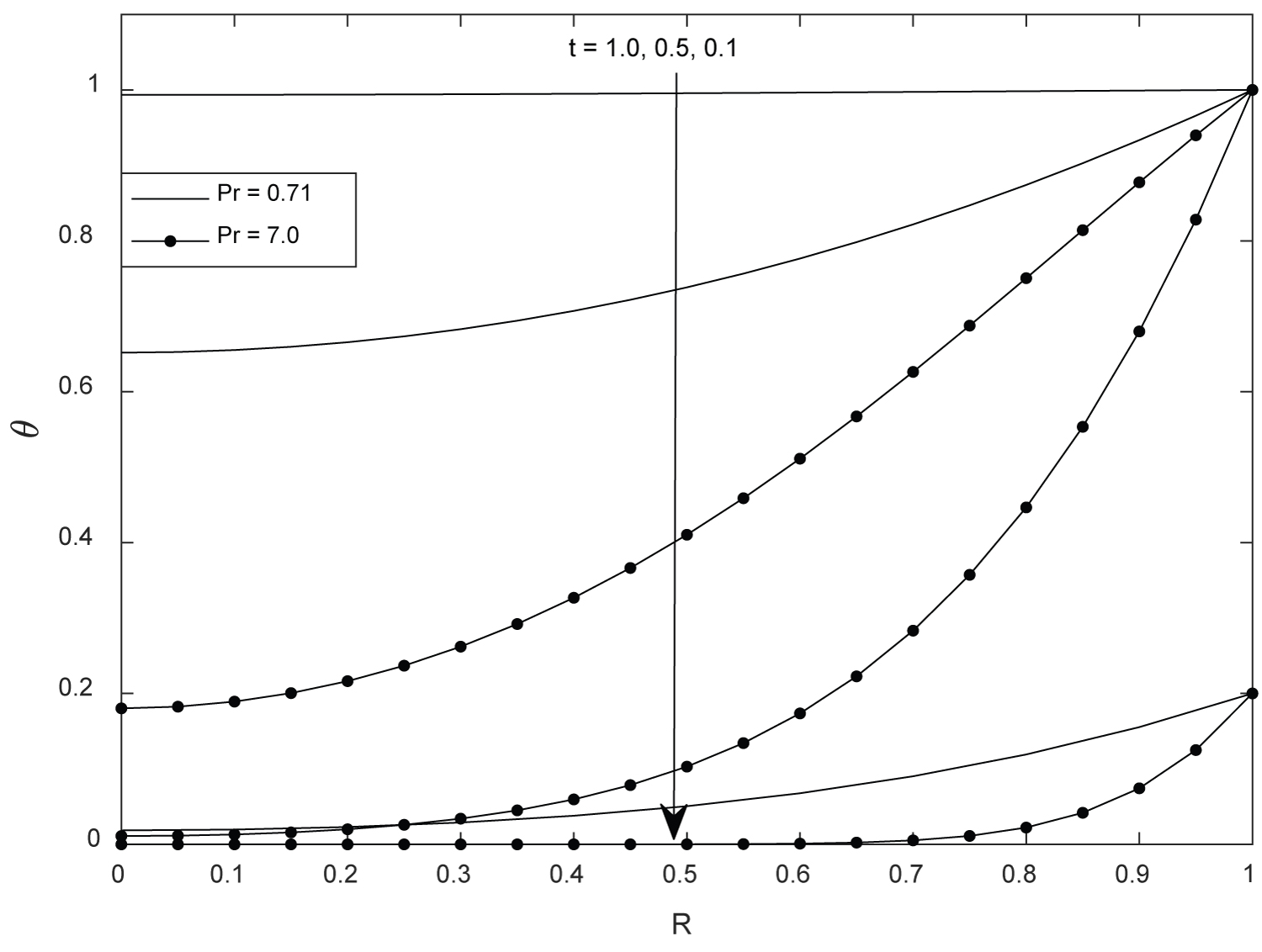
Figure 2 depicts temperature distribution in the tube for different values of Pr at different time with ramped temperature. It is obvious form this figure that fluid temperature increases with time and decreases with increase in Pr. This an expected result since the continual heating of the surface of the tube leads to corresponding increase temperature distribution in the tube until steady state is reached. It is good to state that there exists unchanging temperature profile for clear case and porous medium case. This could be attributed to the fact that this current article is restricted to fully developed region and as such the Darcy number only appears in the momentum equation.
Figure 3 and Figure 4 portray velocity profiles of different physical situations at different time in a vertical tube for air and water respectively. It is clear from these figures that velocity profiles increase with time regardless of the physical situation considered. In addition, the peak magnitude of velocity in the tube is found for the case of isothermal surface heating of the tube compared to ramped wall temperature. Also, the role of porous material is to retard fluid motion. This is physically true since the presence of homogeneous porous material hinders free motion of flow. Further, it is found that at steady state, the thermal boundary conditions (ramped temperature or isothermal heating) have no influence on velocity profile. This is can be seen in Figure 4 where fluid velocity for ramped and isothermal cases corresponds for both and non-porous material respectively for t = 7.0.
Figure 5 illustrates velocity profiles for porous case as a function of ratio of viscosity for ramped surface heating and isothermal surface heating. It is observed that fluid velocity is maximum when the effective kinematic viscosity of the porous medium is lower than the kinematic viscosity of the fluid. In addition, it is further seen that the role of ramped surface temperature is to reduce fluid velocity in the vertical tube.
Figure 6 on the other hand exhibits the significance of porous medium on flow formation in the vertical tube. It is obvious from this graph that fluid velocity is an increasing function of Da regardless of the thermal imposed condition. This could be attributed to the fact that Darcy number (Da) is directly proportional to permeability of the porous material, therefore increase in permeability leads to enhances of flow formation. A critical look at the figure suggests that as , there will be stoppage of flow formation regardless of the thermal conditions.
Figure 7 shows the rate of heat transfer between the surface of the tube and the fluid (represented by Nusselt number) at different time for different values of Pr for the case of ramped surface temperature of the fluid. It is established from this figure that heat transfer increases with time for and then decreases for t > 0. This could be attributed to the ramped nature of heat supplied. Also, fluids with higher Pr tends to have higher Nusselt number compared to fluid with relatively low Pr A critical look at this figure confirms that Nusselt number is zero at steady state and is independent on fluid considered. It is good to state that, heat transfer for both porous and non-porous case are exactly the same, since thus current analysis is concern with fully developed region, hence, fluid temperature is independent on porous material.
Figure 8 depicts skin-friction for different physical situations and different values of Pr at different time. It is found that skin-friction is independent of thermal boundary conditions imposed at steady state, but only depend on the porous or non-porous case. It can also be observed that the non-porous case has a higher drag that the porous case. In addition, it is obvious that the role of ramped surface heating is to reduce the skin-friction at this surface.
Table 1 presents a numerical comparison of RSA and steady state solution for different values of time. As expected, it is found that at sufficiently large time, RSA corresponds the steady state solution and thereby justifying the accuracy and reliability of RSA. In all cases considered, fluid velocity is found to increase with time.
Table 2 on the other hand illustrates the role of time on temperature and velocity for ramped and isothermal cases. It shows the degree of responsiveness of temperature and velocity with change in time. It is found that the ramped boundary conditions respond speedily than the isothermal case. In addition, the case of fluid flow filled with porous material exhibits sluggish respond to time compared to clear fluid.
Conclusion
A semi-analytical study is carried out on unsteady natural convection flow in a tube inspired by ramped surface heating. The governing momentum and energy equations are presented with relevant boundary conditions. Using the Laplace transform technique, exact solutions are obtained for both the clear fluid and the fluid filled with porous material. Based on the solutions obtained and graphical representations, the following conclusions can be drawn:
1. Fluid temperature, velocity and skin-friction increases with time regardless of the case considered.
2. The existence of homogeneous porous material eliminates the discontinuity of flow velocity for unity Prandtl number.
3. Ramped surface temperature leads to decrease in temperature, velocity and skin-friction.
4. Flow formation can be enhanced by eliminating porous materials.
5. Nusselt number increasing with Prandtl number until steady state is attained.