Electric Field Theory Based on Weber's Electrodynamics

International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 7, Issue 2
Research Article
DOI: 10.35840/2631-5068/6539
Electric Field Theory Based on Weber's Electrodynamics
Qingsong Li
Table of Content
Figures

Figure 1: The electric force exerted...
The electric force exerted by the charge Q with velocity and acceleration on to the charge with velocity and acceleration .
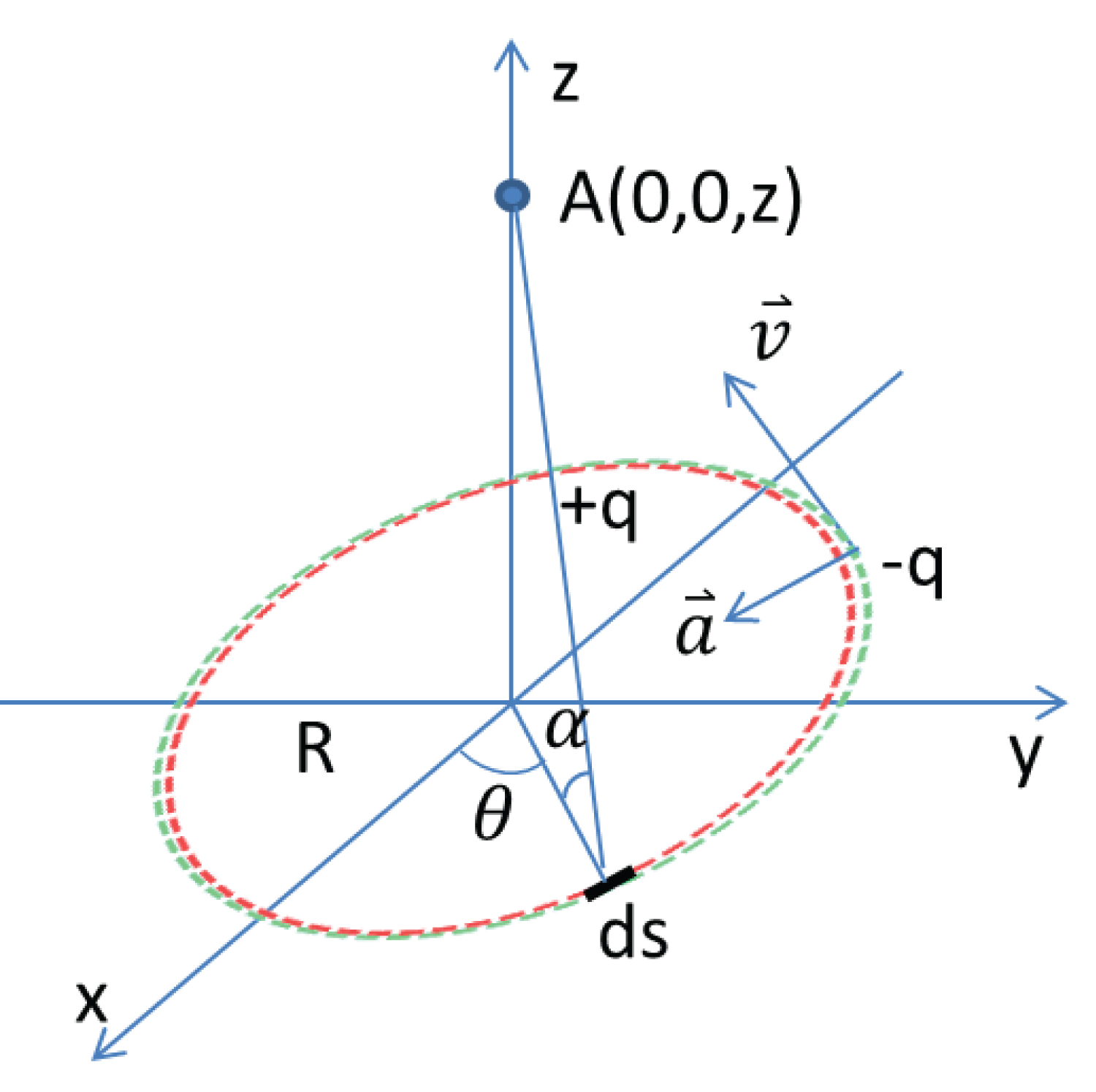
Figure 2: Schematic diagram of the electrical....
Schematic diagram of the electrical fields at point A (0,0,z) from a circular current, which has a radius R.
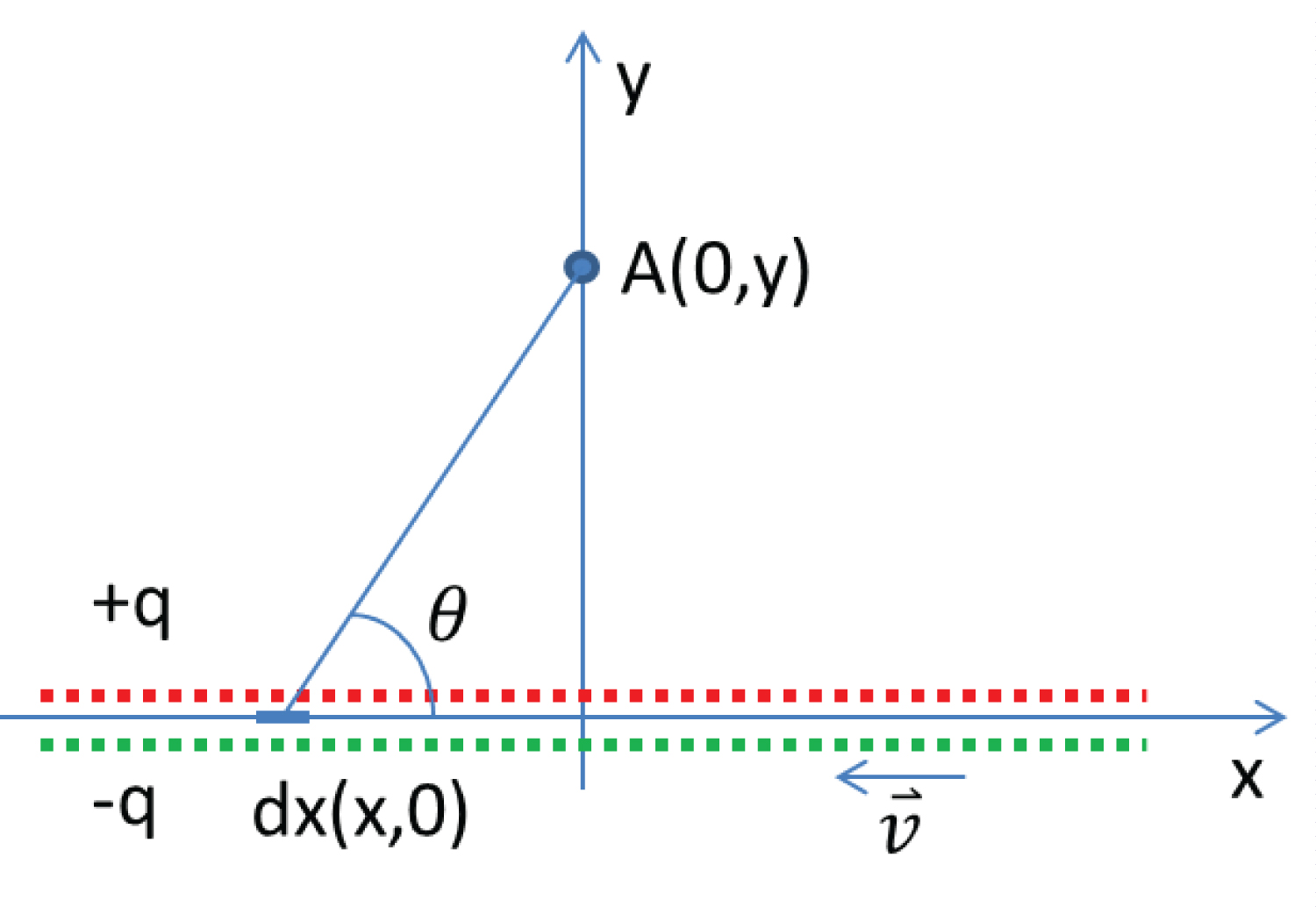
Figure 3: Schematic diagram of the electrical....
Schematic diagram of the electrical field of an infinite long straight current along the x-axis. The positive charge of the current is stationary, and the negative charge moves in the opposite direction of the x-axis.
References
- Griffiths DJ (1998) Introduction to electrodynamics. (3rd edn), Prentice Hall, New Jersey, USA, 204-541.
- Maxwell JC (1865) A dynamical theory of the electromagnetic field. Phil Trans R Soc Lond 155: 459-512.
- Nussbaum A (1972) Faraday's law paradoxes. Physics Education 7: 231.
- Cullwick E (1952) Electromagnetic momentum and Newton's third law. Nature 170: 425.
- Weber W (2007) Determinations of electrodynamic measure: Concerning a universal law of electrical action. 21st Century Science and Technology.
- Junginger JE, Popovic ZD (2004) An experimental investigation of the influence of an electrostatic potential on electron mass as predicted by Weber's force law. Can J Phys 82: 731-735.
- Weikert M, Tajmar M (2019) Investigation of the Influence of a field-free electrostatic potential on the electron mass with Barkhausen-Kurz oscillation. Physics.
- Assis KT, Tajmar M (2019) Rotation of a superconductor due to electromagnetic induction using Weber's electrodynamics. Annales de la Fondation Louis de Broglie 44: 111-123.
- Lemon DK, Edwards WF, Kenyon CS (1992) Electric potentials associated with steady currents in superconducting coils. Physics Letters A 162: 105-114.
Author Details
Qingsong Li*
Independent Researcher, Sugar Land, USA
Corresponding author
Qingsong Li, Independent Researcher, Sugar Land, Texas, USA.
Accepted: December 29, 2021 | Published Online: December 31, 2021
Citation: Li Q (2021) Electric Field Theory Based on Weber's Electrodynamics. Int J Magnetics Electromagnetism 7:039.
Copyright: © 2021 Li Q. This This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Weber's electrodynamics, as an alternative to classical electromagnetic field theory, can successfully explain many electromagnetic phenomena. However, the Weber's electrodynamics involves integrating interactions among electric particles for each application, which can be sometimes very tedious. In this study, we try to develop an electric field theory, which sums the contribution of each particle as a field, and then apply this field to the particle of interest. This way, the application of Weber's electrodynamics is greatly simplified.
Introduction
More than a century ago, physicists proposed a series of theories and equations regarding electromagnetic phenomena, such as Coulomb's law, Ohm's law, Ampere's law, and Faraday's law of electromagnetic induction, etc. And Maxwell formed some of these equations into a system of equations, namely Maxwell's equations [1]. Later physicists simplified it, and they became four well-known equations, including Gauss's law, Gaussian magnetic law, Faraday's law of induction, and Maxwell-Ampere's law. In this system of equations, a changing electric field and/or an electric current produce a magnetic field, and a changing magnetic field also produces an electric field. The Lorentz force equation cannot be derived from the four Maxwell's equations, but becomes a separate axiom [2].
Classical electromagnetic field theory has been widely and successfully used to explain macroscopic electromagnetic phenomena. However, in some special cases, such as Faraday's Paradox [3], the explanation given by the classical electromagnetic field theory is not intuitive. In addition, the conformity between classical electromagnetic field theory and Newton's third law is not simple, and electromagnetic momentum needs to be introduced [4].
Besides classical electromagnetic field theory, Weber's electrodynamics was introduced in similar time [5], which is much less known in the physics community. Both Weber's electrodynamics and classical electromagnetic field theory can explain a lot electromagnetic phenomena. And experiments had been conducted to differentiate these two theories [6], but appeared inclusive [7].
Weber's electrodynamics can be described in the formula below [8]:
Where Q and q are two electrical charges, is the force that charge Q exerted on charge q, r is the distance between the two charges, is the unit vector pointing from charge Q to charge q, and are velocity and acceleration of charge q relative to charge Q, is the dielectric constant, c is the speed of light.
To apply Weber's electrodynamics, we need do integration over particles in each application. This can be sometimes very tedious if a large amount of particles are involved. In this study, we try to develop an electric field theory to simplify this process. We will also show two applications of this theory as examples.
Electric Field with Weber's Electrodynamics
First, we set a reference coordinate frame (Figure 1). Inside it, there is a charge Q with velocity and acceleration , and a charge q with velocity and acceleration . The distance between two charges is r, and is the unit vector pointing from charge Q to charge q. Then the force that charge Q exerted on charge q is:
If we use Einstein notation, the equation above can be rewritten to:
Let
The equation above can be rewritten to:
Let's use Kronecker delta , then:
Let's simplify above equation:
The above equation can be rewritten as:
Where
In Weber's electrodynamics, the force has the property of linear addition. Then the above 6 quantities, including , , , , , also have the property of linear addition. They are also the full representation of electrical field of Weber's electrodynamics. For the field of multiple electrical charges, we can add up the field of individual charge. To calculate the force from multiple charges to a single charge, we can apply equation (8) with both the single charge's property (charge amount, velocity, and acceleration) and the superposed electric field.
Circular Electric Current
There is a circular electric current on the x-y plain, centered at the origin (Figure 2). Let's calculate the electrical fields at point A on the z-axis (0, 0, z). The current is in steady state, the positive charges are stationary, and the negative charges have a velocity along the circle, and an acceleration pointing to the origin.
Because of the coexistence of positive and negative charges, apparently the integrated , , equal to zero.
For the current segment ds, the unit vector pointing from ds to point A is . Assume that negative charge has a linear density of . Let's calculate the electric field contributed by moving negative charges in the circle. First, the properties of the current segment ds are:
Then from the current segment is derived from equation (9).
We integrate it along the current circle, then we get .
Similarly, we can get:
For a charge q at point A with velocity and acceleration , the force exerted on it can be calculated with equation (8).
This force is consistent with the Lorentz force of the magnetic field that can be derived from the classical magnetic theory.
Infinity Long Straight Electric Current
There is an infinity long straight electric current along the x-axis (Figure 3). Let's calculate the electric field of this current at point A on the y-axis (0,y). Assume that the current is in steady state, the positive charges are stationary and the negative charges have a velocity .
Because of the coexistence of positive and negative charges, apparently the integrated , , equal to zero. Also because there is no acceleration of negative charges, the integrated equals to zero.
For the current segment dx, the unit vector pointing from dx to point A is . Assume that negative charge has a linear density of . Let's calculate the electric field contributed by moving negative charges. First, the properties of the current segment dx are:
Then from the current segment is derived from equation (9).
We integrate it along the x-axis, then with some math we get .
Similarly, we can get:
For a charge q at point A with velocity and acceleration , the force exerted on it can be calculated with equation (8).
The first term of the force is the same as the Lorentz force of the magnetic field from classical magnetic theory. The second term is unique to Weber's electrodynamics, comparing to the classical magnetic theory without introducing special relativity.
Discussion
We derived a new electric field theory from Weber's electrodynamics. In this theory, the electric field in general consists of 6 terms, including (1) static first-order tensor field , (2) velocity related third-order tensor field , (3) velocity related second-order tensor field , (4) velocity related first-order tensor field , (5) acceleration related second-order tensor field , and (6) acceleration related first-order tensor field . To calculate forces exerted on electric charges, we can use these field terms instead of integrating particle-particle interactions directly. This can greatly simplify the calculation process.
The electric field is dependent on the choice of reference frames. However, the final calculated forces are independent to choices of reference frames, because the field is derived from Weber's electrodynamics. As we know, Weber's electrodynamics only depends on the relative velocity and relative acceleration among particles.
The results of this paper indicate that the new electric field theory can be equivalent to classic electromagnetic theory in some special cases. For example, a special case can be (1) positive charge is always accompanied by negative charge and there is no net summed charge, (2) the current forms a loop, (3) the current is steady. Then all other terms in equation (9) may become zero or cancel each other, except velocity related second-order tensor field . And becomes the magnetic field of classical electromagnetic theory.
In the example of infinite long straight electric current, we show that the new field theory differs from classical magnetic theory with a term (equation 19). However, this difference may not be detected currently. This is due to the fact that this difference is proportional to the square of the electro drift velocity which is small (in order of 10-4 m/s). Also electric current generally needs a loop, in which case the assumption of infinite long straight current may not hold.
Even though Weber's electrodynamics (and the field theory in this paper) is velocity dependent, the induced electric field could be still zero in a special case, i.e. steady circular current. Previously, some experiments were done for detecting the velocity induced electric field using coils of current [9]. However, the measurements are significantly below prediction [9]. This paper's result may give a potential explanation: with the loop current, the velocity induced and acceleration induced electric fields cancel each other (equation 13).
Conclusion
This article presents a new theory of the electric field, which is derived from Weber's electrodynamics. With this theory, the calculation of forces exerted to electric charges can be greatly simplified. First, we sum up the electric field contributed from individual particles; second, we apply the field to particles of interest.
Acknowledgment
The author thanks Ronghua Li for showing the beauty of physics when the author was young.

