Optical Properties of Asymmetric Transmission Devices for One-Dimensional Photonic Crystals

International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 6, Issue 2
Research Article
DOI: 10.35840/2631-5092/4545
Optical Properties of Asymmetric Transmission Devices for One-Dimensional Photonic Crystals
Ming-Li Ren, Meng Han, Xiao-Jing Liu and Xiang-Yao Wu
Table of Content
Figures
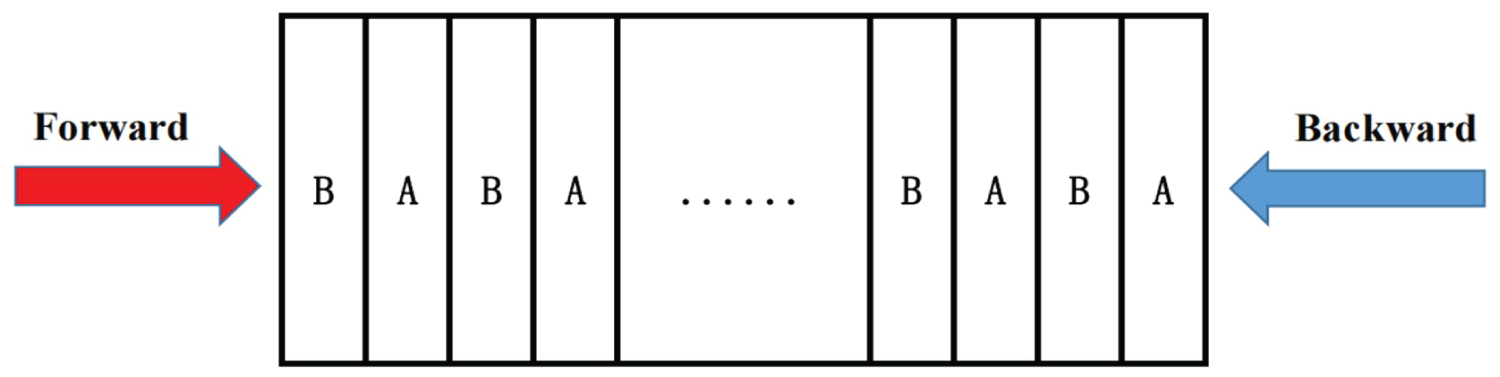
Figure 1: The light forward incident (red arrows) and....
The light forward incident (red arrows) and backward incident (blue arrows) to the FPCs.
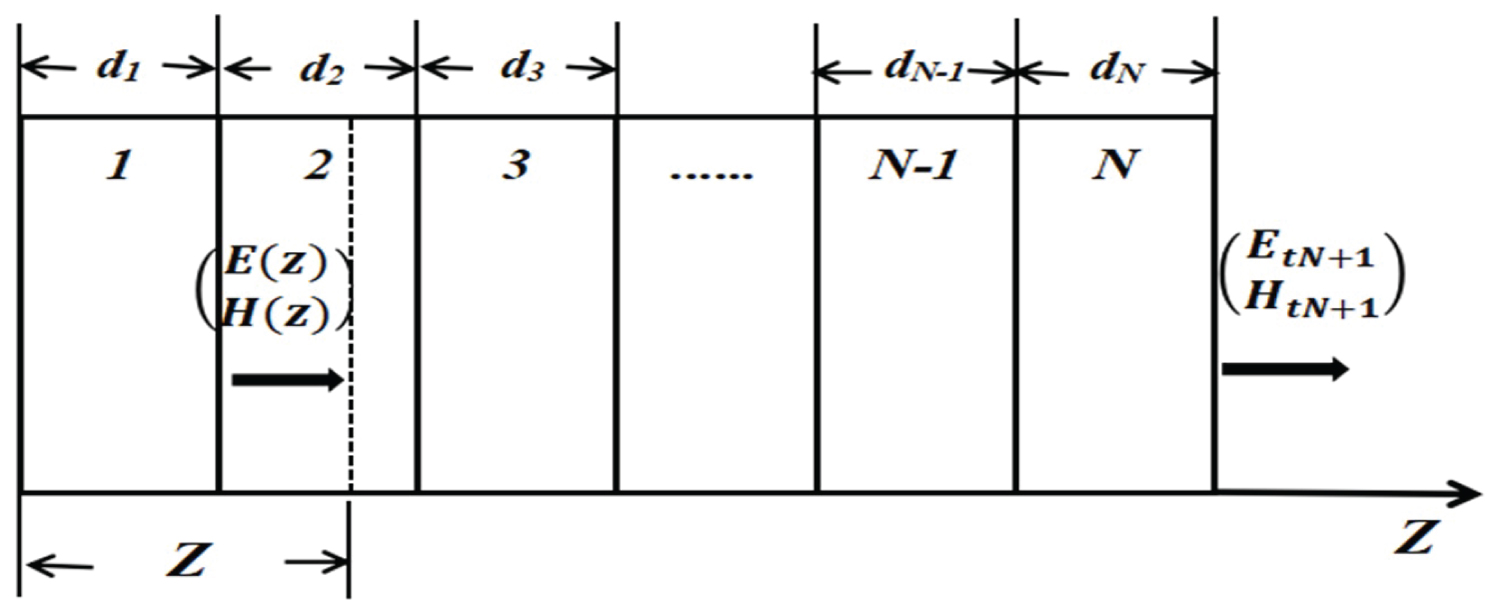
Figure 2: The input and output electric field and....
The input and output electric field and magnetic field in the FPCs.
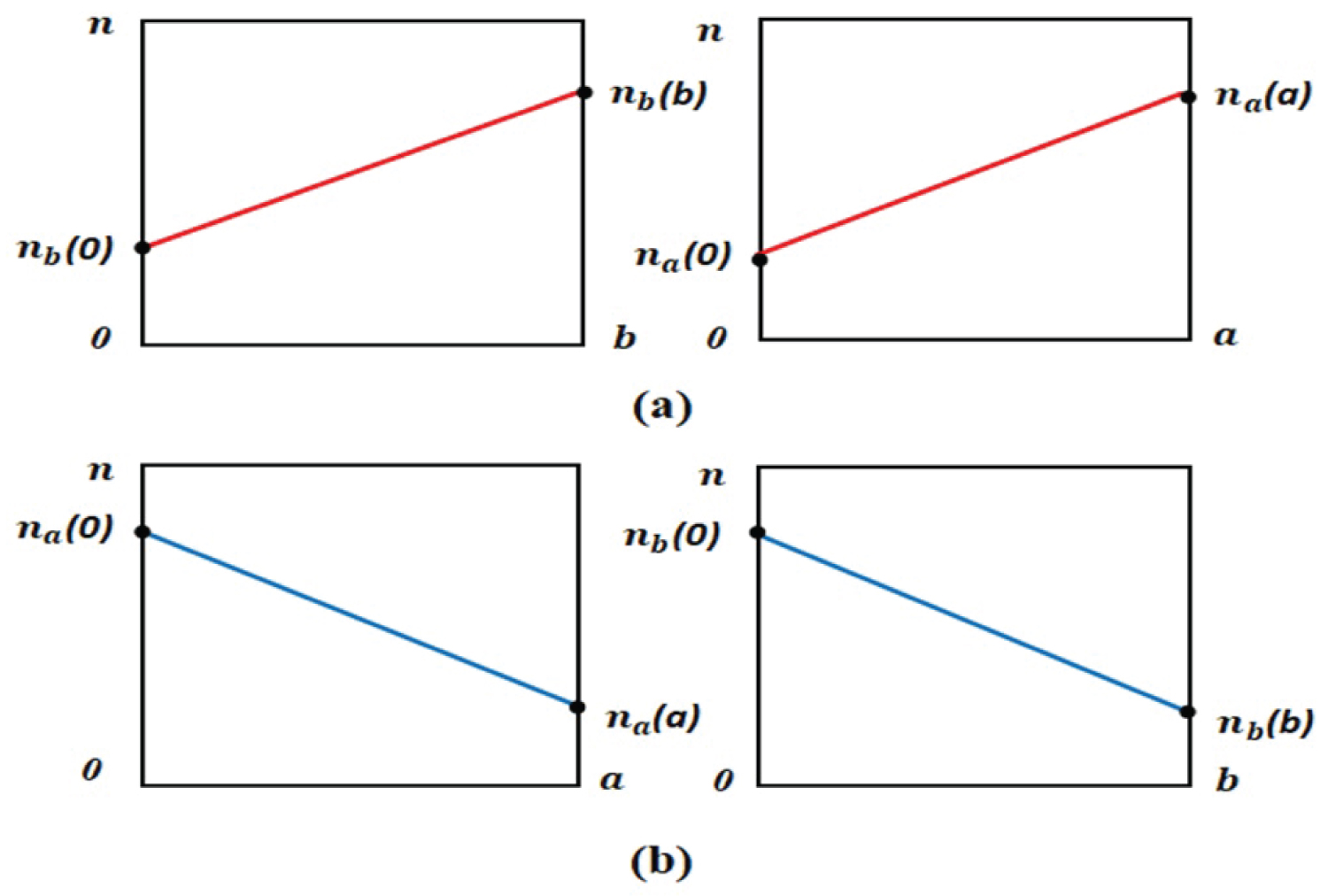
Figure 3: The line refractive indices functions as space....
The line refractive indices functions as space coordinates in a period. The (a) is the refractive indices function of linear increase for forward incident. The (b) is the refractive indices function of linear decrease for backward incident.
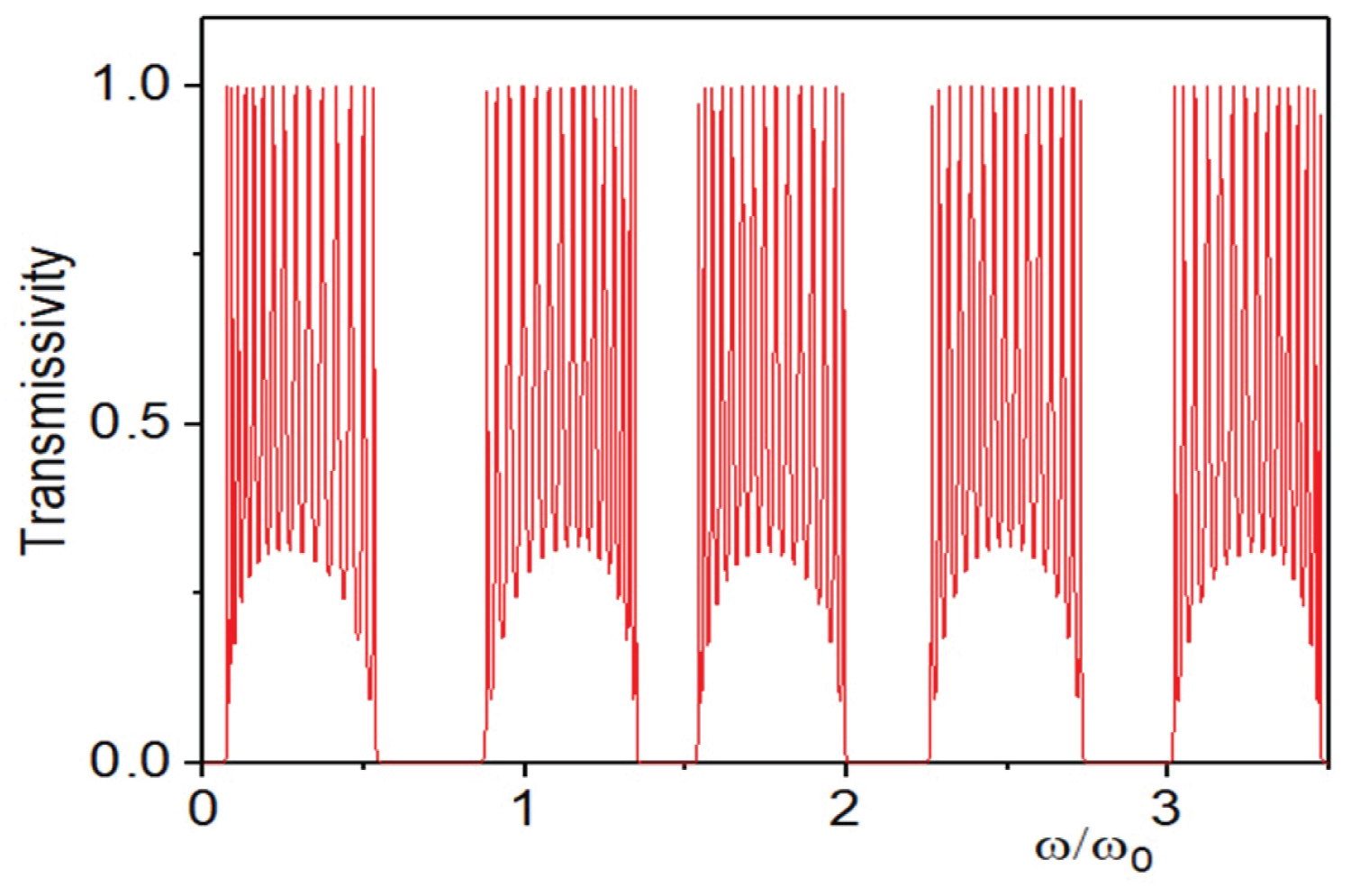
Figure 4: The distribution of transmissivity with...
The distribution of transmissivity with the forward incident (red line).
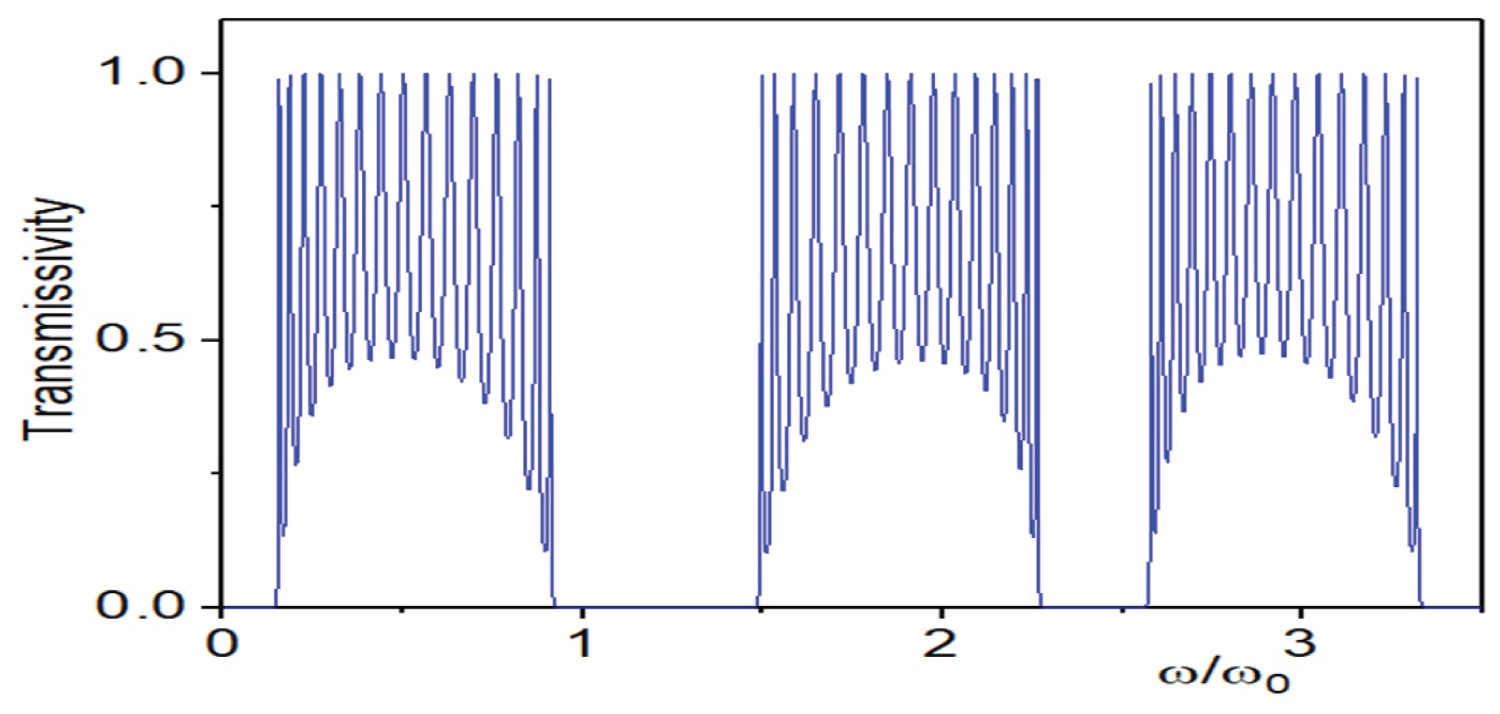
Figure 5: The distribution of transmissivity...
The distribution of transmissivity with the backward incident (blue line).
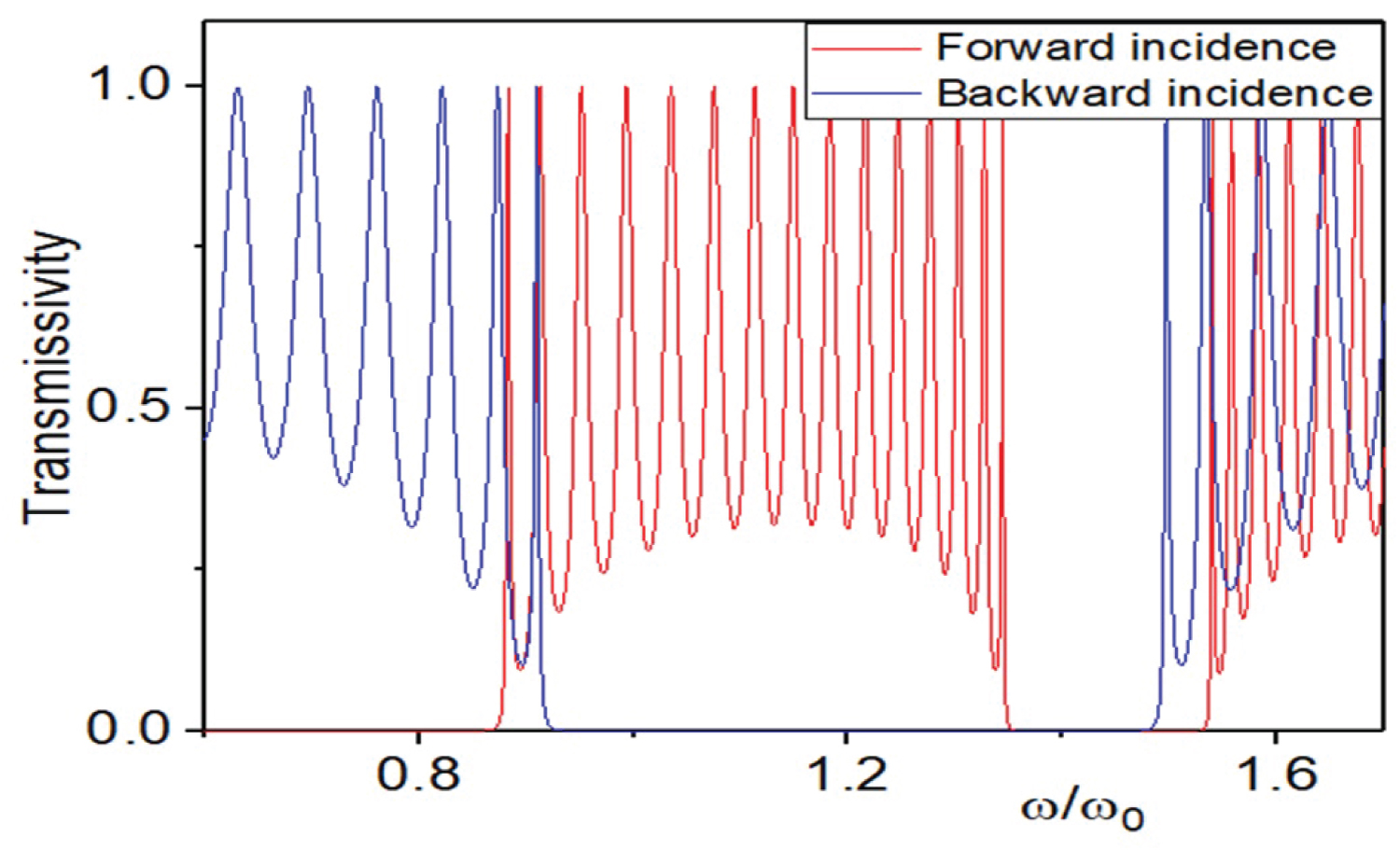
Figure 6: The distribution of transmissivity with the...
The distribution of transmissivity with the forward incident (red line) and the backward incident (blue line) when .
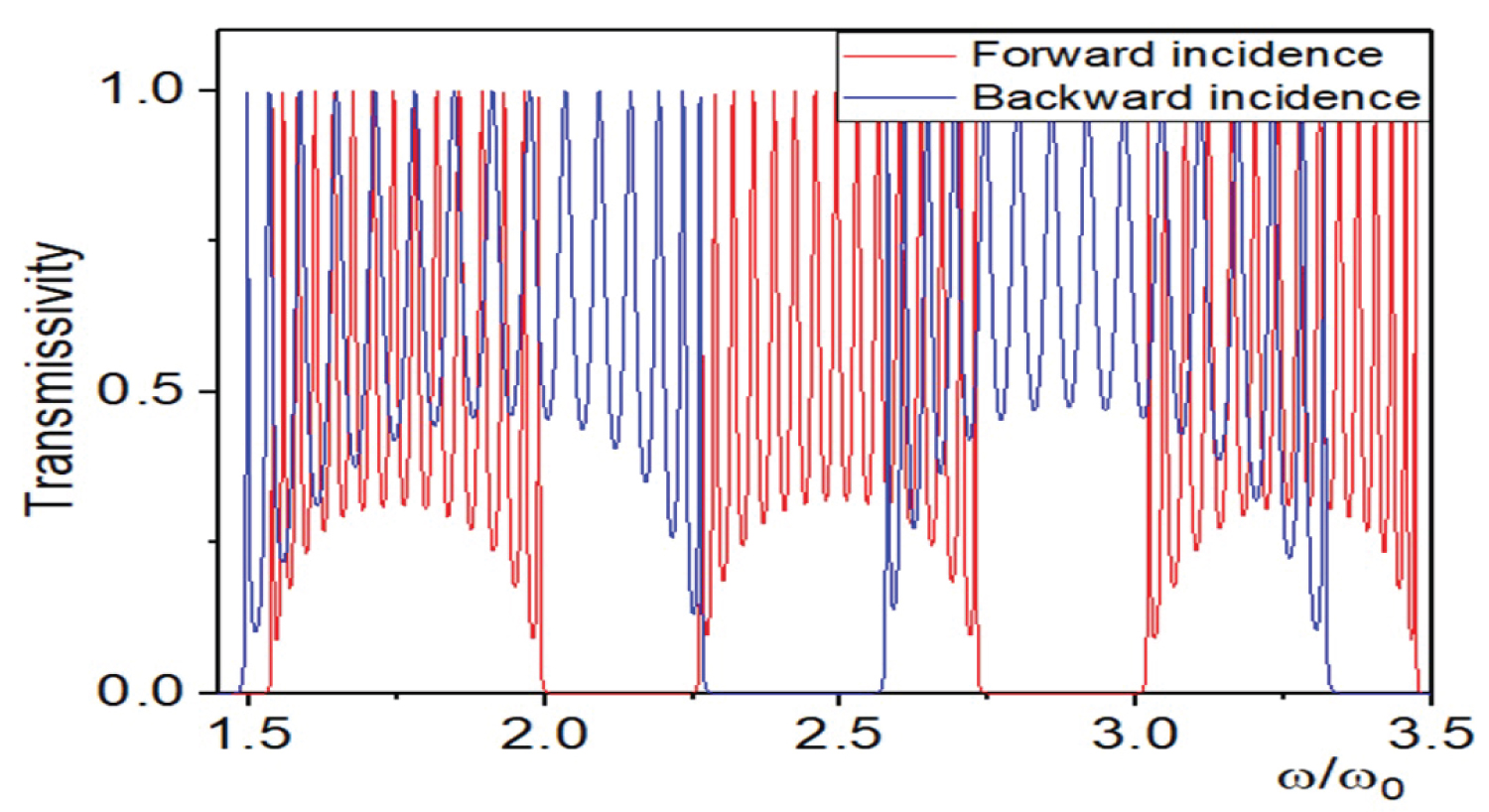
Figure 7: The distribution of transmissivity with the...
The distribution of transmissivity with the forward incident (red line) and the backward incident (blue line) when .

Figure 8: The distribution of transmissivity with...
The distribution of transmissivity with the forward incident (red line) and the backward incident (blue line) when .
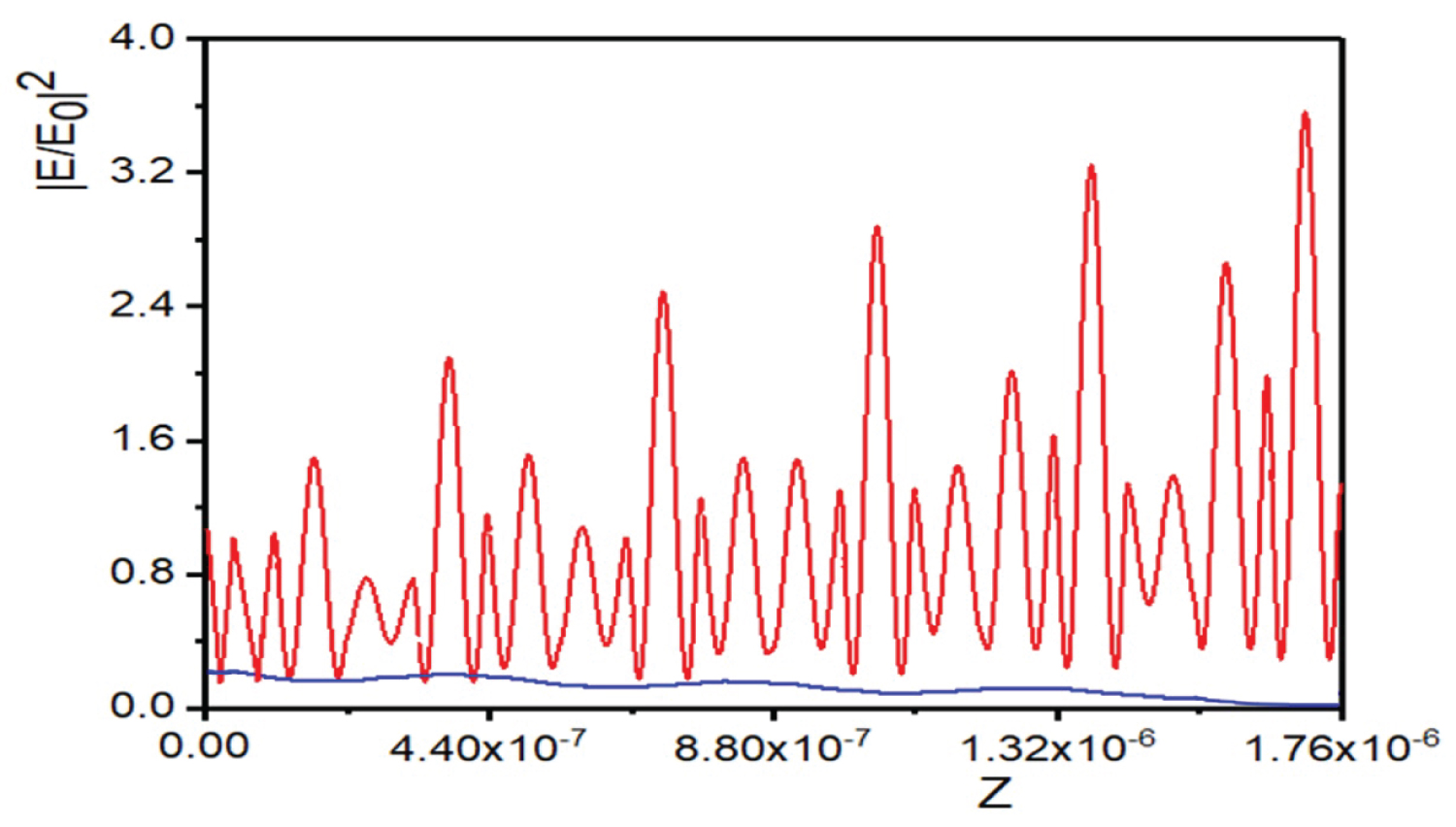
Figure 9: The electric field distribution of the forward...
The electric field distribution of the forward incident (red line) and backward incident (blue line) with .
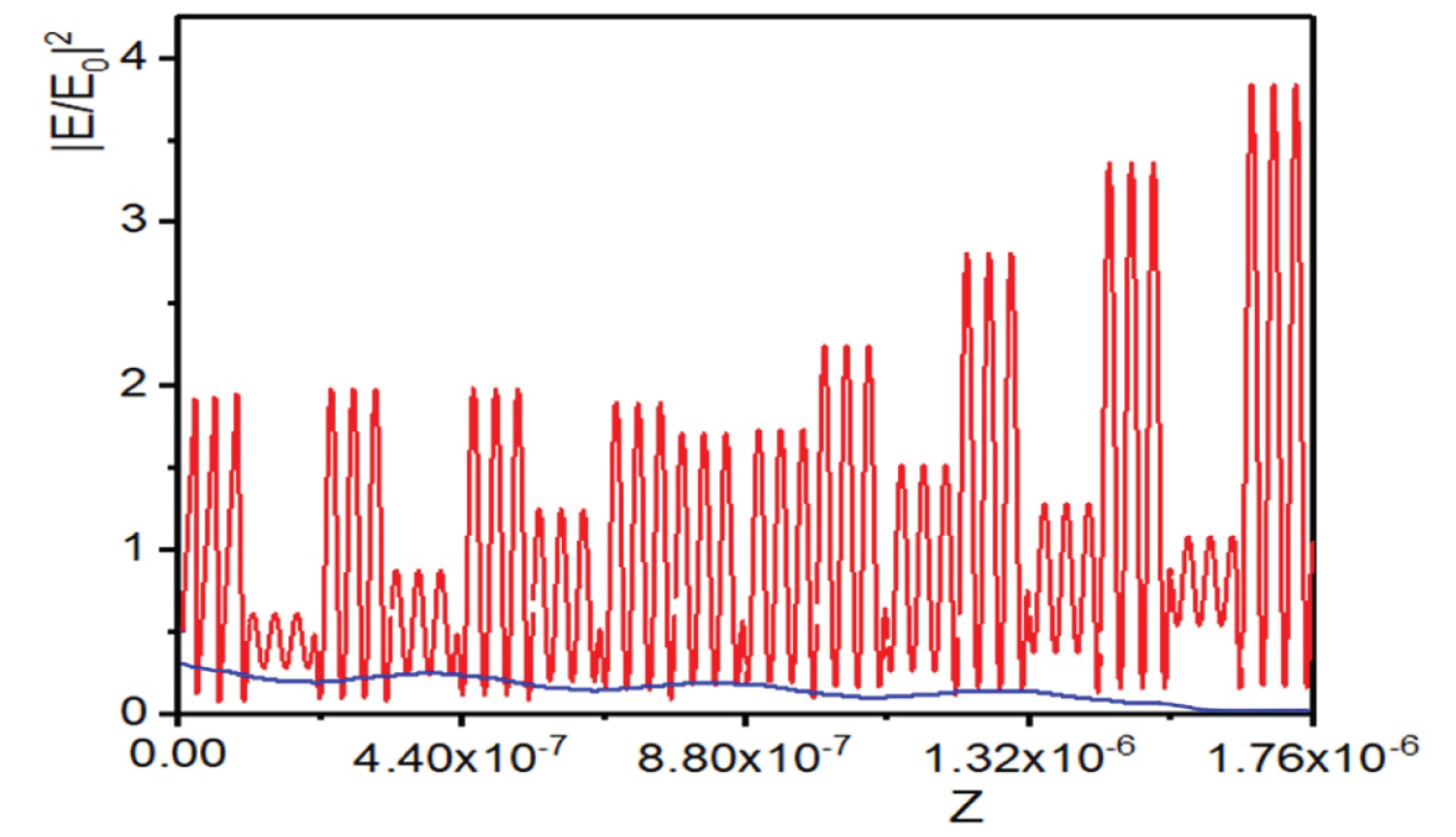
Figure 10: The electric field distribution of the forward...
The electric field distribution of the forward incident (red line) and backward incident (blue line) with .
References
- Bi L, Hu JJ, Jiang P, Kim DH, Dionne GF, et al. (2011) On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nat Photonics 5: 758-762.
- Mingaleev SF, Kivshar YS (2002) Nonlinear transmission and light localization in photonic-crystal waveguides. Opt Soc Am B 19: 2241-2249.
- Hwang J, Song MH, Park B, Nishimura S, Toyooka T, et al. (2005) Electro-tunable optical diode based on photonic bandgap liquid-crystal heterojunctions. Nat Mater 4: 383-387.
- Yu Z, Fan S (2009) Complete optical isolation created by indirect interband photonic transitions. Nat Photonics 3: 91-94.
- Gevorgyan AH (2002) Optical diode based on a highly anisotropic layer of a helical periodic medium subjected to a magnetic field. Tech Phys 47: 1008-1013.
- Kang MS, Butsch A, Russell PSJ (2011) Reconfigurable light-driven opto-acoustic isolators in photonic crystal fibre. Nat Photonics 5: 549-553.
- Shijua E, Bharat M, SijiNarendran NK, Narayana Rao D, Chandrasekharan K (2019) Optical diode activity in an axially asymmetric nonlinear medium incorporated with phenothiazine and silver nanoparticles. Optical Materials 99: 109557.
- Fan L, Wang J, Varghese LT, Shen H, Niu B, et al. (2012) An all-silicon passive optical diode. Science 335: 447-450.
- Mujumdar S, Ramachandran H (2001) Use of a graded gain random amplifier as an optical diode. Opt Lett 26: 929.
- Rostami A (2007) Piecewise linear integrated optical device as an optical isolator using two-port nonlinear ring resonators. Opt Laser Technol 39: 1059-1065.
- Feise MW, Shadrivov IV, Kivshar YS (2005) Bistable diode action in left-handed periodic structures. Phys Rev E Stat Nonlin Soft Matter Phys 71: 037602.
- Tocci MD, Bloemer MJ, Scalora M, Dowling JP, Bowden CM (1995) Thinfilm nonlinear optical diode. Appl Phys Lett 66: 2324.
- Jia X-H (2007) Random fiber laser formed by mixing dispersion compensated fiber and single mode fiber. Opt Soc Am B 24: 2746.
- Lin X-S, Wu W-Q, Zhou H, Zhou K-F, Lan S (2006) Enhancement of unidirectional transmission through the coupling of nonlinear photonic crystal defects. Opt Express 14: 2429-2439.
- Miroshnichenko AE, Pinkevych I, Kivshar YS (2006) All-optical switching in photonic structures with liquidcrystal defects. Opt Express 14: 2839.
- Alexander D, Bruce III J, Zuhlke C, Koch B, Rudebusch R, et al. (2006) Demonstration of a nanoparticle-based optical diode. Opt Lett 31: 1957-1959.
- Gallo K, Assanto G, Parameswaran KR, Fejer MM (2001) All-optical diode in a periodically poled lithium niobate waveguide. Appl Phys Lett 79: 314-316.
- Wang Z, Chong Y, Joannopoulos JD, Soljacic M (2009) Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461: 772-775.
- Lepri S, Casati G (2011) Asymmetric Wave Propagation in Nonlinear Systems. Phys Rev Lett 106: 164101.
- Lira H, Yu Z, Fan S, Lipson M (2012) Electrically driven nonreciprocity induced by interband photonic transition on a silicon chip. Phys Rev Lett 109: 033901.
- Espinola RL, Izuhara T, Tsai MC, Osgood RM, Dotsch H (2004) Magneto-optical nonreciprocal phase shift in garnet/silicon-on-insulator waveguides. Opt Lett 29: 941-943.
- Wu X-Y, Zhang B-J, Yang J-H, Liu X-J, Ba N, et al. (2011) Function photonic crystals. Physica E 43: 1694-1700.
- Wu X-Y, Zhang B-J, Yang J-H, Liu X-J, Ba N, et al. (2012) The characteristic of light transmission of function photonic crystals. Physica E: Low-dimensional Systems and Nanostructures 44: 1223-1229.
- Chot KH, Ling CW, Lee KF, Tsang YH, Fung KH (2016) Simultaneous multi-frequency topological edge modes between one-dimensional photonic crystals. Opt Lett 41: 1644-1647.
- Sedrakian DM, Gevorgyan AH, Khachatrian AZ, Badalian VD (2007) Photonic band gap in 1D Photonic crystals with gradient profifile of pitch and amplitude of modulation. Optics Communications 271: 451-456.
- Harutyunyan EM, Harutyunyan SH, Gevorgyan AH, Movsisyan AH (2009) Optical Properties of Chiral Photonic Crystals with Graded Modulation Parameters. Journal of Contemporary Physics (Armenian Academy of Sciences) 44: 155-160.
- Gevorgyan AH, Harutyunyan EM (2009) Optical properties of chiral photonic crystals with linear profiles of modulation parameters. Optics and Spectroscopy 107: 136-143.
- Gevorgyan AH (2016) Optical diodes and omnidirectional reflectors based on one-dimensional quasiperiodic photonic crystals. Technical Physics Letters 34: 5714-5719.
Author Details
Ming-Li Ren, Meng Han, Xiao-Jing Liu and Xiang-Yao Wu*
Institute of Physics, Jilin Normal University, Siping, China
Corresponding author
Xiang-Yao Wu, Institute of Physics, Jilin Normal University, Siping, 136000, China
Accepted: December 18, 2021 | Published Online: December 20, 2021
Citation: Ming-Li R, Han M, Xiao-Jing L, Xiang-Yao W (2021) Optical Properties of Asymmetric Transmission Devices for One-Dimensional Photonic Crystals. Int J Opt Photonic Eng 6:045
Copyright: © 2021 Ming-Li R, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this paper, we researched the optical properties of asymmetric transmission devices for one-dimensional functions photonic crystals. The refractive indices of media A and B are not constant, it is the functions of space coordinate. By calculated the transmissivity and electric field distribution of asymmetric transmission devices, we found that when the forward incident light can transmit the function photonic crystals, but the backward incident light did not transmit through it, the function photonic crystals can be made into asymmetric transmission devices. Such as optical diodes or optical triode, etc.
Keywords
Function Photonic crystals, Transmissivity, Electric field distribution, Asymmetric transmission
Introduction
Electrical diodes are basic electronic devices and essential building blocks of modern electronics. Such as p-n junction diodes and Schottky diodes. But they have too many limitations. So that we want to overcome the limitations posed by electronic devices, and to satisfy the need for optical elements in integrated photonic circuits, Asymmetric light transmission is essential for fabricating such an all-optics based system. Optical diodes enable asymmetric transmission or one-way transmission of light. So, numerous optical diodes have been manufactured using the magneto-optic effect, the acousto-optic effect, photonic crystals, second harmonic generators, the thermo-optic effect, dynamically modulated ring resonator structures or absorbing multilayer systems [1-7] in the past.
Various optical diodes and optical triodes have been put forward nowadays, such as nonreciprocal reflection transmission in anisotropic media, ring resonators, graded dissipative media and left-handed materials [8-11]. A great deal of attention has been paid to periodic or quasi-periodic systems: Photonic band-gaps with a linear index variation [12,13] photonic crystals with defects [14,15] nanoparticles [16], and quadratic waveguides with quasi-phase matching [17].
There has been rapidly growing interest in optical-diode phenomenon, we can employ magneto-optical materials [1,18] nonlinear media [19] or spatial-temporal modulations of refractive indices [4,20]. All the three approaches could implement an optical diode that can transmit and block any spatial mode in the opposite two directions. It's characterized by cheap, don't need require large magnetic fields and it can be used to miniaturized optical circuits straightforward [21].
An important feature of the photonic crystal is that there are allowed and forbidden ranges of frequencies, and the forbidden frequency range known as photonic band gap (PBG). In Refs. [3-23], we have proposed the function photonic crystals (FPCs), which the medium refractive indices are the function of space position, which can be realized by the electro-optic effect or the optical Kerr effect. On the basis, we have designed the asymmetric transmission devices using one-dimensional FPCs with (AB)N, which the refractive indices of media A and B are not constant [24], but the functions of space coordinate, such as , and . We calculated the distribution of transmissivity and electric field with the forward incident and backward incident of light in one-dimensional FPCs respectively. By calculating, we found the forward incident light can transmit the FPCs, but the backward incident did not transmit it. This is the characteristic of asymmetric transmission devices. The FPCs can be made into asymmetric transmission devices. Such as optical diodes or optical triode, etc.
In Ref. [24-28], they are devoted to one-dimensional quasi periodic photonic crystals (1D-QPCs) with a dielectric permittivity from these four papers. The influence of different parameters on reflection spectrum is studied in detail.
A new type that makes possible the use of broadband optical diodes. It can be realized by using a strong light or ultrasound field in an absorbing medium occurring in a temperature gradient on electric field. They can used to design broadband mirrors, omni-directional reflectors, optical diodes, compressors of optical signals, etc.
For the convention photonic crystals, the refractive indices of media A and B are constant, because its transmissivity and electric field distribution are the same for the forward incident and backward incident, it does not have the characteristic of asymmetric transmission devices.
The Transfer Matrix and Transmissivity of One-Dimensional Function Photonic Crystals (Fpcs)
The period (Λ) of a unit cell is given by [24], where and are the thickness of a single dielectric layer of a and . In this Letter, the optical path length of each unit cell is specified by Eq. (1).
Where and are the refractive indices of the non-dispersive dielectric layer a and b. And is the ratio of optical path length of a unit cell to its period. For the sake of simplicity, we first assume the refractive indices of glass is , and every dielectric medium has negligible dispersion effect and magnetic response. Layer is considered as the "reference" medium because its dielectric property will always remain unchanged in all of our simulations. As an example, we set , and which gives . Using the arguments above, the parameters of refractive indices can be generated at every zone-center gap by choosing some refractive indexes such that and .
In the following, we have given the transfer matrices of media A and B, they are
Where the Angle of incident and refraction from interface B to interface A are and , the Angles of incident and refraction from interface A to interface B were and .
While
And
Where is air refractive indices, and , we can calculate . The Angle of incident from interface A to interface B is .
In one period, the transfer matrix M is
The asymmetric transmission devices model was shown in Figure 1, the light forward incident (red arrow) and backward incident (blue arrow) to the FPCs. In the following, we give the electric field distribution at position z of light in the one-dimensional FPCs, it is shown in Figure 2.
The form of the FPCs transfer matrix M is more complex than the conventional PCs. The characteristic equation of FPCs is
Where, N is the period number. With the transfer matrix M, we can obtain the transmission and reflection coefficient t and r, and the transmissivity and reflectivity T and R, they are
and
Where, , and are incident and reflection electric fields, and
Where and are the thickness of B and A medium, respectively, and are the electric field and magnetic field, when position z changes we can obtain the electric field and magnetic field inmedia. The and are the output electric field and magnetic field. From Eq. 17, we get
and then
Numerical Result
In this section, we report our numerical results of transmissivity and electric field distribution. The refractive indices of media A and B are the linearity functions as space coordinates, they are
The Figure 3 are the line refractive indices figures of media and , the , , and are the endpoint values of refractive indices. The main parameters are: the thickness of media B and A are = 260 nm and = 150 nm. For the forward incident, the endpoints of media B and A are , and , , it is shown in Figure 3a. For the backward incident, the endpoints of media A and B are , and , , it is shown in Figure 3b. The center frequency , corresponding to center wavelength, and the structure of FPCs is .
By calculation, we can obtain the transmissivity of the one-dimensional FPCs for the forward and backward incident of light. We found that when the light backward incident to the one-dimensional FPCs, the broadening of the photonic forbidden band gap takes place. The forward incident (red line) figure and the backward incident (blue line) figure have been shown in Figure 4 and Figure 5.
In the range of = 0.9196 ~1.349 and 2.269 ~2.574 the forward incident light can transmit the one-dimensional FPCs, but the backward incident light cannot transmit the medium, because the backward incident light is in the forbidden band. In the range of = 0.5402 ~0.8759, 1.994 ~2.26 and 2.733 ~3.016 the backward incident light can transmit the one-dimensional FPCs, but the forward incident light did not transmit the medium, because the forward incident light is in the forbidden band. In the range of = 0.1488 ~0.542, 1.536 ~1.994 and 2.574 ~2.733 the forward incident light can transmit the one-dimensional FPCs, and the backward incident light also can transmit the medium, because they are both in the transmission band. In the range of = 0 ~0.0718 and 1.349 ~1.49 the forward incident light did not transmit the one-dimensional FPCs, and the backward incident light also did not be transmitted, because they are both in the forbidden band. It embodies the optical properties of asymmetric transmission devices for one-dimensional photonic crystals. They are shown in Figure 6 and Figure 7. The similar characteristics also apply to wave lengths in Figure 8. The asymmetric profiles of parameters in these systems results in the appearance of non reciprocity of a new type that makes possible their use as the ideal, optical diodes.
In addition, we also calculated the distribution of electric field to study the connection between the connection between the conduction band and the forbidden band. In the forbidden bands of backward incident, we have chosen the frequency and from the range of frequency = 0.9196 ~1.349 and 2.269 ~2.574 respectively. And we have obtained the distribution of electric field for forward incident (red line) and backward incident (blue line), they are shown in Figure 9 and Figure 10. We can find that the forward incident light can be transmitted to the medium, but the backward incident light did not be transmitted to it, i.e., the light can only be transmitted one way in the one-dimensional FPCs, which can be made into one-dimensional optical diodes or bidirectional diodes. For each wavelength, the electric field distribution of the forward has many times different number of oscillations, because we choose different , the higher the frequency, the more oscillations. The field distribution in Figure 9 and Figure 10 for the opposite direction is almost identical, because the backward incident was in a forbidden band, the electric field is attenuate to quickly and there was no periodic change, the change is so small that it is barely noticeable.
Conclusion
In summary, we have theoretically investigated the function photonic crystals (FPCs), which there fractive indices of media are the functions of space position. We have chosen the line refractive indices functions for two media A and B. By calculation the transmissivity and electric field distribution, we find that the optical property of the one-dimensional FPCs is not only one-way transmission, but also two-way transmission. It can be made into asymmetric transmission devices. Such as optical diodes or optical triode, etc.
Back Matter
Funding
Thanks to Research Innovation of Jilin Normal University (Grant N. 201937) and Doctoral research project of Jilin Normal University (Grant N. 2017005) for the funding support.
Disclosures
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability
No data were generated or analyzed in the presented research.

