
International Journal of Signal Processing and Analysis
(ISSN: 2631-5025)
Volume 2, Issue 1
Research Article
DOI: 10.35840/2631-5114/3502
A Novel Color Image Enhancement Method by the Transformation of Color Images to 2-D Grayscale Images
Artyom M Grigoryan1, Aparna John1* and Sos S Agaian2
Table of Content
Figures

Figure 1: a) Original image...
a) Original image "flower.tif"; b) 2-D grayscale image of (a) by 2 × 2 transformation model; c) Alpha-rooting of 2-D grayscale image in (b); d) RGB color image after converting back to color the image in (c); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 2: a) Original Image "flower.tif";...
a) Original Image "flower.tif"; b) 2-D grayscale image of (a) by 2 × 3 Transformation model; c) Alpha-Rooting of 2-D grayscale image in (b); d) RGB color image after converting back to color the image in (c); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 3: a) Original image "flower.tif"; b)...
a) Original image "flower.tif"; b) 2-D grayscale image of (a) by the column transformation model; c) Alpha-rooting of 2-D grayscale image in (b); d) RGB color image after converting back to color the image in (c); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 4: a) Original image...
a) Original image "flower.tif"; b) 2-D grayscale image of (a) by the row transformation model; c) Alpha-rooting of 2-D grayscale image in (b); d) RGB color image after converting back to color the image in (c); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 5: a) Original Image "crane.jpg";...
a) Original Image "crane.jpg"; b) 2-D grayscale image of (a) by 2 × 2 Transformation model; c) Alpha-Rooting of 2-D grayscale image in (b); d) RGB color image after converting back to color the image in (c); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 6: a) Original Image "crane.jpg";...
a) Original Image "crane.jpg"; b) 2-D grayscale image of (a) by 2 × 3 Transformation model; c) Alpha-Rooting of 2-D grayscale image in (b); d) RGB color image after converting back to color the image in (c); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 7: a) Original Image "crane.jpg";...
a) Original Image "crane.jpg"; b) 2-D grayscale image of (a) by column Transformation model; c) Alpha-Rooting of 2-D grayscale image in (b); d) RGB color image after converting back to color the image in (c); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 8: a) Original image "crane.jpg";...
a) Original image "crane.jpg"; b) RGB color image after converting back to color the image in (c); c) 2-D grayscale image of (a) by row transformation model; d) Alpha-rooting of 2-D grayscale image in (b); e) 2-D DFT of image in (b); f) Center-shifted 2-D DFT in (e).

Figure 9: a) Original image "flower.tif";...
a) Original image "flower.tif"; b) 2-D Grayscale image transformed by 2 × 2 model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.

Figure 10: a) Original Image "flower.tif";...
a) Original Image "flower.tif"; b) 2-D Grayscale image transformed by 2 × 3 model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.

Figure 11: a) Original Image "flower.tif";...
a) Original Image "flower.tif"; b) 2-D Grayscale image transformed by column model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.

Figure 12: a) Original Image "flower.tif";...
a) Original Image "flower.tif"; b) 2-D Grayscale image transformed by row model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.
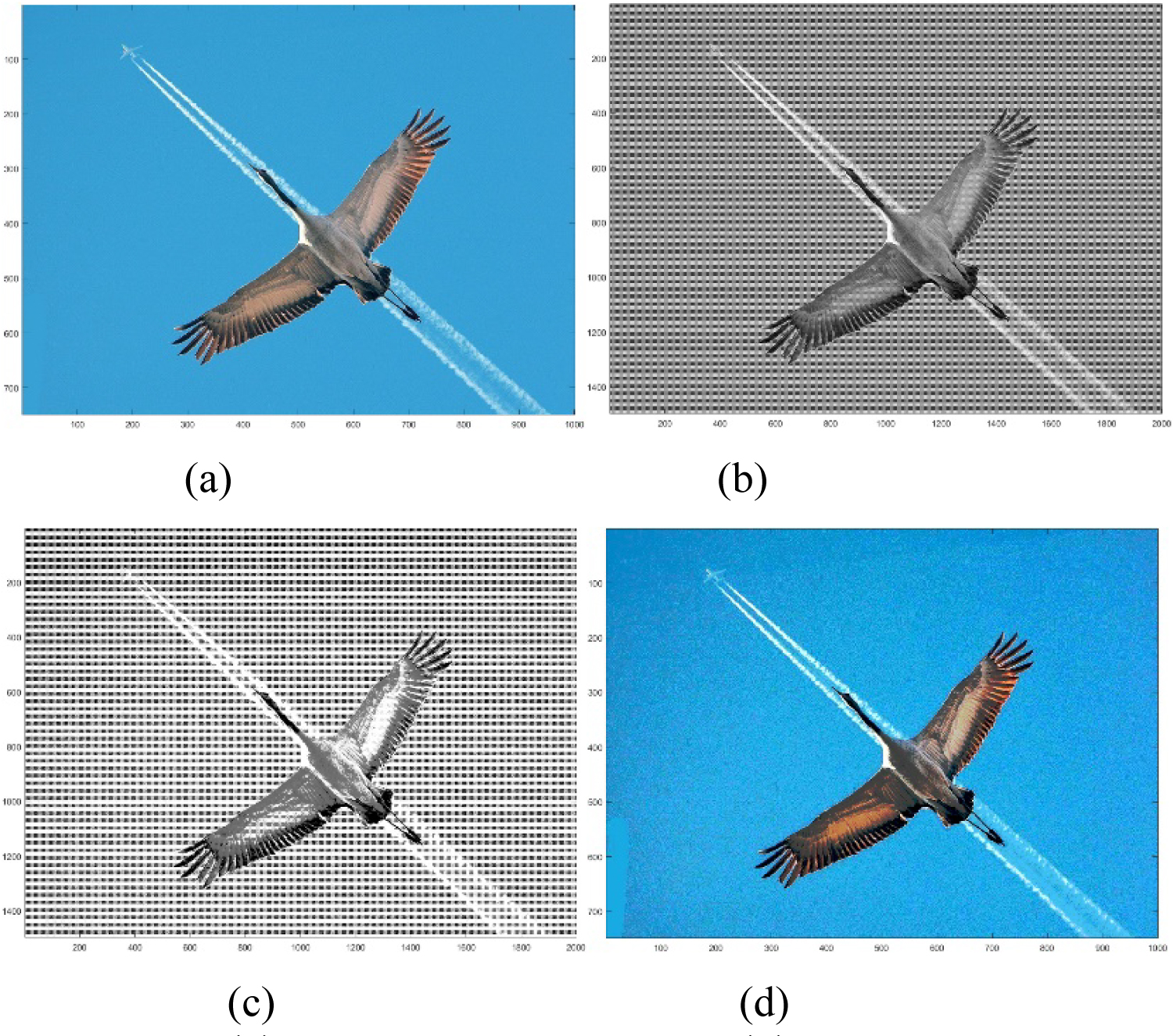
Figure 13: a) Original Image "crane.jpg";...
a) Original Image "crane.jpg"; b) 2-D Grayscale image transformed by 2 × 2 model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.

Figure 14: a) Original Image "crane.jpg";...
a) Original Image "crane.jpg"; b) 2-D Grayscale image transformed by 2 × 3 model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.
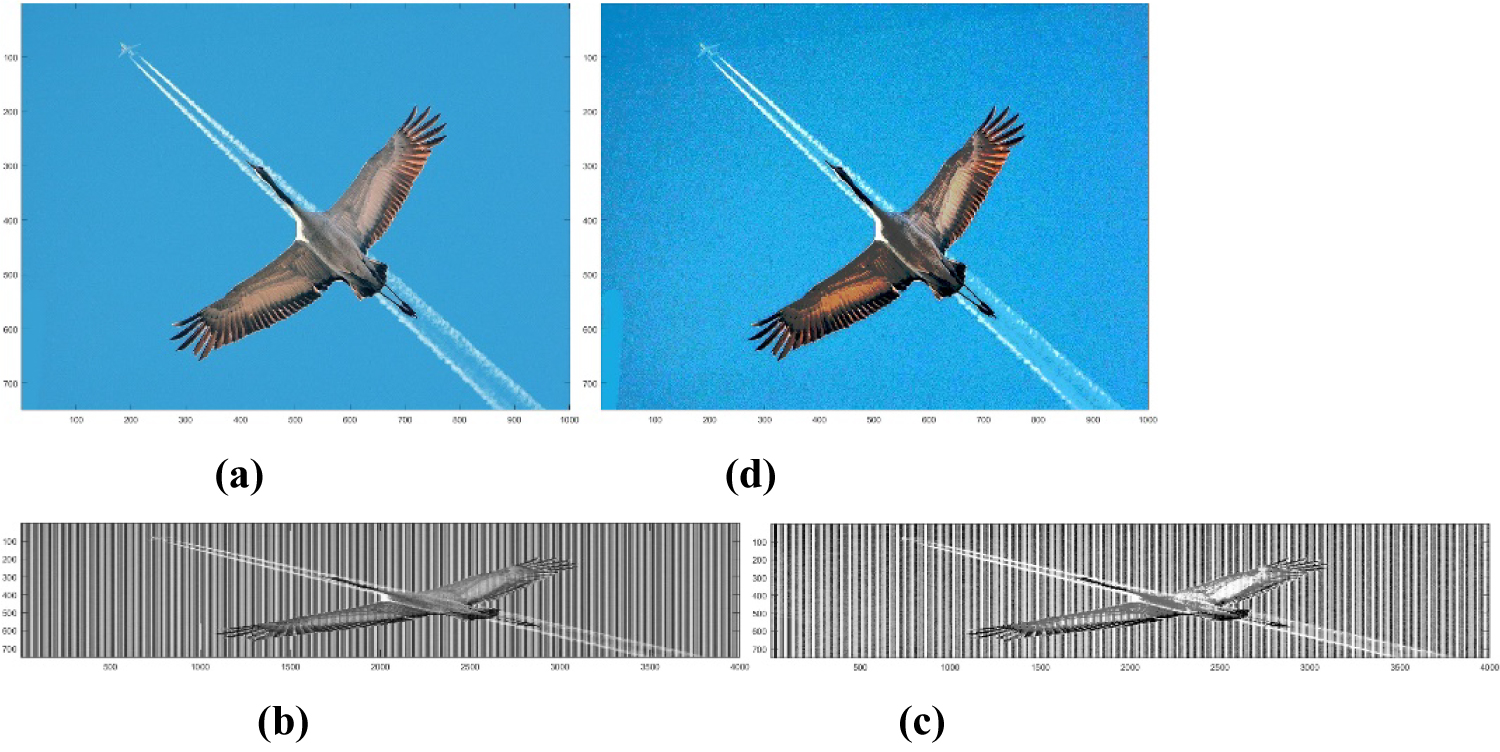
Figure 15: a) Original Image "crane.jpg";...
a) Original Image "crane.jpg"; b) 2-D Grayscale image transformed by column model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.

Figure 16: a) Original Image "crane.jpg";...
a) Original Image "crane.jpg"; b) 2-D Grayscale image transformed by row model; c) Histogram equalized 2-D grayscale image in (b); d) RGB color image after converting the 2-D grayscale image in (c) to color image.

Figure 17: a) Original Image "tree.tiff";...
a) Original Image "tree.tiff"; b) Alpha-rooting (alpha = 0.98) on 2-D Grayscale transformed image by 2 × 3 model of RGB image; c) Alpha-rooting (alpha = 0.97) on 2-D Grayscale transformed image by 2 × 3 model of XYZ model of image in (a); d) Alpha-rooting (alpha = 0.99) on 2-D Grayscale transformed image by 2 × 3 model of CMY model of image in (a); e) Alpha-rooting (alpha = 0.96) is done on Y component of YUV model of image in (a).

Figure 18: a) Original Image "tree.tiff";...
a) Original Image "tree.tiff"; b) Histogram Equalization on 2-D Grayscale transformed image by 2 × 3 model of RGB image; c) Histogram Equalization on 2-D Grayscale transformed image by 2 × 3 model of XYZ model of image in (a); d) Histogram Equalization on 2-D Grayscale transformed image by 2 × 3 model of CMY model of image in (a); e) Histogram Equalization is done on Y component of YUV model of image in (a).
Tables
Table 1: Alpha, EME and CEME values of alpha-rooting method on "flower.tif".
Table 2: Alpha, EME and CEME values of alpha-rooting method on "crane.jpg".
Table 3: EME and CEME values of histogram equalization of "flower.tif".
Table 4: EME and CEME values of histogram equalization of "crane.jpg".
Table 5: CEME values of original and enhanced image of "tree.tiff".
References
- M Grigoryan, SS Agaian (2016) 2-D Left-side quaternion discrete fourier transform: Fast algorithm. Electronic Imaging 1-8.
- AM Grigoryan, SS Again (2015) Tensor representation of color images and fast 2-D quaternion discrete Fourier transform. Image Processing, Algorithms and Systems XIII 9399.
- AM Grigoryan, MM Grigoryan (2009) Brief notes in advanced DSP: Fourier analysis with MATLAB. CRC Press Taylor and Francis Group.
- AM Grigoryan, SS Agaian (2014) Retooling of color imaging in the quaternion algebra. Applied Mathematics and Sciences: An International Journal 1: 23-39.
- TA Ell, N Bihan, SJ Sangwine (2014) Quaternion fourier transforms for signal and image processing. Wiley NJ and ISTE UK.
- WR Hamilton (1886) Elements of Quaternions. Logmans, Green and Co., London.
- TA Ell (1993) Quaternion-fourier transforms for analysis of 2-dimensional linear time-invariant partial differential systems. Proceedings of the 3rd IEEE Conference on Decision and Control 1: 1830-1841.
- SJ Sangwine (1996) Fourier transforms of colour images using quaternion, or hypercomplex, numbers. Electronics Letters 32: 1979-1980.
- SJ Sangwine (1997) The discrete quaternion-fourier transform. IPA97, Conference Publication, 443: 790-793.
- SJ Sangwine, TA Ell, JM Blackledge, MJ Turner (2000) The discrete fourier transform of a color image. In: Proc. Image Processing II Mathematical Methods, Algorithms and Applications. 430-441.
- SJ Sangwine, TA Ell (2001) Hypercomplex Fourier transforms of color images. Proc IEEE Intl Conf Image Process 16: 137-140.
- AM Grigoryan, SS Agaian (2014) Alpha-rooting method of color image enhancement by discrete quaternion Fourier transform. Proc SPIE, Image Processing: Algorithms and Systems XII 9019: 12.
- AM Grigoryan, SS Agaian (2016) Color enhancement and correction for camera cell phone medical images using quaternion tools. In: J Tang, SS Agaian, J Tan, Electronic Imaging Applications in Mobile Healthcare. SPIE Press, Bellingham, Washington, 77-117.
- AM Grigoryan, SS Agaian (2017) Alpha-Rooting method of gray-scale image enhancement in the quaternion frequency domain. Proceedings of IS&T International Symposium, Electronic Imaging: Algorithms and Systems XV, 29 Burlingame.
- AM Grigoryan, A John, SS Agaian (2017) Color image enhancement of medical images using alpha-rooting and zonal alpha-rooting methods on 2-D QDFT. Proceedings of SPIE Medical Imaging Symposium, Image Perception, Observer Performance, and Technology Assessment, 1-9.
- AM Grigoryan, A John, S Agaian (2016) Zonal-alpha-rooting color image enhancement by the two-side 2D quaternion discrete Fourier transform. Proceedings of IS&T International Symposium, Electronic Imaging: Algorithms and Systems XIV, San Francisco, California.
- AM Grigoryan, SS Agaian (2016) 2-D Left-side quaternion discrete Fourier transform fast algorithms. Proceedings of IS&T International Symposium, Electronic Imaging: Algorithms and Systems XIV, SanFrancisco, California.
- AM Grigoryan, SS Agaian (2017) Image processing contrast enhancement. Wiley Encyclopedia of Electrical and Electronics Engineering.
- M Grigoryan, A John, SS Agaian (2017) Modified alpha-rooting color image enhancement method on the two-side 2-D quaternion discrete fourier transform and the 2-D discrete fourier transform. Applied Mathematics and Sciences: An International Journal (MathSJ ) 4: 1-2.
- AM Grigoryan, SS Agaian (2016) Systems and Methods for Fast Quaternion Convolution with multimedia. US Patent Application, Attorney Docket Number 292007-8240.
- JH McClellan (1980) Artifacts in alpha-rooting of images. Proc. IEEE Int. Conf. Acoustics, Speech, and Signal Processing, 449-452.
- FT Arslan, AM Grigoryan (2006) Fast splitting alpha-rooting method of image enhancement: Tensor representation. IEEE Trans on Image Process 15: 3375-3384.
- AM Grigoryan, SS Again, AM Gonzales (2015) Fast Fourier transform-based retinex and alpha-rooting color image enhancement," [9497-29]. Proc. SPIE Conf., Mobile Multimedia/Image Processing, Security, and Applications, Baltimore, Maryland United States.
- AM Grigoryan, J Jenkinson, SS Agaian (2015) Quaternion fourier transform based alpha-rooting method for color image measurement and enhancement. Signal Processing 109: 269-289.
- SS Agaian, K Panetta, AM Grigoryan (2000) A new measure of image enhancement.
- AM Grigoryan, SS Agaian (2004) Transform-based image enhancement algorithms with performance measure. Advances in Imaging and Electron Physics 130: 165-242.
- AM Grigoryan, SS Agaian (2015) Optimal color image restoration: Wiener filter and quaternion Fourier transform. Proceedings of SPIE 9411.
- SS Agaian, K Panetta, AM Grigoryan (2001) Transform-based image enhancement algorithms. IEEE Trans on Image Processing 10: 367-382.
Author Details
Artyom M Grigoryan1, Aparna John1* and Sos S Agaian2
1Department of Electrical and Computer Engineering, The University of Texas at San Antonio, USA
2City University of New York, USA
Corresponding author
Aparna John, Department of Electrical and Computer Engineering, The University of Texas at San Antonio, One UTSA Circle, San Antonio, TX-78249, USA, E-mail: aparna.john@utsa.edu
Accepted: December 11, 2017 | Published Online: December 13, 2017
Citation: Grigoryan AM, John A, Agaian SS (2017) A Novel Color Image Enhancement Method by the Transformation of Color Images to 2-D Grayscale Images. Int J Signal Process Anal 2:002 .
Copyright: © 2017 Grigoryan AM, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
A novel method of color image enhancement is proposed, in which three or four color channels of the image are transformed to one channel 2-D grayscale image. This paper describes different models of such transformations in the RGB and other color models. Color image enhancement is achieved by enhancing first the transformed grayscale image and, then, transforming back the grayscale image into the colors. The color image enhancement is done on the transformed 2-D grayscale image rather than on the color image. New algorithms of color image enhancement are described in both frequency and time domains. The enhancement by this novel method shows good enhancement results. The enhancement of the image is measured with respect to a metric referred as the Color Enhancement Measure Estimation (CEME).
Introduction
A typical color image consists of three channels with each channel consisting of the image corresponding to the intensity values of particular color. In other words, color of the image is decomposed to color components and image corresponding to each of the color components are composed together to form a color image. Usually the image processing of the color image is done considering images in each channel as separate. In one of the most popular color image processing methods, the processing is done on each channel separately and the final enhanced image is composed by these enhanced channels. That is, image processing is done channel by channel. Another method of color image processing is based on the quaternion approach of color image processing [1-11]. In the quaternion approach, the color image is considered as the quaternion image and the three channels in the color image considered as the components in the quaternion number [12-19]. In both these methods, processing is done on three channels of image, or on the 3-D images. We are proposing a novel color image enhancement method in which all the image processing is done on 2-D grayscale image. In our method, the color image is transformed first to the 2-D grayscale image and image processing is done on 2-D grayscale image. This paper describes transformation of color image to 2-D grayscale image by a few proposed transformation models like 2 × 2, 2 × 3, column and row transformation models. The image enhancement effects by frequency domain enhancement method such as the alpha-rooting method and spatial domain enhancement method by the histogram equalization by the novel method is studied.
Transformation Models
In the novel method of color image enhancement, color images are transformed to 2-D grayscale images and the enhancement algorithms, which work well in 2-D grayscale images, can be used in the newly transformed 2-D grayscale-color image [20]. This color image enhancement mainly consists of the transformation of the color image to the 2-D grayscale image. There are many different models which can be considered for this transformation. A few of these transformation models are the 2 × 2 model, 2 × 3 model, column model and row model. First, we describe the 2 × 2 model of color-to-gray transformation for RGB color image. There are three channels of RGB image R, G, and B, and the luminous of this RGB image is obtained by the relation.
In the 2 × 2 model, the new transformed 2-D grayscale image is obtained by arranging side by side the pixel values of I, R, G, and B of each pixel. For instance the table below depicts one of the ways the 2 × 2 model is obtained.
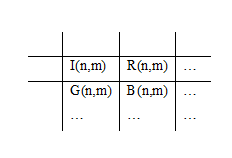
Therefore, the image of size M × N × 3 is transformed to (2M) × (2N) 2-D grayscale image.
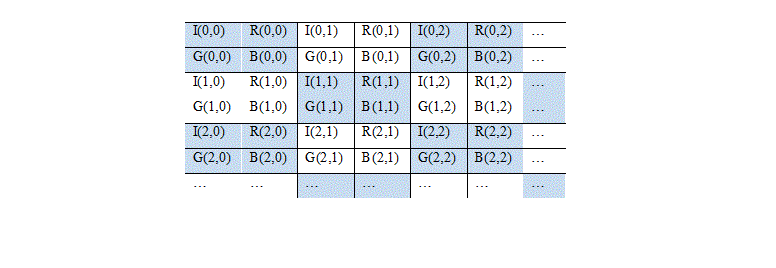
The 2 × 3 model is another transformation model, in which the R, G, and B are arranged in such a way that a single unit so formed is a 2 × 3 in size. There are many different ways to arrange R, G, and B pixel values. One of the many different possibilities is as depicted below in the table.
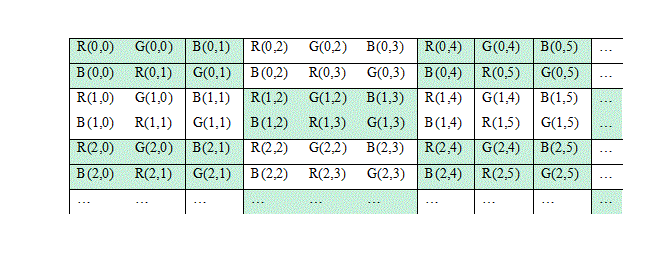
The color image of size M × N × 3 is transformed to a 2-D grayscale image of size (2M) × (3N/2).
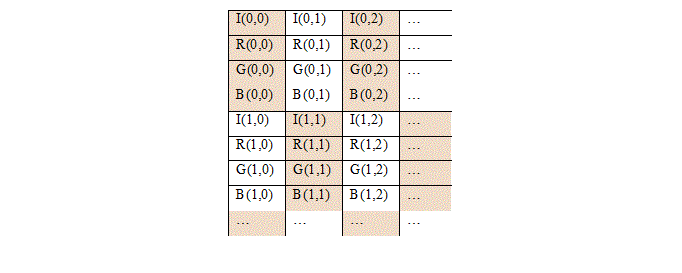
The table above depicts the row model and in a row model the color image of size M × N × 3 together with the luminous component I is transformed to a 2-D grayscale image of size (4M) × N. We can also opt out the luminous component in the new model. Then the new transformed image is of size (3M) × N.
And the column model of transformation is as depicted in table below. The color image of size M × N × 3 together with the luminous component I is transformed to an image of size M × (4N). It is optional to include the luminous component I in the new transformed model.

Enhancement Methods
Alpha-rooting method
In the alpha-rooting method of image enhancement [14,16,21-24], for each frequency point (p,s), the magnitude of the discrete transform are transformed as
Histogram equalization of color images
The histogram is an important concept in imaging, which gives the number (cardinality) of pixels of the image with the given level of intensity r. For the image fn,m of size M × N, the histogram is a non-negative function.
The histogram is normalized, h(r) = h(r)/(MN) so that 0 < h(r) < 1. In the method of histogram equalization, a monotonic increasing gray-scale transformation w is used to straighten the curve of the histogram.
It is assumed that the value of the image as random number r from the interval [fmin, fmax] is transformed to the random value s which is approximately uniformly distributed in the interval [wmin, wmax] = [w(fmin), w( fmax)]. This monotonic transformation w is calculated as
Where F(r) is the distribution function of the intensity and is calculated as
and F(r) = 0 when r < fmin. In the case when [wmin, wmax] = [0, 255], the histogram equalization is calculated by the transformation
Enhancement Measure Estimation (EME)
The Enhancement Measure Estimation (EME) for grayscale images, is an enhancement measure [25-28] based on the contrast of the images in one channel 2D image or grayscale image. The proposed enhancement measure is a modification of Weber's law which basically explains that the visual perception of the contrast is independent of luminance and low spatial frequency. The metric EME relates to the Weber's law that states that the perceived change in stimulus proportional to initial stimuli, and the Fechner's law, which states that the perception and stimulus are logarithmically related. That is, the visually perceived intensity value is proportional to the logarithm of the actual intensity. To calculate the EME value, the 2-D discrete image of size N × M is divided by k1k2 blocks of size L1 × L2 blocks each, where kn = [Nn/Ln], for n = 1, 2. When an image is enhanced,
Where f and , referring to the original and enhanced image respectively, the EME value of enhanced image is calculated by
And, EME of the original image is obtained by replacing in Eq. 9 by f.
Color Enhancement Measure Estimation (CEME)
The Color Enhancement Measure Estimation (CEME), is an enhancement measure [25-28] is equivalent of EME measure but CEME metric is the measure of visual perception of color images. To calculate the CEME value, the 2-D discrete image of size N × M is divided [12] by k1k2 blocks of size L1 × L2 blocks each, where kn = [Nn/Ln], for n = 1, 2. When the original image f is enhanced to ,
The CEME value of the enhanced color image is calculated by
Here, fR, fG, fB and , refer respectively to R, G, and B channel of the original and enhanced image. In our experiment, are the enhanced color channels that are obtained by reconverting back the enhanced 2-D grayscale image. And, the CEME of the original image is similar to Eq. 11 but replaced by f.
Experimental Results
A few image results of the enhancement by the novel method is shown below. The enhancement in the frequency domain by the alpha-rooting method and the enhancement in the spatial domain by the histogram equalization show good enhancement of images. Figure 1 shows the original image "flower.tif" and the transformation of the color image to 2-D grayscale image by the 2 × 2 transformation model (Figure 1a and Figure 1b). The alpha-rooting method is applied onto the transformed 2-D grayscale image and then converted back to the color image (Figure 1c and Figure 1d). The optimum value of alpha chosen for the enhancement is the alpha that gives a maximum CEME value for the enhanced color image. For "flower.tif" image, the alpha value is 0.97. The EME value of the 2-D grayscale image after transforming by 2 × 2 transformation model and after doing alpha-rooting method is tabulated in Table 1. The CEME value of the image after converting back to the color image is higher than the CEME value of the original image. Figure 1e and Figure 1f shows the 2-D DFT and the center-shifter 2-D DFT of the image in Figure 1b respectively. The periodicity in the row and column in 2-D DFT is seen based on the 2 × 2 model.
Figure 2 shows the results of the transformation of the color image by 2 × 3 transformation model. Figure 2a and Figure 2b show the original image and its transformation to 2-D grayscale image by the 2 × 3 models. Figure 2c shows the image after performing alpha-rooting method of enhancement. The optimum choice of alpha in this case is also 0.97 and at alpha equals 0.97 the CEME value of the color image is maximum. Figure 2d shows the color image after converting back the 2-D grayscale image after performing alpha-rooting method. Figure 2e and Figure 2f shows the 2-D DFT and the center-shifted 2-D DFT of the transformed grayscale image shown in part 2b.
Figure 3 shows the results of alpha-rooting method of color image when transformed by the column model. The alpha value chosen in this method is 0.97. The 2-D DFT and center-shifted 2-D DFT show a periodicity in the column. Figure 4 shows image results after the color image is transformed by the row model. The alpha values chosen in alpha-rooting method in each transformation model and the respective EME and CEME value of the images are tabulated in Table 1.
In Table 1, we see that the best alpha value for alpha-rooting of "flower.tif" is 0.97, irrespective of the transformation model used for transforming the color image to the 2-D grayscale image. The CEME value of the enhanced color image is higher than the CEME value of the original image which is 28.7506. The CEME value of the enhanced color image is almost the same for all four different models of transformation. The EME value of the 2-D grayscale image of the enhanced image is also higher than the EME of the transformed 2-D grayscale image of the original image. The EME value also show almost nearby values for all transformation models.
Figure 5 is the image results of the alpha-rooting method of the original image "crane.jpg" (Figure 5a) after transforming the color image to 2-D grayscale image by 2 × 2 model. (Figure 5b and Figure 5c) shows respectively the 2-D grayscale image of the original image and after enhancing by alpha-rooting method with alpha equals 0.88. When alpha equals 0.88, the CEME value is maximum for the color image obtained after converting back the enhanced 2-D grayscale image. Figure 5d shows the final enhanced color image. Figure 5e and Figure 5f shows the 2-D DFT and the center-shifted 2-D DFT of the 2-D grayscale image in Figure 5b. Since the transformation model chosen is 2 × 2, the 2-D DFT shows a periodicity in the row and column direction similar to the spatial domain transformation of the 2-D grayscale image.
Figure 6 shows the image results of the original image "crane.jpg" after transforming the color image by 2 × 3 model. Figure 6a shows the 2-D grayscale image after transforming by the 2 × 3 model. When the transformed image in Figure 6b is enhanced by the alpha-rooting method, the enhancement of the image is as shown in Figure 6c. The optimum alpha value for the alpha-rooting method is 0.88. Figure 6d shows the color image after converting back the enhanced 2-D grayscale image in Figure 6c. When alpha equals 0.88 the color image in Figure 6d gives the maximum CEME value. Figure 6e and Figure 6f shows respectively the 2-D DFT and centershifted 2-D DFT of the image in Figure 6b. The Fourier transform shows a periodicity in the 2 × 3 model in the row and column direction.
In Figure 7, the original image "crane.jpg" (Figure 7a) is transformed by the column model to the corresponding 2-D grayscale image. Figure 7b shows that the image is four times wider in the column direction as compared to the column width of the original image while the row size of the transformed image remains same as the original image. The transformed 2-D grayscale image in Figure 7b is enhanced by the alpha-rooting method with the best alpha which is 0.88 and the enhanced image is shown in Figure 7c. The enhanced color image is shown in Figure 7d. The 2-D DFT and the center-shifted 2-D DFT in (Figure 7e and Figure 7f) show a periodicity in the column direction.
Figure 8 shows enhancement results after transforming the color image (Figure 8a) to 2-D grayscale image by row method. The row size of the transformed grayscale image (Figure 8b) is four times the row size of the original image while the column size is same for both original image and transformed grayscale image. Figure 8c is the enhanced 2-D grayscale image after performing alpha-rooting method with alpha equals 0.88. The 2-D DFT and the centershifted 2-D DFT shown in Figure 8e and Figure 8f shows a periodicity in the row direction.
In Table 2, we can see that the alpha value chosen for the alpha-rooting method is the same in all transformation models. The CEME of the color image after enhancing by the novel transformation method is higher than the CEME value of the original image (CEME = 28.7627). The CEME value of the obtained by all transformation models has values close to 46. The EME value of the 2-D grayscale transformed image has value close to 27 and EME of the enhanced grayscale image by the alpha-rooting method has value in the range 42-44 for all models.
The figures that follow show the image results by the spatial transformation by histogram equalization after transforming the color image by different transformation models. In Figure 9, the original image "flower.tif" (Figure 9a) is first transformed to the 2-D grayscale image by the 2 × 2 model (Figure 9b) and the histogram equalization is calculated on the 2-D grayscale image; the result is shown in Figure 9c. Figure 9d shows the final color image after converting back the histogram equalized grayscale image in Figure 9c.
Figure 10 is the enhancement result after the color image is transformed to 2 × 3 model 2-D grayscale image. Figure 10b and Figure 10c are respectively the 2 × 2 model 2-D grayscale image of the original image in Figure 10a, and the histogram equalized image in Figure 10b. After enhancing the transformed 2-D grayscale image by histogram equalization, it is converted back to color image and the result is shown in Figure 10d.
Figure 11 shows results of column model transformation (Figure 11b) of the original color image (Figure 11a). After transforming to the column model 2-D grayscale image, the histogram equalization is calculated on the image; the enhanced grayscale image is as shown in Figure 11c and the corresponding color image in Figure 11d.
Figure 12 shows the row transformed 2-D grayscale image (Figure 12b) of the orignal image (Figure 12a). The image processing is done on the transformed grayscale image and the histogram equalized grayscale image is shown in Figure 12c and the corresponding color image in Figure 12c is shown in Figure 12d.
Table 3 shows that the CEME value of the histogram equalized color image is slightly higher than the CEME of the original image. The CEME value of the 2 × 2 column and row model are exactly the same value. But the CEME value of the 2 × 3 model is slightly different but close to the other CEME values. EME value of the histogram equalized grayscale image is slightly higher than the transformed 2-D grayscale image of the original image. But the EME value of the histogram equalized grayscale image is different for the transformation done by different models.
In Figure 13, the original image "crane.jpg" (Figure 13a) is first transformed to 2-D grayscale image by 2 × 2 model (Figure 13b). Then, the histogram equalization is done on the transformed grayscale image and is shown in Figure 13c. Figure 13d is the color image of the histogram equalized image in Figure 13c.
Figure 14 shows the image after transforming the image "crane.jpg" in (Figure 14a) by 2 × 3 model (Figure 14b). The enhancement algorithm of histogram equalization is done on the transformed grayscale image and the enhanced grayscale image is shown in Figure 14c. This image converted back to the color image and is shown in Figure 14d.
Figure 15 and Figure 16 are respectively the image results after transforming the original color imageby column transformation model and row transformation model. The transformed image of the original image in Figure 15a and Figure 16a is shown respectively in Figure 15b and Figure 16b. The histogram equalized grayscale image is shown in Figure 15c and Figure 16c. The enhancement effects by histogram equalization on color image is shown in Figure 15d and Figure 16d.
Table 4 shows that the CEME value of enhanced color image is much higher than the CEME value of the original image. In this case also, CEME value of enhanced color image by 2 × 2, column and row model are exactly the same and the CEME value of 2 × 3 model is slightly different but close to the rest of CEME values. The EME value of the enhanced grayscale image is also higher than the corresponding grayscale image of the color image. The EME values is showing nearby values for the images transformed by the different transformation model.
We also did a comparative study of enhancement by the proposed method for different color models. Figure 17 show enhanced image results of the proposed algorithm when applied to RGB, XYZ and CMY color models of the original image "tree.tiff" for frequency domain enhancement technique alpha-rooting method. While Figure 18 show the image results for spatial domain enhancement techniques histogram equalization by the proposed method for image "tree.tiff" in color models RGB, XYZ and CMY. The transformation model used in Figure 17a, Figure 17b, Figure 17c, Figure 17d, Figure 18a, Figure 18b, Figure 18c and Figure 18d are 2 × 3 model. Figure 17e and Figure 18e show respectively image results of alpha-rooting method and histogram equalization on color model YUV. In YUV model, the Y component is enhanced by the enhancement technique. The Table 5 below shows the CEME values of the original and enhanced image of "tree.tiff" for both alpha-rooting method and histogram equalization for color models RGB, XYZ, CMY and YUV.
Conclusions
The novel method of color image enhancement method shows good enhancement results for enhancement algorithms in both frequency domain as in the alpha-rooting method, and in the spatial domain, as in the histogram equalization. The CEME metric shows that enhancement by all the different transformations gives better CEME than the original image. It is also seen that the CEME value of the enhanced image gives almost nearby range values for all different models. In spatial domain enhancement by histogram equalization, it is seen that the CEME value of the enhanced image is exactly the same value for color image transformed by the proposed 2 × 2, column and row models and slightly different from that of 2 × 3 model. This is because in the 2 × 3 model, we do not consider the luminous part I(n, m) separately. But in all other models, the I(n, m) is also included in experimental methods.

