International Journal of Biomechanics and Movement Science
(ISSN: 2631-5114)
Volume 3, Issue 1
Research Article
DOI: 10.35840/2633-8955/9724
Numerical Investigation of the Femur Mechanical Behavior
Benchikh Lehocine Hala* and Khalfallah Salah
Table of Content
Figures
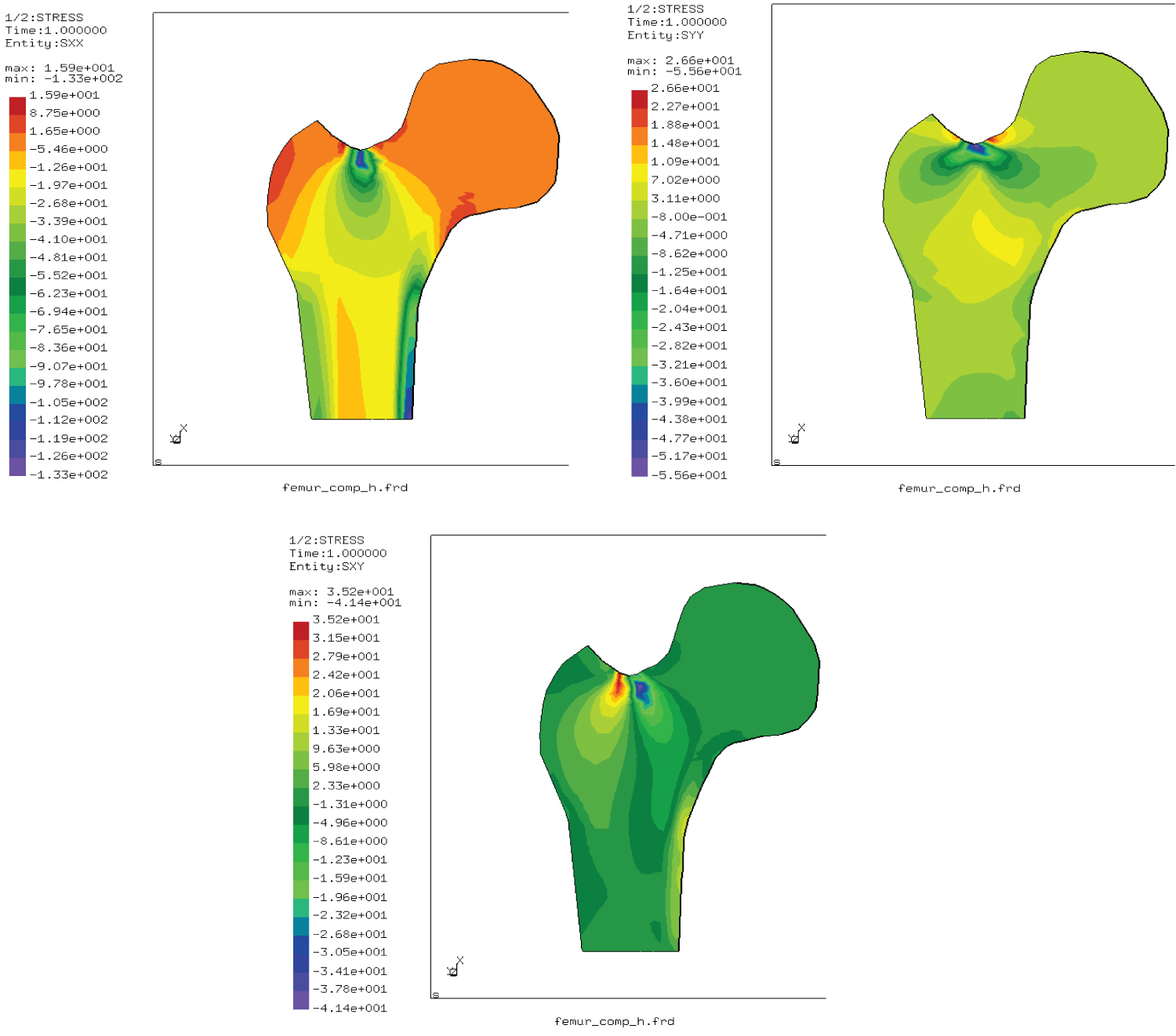
Figure 2: σxx, σyy and σxy distributions....
σxx, σyy and σxy distributions in the femur under compressive load.
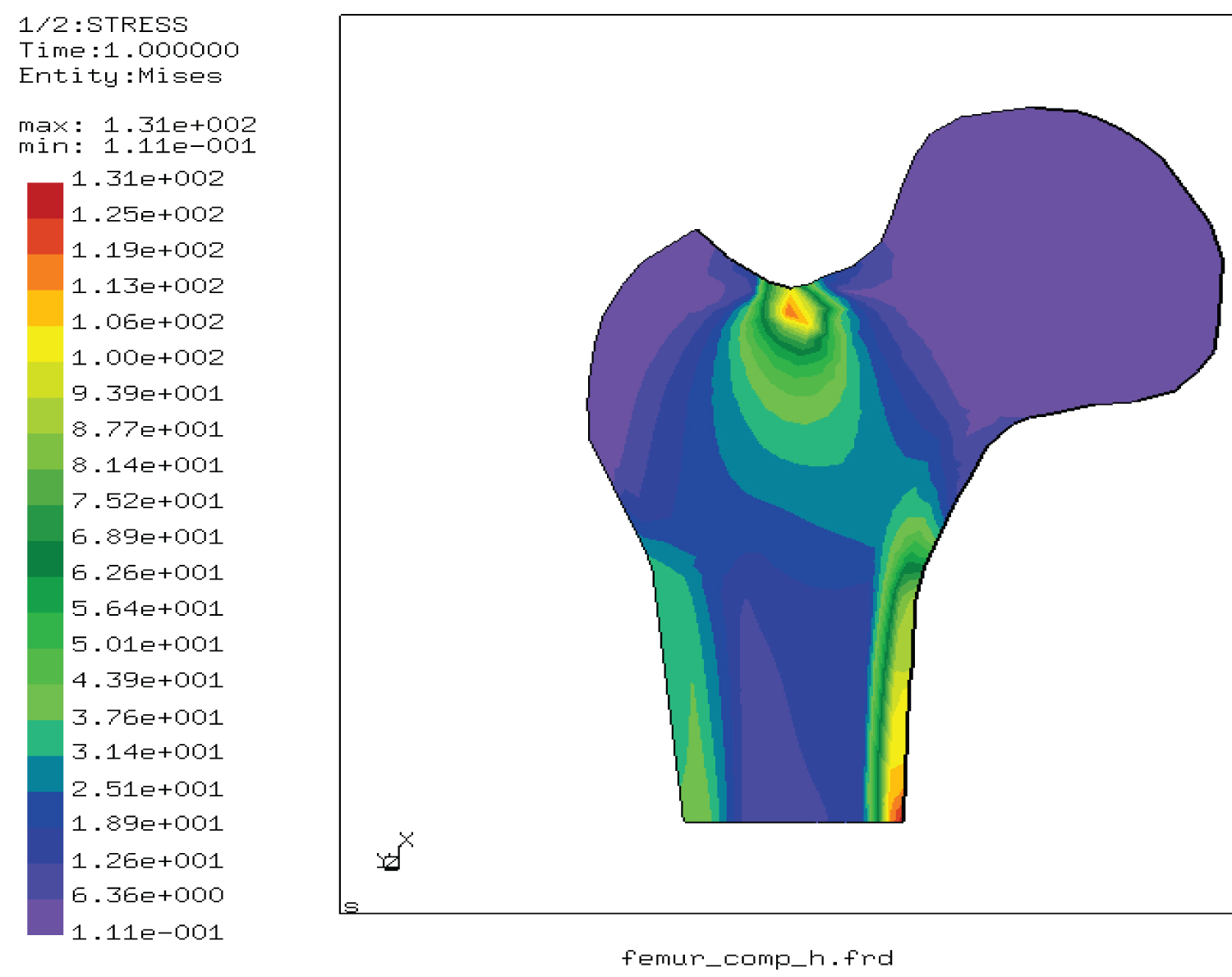
Figure 3: Von Mises stress distribution....
Von Mises stress distribution in the femur under compressive load.
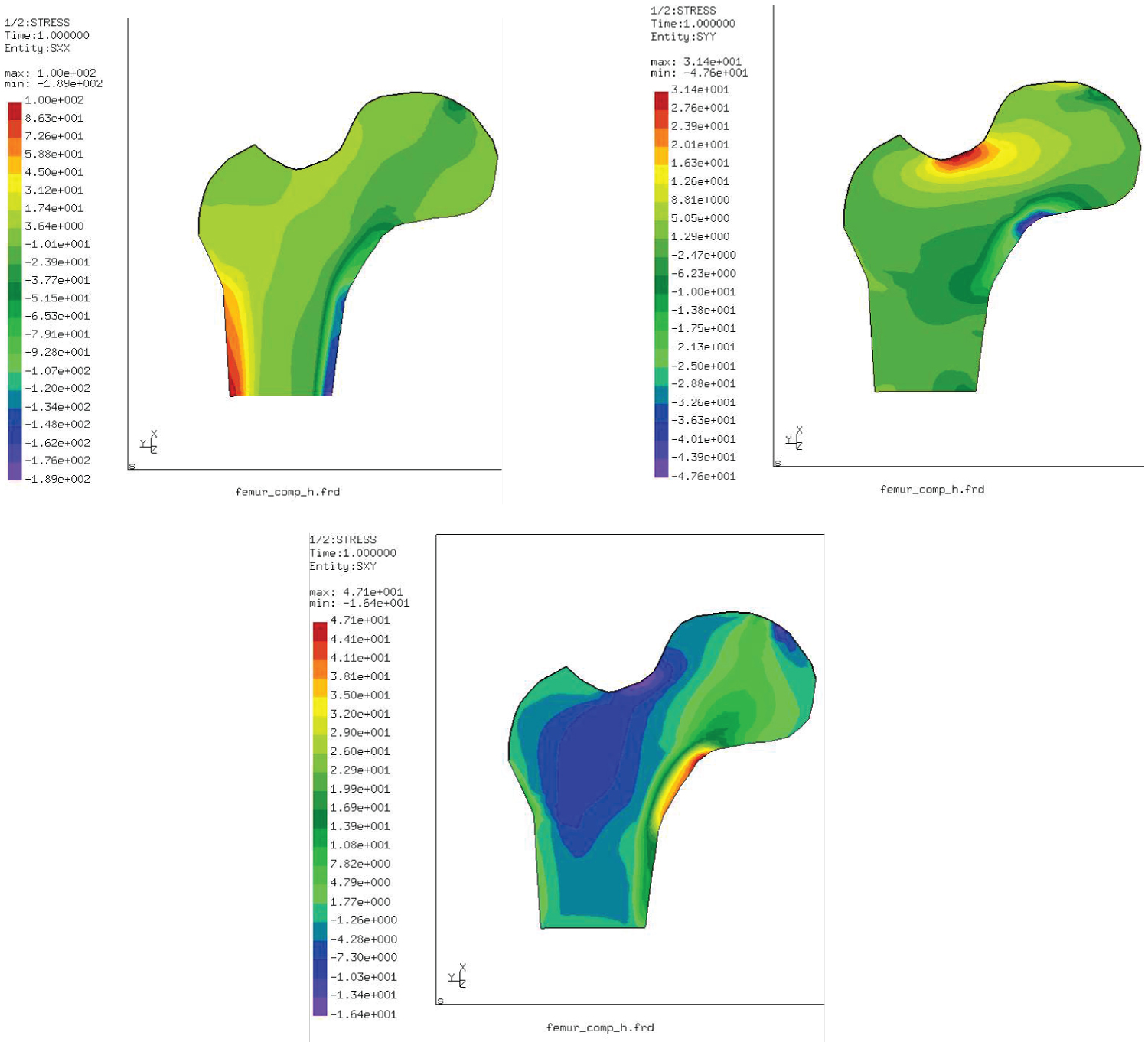
Figure 4: σxx, σyy and σxy distributions....
σxx, σyy and σxy distributions in the femur under bending load.
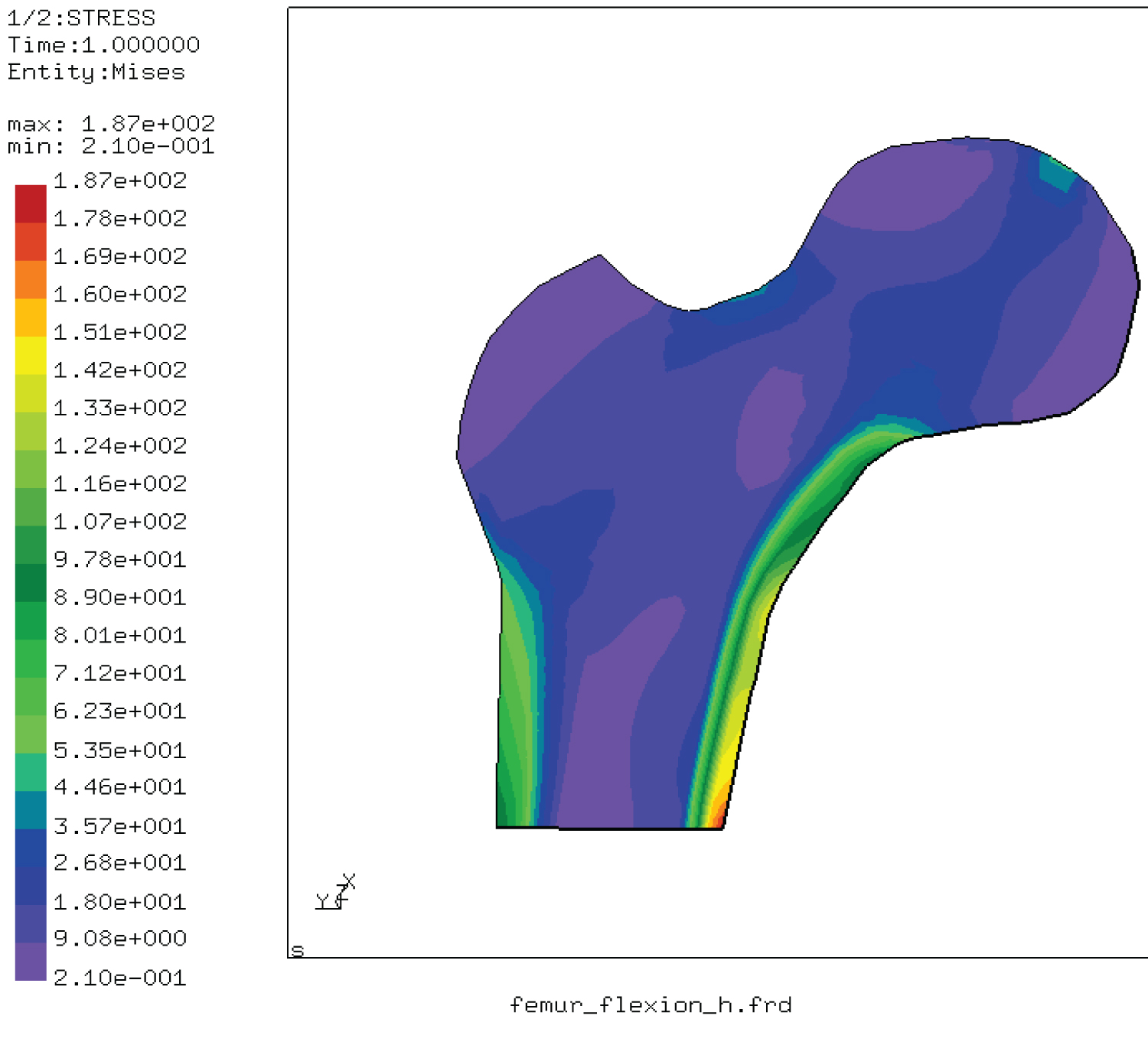
Figure 5: Von Mises stress distribution....
Von Mises stress distribution in the femur under bending load.
Tables
Table 1: Extreme planar stresses and von Mises stress under compressive force.
Table 2: Extreme planar stresses and von Mises stress under bending effect.
References
- Bailey AM, McMurry TL, Poplin GS, Salzar RS, Crandall JR (2015) Survival model forfoot and leg high rate axial impact injury data. Traffic Inj Prev 16: S96-S102.
- Cohen H, Kugel C, May H, Medlej B, Stein D, et al. (2016) The impact velocity and bone fracture pattern: Forensic perspective. Forensic Sci Int 266: 54-62.
- Enns-Bray WS, Bahaloo H, Fleps I, Ariza O, Gilchrist S, et al. (2018) Material mapping strategy to improve the predicted response of the proximal femur to a sideways fall impact. J Mech Behav Biomed Mater 78: 196-205.
- Zellagui S, Hivet A, El Mouss M, Hambli R (2021) Prediction of proximal femur fracture risk from DXA images based on novel fracture indexes. Comput Method Biomech Biomed Eng 9: 205-216.
- Schmidt I, Papastavrou A, Steinmann P (2021) Concurrent consideration of cortical and cancellous bone within continuum bone remodeling. Comput Method Biomech Biomed Eng 24: 1274-1285.
- Sanfilippo JA, Austin MS (2006) Implants for total hip arthroplasty. Futur drugs Ltd 3: 769.
- Nordin M, Frankel VH (2001) Basic biomechanics of the musculoskeletal system. Lippincott Williams & Wilkins.
- Halgrin J, Chaari F, Markiewicz É (2012) On the effect of marrow in the mechanical behavior and crush response of trabecular bone. J Mech Behav Biomed Mater 5: 231-237.
- Imbert L, Aurégan J-C, Pernelle K, Hoc T (2014) Mechanical and mineral properties of osteogenesis imperfecta human bones at the tissue level. Bone 65: 18-24.
- Khorshidi MA (2020) Length scale parameter of single trabecula in cancellous bone. Biomech Model Mechanobiol 19: 1917-1923.
- Mobasseri S, Karami B, Sadeghi M, Tounsi A (2022) Bending and torsional rigidities of defected femur bone using finite element method. Biomedical Engineering Advances 3: 100028.
- Xingdong S, Ke X, Jie W, Liangyuan X, Liangfei F, et al. (2002) Investigation of the mechanical response and deformation mechanism of cortical bone material under combined compression and bending loads. Materials Research Express 9: 025402.
- Frost HM (1987) Bone “mass” and the “mechanostat”. A proposal. Anat Rec 219: 1-9.
- Martin RB (1991) Determinants of the mechanical properties of bone. J Biomech 24: 79-88.
- Varfolomeev D, Samodai V (2021) A Device for Installation of the Femoral Component of Hip Joint Endoprostheses. Biomed Eng 54: 384-387.
- Hambli R (2011) Numerical procedure for multiscale bone adaptation prediction based on neural networks and finite element simulation. Finite Element Anal Des 47: 835-842.
- Mircheski I, Gradišar M (2016) 3D finite element analysis of porous Ti-based alloy prostheses. Comput Methods Biomech Biomed Eng 19: 1531-1540.
- Kraiem T, Barkaoui A, Chafra M, Hambli R, Tavares JMR (2017) New three-dimensional model based on finite element method of bone nanostructure: single TC molecule scale level. Comput Method Biomech Biomed Eng 20: 617-625.
- Rahchamani R, Soheilifard R (2020) Three-dimensional structural optimization of a cementless hip stem using a bi- directional evolutionary method. Comput Method Biomech Biomed Eng 23: 1-11.
- Warren JM, Hey LA, Mazzoleni AP (2021) A finite element study of the relationship between upper body weight and the loads experienced by the human lumbosacral spine, and fusion instrumentation, in a standing upright posture. Biomed Eng Adv 2: 100023.
- Apel Z, Vafaeian B, Apel DB, Hussain A (2021) Occlusal stresses in beveled versus non-beveled tooth preparation. Biomed Eng Adv 2: 100010.
- Papastavrou A, Schmidt I, Steinmann P (2020) On biological availability dependent bone remodeling. Comput Methods Biomech Biomed Eng 23: 432-444.
- Kluess D, Soodmand E, Lorenz A, Pahr D, Schwarze M, et al. (2019) A round-robin finite element analysis of human femur mechanics between seven participating laboratories with experimental validation. Comput Method Biomech Biomed Eng 22: 1020-1031.
- Lerner AM, Tagliari I, Israel CL, Pagnussato F, de Freitas Spinelli L (2021) Mechanical resistance of hydroxyapatite-based bio components for use in bone grafting. Res Biomed Eng 37: 419-428.
- Jadhav MV, Gambhire VR (2015) Experimental analysis of stress in real (preserved) intact proximal human femur (thigh) bone under static load. IJATES 3: 1179-1187.
- Uzair NM, Khawaja HA, Moatamedi M (2015) Finite element analysis of human femur bone. The International Journal of Multiphasic 9: 101-108.
Author Details
Benchikh Lehocine Hala* and Khalfallah Salah
Laboratoire de Mécanique et Systèmes Energétiques Avancés, Ecole Nationale Polytechnique, Constantine, Algeria
Corresponding author
Bencheikh Elhocine Hala, Laboratoire de Mécanique et Systèmes Energétiques Avancés, Ecole Nationale Polytechnique, Constantine, Algeria.
Accepted: July 03, 2023 | Published Online: July 05, 2023
Citation: Hala BL, Salah K (2023) Numerical Investigation of the Femur Mechanical Behavior. Int J Biomech Mov Sci 3:004
Copyright: © 2023 Hala BL, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
This work aims to model the structural behavior of the femur upper under two types of loading: A pure compressive loading and compressive bending force. Therefore, the finite element method (FEM) is adopted to build the 2D-geometrical model. The numerical analysis is carried out based on the finite element method considering the trabecular and cortical bones, simultaneously, to achieve the objectives of this work by using an open source program (Calculix). This study deals to evaluate the stress and their distributions throughout the femur and precisely at the neck level in order to understand the mechanical behavior of the femur and the failure modes. Based on obtained results, the maximum stresses and theirs locations were mentioned and localized throughout the femur and the bone fracture load was also evaluated. More, results appear the significant importance in replication of the natural design parameters in creating the synthetic bone substitutes and bring more information and techniques to practitioners and clinicians.
Keywords
Femur neck, Modeling, Cortical bone, Cancellous bone, Compressive loading, Bending, Calculix, FEM, Simulation
Introduction
Materials Sciences and mechanics are effective tools that can be used to study and analyze different effects that can be applied on bone structures. Modeling of biological limb bone serviceability using experimental or numerical methods provide a deeper understanding of their responses and behaviors. Therefore, these studies lead to show pattern stresses throughout even each biological members. The mechanical complexity of bone tissue composed of trabecular and cortical bone exceeds that of most material used in engineering field.
Study of mechanical behavior of long bone tissues using the finite element method has been performed by many researchers [1-5]. The femur bone is one of important bone members constituting the hip joint exposing to different forces during working, standing, walking, or running [6]. As example, in United States of America, more than 300000 people sustain a hip fracture each year and most of them occur in patients having 65-years-older. The percentage of registered cases is more than double and it is expected an increase in next year. Particularly, women are more affected by this disease compared to men. Hip fractures have a severe impact on the elderly population with relevant risks, such as high mobility and mortality, high postoperalae disability index and increasing costs to society with less beneficial results related to treatment.
The femur is the longest, strongest and the thigh bone in the human body. It takes care of a critical part of the body ability to stand and move. Thus, it is the principal member transferring various actions of upper limbs to the feet and then to the ground. Therefore, any damage or harm of this element blocks the living activities, which can be due to an illness or an external effect: fall, accident,… etc. The femur can be decomposed into neck, greater and lesser trochanters, shaft distal and proximal, which form the hip joint constituting the femur head.
During daily activities, the proximal femur can be subjected to various loads that engender damage and deterioration of the joint between the acetabulum and the head of the femur. In this environment with aging, the bone becomes very weaker and it can be easily break. One of main topics that attracted an attention is the rigorous evaluation of the mechanical behavior of the human femur. In this case, many studies have been published, in order to establish the femur response subjecting to compression loading and or bending effects.
Hip fractures are called cracks in the top of the thigh bone near to the hip joint. These fractures are usually due to a fall or an injury to the side of the hip as it may be caused by a health conditions. Most hip fractures result from accident of older people that can result from fall or from twisting or pivoting suddenly. It is concluded that the fall is the most common reason for the hip fracture and a few people have it happen spontaneously. Really, the hip fracture is a serious injury with complications that can be life-threatening.
Most members are composed of bone tissues with different mechanical properties characteristics and various geometrical cross sections. These bone structures can be subjected to various types of forces and moments [7]. The femur shape is an irregular form therefore, its cross section is asymmetric and the exact evaluation of the resultant stress field is a difficult task. Due to these complications, experimental studies are more numerous compared to numerical or analytical studies. These studies do not take into account the internal architecture of the femur, the bone areas occupied by the cortical or spongy bones and the geometric shape. Then, an accurate understanding of the properties and behaviors of bone structures seems to be necessary. In this topic, the effect of the loading impact and their fracture which may be the result of high force impact, stress or other phenomena [6,8], have been studied. Some researches focused on the mechanical behavior of bone structures [8-10] in which the effect of bending and torsional rigidies of the femur bone have been recently elaborated [11]. Adding, the deformation mechanisms of cortical bone material under combined compression and bending loads is investigated [12]. Really, bone material can’t remain healthy and defects arise in their structure. So, in order to investigate bones in a real situation, it is proper to consider these defects [11].
The mineral mass is the principal indicator of the quality of bone or its strength. Really, the geometric, mass, structural and material properties are the factors influencing the biological strength. H.M. Frost [13] studies the correlation between the geometric and material properties of bone using the feedback mechanism. Martin [14] defined the structural properties of bone by the material and architectonic properties.
This work performs a comprehensive study on static bending and pure compressive force in human femur. To reach objectives, an analyze based on the finite element method [11,15-20] is used to study the response of human femur bone [21-24]. The mechanical characteristics of the cancellous and cortical bones are of interesting role in process of structural supports and flexibility during physical activity. According to the robustness of cortical bone tissue, the mechanical properties and mechanical behavior of the cancellous bone were found crucial as information of the elastic and failure properties of the tissue may potentially be used to study the effects of druy treatments, aging and disease at the tissue level.
Methods of the Analysis
In this domain, various tests have already been shown many attempts evaluating the high stress concentration of femur bone by experimental analyzes involving damage and fracture [25]. These studies have been elaborated to study strain patterns using various methods. They are for object to investigate the mechanical behavior of the femur under different loading scenarios. Experimental tests are due to availability of test tools equipped with devices characterized with high precision. Really, these researches have provided satisfactory results and recommendations for orthopedic practitioners.
This work leads to show the concordance between experimental and numerical tests. Certainly, the geometric complexity and material composition of bone structures make analytical analysis quite difficult. For this reason, numerical analysis remains as requirement for this type of structure.
The biomechanical orthopedics was introduced fifty years ago to compute stresses distribution in human bones. The Finite element method has become the most used numerical method for its efficiently to analyze complex structures as mechanical, civil structures and human organs. This technique allows studying stresses and strains and helps to predict fractures of biological members in specific locations. This analysis performed assumes distinct bone tissues of cortical and cancellous bone as isotropic linear elastic behavior.
Geometrical model
In this analysis, the bi-dimensional (2D) model is used to mesh the proximal human femur. The model of the proximal femur was developed based on X-ray image that is of an anonymous patient. Thus, the corresponding file was generated and exported to the program developed for this concern. The numerical model is composed of two different materials: the cortical bone and the trabecular one. Therefore, the final 2D model is composed by 658 rectangular elements and 725 nodes for the upper half of the femur. The two-dimensional (2D) model of the proximal femur was developed based on pre- processor developed for geometrical modeling of structures.
Material model
In this work, two distinct materials were considered: cortical and cancellous bone tissue. The mechanical properties of the constitutive law used are the Young's modulus and the Poisson's coefficient. Thus, the Young's modulus E = 18000 MPa and E = 3200 MPa for cortical and trabecular bone, respectively, are chosen. The Poisson's ratio v = 0.30 and v = 0.20 for cortical and trabecular bone, respectively, are selected. In this study, even cortical and trabecular bone behaves as an isotropic material and mechanical characteristics may be related to external loading. Therefore analyzing the failure modes of biological members under different loading conditions is necessary to explore the modes of failure and this leads to reinforcing members.
Boundary conditions
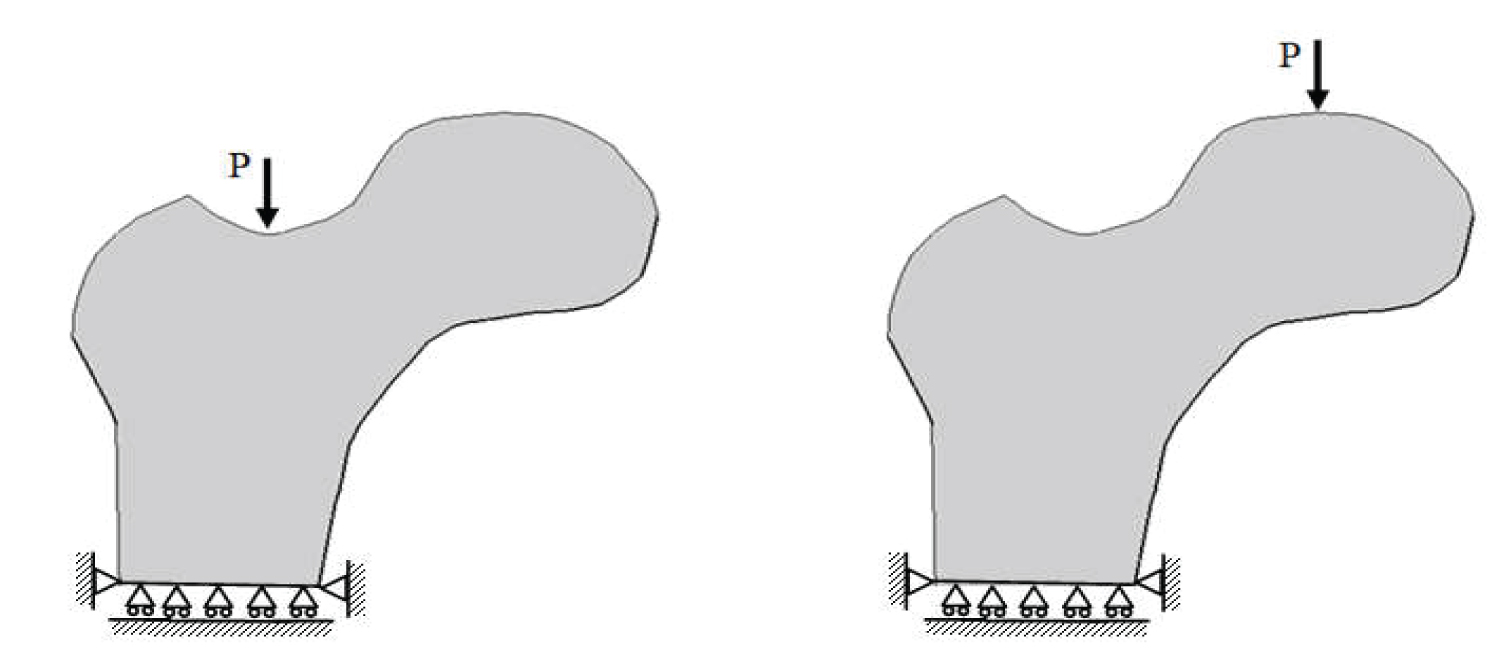
This section describes boundary conditions of the femur. In this contribution, only the upper part of the femur is considered according to the study referred. For this reason, the degrees of freedom of the cutting section are locked according to the vertical degree of freedom while limited nodes are blocked in the vertical and horizontal directions (Figure 1).
Loads scenarios
The loads applied on the femur are divided into two categories, in the first case, on the femur neck engendering a pure compressive force and in the second case, the load in applied on the femur head. This engenders a compression and bending effect (Figure 1).
Finite element analysis: Material models
The Finite Element Method is a numerical tool, largely used for obtaining solutions of static or dynamic equations. The practical applications of the finite element method are a computational means for performing engineering analysis. Among, the biomechanical analysis can be studied involving with mechanical aspects of the biological elements.
This section explains the analytical formulations of different material models, like linear isotropic linear elastic material. In this study, the bone is considered as elastic and after orthotropic material. Firstly, the constitutive law for a linear elastic material can be described by
and are the second order tensors of stress and strain, respectively and is the fourth order tensor of elasticity In indicial form, the equation (1) can be rewritten as
l and m are the Lamé constants.
For plane stress state, the stress according the third axis, this leads to and
Thus, the constitutive law can be written
Lamé constants can be written in fonction of Young’s modulus, E, and Poission ratio, v as
The failure mode according von Mises yield creterion is also performed. Thus, the octaedral stress of von Mises approach can be computed by
Numerical Results
In this section, the results obtained using the simulation of the femur model based on the finite element method software (Calculix), are presented. As mentioned above, it was considered that the femur bone has two types of tissues: trabecular and cortical bone. Therefore, the head and neck femur are constituted of bone cancellous tissues but the rest is surrounded by cortical bone having a thin thickness. This composition was considered in the development of the finite element approach. The transition between to sort of tissues takes place on the upper part of the diaphysis and the rest of the model was considered as cortical bone.
The elaborated mesh has 720 nodes. Accordingly, the trabecular portion was modeled with 628 membranous elements of four nodes. Loads considered were applied over the femur head and at femur neck level. The first load engenders a bending effect but the second one can be considered as a compressive load. Besides, the bone was considered as fixed at its bottom nodes (Figure 1).
The finite element analysis is performed on the femur bone model by varying the nature of loading excitation. The maximum stresses generated in the analysis and the fracture stress is adopted about of 100 MPa in tension and of 133 MPa in compression based on the experimental test elaborated by Uzair [26].
Compressive loading effect
Figure 2 shows the distributions of planar stresses ( σ xx , σ yy and σ xy ) in the femur which is subjected to compressive force at the femur neck. As can be seen from Figure 2, nodes around the loaded point are the most stressed. These nodes record maximum result stresses and they are of σ xx = 133 MPa (in compression), σ yy = 55.6 MPa (in compression) and σ xy = -41.40 MPa for a force of 2 KN (Table 1).
For the compression case, stresses σ xx , σ yy and σ xy are clearly concentrated in the vicinity of the loading region. This is accompanied by a second localization at femoral shaft (Figure 2). The computing was made until the yielding stresses of the cortical and spongy bones.
Figure 3 shows the Von Mises stress distribution that is concentrated in the vicinity of the loaded point and along the inner of the femoral shift. This distribution decreases from the limit stress of the cortical bone to the minimum value of stress in the spongy bone.
The Table 1 regroups the extreme values of σ xx , σ yy and σ xy stresses according to the geometrical axes of the femoral structure.
Bending effect
For the bending case, the stress σ xx is distributed along the inner side (compression) and the outer side (traction) of the femoral shift. In this case, the femoral head is less stressed while the stress σ yy is clearly focused at the level of the femoral neck with opposite signs. These stresses generate a shearing of the neck of femur and the effect is much underlined with shear stresses σ xy (Figure 4).
In this case, this distribution shows clearly the location of the maximum stresses in the femoral shaft of the femur and at the level of the femoral neck. The mechanical damage can be shown at the femur neck (Figure 5 and Table 2).
Conclusions
In this paper, 2D model is proposed based on analyzing the mechanical behavior under compressive and bending loadings. In this analysis, the cortical and spongy bones are taken into account where each material is considered with its proper mechanical properties. The analysis is performed by using open source software. Conclusions can be drowning are:
- Higher stresses are observed in the shaft of the femur when the bending load is applied but they are dominant around the femur neck under compressive loading.
- Results appear that the failure of femur bone under compressive loading of 2000 N and 645 N of load under bending load. Thus, the axial strength of femur is about 3.10 times than bending loading.
- For the compression case, planar stresses are localized in the vicinity of the loading region and at femoral shaft.
- Von Mises stress distribution is considerable around the loaded point and along the inner of the femoral shift.
- For bending effect, stresses distribution shows clearly the location of the maximum stresses in the femoral shaft of the femur and at the level of the femoral neck.