International Journal of Experimental Spectroscopic Techniques
(ISSN: 2631-505X)
Volume 8, Issue 1
Research Article
DOI: 10.35840/2631-505X/8532
Laser-Induced Fluorescence in a Quest to Detect Quantum Size Flumps in Counterion-Mediated Long-Range Attraction of Colloids by Surfaces with Surface Potential Ψ0 Greater than 70 mV
Leonid A Kaledin*
Table of Content
Figures
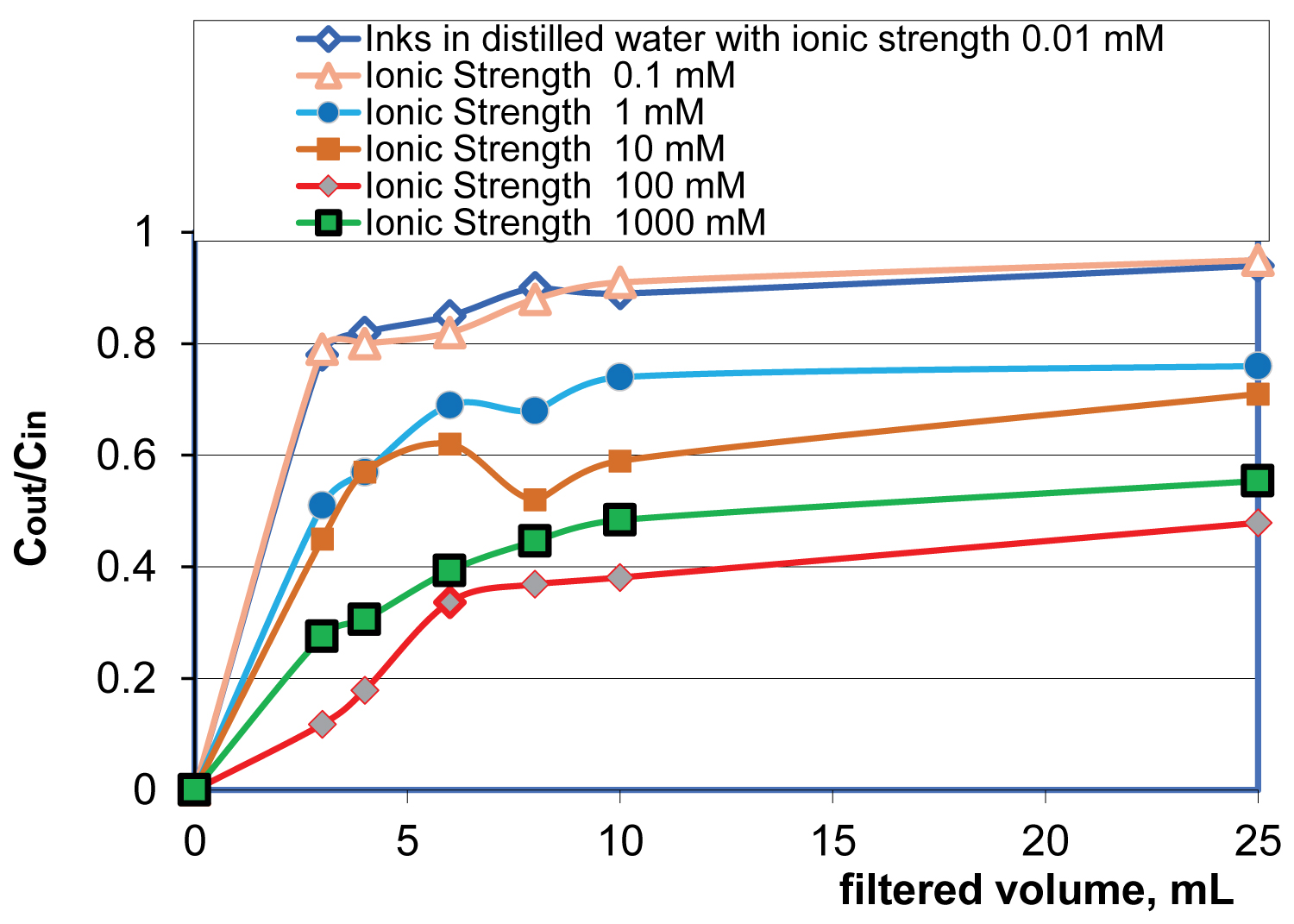
Figure 1: Ink adsorption by....
Ink adsorption by non-woven high flow disruptor filter media with pore size of 8 μm and largest pore size of 20 μm.
Tables
Table 1: Counterion-mediated attractive interaction between highly charged surfaces surface potential Ψ0 greater than 70 mV and colloidal particles.
References
- Spedding FH. In: Gschneidner KA, Handbook on the physics and chemistry of rare earth.
- Martin WC, Zalubas R, Hagan L (1978) Atomic energy levels-the rare-earth elements. NSRDS-NBS No. 60, U.S. Government Printing Office, Washington, DC.
- Kaledin LA, Kaledin AL, Heaven MC (2021) The electronic structure of the actinide oxides and their singly and doubly charged cations: A ligand field approach. Int J Quantum Chem 121.
- Kaledin AL, Heaven MC, Field RW, Kaledin LA (1996) The electronic structure of the lanthanide monohalides: A ligand field approach. J Mol Spectrosc 179: 310-319.
- Dieke GH, Crosswhite HM, Crosswhite Hs (1968) Spectra and energy levels of rare earth ions. Interscience Publishers.
- Carnall WT, Crosswhite H, Crosswhite HM (1978) Energy level structure and transition probabilities in the spectra of the trivalent lanthanides in LaF 3 . Report: ANL-78-XX-95; TRN: 79-005910, US.
- Bethe HA (1929) Splitting of terms in crystals. Ann Der Physik 3: 133-206.
- Demtröder W (1981) Laser spectroscopy. Basic concepts and instrumentation. 2 nd Printing, Springer-Verlag, Berlin.
- Hahn EL (1950) Spin Echoes. Phys Rev 80: 580.
- Sternheimer RM, Blume M, Peierls RF (1968) Shielding of crystal fields at rare earth ions. Phys Rev 173: 376-389.
- Kaledin LA, McCord JE, Heaven MC (1994) Laser spectroscopy of UO: Characterization and assignment of states in the 0- to 3-eV range, with a comparison to the eectronic structure of ThO. J Mol Spectrosc 164: 27-65.
- Field RW (1982) Diatomic molecule electronic structure beyond simple molecular constants. Berichte der Bunsengesellschaft für physikalische Chemie 86: 771-779.
- Tepper F, Kaledin LA (2003) Nanosize electropositive fibrous adsorbent. US 6,838,005B2.
- Tepper F, Kaledin L (2009) Sub-micron filter. US Patent 7,601,262B1.
- Tepper F, Kaledin LA (2008) Drinking water filtration device. US Patent 7,390,343B2.
- Tepper F, Kaledin LA (2007) Electrostatic air filter. US Patent.
- Tepper F, Kaledin LA (2005) Removing pathogens using nano-ceramic-fiber filters. NASA Tech Briefs, MSC-23478.
- Bugash J (1959) US Patent 2,915,475.
- Penrod SL, Olson TM, Grant SB (1996) Deposition kinetics of two viruses in packed beds of quartz granular media. Langmuir 12: 5576-5587.
- Lyklema J (1991) Fundamentals of interface and colloid science: Fundamentals. 1, Academic Press, London.
- Kaledin LA, Tepper F, Kaledin TG (2016) Aluminized silicious powder and water purification device incorporating the same. US Patent 9,309,131B2.
- Kaledin LA, Tepper F, Kaledin TG (2014) Long-range attractive forces extending from alumina nanofiber surface. International Journal of Smart and Nano Materials 5: 133-151.
- Kaledin LA, Tepper F, Kaledin TG (2015) Long-range attractive forces extending from the alumina’s nanolayer surface in aqueous solutions. Int J Smart & Nano Materials 6: 171-194.
- Wefers K, Misra C (1987) Oxides and hydroxides of aluminum. Alcoa Technical Paper No. 19, Alcoa Laboratory.
- Kaledin LA, Tepper F, Kaledin TG (2017) Electrokinetic aspects of water filtration by AlOOH-coated siliceous particles with nanoscale roughness. AIMS Materials Science 4: 470-486.
- Kaledin L, Tepper F, Vesga Y, Kaledin T (2019) Boehmite and akageneite 1D and 2D mesostructures: Synthesis, growth mechanism, ageing characteristics and surface nanoscale roughness effect on water purification. Journal of Nanomaterials 2019: 9516156.
- Appelo CAJ (2017) Solute transport solved with the Nernst-Planck equation for concrete pores with ‘free’ water and a double layer. Cement and Concrete Research 101: 102-113.
- van Loosdrecht MC, Lyklema J, Norde W, Schraa G, Zehnder AJB (1987) Electrophoretic mobility and hydrophobicity as a measure to predict the initial steps of bacterial adhesion. Appl Environ Microbiol 53: 1898-1901.
- Einstein (1905) Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen 17 Physik 322: 549-560.
- Furth R, Cowper AD (1956) Investigations on the theory of the Brownian Movement. Dover Publications, New York.
- Feynman RP, Leighton RB, Sands M (1977) The feynman lectures on physics. The New Millennium Edition, Volume I, Basic Books, New York.
- Yu Q, Qu C, Houston PL, Conte R, Nandi A, et al. (2022) q-AQUA: A many-body CCSD(T) water potential, including 4-body interactions, demonstrates the quantum nature of water from clusters to the liquid phase. Phys Chem Lett 13: 5068-5074.
- Elimelech M, O'Melia CR (1990) Kinetics of deposition of colloidal particles in porous media. Environ Sci Technol 24: 1528-1536.
- Silfvast WT, Meyers RA (2003) Encyclopaedia of physical science and technology. (3 rd edn), Academic Press, 267-281.
- Dirac PAM (1950) Generalized hamiltonian dynamics. Canadian Journal of Mathematics 2: 129-148.
- Dirac PAM (1957) The principles of quantum mechanics.
- Dirac PAM (1964) Lectures on quantum mechanics, Dover, New York.
- Shank Y, Wang A, Kaledin B, Braams J, Bowman JM (2009) Accurate ab initio and “hybrid” potential energy surfaces, intramolecular vibrational energies, and classical ir spectrum of the water dimer. J Chem Phys 130: 144314.
- Ise N (1999) Recent study of counterion-mediated attraction between colloidal particles. Colloids and Surfaces A: Physicochemical and Engineering Aspects 146: 347-357.
- Ise N (2010) Like likes like: counterion-mediated attraction in macroionic and colloidal interaction. Phys Chem Chem Phys.
- Ise N, Ito K, Okubo T, Dosho S, Sogami I (1985) Ordered” structures in dilute suspensions. J Am Chem Soc 107: 8074-8077.
- Ise N (1999) Recent study on counterion-mediated attraction between colloidal particles. Colloids and Surfaces A: Physicochemical and Engineering Aspects 146: 347-357.
- Shinohara T, Smalley MV, Sogami IS (2003) Helmholtz free energy of a multilayer system of highly charged plates immersed in an electrolyte. Mol Physics 101: 1883-1900.
- Konishi T, Yamahara E, Ise N (1996) Characterization of colloidal silica particles by ultra-small-angle x-ray scattering. Langmuir 12: 2608-2610.
- https://www.entegris.com/content/dam/product-assets/accusizerspossystems/appnote-particle-size-of-inkjet-inks-10526.pdf
- Stumm W, Morgan JJ (1981) Aquatic chemistry. An introduction emphasizing chemical equilibria in natural waters. Wiley-Interscience, New York.
- Everett DH, Koopal LK (1971) International union of pure and applied chemistry. Manual of symbols and terminology for physicochemical quantities and units. Appendix I: Definitions, Terminology and Symbols in Colloid and Surface Chemistry, part I, IUPAC, Washington DC.
- Sogami I (1983) Effective potential between charged spherical particles in dilute suspension. Phys Lett A 96: 199-203.
- Sogami IS, Shinohara T, Smalley MV (1992) Adiabatic pair potential of highly charged plates in an electrolyte. Mol Phys 76: 1-19.
- Sogami IS, lse N (1984) On the electrostatic interaction in macroionic solutions. J Chem Phys 81: 6320-6332.
- lse N, Sogami IS (1914) Structure formation in solution: Ionic polymers and colloidal particles. Springer, Berlin/Heidelberg.
- Sogami IS, lse N (2005) Structure formation in solution: Ionic polymers and colloidal particles. Springer.
- Derjaguin B, Landau L (1993) Theory of stability of strongly charged lyophobic sols of the adhesion of strongly charge particles in solution of electrolytes. Progress in Surface Science 43: 30-59.
- Smalley M (2006) Clay swelling and colloid stability. CRC Taylor & Francis Group, Boca Raton.
- Haynes WM, Lide DR, Bruno TJ (2012) CRC handbook of chemistry and physics. (93 rd edn), CRC Press, Boca Raton.
- Langmuir I (1938) The role of attractive and repulsive forces in the formation of tactoids, thixotropic gels, protein crystals and coacervates. J Chem Phys 6: 873.
- Verwey EJ, Overbeek JTG (1948) Theory of the stability of lyophobic colloids. Elsevier, Amsterdam.
- Langmuir I (1938) Repulsive forces between charged surfaces in water, and the cause of the Jones-Ray effect. Science 88: 430-432.
- Schwalb S, Thirring T (1964) Quantum theory of laser radiation. In: Herausgegenben, von G. Hohler, Ergebnisse der exakten Naturwissenschaften. 36: 61.
- Weyl H (1950) Theory of groups and quantum mechanics. Dover.
- Klauber RD (2014) Basic principles and quantum electrodynamics. 2 nd edition with corrections.
- Zare RN (2012) My life with LIF: A personal account of developing laser-induced fluorescence. Annu Rev Anal Chem 5: 1-14.
- Schultz HW, Cruse RN, Zare (1972) Laser-induced fluorescence: A method to measure the internal state distribution of reaction products. J Chem Phys 57: 1354-1355.
- Feldman DL, Lengel RK, Zar RN (1977) Multiphoton ionization: A method for characterizing molecular beams and beam reaction products. Chem Phys Lett 52: 413-417.
- Han J, Goncharov V, Kaledin LA, Komissarov AV, Heaven MC (2004) Electronic spectroscopy and ionization potential of UO 2 in the Gas Phase. J Chem Phys 120: 5155-5163.
- Burolla VP, Pentoney Jr SL, Zare RN (1989) High-performance capillary electrophoresis. Am Biotechnol La 7: 20-26.
- Patterson G, Davidson M, Manley S, Lippincott-Schwartz J (2010) Superresolution imaging using single-molecule localization. Annu Rev Phys Chem 61: 345-367.
Author Details
Leonid A Kaledin*
Quantum Structures Technologies, 1665 Promenade Cir., Port Orange, FL 32129, USA
Corresponding author
Leonid A Kaledin, Quantum Structures Technologies, 1665 Promenade Cir., Port Orange, FL 32129, USA.
Accepted: March 10, 2023 | Published Online: March 12, 2023
Citation: Kaledin LA (2023) Laser-Induced Fluorescence in a Quest to Detect Quantum Size Flumps in Counterion-Mediated Long-Range Attraction of Colloids by Surfaces with Surface Potential Ψ0 Greater than 70 mV. Int J Exp Spectroscopic Tech 8:032
Copyright: © 2023 Kaledin LA. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
This Perspective describes experimental and initial theoretical efforts in the field of simulating excited state photodynamic of rare earth metal complexes in polar solutions using Laser-induced fluorescence (LIF) in a quest to detect quantum size flumps in counterion-mediated long-range attraction of colloids by surfaces with surface potential Ψ0 greater than 70 mV. It presents the typical workflows starting from electronic structure methods suitable to describe the crystal and liquid complexes to approaches able to simulate their dynamics under the effect of stimulating light and/or magnetic fields. It gives particular attention to build a bridge between theory and experiment by discussing the different quantum field approached such as Dirac's Legendre transformations to Hamiltonian densities in terms of complex fields as well as classical Poisson Boltzmann Hamiltonians. The former is adopted in the present work because it contains the acceleration terms that are not in thermodynamic equilibrium with environtment, and the latter is commonly adopted in the interpretation of experiments and the simulation of colloid removal from polar solutions using equilibrium thermodynamic approach. The Dirac's dynamic approach is more suitable to experimental conditions that are far from the thermodynamic equilibrium and appears to be preferred for describing physical reality of the adsorption processes of removal colloids by surfaces with surface potential Ψ0 greater than 70 mV in polar solutions. It discusses excited state dynamics on these complexes in solution from reduced (1D- and 2D- Poisson-Boltzmann equation) to full 4D (3D + time) dimensionality.
Keywords
Rare earths, Lanthanides, Actinides, Metal complexes, Photochemistry, Excited-state dynamics, Wave packet dynamics, Electronic structure theory, Laser spectroscopy, Laser induced fluorescence, Quantum fields, Dirac legendre transformations, Hamiltonian density
Introduction
Lanthanides and actinides among the rare earthsa elements provide a rich photochemistry due to partially filled f-shells with density of states up to one state per a reciprocal centimeter (cm-1) [1-4]. The radial wavefunctions for 4f- and 5f- are all within the outer 6s, 6p and 7s, 7p orbitals respectively. Therefore, the environment surrounding the ions, that is, either vacuum, noble gases, liquids, or crystals has limited impact on the spectra of the ions [5,6]. We are using this property to predict spectra of rare earth ions in liquid and crystal environments based on their spectra [5-7]. The splitting of an individual term in gaseous, liquid and crystal environments is rather different in details [1-6], such as in laser induced fluorescence (LIF) spectra (see Section 8.7 of Ref. [8]). The present project is aimed at combined use of the LIF and Hahn spin-echo Nuclear Magnetic Resonance (NMR) [9] technologies involving of pulses of different intensity or duration for remote sensing of large variety of densely packed electronic states with different electronic symmetry in different symmetry groups created in liquid or condensed phase [7,10]. The behavior of these metal complexes after light irradiation is controlled by short-lived or long lived excited states that may either emit light or go via nonradiative transitions to other electronic states ultimately decaying back to the ground state or return to the ground state or via luminescence when the molecule ends up in a state with no possibility of transition to any other state. The LIF technique on gas phase is a very powerful tool to probe the lower and excited states symmetries [7] and for viable laser-based enrichment procedure for the lighter isotope U-235 with a natural abundance of only 0.72% of lighter uranium that sustains a nuclear fusion chain reaction and is the material for nuclear reactors. This enrichment is easier to achieve with uranium oxide in gas phase rather than with atoms or ions since the difference between two band-heads of UO is greater than the linewidth of pulsed dye laser in visible region of the spectrum [11]. Ligand Field theory [12] is a powerful tool to assign the excited states of actinide monooxide [2], and lanthanide monohalides [3] diatomic molecules in C∞v symmetry. Crystal field [7] and Ligand Field [2,3,12] theories describe splitting of electronic terns of free ions [2].
aThe name of "Rare earths" is reserved for Sc, Y, La and lanthanides [1].An electric field of definite symmetry causes a splitting and reordering of the terms of the unperturbed ion. Therefore, the unperturbed free ion in vacuo, in water electrolyte, and in crystals could have similar excitation wavelengths and very different LIF spectra.
Experimental
Materials and methods
A family of sorbents with surface potential Ψ0 greater than 70 mV and ζ-potential greater than 50 mV at pH in the range from 3 to 10 that highly efficiently adsorb colloidal particles from salt water with salinity up to 3 M were recently described [13-19].
NanoCeram and Disruptor non-woven filter media: An electro adsorptive non-woven filter media called NanoCeram® (NC) have been developed under NASA contracts to develop a filter for removing pathogens from recycled water in space cabins [20,21] by dispersing the nano boehmite (γ-AlOOH)b fibers [22] onto a second fibrous structures [13-16] that attracts and tightly retains colloid particles including bacteria, viruses, bacteriophages, many biological molecules such as Ribonucleic acid (RNA) protein as well as PFOA/PFOS without the adverse high pressure of polymeric membranes that manufactured and sold by Ahlstrom-Munksjo as Disruptor® filter media under an exclusive, global license. The two-dimensional (2D) quantum-sized and one-dimensional (1D) nanometer size γ-AlOOH (Boehmite) structures [13-16] and 2D atomically-thin β-FeOOH (Akaganeite) nanobelts [23] with a mean width of approximately 10 nm were deposited onto siliceous substrates in aqueous processes at moderate temperatures. Low cost and large-scale manufacturing of siliceous substrates coated with 2D and 1D γ-AlOOH (Boehmite) crystallites of 2.7 ± 0.5 nm in diameter, with an average length of 2.9 ± 0.9 nm and 250 ± 50 nm, respectively, that were further functionalized with atomically thin 2D β-FeOOH (Akaganeite) nanobelts [23] was demonstrated.
bAluminum oxide/hydroxide (α-AlOOH) in current international nomenclature, was also known as α-Al2O3•H2O according to the Alcoa system of nomenclature which was in general use in North Americas [21] in early 1950es when one of us (FT) was using itDiffusion coefficients of ions, viruses, bacteria in NaCl aqueous suspensions at 25 ℃: The adsorption tests of pleated NanoCeram cartridges [23] and porous polymeric DEAL® [24] and DEAL-FeOOH blocks were conducted in batches at temperature 25 ± 2 ℃. Each individual batch was ten litre volume of microbial suspension of MS2 bacteriophages (ATCC 15597-B1) and RT bacteria (ATCC 33257) mixed and filtered through a cartridge at different superficial velocity through the media with a desired solution chemistry (i.e., solution pH and NaCl concentration).
The diffusion coefficients as a function of NaCl concentration in suspensions at 25 ± 2 ℃ and pH7 were calculated with the use of data in Ref. [25] for of Na+, Cl-, OH-, H+ ions, Ref. [26] for viruses, and Ref. [27].
The measurable Brownian diffusion velocity of colloidal particles and/or ions in a suspension is the mean square displacement of the particle given by the Einstein equation for a spherical particle suspended in liquids [28]:
Where t is the time elapsed from the moment when particle or ion was in its initial position and D is translational diffusion coefficient in a liquid is defined by Stokes-Einstein relation (see equation 1). Furthermore, the electrostatic attraction should not play significant role due to highly efficient shielding by the EDL layer with Debye length as short as 1.6 Å in the case of RT suspension in the 3.0 M NaCl electrolyte [29].
The diffusion coefficients for MS2 bacteriophage and Raoultella Terrigena (RT) bacteria in 0.01 mM and 0.1 mM NaCl electrolytes [18,19] were found to be 1.4.10-7 and 4.8.10-9 cm2/s, that are within accuracy with corresponding diffusion coefficients for MS2 bacteriophage (1.47.10-7 cm2/s) and RT bacteria (3.0.10-9 cm2/s. According to Feynman (Ref. [30] Figure 1, Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6) in the case of NaCl electrolyte: "The hydrogen ends of the water molecules are more likely to be near the chlorine ion, while near the sodium ion we are more likely to find the oxygen end, because the sodium is positive and the oxygen end of the water is negative, and they attract electrically". Moreover, the quantum effects are shown to be substantial for the self-diffusion constant of water for the isomers of the water such as hexamer and several isomers such as 20-mers [31] and dimers [32,33].
Ise, et al. [34] studied "ordered" structures in dilute suspension of highly charged polymer lattices using an ultramicroscope with resolving power much higher than that of the ordinary optical microscope and concluded that [35] the like-likes-like attraction [36] appears for highly charge ones [37]. Ise [38] concluded that lattice-like ionic distribution exists in the solutions because of interaction linkage through the intermediary of counterions following experimental supports for such an ordered structure have recently been documented.
Adsorption of inks: Removal efficiency of inkjet ink particles (Canon PGI-5/PGI-220 BK Pigment) by one layer of High Flow Disruptor at a flow velocity of 0.7 mm/s and at neutral pH from distilled water (DW) and salted waters was measured by Genesis-10 UV spectrophotometer in a 1 cm long cuvette at wavelength of 300 nm. Figure 1 shows removal efficiency of inkjet ink with mean particle size of 127.49 nm and with zeta potential ζ = -32.1 mV [39] at dilution ratio of 10,000:1. At this dilution ratio the ionic strength of the suspension was measured to be 0.01 mM. Ink stock in distilled suspension was filtered through a polymeric membrane with rating of 0.22 μm and kept in polypropylene bottle with a cap to reduce CO2 acidification of the suspension. Salt was added just before the experiment. The filter disk was flushed with 50 mL of DW and the residual of DW water was removed out from filter the holder and partially from the filter disk flushing with 50 cm3 of air at flow velocity 0.7 mm/s. Average values of LRV = -log(Cout/Cin) were used based on at least three replicates at a given NaCl concentration.
Local potential of ink suspension in distilled water at 0.5 μm from the capillary wall assuming that it can be modeled by a flat surface is estimated to be 0.13 mV (See equation 12 in Table 10.4 of Ref. [40]) rising to Ψ0 ≥ 70 mV close to the capillary surface.
Results of Figure 1 show that the intervening ions play a dominant role in removing ink particles allowing the clouds of counterions compress around charged ink particles around and between highly charge capillary wall and colloidal particle, generating attraction via the intervening Cl counter-ions of NaCl electrolyte. The adsorption occurs in a stepwise fashion: (i) The nearby to the capillary wall ion clouds attract by the electrostatic forces at a given point of the capillary until the electrical double layer (EDL) is saturated, that is, for the case of NaCl electrolyte the ionic strength is up to 6.1 M at ambient temperature of 298 K; (ii) The closest to the removed ion cloud ions replace the space occupied by the adsorbed ions and so on.
Complex field extension: We define complex field (see Section 2.1.6) extension from boehmite nanofiber surface to be equal to a distance that colloidal particle with dimensions from 1 nm to 1 μm (Ref. [41], Chapter 1.3. Page 37)] travels from the farthest point P in the plane of the assembly (Figure 1) with x = r0 at the center of colloidal particle and x = 0 to the surface of the assembly either as a much [18] or in the capillary pore [19] during a certain time interval. This distance can be viewed as the complex field extension established via counterion-mediated electrostatic attractive interaction in macroionic solution that could be accounted for by using the Sogami pair potential with Rmin minimum defined by equation (42) of Ref. [42] that has depth well surpassing the thermal energy kT. However, at ka > 3.2 ordered structures are destroying (see below). Sogami-Ise theory [43-45] combined with the Dirichlet boundary condition (constant surface potential) yields the prediction that the ratio(s) of the salt concentration in the supernatant fluid to the average salt concentration in the gel phase be constant. This is a central prediction of the Sogami-Ise theory, in which there is a weak attractive tail in the electrical interaction potential. The standard theory of colloid stability, the DLVO theory [46,47], is shown to be a limiting case of the Coulombic attraction theory [48], in the one-phase region.
Table 1 show counterion-mediated attractive interaction translational velocities for ink particles with mean dimension of 127 nm and MS2 bacteriophage with mean dimension of 27 nm.
Results of Table 1 show that counterion-mediated attractive interaction translational velocities for ink particles and MS2 bacteriophages in the cases of 0.1 mM and 0.01 mM NaCl electrolyte are equal to the average velocity V = 0.20 ± 0.05 μm/s within 2σ of standard deviations within each other even though the sizes of colloidal particles are different by a factor of 5 and the travel distances by a factor of 129 ± 46 for 1 mM NaCl electrolyte and 780 ± 135 for the 0.1 mM NaCl electrolyte. Figure 1 suggests that counterion-mediated attractive interaction via the intervening ions play a dominant role in removing colloidal particles allowing the clouds of counterions compress around charged colloidal particles and around and between the highly charged surfaces with surface potential greater than 70 mV in either the capillary wall or in the mulch suspension generating attraction via the intervening counter-ions. The NC assemblies with high surface area and high surface potential adsorb the nearby to the capillary wall ion clouds until the EDL layer is saturated, that is, in the case of NaCl 1:1 electrolyte it reaches ionic strength of 6.1 M at 298 K (Ref. [49], page 5-199 With the use of mean field approach Sogami [42-44] formulated Langmuir's idea [50,51] and showed that the electrostatic Helmholtz free energy Fel is not equal to the corresponding Gibbs free energy Gel, at variance with the DLVO assumption Fel = Gel. Ise, et al. also found that the center-to-center interparticle distance decreased with increasing concentration of NaCl 1:1 coexisting salt with ionic strength from 1.71 μM to 68.4 μM, and further increase in the ionic strength to still very dilute 0.137 mM naturally destroyed the ordered structure (see Table 2 of Ref. [35]) and particles showed Brownian motion (see Åbstract of Ref. [35]). These observations indicate that Sogami Ise theory has limitations at ka > 6.19 ± 0.14 where k-1 = lDebye ~ 367Å with type SS-37 latex particles with radius of a = 2270 ± 50 Å. Smalley [48] indicated that in the case of swelling clays the inverse Debye screening length in salt soaking solution kex significantly different (see Ref. [48], page 52, equations 3.4 and 3.15, Table 3.5 and Figure 3.11) from these obtained from the least-squares fits referring to the internal kappa (kin inside the gel) with one point obtained at cex = 0.03 M/L far outside the trend presented in Figure 3.11 and Table 3.5 of Ref. [48].
Experimental results [24] for sorbents with surface potential Ψ0 greater than 70 mV in aqueous solutions with ionic strength up to 4M, show the constancy of the ratio of Cfinal/Cinitial where Cinitial and Cfinal are the initial and final concentrations of colloidal particles as well as associated quantities such as removal efficiency = (1-Cfinal/Cinitial) 100% and logarithm reduction value LRV = -log10(Cfinal/Cinitial) for a given adsorptive media with surface potential Ψ0 greater than 70 mV defined as:
Cfinal/Cinitial = Constant (2)
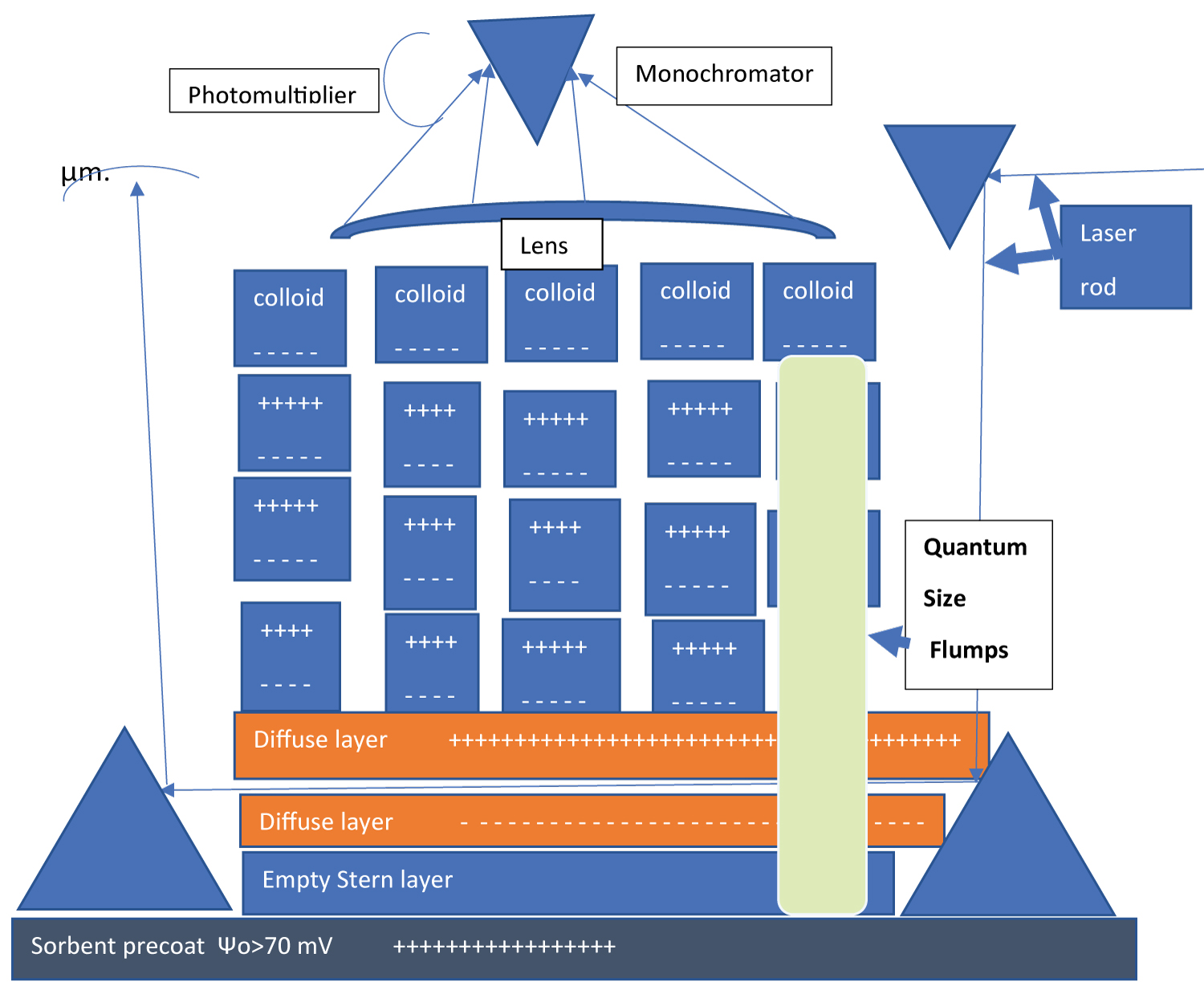
Where the constant is independent of electrolyte ionic strength in the range from 0.01 mM to 3M, of pH in the range from pH3 to pH10, of flow velocity in the capillary pores in the range from 0.1 mm/s to 10 mm/s [24] for 1:1 electrolyte and for either an adsorptive media or a device with average pore size less than 8 μm. Equation (2) is in disagreement with theory [52]. We argue in the present work that counterion-mediated quantum enhanced long range interaction contribute to the validity of equation 2. The proposed mechanism of adsorption is sketched in Figure 2 where negatively charged surface of a colloidal particle is linked with highly positively charged sorbent with surface potential greater than 70 mV in water via counterion-mediated quantum enhanced long range interaction that can be visualized as quantum size famous British flumps sweet which is a combination of long marshmallow cables, twisted together in a helix shape. It attaches itself by one side to negatively charged part of the colloidal surface (The entire colloidal particle could be positively charged in water at a given pH as e.g., the fr bacteriophage (ATCC 15767-B1) that is also effectively adsorbed by the highly positively charges surface with surface potential greater than 70 mV in water) and by the other side either attached in still water (Figure 2) or is sliding along the sorbent surface in moving water. When the strength of either of these bonds became weaker than the energy of the thermal motion kT, the flumps detach from the surfaces and ordered structure is destroying.
Scanning experiments with continuous wave ring dye laser: To clarify problems of this nature we propose to study some models of flumps formation in a static mode when colloidal particles are buoyant on a 2D surface (not as a 3D ordered structures) of a supernatant fluid above the 3-5 mm thick precoat layer made from a sorbent as described in Ref. [19].
The depth of the supernatant layer should be approximately 1 mm to where the flump links can reach from the sorbent surface (see Refs. [18,19]). The light source is suggested to be a continuous wave dye laser (e.g., Coherent ring dye laser) with a narrow laser beam rod. Dye lasers are available in either pulsed (up to 50-100 mJ) or continuous output (up to a few Watts) in table-top systems that are pumped by either flash lamps or lasers [53]. Schematic of setup for a scanning LIF experiment is presented in Figure 2. The continuous ring dye lasers are preferred to pulse lasers for the purpose of the present work since the angle of the radiation goes like the root of the relative width of the line and deviation from parallelism is related to the fact that laser radiation is not completely monochromatic (see, e.g., Ref. [54], page 242]). The laser rod will be adjusted by lifting the dye laser unit up and down while tilting the angle to direct the laser rod with the use of two prisms situated above the precoat and several lenses on the optical bench to be parallel to the precoat and propagated through 1 mm deep supernatant. The precoat is created with the use of a Buckner funnel with a vacuum pump with a receiver (see Ref. [19] with diameter 38 mm and surface area 11 cm2). The precoat build-up is terminated when the supernatant depth reaches approximately 1 mm with total volume of the supernatant fluid of approximately 1 cm3. Then the two bottom prisms (entrance and exit) are immersed into the supernatant with the use of two independent micro-screws while the bottom parts of the prisms are touching the precoat. Then the laser rod is readjusted and approximately 0.1 cm3 of a colloidal suspension that stays buoyant in each fluid, (for example, the porous spheres coated with a nanolayer of boehmite) is added carefully (not disturbing the precoat) on the top of a given supernatant fluid through multiple microjets from different directions. The laser induced fluorescence (LIF) light is collected with the use of double-convex lens and steered onto a fifth prism that images the focused LIF light from the laser rod propagated through the supernatant onto a photomultiplier equipped with a broad-band filter and onto an input slit of a monochromator. When the photomultiplier detects a fluorescent signal the signal is adjusted for both, the multiplier and the monochromator tilting the double-convex lens with the micrometre screws and the LIF spectra is recorded and the energy linkages of the lowest states and the symmetries of flumps are established.
Quantization of Maxwell-Dirac field equations: The field laws arise from a Hamiltonian principle [55-57] which is analogous to the Hamiltonian principle of classical mechanics expressed in term of Lagrangian function L which depends on the position qi and their derivatives with respect to time ([58], page 253). It is, however, more convenient to work with the momentum components instead of the velocity components [56] p.85]. Let us call the coordinates qr r going from 1 to 3 times the number of particles, and corresponding momentum components pr that are called canonical coordinates and moment a [56] p. 85]. An important concept in general dynamic theory is the Poisson Bracket (PB) [59] and quantum PB [59] of any two dynamical variables u and v. The equation of motion for generalized coordinates are expresse, d in three different but equivalent ways: The Lagrange equation formulation, the Hamilton's equation formulation, and the Poisson bracket formulation (Ref. [59] equations 2-23 and 2-24). Classical particle theories contain rarely used PB entities ([59] page 3). The process of extrapolating from classical theory to quantum theory becomes known as quantization (Ref. [59], page 4). Quantization for both non-relativistic and relativistic particle theories, entails (i) Using the classical form of the Hamiltonian as the quantum form of the Hamiltonian (Ref. [59] page 41]) and (ii) Changing PB to commutators. The classical non relativistic particle and non-relativistic quantum mechanics (NRQM) theories have the same relations except that the commutators of quantum theory correspond to PBs of classical theory times a factor of -i/h (Ref. [59] chapters 2.7.2 and 3.1.1, pp. 29 and 42). If we postulate that the solution φ of the Klein-Gordon equation describes a field instead of a particle (Ref. [59] page 48). Because the QFT describes the real world so well, it justifies the above postulate. We further postulate that the field φ to be complex. This means re-expressing values for and in term of a complex field, but such as and remain real (energy and energy density H, must be real numbers) (Ref. [59]). This yields the free complex field Lagrangian and Hamiltonian densities (Ref. [59] equations 3-32, 3-33, 3-150, 3-151) For a dynamical system with classical analogue, the state for which the classical description is valid as an approximation is represented in quantum mechanics by a wave packet. The result is that Schrodinger's wave equation fixes how such wave packet varies with time. We suppose that the time-dependent wave function in Schrodinger's representation is of the form (Ref. [56] page 121):
Where the S is the quantum analogue of the classical action function and equals it in the limit h→0. In classical mechanics a Gibbs ensemble is defined in the phase space, whose number of dimensions is twice the number of degrees of freedom of the system [Ref. [56] page 131]. Suppose that we are not given that the system is in a definite state at any time, but only that it is in one or other of several possible states according to a definite probability law. We should be able to represent it by fluid in the phase space, the mass of fluid in any volume of the phase space being the total probability of the system being in any state whose representative point lies in that volume. Each particle of the fluid will be moving according to the equation of motion. If we introduce the density ρ of the fluid at any point, equal to the probability per unit volume of phase space of the system being in the neighbourhood of the corresponding state, the equation of conservation is (Ref. [56] equation 65):
This may be considered as the equation of motion for the fluid, since it determines the density ρ for all time if ρ is given initially as a function of the q's and p's with normalizing condition for ρ
In classical mechanics the Gibbs ensemble for a dynamical system in thermodynamic equilibrium with the surroundings at a given temperature T is represented by a density (Ref. [56] equation 74, page 74).
H being the Hamiltonian independent of the time. Dirac described the above procedure in Reference [55].
LIF experimental methods: To clarify problems of this nature we propose to study some models of flumps formation not only in the static mode (Section 2.1.5 and Figure 2) when colloidal particles are buoyant on a 2D surface but also as a 3D ordered structures [35-37] with surface potential of greater than 70 mV. The LIF method allows capture the nascent reaction products including flumps formation under single-collision conditions [60,61]. Since the flumps consist of ions, the state-specific resonance enhanced multiphoton ionization (REMPI) process [62,63]. In the present work we propose to use the supersonic expansion that causes extensive cooling of the ion complexes, which greatly simplified the spectral analysis. The capillary electrophoresis (CE) method that applies a strong electric field across the length of the capillary filled with liquid and loaded with flumps. The electric field cases ions and flumps to move at different speed along the capillary [64,65]. The spatual resolution of visible light microscopy has been increased to approximately 10 to 20 nm, allowing some processes to be described at the molecular scale [50,51]. Experimental results make it clear that colloidal particles are buoyant on a 2D surface (not as a 3D ordered structures) that colloidal transport mechanism in highly charge capillary pores or in mulches is driving by the intervening ions, the mechanism first proposed in the 1930s [66,67], and is responsible for high removal efficiency of charged colloidal particles from polar fluids not only at high flow velocities but also at high salt concentrations.
Conclusions
Experimental colloidal particle removal efficiencies by three adsorptive media all with surface potential greater than 70 mV were found to be insensitive to the superficial velocity through the media, pH, and to salt concentrations. That electrostatic mechanism plays a major role in kinetics of deposition of Brownian colloidal particles in highly positively charged porous media immersed in the polar suspensions. Interfacial electrodynamics of colloidal particle-collector interaction coupled with hydrodynamics of pressure driven flow in the filter media capillary pores together with effects of surface roughness on dynamics of interaction are presumed to have significant effects on the dynamics of adsorption.
The liquid for preparation of colloidal suspension could be either water (H2O), heavy water (D2O), or their mixture with possible formation of mixed heavy water HOD molecules or any other polar liquid such as alcohols.
Acknowledgements
The author gratefully acknowledges the use of the resources of the Cherry L. Emerson Center for Scientific Computation.
Conflicts of Interest
There are no conflicts to declare.