Effects of Expansion Rate on Stress Evolution of TWIP Expandable Tubular Based on TSS Criterion

International Journal of Metallurgy and Metal Physics
(ISSN: 2631-5076)
Volume 5, Issue 3
Research Article
DOI: 10.35840/2631-5076/9259
Effects of Expansion Rate on Stress Evolution of TWIP Expandable Tubular Based on TSS Criterion
Yun Luo, Wenchun Jiang, Fan Zhou and Shengjun Huang
Table of Content
Figures

Figure 3: The true and engineering stress-strain....
The true and engineering stress-strain curve of TWIP steel.

Figure 4: (a) The expansion experiment device in....
(a) The expansion experiment device in site; and (b) XRD setup of residual stress.
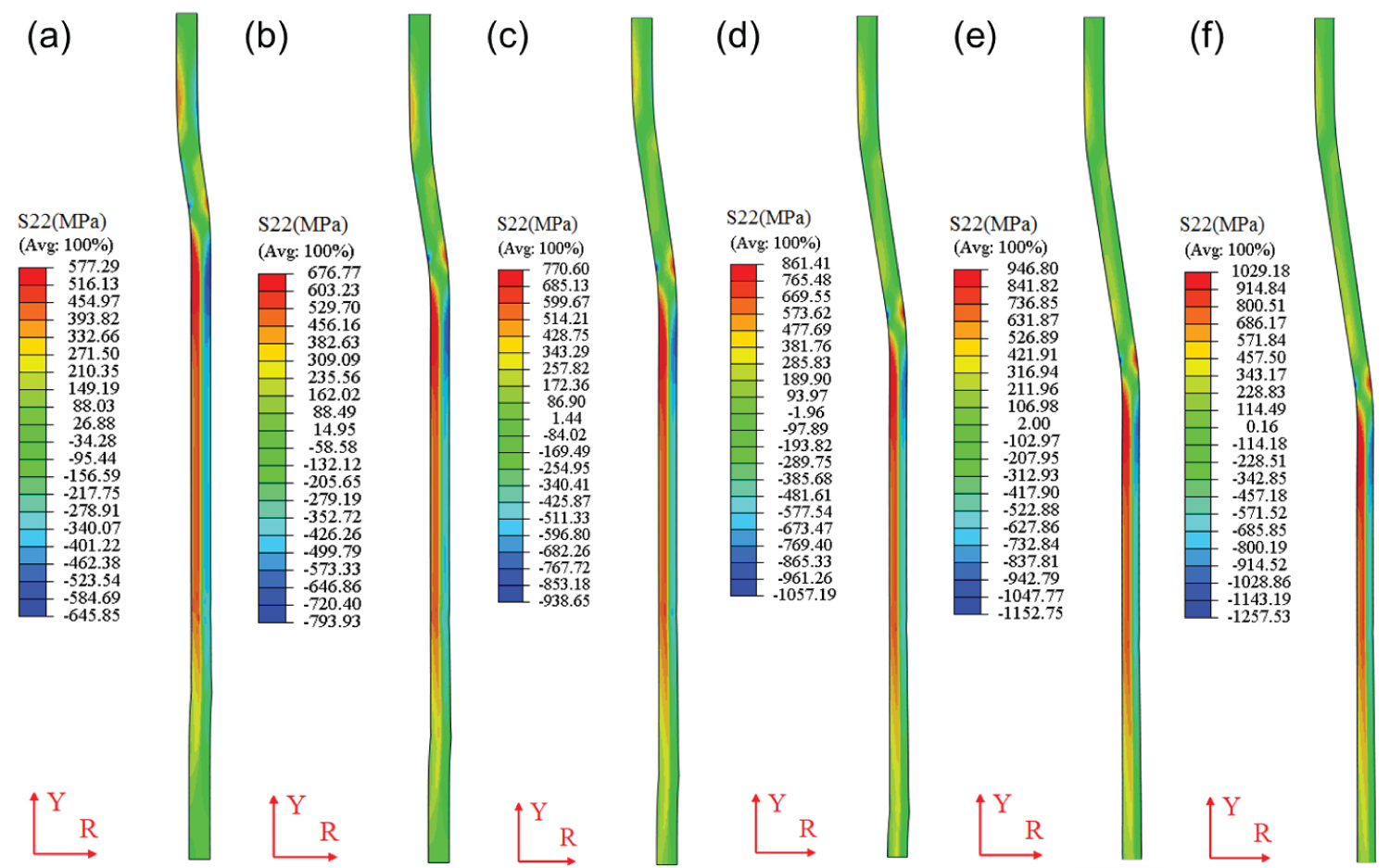
Figure 5: The effects of expansion rate on the contour....
The effects of expansion rate on the contour distribution of axial stress during expanding process: (a) 10%, (b) 15%, (c) 20%, (d) 25%, (e) 30%, (f) 35%.

Figure 6: The effects of expansion rate on the contour....
The effects of expansion rate on the contour distribution of hoop stress during expanding process: (a)10%, (b) 15%, (c) 20%, (d) 25%, (e) 30%, (f) 35%.
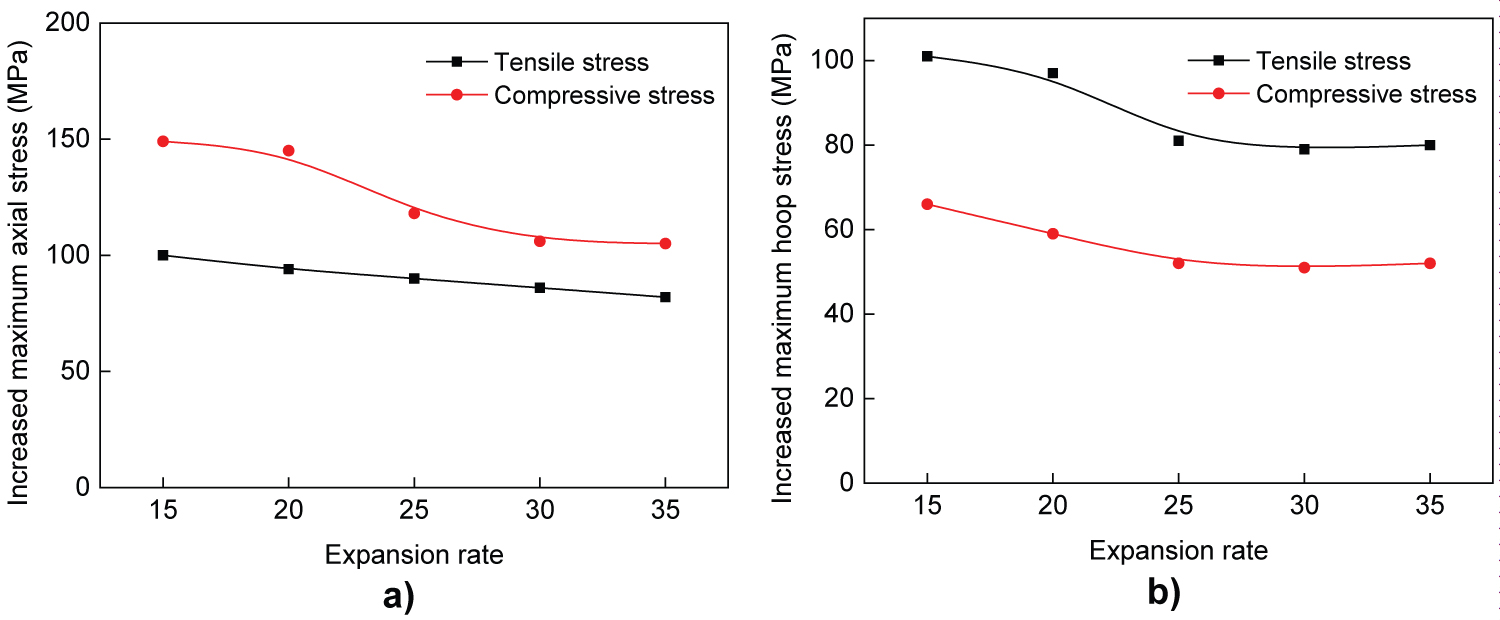
Figure 7: (a) The increased maximum axial stress...
(a) The increased maximum axial stress; and (b) The increased maximum hoop stress; during expanding process for different expansion rates compared to expansion rate 10%.
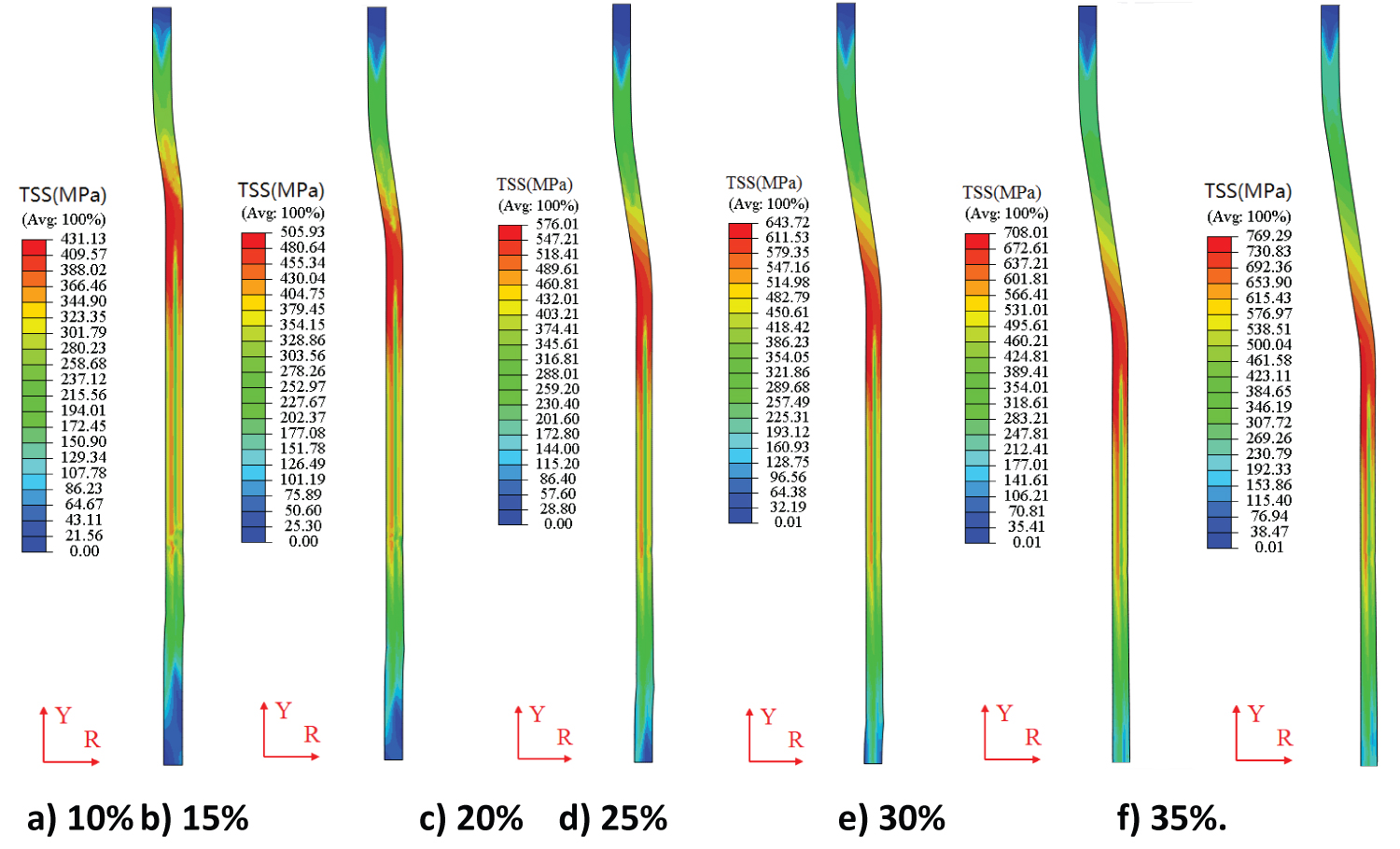
Figure 8: The effects of expansion rate on...
The effects of expansion rate on the contour distribution of TSS equivalent stress during expanding process.

Figure 9: The increased maximum TSS during expanding ...
The increased maximum TSS during expanding process for different expansion rates compared to expansion rate 10%.
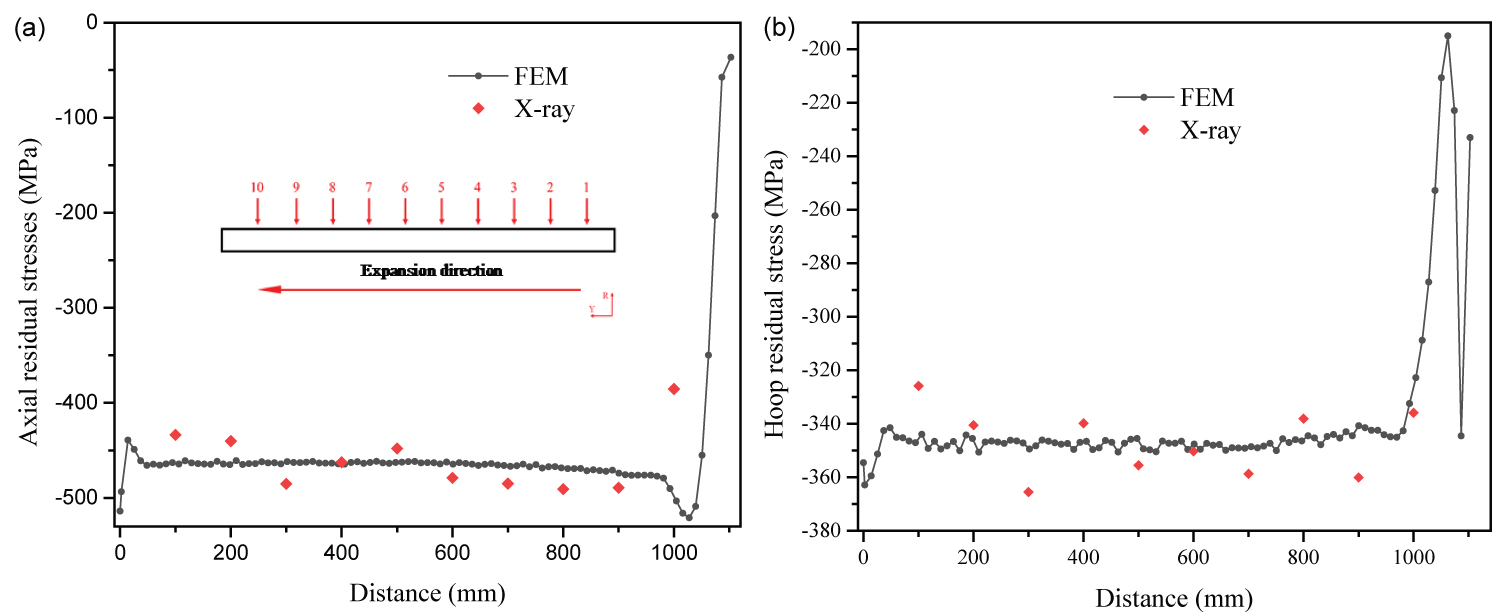
Figure 10: Comparison of: (a) Axial residual stress...
Comparison of: (a) Axial residual stress; and (b) Hoop residual stress; on the outer surface by simulation and experiment.
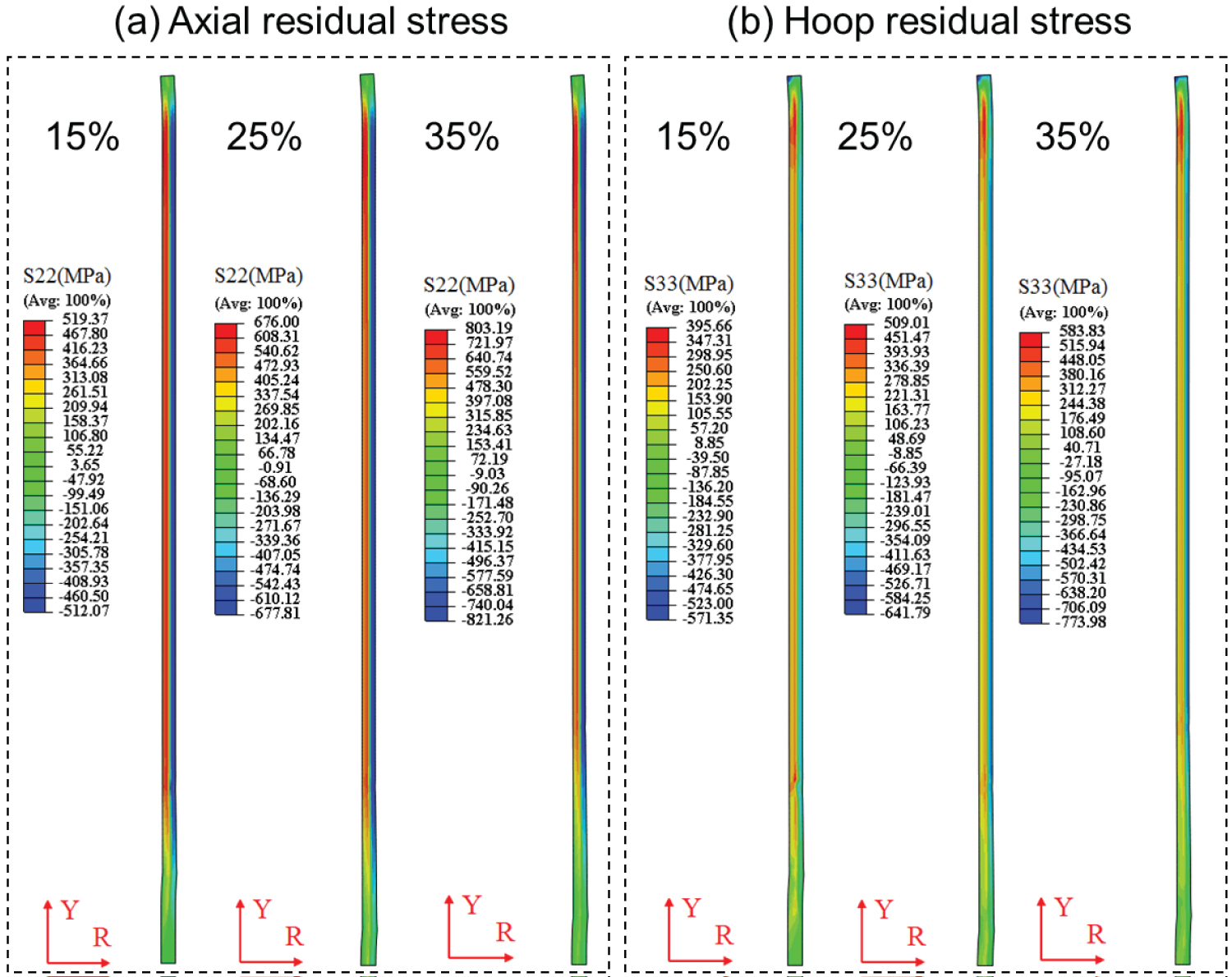
Figure 11: The contour distribution of: (a) Axial...
The contour distribution of: (a) Axial residual stres; and (b) Hoop residual stress; for different expansion rates.
References
- Xu B, Zhang Y, Hui W, Yin H, Tao J (2009) Application of numerical simulation in the solid expandable tubular repair for casing damaged wells. Pet Explor Dev 36: 651-657.
- Pervez T (2010) Experimental and numerical investigation of expandable tubular structural integrity for well applications. Journal of Achievements in Materials & Manufacturing Engineering 41: 147-154.
- Akisanya AR, Khan FU, Deans WF, Wood P (2011) Cold hydraulic expansion of oil well tubulars. International Journal of Pressure Vessels and Piping 88: 465-472.
- Al-Abri OS, Pervez T (2013) Structural behavior of solid expandable tubular undergoes radial expansion process-analytical, numerical, and experimental approaches. International Journal of Solids & Structures 50: 2980-2994.
- Pervez T, Qamar SZ, Al-Abri OS, Khan R (2012) Experimental and numerical simulation of in-situ tube expansion for deep gas wells. Mater Manuf Process 27: 727-732.
- Wilson A (2013) New design of solid-expandable tubular aids patching of hard-to-reach casing. J Pet Technol 65: 112-114.
- Khan R, Pervez T, Alrasheedi NH, Al-Abri O, Sajid A (2017) Effects of expansion rate on plasticity and structural integrity of downhole tubular. International Journal of Pressure Vessels and Piping 151: 1-10.
- Liu YZ, Qiu XM (2016) A theoretical study of the expansion metal tubes. International Journal of Mechanical Sciences 114: 157-165.
- Liu YZ, Qiu XM, Yu TX (2018) A theoretical model of the inversion tube over a conical die. Thin-Walled Structures 127: 31-39.
- Liu YZ, Qiu X (2018) A theoretical model of the shrinking metal tubes. International Journal of Mechanical Sciences 144: 564-575.
- Agata J, Tsuru E, Sawamura M, Asahi H, Tsugihara H (2013) An experimental and numerical approach to the prediction of expandability and collapse resistance for solid expandable tubulars. Society of Petroleum Engineers 18: 406-415.
- Li T, Gao S, Chen Q, Li YL, Han WY, et al. (2013) Innovative design of the solid expandable tubular to patch the casing: area below the previously installed expandable tubular. International Petroleum Technology Conference, China.
- Xu SG, Wang C, Wang SK, Zhang L, Li XC, et al. (2017) Experimental study of mechanical properties and residual stresses of expandable tubulars with a thread joint. Thin-Walled Struct 115: 247-254.
- Xu S, Wang S, Meng W, Wang C, Sun Z (2017) Study of the effect of the expansion cone on the expansion process in solid expandable tubulars with thread joints. Journal of Petroleum Science and Engineering 158: 175-185.
- Zhang S, Wang Q, Zhou W (2019) Implementation of the Tresca yield criterion in finite element analysis of burst capacity of pipelines. International Journal of Pressure Vessels and Piping 172: 180-187.
- Khanna K, Gupta VK, Nigam SP (2017) Creep analysis in functionally graded rotating disc using Tresca criterion and comparison with von-mises criterion. Materialstoday: Proceedings 4: 2431-2438.
- Yu MH (1983) Twin shear stress yield criterion. International Journal of Mechanical Sciences 25: 71-74.
- Yu MH, He LN, Liu CY (1992) Generalized twin shear stress yield criterion and its generalization. Chinese Science Bulletin 37: 2085-2089.
- Yu MH (2004) Unified strength theory and its applications. (2nd edn), Springer-Verlag, Berlin, Germany.
- Taylor GI, Quinney H (1932) The plastic distortion of metals. Philosophical Transactions of the Royal Society A Mathematical Physical & Engineering Sciences 230: 323-362.
- Ivey HJ (1961) Plastic stress-strain relations and yield surfaces for aluminium alloys. Archive Journal of Mechanical Engineering Science 3: 15-31.
- Winstone MR (1984) Influence of prestress on the yield surface of the cast nickel superalloy marm002 at elevated temperature. Mechanical Behaviour of Materials 1984: 199-205.
- Wu HC, Yeh WC (1991) On the experimental determination of yield surfaces and some results of annealed 304 stainless steel. International Journal of Plasticity 7: 803-826.
- Ishikawa H (1997) Subsequent yield surface probed from its current center. International Journal of Plasticity 13: 533-549.
- Pervez T, Seibi AC, Karrech A (2005) Simulation of solid tubular expansion in well drilling using finite element method. Petroleum Sci Technol 23: 775-794.
- Zhang JB, Jia YL, Lv XH (2011) Finite element simulations of mechanical properties of solid expandable tubular threaded joint. Adv Mater Res 421: 258-262.
- Pervez T, Qamar SZ (2011) Finite element analysis of tubular ovality in oil well. Adv Mater Res 264-265: 1654-1659.
- Jiang W, Luo Y, Li JH, Woo W (2016) Residual stress distribution in a dissimilar weld joint by experimental and simulation study. J Pressure Vessel Technol 139: 011402.
- Liao X, Qi Y, Zhu X, Cheng F, Qin F (2019) Failure analysis and solution study of 203?mm solid expandable tubular. Engineering Failure Analysis 106: 104135.
- Khajeian A, Mahmoudi AH, Mehmanparast A (2019) Shot peening effects on residual stresses redistribution of offshore wind monopile multi-pass weldments. Marine Structures 66: 106-120.
- Ren S, Li S, Wang Y, Deng D, Ma N (2019) Finite element analysis of residual stress in 2.25Cr-1Mo steel pipe during welding and heat treatment process. Journal of Manufacturing Processes 47: 110-118.
Author Details
Yun Luo*, Wenchun Jiang, Fan Zhou and Shengjun Huang
College of New Energy, China University of Petroleum (East China), China
Corresponding author
Yun Luo, College of New Energy, China University of Petroleum (East China), Qingdao, 266580, China, Tel/Fax: +86-532-86983481; +86-532-86980609.
Accepted: October 01, 2020 | Published Online: October 03, 2020
Citation: Luo Y, Jiang W, Zhou F, Huang S (2020) Effects of Expansion Rate on Stress Evolution of TWIP Expandable Tubular Based on TSS Criterion. Int J Metall Met Phys 5:059
Copyright: © 2020 Luo Y, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Expansion rate is key parameter to the manufacture of expandable tubular. In this paper, the effects of expansion rate on stress evolution of twinning induced plasticity (TWIP) steel expansion tubular were discussed in detail. A user subroutine UMAT using twin shear stress (TSS) yield criterion is employed to simulate the expanding process. The results show that the predicted residual stresses agree with the experiment very well. The axial expanding stress showed the layered distribution along the thickness direction and the hoop tensile stress is mainly located in the corner of expanded area. With the steady increases of expansion rate, the expanding axial, hoop and TSS stresses are all increased, and the increasing rate is decreased gradually. The residual stresses are tensile in inner surface and compressive in outer surface. Both the hoop and axial stresses are all increased with the increases of expansion rate. The suggested expansion rate should be controlled below 35%.
Keywords
Expandable tubular, Expansion rate, Residual stress, Expanding stress, TWIP steel
Introduction
The expandable tubular technology is regarded as a revolutionary new technology in the field of petroleum drilling and production, and has been widely used in the construction operations such as drilling, completion, oil recovery and workover [1]. The expansion tubular is formed by generating permanent plastic deformation using expansion cone. After expansion, the diameter of expanded tubular is increased compared to old dimension. The expansion rate (the ratio of increased diameter to old diameter) is an important parameter to characterize the expansion properties of tubular [2]. In general, the expansion rate used for originally casing patch is usually less than 15%. However, the expansion rate of equal well tubular used in deep well drilling reached more than 20%, which brings new challenges to the application of bigger expansion rate tubular [3]. Therefore, it is very important to study the effects of expansion rate on mechanical properties of expansion tubular, so as to provide guidance to the manufacture of expansion tubular.
Expandable tubular technology was proposed by Royal Dutch Shell in 1990 [4]. After more than 20 years of development, expandable tubular technology has become one of the advanced technologies widely used in drilling engineering [5]. It is mainly used to solve the problems of casing placement, pipe sleeve leakage and so on [6]. Up to now, there are many researchers investigated the expansion theory, expansion tube design, and manufacture technology of expandable tubular by experiment, theoretical and simulation methods. Khan, et al. [7] investigated the effects of expansion rate on plasticity and structural integrity of down-hole solid tubular. They found that there is variation in effective stress, equivalent plastic strain, and thickness reduction, thus ultimately influence expansion properties, collapse and burst strengths of tubular. Liu, et al. [8-10] systematically studied the process of expansion, reversal and shrinkage of metal tube, and the corresponding theoretical models have been established. Agata, et al. [11] extended the experimental and numerical models to investigate the effect of material factors on the collapse resistance of solid expandable tubulars, and a formula was determined based on the results. Li, et al. [12] and Wilson [6] developed innovative designs of solid expandable tubulars to successfully perform casing patch in difficult conditions, and the designs proved to be cost effective. Xu, et al. [13,14] investigated the deformation, residual stress, mechanical properties, and microstructure variation of the expansion process for J55 steel expandable tube with thread joints by experiment and simulation. And the effect of expansion cone geometry was investigated. A cone angle of 9° and sizing section length of 65-75 mm were proposed [14]. In their study, the research models are based on the Tresca or Mises yield criterion, and the effects of the intermediate principal stress were ignored in the yield model.
Expansion theory is the basis of equal well diameter expandable tubular technology. And the yield criterion is key part of expansion theory. Nowadays, the yield criterion is mainly divided into three types: Single-shear yield, twin-shear yield, and three-shear yield criterion. The single-shear yield criterion is Tresca yield criterion proposed by Tresca in 1864 [15]. The typical three-shear yield criterion is von Mises yield criterion proposed in 1913 [16], which is a popular yield criterion widely used in engineering assessment. The twin-shear stress (TSS) yield criterion was proposed by Yu Mao-hong in 1961 [17] and the extension of the development into the unified yield condition in 1991 [18]. All kinds of yield conditions have their own characteristics and corresponding application scope, and different types of materials need to choose the applicable yield criterion in plastic behavior analysis, especially for different ratios of shear yield strength to tensile yield strength (η). Yu [19] pointed out that the suitable yield criterion for ratio η 0.5, 0.577 and 0.6687 are Tresca, Mises and twin-shear yield criterion, respectively. Taylor [20] and Ivey [21] carried out a large amount of axial force-torsion tests on thin-walled steel tubes, and found that the measured experimental data of shear-axial stress were in good agreement with the twin-shear yield condition, while it has a large difference with the Mises yield condition. Winston [22] measured initial yield surface of nickel at 750 °C by acoustic emission technique and found the ratio η is 0.7, which is similar to that of TSS yield criterion. Wu, et al. [23] investigated the initial yield surface of 304 stainless steel by the axial force-torsion test and found that is different from the Mises yield surface, and the ratio η is larger than 0.66. Ishikawa, et al. [24] also found the measured yield surface of 304 stainless steel is quite different from that of Mises yield criterion. Because the TSS yield condition has a simple linear form and has a good degree of coincidence with the experimental results, the TSS yield condition has been paid more attention at home and abroad, and gradually applied to the stress analysis of engineering structures.
Up to now, there are many experiment and finite element analysis were performed on the study of expansion process of tubular [25-27], but theoretical analysis is almost based on von Mises yield criterion. And little studies were performed on the expansion forming by the combination method of theoretical, experimental and simulation. For the larger expansion rate tubular, the twinning-induced plasticity (TWIP) steel is a potential material because of good strengthening properties (small ratio of yield strength to tensile strength). By using tensile and torsional experiments, the yield and torsional strength of TWIP steel are 250 and 161 MPa, respectively. The ratio of shear to tensile strength ratio η for TWIP steel is 0.64, so the TSS yield criterion is more suitable for the TWIP steel. In this study, the finite element modeling (FEM) based TSS yield criterion was employed to study the expanding process of TWIP steel. First, a two dimensional (2D) axisymmetric finite element model of the expandable tubular was developed using the software ABAQUS complained by user subroutine UMAT by considering TSS yield criterion. Then, an expandable tubular experiment was carried out in the laboratory to verify the validity of simulation results. Last, the effect of the expansion rate on the expansion stress and residual stress were discussed, and then an optimal design of the expansion rate was attained.
Finite Element Analysis
Finite element model
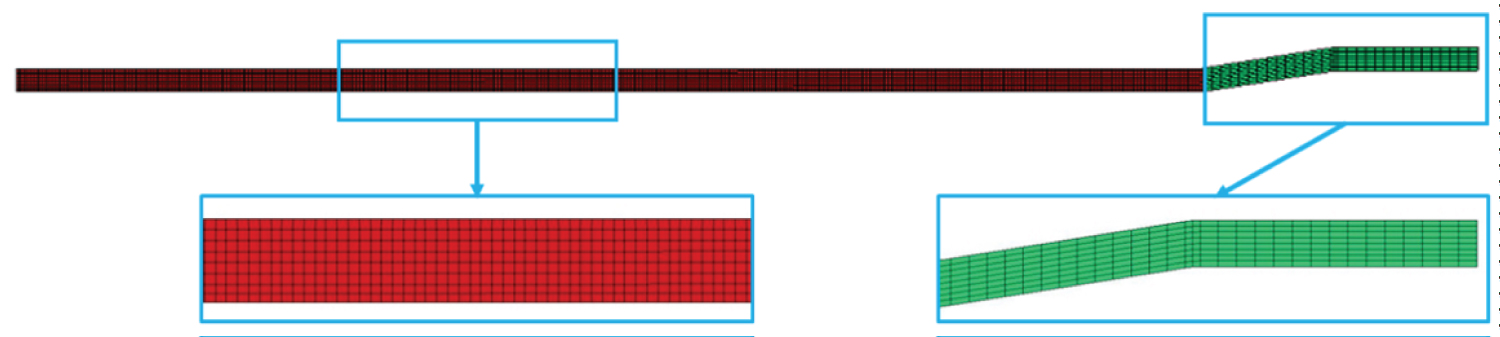
The external diameter and wall thickness of expansion tubular before expanding are 139.7 and 9.85 mm, respectively, as shown in Figure 1. In order to improving calculation efficiency, 2D axisymmetric model is used in the finite element analysis. The half cone angle of expansion cone is 9°. The length of unexpanded section of the expansion tube is 500 mm. The diameter of the expansion cone is determined by the expansion rate. So, the calibrating section diameter of the expansion cone for the expansion rate 10%, 15%, 20%, 25%, 30% and 35% are 151.7 mm, 155.7 mm, 163.7 mm, 169.7 mm, 175.7 mm, and 181.7 mm, respectively.
Considering that the wall thickness is relatively thin, the mesh size of the expansion tube region is controlled to be about 1 mm. The mesh of the expansion section is relatively dense, and it is sparse in other areas. Figure 2 shows the finite element meshing of expandable tubular. The red area is the expansion tube, and the green area is the expansion introduction section. The element is an axisymmetric linear reduction integral element (CAX4R). During the finite element analysis, the expansion cone is regarded as a rigid body and no deformation is generated.
Material properties
The material of expansion tubular is TWIP steel, which has excellent extension and strengthening properties, and can meet the requirements of mechanical properties under large expansion rate. The true stress-strain curve was shown in Figure 3. The elastic modulus and poisson ratio are 300 GPa and 0.3, respectively. And the yield strength and tensile strength are 250 MPa and 800 MPa, respectively. The ideal elastic-plastic model, ideal rigid plastic model and power exponential hardening model were used. The parameter A and m for the power exponential hardening model are 1099.5 MPa and 0.384.
In the finite element analysis, the node in the end of expansion tubular is fixed. The displacement load was applied in the expansion direction. The friction coefficient between the inner wall of the expansion tube and the surface of the expansion cone is assumed as 0.15.
Constitutive model
The total strain is decomposed into the elastic and plastic strain under the assumption of small deformation:
Where the εe and εp represent the elastic and plastic strain tensors, respectively. Elastic strain was modeled using the isotropic Hooke's law with temperature-dependent Young's modulus and Poisson's ratio. For the plastic strain, a rate-independent plastic model was employed with TSS yield surface and isotropic hardening model.
The TSS yield criterion is proposed by Mao-hong Yu [17] based on Tresca yield criterion. The yield condition is established by using all independent principal shear stress, and it can make up the shortcomings of only applying to main principal shear stress for Tresca yield criterion. The yield equation is described as follows:
Where C is the material strength parameter, which can be obtained by simple mechanical test. Compared to Tresca yield criterion, TSS yield criterion takes into account the intermediate principal stress, and it is piecewise linear function.
The isotropic strengthening model is used in this paper due to its simple type. For this model, the yield surface dimension is uniformly changed in various directions of the stress space, but the center and shape of the yield surface remain unchanged. The yield function is defined as follows:
Where is strengthening function which can determine the shape of yield surface. For the von Mises yield rule:
Where is deviatoric stress tensor, σeq is equivalent von Mises stress, which is the function of equivalent plastic strain .
In the analysis process, the constitutive equations described before are employed to calculate the stress and strain, which are defined by ABAQUS user subroutine UMAT compiled by FORTRAN program. In the finite element calculation, an elastic-plastic stiffness matrix is required to be updated each time, and the analysis calculation applied to the next incremental step is to be applied.
Experiment Details
Before the expanding experiment, the expandable tubular and expansion cone were prepared. The material of expansion cone is 42CrMo steel, which has high strength and good deformation resistance, and can ensure that plastic deformation does not occur in the process of expansion. The half cone angle of the expansion cone is 9°, and the expansion rate is 20%. The diameters of two ends are 183 and 220 mm, respectively. The grease was applied uniform between friction surfaces. Then, the steel pipe is fixed, and the expansion load is applied until the expansion test is completed, as shown in Figure 4a.
The residual stress at the outer wall of the expandable tubular was measured by X-ray diffraction method. This method is based on Bragg's equation [28]:
Where n is an integer and 2θ is the diffraction angle.
The residual stress is calculated by [28]:
Where, is the diffraction angle at stress-free state, ψ is the angle between the normals of crystal surface and the material surface, K is stress constant. There is a linear relationship between 2θ and , and M is the slope between diffraction angle 2θ and . M is calculated if more than three points (2θ, ) are determined.
The test machine is X-350A type X-Ray diffraction instrument, as shown in Figure 4b. The operation voltage of the device is 25 kV and the working current is from 7 mA. Before the residual stress measurement, the electrolytic polishing machine is used to remove the oxide on the surface of expanded tubular. The axial and circumferential residual stresses of 10 points were measured. The axial spacing between test points is 100 mm.
Results and Discussion
Distribution of expansion stress
In the process of casing expansion, the expansion cone moves slowly along the expansion direction from bottom to top under the action of driving force, which makes the casing produce permanent plastic deformation and thus increase the pipe diameter. The stress state in the expansion process is an important basis for judging whether there is plastic failure behavior in the expansion process. In particular, for the expansion process of large expansion rate, the plastic failure is easy to occur because of the large deformation and strong plastic flow. Therefore, the stress state of the casing during the expansion process should be evaluated.
Because the radial stress (S11) is relatively small, only the axial (S22) and hoop (S33) stress were analyzed in the following analysis. Figure 5 shows the effects of expansion rate on the contour distribution of axial stress. The axial stress is mainly distributed in the expanded area, and showed the layered distribution along the thickness direction. The distribution of axial stress along the thickness direction can be roughly three layers: The first layer, located at the inner wall of the pipe, is mainly tensile stress. The second layer, located in the middle layer of the pipe thickness, has a small stress value. The third layer is located at the outer wall of the pipe, and the stress is mainly compressive stress. The maximum stress appears at the end of expanded section and decreases gradually in the opposite direction of expansion.
The distribution and size are almost the same (~300 MPa) in the unexpanded area for different expansion rates. The axial stress in the inner surface of expanded area is very larger, exceed the value of yield strength, indicating the plastic deformation are generated. The maximum axial stresses increase with the increases of expansion rate, which is located in the inner surface of tubular. As the expansion rate increases from 10% to 35%, the maximum axial tensile stress in inner surface increases from 577 MPa to 1029 MPa, and the maximum axial compressive stress in outer surface decreases from -646 MPa to -1258 MPa. The maximum axial tensile and compressive stresses are located in the expanded area at last time, which is adjacent to the end of expansion cone.
Figure 6 shows the contour distribution of hoop stress for different expansion rates. Similarly, the hoop stress during expanding process increases with the increases of expansion rate. When the expansion rate increases from 10% to 35%, the maximum hoop tensile stress increases from 550 MPa to 989 MPa, and it is located in the corner of expanded area, which is different from the distribution of axial stress. The maximum axial compressive stress located in outer surface decreases from -367 MPa to -593 MPa. Different to the axial stress, the hoop stress in inner surface of expanded area is very small. The hoop tensile stress is mainly located in the expanding area.
Figure 7 shows the increased value of maximum axial and hoop stress for different expansion rates compared to those of expansion rate 10%. It can be seen that both the enhanced maximum axial and hoop stress are decreased with the increases of expansion rate. When the expansion rate increases to 25%, the increasing extent of expansion stress becomes stable. That is to say, when the expansion rate exceeds 25%, the increased expansion stress has a linear relationship with increased expansion rate. For the expansion rate bellows 25%, the increased expansion rate can lead to a great variation of hoop and axial expansion stress. In addition, the tensile and compressive stresses have a similar variation law.
The equivalent TSS can also be obtained by defining a user defined field SDV in UMAT subroutine. In order to assessment the effect of expansion rate on the safety of tubular, the contour distributions of equivalent TSS stress for different expansion rates were shown in Figure 8. The distributions of equivalent TSS stress for different expansion rates are almost the same. The maximum TSS is located in the corner area between expanding zone and expanded zone. All the TSS in expanded area have exceed the yield strength of TWIP steel, so the plastic deformation was generated in all expanded area. The TSS is increased with the increases of expansion rate. As the expansion rate increases from 10% to 35%, the TSS increases from 431 MPa to 769 MPa. The maximum TSS is still smaller than tensile strength, indicating that all the tubulars for expansion rate below 35% will not occur plastic failure.
Based on the maximum TSS for expansion rate 10%, the enhanced maximum TSS for different expansion rates were shown in Figure 9. Obviously, the enhanced maximum TSS value has a linear relationship with expansion rate. With the increases of expansion rate, the enhanced maximum TSS is decreased gradually. If the expansion rate is increased continually, the TSS may exceed the tensile strength, thus leading to plastic failure. Therefore, the expansion rate is suggested to not exceed 35%.
Analysis of residual stress
The formation of residual stress is inevitably generated in the expanded tubular, which is formed in the cold working plastic forming process of tubular. Figure 10 shows the comparison of axial and hoop residual stress on the outer surface by simulation and experiment. The predicted axial or hoop residual stress by simulation with TSS yield criterion are in good agreement with experimental results. The predicted axial and hoop residual stress are about -470 MPa and -350 MPa, respectively. In the end section of expansion, both the axial and hoop residual stress are increased sharply. Except for end section, the average error of axial and hoop residual stress between simulation and experiment are 5% and 4%, respectively, and it can be acceptable. Therefore, the simulation method of expansion rate can predict the residual stress very well.
Figure 11a shows the contour distribution of axial residual stress for different expansion rates. It is tensile and compressive residual stresses in inner and outer surface, respectively. And the tensile stress in inner surface is smaller than the compressive stress in outer surface. Except for the end section of expanded tubular, the axial stresses are distributed uniformly in inner and outer surface. The value of axial stress in inner surface and outer surface are decreased greatly because of non-uniform plastic deformation in end section. With the increases of expansion rate, the axial tensile stress in inner surface and axial compressive stress in outer surface are all increased. The larger the expansion rate is, the more uneven deformation occurs in the expansion process, so the larger increased residual stress is.
Similarly, the contour distributions of axial residual stress for different expansion rates were shown in Figure 11b. The hoop stress distribution along entire path is similar to axial stress distribution. The hoop stress in inner wall and outer wall are tensile stress and compressive stress, respectively. That is different to the stress distribution of thick-wall cylinder subjected to uniform internal pressure. Thus, in the theoretical analysis, the expansion model of tubular could not be simplified to the cylinder model with thicker wall subjected to internal pressure. What' more, the expansion rate has little influence on the stress distribution in end section. With the steady increase of expansion rate, the uneven deformation inside the tube increases, leading to the hoop residual stresses of the inner and outer wall increase.
Discussion
The basic principle of expandable tubular technology is to make use of the plastic deformation ability of metal material to produce unrecoverable permanent plastic deformation under the extrusion of expansion cone, so as to reach the designed diameter of expanded tubular. The dimension of tubular is inevitably changed after expansion because of plastic flow in tubular. For the large expansion rate, there must be a large length shrinkage and thickness thinning. The effects of reduced length and thickness should be considered in the design of expansion tubular in case the criteria for strength of expanded tubular cannot be met.
Based on above analysis, we can conclude that the expansion rate has a great influence on the expansion stress and residual stress. The influence law was grasped by a number of experimental and simulation investigations. Under the condition of ensuring safety and reliability, the larger expansion rate for tubular will be more favorable to the engineering application. But the expansion rate of tubular can not be enhanced all the time. First, the larger expansion rate generates bigger plastic deformation in inner and outer wall of tubular. The expansion stress during expanding process may exceed the tensile strength, then leading to plastic failure, even fracture. This phenomenon was also reported by Liao, et al. [29]. And the large residual stress also has a great effect on the structure integrity of expanded tubular. Second, the larger expansion rate needs larger expansion thrust. It needs higher requirements for expander. Last but not the least, the tubular dimensions are greatly changed after bigger expansion rate, then may not meet the standards. Therefore, the expansion rate should be controlled within a certain range. In this study, the equivalent TSS stress for the expansion rate 35% is 760 MPa, which is close to the tensile strength of TWIP steel. So, the expansion rate should be controlled below 35%. The expansion rate is linked to the size of expansion cone. Xu, et al. [14] proposed that the cone angle and sizing section length should be 9° and 65-75 mm, respectively, in which the expansion rate is 15%. Khan, et al. [7] also pointed that higher expansion ratios will be limited by the burst and collapse strengths, which is the main factor in governing the structural integrity of the expanded tubular. On the other hand, the larger residual stress for large expansion rate should be reduced by some methods, such as shot peening [30], heat treatment [31], in order to get a good service performance.
Conclusions
In this study, the effects of expansion rate on expansion stress and residual stress of TWIP steel expansion tubular were investigated by experimental and finite element method. Based on the above investigations, the following conclusions can be drawn:
1) The axial expanding stress showed the layered distribution along the thickness direction. During the expanding process, the axial stress in inner and outer wall is tensile and compressive stress, respectively. The maximum axial stresses are located in the expanded area adjacent to the end of expansion cone.
2) The hoop tensile stress is mainly located in the corner of expanded area. The maximum hoop tensile stress is located in the corner of expanded area, while the maximum axial compressive stress located in outer surface. The hoop stress in inner surface of expanded area is very small.
3) The axial, hoop and TSS stresses increase with the increases of expansion rate. And the enhanced maximum axial, hoop and TSS stress are decreased with the increases of expansion rate. The maximum TSS is located in the corner area between expanding zone and expanded zone. The suggested expansion rate should be controlled below 35%.
4) The predicted axial and hoop residual stress based on TSS yield criterion are in good agreement with experimental results. It is tensile and compressive residual stresses in inner and outer surface, respectively. Both the hoop and axial stresses are all increased with the increases of expansion rate.
Acknowledgments
The authors gratefully acknowledge the support provided by National Natural Science Foundation of China (51905545), China Postdoctoral Science Foundation (2018M642723), Fundamental Research Funds for the Central Universities (20CX02219A; 18CX05002A) and the Natural Science Foundation of Shandong Province (ZR2019MEE108).