
International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 3, Issue 1
Research Article
DOI: 10.35840/2631-5092/4508
Quantum Filtering for Tavis-Cummings System
Zahra Rahimkhani*
Table of Content
Figures
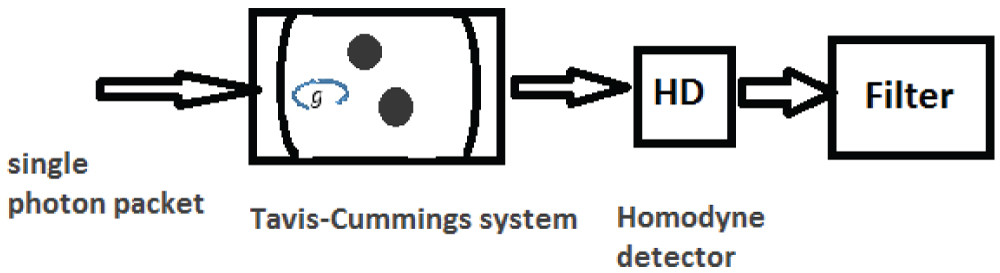
Figure 1: Behavior of interaction two of non-interacting two-level...
Behavior of interaction two of non-interacting two-level atoms with single photon.
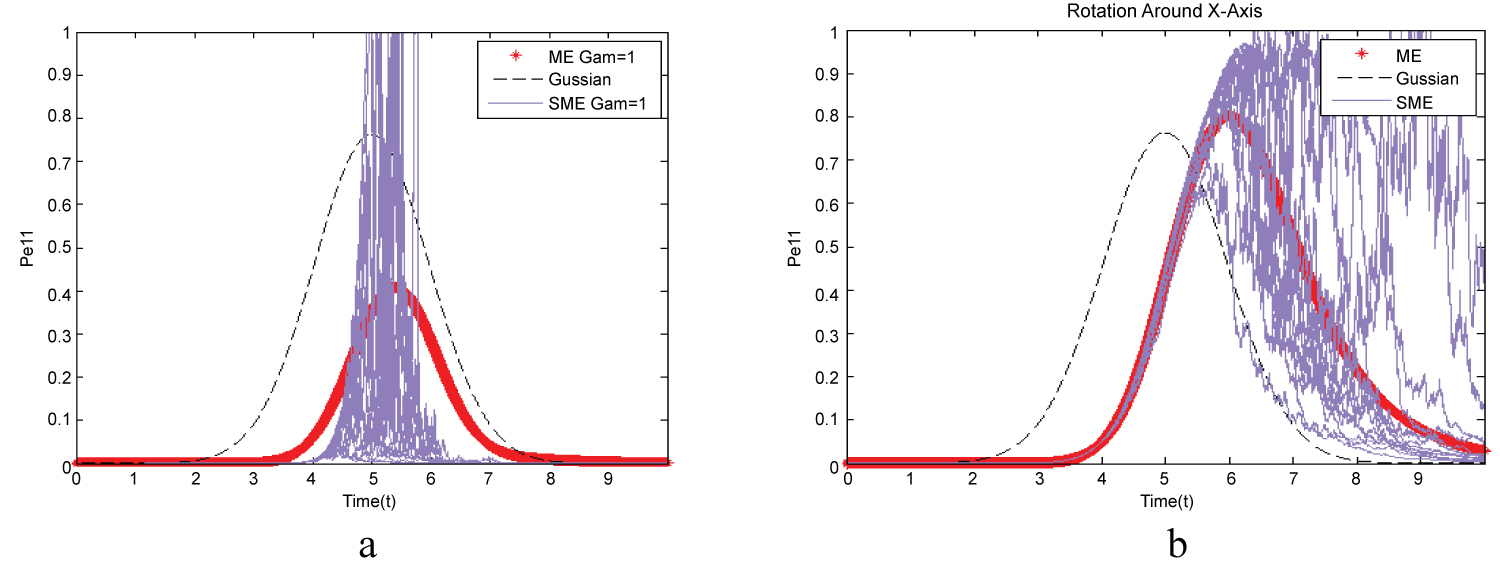
Figure 2: Behavior of two atom of two-level in interact with single...
Behavior of two atom of two-level in interact with single photon with initial state that both of atoms are in ground state. Black line is photon packet, red line is ME (Master equation), purple lines are SME. Figure 2a shows probability of finding atoms in excited state for two two-level atoms and Figure 2b shows this probability for a two-level atom.
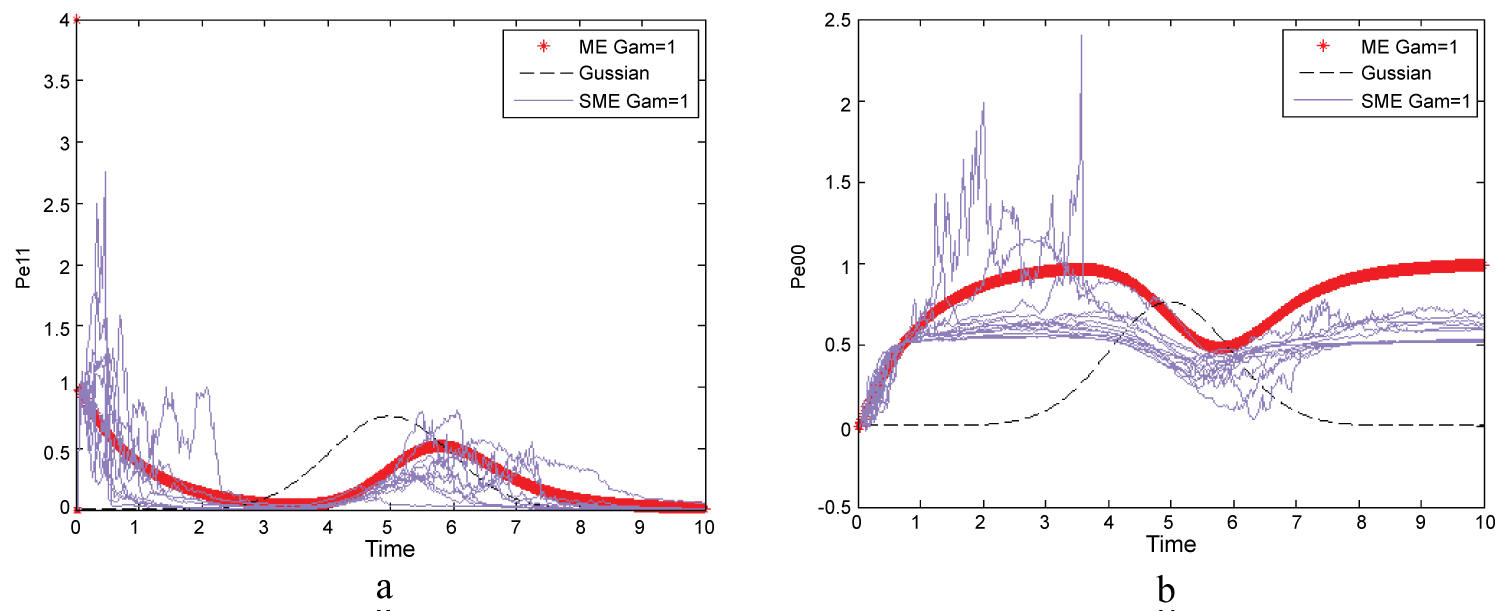
Figure 3: Behavior of two atom of two-level in interact with single...
Behavior of two atom of two-level in interact with single photon with initial state that both of atoms are in exited state. black line is photon packet, red line is ME (Master equation), purple lines are SME.
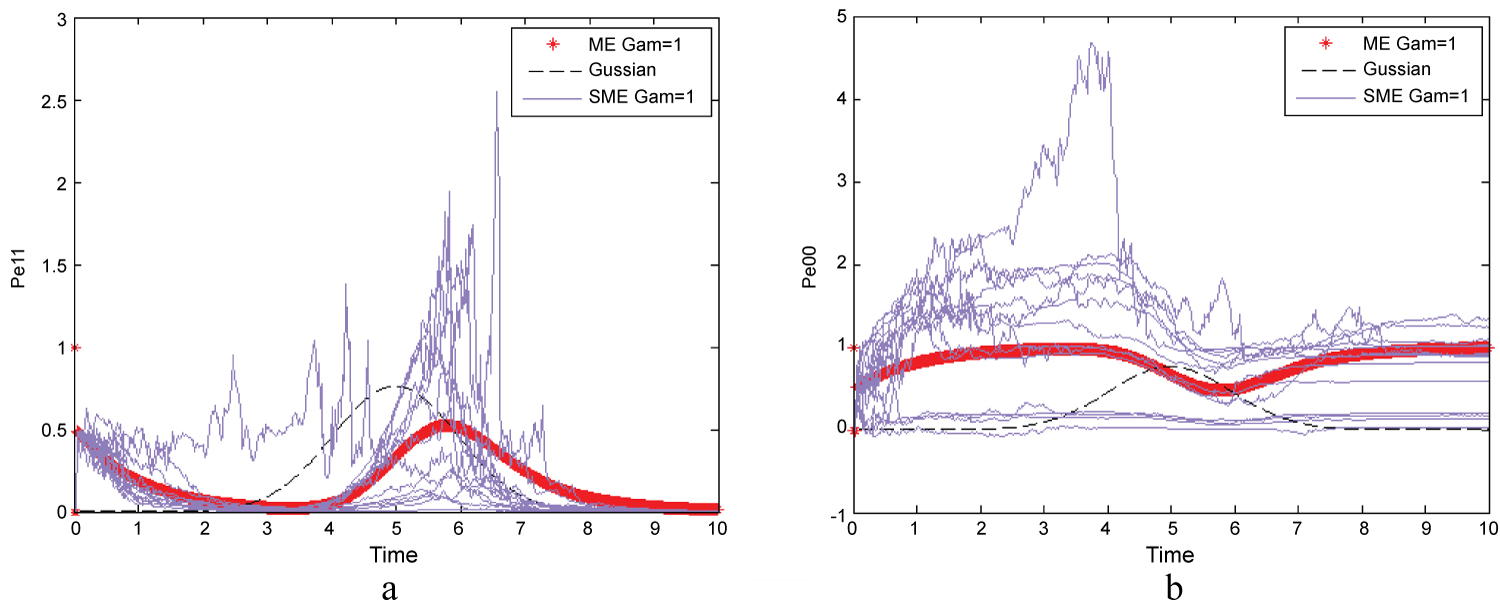
Figure 4: Behavior of two atom of two-level in interact with single...
Behavior of two atom of two-level in interact with single photon with initial state that one of two of atoms be in ground state and other atom be in excited state black line is photon packet, red line is ME (Master equation), purple lines are SME.
References
- Y Wang, J Minar, L Sheridan, V Scarani (2011) Efficient excitation of a two-level atom by a single photon in a propagating mode. Phys Rev A 83: 63842.
- E Rephaeli, JT Shen, S Fan (2011) Full inversion of a two-level atom with a single-photon pulse in one-dimensional geometries. Phys Rev A 82: 33804.
- A Daeichian, F Sheikholeslam (2013) Behaviour of two-level quantum system driven by non-classical inputs. IET Control Theory and Applications 7: 1877-1887.
- JE Gough, MR James, HI Nurdin (2011) Quantum master equation and filter for systems driven by fields in a single photon state. Proc IEEE Conf Decis Control 5570-5576.
- Z Rahimkhani, M Yaghobi, K Javidan (2017) Quantum filtering equations for atom-single photon interaction by homodyne detection: Considering full interaction Rabi model. Opt Int J Light Electron Op 140: 619-625.
- J Sharifi, H Momeni (2011) Lyapunov control of squeezed noise quantum trajectory. Phys Lett A 375: 522-528.
- M Mirrahimi, RVAN Handel (2007) Stabilizing feedback controls for quantum systems. SIAM J Control Optim 46: 445-467.
- VP Belavkin (1979) Optimal measurement and control in quantum dynamical systems. Preprint.
- BQ Baragiola, RL Cook, AM Brańczyk, J Combes (2012) N-photon wave packets interacting with an arbitrary quantum system. Phys Rev A 86: 13811.
- TE Tessier, IH Deutsch, A Delgado, I Fuentes-Guridi (2003) Entanglement sharing in the two-atom Tavis-Cummings model. Phys Rev A 68: 62316.
- S Arash Ghoreishi, M Sarbishaei, K Javidan (2012) Entanglement between Two Tavis-Cummings Systems with N=2. Int J Theor Math Phys 2: 187-195.
- X Maître, E Hagley, G Nogues, C Wunderlich, P Goy, et al. (1997) Quantum memory with a single photon in a cavity. Phys Rev Lett 79: 769-772.
- JM Fink, R Bianchetti, M Baur, M Goppl, L Steffen, et al. (2009) Dressed collective qubit states and the Tavis-Cummings model in circuit QED. Phys Rev Lett 103: 1-4.
- JE Gough, MR James, HI Nurdin, J Combes (2011) Quantum Filtering (Quantum Trajectories) for systems driven by fields in single photon and superposition of coherent states. Phys Rev A 86: 043819.
- F Zhang, MR James (2012) Quantum feedback networks and control: A brief survey. Chinese Sci Bull 57: 2200-2214.
- D Dong, IR Petersen (2009) Quantum control theory and applications: A survey. Engineering 1-37.
- RL Hudson, KR Parthasarathy (1984) Quantum Ito's formula and stochastic evolutions. Commun Math Phys 93: 301-323.
Author Details
Zahra Rahimkhani*
Department of Electrical Engineering and Computer, Islamic Azad University Mashhad, Iran
Corresponding author
Zahra Rahimkhani, Department of Electrical Engineering and Computer, Islamic Azad University Mashhad, Iran.
Accepted: March 24, 2018 | Published Online: March 26, 2018
Citation: Rahimkhani Z (2018) Quantum Filtering for Tavis-Cummings System. Int J Opt Photonic Eng 3:008.
Copyright: © 2018 Rahimkhani Z. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this work, Interaction of a Tavis-Cummings system with single photon packet is studied by quantum master and filter equations with considering homodyne detector. We present result of simulation for two two-level atoms and analyze effects of adding an external single-photon magnetic field.
Keywords
Tavis-Cummings Model, Two level atom, Quantum ?f?iltering
Introduction
Quantum technologies in the current world have a wide range of applications in different areas. The interaction between a field and two-level atom was investigated in different papers [1-5]. In this interaction, ?the field can be classic or non-classic. A non-classic state of light that is vital in quantum systems and quantum communication protocols is single photon ?that is used in quantum filtering of open quantum systems [4,5].
Quantum control systems are studied by two classical and quantum approaches that in classic approach, system was measured by a system and then can use a classical system as controller for control it [6,7]. Besides, Quantum filtering plays an important role in quantum measurement. Belavkin shows that quantum systems are measurement in 1979 [8]. Also, he did different studies about control and quantum filtering [2,9].
A generalization of the JC (Jaynes-Cummings) model, is called the Tavis Cummings (TC) model (also known as the Dicke model), was introduced in 1968. This model describes interaction between a quantized field and a collection of N atoms with approximation RWA (rotating wave approximations) [10,11]. The Tavis Cummings model was considered to describe strongly couple N atoms to a cavity mode. Tavis Cummings system can interact with a field specially single photon that is used in quantum dots, cavity quantum electrodynamics (QED) and semiconductors and circuit QED [5,12].
In this paper, In section 2, we show interaction single photon packet with two non-interacting two-level atoms and study transition probability of atoms. In section 3, The output field is measured by homodyne detection and is estimated by quantum filtering. In section 4, we present summary of the obtained results.
Tavis-Cummings System Model
We consider two of non-interacting two-level atoms in a cavity. We studied the behavior of two atoms that interact with single-photon wave packet. Density matrix of a two-level quantum system is:
that , and are Pauli matrices. We get operations for Tavis-Cummings system by tensor products of Pauli matrices as we have
Interaction atoms and single photon is assumed of the Jaynes-Cummings type. So, Hamiltonian of the system is as [10,13]
and , and and are annihilation and creation operators and is coupling strength in Jaynes-Cummings model.
We consider a non-classical state of light in the sense that it cannot be described in terms of a classical electric field that is single photon packet. Single photon is important in realization of quantum systems and quantum communication protocols. The creation operator for a photon with wave packet in time domain is defined as
And we define wave packet as Gaussian stat where is the frequency bandwidth of the pulse and t stands for the peak arrival time [5,14].
Quantum Filter for the Tavis-Cummings System
Quantum filtering is used to process of extracting information in quantum systems. Dynamic of system is described by Unitary equation. Figure 1 describes interaction an input field, in a single photon State, with a Tavis-Cummings system, output field is continuously measured by homodyne detection then the output light is estimated by stochastic master equation (Quantum filtering). We can use output signal for control quantum systems [15].
That is defined as
In quantum filtering we should continuously measure a quantum system to obtain output field. In this way, the evolution of a quantum system can be described as [16]
Where this is stochastic master equation (SME) and in this equation k is a parameter related to the measurement strength, is a Wiener process that have variance and zero mean that have
Now we consider to calculate the transition rate of population as a function of time?. ?We solve the master equations and also stochastic equations to find expectation value of different possible transitions [14].? For example time evolution of transition rate for two atoms in state becomes?:
that for master equation is calculated based on this equation [14]
That Lindbladian equation is and Liouvillian equation is and master equation is calculated based on this equation [15]
Overall, we considered two two-level atoms and used equations (10) and (11) that they were derived from the paper [14]. We have two two-level atoms that interact with a single-photon.
We get probability of finding atom in excited state and in ground state based on
That is calculated by Master equation that was get based on equation (10) and is calculated Stochastic Master equation was get based on equation (11). This equations were calculated based on quantum stochastic differential equations [17]. We consider Ω = 1.46 in a Gaussian pulse that dotted line is the Gaussian wave packet.
In this section, we simulate transition probability two two-level atoms by considering Homodyne detector then compare them with a two-level atom in same conditions. In Figure 2a, both of two of atoms are in ground state as and probability of finding atom in excited state is as that . In t = 0, both of atoms are in ground state, probability of finding atoms in excited state is zero but with arrival the single photon packet, at least one of the atoms is excited and probability of finding atom in excited state become 0.5. But, in Figure 2b, we show a two-level atom that it got in initial state and probability of finding atom in excited state with arrival the single photon packet is one.
Figure 3a shows probability arrival atom to excited state when is gotten. In this state, in t = 0, probability of finding atoms in excited state is one because both of atoms are in excited state. Over time due to spontaneous emission, atoms get to the ground state. With the arrival single photon, the state atom changes and is excited and probability of finding one of atoms in excited state is 0.5 and then with passing single photon, atom come back to ground state. Figure 3b presents probability of arrival one of atoms in ground state.
Figure 4a shows if in initial state, one of two of atoms be in ground state and other atom be in excited state that and In t = 0, one of atoms is in excited state and other is in ground state so probability of finding atom in excited state is 0.5 and due to spontaneous emission, atoms get to the ground state and with arrival photon, one of atoms is excited probability of arrival atom to excited state become 0.5. Figure 4b shows if initial state be like previous state, probability of finding one of atoms in ground state is 0.5.
Conclusion
In this paper, Two-atom of two level in interaction with single photon field was investigated. filter equations are used to calculated state of system conditioned on Homodyne detection. We have shown that probability of excited one of atoms in Tavis-Cummings system and simulate result it with master and stochastic master equation and in a part compare a two-level system with two two-level atoms.

