International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 3, Issue 3
Research Article
DOI: 10.35840/2631-5092/4513
Research on the Strain Transfer Mechanism of FBG Radian Strain Sensor
Shanchao Jiang*
Table of Content
Figures
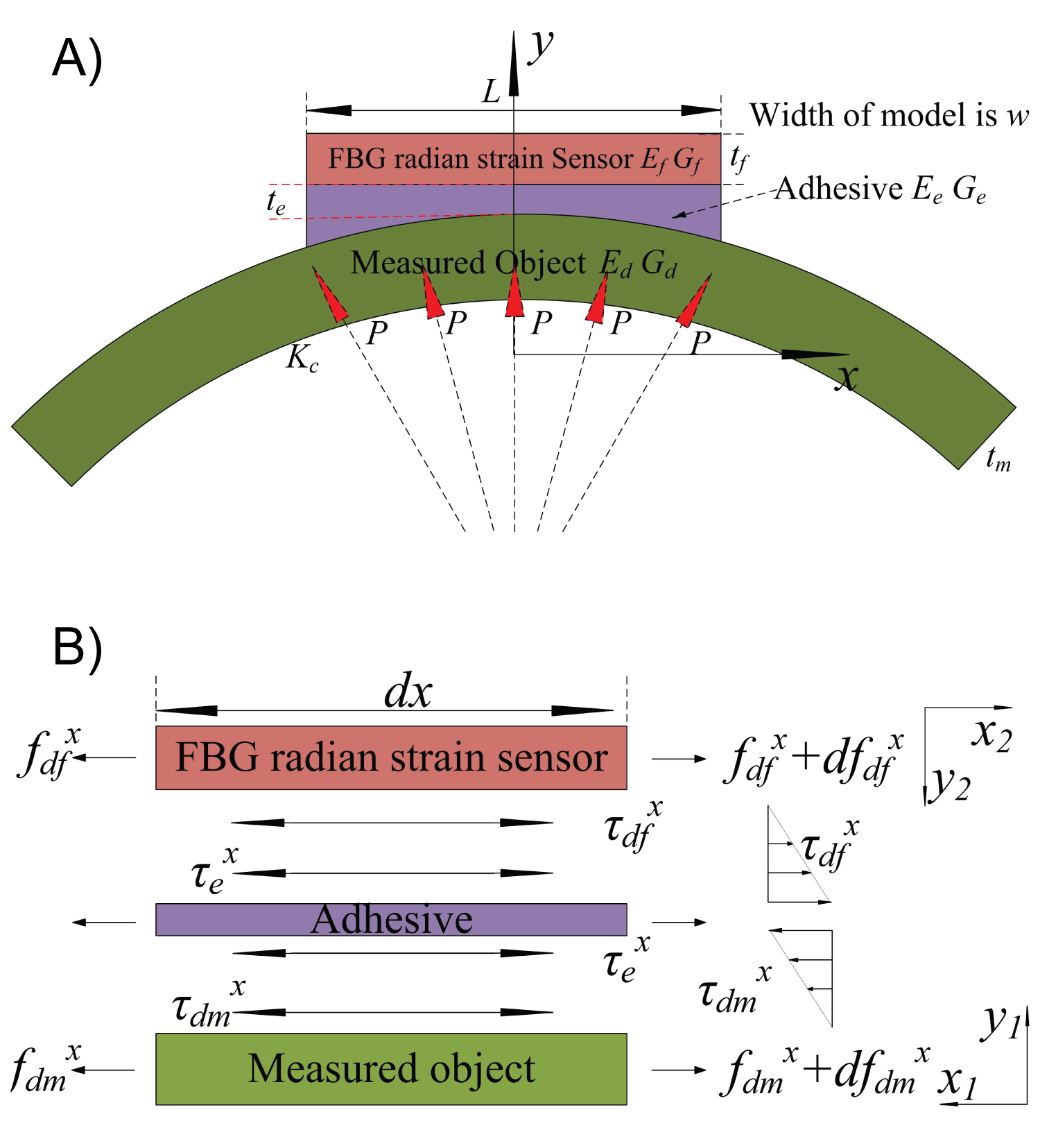
Figure 1: Theory calculation and regional...
Theory calculation and regional infinitesimal model of FBG radian strain sensor. a) Theory calculation model; b) Regional infinitesimal model.
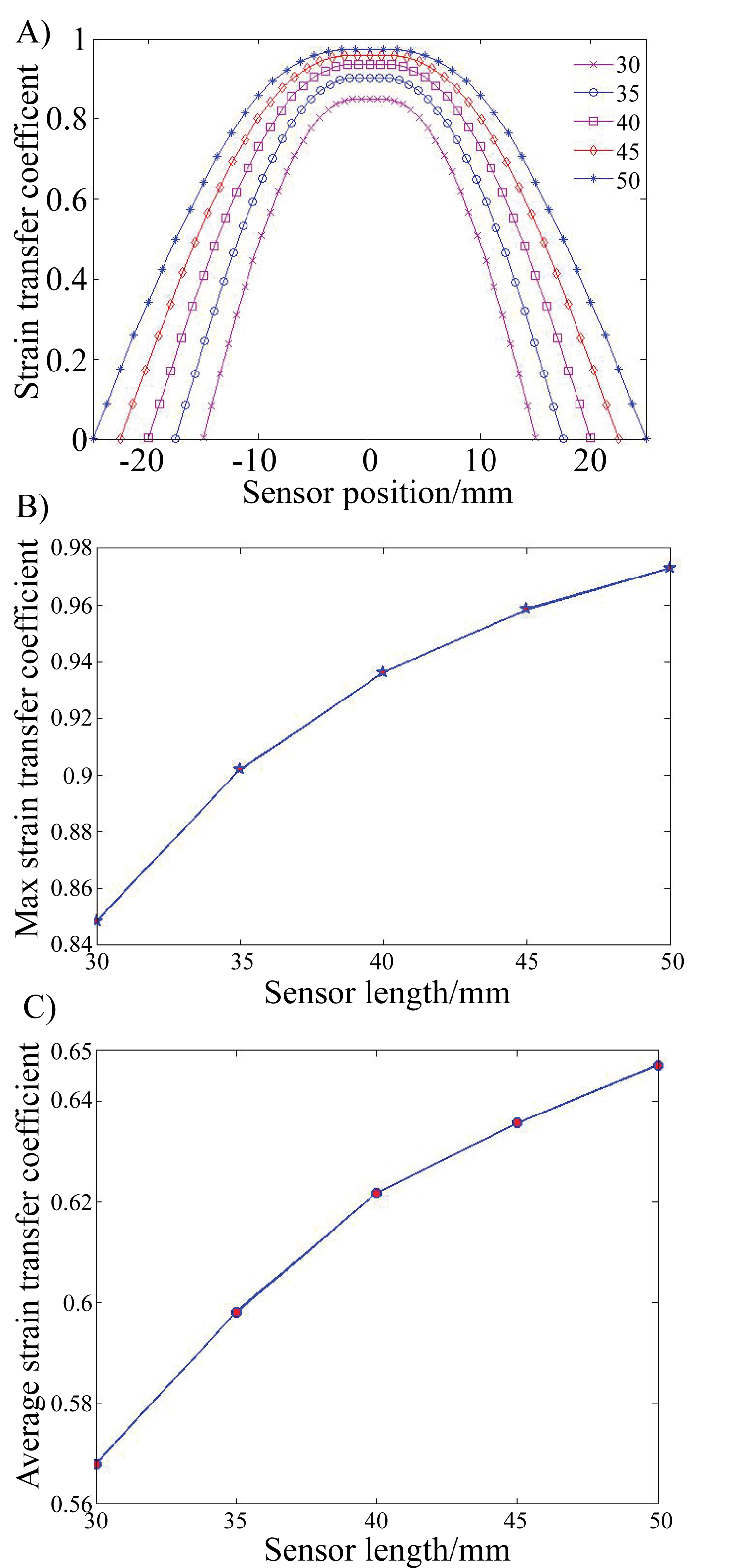
Figure 2: Influence of sensor length to...
Influence of sensor length to coefficient. a) Coefficient distribution; b) Max coefficient; c) Average coefficient.

Figure 3: Influence of adhesive layer...
Influence of adhesive layer thickness to coefficient. a) Coefficient distribution; b) Max coefficient; c) Average coefficient.
Tables
Table 1: Material properties and geometrical parameters.
Table 2: Material parameters of FBG.
References
- H Ahmad, A Zulkhairi, S Azzuhri (2018) Temperature sensor and fiber laser based on optical microfiber knot resonator. Optik 154: 294-302.
- S Wang, P Lu, L Mao, D Liu, S Jiang (2015) Cascaded interferometers structure based on dual-pass Mach-Zehnder interferometer and Sagnac interferometer for dual-parameter sensing. Opt Express 23: 674-680.
- H Zhang, Y Dong, J Leeson, L Chen, X Bao (2011) High sensitivity optical fiber current sensor based on polarization diversity and a Faraday rotation mirror cavity. Appl Opt 50: 924-929.
- M Xiong, H Gong, Z Wang, C-L Zhao, X Dong (2016) Optical modal interferometer fiber strain sensor based on waist-enlarge fusion splicing. Optik 127: 6862-6866.
- Huaping Wang, Lizhong Jiang, Ping Xiang (2018) Priority design parameters of industrialized optical fiber sensors in civil engineering. Optics & Laser Technology 100: 119-128.
- J Zhang, X Wan, Y Li, Z Zhao, C Li (2018) An integrated electro-optic magnetic field sensor based on reflected Mach-Zehnder interferometer. Optik 157: 315-318.
- C-L Zhao, R Wang, Y Zhou, L Niu, H Gong (2017) Angle sensor based on two cascading abrupt-tapers modal interferometer in single mode fiber. Optik 132: 236-242.
- Wei Shen, XIaoxing Wag, Lin Xu, Yingjiang Zhao (2018) Strain tranferring mechanism analysis of the substrate bonded FBG sensor. Optik 154: 441-452.
- Dong Sheng Li, Hong Nan Li (2005) Strain transfer analysis of embedded fiber Bragg grating sensors. Chin J Theor Appl Mech 37: 435-441.
- Qingbin Li, Guang Li, Guanglun Wang (2003) Effect of the plastic coating on strain measurement of concrete by fiber optic sensor. Measurement 34: 215-227.
- Zhi Zhou, Jilong Li, Jinping Ou (2004) Interface strain transfer mechanism and error modification of embedded FBG strain sensors. Smart Mater Struct 5384: 190-198.
- Dezhi Liang, Li Sun, Changtie Huang (2008) Comparison of strain transfer of embedded FBG sensors calculated by FEM and theory formula. J Shenyang Jianzhu Univ Nat Sci 24: 72-76.
- Wei Wang, Yuchi Lin, Yinguo Huang (2008) Research on strain transfer of surface FBG sensor. Laser Infrared 38: 1218-1220.
- Wei Guo, Xinliang Li, Hao Song (2011) Analysis of strain transfer of fiber grating sensors adhered to the structure surface. Metrol Meas Technol 31: 1-3.
- Rujun Wu, Bailin Zheng, Zhigang Liu (2014) Analysis on strain transfer of a pasted FBG strain sensor. Optik 125: 4924-4928.
- Huaping Wang, Lizhong Jiang, Ping Xiang (2016) Theoretical analysis on strain transfer error of FBG sensors attached on steel structures subjected to fatigue load. Strain 52: 522-530.
- Huaping Wang, Lizhong Jiang, Ping Xiang (2018) Improving the durability of optical fiber sensor based on strain transfer analysis. Optical Fiber Technology 42: 97-104.
- Haiting Di, Ying Xin, Jinquan Jian (2018) Review of optical fiber sensors for deformation measurement. Optik 168: 703-713.
- Yu Chen, Jianfeng Li, Yi Yang, Ming Chen, Jing Li, et al. (2013) Numerical modeling and design of mid-infrared FBG with high reflectivity. Optik 124: 2565-2568.
Author Details
Shanchao Jiang*
School of Electrical Engineering, Yancheng Institute of Technology, Yancheng, China
Corresponding author
Shanchao Jiang, School of Electrical Engineering, Yancheng Institute of Technology, Yancheng, 224051, China.
Accepted: November 24, 2018 | Published Online: November 26, 2018
Citation: Jiang S (2018) Research on the Strain Transfer Mechanism of FBG Radian Strain Sensor. Int J Opt Photonic Eng 3:013.
Copyright: © 2018 Jiang S. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The proposed transfer mechanism theories of FBG strain sensor rarely involve influence of curvature of the measured object which is an important parameter in the field of material strength. This paper analyzes the strain transfer mechanism of FBG radian strain sensor between curved plane and plane, proposes the stress distribution, and obtains that the influential parameters of strain transfer are FBG strain sensor length, measured object curvature and adhesive layer thickness. Meanwhile, influence of the stress distribution on FBG reflectance spectrum is also analyzed. Further, calibration model is carried out on one FBG radian strain sensor to analyze the influential parameters. Through the influential parameter's analyses, the practice guidance for FBG radian strain sensor which have highly significant in improving the curvature detection accuracy is given.
Keywords
FBG radian strain sensor, Strain transfer mechanism, Influential parameter, Curvature detection accuracy
Introduction
Due to its overwhelming advantages, such as high sensitivity, light weight, immunity to electromagnetic interference, remote sensing, multiplexing capability and so on, fiber Bragg grating (FBG) sensors have been successfully used in the measurement of temperature [1], pressure [2], current [3], strain [4,5], magnetic field [6], angle [7], and so on.
One of the most important application forms of FBG sensors is strain measurement [8]. However, the FBG strain sensor has to be packaged in use because of that the shear resistance of FBG is very poor. The package types can be roughly divided into embedded type and surface type. The embedded type FBG strain sensor is mostly pasted on the interior of measured object by adhesive, such as epoxy resin and instantaneous drying glue 502. The surface FBG strain sensor is pasted on the substrate, and then pasted on the surface of the measured object [9,10].
Caused by adhesive or substrate of FBG strain sensor, the FBG which is the core sensitive element in FBG strain sensor does not directly measure the strain of the measured object, and the strain transfer error will be generated in practice. There are lots of researches on the transfer mechanism of FBG strain sensor. Zhou, et al. [11] have got the general expression function of the strain transfer by using the relation between the axial normal stress and the shear stress. Liang, et al. [12] have studied the discipline of the strain transfer through the numerical method and have verified the transfer function proposed by Ansari and Libo. Wang, et al. [13] have got the transfer function by assuming the interlaminar shear changes in linear pattern and the strain gradient equals between each layer. Guo, et al. [14] have got discipline of strain transfer through establishing the equilibrium equation by material mechanics method and assuming the strain gradient is the same. Rujun, et al. [15] analyze the transfer mechanism of FBG strain sensor in detail and propose the shear stress distribution of polynomial form. All these research works establish the strain transfer theoretical foundation of FBG strain sensor [16,17].
Due to that traditional curvature measurement methods have their limitations in flammable, explosive and electromagnetic environments, FBG strain sensor has been widely used in the curvature measurement of loaded structures [18]. The curvature of loaded structures is an important parameter in the field of materials strength. While, the proposed transfer mechanism theories of FBG strain sensor are mostly focus on the strain transfer between plane and plane, and rarely involve the strain transfer between curved plane and plane [8]. Based on above discussion and analysis, this paper focuses on the strain transfer mechanism of FBG radian strain sensor which can achieve curvature measurement between curved plane and plane and analyzes the influential parameters on strain transfer coefficient between FBG radian strain sensor and measured object. This research work will further improve the detection accuracy of curvature measurement and promote the development of FBG radian strain sensor.
Strain Transfer Mechanism Model
Stress distribution and strain transfer model
Considering the shear lag effect and thickness of adhesive, one theoretical calculation model of FBG radian strain sensor stress distribution between curved plane and plane is established and shown in Figure 1. Kc and P represent the curvature and radical force of the measured object, and w is the width of the stress distribution model.
To simplify the theoretical calculation model, the strain transfer loss of FBG radian strain sensor between FBG and its substrate is ignored. Due to the influence of the measured object curvature, the thickness of the adhesive in the FBG radian strain sensor range is not a constant value. Suppose that the minimum adhesive thickness is te, the relationship between adhesive thickness, curvature and length of FBG radian strain sensor can be expressed as:
Where, L(x) represents the length distribution of FBG radian strain sensor along with the x axis.
Due to the function of curvature and length of FBG radian strain sensor, the radical force of measured object can be expressed as:
Where, Px and Py represent the force distribution of measured object along with the x and y axis, respectively. Through analyses of Figure 1, Py can act on the FBG strain sensor directly, and the influence of Px on the FBG radian strain sensor is analyzed as follows.
The thickness of adhesive can be considered as a constant in the regional infinitesimal model (Figure 1b). Deformations of adhesive at x direction are caused by combined effects of tension f and shear stress τ. So, displacement u of adhesive at x direction can be expressed as:
Where, uf and uτ represent the displacement caused by f and τ, respectively. Displacement uτ can be expressed as:
Where, γ is the shear strain of adhesive. According to the Hooke's law, γ is expressed as:
The resultant force at x direction can be expressed as:
Where, εx d is the strain of measured object at x direction.
Combining Eqs. (1) ~ (4), we can obtain that:
Where, τx e is the shear stress of adhesive and it can be expressed as:
Combining Eqs. (3) ~ (8), the following equation is obtained and expressed as:
Due to force balance of adhesive and FBG radian strain sensor, we can get that:
and
Bring Eqs. (6) (10) (11) into (9), second-order ordinary differential equation of fx df is expressed as:
With, ω is a constant value which is determined by material and geometrical parameters of the calculation model and shown as:
Boundary conditions of this theory calculation model are expressed as:
So, the solution of the eq. (12) is
Where, A and B are constant coefficients and expressed as:
Further, the strain transfer coefficient k(x) between the measured object and FBG radian strain sensor can be expressed as:
Through analyses of stress distribution and strain transfer model, the parameters which influence the strain transfer coefficient are FBG radian strain sensor length, measured object curvature and adhesive layer thickness.
Influence of stress on FBG reflectance spectrum
To further obtain the effect of FBG radian strain sensor stress distribution on the FBG reflectance spectrum, transmission matrix theory [19] is introduced. Assuming that the grating area lf is evenly divided into N, each of them can be treated as uniform fiber grating. Major optical properties of FBG are the coupling effect of the forward mode A(z) and the reverse mode B(z). With the initial conditions A(-L/2) = 1, B(-L/2) = 0 and A(L/2) = 0, B(L/2) = 1, the transmission matrix theory can be expressed as follows.
Where, neff is the effective reflective index, λ is the Bragg wavelength, v is the passion ratio of fiber, pij is the photo-elastic constant, and Ef is elasticity modulus of fiber. According to Eqs. (22) ~ (24), length and effective reflective index of FBG are all affected by the stress fx df which may be able to broaden reflectance spectrum. Finally, reflectance spectrum R of FBG can be described by:
Establishment of Calculation Model
In order to verify the strain transfer mechanism model, one FBG radian strain sensor model is established to calculate the strain transfer coefficient with the changes of length of FBG radian strain sensor, measured object curvature and adhesive thickness.
According to the strain transfer mechanism model, there are three layers in the theoretical calculation model which are FBG radian strain sensor, adhesive and measured object. To obtain the influence of FBG radian stain sensor length, the measured object curvature and adhesive thickness on the strain transfer coefficient, their values are uncertain in the calculation model. The rest material properties and geometrical parameters of the strain transfer mechanism model are shown in Table 1. Same material properties of measured object and FBG radian strain sensor are chosen to simplified calculation model. Material properties and geometrical parameters of FBG are shown in Table 2 to analyze the influence of stress on FBG reflectance spectrum.
Influential Parameters Analyses
Analyses of strain transfer coefficient
According to the strain transfer mechanism model, the parameters which influence the strain transfer coefficient are FBG radian strain sensor length, measured object curvature and adhesive thickness. Firstly, the influence of FBG radian strain sensor length and measured object curvature are analyzed. Assuming that measured object curvature is 2.5·10-3 mm-1 and adhesive layer thickness te is 1 mm, Figure 2 shows influence of FBG radian strain sensor length on strain transfer coefficient along with sensor length changes from 30 mm to 50 mm with interval 5 mm.
As shown in Figure 2, the strain transfer coefficient in the middle range is bigger than two ends, and the coefficients from the middle to two ends trend to 0. In the middle of FBG radian strain sensor, the strain transfer coefficient is approximately a constant, and constant range is wider with the length of FBG radian strain sensor getting bigger. The strain transfer coefficient, its max value, average value and width of strain transfer coefficient constant range are bigger with the length of FBG radian strain sensor getting bigger. If max and average strain transfer coefficient threshold are 0.9 and 0.6, the FBG radian strain sensor length should be larger than 35 mm, and the width of strain transfer coefficient constant range is 11.2 mm which is bigger than the length of FBG. In other word, the ratio between FBG radian strain sensor length and measured object radius should be larger than 8.75%. The reciprocal of curvature is radius. It is important to ensure the ratio between FBG radian strain sensor length and measured object radius to guarantee the curvature measurement accuracy in practice.
Further, the influence of adhesive thickness is analyzed. Assuming that measured object curvature is 2.5·10-3 mm-1 and the FBG radian strain sensor length is 35 mm, adhesive layer thickness te is set from 0.5 mm to 2 mm with interval 0.5 mm. Calculation results of strain transfer coefficient are shown in Figure 3.
As shown in Figure 3, the changes of strain transfer coefficient along with the FBG radian strain sensor position have same laws as Figure 2a. Strain transfer coefficient in the middle range is bigger than two ends, and the coefficients from the middle to two ends trend to 0. While, the strain transfer coefficient, its max value and average are smaller with the adhesive thickness getting bigger. The reduced changes of max strain transfer coefficient and its average are approximately linear with the increases of adhesive thickness. Least square method is introduced to obtain the approximate function. The function between max strain transfer coefficient ymax and adhesive thickness te is
ymax = -0.1078te + 1.0409 (29).
Then, the changes of strain transfer coefficient average yave can be expressed as
ymax = -0.0736te + 0.6959 (30).
When the adhesive thickness te is zero, the max value of strain transfer coefficient is 1.0409 which is bigger than 1. This phenomenon is caused the influence of the adhesive thickness at two ends of FBG radian strain sensor. The smaller thickness of adhesive leads to the bigger strain transfer coefficient. While, if the thickness of adhesive is too small and does not have effective bonding effect, the sensor will be fail. If max and average strain transfer coefficient threshold is 0.9 and 0.6, the adhesive thickness should be 1.307 mm (calculated through eq. (29)) and 1.302 mm (calculated through eq. (30)). So, thickness value of the adhesive can chose 1.3 mm after considering both effective bonding effect and larger strain transfer coefficient.
In conclusion, in order to guarantee larger strain transfer coefficient and the curvature measurement accuracy of FBG radian strain sensor in practice, the ratio between FBG radian strain sensor length and measured object radius should be larger than 8.75%, and the thickness value of the adhesive layer can be set to 1.3 mm.
FBG reflectance spectrum analyses
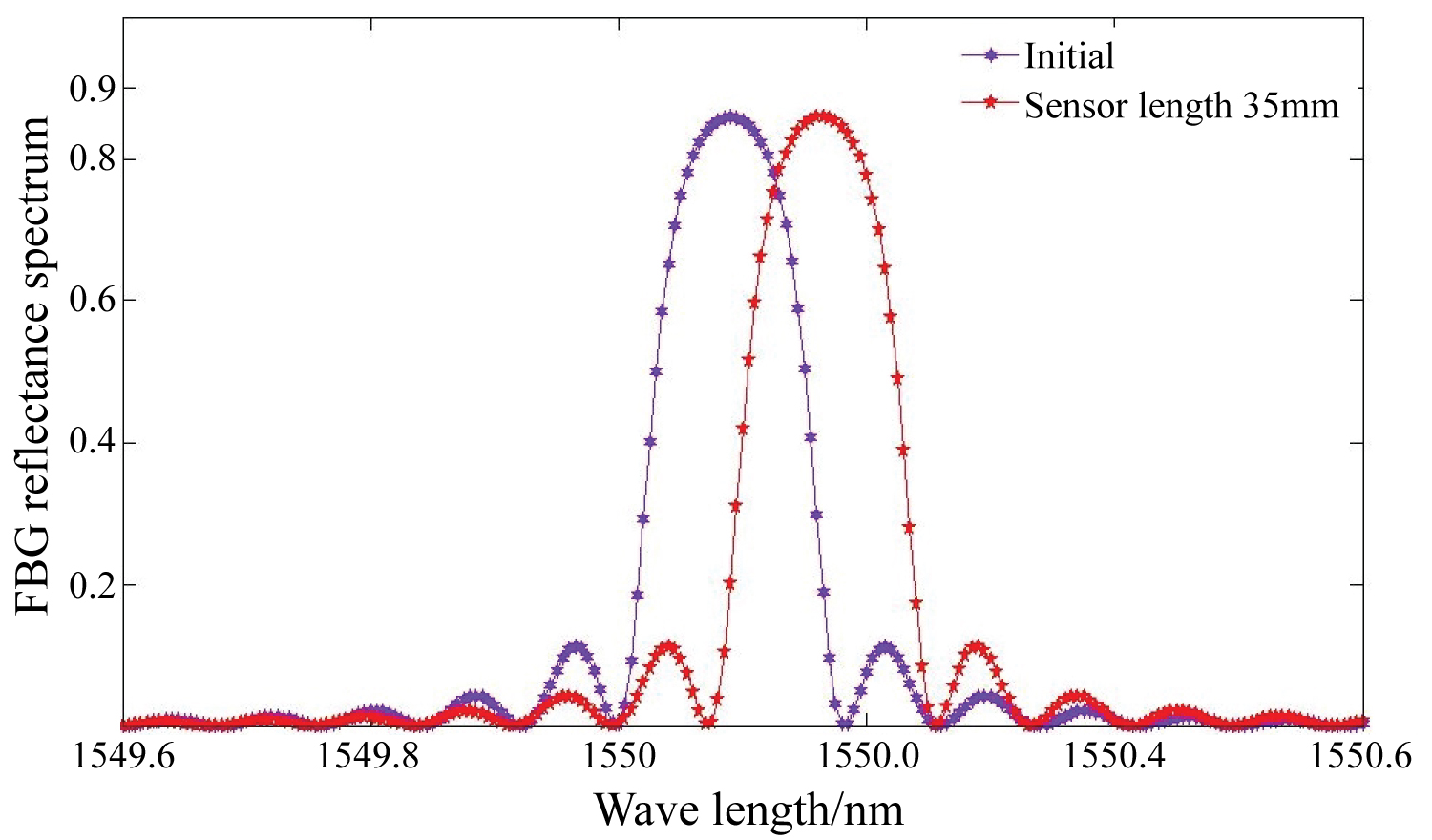
Further, the effect of FBG radian strain sensor stress distribution on the FBG reflectance spectrum is also analyzed. Assuming that the max strain change of the measured object caused by radical force is 100 με, Figure 4 shows the FBG reflectance spectrum comparison of FBG radian strain sensor between the initial and sensor length 35 mm.
After analyses of Figure 4, the FBG reflectance spectrum of FBG radian strain sensor is not broadened between the initial and sensor length 35 mm, and their 3dB wavelength width are both 0.125 nm. The results show that the FBG in the FBG radian strain sensor is under the uniform axial force which is in good agreement with Figure 2a. So, just center wavelength analyses of FBG radian strain sensor can achieve the curvature measurement of measured object.
Conclusion
Strain transfer mechanism model of FBG radian strain sensor between curved plane and plane is established, and its influence model on the FBG reflectance spectrum is also proposed in this paper. After analyses of strain transfer mechanism model, the influential parameters of the strain transfer coefficient are FBG radian strain sensor length, measured object curvature and adhesive thickness. Further, calculation model of FBG radian strain sensor is established to analyze the influential parameters, and the following conclusions are obtained.
1. The strain transfer coefficient, its max value and average value are bigger with the length of the FBG radian strain sensor getting bigger. While, the strain transfer coefficient, its max value and average are smaller with the adhesive thickness getting bigger. The reduced changes of strain transfer coefficient max value and its average are approximately linear with the increases of adhesive thickness.
2. In order to guarantee larger strain transfer coefficient and the accuracy of FBG radian strain sensor in practice, the ratio between FBG strain sensor length and measured object radius should be larger than 8.75%, and the thickness value of the adhesive layer can chose 1.3 mm.
3. Under these above-mentioned conditions, the FBG reflectance spectrum of FBG radian strain sensor is not broadened. It means that the FBG is under the uniform axial force and not influenced by measured object curvature. The curvature measurement of measured object can be obtained by just center wavelength analyses of FBG radian strain sensor.
Acknowledgement
This paper is supported by National natural science foundation of China (NO. 61803325), the Natural Science Foundation of Jiangsu Province (Grants No. BK20181049) and the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No. 18KJB510046).