
International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 4, Issue 1
Research Article
DOI: 10.35840/2631-5092/4514
Bit Error Rate Analysis of an OFDM Subcarrier Modulated FSO Link with Optical Intensity Modulation and a Direct Detection Receiver
Bobby Barua1* and SP Majumder2
Table of Content
Figures
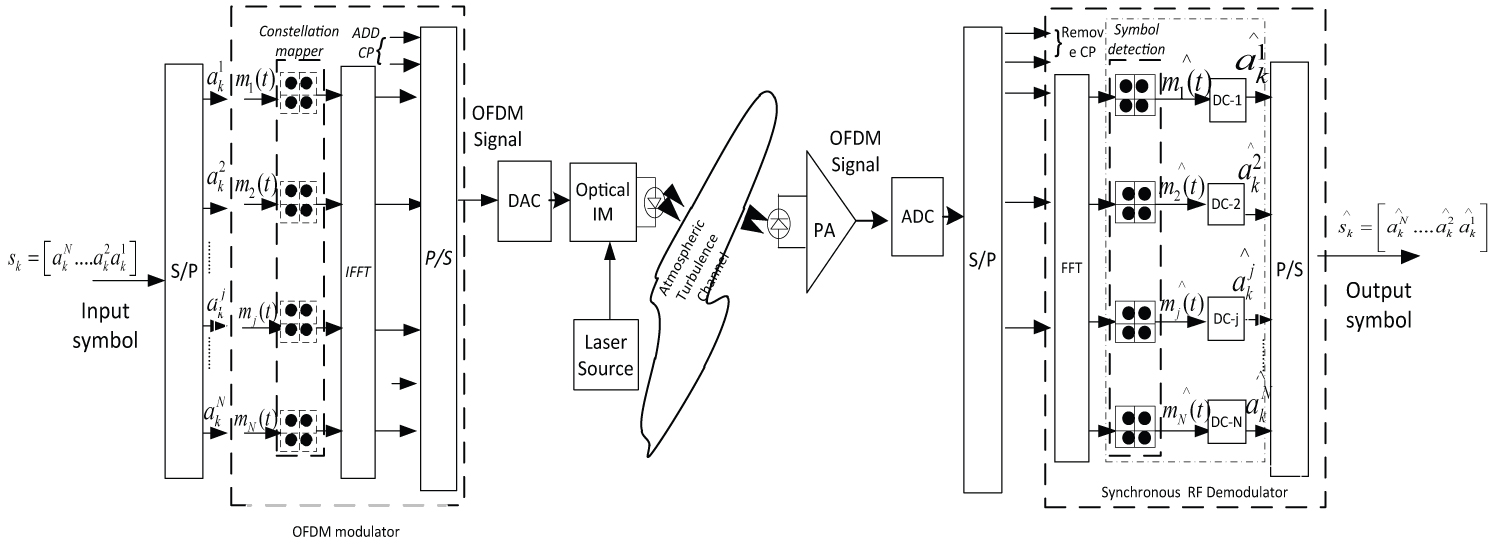
Figure 1: Block diagram of ASK Mapped...
Block diagram of ASK Mapped OFDM FSO communication system with an optical direct detection receiver followed by RF synchronous demodulator.
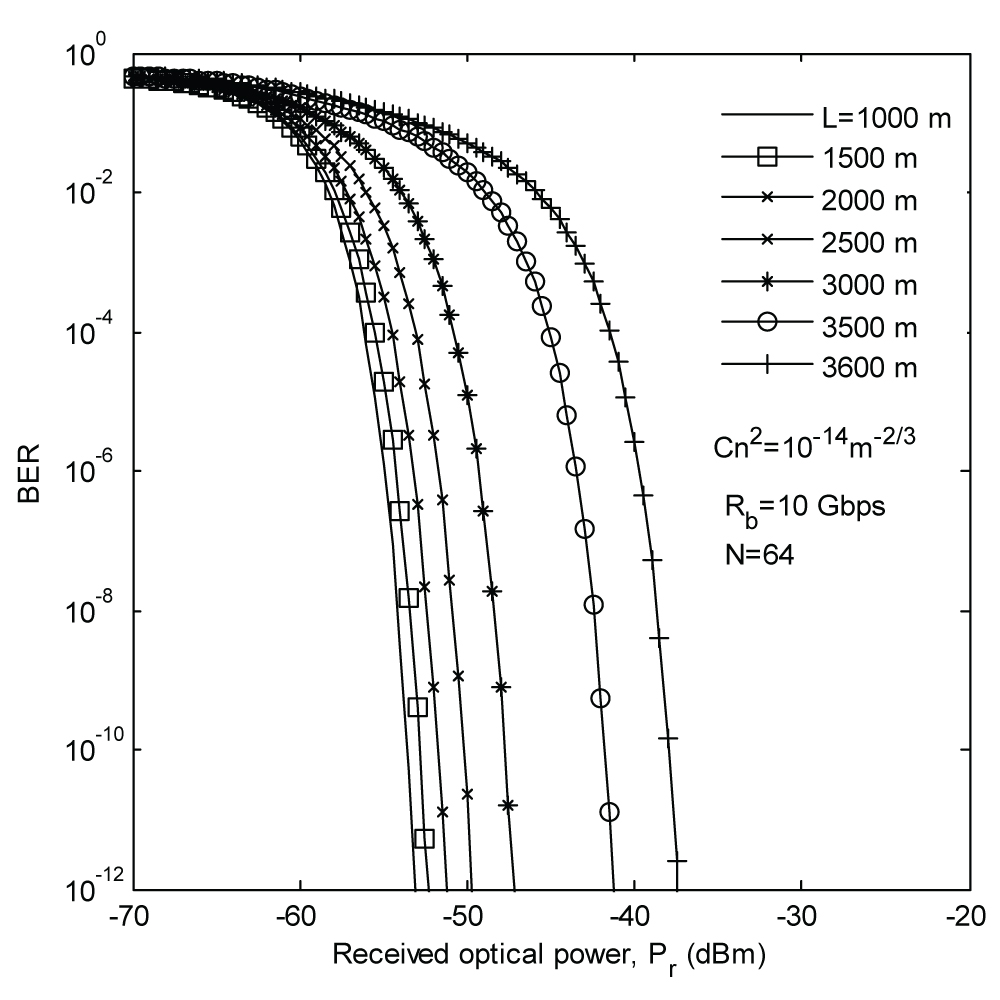
Figure 2: Plots of BER versus received...
Plots of BER versus received opt. power with variation of link distance (meter) for OFDM FSO system.

Figure 3: Plots of power penalty versus...
Plots of power penalty versus link distance with different BER for multiple subcarriers OFDM FSO system.
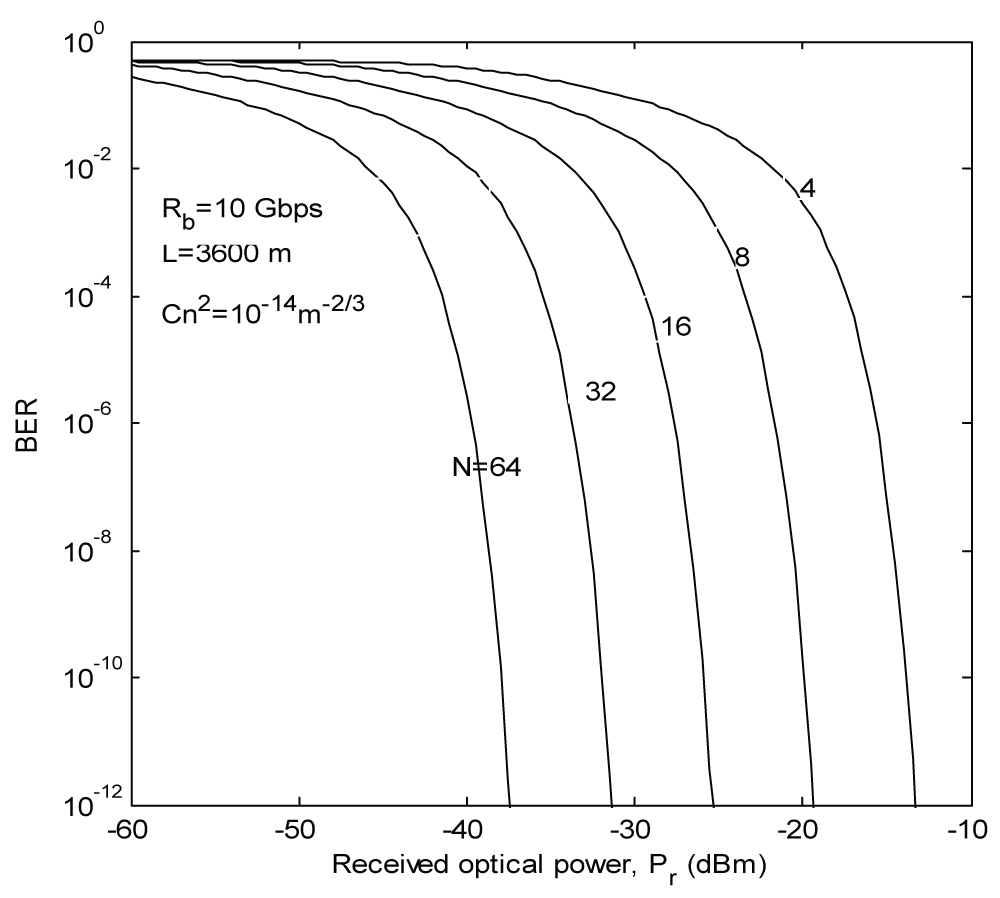
Figure 4: Plots of BER versus received...
Plots of BER versus received optical power with number of OFDM subcarriers as a parameter.

Figure 5: Plots of receiver sensitivity versus...
Plots of receiver sensitivity versus number of OFDM subcarrier in FSO system as a function of link distance under turbulent condition.

Figure 6: Plots of BER versus received...
Plots of BER versus received optical power for OFDM FSO system under as a function of data rate.

Figure 7: Plots of power penalty versus...
Plots of power penalty versus data rate for variable number of OFDM subcarrier in FSO system.
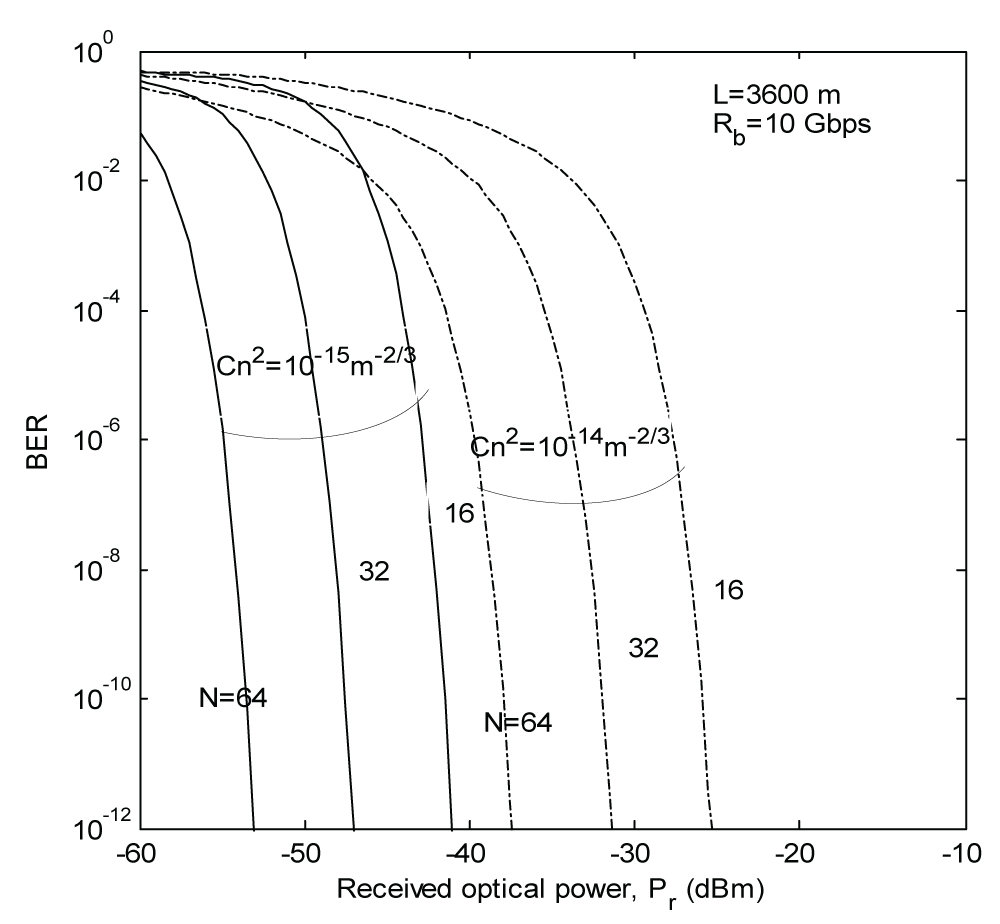
Figure 8: Plots of BER versus received...
Plots of BER versus received power under OFDM for variable combinations of OFDM subcarriers with two different value of refractive index structure parameter.
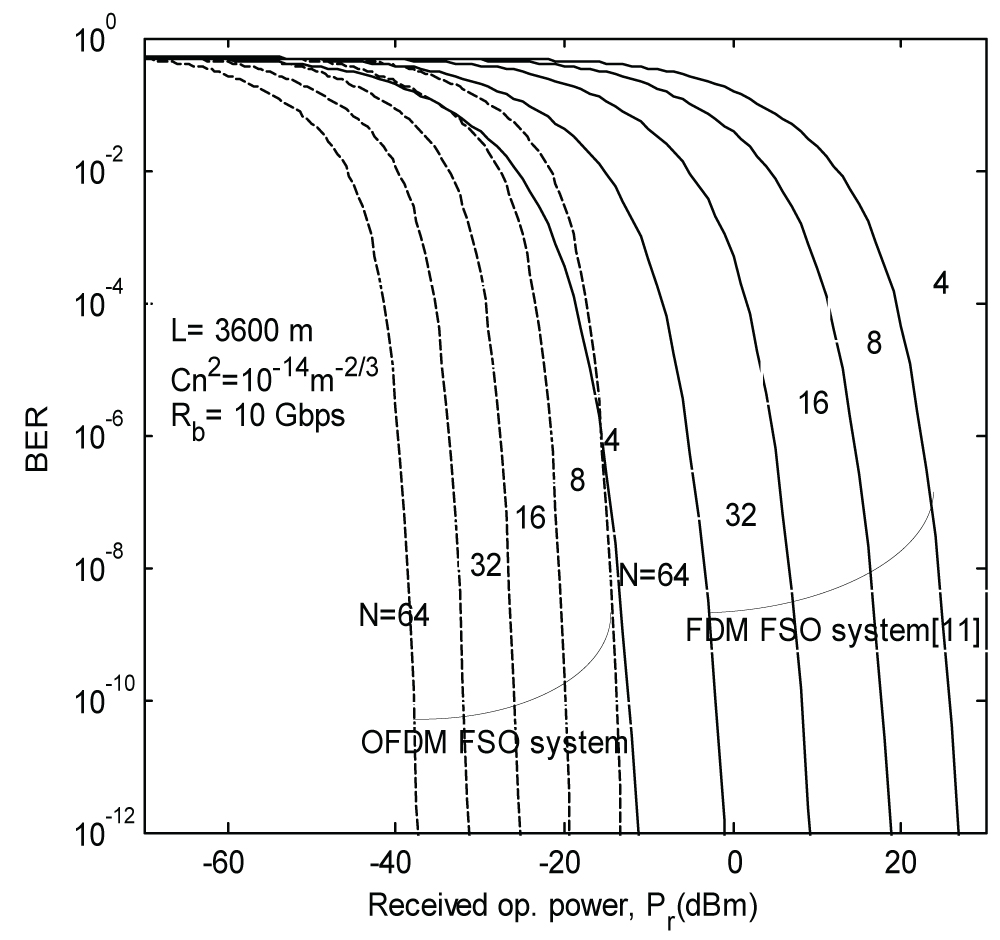
Figure 9: Plots of BER versus received optical...
Plots of BER versus received optical power for FDM and OFDM FSO system with variable combinations of subcarriers.

Figure 10: Plots of power penalty versus number...
Plots of power penalty versus number of subcarriers with two different refractive index structure parameters for both FDM and OFDM FSO systems.

Figure 11: Plots of BER versus received optical...
Plots of BER versus received optical power for OFDM FSO system under different turbulent condition.
References
- J Kaufmann (2011) Free space optical communications: An overview of applications and technologies. Proceedings of the Boston IEEE Communications Society Meeting.
- MNO Sadiku, SM Musa (2016) Free space optical communications: An overview. European Scientific Journal 12: 55-68.
- H Kaushal, A Viswanath, VK Jain, S Kar (2014) Evaluation of performance of ground to satellite free space optical link under turbulence conditions for different intensity modulation schemes. Proc SPIE, Free Space Laser Comm and Atmosph Prop (XXVI).
- W Gappmair, M Flohberger (2009) Error performance of coded FSO links in turbulent atmosphere modeled by gamma-gamma distribution. IEEE Trans Wireless Commun 8: 2209-2213.
- MA Al-Habash, LC Andrews, RL Phillips (2001) Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt Eng 40: 1554-1562.
- Y Wang, F Du, Jing Ma, Liying Tan (2014) Employing circle polarization shift keying in free space optical communication with gamma-gamma atmospheric turbulence channel. Opt Commun 333: 167-174.
- T Ohtsuki (2003) Multiple subcarrier modulation in optical wireless communications. Opt Wireless Communication 1: 74-79.
- WO Popoola, Z Ghassemlooy, JIH Allen, E Leitgeb, S Gao (2008) Free-space optical communication employing subcarrier modulation and spatial diversity in atmospheric turbulence channel. Optoelectronics IET 2: 16-23.
- WO Popoola, Z Ghassemlooy (2009) BPSK subcarrier intensity modulated free-space optical communications in atmospheric turbulence. J Light wave Technol 27: 967-973.
- X Tang, S Rajbhandari, WO Popoola, Z Ghassemlooy, SS Muhammad, et al. (2010) Performance of BPSK subcarrier intensity modulation free-space optical communications using a lognormal atmospheric turbulence model. IEEE Conference.
- B Barua, SP Majumder (2018) Performance analysis of a multiple subcarrier modulated FSO communication system using direct detection optical receiver under the effect of weak atmospheric turbulence. J Opt Communications, 1-8.
- H Samimi, P Azmi (2011) Performance analysis of adaptive subcarrier intensity-modulated free-space optical systems. IET Optoelectronic 5: 168-174.
- Zhan-Qiang Hui, Jian-Guo Zhang (2015) Design of optical time-division multiplexed systems using the cascaded Four-Wave Mixing in a highly nonlinear photonic crystal fiber for simultaneous time demultiplexing and wavelength multicasting. Journal of Optics 17: 1-16.
- Zhan-Qiang Hui, Jian-Guo Zhang (2014) Demonstration of 100 Gbit/s optical time-division demultiplexing with 1-to-4 wavelength multicasting by using the cascaded four-wave mixing in photonic crystal fiber with a single control light source. Microwave and Optical Technology Letters 56: 2330-2335.
- W Shieh, C Athaudage (2009) Coherent optical orthogonal frequency division multiplexing. Electron ett 42: 587-588.
- HE Nistazakis, AN Stassinakis, S Sinanovic, WO Popoola, GS Tombras (2015) Performance of quadrature amplitude modulation orthogonal frequency division multiplexing based free space optical links with nonlinear clipping effect over Gamma-Gamma modeled turbulence channels. IET Optoelectronic 9: 269-274.
- A Bekkali, CB Naila, K Kazaura, K Wakamori, M Matsumoto (2010) Transmission analysis of OFDM based wireless services over turbulent radio-on-FSO links modeled by gamma-gamma distribution. IEEE Photonics Journal 2: 510-520.
- J Armstrong (2009) OFDM for optical communications. IEEE/OSA Journal of Lightwave Technology 27: 189-204.
- Cvijetic, T Wang (2006) WiMAX over free-space optics-evaluating OFDM multi-subcarrier modulation in optical wireless channels. IEEE Sarnoff Symposium, Princeton, USA, 1-4.
Author Details
Bobby Barua1* and SP Majumder2
1Department of Electrical and Electronic Engineering, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh
2Department of Electrical and Electronic Engineering, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh
Corresponding author
Bobby Barua, Department of Electrical and Electronic Engineering, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh.
Accepted: January 22, 2019 | Published Online: January 24, 2019
Citation: Barua B, Majumder SP (2019) Bit Error Rate Analysis of an OFDM Subcarrier Modulated FSO Link with Optical Intensity Modulation and a Direct Detection Receiver. Int J Opt Photonic Eng 4:014.
Copyright: © 2019 Barua B, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
An analytical approach is developed to evaluate the BER performance of a FSO communication link using RF OFDM subcarrier modulation with optical intensity modulation and a direct detection receiver. Analysis is carried out to find expressions for the output photodetector current and carrier to noise power ratio at the output of the OFDM demodulator taking into account the effect of atmospheric turbulence of the free space optical channel. The average bit error rate is evaluated numerically considering log-normal and gamma-gamma distributions for weak and strong atmospheric turbulence. The analytical results are evaluated for different system and channel parameters such as number of OFDM subcarriers, turbulence variance, link distance etc. The computed results show that the system suffers power penalty due to atmospheric turbulence which can be significantly reduced by increasing the number of OFDM subcarriers at a given data rate. For example, for weak turbulence power penalty at a BER of 10-9 is found to be 18 dB, 14.5 dB and 12 dB corresponding to the number of OFDM subcarrier of 16, 32 and 64 respectively for link distance of 3.6 km at a data rate of 10 Gbps. It is also noticed that OFDM system provides 10 to 20 dB improvements over FDM system reported earlier.
Keywords
Carrier to noise ratio (CNR), Direct detection (DD), Free space optical (FSO) communication, Lognormal distribution, Subcarrier multiplexing
Introduction
Free space optical (FSO) communication systems are very much promising for future optical wireless communications [1-4]. However, the performance is highly degraded due to the effect of atmospheric turbulence which leads to intensity and phase fluctuations and seriously affects the stability and reliability of the FSO communication system [5-6].
Further, compared to a multiple subcarrier modulated system a single carrier modulated system suffers more severely due to inter symbol interference (ISI) caused by the dispersive fading of FSO channels and thereby needs more complex equalization [7-12].
OTDM and OFDM schemes are in literature to increase the data rate in optical fiber communication [13-16], but each of them reaches the desired capacity in a different way. OTDM allows us to time-interleave low duty-cycle and low rate data tributaries which simplifies the speed requirements of the transmitter equipment [13,14]. The challenging points in OTDM are the time-demultiplexer which relies on the femto-second response applicable on guided wave system.
On the other hand, orthogonal frequency division multiplexing (OFDM) is attractive for its capability of overcoming the effect of ISI due to increased robustness against frequency selective fading and narrow-band interference [15-17]. The flexibility of OFDM provides opportunities to use advanced techniques such as adaptive loading, transmit diversity and receiver diversity to improve transmission efficiency. A hybrid optical communication system consists of RF OFDM and optical intensity modulation can be used to improve the performances of FSO communication system [18,19]. Previous works [18,19] on OFDM based optical wireless communication are carried out by simulation and experimental demonstrations.
In this paper, we develop an analytical approach to investigate the performance of a FSO communication link using RF OFDM modulation with optical intensity modulation considering weak and strong atmospheric turbulence. Analysis is developed to find the BER performance results analytically in terms of carrier to noise ratio and optimum number of OFDM subcarriers, link distance etc. for several values of other parameters. The analytical results are verified with the computer simulation work that is reported in literature.
System Model
Figure 1 shows the block diagram of an OFDM FSO communication system with an optical direct detection receiver followed by RF synchronous demodulator. According to the diagram the input data stream is converted to parallel bit stream which is transmitted using N OFDM subcarriers. Each data channel is mapped with ASK modulator and the outputs of the modulators are given input to Inverse Fast Fourier Transform (IFFT) block. After that, Cyclic Prefix (CP) is added to mitigate the ISI effect and the overall output is sent to parallel to serial convertor. The output OFDM signal is then given input to an electro optic intensity modulator (EOIM) and the output of EOIM signal is then transmitted over an atmospheric turbulent channel.
At the receiving end the optical signal is detected by a direct detection receiver and the output photodetector current is amplified by a preamplifier. The output of the preamplifier is the OFDM signal with the effect of atmospheric turbulence along with receiver noise. The received OFDM signal is passed through a serial to parallel converter and cyclic prefix is removed. After removing the CP, the received samples are put to a Fast Fourier Transform (FFT) block. Finally, the RF outputs are demodulated using synchronous demodulators followed by decision circuit (DC). The output of the DC is sent to parallel to serial converter to get the original data stream.
Theoretical Analysis
Let, Sk represents the k-th input data symbol consisting of N number of bits ranging from ɑk1 to ɑkN. The symbol is given input to a serial to parallel converter and output parallel bits {ɑkj, j = 1: N} are transmitted using N subcarriers. Thus, ɑkj is the j-th bit of the k-th symbol and is used to modulate the j-th subcarrier.
Let mj(t) represents the message at the j-th branch of the serial to parallel converter. Then mj(t) can be given as:
Where { = 0,1}, Ts = N Tb, Tb representing the bit period while Ts represents the symbol period and p(t) is the pulse shape.
The electrical field output of j-th subcarrier ASK modulator is given by:
Where ωj is the j-th RF angular frequency and Aj is the amplitude of the j-th subcarrier.
The output of the subcarrier modulator corresponds to k-th symbol is given by:
Now the output of the subcarrier modulates, sk are given input to IFFT block and the output of IFFT can be represented as:
The IFFT block samples SIFFT(t) at t = lTs which provides
To deal with inter carrier interference, a cyclic extension is added with the output of IFFT block. With the cyclic extension, the actual OFDM symbol duration is increased from Ts to T = Ts + Tg, where Tg denote the length of a cyclic extension. The samples are passed through a parallel to serial converter to produce OFDM signal.
The output OFDM signal is then used to intensity modulate the laser diode using an electro optic intensity modulator.
The output of the optical intensity modulator can be expressed as:
Where PT represents the transmitter laser power and ka is the intensity modulation index and ωc is the optical carrier angular frequency.
The received optical signal at the input to receiver photodetector can be expressed as:
Where PR = PT e-αL is the received optical power, α is the attenuation coefficient of the atmospheric channel, L represents the link distance, nb is the background radiation intensity and I(t) represents the turbulence induced fading.
The signal photocurrent id at the output of the PD is given by:
Where Rd is the responsivity of the photodetector.
The received OFDM signal is then given by:
Now the received OFDM signal is put to a serial to parallel converter and cyclic extension is removed from the output. Then the output is fed to FFT block and the output of the FFT block can be expressed as:
The output of the FFT is given input to RF synchronous demodulators. The signal at the output of the RF synchronous demodulator can be shown to be:
Where no(t) represents the noise due to photodetector shot noise and receiver thermal noise.
Considering Aj = Asc (for j=1: N), the variance of the output noise no(t) for a given value of I(t) = I can be expressed as:
Where σsh2 and σth2 represents variance of shot and thermal noise respectively, T is the receiver noise temperature and RL is the load resistance.
Now the Carrier to Noise Power Ratio conditioned on a given turbulence induced fading I can be expressed as:
The conditional BER for n-th subcarrier channel can be found as [17]:
and the average BER can be obtained by averaging the conditional BER over the pdf of I as:
Where p(I) represents the probability density function of the turbulence induced irradiance.
For weak turbulence p(I) is represented by a lognormal distribution given by [5]:
Where I0 is the signal irradiance without scintillation represents the σI2 ryotov variance given by [5]:
and Cn2 is the Refractive index structure parameter and k represents the wave number which is 2π/λ and λ represents the operating wave length which is 1550 nm.
For strong turbulent condition p(I) is given by a gamma-gamma distribution [16]:
Where α and β are PDF parameters describing the scintillation experienced by plane waves, and in the case of zero-inner scale.
The average bit error rate can be obtained as:
Results and Discussion
Following the analytical approach presented in previous section, we evaluate the performance results of an OFDM FSO communication with system parameters shown in Table 1.
The plots of BER versus received optical power are shown in Figure 2 as a function of the link distance, L. From the plots it is observed that the error performance deteriorates as link distance is varied from 1000 m to 3600 m. Additionally, an expansion in L over 2600 m results in a progressively extreme execution disintegration contrasted with link separation of 1000 m to 2500 m. It is apparent that, the BER execution is less instigated by the environmental disturbance up to the connection separation of 2500 m.
The plots of power penalty due to the effect of weak atmospheric turbulence at BER 10-3, 10-6 and 10-9 with respect to the link distance are shown in Figure 3. The power penalties are calculated numerically from the plots of BER curves with respect to the link distance. It is found that for same system configuration the power penalty is higher at higher link distance. Further power penalty is found to be more for BER of 10-9 compared to 10-3 and 10-6.
Figure 4 shows the plots of BER versus received optical power for various number of OFDM subcarriers for a FSO system. As expected, the system performance gradually improves with increase in number of subcarriers.
Figure 5 shows the plots of receiver sensitivity at BER of 10-9 versus number of OFDM subcarrier in FSO communication system as a function of link distance under turbulent condition. It is found that with increase in number of OFDM subcarrier the receiver sensitivity gradually improves at a given BER.
Figure 6 shows the BER performance with respect to the received optical power for OFDM FSO system with different values of the data rate. At higher data rate, system is more affected due to atmospheric turbulence.
The plots of power penalty at BER = 10-9, versus data rate for various number of OFDM subcarrier in FSO system are shown in Figure 7. From the figure it is found that the power penalty increases with increase in data rate to a certain value. For example, for 1 Gbps data rate the system suffers in power penalty of 3 dB for 64 OFDM subcarriers and power penalty gradually increases with increase in data rate till 15 Gbps. After that the power penalty remains unchanged.
The error performances of OFDM FSO link for combinations of OFDM subcarriers with variable refractive index structure parameter, Cn2 are shown in Figure 8. The error performance improves with the improvement of refractive index structure parameter, Cn2 from 1 × 10-14 m-2/3 to 1 × 10-15 m-2/3 for same number of OFDM subcarriers.
The BER performances under orthogonal and non-orthogonal conditions with various RF subcarriers are shown in Figure 9. From the analysis of the figure it is found that, by applying RF OFDM subcarrier modulation in FSO communication the link performance improves gradually with increasing the number of subcarriers. Overall the system demands less power compared to non-orthogonal condition. For example, the required power for 64 subcarriers under non-orthogonal condition is almost similar to the power required for 4 subcarriers under orthogonal condition.
The plots of power penalty at a BER of 10-9 as a function of OFDM subcarriers are shown in Figure 10 with two different refractive index structure parameters for both strong and weak turbulent condition. It is found that by changing the value of refractive index structure parameter, Cn2 from 10-14 to 10-15, the system power penalty reduces significantly. Moreover, the system suffers huge power penalty under strong turbulent condition.
The BER performance comparisons of our analytical results with the simulation results reported in Ref [16] are shown in Figure 11. In Ref [16] the simulation is performed for strong turbulent condition with 5617 OFDM subcarriers considering the effect of laser nonlinearities. In our results, non-linearities of Laser diode are not included. Our analytical results shows better BER performance without non-linear effects. And the analytical result for weak turbulent condition also included in figure which represents the better performance.
Conclusions
An analytical approach is presented to evaluate the bit error rate (BER) performance of an OFDM FSO link in presence of atmospheric turbulence. The results show that the BER performance is strongly degraded due to the effect of atmospheric turbulence. However, the BER performance results can be improved and the power penalty can be greatly reduced by increasing in the number of OFDM subcarriers. Finally, the analytical results are compared with the computer simulation work that is reported in ref. [16]. The results of this research will find applications in design of RF OFDM modulated optical intensity modulation FSO link with direct detection receiver for high data rate application.
Acknowledgements
The authors would like to acknowledge with gratitude the support provides the Department of EEE, BUET.

