
International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 5, Issue 1
Research Article
DOI: 10.35840/2631-5092/4522
On the Velocity and Acceleration of Light
Richard Sauerheber1* and Kalvin McCallum2
Figures

Figure 1a: A light ray travels 1 meter in the horizontal...
A light ray travels 1 meter in the horizontal X direction and is reflected by a 45° tilted mirror and then travels an additional meter in its new vertical Y propagation direction. The total distance traveled is 2 meters in time t = d/c = 2/c. The net velocity vector v of the light for the event is the net displacement divided by the time, or .
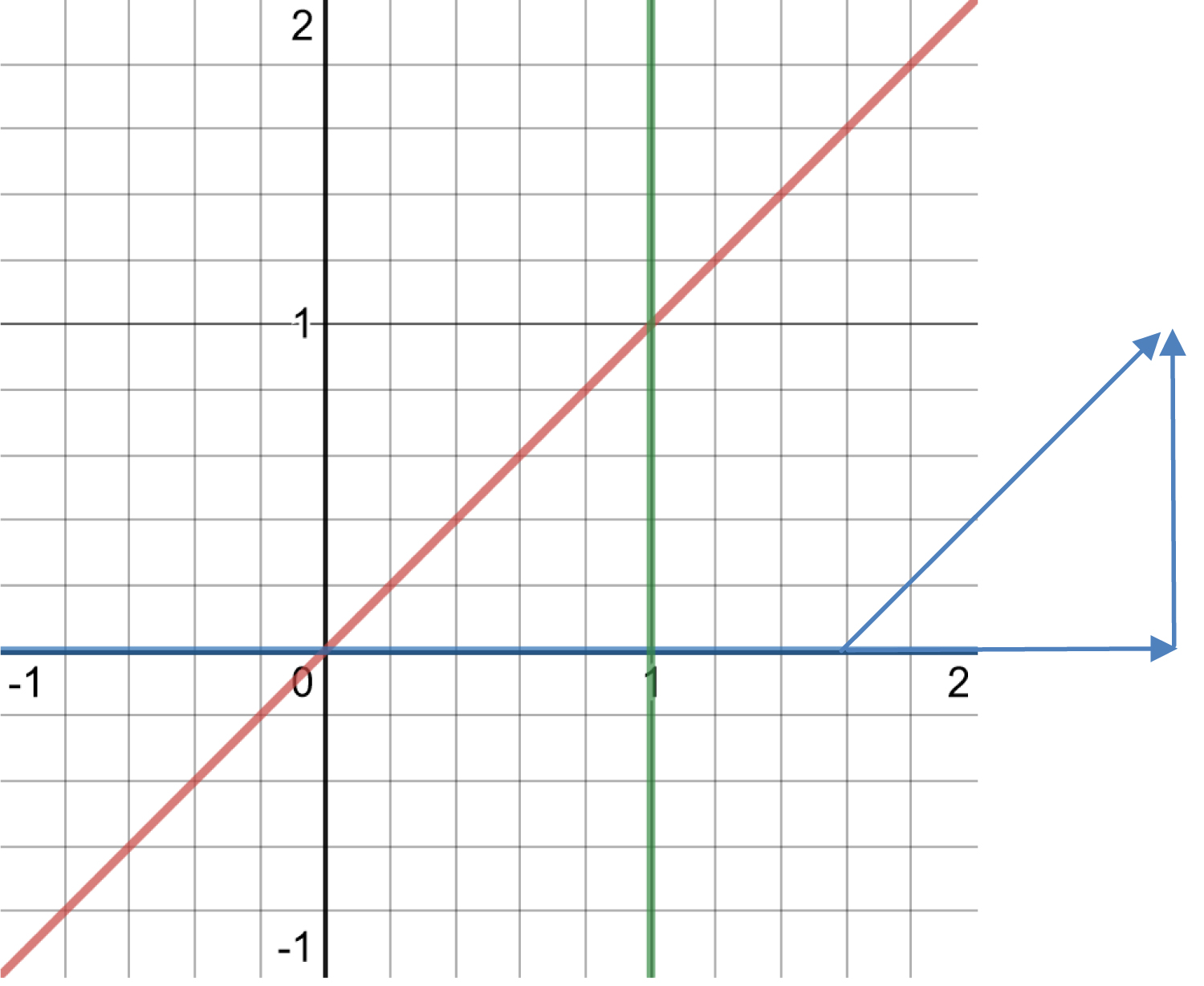
Figure 1b: a) THz signal generated from the system...
a) THz signal generated from the system; b) Schematic Diagram of the solution of using THz for skin evaluation.
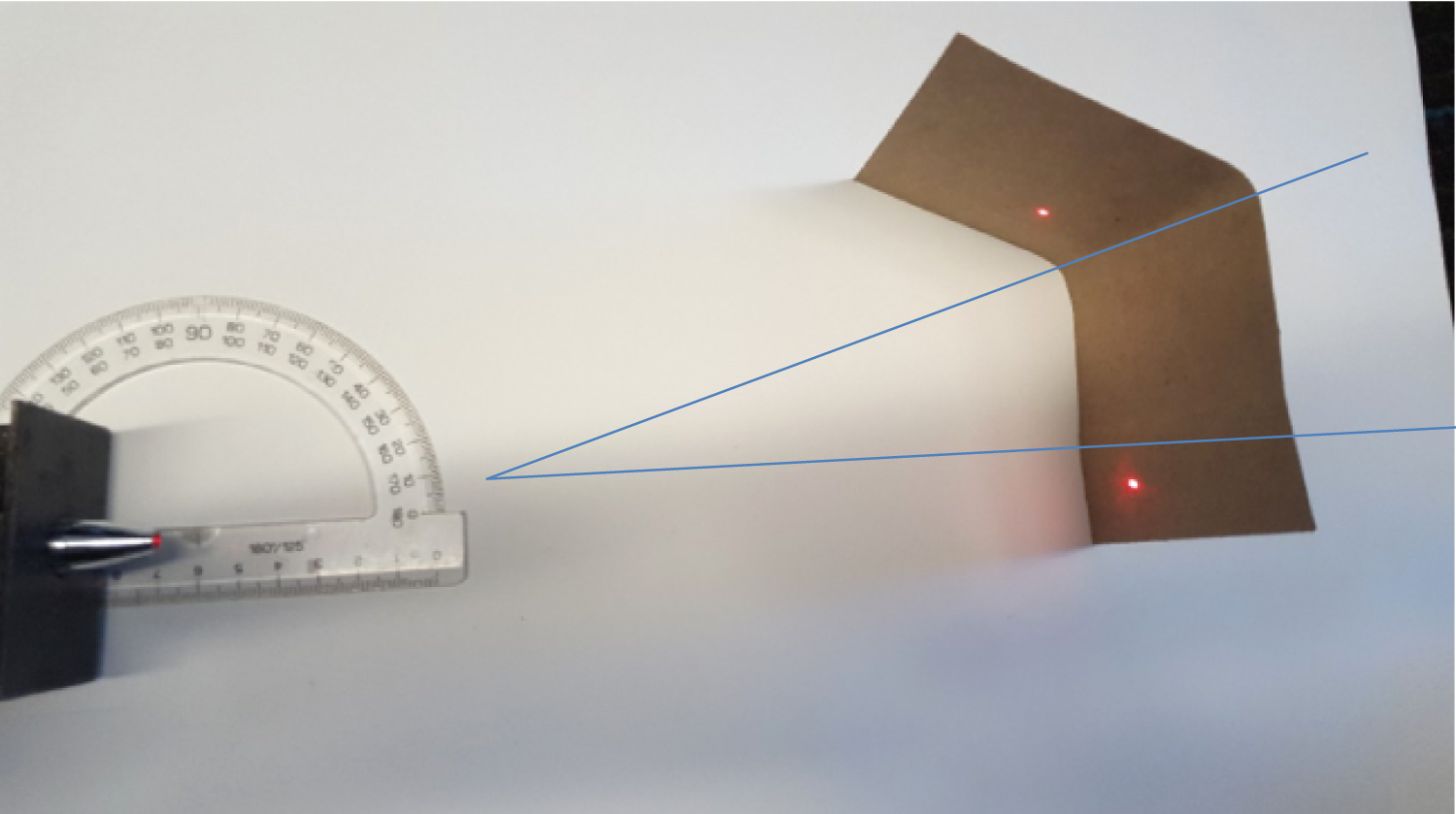
Figure 2a: Two red laser light rays from a source travel...
Two red laser light rays from a source travel 1 meter each in distinct directions to a reflective barrier. The angle between the rays is θ = 20°. The total distance illuminated by the beams is 2 meters and occurs in time t = (1 m)/(cm/s) or 3.33 nanoseconds. The speed with which distance is illuminated is 2m/t = 2m/3.33 × 10-9 s = 6.0 × 108 m/s = 2c.
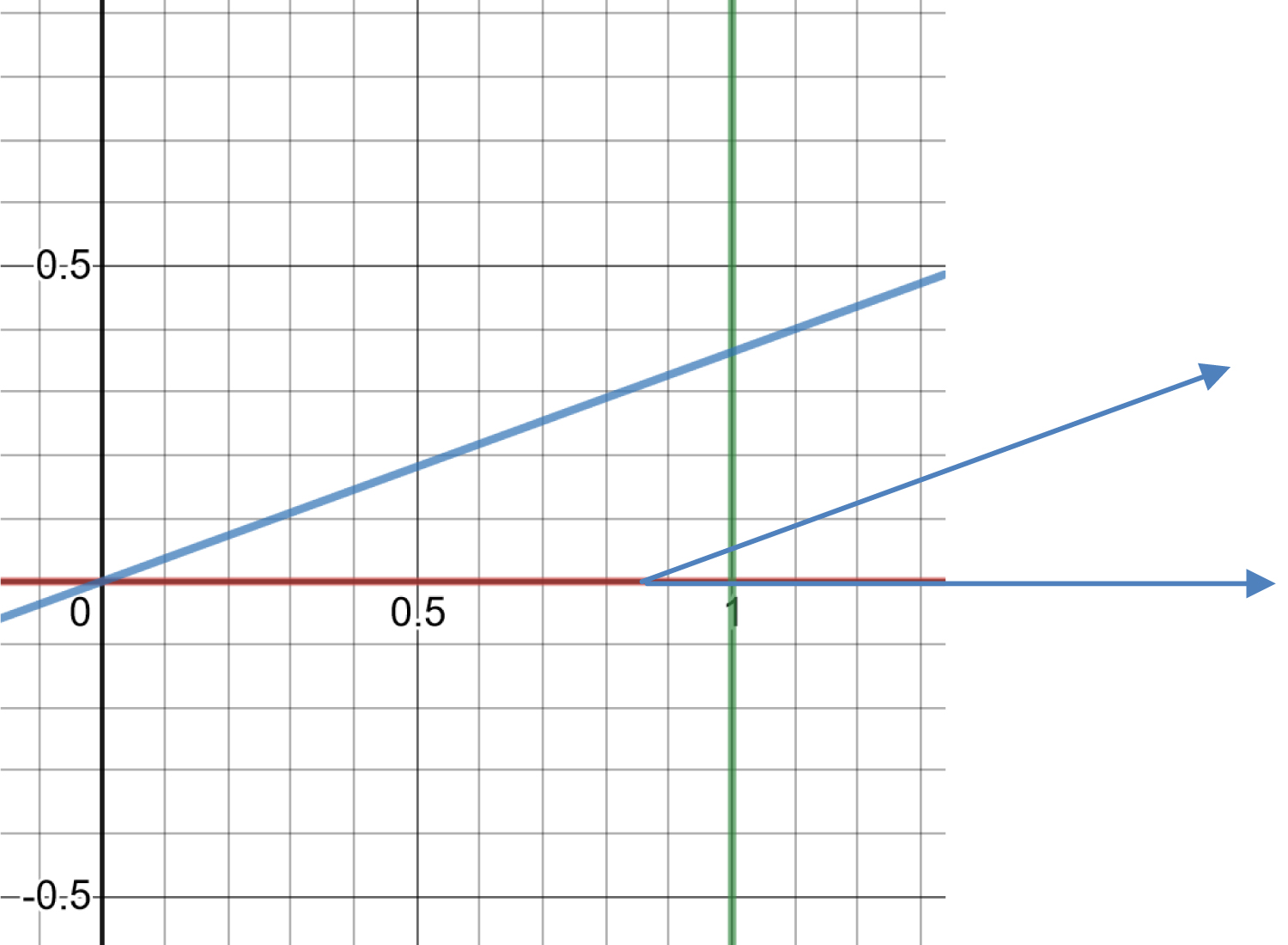
Figure 2b: The equations y = 0, and y = tan(20°)x describe...
The equations y = 0, and y = tan(20°)x describe the paths the two light rays take that are shown in the Figure 2 photograph. The horizontal ray and the angled ray travel one meter in a time given by t = 1/c = 1.33 nanoseconds because both rays travel simultaneously.
References
- Giancoli D (2005) Physics. (5th edn), Prentice-Hall, Upper Saddle River, New Jersey, USA.
- Halliday D, Resnick R, Walker J (2001) Fundamentals of physics. (6th edn), John Wiley and Sons, Inc., New York.
- Otis A (1960) Light velocity and relativity. Burckel and Associates, Yonkers-on-Hudson, New York.
- Sauerheber R (2018) Characteristics of light: Velocity, massless energy, and special relativity. Optik 168: 974-986.
- Sauerheber R (2014) On the nature of light and relativity. Physics Essays 27: 116-125.
- McCausland I (1999) Anomalies in the history of relativity. Journal of Scientific Exploration 13: 271-290.
- Reddy F (2019) NASA visualization shows a black hole's warped world. Goddard Space Flight Center, Greenbelt, MD, USA.
- (2014) Moon Bumps: Earth's Gravity Created Lunar Bulges, NASA's Moon Gravity Mission, Space.com, USA.
Author Details
Richard Sauerheber1* and Kalvin McCallum2
1STAR Center, Palomar Community College, San Marcos, USA
2Bioengineering, University of Massachusetts Lowell, Massachusetts, USA
Corresponding author
Richard Sauerheber, STAR Center, Palomar Community College, San Marcos, CA 92069, California, USA.
Accepted: May 18, 2020 | Published Online: May 20, 2020
Citation: Sauerheber R, McCallum K (2020) On the Velocity and Acceleration of Light. Int J Opt Photonic Eng 5:022
Copyright: © 2020 Sauerheber R, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Commonly argued tenets in Physics are that the velocity of light is a fixed constant in any particular medium, and the velocity of light cannot be exceeded. Here the factual and false portions of these claims are delineated with simple demonstrations that distinguish between the speed versus the velocity of light. Also demonstrated is how indeed light velocity can be other than c and thus can be exceeded, and that light itself can be accelerated. This description is essential to understand claims made in the theory of special relativity, the interaction of light with matter, and the behavior of light in the physical universe. Although a light box is not useful as a timepiece since the earth itself undergoes several rapid states of motion, a light ray may be used as a sensitive motion detector.
Introduction
The special theory of relativity states that light velocity is fixed in a given medium and that light velocity is limiting and thus cannot be exceeded by any known entity [1,2]. These statements have led to many inconsistent proposals. For example, it has been proposed and widely written that absolute time itself 'dilates' or becomes prolonged for objects or observers in motion, even though absolute time itself is not subject to human activity and does not require the existence of matter. Second, the total relative velocity of an observer moving in relation to a light front has been argued to remain fixed at magnitude c, even though total relative velocity is different from the intrinsic velocity of an entity even though that itself might be fixed [3]. Indeed, sound speed is fixed and yet the relative velocity between a sound wave front and a moving observer differs from the speed of sound alone. Since velocity is a vector quantity and speed is not, the distinction between these quantities for light is crucial in order to understand the correct and incorrect parts of relativity theory. Shown here are the facts that light velocity can vary from -c to +c, that observer and light velocities are additive, that light can be accelerated, and that light speed and velocity can technically be exceeded.
Methods
A laser light source, protractor, mirror, and reflective barrier are photographed in various arrangements to demonstrate the distinct properties of velocity and speed for light. The acceleration of light may be computed as a change in velocity after reflection from a surface by measuring the total distance traveled by light and the net distance traveled by light for a particular event. Two light sources combine in arrangements that demonstrate that light velocity can be exceeded. For the sake of clarity, the velocity of light in air is here rounded to throughout and is the velocity that is intrinsic to light with respect to the location at which it leaves its source. Time for light to travel a given distance is computed from ground displacement divided by the linear speed of light, which ignores earth orbital and rotational velocity and solar system rotation about its axis, which are not necessary to conceptualize the phenomena described here. The experiments were not done in a cloud chamber to directly visualize the path of light, so the paths are drawn between the positions at which light is reflected. Constants are shown in boldface lower letters, variables in boldface higher letters, vector quantities in boldface italics, and abbreviated units of measure in italics.
Results
Light rays of photons from a stationary source form vectors in the propagation direction, which in a two-dimensional plane of travel may be described with horizontal and vertical components.
Net velocity for a light event
In Figure 1 a light ray indicates the path of photons taken from the laser source on the left to a mirror 1 meter distant which is 45° rotated from the horizontal. The photons in the ray are reflected to travel an additional 1 meter to the upper barrier. Velocity is a vector quantity with both a magnitude and a direction. The velocity for the photons from the source to the mirror may be written as v1 = ci + 0j, and the velocity of the reflected photons as v2 = 0i + cjm/s. Here the time required to travel the entire event is or 6.67 × 10-9 seconds. The total net velocity for the event is the total distance traveled, the magnitude of the vector from the origin to the barrier, or , divided by the time for the event, so the actual velocity of the event for light traveling from (0, 0) to position (1, 1) is less than c.
A Cartesian graph of three equations describes the light ray paths as shown in Figure 1A. Since light rays are vector quantities, the net displacement is the sum of the two vectors. The net displacement is meters during the time for the event.The time required for the event is the total distance the light ray traveled, 2 meters, divided by the intrinsic speed of light c, or t = 2/c = 6.67 × 10-9 seconds. Thus the net velocity for light in this event is .
Acceleration of light
The acceleration of light may be described as its change in velocity per second. Although the magnitude of the velocity of the photons, the speed, remains c during the entire event, the velocity of the photons changed because of a change in direction. If this change had occurred smoothly over the duration of the event, or if we desire the average acceleration, we could compute it as the magnitude of the final velocity minus the initial velocity, divided by the time, or from the vector analysis ||v2 – v1||/t = ||-ci + cj||/(2/c)= 0.707 c(c/2) = 1.32 × 1016 m/s2. Using the Cartesian analysis, (v2 = v1)/t = (0.707c - c)/(2/c) = 1.32 × 1016 m/s2 as well. Light re-direction from reflective surfaces causes enormous acceleration with change in velocity. In reality the accelerative event took place when the photon experiences a frictionless interaction with the EM field near the mirror.
Light velocity exceeded in several ways
Two light rays travel from the origin at one instant to two separate locations 1 meter distant as shown in Figure 2. Whether the angle between the beams is 180°, forming a total linear path of illumination, or not, the total velocity with which the 2 meters distance is illuminated by light would be 2c. This is because the time required to illuminate the involved distances is determined by the 1 meter distance traveled by both at the same time, which is t = d/c = 3.33 × 10-9 seconds. This demonstrates that the speed and the velocity for light can be exceeded in certain physical arrangements. The velocity of light in its propagation direction is fixed at c, which means that the velocity for light in any other direction is a component that is less than c. For light to reach a 1 meter distance along the horizon requires time t = (1 m)/(cm/s) = 3.33 nanoseconds, but for the beam with a North East propagation direction, the time to travel 1 meter along the horizon is greater than 1/c, where t = 1/[c(cos20°)] = 3.55 nanoseconds. The necessary component of velocity in the desired horizontal direction is less than c. Also, the total distance of travel L in its propagation direction would be greater than 1 meter while attaining a 1 meter span along the horizon, where L = 1/cos(θ) = 1.06 m.
From the Cartesian graphs of the situation shown in Figure 2A, notice that the horizontal ray travels at velocity c to span distance x = ct = 1 meter in a time t = 1/c, from (0, 0) to (1, 0). The angled ray propagates with horizontal component velocity c[cos(20°)] to accumulate a horizontal distance x = cos(20°)ct = 0.939 m and with vertical component velocity c[sin(20°)] to accumulate vertical distance y = sin(20°)ct = 0.342 m, traveling from (0, 0) to (0.939, 0.342). The propagation distance for both rays is 1 m, where the angled ray travel distance is L = (0.9392 + 0.3422)0.5 = 1 m as well.
Discussion
Light photons are orthogonal electromagnetic field sets that self-induce and self-annihilate each other that thus must travel at intrinsic fixed speed c = E/B in its propagation direction from the location in space at which it departs its source. When uninterrupted, light travels at fixed speed (and velocity magnitude in its propagation direction) c without acceleration in perpetuity. However, the presentation here demonstrates that the speed and velocity of light can be exceeded in physical experiments.
Light in space
In nature, notice that all light rays from the sun or other stars propagate in 3-dimensional space, where each ray has a distinct velocity vector in i,j,k space while each travel at magnitude speed c in their respective directions. Each has distinct velocities where rays traveling in one octant of a sphere do not ever exist in other octants. The speeds for any ray from the sun technically can be represented as c for one direction of travel and -c for the opposite direction, and velocity components for light can vary from -c to 0 to +c for any particular stationary coordinate system. Any light ray has components with velocity less than c in any direction other than the propagation direction. Starlight rays from two stars traveling in opposite directions toward each other require less time to span this total distance than required for a single beam, where the total relative velocity can be as large as 2c.
Component velocity
Thus, the velocity of light can be exceeded in a direction other than the propagation direction for light [4,5]. For example, a jet traveling from Los Angeles (-118° longitude) to New York City (-74°) travels 2,791 miles at 500 mph in approximately 15,000 seconds. This exceeds the velocity of light in that direction for light if it propagates North East at a bearing angle less than θ = 0.15°. Here the light would require more than 15,000 seconds to reach the longitude of NYC, so the velocity of the plane exceeds the velocity component of light traveling East.
Light can be accelerated, without change in intrinsic propagation speed c, by a reflective surface so that the velocity of such a ray changes due to that acceleration. Although massive acceleration such as reported here would first seem impossible, recall that light is massless EM radiation and thus does not require a force, from F = ma, to be accelerated and redirected because m = 0. This is also why there is no friction when light is reflected by matter. Acceleration of a massless entity does not involve a force. The precise mechanisms by which light is accelerated by reflective surfaces, or by matter that refracts, diffracts, or scatters light, are not well characterized.
A light photon traveling toward a reflective surface or mirror propagates at speed c, and after reflection in the reverse direction away from the surface travels at speed c as well. However, the horizontal velocity of the photon before reflection is v = +c and after reflection is v = -c. Since the angle of incidence is always equal to the angle of reflection for a mirror, light is not absorbed and re-emitted in random directions. Therefore it must be that the center of the photon, which itself is not a wave but is an infinitesimal packet of EM energy, must have a horizontal velocity that is zero at the location at which it is reflected. This does not however alter the fact that for light to exist it must propagate at speed c. The precise mechanism by which photons are reflected is not analogous to a collision of two masses and could involve for example an internal fold on itself with a front that still proceeds at speed c. The miniscule reflection time for this event might be estimated at the wavelength the light generates divided by c, which here would be 450 × 10-9 m/(3 × 108 m/s) = 1.5 × 10-15 s.
Time does not respond to motion of matter
These results are necessary to understand why time does not 'dilate' due to motion in widely published light clock diagrams, and why the relative velocity of light can be different from c and can exceed c in natural and artificial systems. Light travels about 93 million miles from the sun to the earth in a direct path in approximately 8 minutes and 18 seconds. Sunlight that arrives on earth that is reflected from the moon, which allows the moon to be seen with the naked eye, travels 93 million (149.6 × 109 m) plus about 241,000 miles (384 × 106 m) all at intrinsic propagation speed c. Thus it takes 8 minutes and 20 seconds for sunlight to reach earth after being accelerated by the moon. This extra time required for light to be observed, compared to that directly observed from sun's rays, is not due to "time dilation" but simply reflects classical relativity, that a longer time is required for light to travel a longer linear distance. The net velocity of the light for the displacement L/c = 0.997c, compared to c for the beams that directly travel from sun to earth.
Now that these features of light have been explained, it is then possible to discern the very common blunder that time "dilates" due to motion of an observer, as widely described in most Physics texts. The mistake may be revealed by examining Figure 2. The light ray traveling 20° North of the horizontal travels actually 1 meter in 3.33 nanoseconds as discussed (ignoring the motion of the planets and solar system for clarity). However, if an observer were in motion along with the traveling ray vertically at the same vertical velocity of the ray at c[sin(20°)] = 1.03 × 108 m/s, then the vertical distance accumulated by the beam would not be observed. It would then be presumed that the beam merely traveled the horizontal component of [1 m][cos(20°)] or 0.94 m because this is the only displacement that is observed. Further, it is always assumed that light velocity is fixed at c no matter the physical configuration of a system, so the time for this event would be mistakenly calculated as 0.94/c = 3.1 nanoseconds. But both the distance accumulated by a light beam in a particular direction, and the component velocity of light in a particular direction, is vectors, so this blunders of course here is a simple mismatch of vector quantities.
The difference between the true time and the mistaken time is usually referred to as ∆t, that is claimed to be the amount of time that "dilates due to motion", and represents the "slowing" of biological processes due to motion, and the difference in age for twins when one travels more rapidly than the other. However, notice that ∆t is actually the amount of error between the true travel time for the light ray and the mistakenly computed time. It is the magnitude of error in the measurement, which is here an error of [(3.33 - 3.10)/3.33] × 100 = 6.9% for the moving observer. The stationary observer computes the correct time, but the moving observer is in error, where the extent and sign of the error depend on the direction of motion of the observer. If the time had been computed by the moving observer as the horizontal component of distance divided by the horizontal velocity component for the ray of [c][cos(20°)], then the correct time would have been obtained by the moving observer as well, just as for the stationary observer. In other words, L/c and L[cos20°]/{[c][cos20°]} are identical. But L[cos20°]/c and L/{[c][cos20°]} are both false computations, being mismatched vectors.
The same outcome occurs if the source and target are in motion together, for the stationary and moving observers computing time [5]. An observer moving along with the moving source notices a false displacement for a light event because the target moves during the event, where light requires a different distance than the ground distance between source and target. This is seen properly by a theoretic stationary observer, so the moving observer again computes an incorrect time. In conclusion, there is no such thing as dilation of absolute time due to motion for a given event involving light. Indeed, absolute time has no beginning or ending, having a domain of (-∞ to +∞), and does not adjust itself based on the motional behavior of mass, and indeed existed long before matter or even light ever did. This of course does not detract from the classical relativity fact that a prolonged time occurs for two different light events if one distance traveled by light is longer than another.
Relative velocity
Notice that the relative velocity between alight front and a moving detector, or between two light fronts, is not c. Even though the intrinsic speed of a single light ray in its propagation direction is fixed at c (as originally derived mathematically by James Clerk Maxwell as c = E/B), total relative velocity with respect to moving detectors or other rays is obtained by classical velocity addition. The relative velocity between the two rays at the points of deflection by the targets in Figure 2 is less than c because after the travel time the two positions only differ by a distance of [0.9392 + (1 - 0.342)2]0.5 = 1.15 m, compared to the 2 meters separation if the beams had been traveling in opposite directions. Also, if a detector in Figure 2 could theoretically move at light speed c in the propagation direction for the angled ray, then no net displacement would be detected at all, and the relative velocity would be c - c = 0. Likewise, for two beams traveling in opposite directions, either both away from a common source, or both toward a common destination from separate sources, the relative velocity between the two fronts is 2c, where space is illuminated at a rate twice as quickly as a single ray could. Recent published discussions have been presented regarding the possibility that an entity could even travel in excess of speed c in the propagation direction.
Special classical relativity; massless light
The special characteristics of light, having no mass, and traveling at fixed intrinsic speed c in its propagation direction from a coordinate in space at which it departs its source, do not interfere with classical relativity [3], but rather add to it. Special Classical relativity would be an appropriate label to describe light and its interaction with matter. That light is massless is not only demonstrated here with the massive acceleration magnitudes, but this has also been demonstrated experimentally [3] where light velocity increases while leaving glass to enter air, which is a property that masses do not have. Further, it is widely accepted that electric and magnetic fields have no mass, containing no physical particles [1,2]. A charged body emanates an electric field around it and a magnetic body is surrounded by a magnetic field, and neither requires an expenditure of energy or loss of mass to exist. It is clear then that EM radiation is massless. The problems with the interpretation of the original photographs of starlight at different times of day, suggesting that this may not be the case, have been amply reviewed [6].
Black "holes"/bodies
The National Aeronautics and Space Administration recently published an animation from a space telescope photograph of an object in deep space [7] commonly labeled a "black hole." It is believed that the object contains dense matter at its core with gravity that is said to be responsible for gas molecules swirling around it. Thus the object could be better called a black body rather than a hole. Light detected from gas particles surrounding the body in a flat pattern indeed may be due to light-emitting (or light-reflecting) molecules that orbit a gravity-producing center. It is improper however to ascribe the animation to being due to gravity altering the path of light itself since light is massless and not subject to gravity, while the gas particles themselves would be. Recall that light displaces darkness since darkness is merely the absence of light. What appears to be dark empty space between stars is not known necessarily to be actually dark since light is emitted from all stars in 3-dimensional space. The moon for example is visible while it traverses the entire skyline because it is intercepting and reflecting sunlight that is otherwise invisible. Massive quantities of light energy exist in deep space that is not seen because it is not reflected to earth. So it is not certain that a black body (or 'hole') is totally devoid of light; and if it were, it is possible that light arriving there might merely be efficiently absorbed and not reflected, as for an actual blackbody.
Motional effects on light
A light box is not a useful device to measure time for a physical event since the intrinsic speed is always c in its propagation direction, while material objects travel at unknown total speeds due to earth's orbit and rotation, the angular rotation of the galaxy, and possible translational motion of the universe, etc. However, a light ray can be used as a highly sensitive relative motion sensor. A light ray from a typical public available laser source is reflected by a target 30 meters distant without appreciable distortion of the circular-shaped reflection spot. Therefore a readily visible shift of 1 millimeter in the position of a reflected spot on a 30 m distant target is caused by a mere [0.0019° = tan-1 (0.001 m/30 m)] shift in the angle made by the ray and source-target axis. It is possible to determine the extent of stress buildup across an earthquake fault by noting the shift in laser light angle over time as a possible warning device to better predict the time of an impending earthquake. The relative drift between positions on the North American Plate and the Pacific Plate is approximately 100 mm per year.
A light ray may be used to sense any relative ground motion between source and target because light produced from lateral moving sources picks up lateral momentum from the source and shifts along with the moving target without shifting the reflected spot location on the target [4]. This effect destroys the ability to use a light ray in a box as a timepiece, but the phenomenon ensures a light ray may be used as a sensitive motion detector or position sensor. The exquisite sensitivity of a light ray to relative motion between a source and target makes this detection possible. NASA scientists found a 50 cm bulge on the surface of the moon closest to earth due to earth's gravity pulling the non-spinning moon [8]. It was also argued that the moon's gravity pulls on the earth to contribute to its bulged equator, but this is uncertain since the earth rotates so that more centripetal force is at the equator. Preliminary detected evidence indicates that localized earth movements or bulges as a function of time may reflect changes in gravity as the moon orbits. Gravity from the moon of mass mat earth's surface a distance r is approximately g' = mG/r2 = (7.35 × 1022 kg) (6.67 × 10-11 N-m2/kg2)/(384 × 106 m)2 = 3.3 × 10-5 m/s2 where G is the universal gravitation constant. This appears negligible but is of course able to bulge the oceans as the earth rotates to produce tides. Time-dependent daily shifts in a reflected light spot on a target may correlate with the position of the moon, as due ocean tides, if the target and light source are not physically attached and are anchored on different types of surfaces.

