
International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 5, Issue 1
Research Article
DOI: 10.35840/2631-5092/4523
Coherent Control of Optical Nonreciprocal Propagation in a V-Type Atomic System
Yihong Qi1*, Peng Wang2, Yueping Niu1 and Shangqing Gong1
Table of Content
Figures

Figure 1: (Color online) a) Coupling schemes of the V-type...
(Color online) a) Coupling schemes of the V-type atomic model; b) Laser arrangement and experimental setup. PB: Polarized Beamsplitter; PD: Photoelectric Detector; HWP: Half-Wave Plate; PL: Probe Laser, CL: Control Laser; Rb: Rubidium Cell; OI: Optical Isolator; AR-Rb: Antireflection Coated Rb Vapor Cell; SAS: The Laser System Stabilized on the Saturated Absorption Lines of Rubidium.
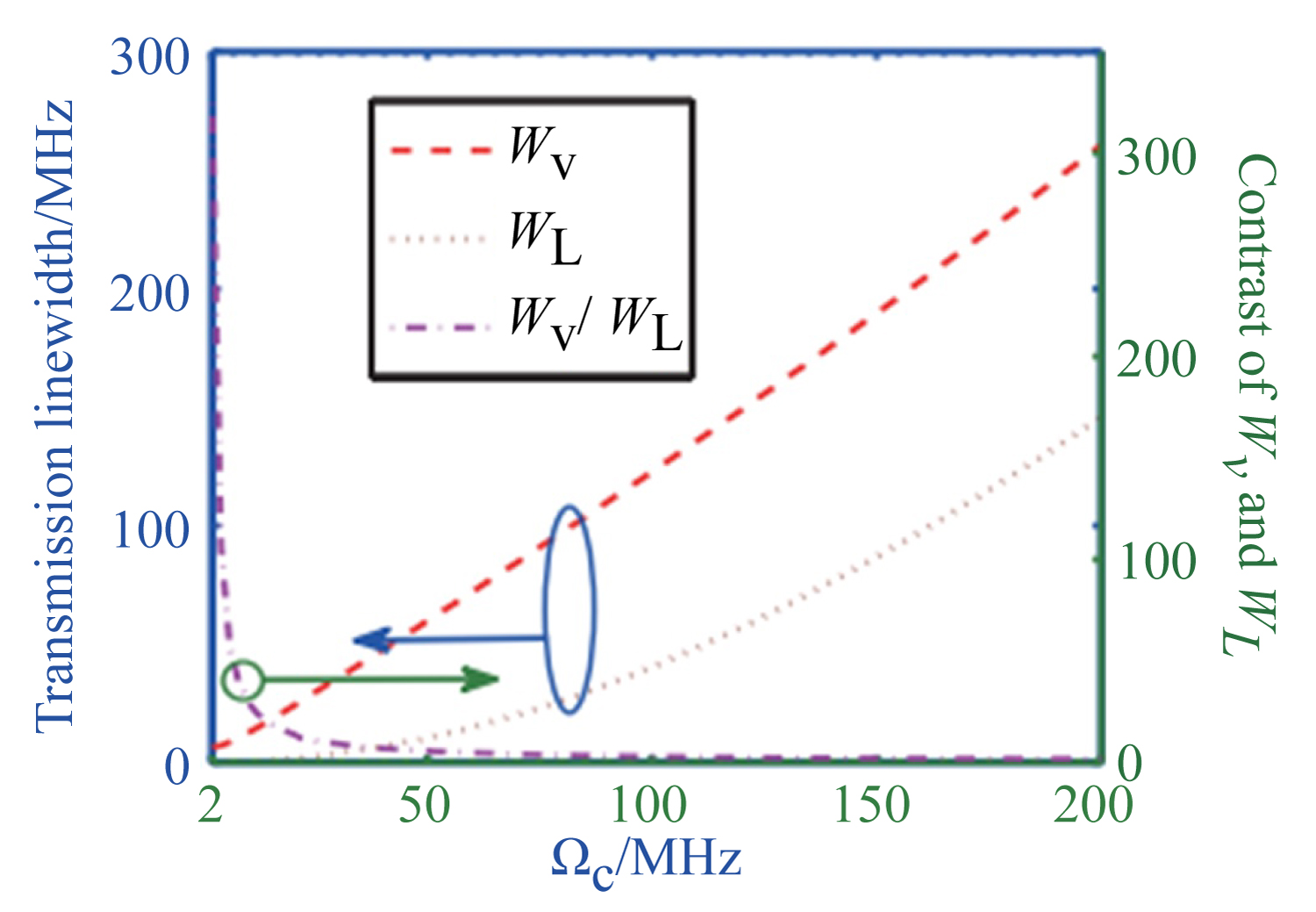
Figure 2: (Color online) Comparison of transmission...
(Color online) Comparison of transmission bandwidth in Λ and V-type thermal atoms. The parameters used in the calculation are Δc = 0, N = 5.0 × 1010 cm-3, γ = 5.746 MHz and γ23 = γ (γ23 = 0.001γ) in the V-type (Λ-type) atomic system.
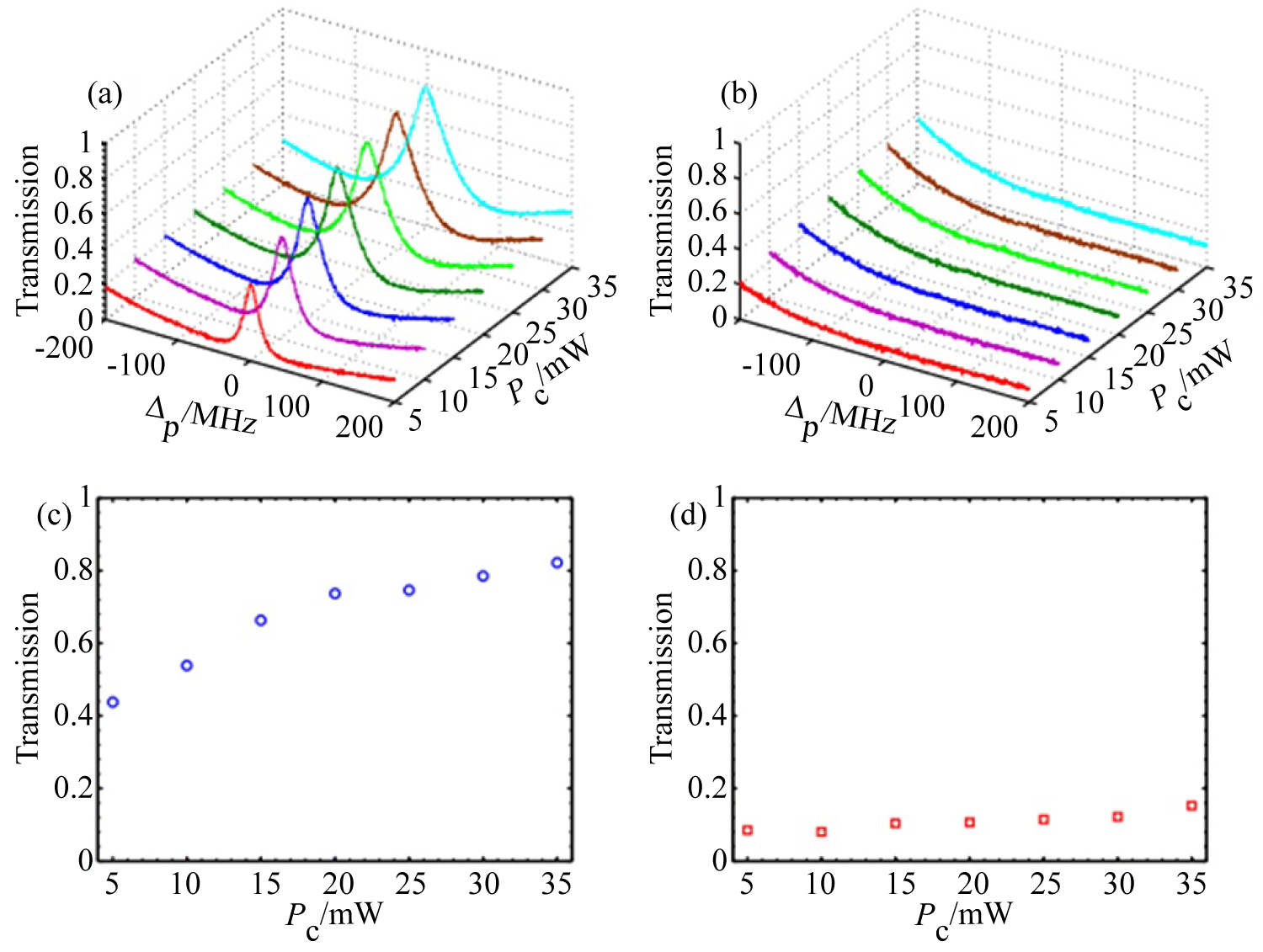
Figure 3: (Color online) Transmissions of the probe...
(Color online) Transmissions of the probe field under different powers of the control field in the Rb87 thermal atoms. a) Forward and b) Backward transmissions versus the probe detuning and the control power; c) Forward and d) Backward transmissions at the resonant frequency .
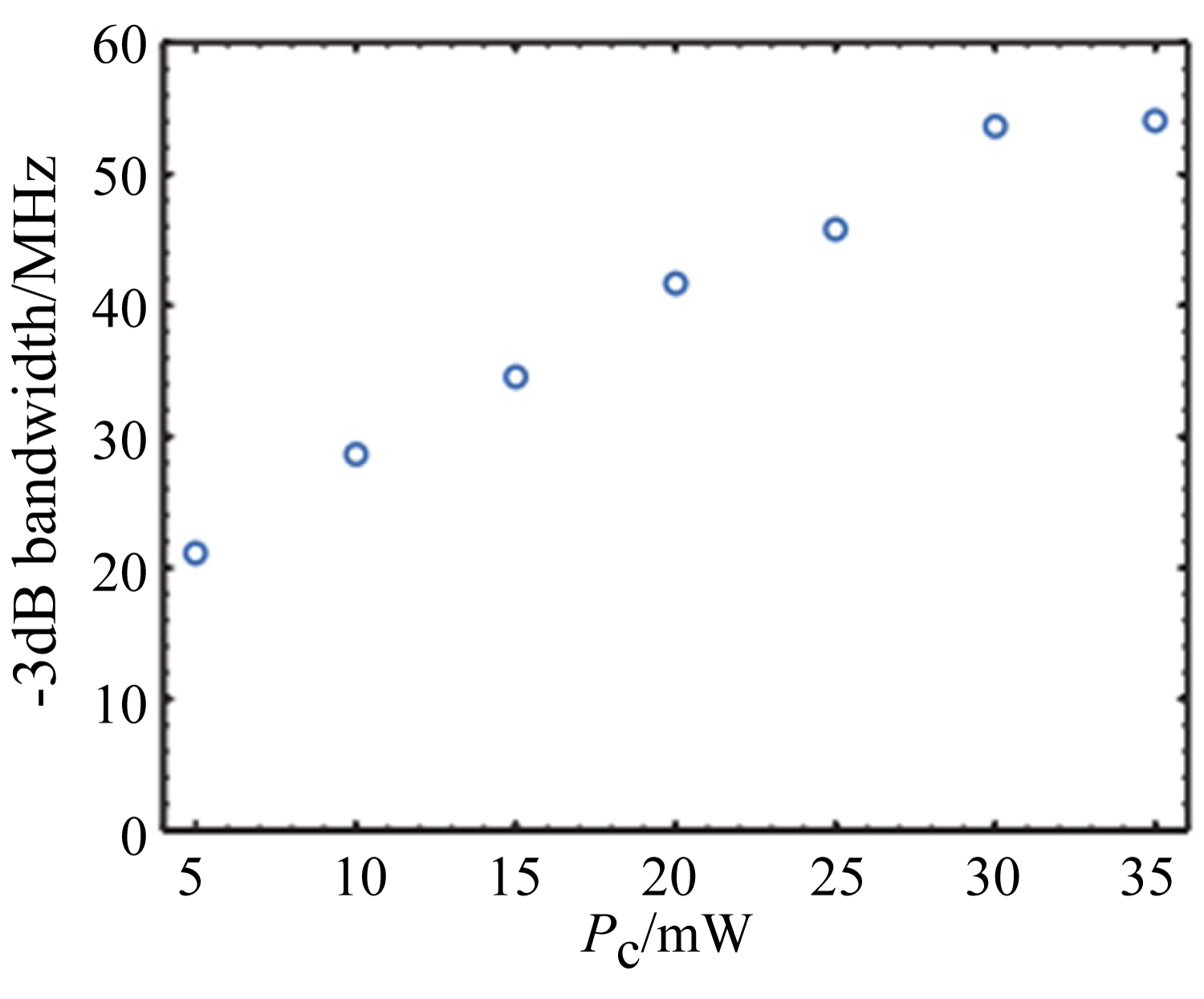
Figure 4: (Color online) Variation of -3dB bandwidth...
(Color online) Variation of -3dB bandwidth for the forward probe field with the power of control field.
References
- D Jalas, A Petrov, M Eich, W Freude, S Fan, et al. (2013) What is and what is not an optical isolator. Nat Photon 7: 579-582.
- AH Gevorgyan (2002) Optical diode based on a highly anisotropic layer of a helical periodic medium subjected to a magnetic field. Tech Phys 47: 1008.
- FDM Haldane, S Raghu (2008) Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys Rev Lett 100: 013904.
- Z Wang, Y Chong, JD Joannopoulos, M Soljacic (2009) Observation of unidirectional backscattering immune topological electromagnetic states. Nature 461: 772-775.
- B Khanikaev, SH Mousavi, G Shvets, YS Kivshar (2010) One-way extraordinary optical transmission and nonreciprocal spoof plasmons. Phys Rev Lett 105: 126804.
- L Bi, J Hu, P Jiang, DH Kim, GF Dionne, et al. (2011) On-chip optical isolation in monolithically integrated non-reciprocal optical resonators. Nat Photon 5: 758.
- M Scalora, JP Dowling, CM Bowden, MJ Bloemer (1994) The photonic band edge optical diode. J Appl Phys 76: 2023.
- K Fang, Z Yu, S Fan (2012) Photonic Aharonov-Bohm effect based on dynamic modulation. Phys Rev Lett 108: 153901.
- LD Tzuang, K Fang, P Nussenzveig, S Fan, M Lipson (2014) Non-reciprocal phase shift induced by an effective magnetic flux for light. Nat Photon 8: 701-705.
- Z Yu, S Fan (2009) Complete optical isolation created by indirect interband photonic transitions. Nat Photon 3: 91-94.
- MS Kang, A Butsch, PSJ Russell (2011) Reconfigurable light-driven opto-acoustic isolators in photonic crystal fibre. Nat Photon 5: 549-553.
- DL Sounas, C Caloz, A Alu' (2013) Giant non-reciprocity at the subwavelength scale using angular momentum-biased metamaterials. Nat Commun 4: 2407.
- NA Estep, DL Sounas, J Soric, A Alu' (2014) Magnetic-free non-reciprocity and isolation based on parametrically modulated coupled-resonator loops. Nat Phys 10: 923-927.
- DL Sounas, A Alu (2014) Angular-momentum-biased nanorings to realize magnetic-free integrated optical isolation. ACS Photon 1: 198-204.
- Q Wang, F Xu, ZY Yu, XS Qian, XK Hu, et al. (2010) A bidirectional tunable optical diode based on periodically poled LiNbO3. Opt Express 18: 7340-7346.
- L Fan, J Wang, LT Varghese, H Shen, B Niu, et al. (2012) An all-silicon passive optical diode. Science 335: 447-450.
- B Peng, SK Ozdemir, F Lei, F Monifi, M Gianfreda, et al. (2014) Parity-time- symmetric whispering-gallery microcavities. Nat Phys 10: 394-398.
- L Chang, X Jiang, S Hua, C Yang, J Wen, et al. (2014) Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators. Nat Photon 8: 524.
- Y Shi, Z Yu, S Fan (2015) Limitation of nonlinear optical isolators due to dynamic reciprocity. Nat Photon 9: 388-392.
- DW Wang, HT Zhou, MJ Guo, JX Zhang, J Evers, et al. (2013) Optical diode made from a moving photonic crystal. Phys Rev Lett 110: 093901.
- SAR Horsley, JH Wu, M Artoni, GC LaRocca (2013) Optical non-reciprocity of cold atom bragg mirrors in motion. Phys Rev Lett 110: 223602.
- L Yang, Y Zhang, X-B Yan, Y Sheng, C-L Cui, et al. (2015) Dynamically induced two-color non-reciprocity in a tripod system of a moving atomic lattice. Phys Rev A 92: 053859.
- C Hang, G Huang, VV Konotop (2013) PT symmetry with a system of three-level atoms. Phys Rev Lett 110: 083604.
- Y-T Fang, Y-Y Wang, J Xia (2019) Large-range electric field sensor based on parity-time symmetry cavity structure. Acta Phys Sin 68: 194201.
- JH Wu, M Artoni, GC La Rocca (2014) Non-Hermitian degeneracies and unidirectional reflectionless atomic lattices. Phys Rev Lett 113: 123004.
- J Zhang, B Peng, SKO zdemir, Y-X Liu, H Jing, et al. (2015) Giant nonlinearity via breaking parity-time symmetry: A route to low-threshold phonon diodes. Phys Rev B 92: 115407.
- K Fang, J Luo, A Metelmann, MH Matheny, F Marquardt, et al. (2017) Generalized nonreciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat Phys 13: 465-471.
- M Hafezi, P Rabl (2012) Optomechanically induced non-reciprocity in microring resonators. Opt Express 20: 7672- 7684.
- Z Shen, Y-L Zhang, Y Chen, C-L Zou, Y-F Xiao, et al. (2016) Experimental realization of optomechanically induced non-reciprocity. Nat Photon 10: 657-661.
- F Ruesink, M-A Miri, A Alu, E Verhagen (2016) Nonreciprocity and magnetic-free isolation based on optomechanical interactions. Nat Commun 7: 13662.
- XW Xu, Y Li (2015) Optical nonreciprocity and optomechanical circulator in three-mode optomechanical systems. Phys Rev A 91: 053854.
- Y Li, YY Huang, XZ Zhang, L Tian (2017) Optical directional amplification in a three-mode optomechanical system. Opt Express 25: 18907-18916.
- XZ Zhang, L Tian, Y Li (2018) Optomechanical transistor with mechanical gain. Phys Rev A 97: 043818.
- F Ruesink, JP Mathew, M-A Miri, A Alu, E Verhagen (2018) Optical circulation in a multi mode optomechanical resonator. Nat Commun 9: 1798.
- P Lodahl, S Mahmoodian, S Stobbe, A Rauschenbeutel, P Schneeweiss, et al. (2017) Chiral quantum optics. Nature 541: 473-480.
- K Xia, G Lv, G Lin, Y Cheng, Y Niu, et al. (2014) Reversible nonmagnetic single-photon isolation using unbalanced quantum coupling. Phys Rev A 90: 043802.
- M-T Cheng, X Ma, J-W Fan, J Xu, C Zhu (2017) Controllable single-photon nonreciprocal propagation between two wave guides chirally coupled to a quantum emitter. Opt Lett 42: 2914-2917.
- W-B Yan, W-Y Ni, J Zhang, F-Y Zhang, H Fan (2018) Tunable single-photon diode by chiral quantum physics. Phys Rev A 98: 043852.
- M Scheucher, A Hilico, E Will, J Volz, A Rauschenbeutel (2016) Quantum optical circulator controlled by a single chirally coupled atom. Science 354: 1577-1580.
- I Sollner, S Mahmoodian, SL Hansen, L Midolo, A Javadi, et al. (2015) Deterministic photon-emitter coupling in chiral photonic circuits. Nat Nanotech 10: 775-778.
- C Sayrin, C Junge, R Mitsch, B Albrecht, DO Shea, et al. (2015) Nanophotonic optical isolator controlled by the internal state of cold atoms. Phys Rev X 5: 041036.
- B Le Feber, N Rotenberg, L Kuipers (2015) Nanophotonic control of circular dipole emission. Nat Commun 6: 6695.
- C-H Yan, Yong Li, H Yuan, LF Wei (2018) Targeted photonic routers with chiral photon-atom interactions. Phys Rev A 97: 023821.
- S-H Gong, F Alpeggiani, B Sciacca, EC Garnett, L Kuipers (2018) Nanoscale chiral valley-photon interface through optical spin-orbit coupling. Science 359: 443-447.
- T Chervy, S Azzini, E Lorchat, S Wang, Y Gorodetski, et al. (2018) Room temperature chiral coupling of valley excitons with spin-momentum locked surface plasmons. ACS Photon 5: 1281-1287.
- Z Yang, S Aghaeimeibodi, E Waks (2019) Chiral light-matter interactions using spin valley states in transition metal dichalcogenides. Opt Express 27: 21367-21379.
- SE Harris, JE Field, A Imamoglu (1990) Nonlinearoptical processes using electromagnetically induced transparency. Phys Rev Lett 64: 1107-1110.
- M Fleischhauer, A Imamoǧlu, JP Marangos (2005) Electromagnetically induced transparency: Optics in coherent media. Rev Mod Phys 77: 633-673.
- F Zhou, Y Qi, H Sun, D Chen, J Yang, et al. (2013) Electromagnetically induced grating in asymmetric quantum wells via Fano interference. Opt Express 21: 12249-12259.
- R Sadighi-Bonabi, T Naseri, M Navadeh-Toupchi (2015) Electromagnetically induced grating in the microwave-driven four-level atomic systems. Appl Opt 54: 368-377.
- Y You, Y Qi, Y Niu, S Gong (2019) Control of electromagnetically induced grating by surface Plasmon and tunneling in a hybrid quantum dot-metal nanoparticle system. J Phys-Condens Mat 31: 105801.
- C Ding, R Yu, J Li, X Hao, Y Wu (2014) Matched infrared soliton pairs in graphene under Landau quantization via four-wave mixing. Phys Rev A 90: 043819.
- C Li, Z Jiang, Y Zhang, Z Zhang, F Wen, et al. (2017) Controlled correlation and squeezing in Pr3 : Y2SiO5 to yield correlated light beams. Phys Rev Appl 7: 014023.
- JH Li, XY Lv, JM Luo, QJ Huang (2006) Optical bistability and multistability via atomic coherence in an N-type atomic medium. Phys Rev A 74: 035801.
- C Bao, Y Qi, Y Niu, S Gong (2016) Surface plasmon assisted optical bistability in the quantum dot-metal nanoparticle hybrid system. J Mod Opt 63: 1280-1285.
- Y Qi, Y Niu, F Zhou, Y Peng, S Gong (2011) Phase control of coherent pulse propagation and switching based on electromagnetically induced transparency in a four-level atomic system. J Phys B 44: 085502.
- H Schmidt, A Imamoglu (1996) Giant Kerr nonlinearities obtained by electromagnetically induced transparency. Opt Lett 21: 1936-1938.
- Y Qi, Y Niu, Y Xiang, H Wang, S Gong (2011) Phase dependence of cross-phase modulation in asymmetric quantum wells. Opt Commun 284: 276-281.
- Y Peng, A Yang, L Jiang, L Meng, J Liu (2014) Tunable self-Kerr nonlinearity with voltage sensing in double quantum dot system. Eur Phys J D 68: 152.
- Y Peng, A Yang, D Li, H Zhang, Y Niu, et al. (2014) Ultra-narrow line width and high gain of an optical cavity with enhanced self-Kerr nonlinearity in quantum dot molecules. Laser Phys Lett 11: 065201.
- Y Wu, L Deng (2004) Ultraslow optical solitons in a cold four-state medium. Phys Rev Lett 93: 143904.
- G Huang, C Hang, L Deng (2008) Gain-assisted superluminal optical solitons at very low light intensity. Phys Rev A 77: 011803(R).
- WX Yang, JM Hou, YY Lin, RK Lee (2009) Detuning management of optical solitons in coupled quantum wells. Phys Rev A 79: 033825.
- LG Si, WX Yang, XY Lou, XY Hao, X Yang (2010) Formation and propagation of ultra low three-wave-vectoroptical solitons in a cold seven-level triple-Λ atomic system under Raman excitation. Phys Rev A 82: 013836.
- C Hang, VV Konotop (2011) Spatial solitons in a three-level atomic medium supported by a Laguerre-Gaussian control beam. Phys Rev A 83: 053845.
- Y Qi, F Zhou, T Huang, Y Niu, S Gong (2011) Spatial vector solitons in a four-level tripod-type atomic system. Phys Rev A 84: 023814.
- Y Zhang, Z Wang, Z Nie, C Li, H Chen, et al. (2011) Four-wave mixing dipole soliton in laser-induced atomic gratings. Phys Rev Lett 106: 093904.
- Z Zhang, F Li, G Malpuech, O Bleu, S Koniakhin, et al. (2019) Particle like behavior of topological defects in linear wave packets in photonic grapheme. Phys Rev Lett 122: 233905.
- S Zhang, Y Hu, G Lin, Y Niu, K Xia, et al. (2018) Thermal-motion-induced non-reciprocal quantum optical system. Nat Photon 12: 744-748.
- G Lin, S Zhang, Y Hu, Y Niu, J Gong, et al. (2019) Nonreciprocal amplification with four-level hot atoms. Phys Rev Lett 123: 033902.
- K Xia, F Nori, M Xiao (2018) Cavity-free optical isolators and circulators using a chiral cross-Kerrnon linearity. Phys Rev Lett 121: 203602.
- Y Hu, S Zhang, Y Qi, G Lin, Y Niu, et al. (2019) Multiwavelength magnetic-free optical isolator by optical pumping in warm atoms. Phys Rev Appl 12: 054004.
- S Fan, Y Qi, G Lin, Y Niu, S Gong (2020) Broadband optical nonreciprocity in an N-type thermal atomic system. Opt Commun 462: 125343.
Author Details
Yihong Qi1*, Peng Wang2, Yueping Niu1 and Shangqing Gong1
1Department of Physics, East China University of Science and Technology, Shanghai, China
2School of Physics and Electrical Engineering, Anqing Normal University, Anqing, China
Corresponding author
Yihong Qi, Department of Physics, East China University of Science and Technology, Shanghai 200237, China.
Accepted: May 30, 2020 | Published Online: June 01, 2020
Citation: Qi Y, Wang P, Niu Y, Gong S (2020) Coherent Control of Optical Nonreciprocal Propagation in a V-Type Atomic System. Int J Opt Photonic Eng 5:023
Copyright: © 2020 Qi Y, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Optical nonreciprocity and nonreciprocal propagation of light have attracted great research interest, due to not only their fundamental scientific significance, but also their extensive applications in lasing, quantum optical devices and quantum information. In this work, we theoretically and experimentally investigate nonreciprocal propagation of light in a V-type three-level thermal atomic system. By virtue of the EIT effect and the atom thermal motion, nonreciprocal propagation of light is achieved in the Rb87 warm atoms, where high transmission of the probe field is achieved in the co-propagation direction of the control field and the probe field is blocked in the opposite direction of the control field. Transmission and bandwidth for the nonreciprocal propagation of light can be enhanced and controlled by the control field in this system, where the nonreciprocal band width can be broadened significantly in comparison with the Λ-type atomic system. In our experiments, we achieve ~60 MHz nonreciprocal bandwidth for the probe field. This work may have potential applications in quantum nonreciprocal devices such as optical isolator and circulator.
Introduction
Optical nonreciprocity and nonreciprocal devices, which supports drastically asymmetric propagation of light in two opposite directions, are essential in optical communications, laser systems and signal processing [1]. In recent years, optical nonreciprocity has attracted great research interest, and various strategies or physical mechanisms are proposed and studied for nonreciprocal transmission of light. Utilization of magneto-optic effect is a common approach to break the reciprocity [2-6]. However, response of magnetic materials often performs weak, implying bulky, costly and difficulty on integration of devices.
Great efforts dedicate to searching for alternative approaches and mechanisms to break reciprocity without the use of magnetism, especially those for suitable on-chip integration. A photonic band gap material with the combination of linear and nonlinear medium response previously proposed to support unidirectional propagation and optical diode [7]. Spatiotemporal modulation of refractive index of materials is one promising approach for this purpose, which generates optical nonreciprocity via introducing nonreciprocal phase transfer [8,9] and frequency conversion [10,11], or establishing an angular momentum biasing [12-14]. Nonmagnetic optical nonreciprocity can also be achieved by optoacoustic effects [11,15], optical nonlinearity [16-19], and moving systems [20-22]. Great research interest were paid on the parity-time symmetry [23,24] recently. Using parity-time symmetric system, optical nonreciprocity [25] and phonon diode [26] have been studied. Due to the rapid development and the flexibility, optomechanical systems provide a good platform to support nonreciprocal transmission and create nonreciprocal devices such as optical isolator, optical circulator and optical router [27-34]. In chiral quantum physics, photons propagating in opposite directions are of spin-momentum or polarization locking, which drives emitters with different transition levels and rates [35].
It thus naturally offers a novel way to support nonreciprocal propagation of light even in the quantum regime [36-43]. The spin-orbit coupling canal so be used to realize optical nonreciprocity in low-dimensional materials [44-46].
Since the electromagnetically induced transparency (EIT) technology was introduced by Harris, et al. [47,48], many interesting quantum optical phenomena have been observed and realized in multi-level quantum systems based on the EIT effect, such as electromagnetically induced grating (EIG) [49-51], four-wave and six-wave mixing [52,53], optical bistability and multistability [54,55], optical switching [56], Kerr nonlinearity enhancement [57-60], weak-light optical solitons [61-66] etc. Via inducing periodic structures by lasers in the EIT atomic systems, dipole soliton and optical vortices were generated and studied experimentally in thermal atoms [67,68]. The random motion of atoms often takes disadvantage on quantum coherence in warm atoms. However, utilizing the atom thermal motion and EIT effect, our group experimentally investigated and achieved optical nonreciprocity and isolation in a cavity-atom coupling system [69]. And soon, a scheme of unidirectional amplification of light was also proposed and demonstrated in an atomic system [70]. Utilizing the optical nonlinearity of cross phase modulation, Xia, et al. theoretically proposed a scheme for optical isolator and optical circulator in an N-type thermal atomic system [71]. We also proposed a scheme to experimentally achieve optical nonreciprocity via optical pump effect in multi-level atomic systems [72]. Our recent experiment demonstrated that, the nonreciprocal bandwidth can be broadened in the cavity-free N-type atomic system [73]. Three level V-type atomic system is a very common and frequently used quantum system. In this work, based on the EIT effect, we experimentally and theoretically investigate the nonreciprocal propagation of light in a warm Rb87 V-type atomic system. By adjusting the control field, transmission and bandwidth can be controlled and enhanced for nonreciprocal propagation of the probe field in this system. It is shown that, high transmission of the probe light is achieved in the co-propagation direction of the control field, while it is effectively blocked in the opposite direction. In addition, the V-type atomic system can provide a relatively wider band width for nonreciprocal propagation of the probe light in comparison with the Λ-type atomic system. This work may provide reference for broadband applications of optical nonreciprocal devices.
Model and Theoretical Analysis
In this work, we consider a weak probe field of Rabi frequency and a strong control field of Rabi frequency interacting with a V-type atomic system (as shown in Figure 1). Under the slowly varying envelope and paraxial approximations, evolution of the probe field is governed by the following wave equation:
Transmission of the probe field is determined by the macro susceptibility , which can be derived by solving the motion equations of the density matrix elements under steady states. Under electric-dipole and rotating-wave approximation, the interacting Hamiltonian can be written in the interaction picture as
Where and indicate the one-photon detunings respectively for the probe and control lasers. They are defined as and with and being the angular frequencies of the probe and control lights and the relevant transition frequency between states and . is the half Rabi frequency of the probe (control) field with the electric dipole momentum for the transition and the slowly varying electric field amplitudes of the probe and control laser fields.
The macro polarization for the probe field is , in which N is the atomic density, is the vacuum permittivity and represents the corresponding density matrix element. As we consider in the warm atomic gas, the frequencies of the lasers felt by the atoms depend on not only the frequencies of the incident lasers but also the frequency shift caused by the atom thermal motion. Considering all the atoms follow the Maxwell-Boltzman velocity distribution, we need to integrate the macro susceptibility on all the velocities of atoms. Then the susceptibilities for the forward and backward probe light can be written respectively as:
Here is the effective detuning with the wave vector of the lasers and the atom velocity . represents the velocity distribution function of the atoms, where is the most probable velocity with the Boltzmann constant , the absolute temperature T, and the atom mass M. The superscript (F, B) indicates the forward or backward propagation direction for short. Similarly, we can also obtain the susceptibility for the Λ-type atomic system. Transmission of the probe field in the two atomic systems can be calculated by Eqs. (1) and (3).
When the control field propagates along the forward direction, the atomic thermal motion gives rise to the same frequency shift on the forward probe field and opposite frequency shift on the backward probe field if So transmission of the backward probe field can be greatly suppressed due to the destruction of EIT, while transmission of the forward probe field can maintain a high level. Then nonreciprocal propagation of the probe field can be achieved in the two opposite directions. The nonreciprocal bandwidth is mainly determined by the EIT line width of the forward probe field and the Doppler line width of the warm atoms. Figure 2 shows the comparison of the transmission line width of the forward probe field in the V and Λ-type warm atomic systems by solving the Eqs. (1) and (3) directly. In the calculation, the medium length is 5.0 cm and the temperature is 70 ℃. The other parameters are , cm-3, MHz and , in the V-type atomic system while , , in the Λ-type atomic system, in which and indicates the decoherence and population decay rates respectively. It can be seen in Figure 2 that, the transmission line widths and of the forward probe field increases with the Rabi frequency of the control field (or the intensity of the control field), and the transmission line width can be much broader than especially for small . can be dozens or even hundreds of times larger than under the same .
Experiment for Nonreciprocal Propagation of Light
We experimentally investigate the nonreciprocal propagation of light in a warm V-type Rb87 atomic system. We select the levels (52S1/2, F = 2), (52S1/2, F = 2) and (52S3/2, F = 3) of Rb87 atoms as the states , and and set laser couplings as shown in Figure 1a. The strong control laser with wavelength of 780 nm is applied to drive the transition . A weak laser with wavelength of 795 nm is used to probe the transition. Such consideration of laser excitation forms a V-type configuration. The experimental setup and laser paths in experiment are laid out as shown in Figure 1b. With such arrangement of light paths, the coupling lasers is vertically polarized and the probe laser is parallel polarized when they pass through the atoms. The cell length of Rb is about 5.0 cm and the temperature is set at 70 ℃ in experiment. The control laser is locked to be resonant with the transition . For convenience, we define the path from left to right as the forward direction whereas the path from right to left as the backward direction. In our experiment, propagation direction of the control field is fixed to be along the forward direction.
Figure 3a and Figure 3b show the transmissions of the forward and backward probe fields versus the probe detuning and laser power Pc of the control field respectively, where the average background noise has been erased. As shown in Figure 3a, we obtain high transmission for the forward probe field near the resonant frequency. The transmission and bandwidth depend sensitively on the power of the control field Pc. It is obvious that, with the increase of Pc, transmission and band width of the probe field are significantly enhanced (see Figure 3a). Contrarily, as the thermal motion of atoms induces opposite frequency shift for the backward probe field and breaks the EIT effect, backward transmission of the probe field is greatly suppressed (Figure 3b). The reason is that, thermal motion of atoms gives rise to the same frequency shift of the probe field in the forward direction but opposite shift in the backward direction compared with the control field. So, the EIT condition is always satisfied in the forward direction while broken in the backward direction. Forward and backward transmissions of the probe field at the resonant frequency are plotted in Figure 3c and Figure 3d respectively. The probe field obviously realizes high transmission in the forward direction because of the EIT effect (Figure 3c). While in the backward direction, transmission of probe field is very low under certain control powers (Figure 3d). Therefore, nonreciprocal propagation of probe field can be achieved in the two opposite directions.
We further measure bandwidth of the nonreciprocal propagation by evaluating the full width at half maximum (FWHM) of the forward transmission in the EIT window and show the results in Figure 4. It can be found that, with the increase of Pc, bandwidth of the nonreciprocal propagation of the probe field can be broadened significantly, which provides a simple way to enhance the nonreciprocal bandwidth. As the backward transmission of the probe field is limited by the line width of the Doppler broadening of the thermal atoms, it grows evidently once the transmission line width becomes larger than the Doppler line width, which is undesirable for superior nonreciprocal propagation and nonreciprocal devices. Though limited by output power of the lasers, ∼60 MHz band width of nonreciprocal propagation is achieved in the V-type atomic system in our experiments. Broadband nonreciprocal propagation may play important role in some quantum applications such as quantum communications and quantum information processing.
Conclusion
In conclusion, based on the electromagnetically induced transparency and the thermal motion of the atoms, we have investigated nonreciprocal propagation of light in a V-type Rb87 warm atomic system. Transmission of the probe field in two opposite directions can be controlled and enhanced by adjusting the control field. In the same propagation direction of the control field, the thermal motion of the atoms causes approximate frequency shift on the probe field, which guarantees the EIT condition and produce high transmission of the probe field. Conversely, in the opposite direction, the thermal motion induced frequency shift is nearly contrary between the probe field and the control field. So the probe field can be significantly blocked in the backward direction. In addition, bandwidth for nonreciprocal propagation of the probe field in the V-type atomic system can be enhanced and controlled by adjusting the control field. ∼60 MHz bandwidth (FWHM) for nonreciprocal propagation of the probe field is achieved in experiment. This work may provide references for wide band applications of nonreciprocal light propagation.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos.11874146 and 11774089) and University Natural Science Research Project of Anhui Province (Grant No.KJ2019A0567).

