
International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 5, Issue 1
Research Article
DOI: 10.35840/2631-5092/4524
Non-Split Perfectly Matched Layer Boundary Conditions for Numerical Solution of 2D Maxwell Equations
Arnold Abramov*, Yutao Yue and Mingming Wang
Table of Content
Figures
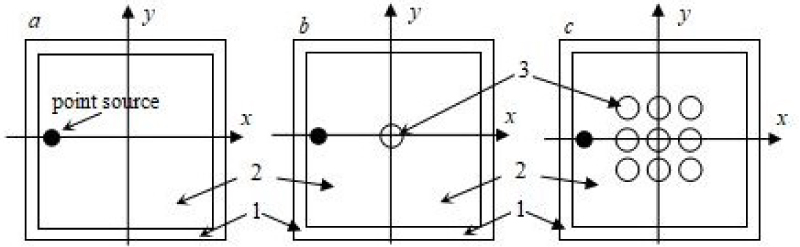
Figure 1: Computational domain of the two dimensional...
Computational domain of the two dimensional problem spaces: 1- PML; 2- Area of real space parameters; 3- Infinite cylinder (top view).
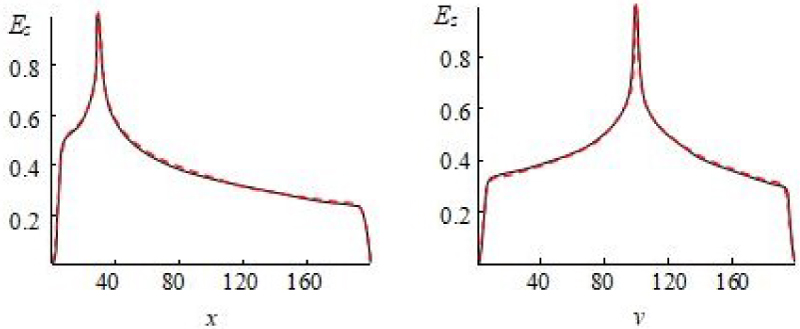
Figure 2: Projections of the field distribution E(x,y)...
Projections of the field distribution E(x,y) inside 2D area (Figure 1a) on the plane of two variables (E, x) (a) and (E, y) (b).
Solid line - Split PML BC; Dashed line - Non-split PML BC.
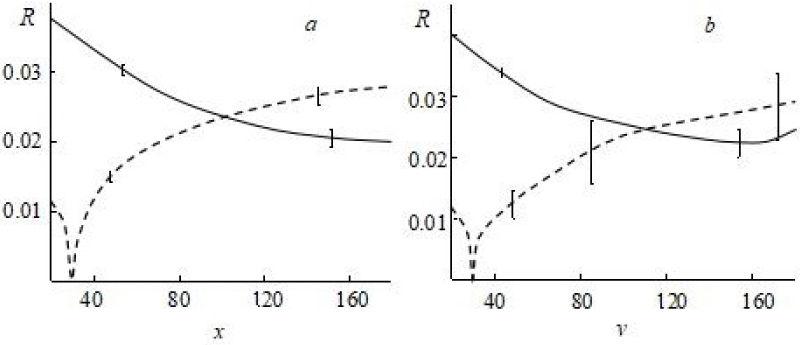
Figure 3: Relative difference between simulation results...
Relative difference between simulation results for non-split and split PML BC along x (dashed line) and y (solid line) axis's for one (a) and nine (b) Cylinders in computational area.
References
- KS Yee (1966) Numerical solution of initial boundary value problems involving maxwell's equations in isotropic media. IEEE Trans Antenn Propag 14: 302-307.
- JP Berenger (1994) A perfectly match layer for the absorption of electromagnetic waves. Journal of Computational Physics 114: 185-200.
- O Ramadan (2003) Auxiliary differential equation formulation: An efficient implementation of the perfectly matched layer. IEEE Microwave and Wireless Components Lett 13: 69-71.
- C Zhang, B Sun, H Yang, J Ma (2016) A non-split perfectly matched layer absorbing boundary condition for the second-order wave equation modeling. Journal of Seismic Exploration 25: 1-9.
- U Basu, AK Chopra (2004) Perfectly matched layers for transient elastodynamics of unbounded domains. International Journal for Numerical Methods in Engineering 59: 1039-1074.
- DM Sullivan (2000) Electromagnetic simulation using the FDTD method. IEEE Press, New York, 165.
- ZA Chen, A Taflove, V Backman (2004) Photonic nanojet enhancement of backscattering of light by nanoparticles: A potential novel visible-light ultramicroscopy technique. Opt Express 12: 1214-1220.
- Z Zhishen, H Yin, F Yuanhua, S Yuecheng, L Zhaohui (2019) An ultra narrow photonic nanojet formed by an engineered two-layer microcylinder of high refractive-index materials. Opt Express 27: 9178-9188.
- CY Liu (2013) Photonic nanojet enhancement of dielectric microcylinders with metallic coating. J Optoelectron Adv Mater 15: 150-154.
- J Schaefer, S-C Lee, A Kienle (2012) Calculation of the near fields for the scattering of electromagnetic waves by multiple infinite cylinders at perpendicular incidence. J Quant Spectrosc Radiat Transf 113: 2113-2123.
- A Abramov, C Ji, R Liu, A Kostikov (2016) Enhancement of the electromagnetic waves intensity by scattering on multiple infinite cylinders. Journal of Photonic Materials and Technology 2: 1-5.
- A Abramov, A Kostikov (2017) Formation of whispering gallery modes by scattering of an electromagnetic plane wave by two cylinders. Phys Lett A 381: 1107-1110.
- A Abramov, A Kostikov, R Liu, C Ji, X Li, et al. (2017) Formation of the high electromagnetic waves intensity areas by multiple cylinders scattering: whispering gallery modes and photonic nanojet. Journal of Electromagn Waves and Applications 31: 820-827.
- A Taflove, S Hagness (2005) Computational electrodynamics: The finite-difference time-domain method. (3rd edn), Artech House, Boston, MA, USA.
Author Details
Arnold Abramov*, Yutao Yue and Mingming Wang
Institute of Deep Perception Technology, Wuxi, China
Corresponding author
Arnold Abramov, Institute of Deep Perception Technology, Wuxi, China.
Accepted: June 15, 2020 | Published Online: June 17, 2020
Citation: Abramov A, Yue Y, Wang M (2020) Non-Split Perfectly Matched Layer Boundary Conditions for Numerical Solution of 2D Maxwell Equations. Int J Opt Photonic Eng 5:024
Copyright: © 2020 Abramov A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
This paper developed a non-split perfectly matched layer (PML) boundary condition (BC) for Finite Difference Time Domain (FDTD) simulation of electromagnetic wave propagation in 2D structure. The point source for electric field has been exploited for propagation of electromagnetic field through 2D structures to validate developed approach. The identity of resulted field distribution to that obtained for split PML BC have been demonstrated.
Keywords
Electromagnetic wave, Non-split, PML, FDTD, Cylinder
Introduction
Electromagnetic field distribution of any system can be known by solving Maxwell's equations. There are many numerical techniques allowing to find appropriate solutions. In this paper we will deal with the finite difference time domain method introduced [1] in 1966 by Kane S. Yee. It has a number of advantages, such as divergence-free (in contrast to the main methods that require a condition div B = 0), the grid is very simple and the data is easily for storage). The FDTD method solves the time-dependent Maxwell's equations in a spatially finite computation domain. The electric and magnetic fields are then represented by their discrete values on the each node of spatial grid, and are extended in time. Without any boundary conditions, Yee's algorithm assumes that the domain is surrounded by a perfect electric conductor (PEC) layer. The presence of the boundaries in the model can affect significantly the simulation results, due to spurious reflection from the boundaries of electromagnetic waves incident on them. To obtain physically reasonable solutions, the calculation area should be interrupted at the edges via special boundary conditions that extend the definite area to infinity, representing it as unbounded volume. Such a boundary condition could be obtained by a reflectionless absorbing layer that surrounds the calculation area and absorbs all incident waves, regardless of the angle of incidence and wavelength. Thus, in the implementation of FDTD, we set the layers of a hypothetical material along the boundaries of computational area specially designed in such a way to completely absorb the radiation incident on it. Such a layers have been called perfectly matching layer (PML) and were first introduced by J. P. Berenger [2]. The PML conditions have a low reflection coefficient, as well as practical independence from the angle of incidence of the wave.
Unfortunately, there is still a reflection: From the first layer of PML; between layers of PML, because to save computing resources, losses increase from layer to layer; after the last layer of PML, since there is a PEC border. Reflection from the first PML layer and between the PML layers is caused by finite-difference discretization errors, and, first of all, by the fact that the vectors E and H do not coincide in space. To reduce reflection within the PML, it is necessary to strict the growth rate of losses to some reasonable limit. Reflection from the PEC boundary after the last PML layer occurs usually for already much attenuated wave. The reflected wave continues to weaken on the way back. But if there are few layers (usually less than 5), then the reflected wave can be significant. To reduce the reflection from the first layer, the value of conductivity σ1 is specially chosen to be small. To reduce the reflection between the layers, the loss profile is selected in such a way to have a limited growth rate of loss. In order to reduce the effect of waves reflected from the PEC boundary, the number of PML layers should be increased.
Berenger's PML is typically referred to as a split field PML because the field components in PML regions are split into two unphysical field components to obtain additional degrees of freedom. This modification allows the creation of a reflectionless interface between a dielectric medium and the PML layer. But extra splitting variables that are introduced in Berenger's PML BC increase computational memory time burden in implementation. In addition, it leads also to the difficulties of numerical implementation. In order to avoid those issues scholars have done a lot of researches on developing of versions of PML absorbing boundary condition for non-splitting fields: Unsplit-field and material independent PML formulations are obtained in [3] incorporating the auxiliary differential equation method into the PML formulations. The non-split PML BC has been used in seismic wave modeling introducing auxiliary variables [4]. A use of non-split PML boundary condition for second-order elastic wave FETD forward modeling with high calculation accuracy and great improvement in calculation efficiency have been demonstrated in [5]. Non-split PML BC formulation developed previously [3] for one dimensional case adopted in the present paper for 2D Maxwell's equations. Another feature of the presented formulations (except non-split PML BC) is that the use of the electric displacement field instead of the electric field. This allows the PML to be independent of the material of the FDTD computational domain.
Basic Equations
The starting point for the construction of an FDTD algorithm is Maxwell's time-domain equations.
Where is the electric field strength vector in volts per meter, is the electric displacement vector in coulombs per square meter, is the magnetic field strength vector, ε0 and μ0 - dielectric and magnetic constant respectively, ε is the permittivity of the material. Using new expressions for the fields
Leads to
Where we used the speed of light in free space .
For specifics, we further consider the case of TE polarizations for which electric field (along z axis) is orthogonal to the plane (x,y) of electromagnetic field propagation. Thus the field has next nonzero components: Ez, Hx, Hy.
In order to implement the FDTD method and calculate the field at all points of the computational domain we have to replace the derivatives by finite-difference approximations and set the field values at the boundaries of the computational domain. But before we will modify these equations assuming the presence of an additional region around the computational domain where the field will be absorbed, excluding its reflection to the back into computational area. For this purpose, we introduce fictitious values that will be selected in such a way as not to affect the field inside the computational domain, and to ensure its absorption outside it. We first write down the system (4) for the case of continuous, time-harmonic fields (i.e. time dependence are described by factor exp(iωt)):
Non-Split PML Boundary Conditions
In order to implement PML we input fictitious constants εx*, εy*, μx*, μy*:
These fictitious parameters should be chosen so both that there are no changes in the medium parameters within the main computational domain and ensure the absorption of the field in the PML domain.
By preserving the electric displacement field Dz in the equations (6), we obtain that all dimensional parameters, as well as all the detailed information about the structure of the computational domain, are enclosed on the input of the dielectric constant. It also allows the PML to be independent of the material in the FDTD computing area.
In [6] it was shown that in order to ensure absorption in the PML layers, the expressions for the ε* and μ* should be as follows
m = x,y, with following selection of parameters
Theoretically, if the condition σi / ε0 = σi* / µ0 is satisfied, then the average velocity of the electromagnetic waves does not change at the interface and the reflection is equal to zero. At the same time, because σi, σi* ≠ 0 the absorption of electromagnetic waves takes place within the PML. PML parameters used in this work will be described below.
Substituting (7-8) into (6) we get:
We can rewrite these equations as follows:
To go back to time dependence, we will perform a formal replacement iω → d/dt. Then instead of (10) we have:
Now we replace the derivatives with their finite-difference approximations and we finally get the PML-modified FDTD equations:
The selection of the fictitious parameters can be determined by the following expressions introduced in Ref. [6]:
With pm = 0.333(i/NPML)3 , i = 1.. NPML, NPML - number of PML.
Finally the FDTD equations are as follow:
Results
The model we used consists of rectangular area of size 200 × 200 unit cells. The size of the unit cell Δx was chosen in such a way that one wavelength λ is equal to integer number N of unit cells: λ = NΔx. Point source generating electric field was defined offset 30 cells from the left edge of the problem space along x-axis. Number of PML layers NPML = 10. As mentioned above a propagation of TE-polarized wave in 2D plane was simulating via solution of Maxwell's equations (1) by FDTD method. The direction of wave propagation is along the x-axis (Figure 1). The origin of the coordinates corresponds to the centre of the computational domain. Three cases were considered: 2D homogeneous space (Figure 1a) and two kinds of structures placed into centre of 2D computational area: Single cylinder (Figure 1b); group of 9 cylinders (Figure 1c). We choose cylinder as main figure in our simulation due to since it is the study of scattering on the cylinder that led to the discovery of photonic nanojet [7] and a further increase in researchers' attention to scattering effects on cylindrical objects [8-14].
Refraction index of each cylinder are nA = 1.59. All results below are presented after 1200 time step simulations. Each time step was equal Δt = Sc*Δx/c, where Sc = 0.5 is Courant stability factor.
Polynomial [12] and power dependence [6] models for medium parameters have been choused for split and non-split PML BC respectively. Effectiveness of those models demonstrates Figure 2: Projections of the calculated field distribution E(x,y) on the plane of two variables (E,x) and (E,y) have been drawn. Field absorption occurs within PML layers (x,y = 0-10 and x,y = 190-200). A maximal value on the dependencies corresponds to position of the point source, where a field magnitude is kept constant.
The difference between two approaches (non-split and split PML BC) was estimated by expression
R = (Ens-Es)/Es
Where Ens and Es are absolute value of calculated electric field for the cases of non-split and split BC respectively.
The Figure 3 demonstrates change of R along and across field propagation for the cases of (0, 1) and 9 cylinders inside a computational area. As it is seen the relative difference is less than 4%. The cases of 0 (empty computational domain, i.e. free propagation of electromagnetic wave) and 1 cylinder are represented by 1 line because the difference in R for them occurred less than 1%. A point where R = 0 corresponds to position of point source. In fact, all the lines on Figure 3 are oscillating and short vertical lines shows an amplitude of those oscillations while main lines itself represent average positions for R dependencies. More complex structure clearly leads to a greater error and oscillations. However, overall these changes are minor, within 4%, those demonstrating efficiency of approximation efficiency and applicability of non-split BC for FDTD method.
Conclusion
The FDTD method to solve 2D Maxwell's equations has been described. Non-split PML BC has been used. This approach allows to avoid electromagnetic field splitting which does not follow from Maxwell's equations, and thus it can lead to the save of the computational time. As result of used approach, all dimensional parameters, as well as all the detailed information about the structure of the computational domain, are enclosed on the input of the dielectric constant. It is because of using the electric displacement field instead of the electric field. This allows also the PML to be independent of the material of the FDTD computational domain.
The developed calculation scheme verified by comparison of final results to those obtained for ordinary (split) version of BC. Calculated field distributions for different parameters of computational domain examined for both cases and are in the good agreement.

