International Journal of Optic and Photonic Engineering
(ISSN: 2631-5092)
Volume 6, Issue 1
Research Article
DOI: 10.35840/2631-5092/4531
Study on the Output Characteristics of the External-Cavity Laser with Corner Cube Resonator
Chang Du*, Kang Yun and Yannan Yang*
Table of Content
Figures
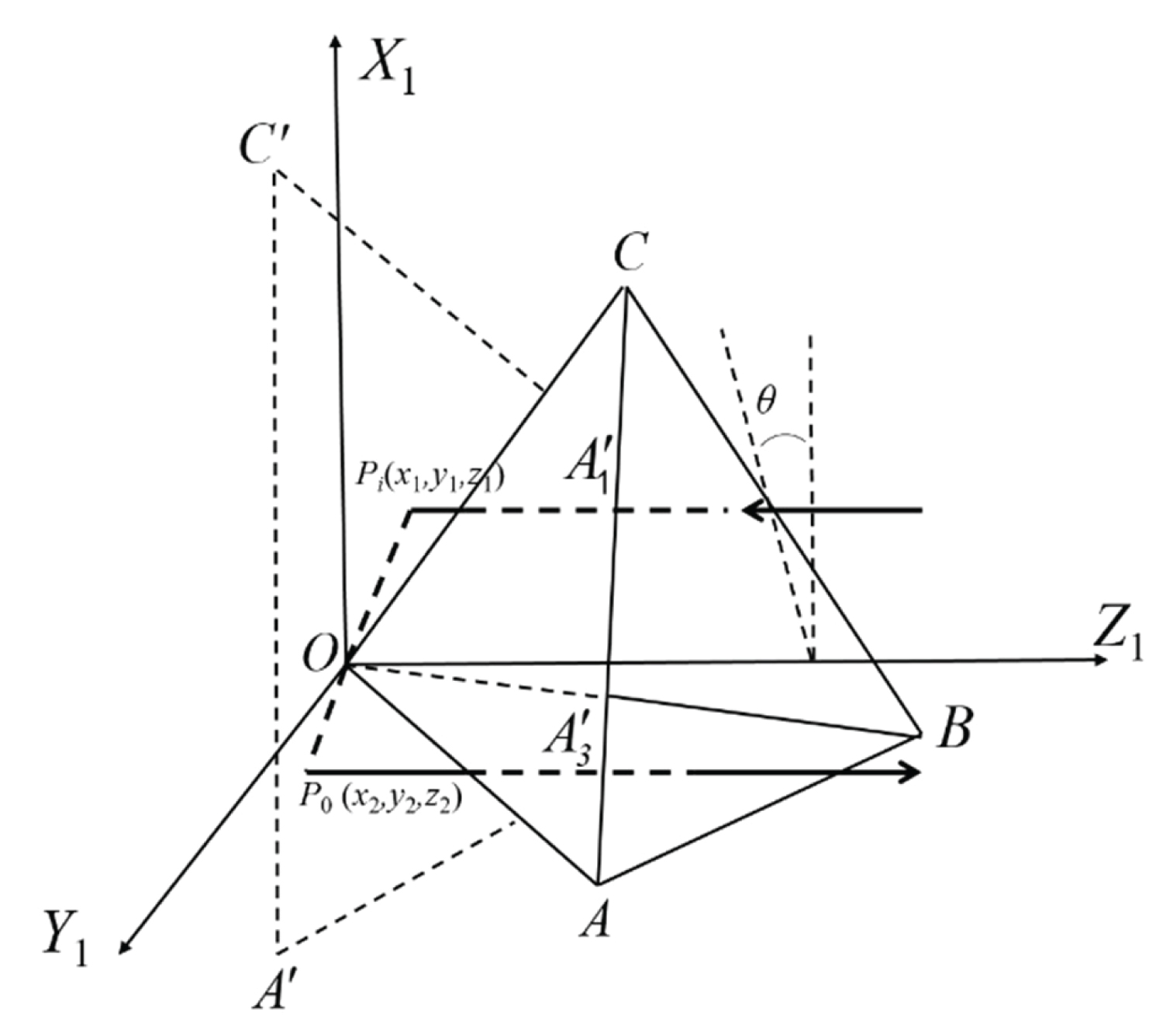
Figure 2: Schematic diagram of the equivalent.....
Schematic diagram of the equivalent surface A'B'C'.
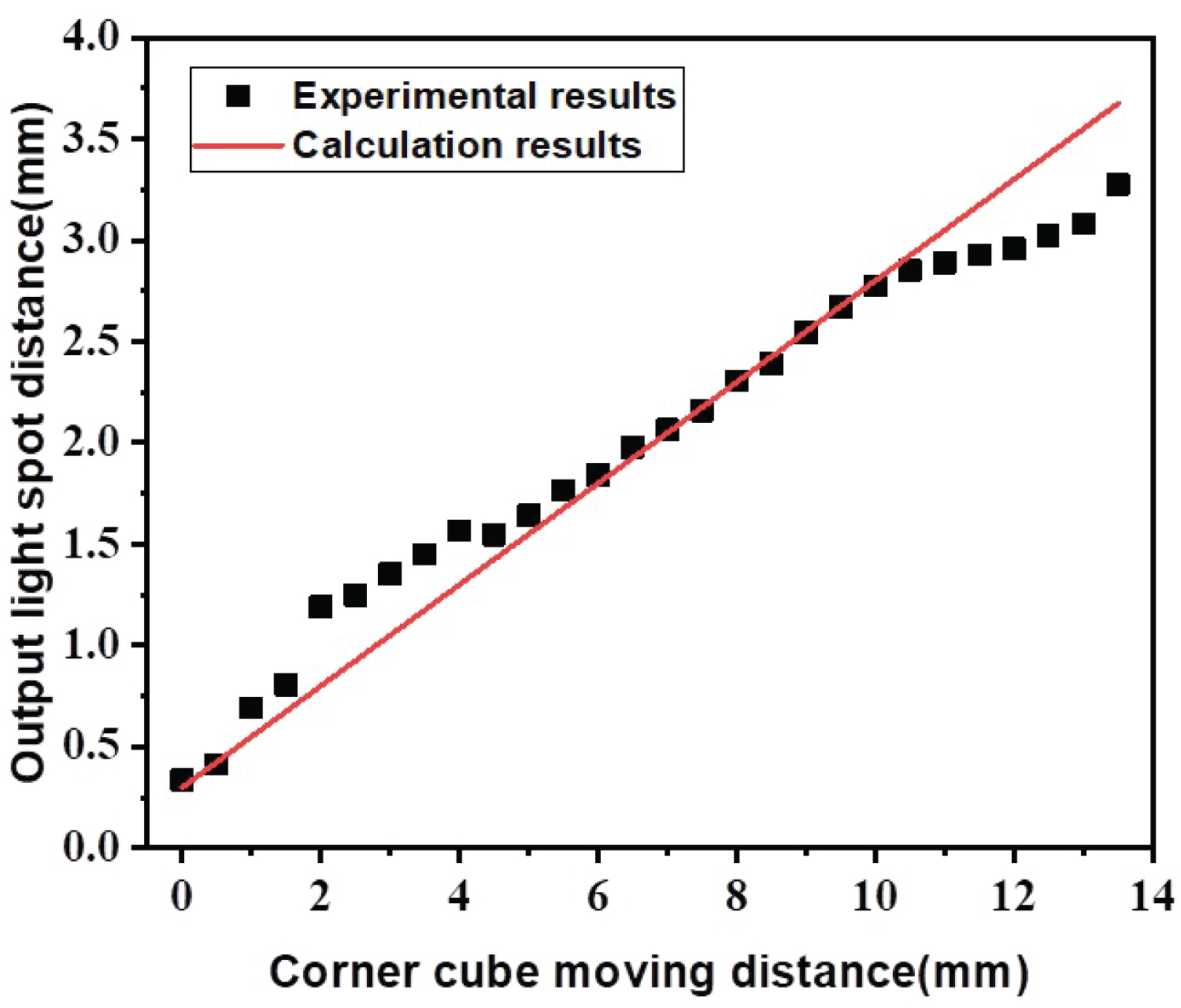
Figure 6: The relationship between the output....
The relationship between the output spot distance and the moving distance of the corner cube.
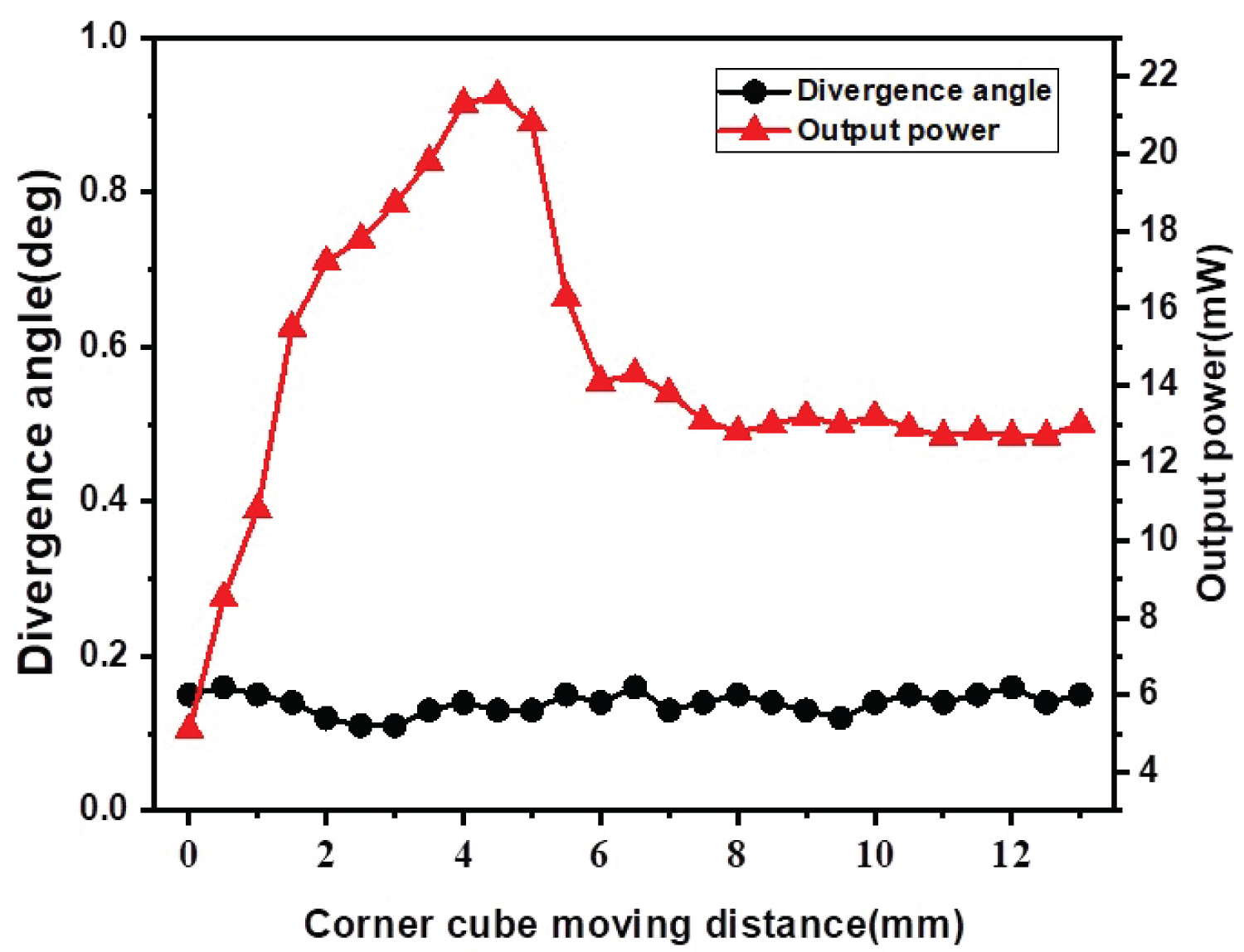
Figure 7: The relationship between the divergence...
The relationship between the divergence angle, output power and the moving distance of corner cube.
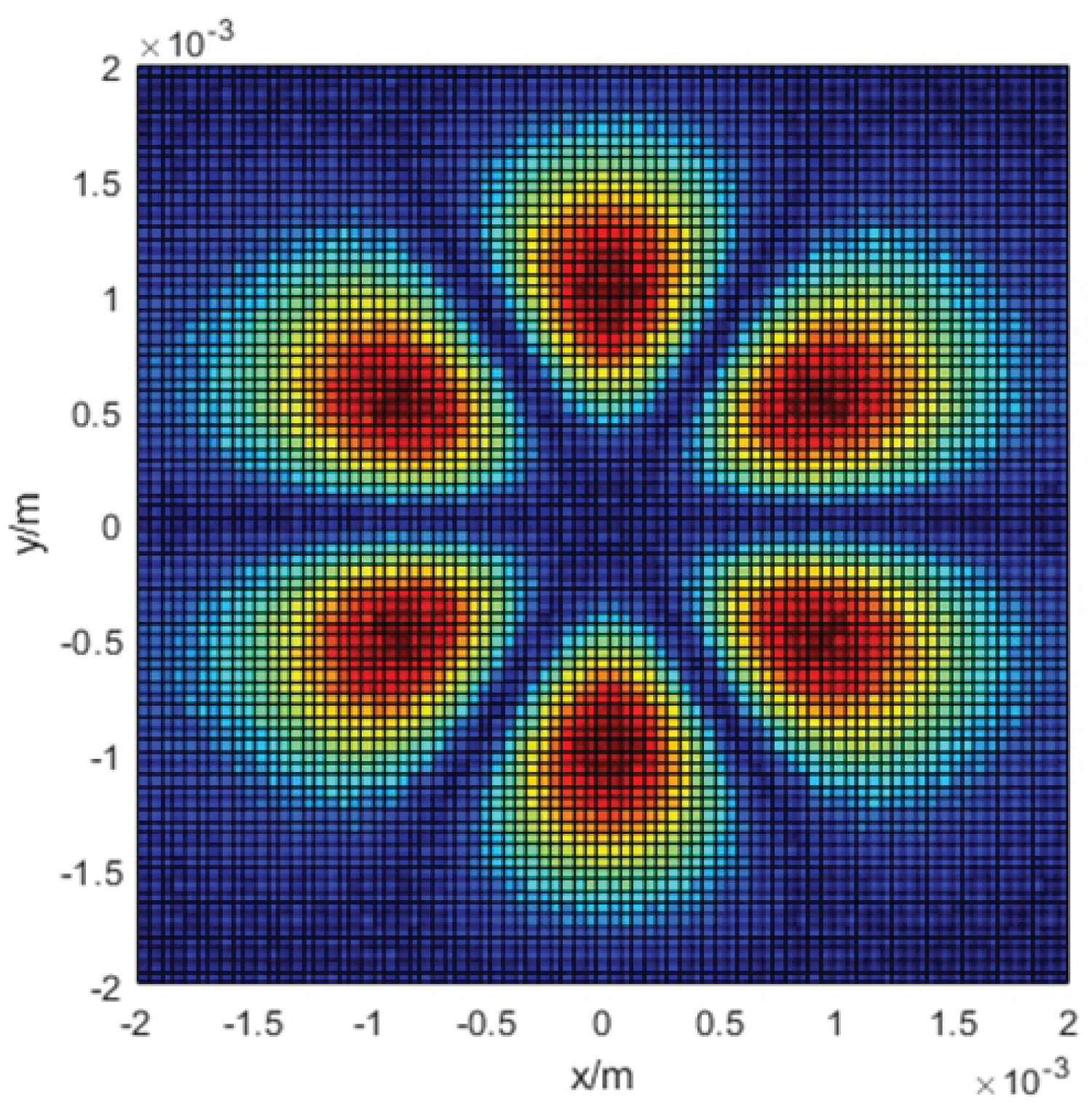
Figure 8: FFT simulation of the output spot of the...
FFT simulation of the output spot of the corner cube resonator.
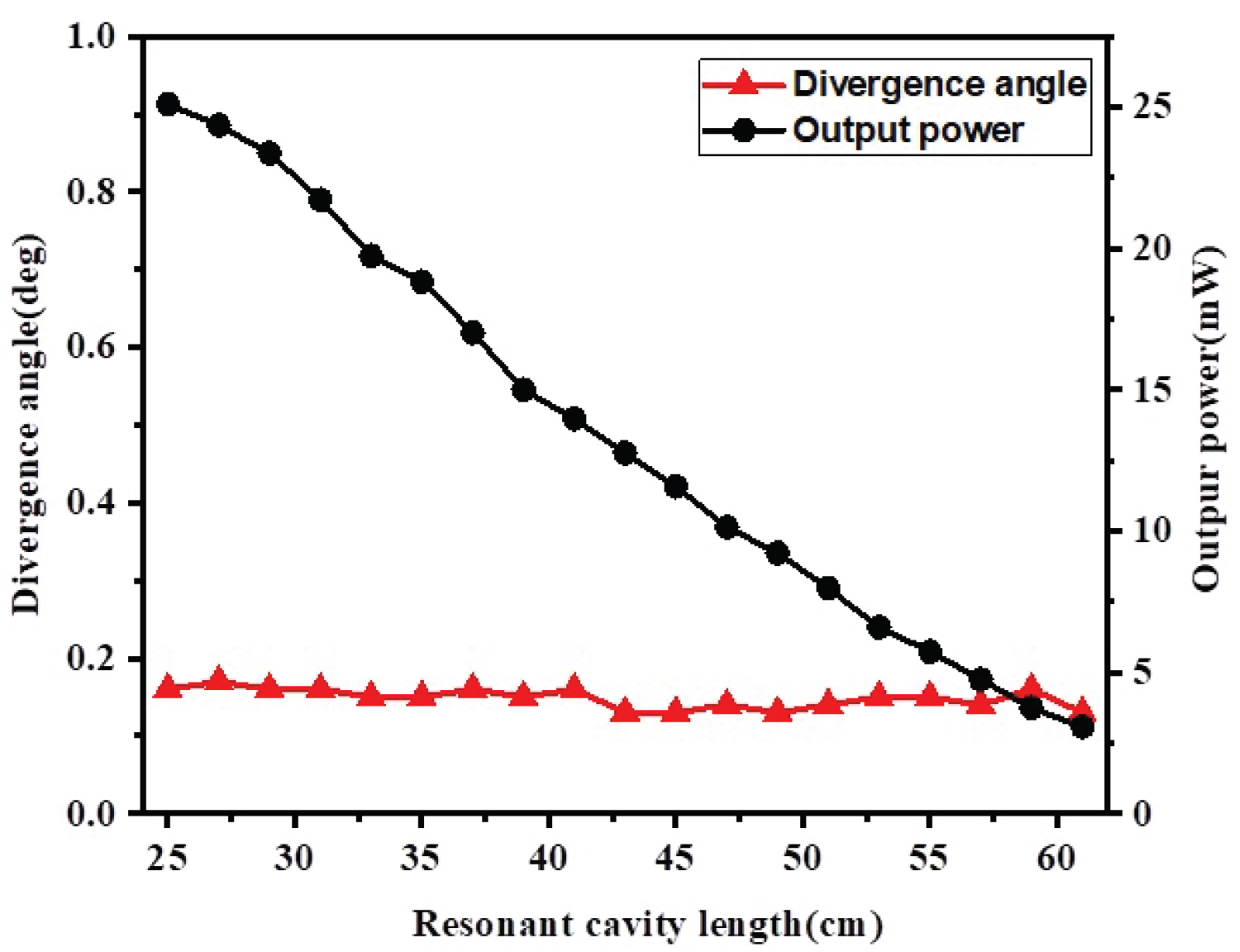
Figure 9: Relationship between divergence angle...
Relationship between divergence angle, output power and cavity length.
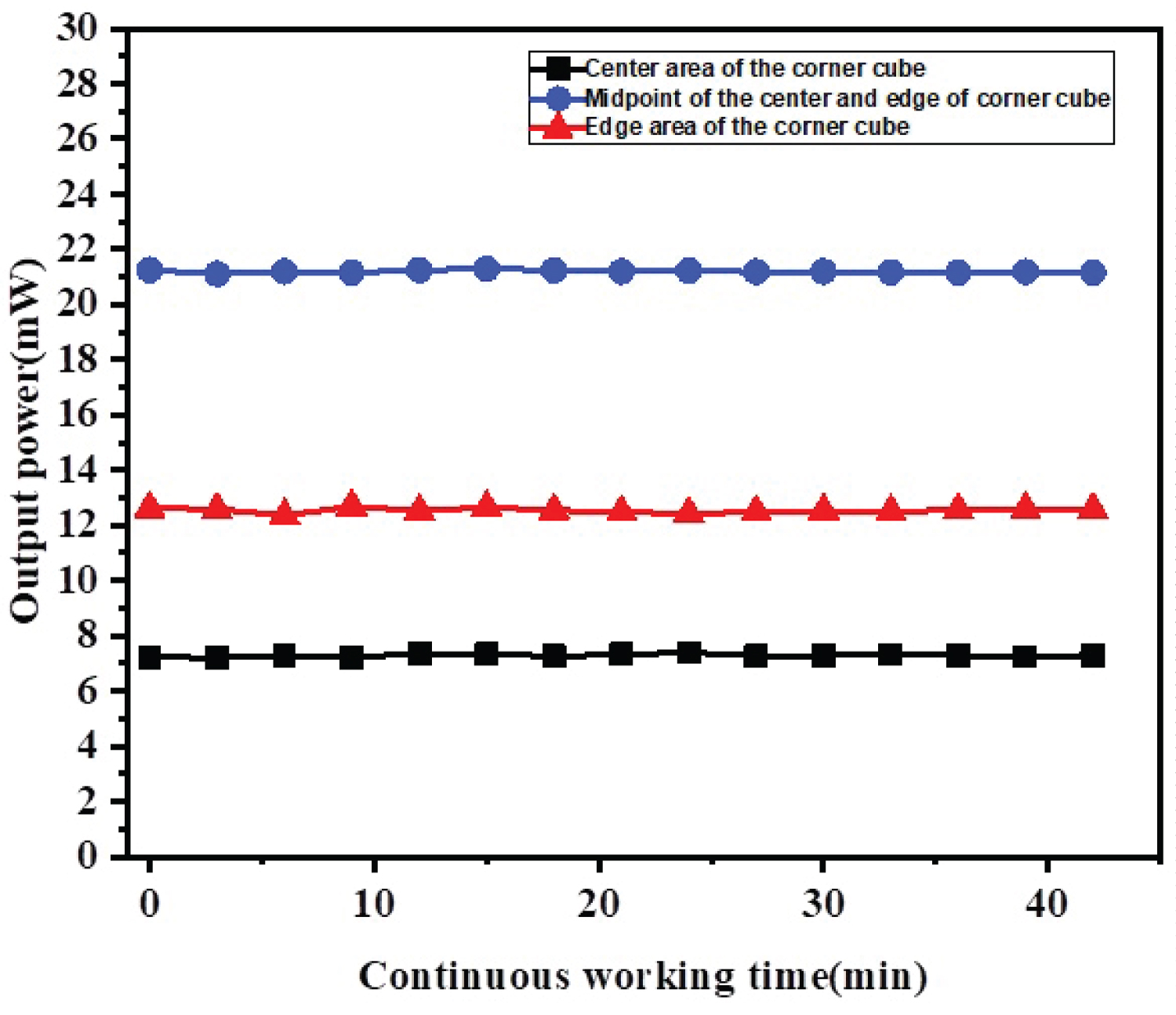
Figure 10: The relationship between output power...
The relationship between output power and continuous working time under different incident points.
References
- Huang H, You Z, Liu YJ, Li B (2012) Design and simulation of an efficient and safe laser power transmission system. J Tsinghua Univ (Sci&Tech) 52: 421-424.
- He T, Yang SH, Zhang HY, Zhao CM, Zhang YC, et al. (2014) High-power high-efficiency laser power transmission at 100 m using optimized multi-cell GaAs converter. Chin Phys Lett 31: 104203.
- Liu JG, Zhang XB, Yu JH, Xu ZY, Ju ZJ (2019) Performance analysis for the magnetically coupled resonant wireless energy transmission system. Complexity 2019: 1-13.
- Nayagam VS, Premalatha L (2000) Optimization of power losses in electric vehicle battery by wireless charging method with consideration of the laser optic effect. Meas Control 53: 441-453.
- Wang JX, Li ZY, Li GC, Xiong K, Ning XW (2017) Investigation of a gravity-immune chip-level spray cooling for thermal protection of laser-based wireless power transmission system. Int J Heat Mass Transf 114: 715-726.
- Kawashima N, Takeda K, Yabe K (2007) Application of the laser energy transmission technology to drive a small airplane. Chin Opt Lett 5: S109-S110.
- Shen MX, Wang SM, Hu LG, Zhao DM (2004) Mode properties produced by a corner-cube cavity. Appl Opt 43: 4091-4094.
- Liu QW, Wu J, Xia PF, Zhao SJ, Yang YP, et al. (2016) Charging unplugged: Will distributed laser charging for mobile wireless power transfer work? IEEE Veh Technol Mag 11: 36-45.
- Zhang Q, Shi X, Liu Q, Wu J, Xia P, et al. (2017) Adaptive distributed laser charging for efficient wireless power transfer. In Proc IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, Canada, 1-5.
- Zhang QQ, Fang W, Liu QW, Wu J, Xia PF, et al. (2018) Distributed laser charging: A wireless power transfer approach. IEEE Internet Things J 5: 3853-3864.
- Wang W, Zhang QQ, Lin H, Liu MQ, Liang XY, et al. (2019) Wireless energy transmission channel modeling in resonant beam charging for IoT devices. IEEE Internet Things J 6: 3976-3986.
- Iyer V, Bayati E, Nandakumar R, Majumdar A, Gollakota S (2018) Charging a smartphone across a room using lasers. Proc ACM Interact Mob Wearable Ubiquitous Technol 1: 1-21.
- Della-Pergola R, Alpert O, Nahmias O, Vaisleib V (2017) Spatially distributed laser resonator. U.S. patent application 9,553,418, B2.
- Yang YC, Luo H (2010) Backward diffractive characteristics analysis of cube-corner prism by Zemax. Infrared Laser Eng 39: 491-495.
- Zhou B, Liu BQ, Zhang Y (2011) Analysis of optical characteristics of cube corner retro-reflector with oblique incident angle. Laser & Infrared 41: 1231-1234.
- Huang CH, Zhai S (2018) Polarization characteristics of corner cube reflectors by Stokes parameters. Infrared Laser Eng 47: 255-261.
- Shi Y, Li S, Zhou H, Wen XT (2005) MATLAB and its application to solve Fresnel diffraction of the cube corner prism. Optoelectron Technol Inf 18: 85-88.
- Zhou XF, Qi ZM, Luo XQ, Liu CA, Zhu JH, et al. (2017) A method to diverge reflected beam uniformly using cube-corner retroreflector array with dihedral angle tolerances. Acta Phys Sin 68: 94-103.
- Chen SQ, Yang GW, Bi MH, Li CS, Li J, et al. (2019) Application of micro-corner prism array in Retro-reflector modulating laser communications. Radio Eng 49: 342-346.
- Cheng Y, Mao SQ, Wang ZH, Wang XB, Sun B, et al. (1999) Avoidance adjust solid state laser. Laser Technol 23: 5-7.
- He Y, Liu Q, Duan HZ, He JJ, Jiang YZ, et al. (2018) Manufacture of a hollow corner cube retroreflector for next generation of lunar laser ranging. Res Astron Astrophys 18: 57-64.
- Ma YF, Li HJ, Lin JP, Yu X, He NL, et al. (2010) Excellent stability of laser passively Q-switched with a retroreflecting corner cube prism. Laser Phys 20: 1791-1793.
- Zhou GS, Alfrey AJ, Casperson LW (1982) Modes of a laser resonator with a retroreflecting corner cube mirror. Appl Opt 21: 1670-1674.
- Xu L, Yang YN (2020) Laser-mode simulation of corner cube resonator. Acta Photonica Sin 49: 193-202.
Author Details
Chang Du*, Kang Yun and Yannan Yang*
College of Science, Nanjing University of Aeronautics and Astronautics, Nanjing, China
Corresponding author
Chang Du and Yannan Yang, College of Science, Nanjing University of Aeronautics and Astronautics, NO. 29, Jiangjun Road, Nanjing 211106, China.
Accepted: March 08, 2021 | Published Online: March 10, 2021
Citation: Du C, Yun K, Yang Y (2021) Study on the Output Characteristics of the External-Cavity Laser with Corner Cube Resonator. Int J Opt Photonic Eng 6:031.
Copyright: © 2021 Du C, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In order to obtain the external cavity lasered with debugging-free and highly stable light energy output in a non-laboratory environment, the corner cube is employed as the optical resonator of the solid laser to build a V-type external cavity solid-state laser. The output characteristics of this type of laser are studied through theoretical analysis and experimental measurement. The results show that, under the given conditions of pump light, the laser oscillation was successfully achieved through the obtained solid-state laser, regardless of changing the lateral position of the corner cube or the angle between the corner cube and the incident light, while the output power and spot position has changed. This type of the obtained solid-state laser has great reference values for the application of external cavity laser in an environment where vibration causes changes in cavity length.
Index Terms
Corner cube, External-cavity laser, Output characteristics
Introduction
Based on the excellent directivity and coherence of the laser, as well as the high energy density, the photovoltaic device can meet the essential requirements of small size and light weight, which was used to convert the receive light energy into electrical energy [1,2]. Therefore, scientists predict that laser wireless energy transmission technology will have broad application prospects in outdoor environments, such as space solar power stations, inter-satellite energy transmission, extend drone battery life [3-6]. Meanwhile, a small laser wireless energy transmission device with good safety protection function also show great high application value for remote wireless charging of mobile intelligent portable devices, such as mobile phones and personal computers which used in an indoor environment. In 2004, Zhejiang University analyzed the mode properties of a corner cube resonator, in which the corner cube is the key element and a flat mirror is used as the output mirror, the results indicates that in the far field the field distribution is a superposition of partially coherent beams [7]. In 2016, Tongji University proposed a segmented laser wireless charging technology which uses a corner cube as a resonant cavity. This technology has a fast and corresponding automatic protection function during the charging process, but there is no specific theory and experiment [8]. Later, they reported a specific scheme to optimize the photoelectric conversion efficiency of the output laser in the photovoltaic cell, and further ascertained through the simulation results [9]. In 2018, they also proposed a multi-module laser wireless charging system model, which has the application background of the Internet of Things (IoT) and a multimodule laser wireless charging system model of Wi-Fi communication function, modeling and analyzing the transmission efficiency of each module of the system [10]. Based on the theoretical model, the experimental platform was built in 2019. The results show that the maximum transmission distance can reach 2.6 meters when the charging power is 2 W [11]. Besides, the University of Washington proposed a laser wireless charging system with the least energy of 2W among the range of 4.3 m to 12.2 m in 2018, which can charge mobile devices such as smartphones [12]. In 2017, Israel's Wi-Charge Company proposed a V-shaped resonant cavity in the patent, laying a theoretical foundation for the practical construction of a distributed laser resonant cavity system [13]. It is worth noting that the external cavity laser with the corner cube as the resonant cavity mirror has great characteristics of large cavity length adjustment range, strong anti-interference ability, laser oscillation can be formed without strict collimation adjustment, and oscillation can be stopped when blocked by obstacles, leading to the excellent laser energy transmission in general living environment.
In this paper, we first used geometrical optics theory to analyze the position and angle relationship between the reflected light and incident light on the corner cube. On this basis, a V-shaped external cavity solid-state laser was set up through combine the Nd: YVO4 crystal as the laser gain medium, a semiconductor laser with a wavelength of 808 nm as the pump source, and a corner cube as the reflector. The wavelength of the output laser was 1064 nm, and the output characteristics of the laser are studied through experiments. The results show that, under the given conditions of pump light, the laser can achieve laser oscillation regardless of changing the lateral position of the corner cube or the angle between the corner cube and the incident light, but the output power and spot position have changed. The obtained laser in this article puts one end of the resonant cavity on the load to form a resonant cavity between the energy emitting end and the charging target. When the resonant cavity is blocked, the light in the cavity will immediately stop oscillating. Therefore, this type of laser is not only suitable for the environment where the cavity length changes due to the movement or vibration of the receiving end, but also has automatic safety protection function.
The Relationship between Reflected and Incident Light on a Corner Cube
Corner cube is a special retro-reflective device, which is a tetrahedron with three mutually perpendicular reflection surfaces. The special feature of the corner cube is that after the incident light is reflected by the three reflecting surfaces, the outgoing light will exit in the opposite direction of the incident light, but there will a certain distance between the outgoing light and the incident light. In addition, the distance varies as the corner cube rotated around its vertex or translated globally, while the two lights remain parallel [14-16]. This feature leads to a widely used in areas ranging from infrared measurement, laser ranging, precision measurement and other fields [17-19] to a mirror of the optical resonator which used in some solid and gas lasers [20-22]. Due to the limitations of the laser gain medium and the size of the pump spot in the solid-state laser, the oscillation is related to the position of the corner cube when the corner cube is used as the laser resonator. Therefore, it is necessary to theoretically analyze and calculate the change law of the distance between the reflected light and the incident light under different circumstances. Based on this, a solid laser with a corner cube resonator cavity can be further constructed, and the output characteristics can be studied.
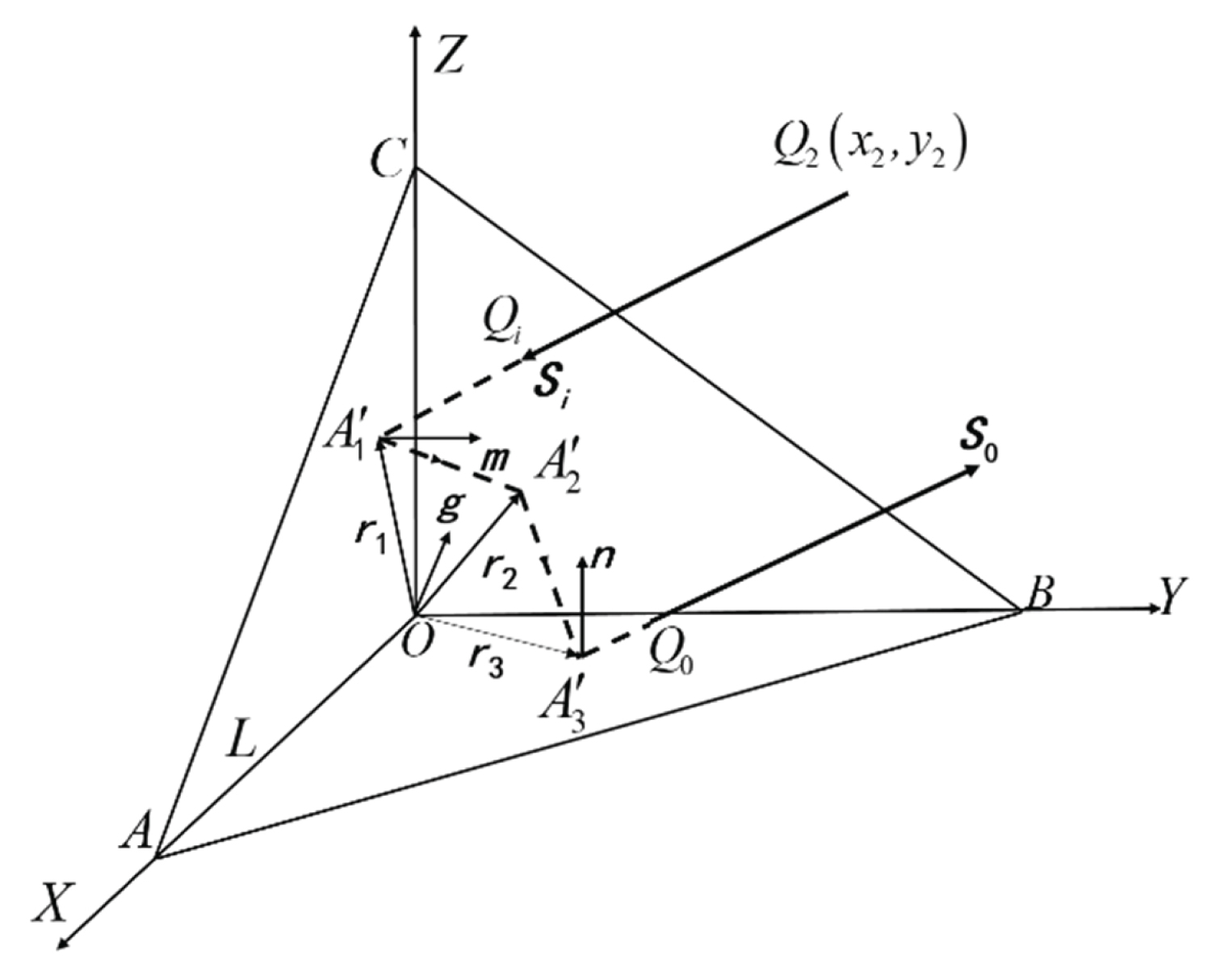
For this, we take the straight line of three arises of the corner cube as the coordinate axis to establish a rectangular coordinate system, as shown in Figure 1. When a beam of light is incident on the point on the plane from any direction, it can be expressed as [23]:
Among them, r = (x, y, z) is a variable vector, ri = (xi , yi , zi) is the vector from the origin of the coordinate to the incident point, Si(a, b, c) is the direction vector of the incident light. Then, the incident ray meets the first reflective surface AOC (which can be expressed as Y = 0), and the point of the incident ray on the plane AOC is , then:
Where r1 is the position vector of point . After the light given by (1) is reflected by , the vector S1 of the reflected light satisfies the following equation according to Snell's rule:
Where m = (0,1,0) is the unit normal vector of the plane AOC, which can be obtained from (3):
Then the light reflected from the plane BOC can be expressed as:
Similarly, the intersection point of the light and the other two reflecting surfaces of the corner cube can be obtained:
After the third reflection of the corner cube, at the point Q0 on the plane ABC, it exits parallel to the incident light, and the position vector at point Q0 is:
Where L is the length of the corner cube, g is a vector perpendicular to the plane ABC from the origin of the coordinate, and g is the length of g. According to (2), (6), (7), and (8), the length from Qi point to Q0 via , , is:
Suppose now that there is a plane A'B'C' that passes through the coordinate origin and is parallel to the plane ABC, this plane can be expressed as:
Increasing the incident light and the outgoing light will intersect the plane A'B'C' at points and , as shown in Figure 2. Can be obtained from (8) and (10):
Pi and P0 are vectors pointing from the origin of the coordinates to points Pi and P0. On the plane A'B'C', the incident point and the exit point are symmetrical about the origin. When the incident light hits a certain point on the corner cube, the coordinates of Pi (x1, y1, z1) and P0 (x2, y2, z2) are determined, the distance between the incident point and the exit point on the plane A'B'C' is:
As the corner cube moves, the coordinates of Pi and P0 on the plane will change accordingly, and the distance h between Pi and P0 will also change accordingly. According to the inclination of the plane A'B'C', the distance between the incident light and the exit light in space is:
Where θ is the angle between the plane A'B'C' and the vertical plane.
We observed from (14) that the distance between the incident light and the reflected light is related to the coordinates of the incident point (The distance between the line of incident light and the axis of the corner cube center) and the angle between incident light and plane ABC when the incident light irradiates one reflection surface of the corner cube and exits after three reflections from the three reflection surfaces. Among them, when θ is unchanged, the distance between the incidents light was linear with the moving distance of the corner cube.
Because the corner cube has the reflection characteristics as described above, the laser composed of the corner cube as a resonant cavity belongs to a ring laser, and the lights oscillating in the cavity are parallel to each other by a certain distance, which depends on the lateral position and azimuth angle of the corner cube relative to the axis.
Corner Cube Resonator Laser and Experimental Results
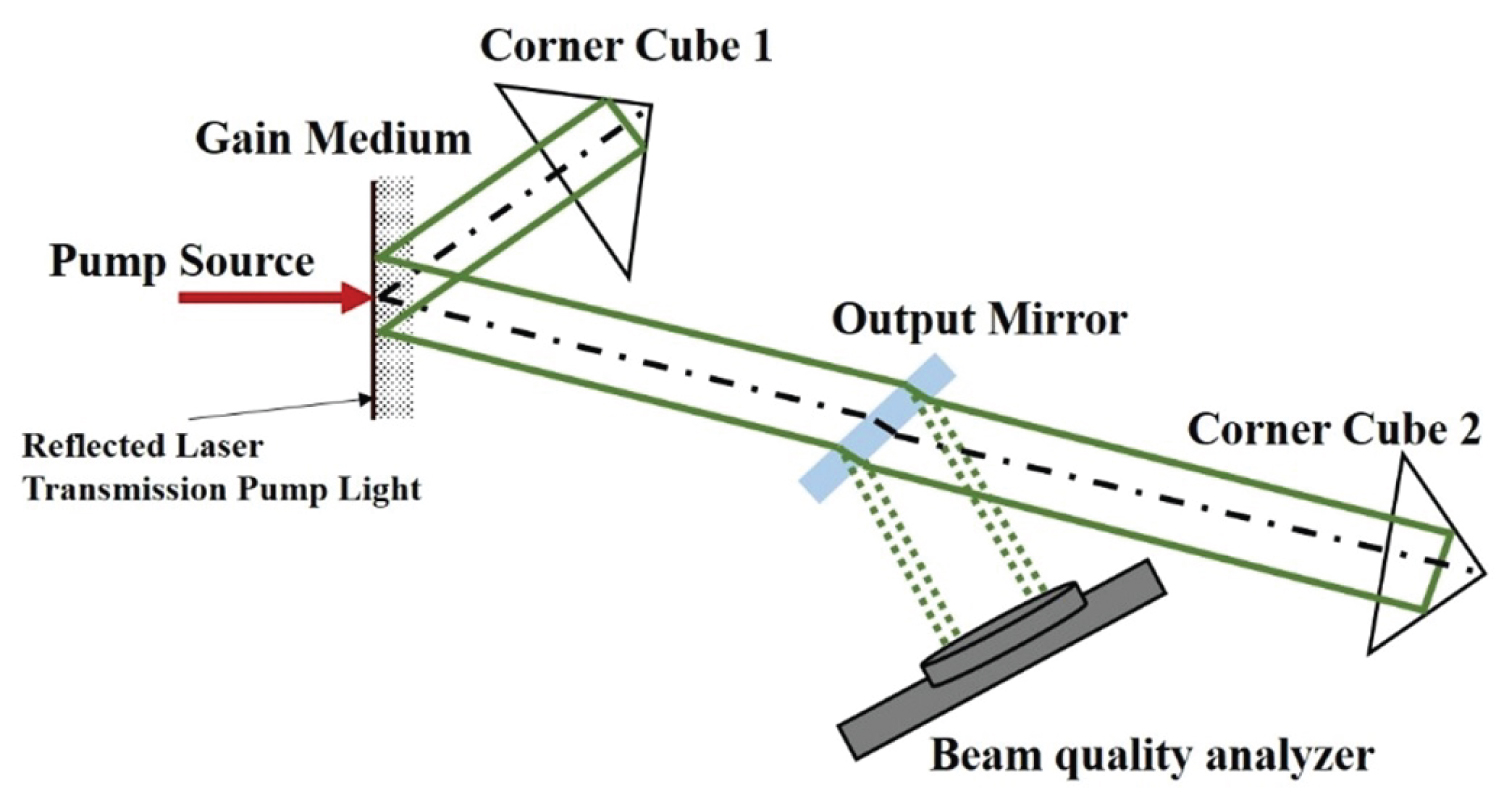
Based on the theoretical calculation results above, we use a corner cube as a reflector, Nd: YVO4 crystal as a laser gain medium, and a semiconductor laser with a wavelength of 808 nm as a pump source to build an external cavity solid-state laser with a V-shaped structure with an output wavelength of 1064 nm, the diameter of the pump light spot on the gain medium is about 1 mm, and the output characteristics of the laser were studied in detail through experiments. The experimental setup is shown in Figure 3 and Figure 4, and the 808 nm laser light source is a semiconductor laser with a maximum output power of 50 W. The gain medium is Nd: YVO4 crystal with a doping concentration of 0.3 at % and a rectangular parallelepiped of 5 mm × 5 mm × 15 mm to make the corner cube 2 have a greater off-axis distance. Besides, considering the formation of the optical path of the resonant cavity and the increase of the pumping efficiency of the pump source, the surface 1 is coated with a film that totally transmits 808 nm laser and reflects 1064 nm laser, and the surface 2 is coated with a film that totally reflects 808 nm laser and transmits 1064 nm laser. The corner cube is a hollow corner cube with a diameter of one inch from Thorlabs, whose error is 2". The output mirror is a flat mirror with 95% transmission and 5% reflection of the 1064 nm laser and located at a position approximately 45° from the optical path. The beam quality analyzer with a wavelength range of 900 nm-1700 nm is from Thorlabs (BP209-IR/M), whose aperture diameter is 9 mm.
Corner cube 1 and 2 are placed symmetrically on both sides of the crystal normal and their axes are approximately parallel to the optical axis, in which corner cube 1 is close to the crystal as the transmitting end resonance mirror, and corner cube 2 is far away from the crystal acting the receiving resonance mirror. Make the corner cube 2 as close to the optical axis as possible, and use this as the initial point to observe the output characteristics of the entire system as the corner cube 2 moves in the horizontal direction (perpendicular to the optical axis direction) and longitudinal direction (along the optical axis direction) when the pump power is 10 W. Due to the limitation of experimental conditions, it was impossible to rotate the corner cube and change the angle of incidence within a small error range without changing the incident point of the incident light, and we did not explore the change in output characteristics with an angular direction.
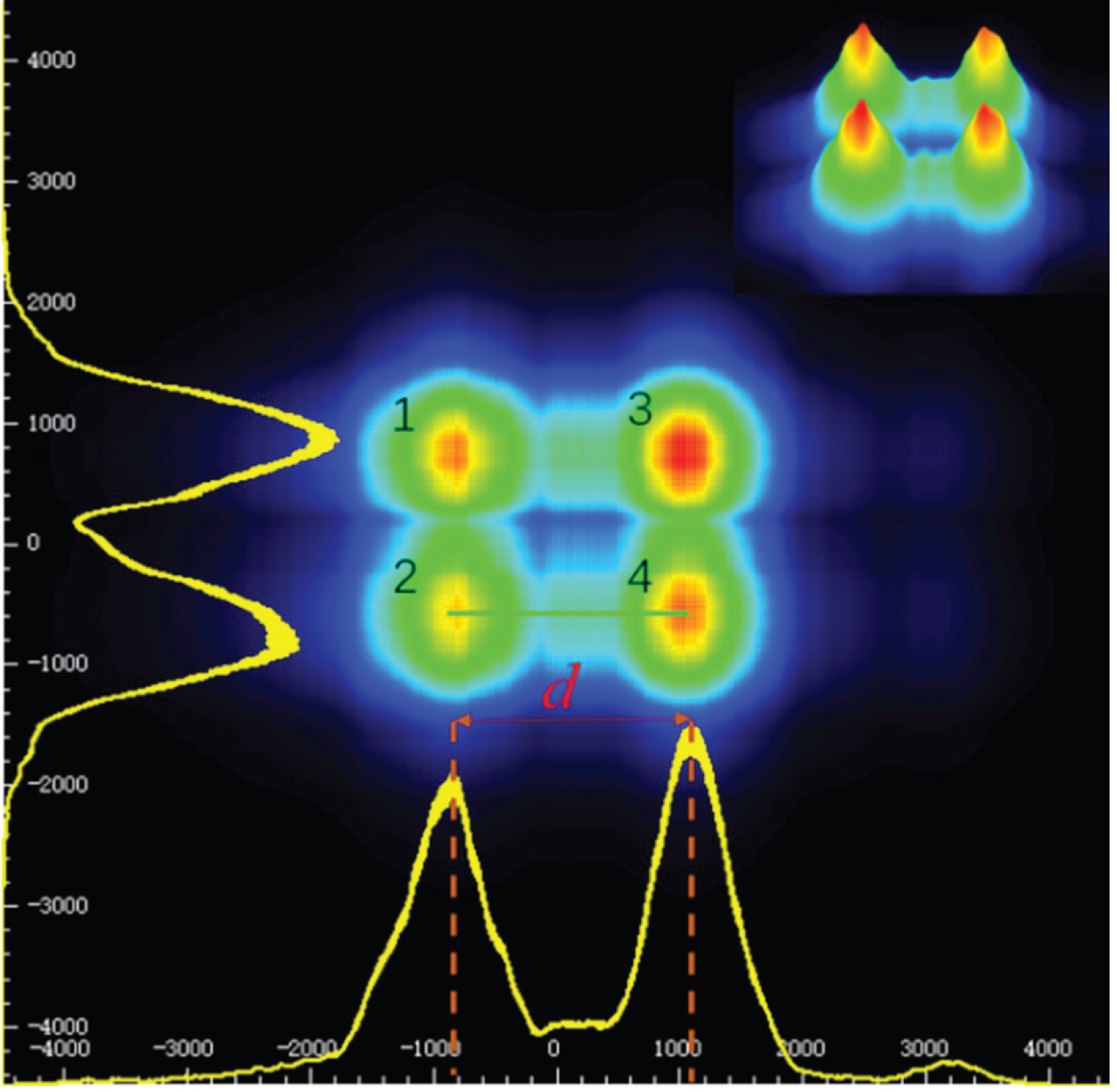
Figure 5 shows the pattern of light spots collected by the scanning beam quality analyzer. In theory, the oscillating light path in the resonant cavity is rectangular, that is, there should be two light spots on any section of the light path. However, since the output mirror placed at 45° in the experiment has a certain thickness, four light spots (1, 3, 2, 4) are discovered after the laser oscillating in the resonator cavity is reflected by the front and rear surfaces of the output mirror. During the experiment, with the movement of the corner cube, the distance between spots 1 and 2 remains unchanged, while the distance between spots 1 and 3 gradually increases. Therefore, the distance between spots 1 and 3 is the output spot spacing, as shown in Figure 5d.
• Horizontal direction
From the initial point, the position of the corner prism 2 is moved in the horizontal direction, and the output spot spacing, output optical power, and divergence angle are measured every 0.5 mm. The measurement results are shown in Figure 6 and Figure 7. We can see from Figure 6 that the distance of the output light spot of the corner cube laser (that is, the oscillating light in the cavity) increases with the distance of the corner cube from the axis. Furthermore, the line fitted in the figure does not pass through the coordinate origin, which is caused by the fact that the axis of the corner cube does not coincide with the axis of the whole system when it starts to move in the experiment. According to the theoretical calculation results above, when the corner cube is fixed in one direction (that is, the angle θ between the incident light and the axis of the corner cube is unchanged), the distance d of the output light spot has a linear relationship with the moving distance of the corner cube, which is consistent with the (14).
We can see from Figure 7 that the divergence angle of the output laser has no significant changes during the entire horizontal movement of the corner cube, which is about 0.15°. The output power varies significantly with the moving distance of the corner cube. When the corner cube starts to move, the output power is the lowest, as the corner cube moves gradually, the output power tends to increase and then decrease. When the moving distance is about 5 mm, the output power reaches the maximum value (21.5 mW), and then decreases to about 13 mW, which is caused by the different losses when the incident light enters the corner cube on different positions. When the vertex of the corner cube is right on the optical axis, since the light incident on the vertex of the corner cube cannot be reflected, the laser oscillation cannot be formed. When the corner cube deviates from the optical axis, the laser oscillation is easily formed. As the distance of the corner cube from the axis increases, the output optical power increases first, and then decreases.
The above output power changes with the position of the corner cube can be explained by the theoretical analysis in Xu's article [24]. Figure 8 is the Fast Fourier Transform (FFT) method numerical simulation of the loss of the light field on different positions of the corner cube. Since the seam of the corner cube has diffraction loss to the light, when the light is incident on the center of the corner cube, the loss is the highest and the output power is the lowest; when the incident light deviates from the center of the corner cube, the loss decreases and the output power increases rapidly; however, when the incident light is far away from the center of the corner cube, although the loss is still low, due to the limitation of the activation volume of the 808 nm pump light in the laser crystal, the two lights cannot be in the area where the number of particles is inversely distributed at the same time, so the output power has decreased again.
• Longitudinal direction
In the case where the position of the oscillating light incident on the corner cube is unchanged, move the corner cube 2 along the longitudinal direction to change the cavity length of the resonant cavity, and measure the divergence angle and output power of the laser under different cavity lengths. The cavity length is increased from 25 cm to 61 cm, and the measurement data are taken every 2 cm, corresponding to moving distance step. The results are shown in Figure 9.
We can see from Figure 9 that the divergence angle of the output laser does not change significantly with the increase of the cavity length and fluctuates are around 0.16°. The output optical power decreases significantly with the increase of cavity length, the main reason for this phenomenon is that the oscillating light in the cavity has a small divergence angle, when the oscillating light starts from the crystal and returns to the crystal after being reflected by the corner cube, the spot area is larger than that of the pump light on the crystal (This area is related to the active area of the crystal irradiated by the pump light), only the part of the oscillated light passing through the active area of the pump light can be amplified. The longer the cavity length is, the larger the area of the laser spot reflected to the crystal, and the higher the proportion of laser light that overflows the pump light activation area, resulting in a lower gain coefficient and a lower output power.
In order to observe the change laws of the laser output power with time, when the cavity length is selected to be a certain value, we recorded the value of output power when the continuous working times of the laser are different. It is found that the output power basically does not change with time, indicating that the output power is very stable under the given resonant cavity structure. Figure 10 shows the measured value of the output power when the cavity oscillated light is irradiated to the vertex of the corner cube (corresponding to ◼ in Figure 10), the distance from the vertex is less (corresponding to • in Figure 10) and the distance from the vertex is more (corresponding to ▲ in Figure 10) when the cavity length is 30 cm.
In addition, according to the results of experimental measurements, we can also find that the output power of the laser obtained in this paper is limited and the efficiency is low. Since this article focuses on whether the corner cube external cavity laser can achieve "self-adaptive oscillation in the case of a long cavity", the focus quality of the pump light is not optimized, which makes the pumping efficiency low. On the other hand, the reflectivity of the output mirror used in this article is only 5%, which will also result in lower output power.
Conclusion
In this paper, based on the reflection characteristics of the corner cube, the output characteristics of a V-cavity solid-state laser are studied through theoretical calculations and experimental measurements. The results show that when the corner cube is used as the cavity mirror of the laser resonator, the oscillating light path in the cavity is rectangular. The distance between the two oscillating lights is related to the coordinates of the incident point (in the spatial rectangular coordinate system with the vertex of the corner cube as the origin) and the angle between the incident lights and the axis of the corner cube. When the angle is fixed, the distance between the two lights in the cavity is proportional to the distance between the incident light and the apex of the corner cube. Based on the results of theoretical calculations and experimental measurements in this article, we can optimize the output performance of the obtained laser by changing the moving distance of the corner cube. That is, let the oscillating light in the resonant cavity enter the corner cube where the loss is small to obtain greater output power and efficiency.
During the horizontal movement of the corner cube, the divergence angle of the output laser does not change significantly with the movement of the corner cube 2.
However, due to the diffraction loss of light on the reflective surface joint of the corner cube, when the light is incident on the center of the corner cube, the output power is the smallest; when the incident light deviates from the center of the corner cube, the output power rises rapidly; but when the incident light is far away from the center of the corner cube, the output power drops again. During the longitudinal movement of the corner cube, the divergence angle of the output laser does not change significantly with the increase of the cavity length, and the output power decreases significantly with the increase of the cavity length.
The anti-fatigue characteristics of the whole system are superior. When the cavity length is a certain value, the output power basically does not change with the continuous working time. The output power is stable and can output laser continuously and stably for a long time to meet the needs of laser wireless charging.
Acknowledgment
The authors are grateful to the reviewers for their valuable suggestions.
Source of Support
This work was supported by the National Natural Science Foundation of China (Nos. 51577091).