
International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 8, Issue 1
Research Article
DOI: 10.35840/2631-5092/4553
Focusing of Anoblique Incident Laguerre-Gaussian Vector Beam by a High Numerical-Aperture Lens
Qiang Xu1*, Shaohui Yan2 and Zhensen Wu1
Table of Content
Figures
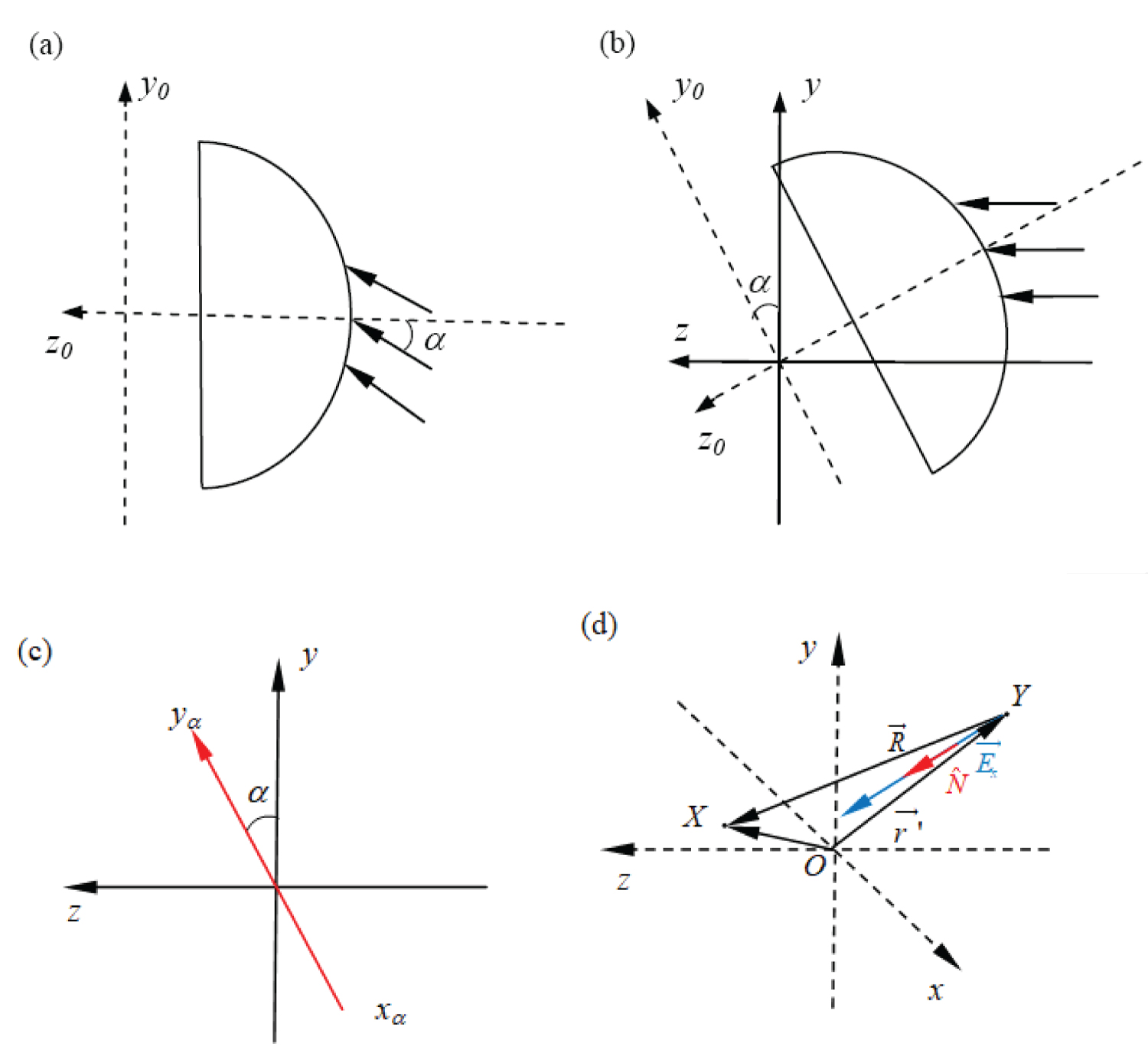
Figure 1: Conceptual diagram of...
Conceptual diagram of oblique lens system. (a) An oblique angle α incident lens system. (b) An oblique plane (xa, ya) inclined by α with respect to the focal plane (x, y). (c) Equivalent lens system image space coordinate representation; (d) O: Geometrical focus; X: An observation point; Y: A point on the exit pupil surface of the lens, the distance YX is .
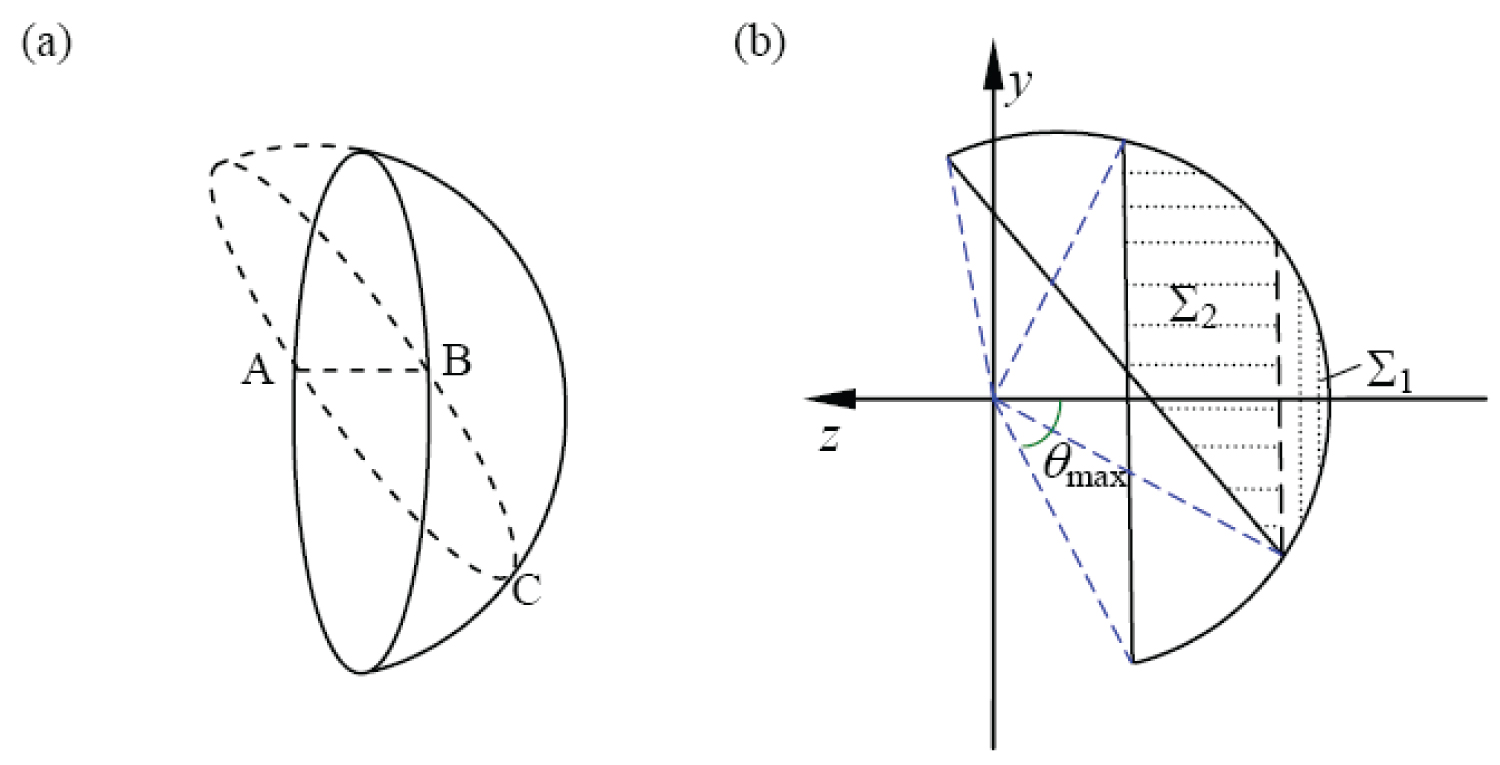
Figure 2: The pupil geometry (a) Effective....
The pupil geometry (a) Effective pupil geometry in the normalized object space; (b) The overlapping area is an effective pupil.
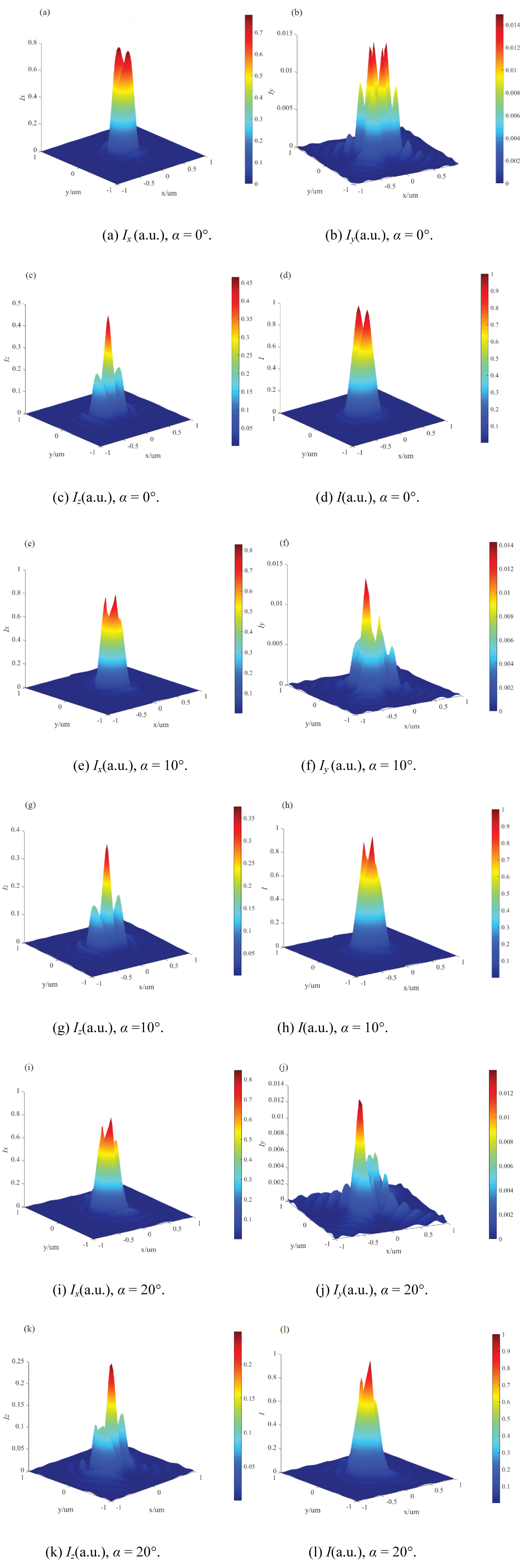
Figure 3: The intensity distribution....
The intensity distribution of an x-polarized Laguerre-Gaussian beam (m = 1, n = 1) on the focal plane with different oblique incident angles α, NA = 1.4.
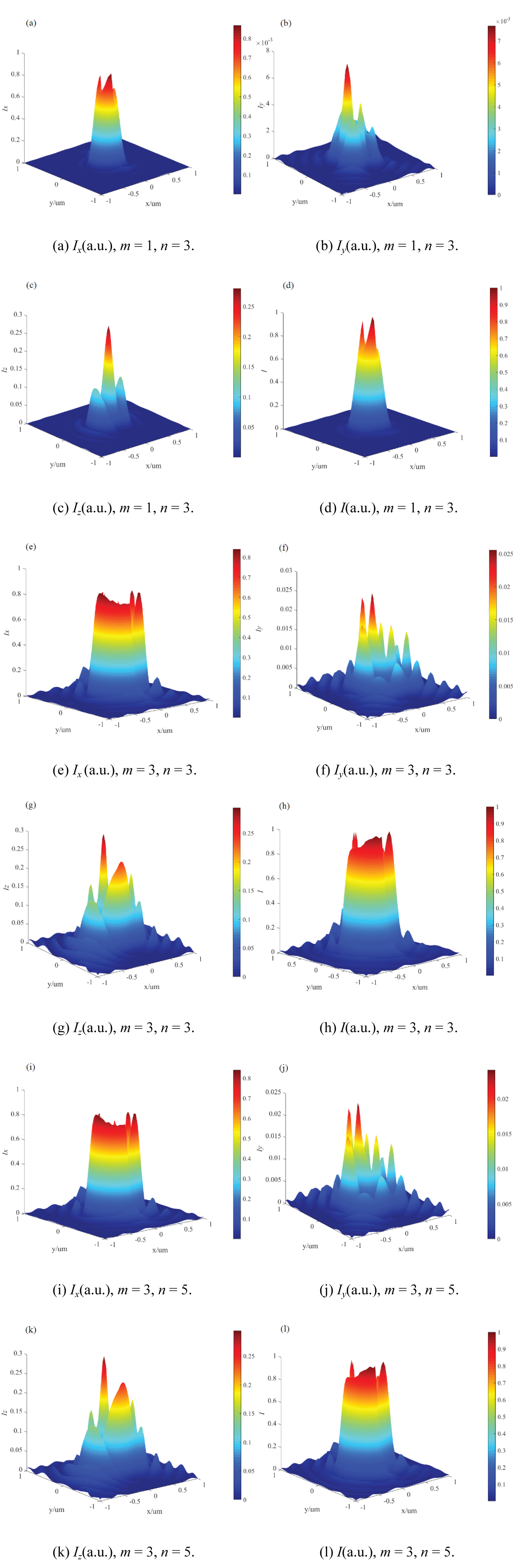
Figure 4: The intensity of an....
The intensity of an x-polarized Laguerre-Gaussian beamon the focal plane with different topological charge, α = 10°, NA = 1.4.
References
- Khonina SN, Karpeev SV, Paranin VD (2018) A technique for simultaneous detection of individual vortex states of Laguerre-Gaussian beams transmitted through an aqueous suspension of microparticles. Opt Laser Eng 105: 68-74.
- Ren Y, Huang H, Xie G, Ahmed N, Yan Y, et al. (2013) Atmospheric turbulence effects on the performance of a free space optical link employing orbital angular momentum multiplexing. Opt Lett 38: 4062-4065.
- Zhu J, Li X, Tang H, Zhu K (2017) Propagation of multi-cosine-Laguerre-Gaussian correlated Schell-model beams in free space and atmospheric turbulence. Opt Express 25: 20071-20086.
- Tamburini F, Anzolin G, Umbriaco G, Bianchini A, Barbieri C (2006) Overcoming the Rayleigh criterion limit with orbital angular momentum of light. Phy Rev Lett 97: 163903.
- Moreno I, Davis JA, Cottrell DM, Zhang N, Yuan X-C (2010) Encoding generalized phase functions on Dammann gratings. Opt Lett 35: 1536-1538.
- Porfirev AP, Ustinov AV, Khonina SN (2016) Polarization conversion when focusing cylindrically polarized vortex beams. Sci Rep 6: 6.
- Khonina SN, Karpeev SV, Paranin VD, Morozov AA (2017) Polarization conversion under focusing of vortex laser beams along the axis of anisotropic crystals. Phys Lett A 381: 2444-2455.
- Toyoda K, Miyamoto K, Aoki N, Morita R, Omatsu T (2012) Using optical vortex to control the chirality of twisted metal nanostructures. Nano Lett 12: 3645-3649.
- Syubaev S, Zhizhchenko A, Porfirev A, Pustovalov E, Vitrik O, et al. (2017) Direct laser printing of chiral plasmonic nanojets by vortex beams. Opt Express 25: 10214-10223.
- Chen Y, Cai Y (2014) Generation of a controllable optical cage by focusing a Laguerre-Gaussian correlated Schell-model beam. Opt Lett 39: 2549-2552.
- Ziyang C, Daomu Z (2012) 4Pi focusing of spatially modulated radially polarized vortex beams. Opt Lett 37: 1286-1288.
- Khonina SN, Golub I (2013) Engineering the smallest 3D symmetrical bright and dark focal spots. J Opt Soc Am A 30: 2029-2033.
- Chen G, Song F, Wang H (2013) Sharper focal spot generated by 4π tight focusing of higher-order Laguerre-Gaussian radially polarized beam. Opt Lett 38: 3937-3940.
- Khonina SN, Porfirev AP (2018) 3D transformations of light fields in the focal region implemented by diffractive axicons. Appl Phys B 124: 191.
- Helseth L (2004) Optical vortices in focal regions. Optics Commun 229: 85-91.
- Kotlyar VV, Khonina SN, Almazov AA, Soifer VA, Jefimovs K, et al. (2006) Elliptic Laguerre-Gaussian beams. J Opt Soc Am A Opt Image Sci Vis 23: 43-56.
- Cui W, Song F, Ju D, Chen G, Song F (2015) Effect of the focal shaping generated from different double-mode cylindrical vector beams. J Opt Soc Am A Opt Image Sci Vis 32: 1576-1580.
- Chen W, Zhan Q (2006) Three-dimensional focus shaping with cylindrical vector beams. Opt Commun 265: 411-417.
- Khonina SN, Kazanskiy NL, Volotovsky SG (2011) Vortex phase transmission function as a factor to reduce the focal spot of high-aperture focusing system. J of Mod Optic 58: 748-760.
- Khonina SN, Golub I (2012) Enlightening darkness to diffraction limit and beyond: comparison and optimization of different polarizations for dark spot generation. J Opt Soc Am A Opt Image Sci Vis 29: 1470-1474.
- Török P, Munro P (2004) The use of Gauss-Laguerre vector beams in STED microscopy. Opt Express 12: 3605-3617.
- Thaning A, Jaroszewicz Z, Friberg AT (2003) Diffractive axicons in oblique illumination: Analysis and experiments and comparison with elliptical axicons. Appl Opt 42: 9-17.
- Abramochkin E, Volostnikov V (1991) Beam transformations and nontransformed beams. Opt Commun 83: 123-135.
- Beijersbergen MW, Allen L, van der Veen HELO, Woerdman JP (1993) Astigmatic laser mode converters and transfer of orbital angular momentum. Opt Commun 96: 123-132.
- Bekshaev AY, Soskin MS, Vasnetsov MV (2004) An optical vortex as a rotating body: mechanical features of a singular light beam. J Opt A Pure Appl Opt 6: S170.
- Bekshaev AY, Karamoch AI (2008) Astigmatic telescopic transformation of a high-order optical vortex. Opt Commun 281: 5687-5696.
- Porfirev AP, Khonina SN, Moiseev OY, Poletaev SD, Larkin AS, et al. (2017) Simple method for efficient reconfigurable optical vortex beam splitting. Opt Express 25: 18722-18735.
- Khonina SN, Degtyarev SA, Porfirev AP, Moiseev OY, Poletaev SD, et al. (2015) Study of focusing into closely spaced spots via illuminating a diffractive optical element by a short-pulse laser beam. Computer Optics 39: 187-196.
- Zhou G (2006) Analytical vectorial structure of Laguerre-Gaussian beam in the far field. Opt Lett 31: 2616-2618.
- Kim J, Li T, Wang Y, Zhang X (2014) Vectorial point spread function and optical transfer function in oblique plane imaging. Opt Express 22: 11140-11151.
- Li Y (2005) Focal shifts in diffracted converging electromagnetic waves. I. Kirchhoff theory. J Opt Soc Am A Opt Image Sci Vis 22: 68-76.
Author Details
Qiang Xu1*, Shaohui Yan2 and Zhensen Wu1
1School of Physics, Xidian University, Xi'an 710071, P.R. China
2The State Key Laboratory of Transient Optics and Photonics, Xi'an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi'an, 710119, P.R. China
Corresponding author
Qiang Xu, School of Physics, Xidian University, Xi'an 710071, PR China.
Accepted: February 17, 2023 | Published Online: February 19, 2023
Citation: Xu Q, Yan S, Wu Z (2023) Focusing of Anoblique Incident Laguerre-Gaussian Vector Beam by a High Numerical-Aperture Lens. Int J Opt Photonic Eng 8:053.
Copyright: © 2023 Xu Q, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We describe diffractive and focusing properties of oblique incident vector vortex beams under tight focusing conditions. By dividing the effective pupil area of the focus lens into two parts for simple integration, using the electromagnetic wave polarization vector diffraction theory, the intensity distributions of oblique incident vector Laguerre-Gaussian beams focused by high numerical aperture lens are calculated and analyzed, the structural changes in the transverse and the axial direction near the focus plane are observed, numerical simulation show that, field intensity distributions are changed with the different oblique incident angle and topological charge of Laguerre-Gaussian beam, the distortion and asymmetry of intensity distribution are shown in different cases. This research can be applied for trapping and manipulating particles, super-resolution fluorescence microscopes.
Keywords
Laguerre-Gaussian vector beam, Vector diffraction theory, Oblique incident, High numerical-aperture Lens, Intensity distribution
Introduction
Recently, vortex beams have been studied extensively and have wide applications, such as optical communications [1-3], optical imaging [4]. Generating multiple vortex patterns beam by a diffraction grating [5], the conversion of polarized laser beams from a radial to an azimuthal polarization, or vice versa [6], the generation of beams with different polarization states in an anisotropic crystal [7]. Application of the vortex beam for trapping and manipulating particles, such as controlling the chirality of metal nanostructures [8], producing chiral nanoneedles on thin films [9]. The use of optical vortices to generate a controllable optical cage [10]. it is quite difficult to create 3D optical cage with identical in all directions light barriers at the usual focusing (from one side), since the axial resolution is several times worse than the transverse one, to decrease the axial extension of the focal spot, different techniques are used, including 4pi scheme with two opposing lenses [11-13]. Also, three-dimensional focus shaping may be realized by supplementing the focusing lens with annular, or choosing the suitable polarization states of vector beams [14], or more complex diffractive optical elements [15,16].
A tight-focusing vortex beam for achieving the smallest possible focal spot is an essential issue in a variety of applications. To reduce the size of the focal spot under sharp focusing, including high-aperture focusing system [17,18], stimulated emission depletion microscopy [19]. Laguerre-Gaussian beams being focused through a stratified medium [20].
The astigmatic transformations of focused vortex beam were studied by many scientists, such as an oblique incidence of an axially symmetric beam onto an optical element produce elliptic beams [21,22]. This effect is closely related to astigmatic transformations, used for the formation of Laguerre-Gauss modes from Hermite-Gauss modes [23,24] and for analyzing the structure of vortex beams [25-27]. Moreover, the sharp focusing of Laguerre-Gauss beams with astigmatic distortion, polarization state affects the longitudinal component of the electric vector of the light field [28].
But by high numerical aperture (NA) lenses, beam field of oblique incident vortex beam have some new character, can be used for trapping and manipulating particles, it need more study, Motivated by these facts, a basic goal of this paper is to examine the diffractive and focusing properties of oblique incident Laguerre-Gaussian (LG) beams focused by high numerical aperture (NA) lenses near the focal region.
Analysis and Methodology
An LG beam oblique is incident on high NA lens, which is schematically shown in Figure 1a. The angle between incident beam and z0 axis is α, we rotate the coordinate system to make incident beam parallel to z axis, shown in Figure 1b.
We note the arrangement of the optical lens system in Figure 1, and use the x-axis polarized Laguerre-Gaussian beam [29].
are the generalized Laguerre polynomials, and the integers n, m obey the relation,
Fresnel approximation of the classical scalar diffraction theory can only be applied to the paraxial optical system or the low numerical aperture. It has lost its effectiveness in the high NA system. In order to accurately predict the performance of high NA, we use the electromagnetic wave polarization vector diffraction theory. The space dependent electric vectors in the image space of the optical system have the integral representation [30,31]
Where is the wavelength, Σ is the wavefront surface over the exit pupil of a lens, is a unit ray vector (normal to the wavefront), is electric field at the exit pupil, k is the wave number in medium. O is geometrical focus, X is an observation point; Y is a point on the exit pupil surface, the distance OX is , the distance OY is , the distance YX is ( shown in Figure 1).
The evaluation of the vector Debye integral requires a mathematical explanation of the effective pupil area in Figure 1. As illustrated in Figure 2a, the original circular pupil region and the oblique region overlap the portion to form an effective pupil. The normalized pupil function is derived from the exit pupil of the image space of the spherical coordinates ( : polar angle, : azimuthal angle). In order to facilitate the calculation of the integral, the circular asymmetric pupil in the oblique plane imaging is divided into (rotationally symmetric part) and (the rest area). The pupil functions for and are [30]
Where , , , and are defined in follow. The values of , are expressed as a function of , NA and n.
In Figure 2, the equation of the plane ABC is , plugging this equation into the unit sphere equation give the coordinate values of the point C as
The electric field near the focal area of the oblique lens can be obtained from equation (1) to be
Here , , , (a Cartesian-to-spherical coordinate relation).
The total intensity can be obtained
Then the two-dimensional electric field over an oblique plane with a oblique angle α is
For the circular symmetry region , the double integration is changed into a single integral. For , integration can be reduced by half. These considerations lead to
The time-averaged electrical energy density or intensity can be obtained by the modulus squared of the electric fields. The total intensity distribution at the focal plane is the sum of the longitudinal and transverse components.
Numerical Simulation Results
In order to probe further the field structure at the focal plane, we have performed numerical calculations for the intensity distributions. Assuming that the light is an x-axis polarized Laguerre-Gaussian beam (the topological charge m = 1, n = 1), the numerical aperture of the lens NA = 1.4, the wavelength of the beam , the diameter of optical aperture is 2.0 cm, the FWHM (full width at half maxima) of the laser beam is 0.5 cm.
In Figure 3a, Figure 3b, Figure 3c and Figure 3d, α = 0°, the intensity is equal to the conventional intensity of the circular aperture system, intensity profile of x component (Ix) has two peaks, intensity profile of y component (Iy) has eight peaks (four secondary peaks around four main peaks), Iy is about 1% of the total intensity, intensity of z components (Iz) is about one third of the total intensity, Iz has three peaks (two secondary peaks around a main peak), the x-direction intensity is the main part of the total intensity. As oblique angle α = 10°, the intensity distribution is distorted, two peaks of Ix become asymmetrical, most peaks of Iy degenerate, Intensity Iz decreases slightly, and the distortion is bigger when the oblique angle α = 20°.
Figure 4a, Figure 4b, Figure 4c, Figure 4d, Figure 4e, Figure 4f, Figure 4g, Figure 4h, Figure 4i, Figure 4j, Figure 4k and Figure 4l shows the oblique incident beam with different the topological charge (m = 1, n = 3; m = 3, n = 3; m = 3, n = 5), the beam incident angle α = 10°, NA = 1.4, other parameters are same as which in Figure 3. The intensity distribution of first mode (the topological charge m = 1, n = 3) is shown in Figure 4a, Figure 4b, Figure 4c and Figure 4d, The intensity Ix is about 75% of total intensity I. The intensity Iy is about 0.1% of total intensity I, there are four main peaks at the center and sub-peaks around. The intensity Iz is about 25% of total intensity I, there is one main intensity peak surrounded by two sub-peaks. The second modes (the topological charge m = 3, n = 3) are shown in Figure 4e, Figure 4f and Figure 4g, Ix is nearly 80% of total intensity I, the intensity Ix distribute in a circle, have eight main lobes, upper (according to y axis direction) two lobes are overlapped. Iy is about 2% of total intensity I, The intensity distribution have ten main lobes. For Iz, is about 20% of total intensity I, some of lobes are overlapped. The intensity distributions of third mode (the topological charge m = 3, n = 5) are shown in Figure 4i, Figure 4j, Figure 4k and Figure 4l, which is similar to that of the second mode. For all these modes, the structure of the field intensity near the focal area significantly changes to an asymmetrical shape, and distribution of I is mainly depended on Ix.
Conclusions
We analyzed focusing of an oblique incident Laguerre-Gaussian vector beam by a high numerical-aperture lens. Based on the Debye-Wolf vector diffraction theory, we formulate the electrical field distribution. Numerical simulation has also been performed, three-dimension intensity distributions of an oblique incident Laguerre-Gaussian beam on the focal plane of the lens were gotten, and the total intensity distribution on the focal plane, which is the sum of the longitudinal and transverse components, were analyzed in detail, the intensity profile of the focused Laguerre-Gaussian beam has several peaks related with topological charge. For normal incident beams, intensity profiles are symmetric, when the beam is obliquedly incident on the lens, value of some intensity peaks increase, as value of others decrease, the distribution profile is asymmetric. The distortion of light beams intensity distribution get greater with the increasing oblique incident angle. We also analyze the distortions of light beams intensity distribution with different topological charge. In practical application, it is an important reference for trapping and manipulating particles, super-resolution fluorescence microscopes.
Funding
This research was funded by the National Natural Science Foundation of China (Grant No. 61975158), State Key Laboratory fund (The State Key Laboratory of Transient Optics and Photonics,Xi'an Institute of Optics and Precision Mechanics).
Data Availability Statement
Data underlying the results presented in this paper can be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.

