International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 3, Issue 2
Research Article
DOI: 10.35840/2631-5009/7516
Thermal and Mechanical Response of Inner Cone Sample of ZrB2-SiC Ceramic under Arc-Jet Conditions
Jun Wei, Lokeswarappa R Dharani* and K Chandrashekhara
Table of Content
Figures
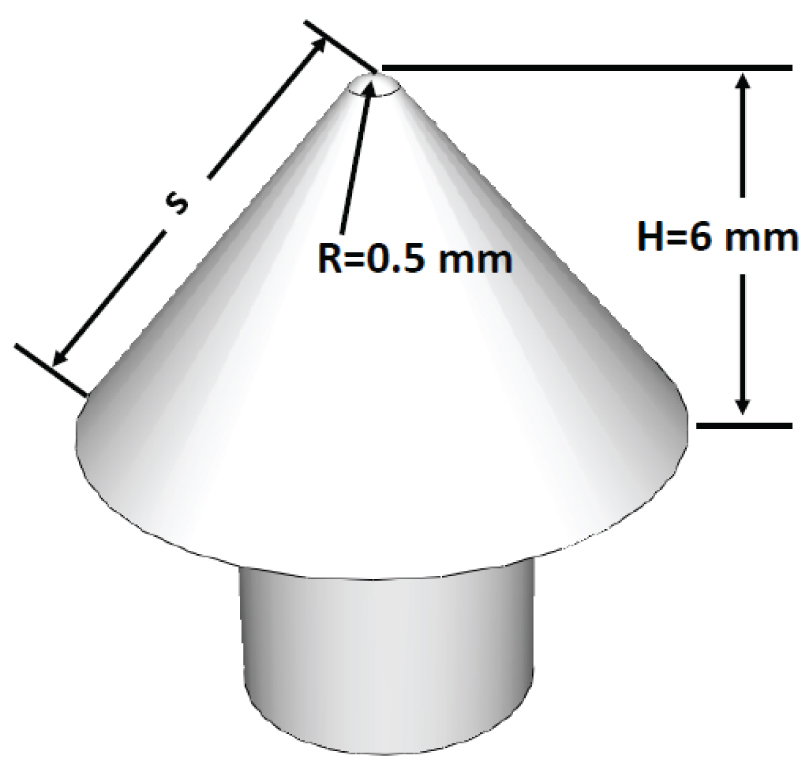
Figure 1: Cone sample with dimensions...
Cone sample with dimensions (after Savino, et al. [13,14] and Monteverde, et al. [15]).
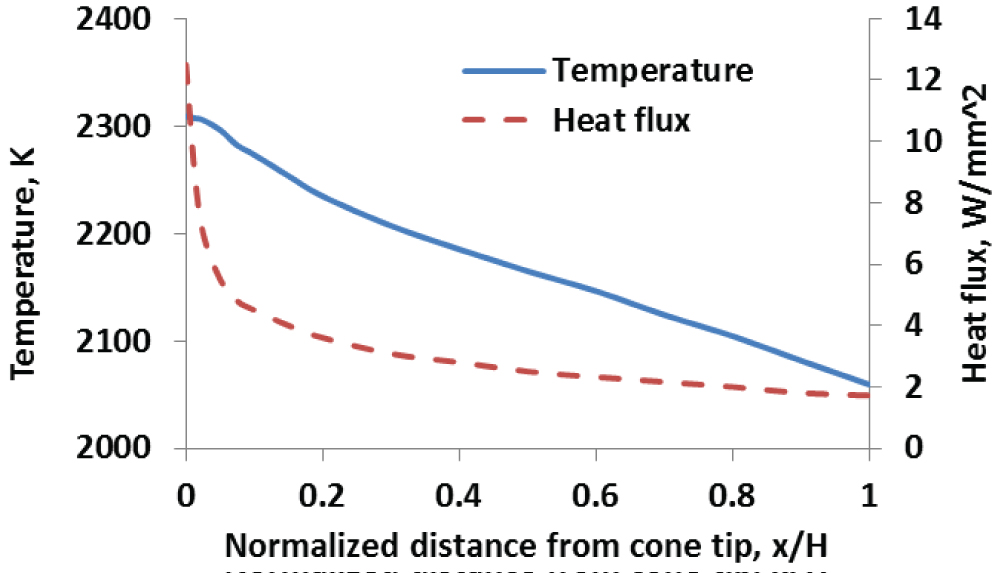
Figure 2: Distribution of surface...
Distribution of surface temperature and surface heat flux along the slant height of the cone with normalized coordinate (x/H) (after Savino, et al. [13,14] and Monteverde, et al. [15]).
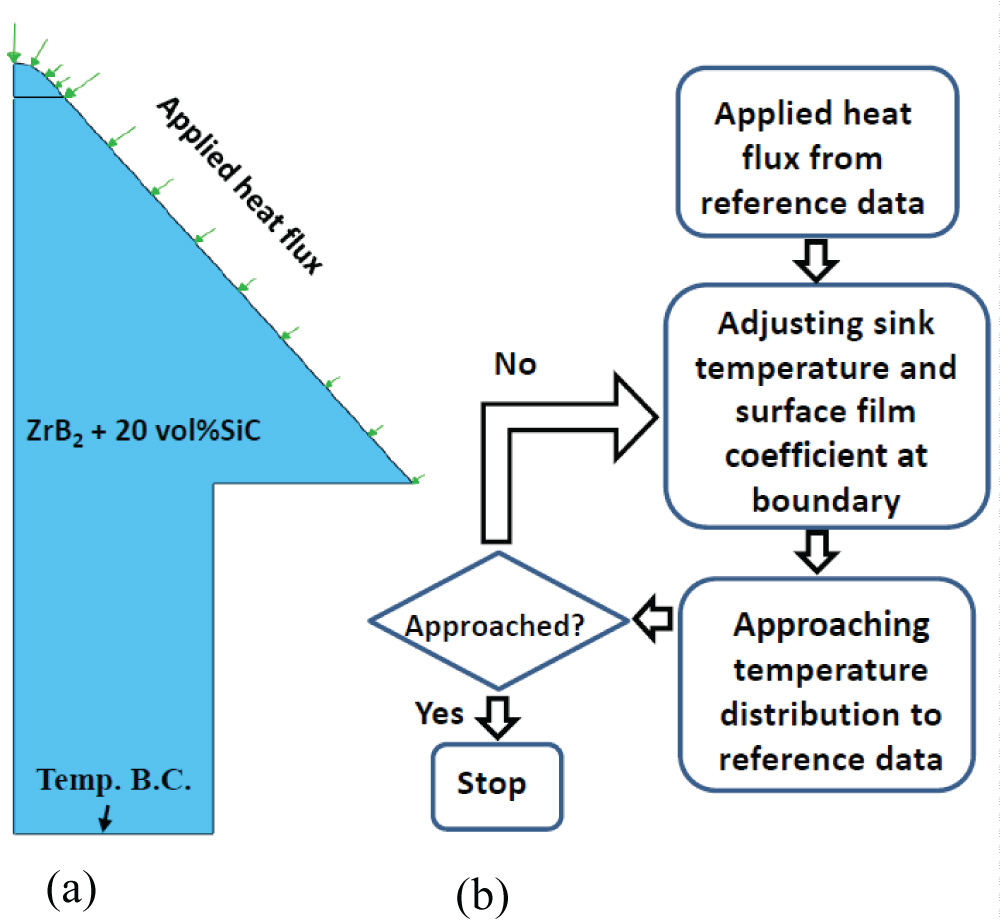
Figure 3: a) The calibration model and...
a) The calibration model and ;b) Flow diagram of the procedure.
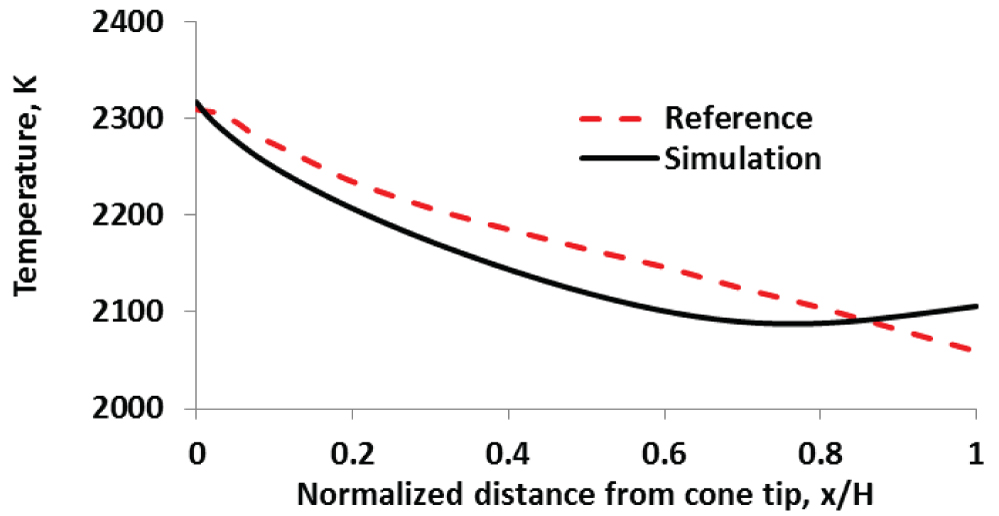
Figure 4: Simulation temperature...
Simulation temperature distribution compared with the reference temperature distribution [13-15].
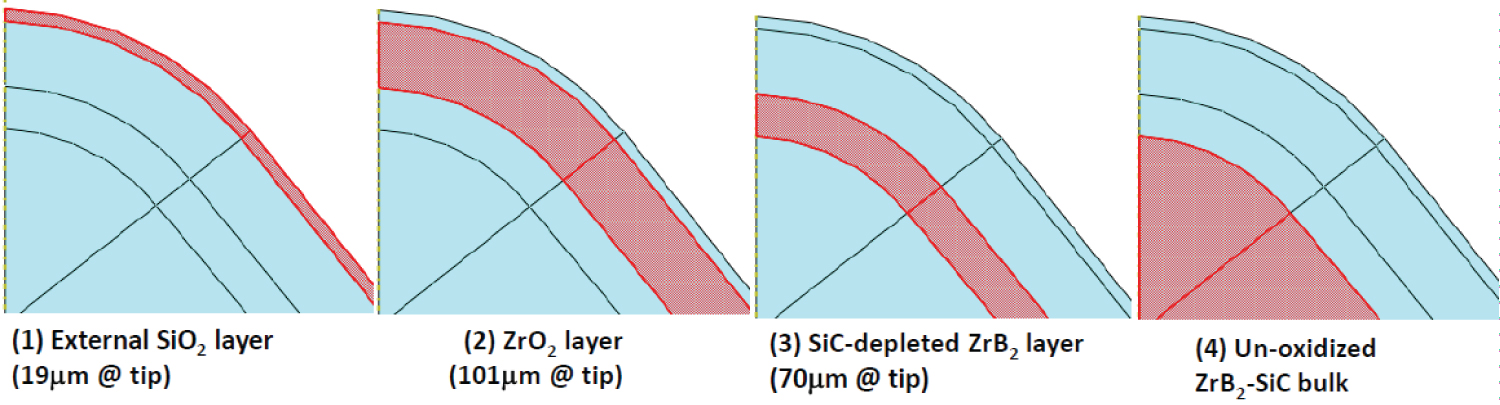
Figure 5: FE model for the multiple...
FE model for the multiple oxide layers with temperature dependent properties. The label numbers and thicknesses correspond to those in reference [15].
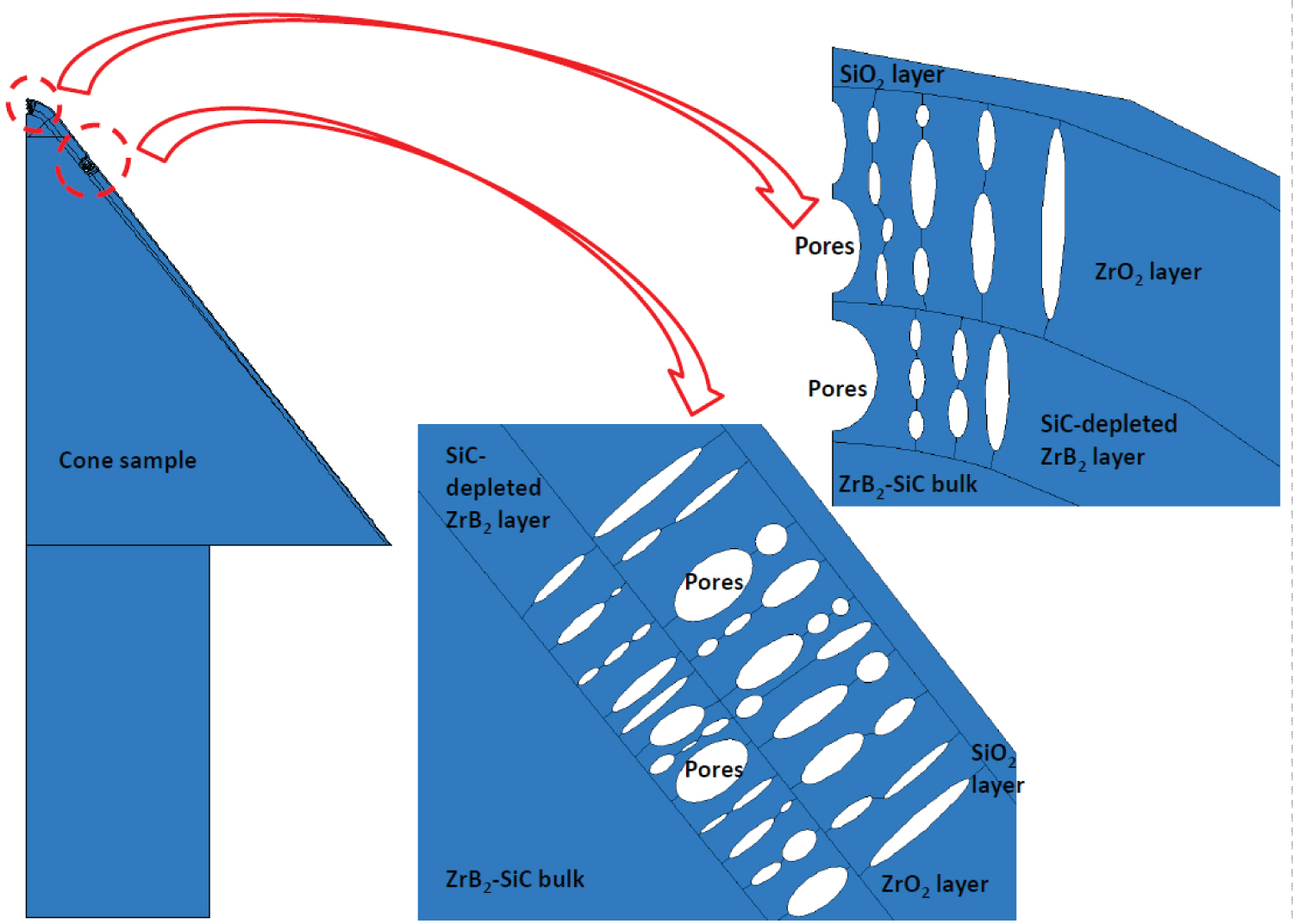
Figure 6: Axisymmetric model with...
Axisymmetric model with artificial ellipses (pores) arbitrarily distributed in the layer.
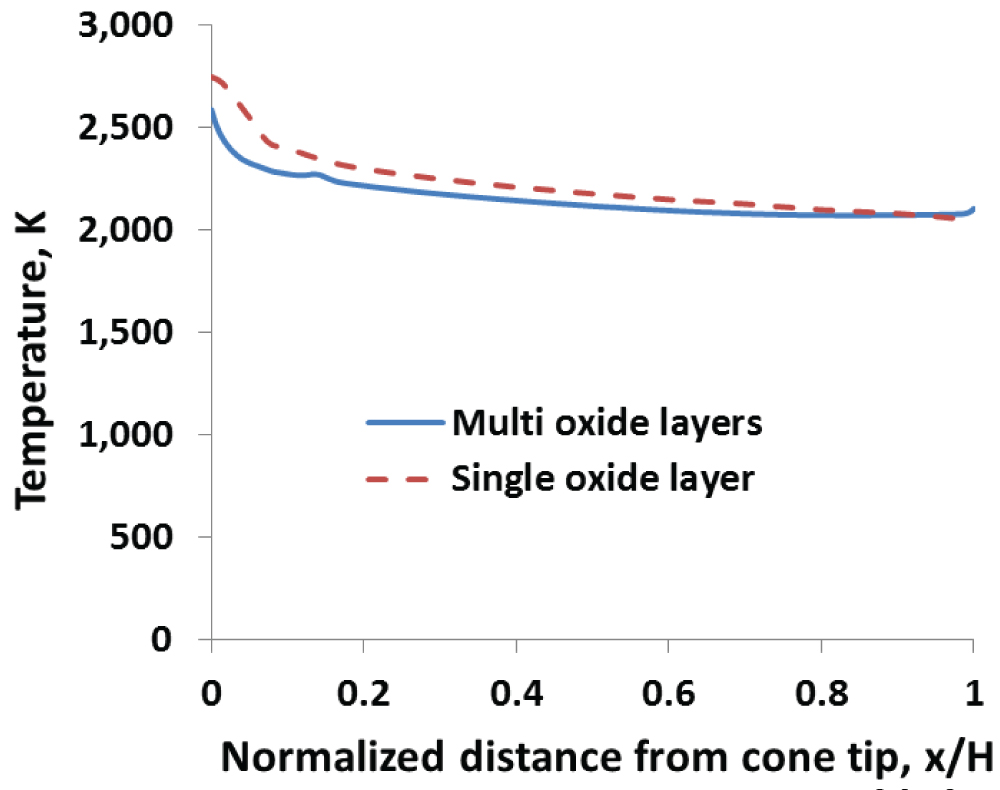
Figure 9: Distribution of the...
Distribution of the surface temperature along the slant height of the cone.
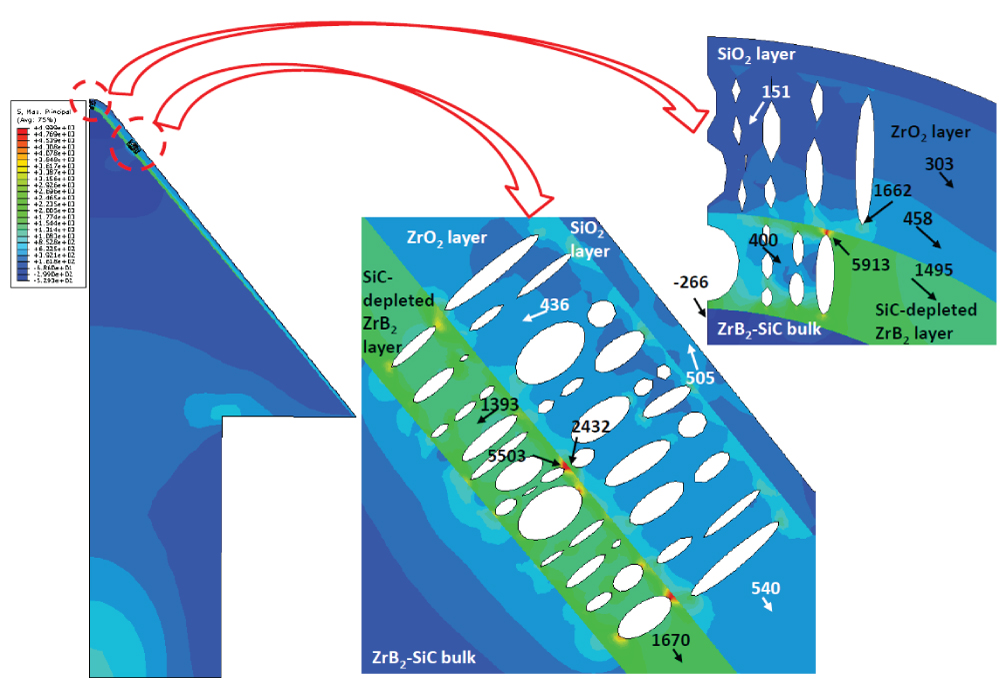
Figure 10: The maximum principal...
The maximum principal stress distribution in the inner cone body (unit: MPa).
References
- R Savino, M De S Fumo, D Paterna, A Di Maso, F Monteverde (2010) Arc-Jet testing of ultra-high-temperature-ceramics. Aerospace Sci Tech 14: 178-187.
- MM Opeka, IG Talmy, JA Zaykoski (2004) Oxidation-based Materials Selection for 2000 ℃+ Hypersonic Aerosurfaces: Theoretical Considerations and Historical Experience. J Mater Sci 39: 5887-5904.
- WG Fahrenholtz, GE Hilmas, AL Chamberlain, JW Zimmermann (2004) Processing and characterization of ZrB2-based ultra-high temperature monolithic and fibrous monolithic ceramics. J Mater Sci 39: 5951-5957.
- R Borrelli, A Riccio, D Tescione, R Gardi, G Marino (2010) Numerical/experimental correlation of a plasma wind tunnel test on a UHTC-made nose cap of a reentry vehicle. J Aerospace Eng 23: 309-316.
- TH Squire, J Marschall (2010) Material property requirements for analysis and design of UHTC components in hypersonic applications. J Eur Ceram Soci 30: 2239-2251.
- DJ Thomas (2002) Design and analysis of UHTC leading edge attachment. NASA/CR-2002-211505.
- T Kowalski, K Buesking, P Kolodziej, J Bull (1996) A thermostructural analysis of a diboride composite leading edge. NASA TM 110407.
- WG Fahrenholtz (2005) The ZrB2 volatility diagram. J Am Ceram Soc 88: 3509-3512.
- TA Parthasarathy, RA Rapp, MM Opeka, RJ Kerans (2007) A model for the oxidaiton of ZrB2, HfB2 and TiB2. Acta Materialia 55: 5999-6010.
- WG Fahrenholtz (2007) Thermodynamic analysis of ZrB2-SiC oxidation: Formation of a SiC-depleted region. J Am Ceram Soc 90: 143-148.
- CM Carney, P Mogilevsky, TA Parthasarathy (2009) Oxidation behavior of zirconium diboride silicon carbide produced by the spark plasma sintering method. J Am Ceram Soc 92: 2046-2052.
- A Rezaie, WG Fahrenholtz, GE Hilmas (2007) Evolution of structure during the oxidation of zirconium diboride-silicon carbide in air up to 1500 ℃. J Eur Ceram Soci 27: 2495-2501.
- R Savino, M De S Fumo, D Paterna, DM Andrea (2010) Arc-Jet testing of ultra-high-temperature-ceramics. The Open Aerospace Engineering Journal 3: 20-31.
- F Monteverde, R Savino, M De S Fumob, A Di Maso (2010) Plasma wind tunnel testing of ultra-high temperature ZrB2-SiC composites under hypersonic re-entry conditions. Journal of the European Ceramic Society 30: 2313-2321.
- J Wei, LR Dharani, K Chandrashekhara, GE Hilmas, WG Fahrenholtz (2012) Modeling of Oxidation Effects on Heat Transfer Behavior of ZrB2 and ZrB2-SiC Ceramics at High Temperature. 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, Hawaii.
- (2011) Material Property Database (MPDB). JAHM Software.
- JB Wachtman, W Roger Cannon, M John Matthewson (1996) Mechanical Properties of Ceramics. John Wiley & Sons, Inc. New York.
Author Details
Jun Wei, Lokeswarappa R Dharani* and K Chandrashekhara
Department of Mechanical and Aerospace Engineering, Missouri University of Science & Technology, USA
Corresponding author
Dr. Lokeswarappa R. Dharani is a Curators' Distinguished Professor of Mechanical and Aerospace Engineering, Department of Mechanical and Aerospace Engineering, Missouri University of Science & Technology, Rolla, MO 65409-0050, USA, Tel: +1-573-341-6504, Fax: +1-573-341-4607.
Accepted: Augsut 06, 2018 | Published Online: Augsut 08, 2018
Citation: Wei J, Dharani LR, Chandrashekhara K (2018) Thermal and Mechanical Response of Inner Cone Sample of ZrB2-SiC Ceramic under Arc-Jet Conditions. Int J Astronaut Aeronautical Eng 3:016.
Copyright: © 2018 Wei J, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Under arc-jet test conditions, ZrB2-SiC ceramic will undergo high temperature oxidation and develop an external glassy layer (SiO2), zirconia sub-layer (ZrO2) and SiC-depleted diboride layer (ZrB2). This study relates to finite element modeling of the effects of oxidation on heat transfer and mechanical behavior of ZrB2-SiC ceramic under arc-jet test conditions. A steady-state heat transfer FE method was employed to conduct the heat transfer analysis to obtain the temperature distribution in the inner body of the cone. The surface thermal conditions available in the literature were used in the heat transfer analysis. The resulting temperature distribution in the inner body of the cone is then applied to the thermomechanical finite element analysis to calculate the thermal stress distribution. The results show that the oxide layers affect both thermal and mechanical response of the ZrB2-SiC ceramic under arc-jet high temperature test conditions. Due to the mismatch of material properties between the bulk ZrB2-SiC and its new products after oxidation, the outer oxide layers constrain the thermal deformation of the inner bulk ZrB2-SiC thereby putting it in compression and outside oxide layers in tension.
Keywords
Finite element, ZrB2-SiC ceramic, Oxidation, Arc-jet
Nomenclature
s: Slant height of the cone; H: Height of the cone; x: Distance from the tip of the cone; ρ: Density; c: Specific heat; k: Thermal conductivity; [D]: Elasticity matrix;α: Coefficient of thermal expansion; T: Temperature; t: Time; r: Polar axis; z: Longitudinal axis; σ: Stress vector; ε: Strain vector; q: Heat flux; h: Surface film coefficient; T0: Sink temperature; p: Porosity; E: Young's modulus; E0: Young's modulus at p = 0; β: Nielson shape factor
Introduction
Experiments show that thermal protection materials on hypersonic aerospace vehicles are exposed to very high temperatures (1500 ℃ and above) [1]. Ultra-High-Temperature Ceramics (UHTCs) such as zirconium and hafnium diborides (ZrB2 and HfB2) have been proposed as candidate materials for such applications. These materials are chemically and physically stable above 1600 ℃ and have high melting points [2]. Among the UHTCs considered so far, ZrB2 has the lowest theoretical density and lower costs, which is attractive for aerospace applications [3]. Even with excellent oxidation resistance, the high temperature exposure of solid zirconium boride (ZrB2 (s)) to air will result in its oxidation to solid ZrO2 (s) and liquid boria (B2O3 (l)). The oxidation resistance of ZrB2 (s) can be improved by adding SiC (s) to promote the formation of a silica-rich scale. Therefore, the behavior of ZrB2-SiC ceramics in the application of hypersonic vehicles is of interest to the aerospace community [1,4-7].
At temperatures above 1100 ℃, SiC (s) oxidizes by reaction to form liquid SiO2 (l) which has low volatility, higher melting point and viscosity compared to liquid B2O3 (l) [8,9]. In summary, the oxidation of ZrB2-SiC ceramic at moderately high temperature in air results in two new products, solid ZrO2 and liquid B2O3 while at high temperature results in two new products, solid ZrO2 and liquid SiO2 [3,10-12]. A SiC-depleted diboride layer was observed as well for the ZrB2-SiC ceramic in high temperature environment [10].
Savino, et al. [1,13] and Monteverde, et al. [14] conducted arc-jet tests on three models of zirconium diboride and silicon carbide ceramic (ZrB2-20 vol% SiC) with different geometries including a rounded wedge, a small hemisphere and a cone with a small nose radius. They [1,13,14] presented experimental data for all the above three configurations. However, the results for the cone sample were relatively more complete. Therefore, the cone sample configuration is considered for calibration and modeling work in this paper. Figure 1 shows the cone sample with dimensions. Stagnation-point temperatures and spectral emissivity were directly measured during the tests using an optical pyrometer. A computational fluid-dynamics (CFD) simulation was performed considering the interaction between the fluid and the solid. The distribution of the surface temperature, wall heat flux, and shear stress for the solid were predicted. The distribution of the surface temperature and surface heat flux along the slant height, s, of the cone with normalized coordinate (x/H) are shown in Figure 2, where H is the height of the cone and x is the distance from the tip of the cone. A microstructure analysis [14] was carried out to observe the features of the oxidized layers such as external glassy layer (SiO2), zirconia sub-layer (ZrO2) and SiC-depleted diboride layer (ZrB2).
The material and geometric changes from the original ZrB2-SiC ceramic after the oxidation at high temperature affect the heat transfer and the mechanical response. The effect of high temperature oxidation on the heat transfer and mechanical behavior of ZrB2-SiC needs to be understood before these materials can be effectively deployed in hypersonic space vehicle structures [2,3]. To conduct heat transfer and mechanical analysis, the thermal and mechanical properties of ZrB2-SiC ceramic and its new oxide products namely solid ZrO2 and liquid SiO2 should be known a priori.
This study relates to a finite element (FE) modeling of oxidation effects on heat transfer and mechanical behavior of ZrB2-SiC ceramic under arc-jet test conditions. A steady-state heat transfer finite element analysis (FEA) was employed to conduct the thermal analysis to obtain the temperature distribution in the inner body of the cone using surface thermal conditions available in the reference literatures [1,13,14]. The resulting temperature distribution in the inner body of the cone is then applied to a FE thermomechanical analysis to calculate the thermal stress distribution. Temperature and thermal stress distributions in the cone sample are presented. This in turn, will facilitate a better understanding of oxidation effects on heat transfer and mechanical behavior of ZrB2-SiC ceramic after oxidation under arc-jet test conditions. The procedure presented in this study can be extended to analyze wing leading-edge geometry of re-entry air-vehicle under high temperature environment.
Calibration of the Temperature Boundary Condition
As mentioned earlier, Savino, et al. [1,13] and Monteverde, et al. [14] performed a CFD analysis and provided the temperature and heat flux distributions on the cone surface. The authors did not present the temperature distribution in the inerior of the cone body nor did they conduct any thermal stress analysis. In this study the thermal surface condition shown in Figure 2 will be used in the finite element analysis to obtain the temperature distribution and the thermal stress distribution in the inner cone specimen accounting for the oxidation and pore effects. Since the temperature boundary conditions are not given by Savino, et al. [1,13] and Monteverde, et al. [14], the calibration for the temperature boundrary condition is conducted first using the geometry, the properties (ZrB2-20 vol% SiC without oxide layer) and the thermal conditions (heat flux distribution shown in Figure 2) used by the authors [1,13,14]. Then, using the calibrated temperature boundary conditions, a steady state heat transfer analysis and a thermal stress analysis are performed for the same cone sample geometry but now consisting of multiple oxide layers. The calibration model and the flow diagram for calibration procedure are shown in Figure 3a and Figure 3b, respectively. Two-dimensional (2D) axisymmetric model (pseudo-3D) is used in this study. With applied heat flux shown in Figure 2, the sink temperature and surface film coefficient at the bottom of the specimen support structure are adjusted. With each set of the sink temperature and surface film coefficient, the resulting surface temperature is checked to see if it approaches the given surface temperature distribution (given in Figure 2). If it does, then, the calibration stops otherwise it will continue as shown in the calibration loop. This procedure is really a trial and error method that employs the available data in the literature [1,13,14] to calibrate the sink temperature and the surafce film coefficient at the bottom of the specimen support structure. The final calibrated sink temperature at the bottom of the cone support is 993 K and the corresponding surface film coefficient is 1.2 × 10-4 Wmm-2K-1. Figure 4 shows the final temperature distributions from the simulation along with the reference temperature distribution [1,13,14] which is same as shown in Figure 2. The difference between the two is small considering the errors and approximations inherent in CFD and FEA. There may also be some uncertainties in the arc-jet experimental test data. Since the difference between the two distributions is small, the calibrated thermal boundary conditions above will be used in the thermal and mechanical modeling to follow.
For a given specimen, the heat flux surface distribution given in [1,13,14] was employed to calculate the temperature and the thermal stress distributions inside the cone specimen. The temperature dependent thermal and mechanical properties were used in the FEA codes. The temperature distribution at the specimen surface was calculated to verify the current model by comparing it with that given by Savino, et al. and Monteverde, et al. [1,13,14]. It is seen that there is a good agreement between the current solid mechanics based FEA model and the CFD model [1,13,14]. The material properties used in this research are all temperature dependent. Since the temperatures are time dependent [1,13,14], to that extent, the material parameters used in this study are time dependent.
Model for Cone Sample after Oxidation
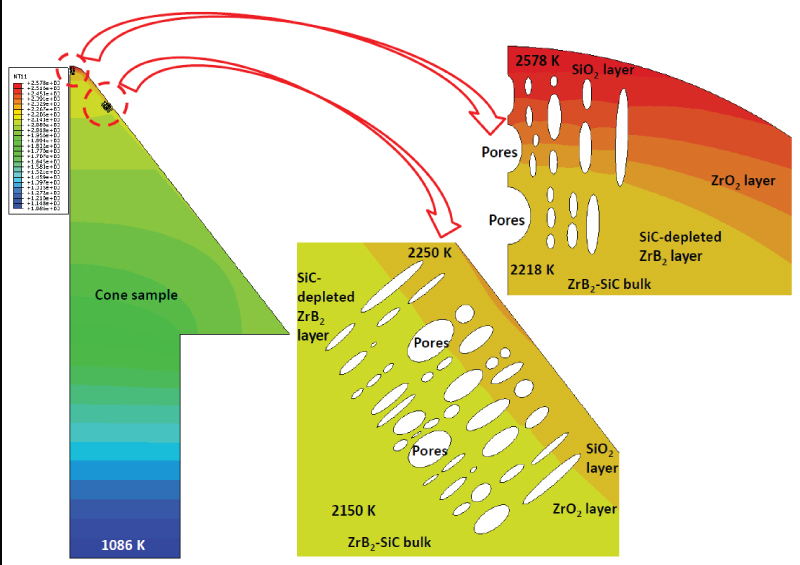
This section will describe a model for ZrB2-SiC ceramic after oxidation under arc-jet test conditions. As mentioned above, the oxidation of ZrB2-SiC ceramic at high temperature results in new products of external glassy layer (SiO2), zirconia sub-layer (ZrO2) and SiC-depleted diboride layer (ZrB2) [1,10,13,14]. The SEM images of the cross-section of a ZrB2-SiC cone sample after oxidation under arc-jet test conditions were shown by Monteverde, et al. [14] for the tip area and the lateral area of the cone. At the cone tip, the external SiO2 layer is about 19 μm, ZrO2 layer is about 101 μm, and SiC-depleted ZrB2 layer is about 70 mm, respectively. The entire thickness of the reaction oxide layer was observed to vary from 50 to 190 μm. The SiC-depleted ZrB2 layer decreases from 70 μm at tip to 0 μm at approximately x/H = 0.75, where H is the height of the cone and x is the distance from the tip. A FE model of the multiple oxide layers was created for the cone sample geometry based on SEM observations [14] shown in Figure 5 in which each shade indicates a different temperature dependent property. The label numbers and thicknesses in Figure 5 correspond to those in reference [14].
The heat conduction equation for axisymmetric problem can be expressed as
Where ρ is the density, c is the specific heat, and k is the thermal conductivity. The thermoelastic model is given by eq. (2),
Where [D] is the elasticity matrix , α is the coefficient of thermal expansion, and T is the temperature. The heat flux condition is
Where q is the heat flux, h is the surface film coefficient, and T0 is the sink temperature. To solve the heat transfer and thermoelastic problem, the temperature dependence of the material properties for solid ZrB2-SiC ceramic and its new products are needed. The properties needed for the analyses are density, specific heat, thermal conductivity, elastic constants and coefficient of thermal expansion.
Most of the temperature dependence of the thermal and mechanical properties of the solid phase can be found in the literature or in databases [15,16]. However, the thermal conductivity and elastic constants of liquid phases of SiO2 is not readily available. A model for the temperature dependence of thermal conductivity of liquid SiO2 was developed by the authors [15] in an earlier work.
It should be noted that the oxidation results in the depletion of SiC and increased porosity to form a SiC-depleted ZrB2 layer as shown in reference [14]. In the absence of any quantitative data, it is reasonable to assume that SiC-depleted ZrB2 layer has a porosity of 0.2 for the 20 vol% SiC addition [14]. All the properties were reduced using the rule of mixture with the exception of the Young's modulus, which uses the Nielson's equation [17] given by
Where p is the porosity, E0 the Young's modulus at p = 0, the Nielson shape factor β = 0.4.
Results and Discussions
Two separate FE models are developed: one for the heat transfer analysis and the other for the thermal stress analysis. The details of the heat transfer analysis and thermal stress analysis models are presented next.
For the heat transfer analysis, the heat flux shown in Figure 2 is applied on the cone surface with the calibrated temperature boundary conditions shown in Figure 3a. The calibration (simulation) model consisted of cone body entirely made of ZrB2-20 vol% SiC. Unlike the calibration model, the cone body now consists of ZrB2-20 vol% SiC ceramic including multiple oxide layers of external glassy layer (SiO2), zirconia sub-layer (ZrO2) and SiC-depleted diboride layer (ZrB2) as shown in Figure 5. Based on the experimental observation by Monteverde, et al. [14], both zirconia sub-layer (ZrO2) and SiC-depleted diboride layer (ZrB2) contain pores. The zirconia layer has columnar microstructures with a series of columns that grow outward from the ceramic surface.
To simulate the columnar microstructure and the pores in the zirconia and SiC-depleted diboride layers, the pores in the sample are represented by a set of arbitrarily distributed three dimensional voids (pores) within the material. A full-blown 3-D model with randomly shaped 3-D pores becomes computationally prohibitive. To simplify the problem, the axial symmetry is assumed as the cone axisymmetric at macroscopic scale. This assumption may lead to some errors in the physical and mechanical results in the circumference direction. However, the distributions of the temperature and the thermal stresses in the radius direction and along the slant height direction should be quite representative of the physical problem. This observation is based on the figures in the literature of [1,13,14] where the cross-sectioned of SEM micrograph and distribution of the surface temperature and the surface heat flux are all shown in the radius and along the slant height directions. In the two-dimensional axisymmetric model, the voids of different shapes that are arbitrarily distributed in the layer as shown in Figure 6. For the current simulation, the major axis is varied between 6.6 μm and 95 μm while the aspect ratio (major to minor axis) varied between 1 and 7.7. To make the problem computationally tractable, the area being modeled is partitioned in to two sub-areas, heterogeneous and homogeneous. The heterogeneous area consists of artificial ellipses so that temperature and stress distributions around pores can be obtained. The homogeneous area consists of the parent solid material without pores. The columnar microstructure is assumed to behave as a transversely isotropic material similar to a transversely isotropic composite material.
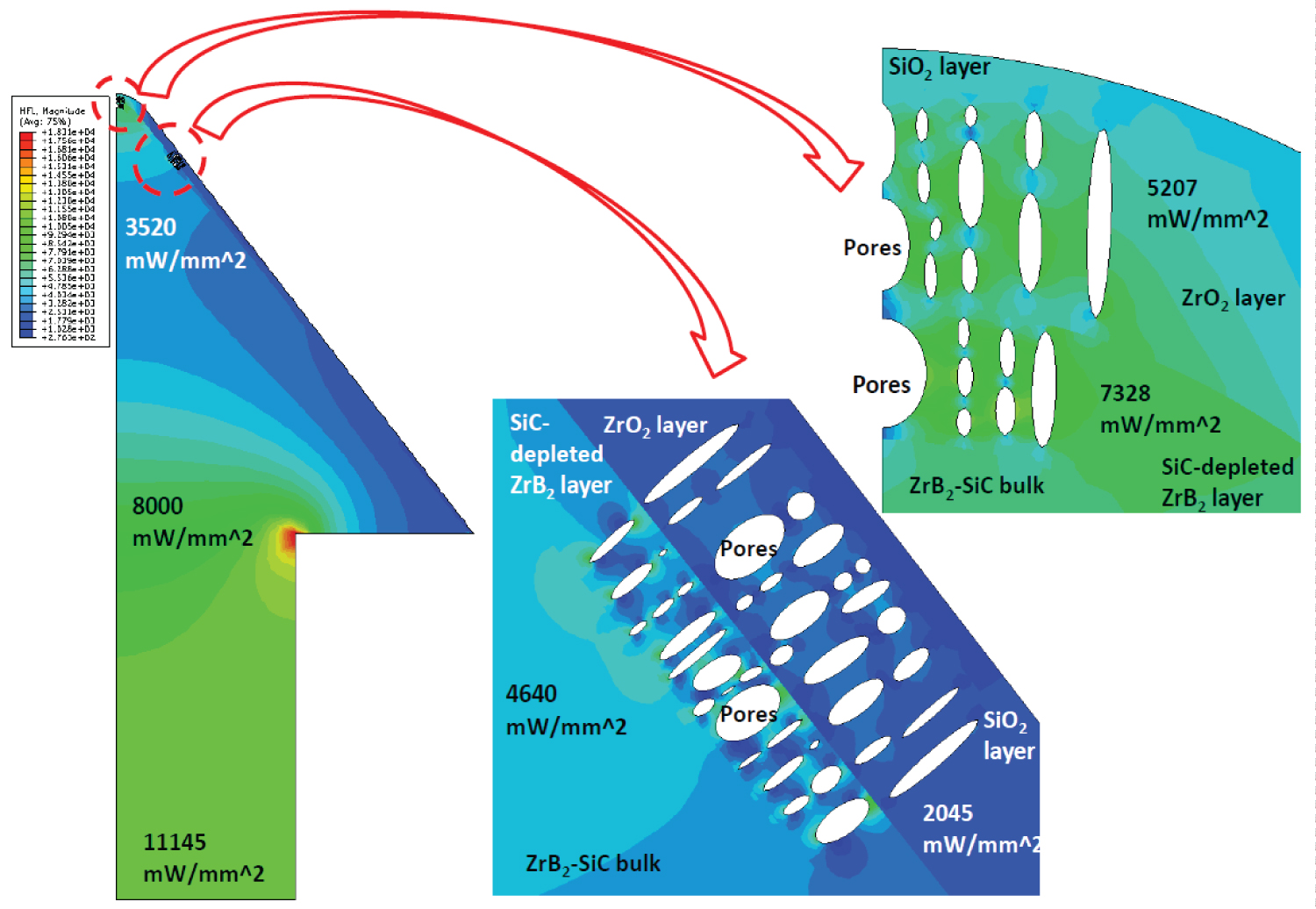
With the applied heat flux on the cone surface the temperature and heat flux distributions in the cone sample are obtained and shown in Figure 7 and Figure 8, respectively. It is seen that the temperature distribution is continuous while the heat flux distribution has concentration at the ellipse and the re-entrant corner of the cone sample due to the heterogeneous of geometry and material properties. Referring to Figure 7, the temperature in the external glassy SiO2 layer ranges from 2218 K to 2578 K at the cone tip while it ranges from 2150 K to 2250 K at the slant surface. The temperature in the bulk ZrB2-SiC ranges from 1086 K to 2218 K. The temperature (1086 K) at the bottom surface of bulk ZrB2-SiC, is higher than the sink temperature of 993 K due to the surface film coefficient effect.
Distribution of the surface temperature along the slant height, s, of the cone with multiple oxide layers is presented in Figure 9 as a function of normalized coordinate (x/H, ratio of the distance from the tip over cone height). For comparison, the temperature distribution at the same location obtained by Monteverde, et al. [14] via CFD is also shown in the Figure 9 and is indicated by "single oxide layer". The temperature at the tip of the cone model with oxide layers is 2589 K and deceases gradually to 2106 K at the bottom surface. There is a steep temperature gradient near the tip and a discontinuity due to the effect of the pores. In their simulation, Monteverde, et al. [14], a single oxide layer of 100 micron thickness with temperature independent thermal conductivity of 1 W/mK was used. The temperature decreased from 2750 K to 2050 K. The difference between the two results may be attributed to differences in the simulation models (CFD and FEA), geometry (single oxide layer versus multiple oxide layers) and material properties (temperature independent versus temperature dependent material properties). In particular, it is interesting to note that the temperatures at tip of the cone are 2750 K and 2589 K for single oxide layer and multiple oxide layers, respectively. The temperature at the same point without any oxide layer is 2309 K (Figure 4). The results clearly show that the oxide layers indeed affect the heat transfer behavior.
Figure 10 shows the principal stress distribution in the cone body. The highest maximum principal stress of 5913 MPa occurs at a pore (ellipse) tip in the SiC-depleted diboride layer (ZrB2) of the tip portion. The far-field stress in this layer is about 1495 MPa. The corresponding stresses in the zirconia sub-layer (ZrO2) in the cone tip region are 1662 MPa at one pore tip and from 303 to 458 MPa for the far-field stress, respectively. The stress in the ZrB2-SiC matrix in the tip is compressive 266 MPa. The stress concentration is 5503 MPa at a pore tip in the pore area of the SiC-depleted diboride layer in the mid region and the far-field stress is 1670 MPa. The stress concentration is 2432 MPa at a pore tip in the pore area in the zirconia layer and the far-field stress is 540 MPa. The external glassy layer (SiO2) has a stress of 505 MPa near the pore area, which is much higher than the far-field stress. This increase in stress in the external glassy layer is due to the reduction in the stiffness of the SiC-depleted diboride and zirconia layers caused by the pores. The outer oxide layers constrain the thermal deformation of the inner ZrB2-SiC bulk at high temperature to put the inner ZrB2-SiC bulk in compression and outer oxide layers in tension.
Conclusion
This study uses the given thermal surface condition available in the literatue to conduct a finite element analysis to obtain temperature and the thermal stress distributions in a conical sample under a simulated arc-jet test condition. The main thrust of the study is to undersatnd the effects of high temperature oxidation and subsequent porosity formation on the thermal and mechanical response. A calibration is first conducted to obtain the applicable thermal boundrary conditions. Then, using these calibrated boundary conditions, a steady state heat transfer analysis and a thermal stress analysis is conducted. The model accounts for multiple oxide layers and porosity in the cone sample. The results show that the oxide layers and the porosity affect both the thermal and mechanical responses of the ZrB2-SiC ceramic under arc-jet high test conditions. Due to the mismatch of material properties between the ZrB2-SiC bulk and its new oxidation products, the outer oxide layers constrain the thermal deformation of the inner bulk ZrB2-SiC of the cone sample and thereby putting it (ZrB2-SiC) in compression and the outer oxide layers (SiO2) in tension. The porosity reduces the effective stiffness of the outer oxide layers and as a result reduces the stresses in the cone body. The stress concentrations occur at the pore tips in the pore area due to the geometry heterogeneity.
Acknowledgements
This project was funded under subcontract 10-S568-0094-01-C1 through the Universal Technology Corporation under prime contract number FA8650-05-D-5807. The authors are grateful for the technical support on the program by the Air Force Research Laboratory, and specifically to Dr. Mike Cinibulk at AFRL for both his collaboration and guidance. The authors thank their colleagues Dr. William Fahrenholtz and Dr. Greg Hilmas for their suggestions and help.