International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 5, Issue 1
Original Article
DOI: 10.35840/2631-5009/7534
Dynamical Model of a Controlled Parawing for Drop Tests Trajectory Reconstruction
C Bettanini1*, M Bartolomei1, A Aboudan2 and G Colombatti2
Table of Content
Figures
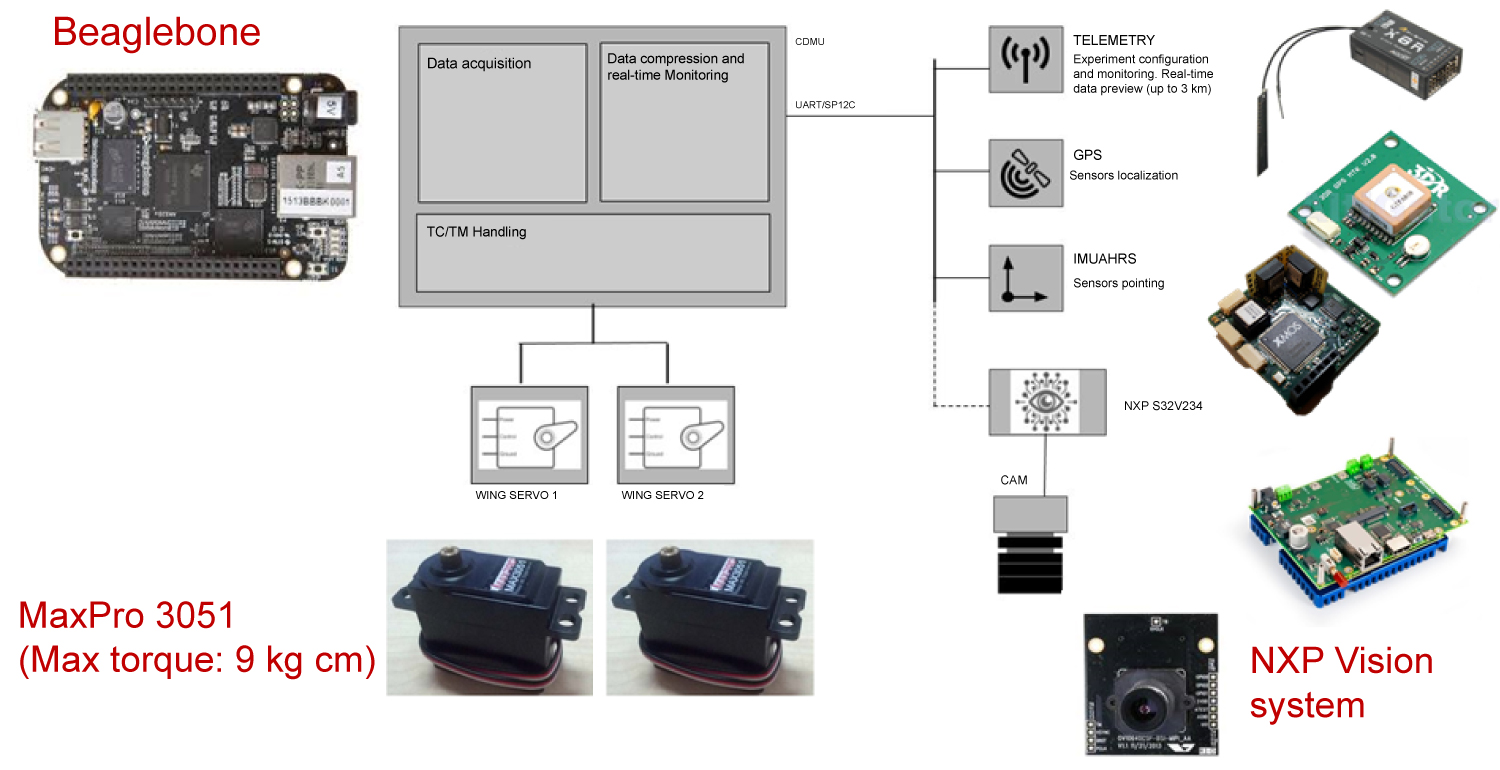
Figure 1: Electronic architecture of the prototype....
Electronic architecture of the prototype parawing.

Figure 2: Safe UAV payload for reduced wing drop test.....
Safe UAV payload for reduced wing drop test (above) and detail of the electronic compartment (below).

Figure 3: Flight chain of the drop tests (left), image.....
Flight chain of the drop tests (left), image of the drone carrying the payload to the desired release altitude (centre) and controlled descent (right).
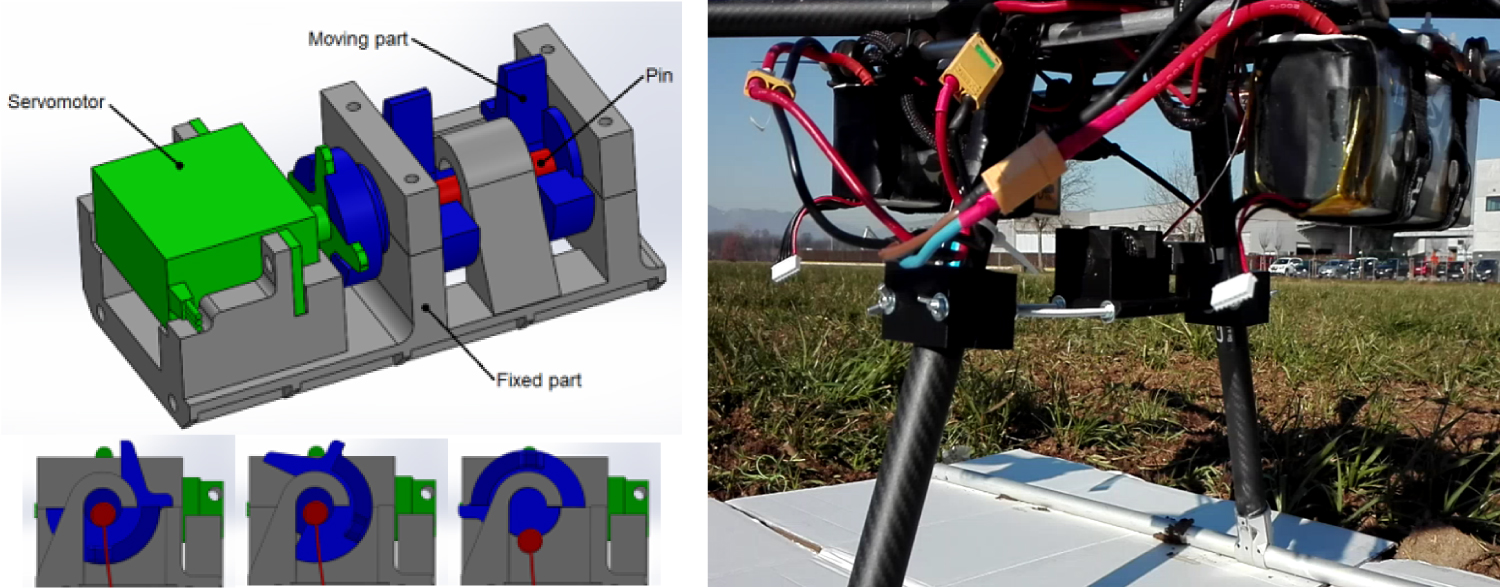
Figure 4: Safe UAV release mechanism in place under the....
Safe UAV release mechanism in place under the drone (left) and 3D impression of the release mechanism and its activation (right).
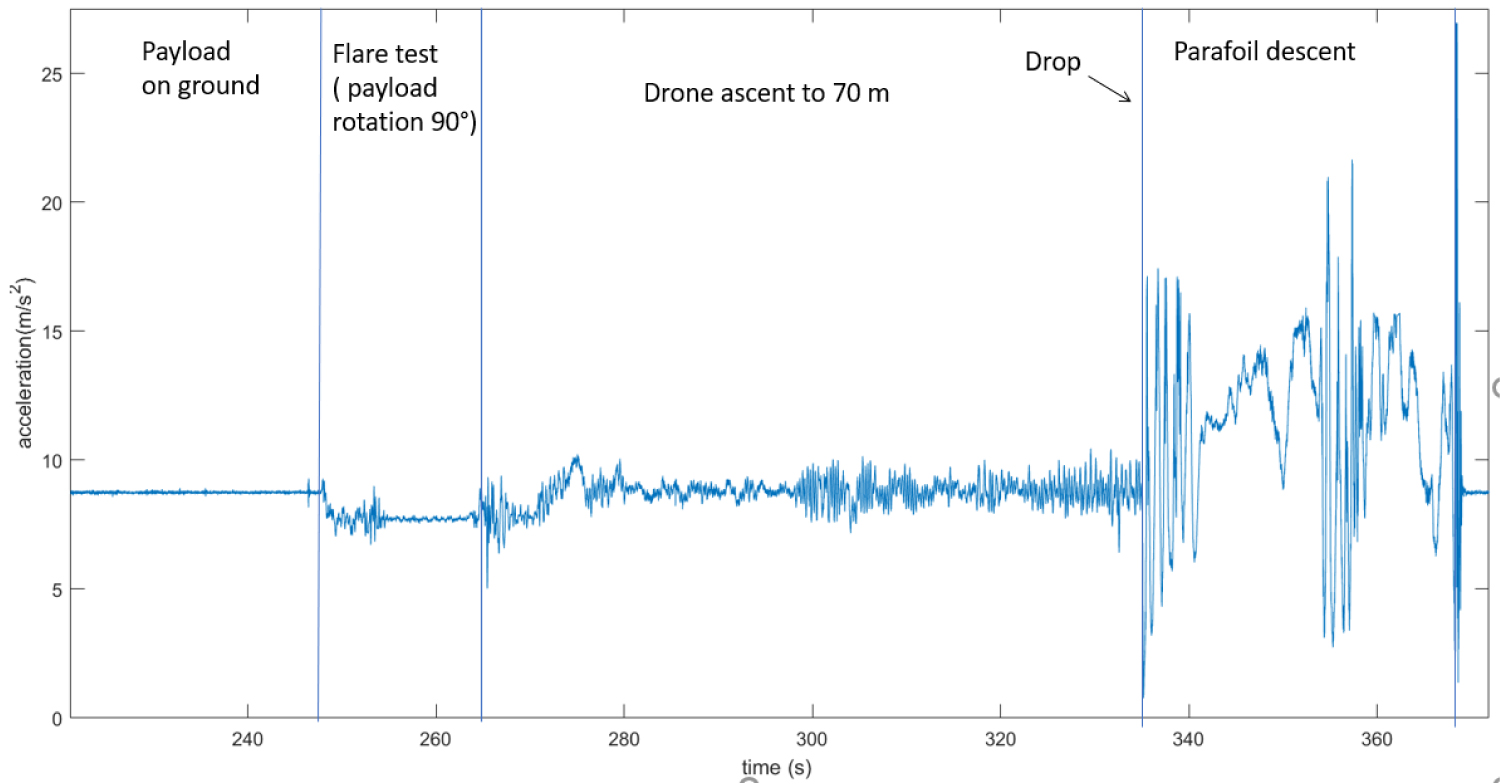
Figure 6: Measured module of accelerations in test.....
Measured module of accelerations in test flight number 7.
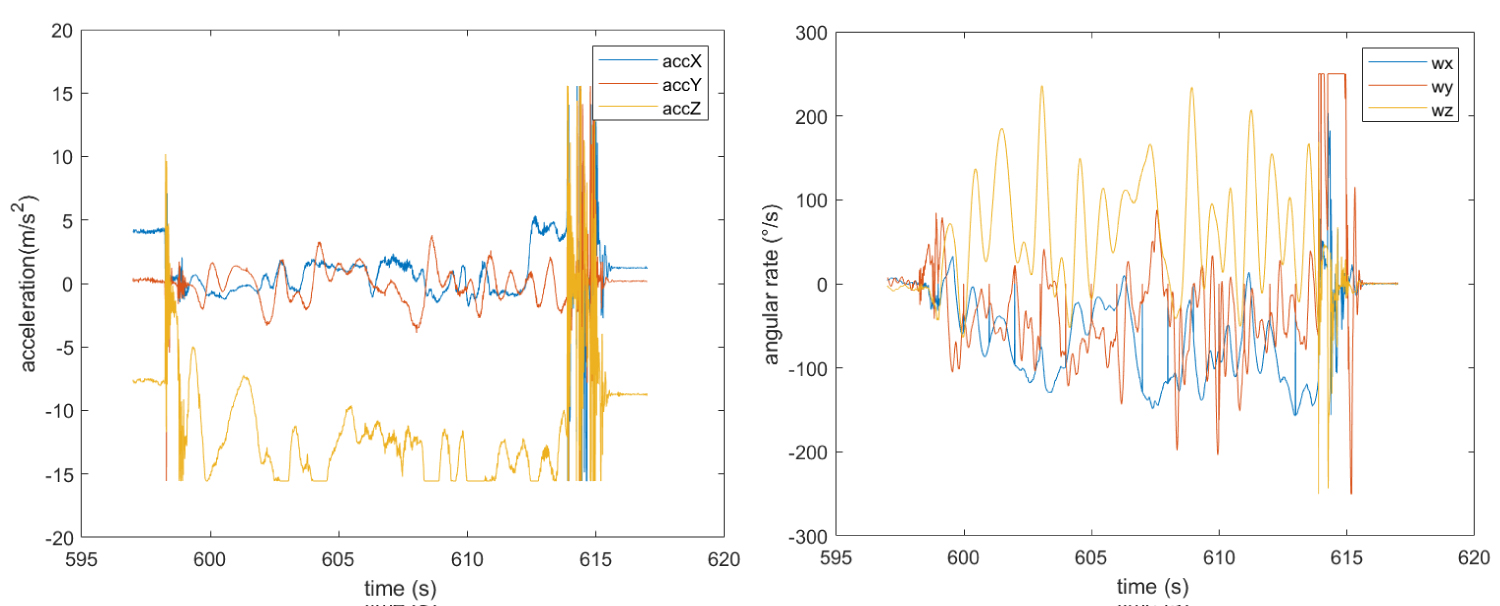
Figure 8: Recorded acceleration and angular rate data during....
Recorded acceleration and angular rate data during descent phase of test flight number 5.
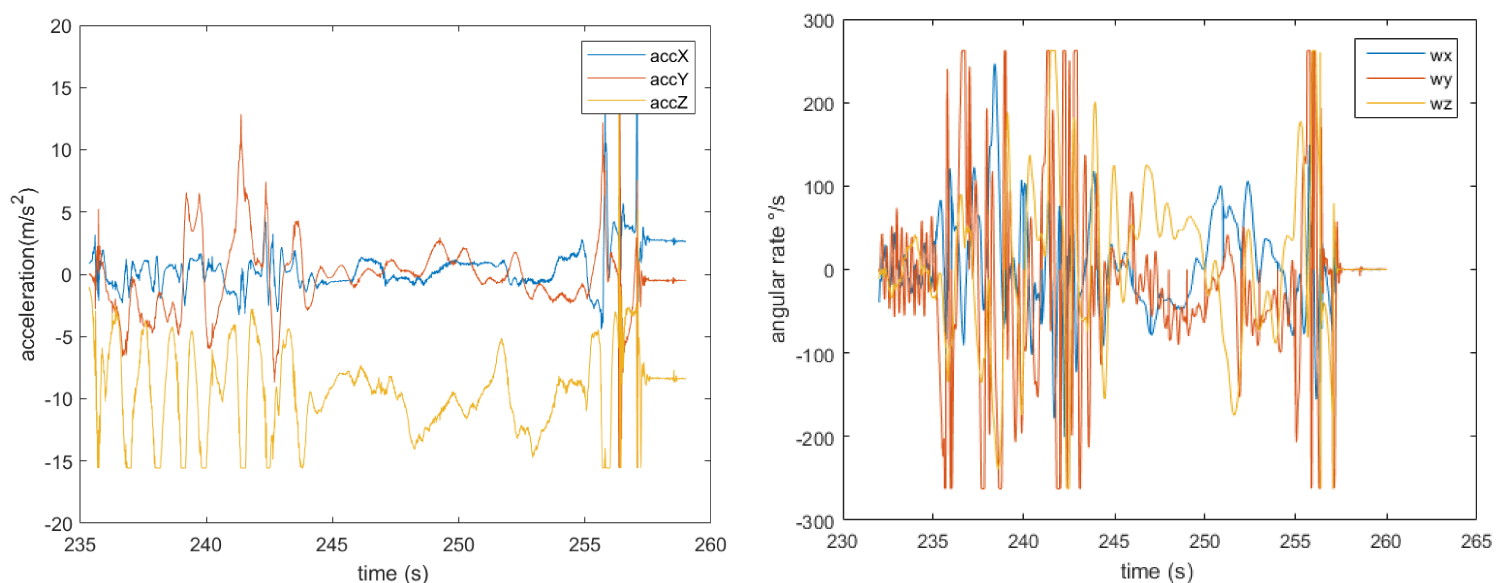
Figure 9: Recorded acceleration and angular rate data during ...
Recorded acceleration and angular rate data during descent phase of test flight number 6.
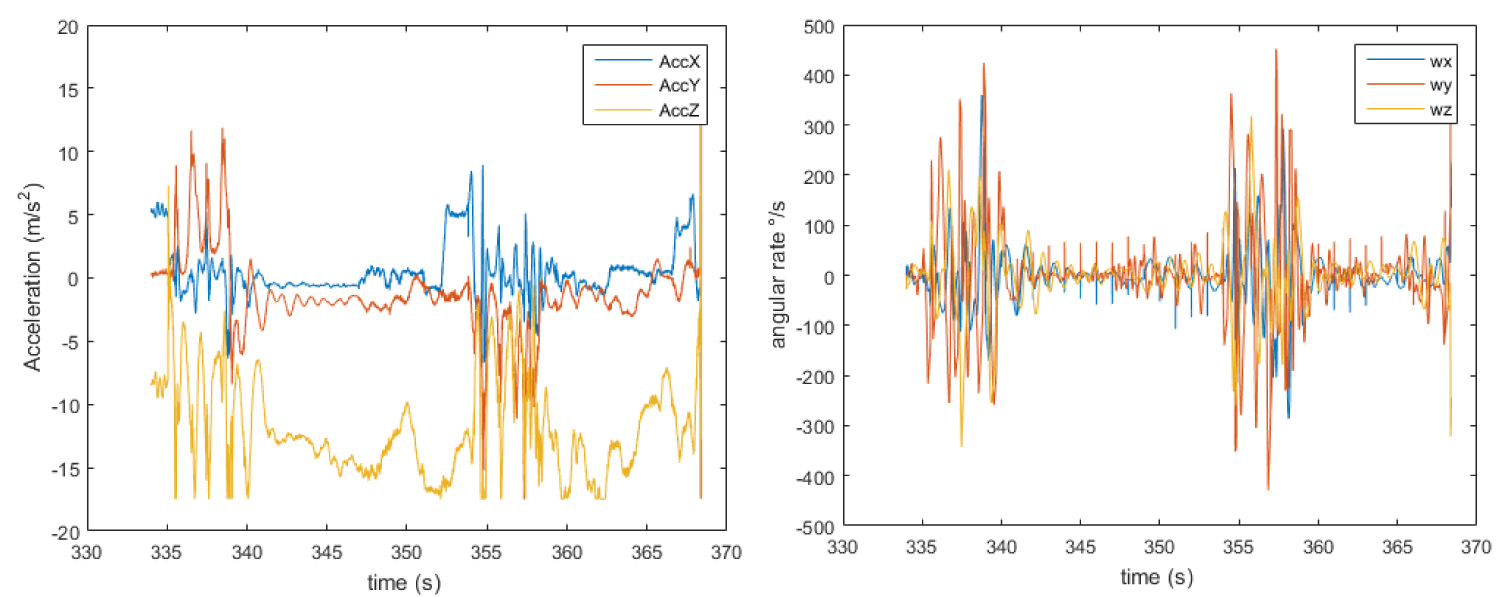
Figure 10: Recorded acceleration and angular rate data during...
Recorded acceleration and angular rate data during descent phase of test flight number 7.
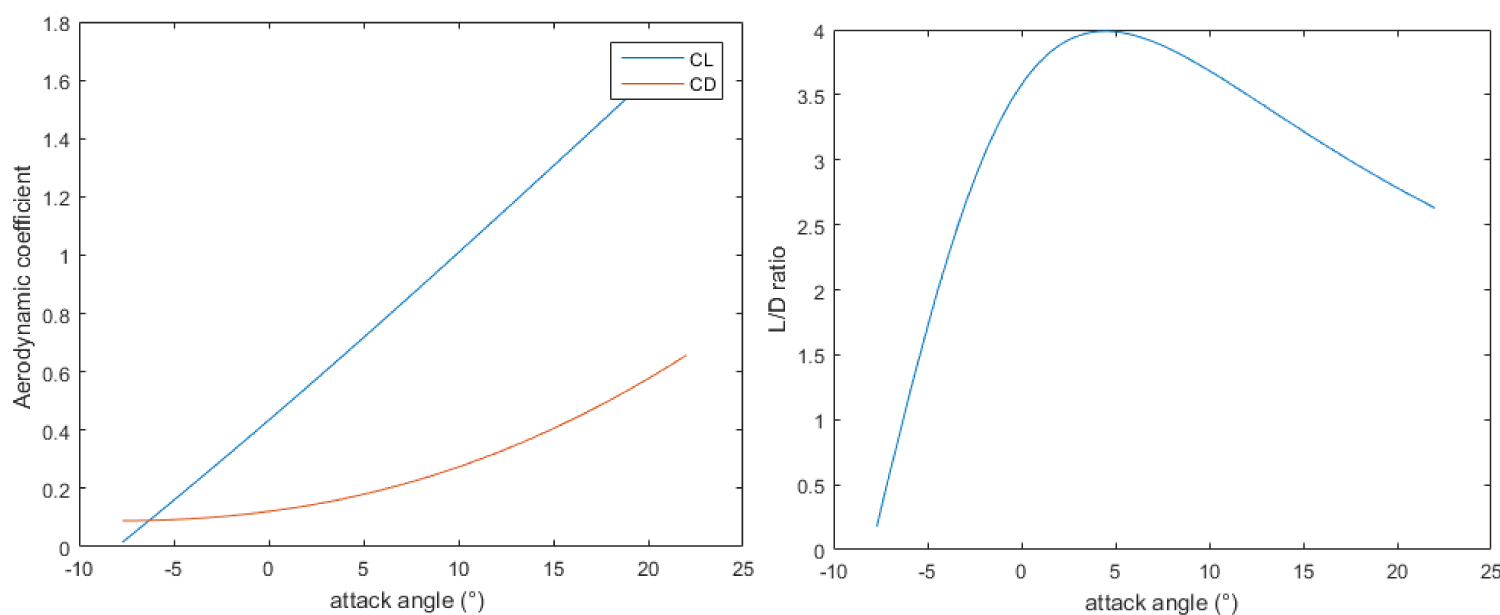
Figure 11: Calculated aerodynamic coefficients (left)....
Calculated aerodynamic coefficients (left) and L/D ratio (right) for the prototype parawing.
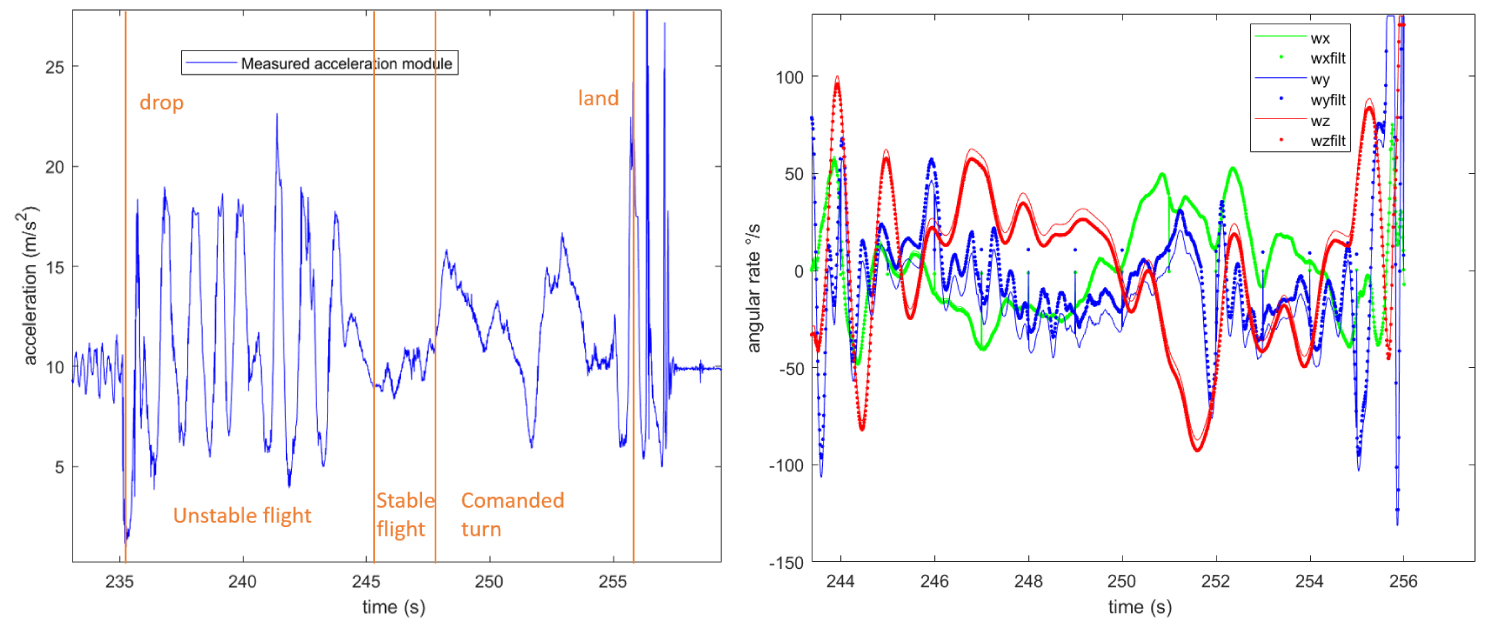
Figure 12: Acceleration module and filtered measures...
Acceleration module and filtered measures of rate gyros during stable part of descent.
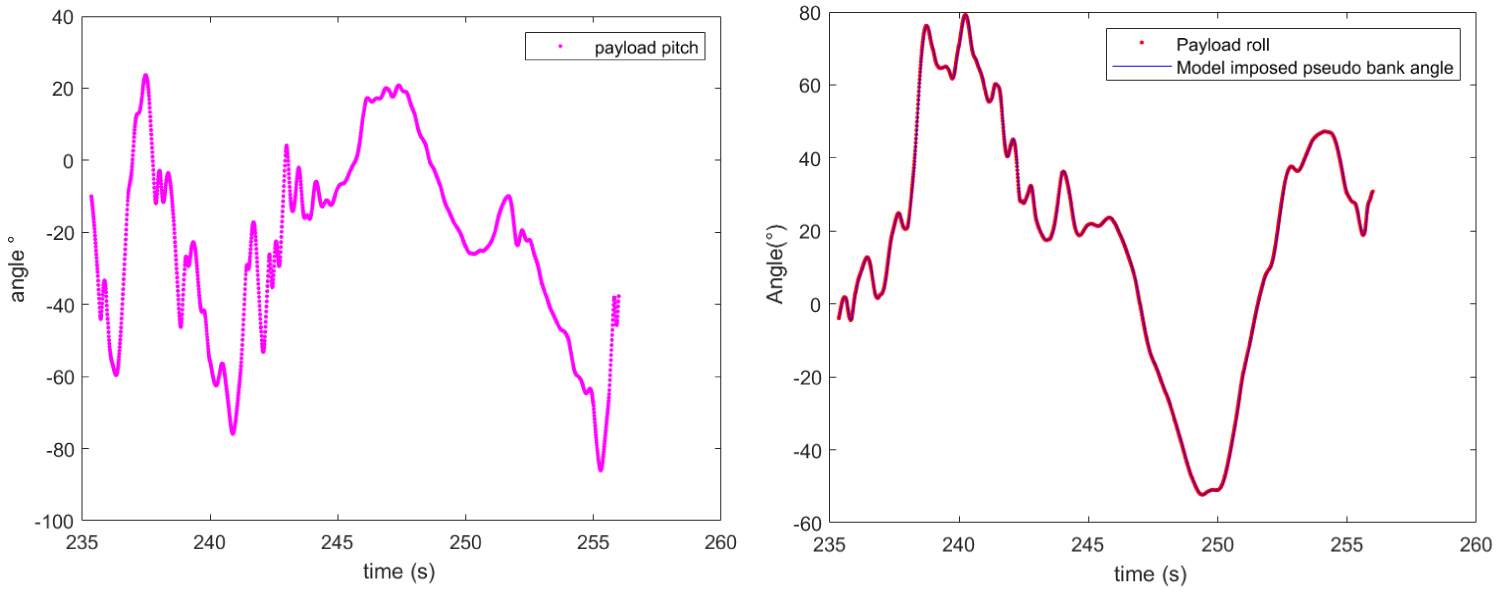
Figure 13: Reconstructed payload pitch angle profile (left)....
Reconstructed payload pitch angle profile (left) and payload roll and model-imposed pseudo bank angle (right).
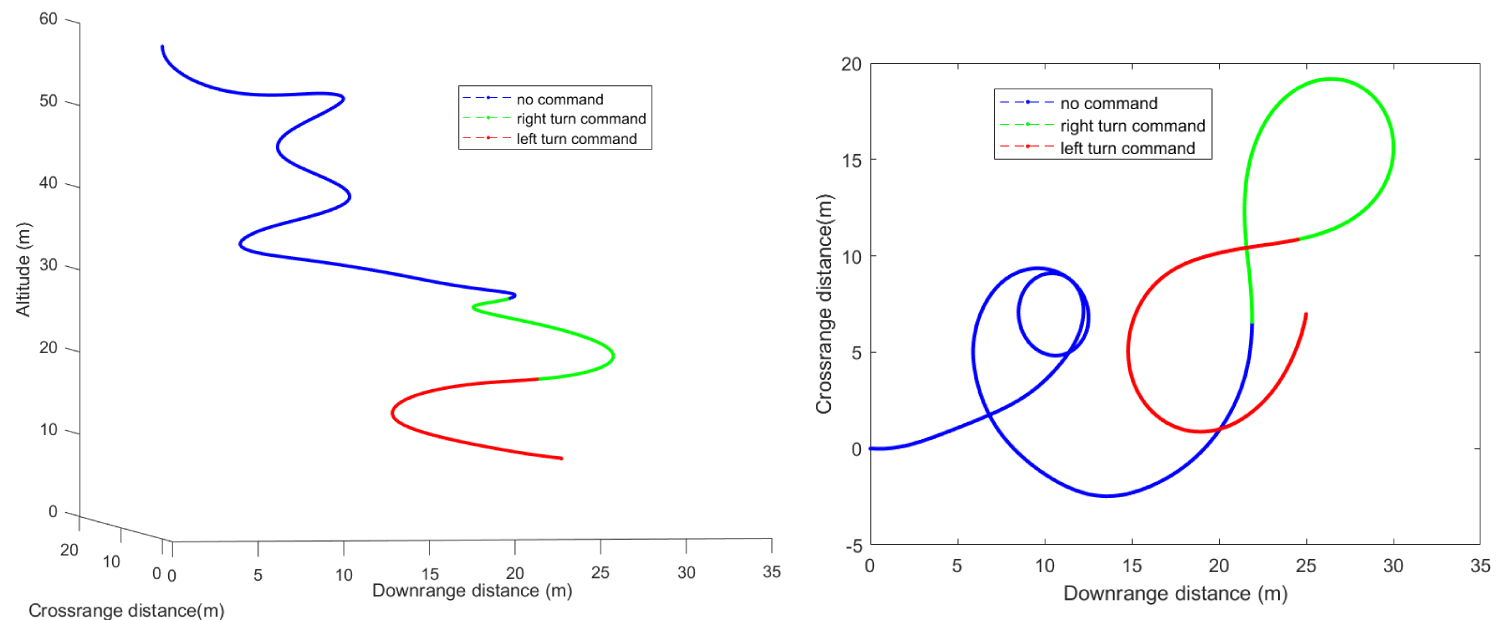
Figure 14: Calculated descent trajectory in NED reference....
Calculated descent trajectory in NED reference (left) and descent trajectory projection on N-E plane (right).
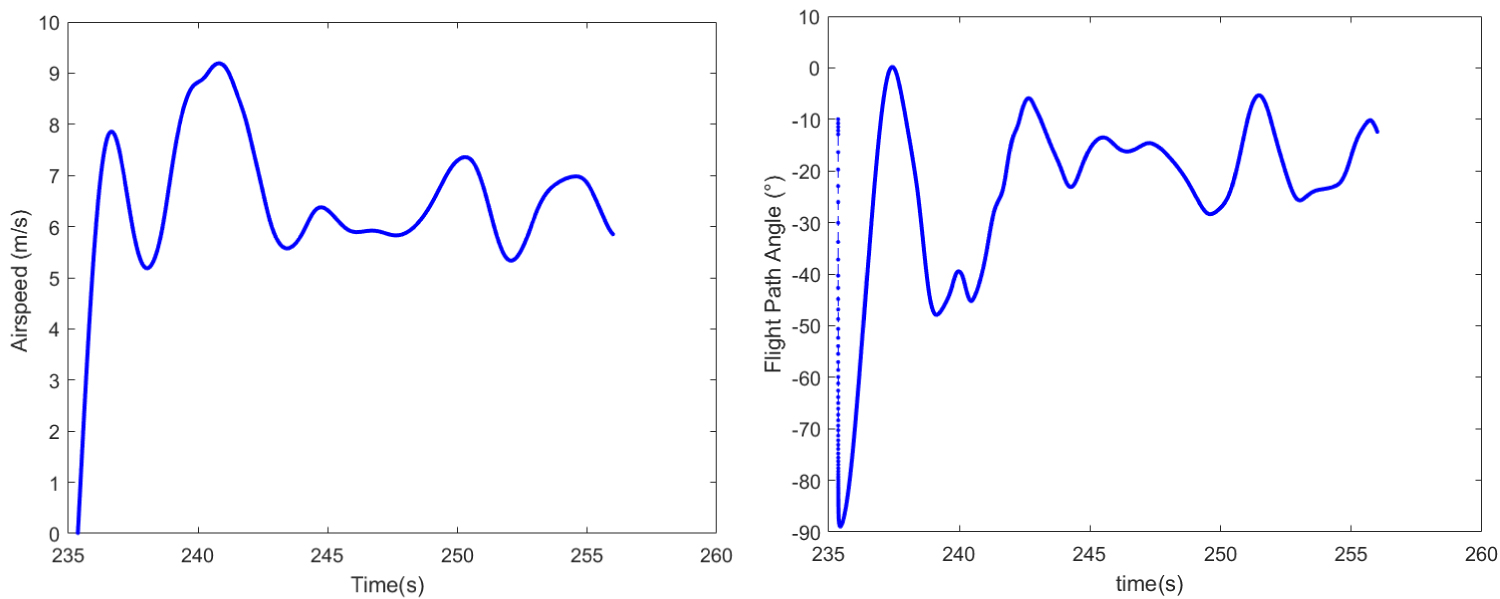
Figure 15: Calculated air speed (left) and flight....
Calculated air speed (left) and flight path angle (right).
References
- Drones for commercial application: The market for unmanned aerial vehicles (UAVs), OMDIA.
- Nicolaides JD, Tragarz MA (1970) Parawing flight performance. AIAA Aerodynamic Decelerator Systems Conference, USA, 14-16.
- Puskas E (1989) The Development of a 10,000 lb capacity ram air parachute. AIAA Aerodynamic Decelerator Systems, USA.
- Berland JC, Dunker S, George S, Barber J (2005) Development of a low cost 10,000 lb capacity ram-air parachute, dragonfly program. 18th AIAA Aerodynamic Decelerator Systems , USA.
- Bennett TW, Fox R (2003) Design, development & flight testing of the NASA X-38 7,500 ft^2 parawing recovery system. AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar, 60-77.
- David C, Sean G, Philip H, Leena S, Steven T (2005) Autonomous guidance, navigation, and control of large parawings.
- Jenny MS, Chris MM, Strahan AL (2005) An overview of the guided parawing system derived from X-38 experience. American Institute of Aeronautics and Astronautics, USA.
- Toglia C, Vendittelli M (2010) Modeling and motion analysis of autonomous paragliders. Sapienza University of Rome, Italy.
- Rademacher BJ (2009) In-flight trajectory planning and guidance for autonomous parafoils. Graduate Theses and Dissertations, 10597.
- Prakash OM (2004) Aerodynamics, longitudinal stability and glide performance of parawing/payload system. Department of Aerospace Engineering Indian Institute of Technology, India.
- Lingard JS (1981) The performance and design of ram-air parachutes. Royal Aircraft Establishment, UK.
Author Details
C Bettanini1*, M Bartolomei1, A Aboudan2 and G Colombatti2
1Department of Industrial Engineering, University of Padova, Italy
2CISAS - Center for Studies and Activities for Space "Giuseppe Colombo", University of Padova, Italy
Corresponding author
C Bettanini, Department of Industrial Engineering, University of Padova, via Venezia 1, Padova, Italy.
Accepted: May 13, 2020 | Published Online: May 15, 2020
Citation: Bettanini C, Bartolomei M, Aboudan A, Colombatti G (2020) Dynamical Model of a Controlled Parawing for Drop Tests Trajectory Reconstruction. Int J Astronaut Aeronautical Eng 5:034.
Copyright: © 2020 Bettanini C, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The work presents the first results of the research activity conducted at University of Padova to develop a remotely controlled parawing system designed to serve as emergency landing device for UAVs. A prototype of the designed system has successfully completed development and has undergone flight testing with airdrop campaigns from an octocopter drone. The prototype, comprising a reduced dimension parawing and flight systems based on commercial off the shelf units, has been carried at test altitude using a dedicated flight chain and released using a custom designed mechanism. Parawing can afterwards be controlled by pulling down the left or right trailing edge of the canopy with two custom designed actuators, activated by manually operated remote controls.
The parawing flight control system is based on a Beaglebone command and data management unit, commercial IMU and GPS sensors for attitude and trajectory data and servo motors for actuation of parawing's control lines.
A total of 10 drop test where conducted in a one-day test campaign and the data measured by on board sensors have been used to verify parawing control performance and to validate the dynamical model of the parawing, which is an 8 d.o.f. dynamical model.
A problem on GPS sensor prevented data utilization for descent trajectory reconstruction, so an integrated approach using IMU data elaboration and dynamical model simulation was implemented to reconstruct the descent profile. The system attitude during descent phases and simulation of commanded manoeuvres was qualitatively compared with images acquired from ground.
Keywords
Controlled parawing, Dynamical model, Release mechanism, Trajectory reconstruction
Introduction
In the last decades, an unprecedented development in on-board computers and sensors miniaturization has driven to the design of new autopilot systems for UAV (Unmanned Aerial Vehicles) with increased performance but lower total cost, thus expanding the range of users of commercial UAV from professionals to semi-professional and amateurs. Recent estimations in fact value the global size of commercial market for drones to step up to 1 mil units in 2021, while there will be around 2.5 mil drones sold in 2025 worldwide [1]. UAVs that are easier to fly may become an issue in the case of unit's subsystem critical malfunction, since smaller expertise is requested to pilots and no recovery action may be performed either due to lack of knowledge or because not authorised at user-side. Flight controllers have been therefore introducing new regulations not only to require a base skill for all UAV pilots but also to guarantee safety conditions during the "critical operations" (as an example imaging above crowded areas) in order to limit the risk of damages or injuries to humans.
The new EASA regulations for drone utilization in EU that will be effective from June 2020 divide UAV operations, whether commercial or recreational, based on the associated risk introducing low risk category ("open category"), medium risk category ("specific category") and high-risk operations. These last will remain in the (manned) aviation domain under the certified category while commercial drone operations will be possible in open category if they do not take place over or near people (30 m), otherwise will fall into the "specific category".
The operations of this last group need approval from National aviation authority and a risk assessment (SORA: Specific Operation Risk Assessment) must be carried out by the operator addressing air risk (the risk of a collision between the drone and another airspace user) and ground risk (the risk of collision of the drone with people, animals or objects on the ground).
If ground risk cannot be mitigated using low energy aircraft or establishing minimum distances with respect to the people on the ground, mitigation measures shall be implemented to protect bystanders on the ground.
Newly engineered failure recovery system shall be therefore taken into the game to cope with every kind of unexpected behaviour. Passive parachute systems are a low expensive solution already available on the market but considering increasing complexity (and cost) of on-board payloads for "scientific" UAVs the parachute system may be improved with controllability to guarantee safe landing and preserve the equipment.
An under estimated 2% of commercial drones (around 20.000 in 2021) [1] is used in "specific operations" linked to research and video survey and will need an on-board dedicated safety system, thus creating an important market for safety landing systems.
Safe UAV project started in late 2018 at Industrial Engineering Department with the objective to design and test a completely autonomous and controlled parawing flight system to be deployed in case of unrecoverable failure of UAVs. Parawings and in general the broader class of gliding parachutes differ from conventional parachute systems for the possibility to generate non-zero lift to drag (L/D) ratios (parawing can achieve lift-to-drag ratios from 1 to 5) and the glide performance coupled with some degree of turn control capability provides the ability to compensate for wind and potentially steer toward a desired landing site minimizing the drift.
The use of autonomously guided parawings for the delivery of quite massive payloads to a desired a target area was first considered in the 1960 and in the 1970's the U.S. Army National Research and Development Center began the development of technologies for autonomously guided parawing [2].
Lately the Draper Laboratories developed dedicated parawing systems [3,4] and collaborated to the Joint Precision Airdrop System (JPADS) program with the goal to develop an autonomous guidance, navigation and control system for precision airdrop capability of high payload capacity. NASA in parallel developed a controlled parachute system to test the technology for a Crew Return Vehicle for the International Space Station [5]. In Europe DLR developed a GNC system with a "T-Approach" guidance algorithm for the control of parawing guided cargos up to 6000 kg [6-8].
Due to complexity of realization and limited budget, it was not possible to address within Safe UAV project all aspects related with the development of an active parachute system.
Short term goals have been therefore limited and have focused on the design and realization of the prototype of the actuated parawing using COTS components and on testing it with a series of drops from an octocopter drone using a custom design release mechanism. Test data have been used to tune and validate a dynamical model of the actuated parawing and to investigate the efficiency of control strategies.
Future developments to be conducted later in the project will focus on the implementation of the flight termination system, investigating failure detection, parachute actuation and expulsion strategies.
Design of the Prototype Parawing
Lightweight and compact size before deployment along with better gliding and steering capability over conventional parachutes identified a parawing as the perfect candidate wing for the Safe UAV project. Among all available wing configurations, a 1.5 square meter NASA wing was chosen for the first flying prototype; the planform is trapezoidal with a chord-wise arc-anhedral profile and suspension lines are attached to the ribs at multiple points both span-wise and chord-wise to distribute the weight of the payload.
The lateral control of the system is achieved by an asymmetric deflection of external portions of the trailing edge of the canopy (outer quarters of the trailing edge) driven by one of the two custom designed actuators commanded by commercial Maxpro digital servo motors with 9 kg cm maximum torque. The deflected portions of the canopy (usually called "brakes") generate a small increase in lift and a large increase in drag on the commanded side, inducing a yaw moment rather than a roll moment as occurs on a conventional aircraft. The drag differential creates a sideslip angle generating the side-force which rolls the canopy into the turn and the adverse yaw moment due to yaw rate brings the system in a steady-state turn.
Longitudinal control is achieved by a symmetric deflection of the brakes commanding the same movement of the two actuators. The symmetric deflection of the brakes typically increases both lift and drag proportionately so that L/D changes very little, essentially resulting in a change in glide airspeed but no change in glide path angle. Same command with full deflection is used for the final flare manoeuvre when approaching ground.
In the first test flights the system has been programmed to use only yaw rate as the primary means of control and no longitudinal control has been commanded during the descent resulting in little or no ability to reduce the along-track trajectory tracking error.
The electronic architecture of the prototype is sketched in Figure 1. The command and Data Management Unit (CDMU) of the system is based on a Beaglebone running a custom developed application software based on Linux OS.
The data-acquisition is synchronous and triggered by the on-board timer; acquired data are correlated with the position retrieved by the GPS sensor and with attitude information provided from an Invensense MPU6050 unit (including three axial MEMS accelerometers and rate gyros). The CDMU can communicate with the ground by means of a commercial telemetry link sending in real-time quick-look data to check on board system configuration and evolution of the control strategy. All the acquired data are also stored on-board in a non-volatile memory for post processing on ground. Parawing control parameters and actuation can be configured either by the on-board software or by means of radio command from ground.
The digital hub of the CDMU may be connected to an imaging subsystem, which includes one NXP S32V234 vision processor board, collecting images from a nadir pointing camera. Processed data on obstacles in the camera FOV may be passed to CDMU for the elaboration of the lowest risk landing trajectory, but the implementation of an autonomous control strategy for obstacle avoidance is to date still in progress. Power for the whole system is provided by rechargeable lithium battery packs powering a distribution unit generating the tension level required by the different subsystems.
Upper part of Figure 2 shows a picture of the final flight configuration: On the left and right side of the mechanical structure is possible to spot the two actuators for lateral and longitudinal control connected to the servo motors. The main electronic box is located in the centre of the payload and hosts the commanding electronics, on board sensors, power unit and balancing ballast. Figure 2 shows also the IMU reference body system, with the X-axis along the front direction, Y along right direction and Z along the down direction. Overall final mass of the payload is slightly below 1.6 kg while canopy and suspension lines mass is 0.2 kg, adding up to a final system mass around 1.8 kg.
Airdrop Tests
Airdrop tests were performed to characterize the flight dynamics of the prototype, to verify the actuation strategies for the lateral control and to test system response in generating simple trajectory profiles. A total of 10 test flights have been conducted in a one-day campaign releasing the payload from the octocopter drone and controlling the descent trajectory manually with inputs from a radio command.
The flight chain (shown on the left of Figure 3) has an overall length of 10 m and is released when at desired altitude using a dedicated mechanism by setting free a cylindrical pin holding the chain cable.
The mechanism consists in two main parts, as shown in the Figure 4: A fixed part, which acts as a support for both the rotating part and the servomotor actuator and a rotating part, that supports the pin on which the payload is connected. Two half-cylindrical elements are used to support the pin on which the payload is connected, one of the two half-cylindrical elements is positioned below the pin, to prevent it from falling, and the other one is positioned over the pin, to avoid any other unwanted movement. A rolling friction system with no sliding friction was designed to minimize actuation force allowing the use of a 5 V servomotor instead of a linear actuator.
By activating the servomotor, the lower half-cylindrical support rotates allowing the cylindrical pin to free fall under the effect of the gravity. On the rotating part, two protrusions have been added to completely fill the spaces at the side of the upper half-cylindrical support to drive the pin when exiting, avoiding any type of jamming. To stop the rotor in the right position during the re-closing phase, two mechanical stops have also been added.
The whole mechanism was printed by a 3D printer and connected to the support legs of the drone.
The series of drop test have been conducted using the same step by step procedure:
1. Raise the parawing to 60 m altitude using the octocopter drone.
2. After system was stable in hoovering position at constant attitude, airdrop was initiated by remotely commanding the release mechanism.
3. After a stable flight configuration of the parawing was achieved (by visual observation from ground), the system was guided in a desired sequence of turns by the operator with a remote control.
4. After landing system was recovered, checked for full functionality and prepared for the following test.
Post-processing of recorded flight data immediately showed a major malfunction of the GPS unit of the parawing system in all tests, preventing the use of its measurements for trajectory reconstruction.
It must be noted that GPS unit of the octocopter drone performed nominally so the drop altitude of the payload was known with good accuracy subtracting the flight chain length from drone altitude.
Data from the IMU (accelerations and rotation rates) were therefore used to investigate system dynamics and effects of the commanded turning manoeuvres.
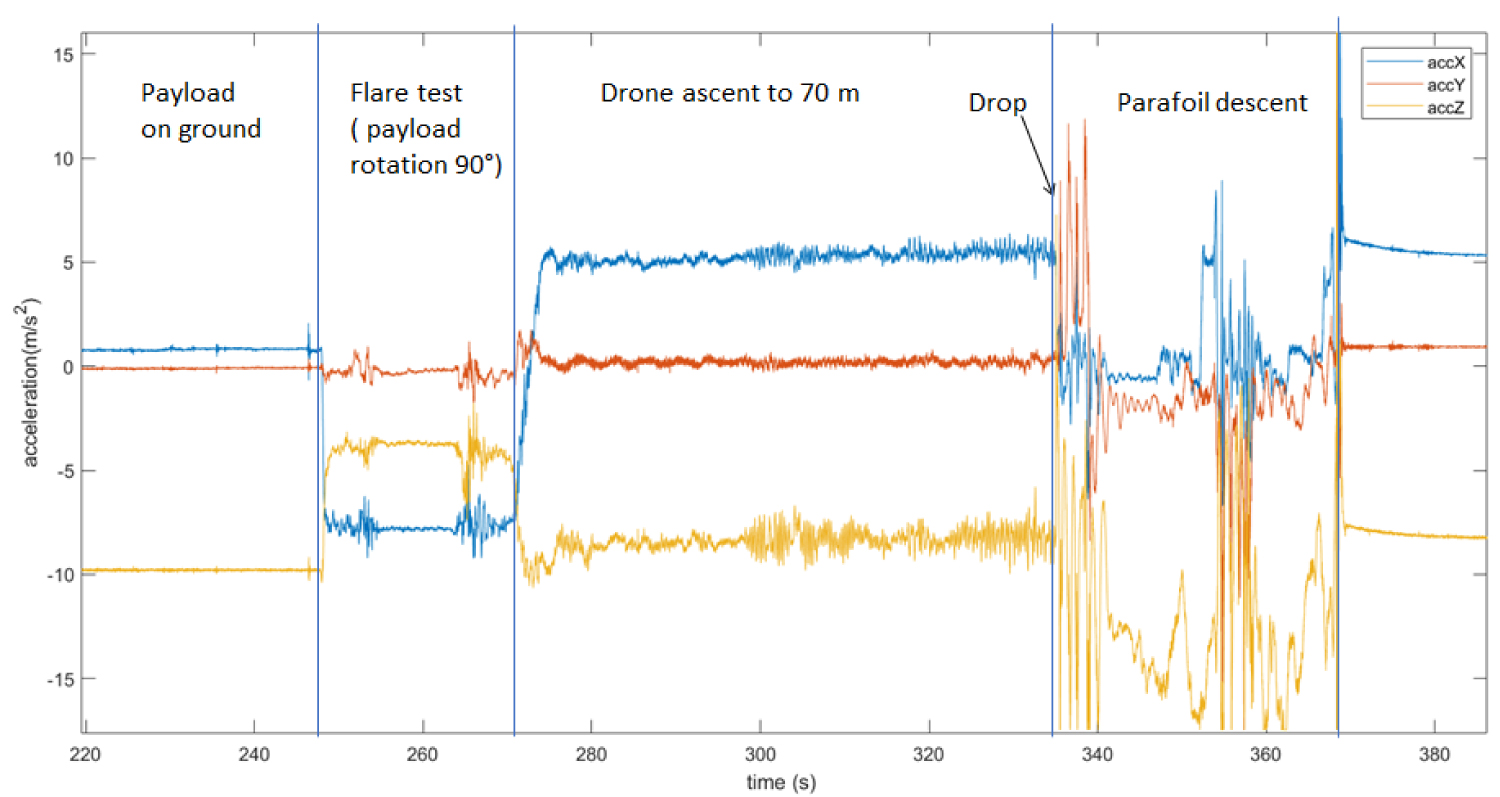
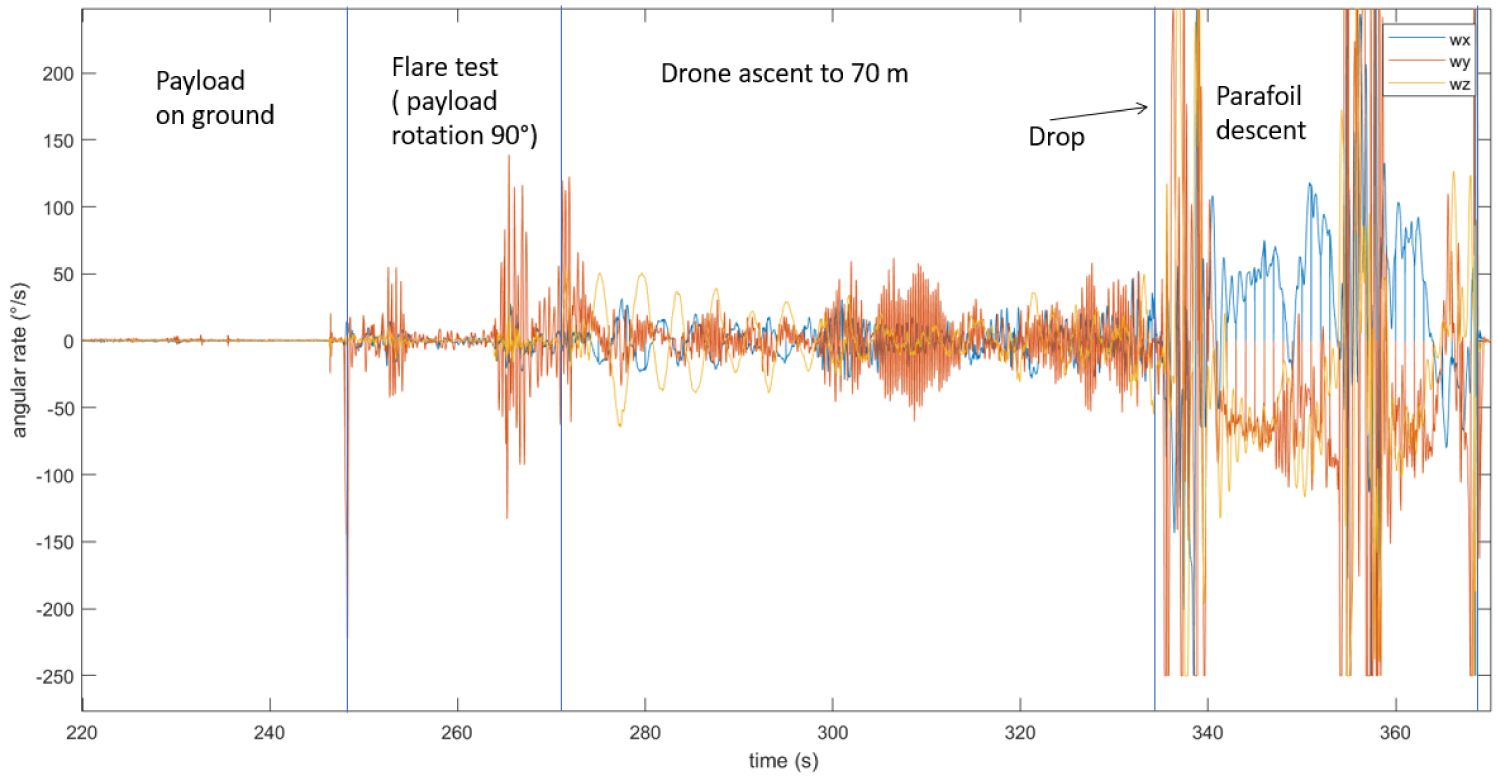
Figure 5 shows the typical acceleration profiles acquired along the three sensing axes during one flight test (test number 7); the data are divided into the different test phases: Payload on ground, lift off and flare test (rotation of payload of 90°), ascent to release altitude, drop and descent. Figure 6 reports the corresponding acceleration module where is possible to spot the free fall condition at 0 g after the drop and afterwards the effect of the complex dynamic of the parawing during canopy inflation. The data acquired by on board rate gyros are reported in Figure 7 and show similar time profiles. As expected the inflation dynamics of the canopy and the impact on ground generate acceleration and rotation rate values which exceed the measured range of the sensors (± 2 g for accelerometer and ± 250°/s for rate gyros). The sensor saturation is visible in Figure 5 and Figure 7 right after the drop from the drone and at landing, but in some flights (as in flight 7) the condition is also encountered during descent when stable glide is lost due to an excess in the commanded turn rate.
For every flight, accelerometer data analysis guided the identification of correct timing of free fall condition and ground impact, allowing to isolate data sets related to parawing descent. The recorded data of the parawing descent for flight 5, 6 and 7 are reported n the following Figure 8, Figure 9 and Figure 10.
The analysis of acceleration and gyro profiles shows that the parawing experienced in all flights a phase of fast spin motion after the drop and preceding a more stable flight condition. In some flights where an excessive pulling of brakes was commanded, the system may re-enter into a spin (as in-flight number # 7 at 355 s), losing aerodynamic lift and recovering a more stable flight attitude after few seconds.
It is also evident from the reported acceleration profiles that the recorded level along the Z-axis reproducing the Lift acceleration may become higher than gravity, due to the added contribution of centripetal acceleration during the turn, which results in a higher final load factor.
Regarding system attitude, the geometrical configuration of attachment points to the wing, contains the lateral inclination at payload level (roll) close to the one of the wings, so payload roll may be used for an estimation of flight bank angle. Same applies for payload yaw angle while payload pitch angle is strongly influenced by local drag and so cannot be directly linked to flight path angle.
Gyro measures may so be used to produce indicative profiles of wing flight condition when integrated and transformed from body reference to inertial reference.
Euler angles have been used to describe system attitude and Euler kinematic equations have been used to transform the measured angular rates into angular velocities in the inertial system.
It is assumed that IMU position is coincident with payload centre of mass, which is also supposed to be the centre of mass of the whole flying system, disregarding wing mass in comparison with payload mass.
Calling φ, θ, ψ the roll, pitch and yaw Euler angles in the quasi inertial North East Down (NED) reference and P, Q, R the roll, pitch and yaw rate components of the payload angular velocity vector in the body front right down (frd) coordinates (aligned with IMU measuring axis), the gyro measured rates have been used to calculate time variation of Euler angles using the well know cinematic system of equations:
Since utilised COTS rate gyro sensors are affected by a significative drift, a high pass filter with no phase shift has been applied on P, Q and R data before transformation to avoid drift integration.
Obtained angular rates in NED reference have been then integrated considering IMU sampling frequency (100 Hz) to reconstruct attitude of payload/parawing system in the inertial frame.
Once attitude of the system is reconstructed the Euler angle-based transformation matrix T can be calculated to project vectors from body (frd) onto inertial reference system (NED) and vice versa.
Where cφ = cosφ, cθ = cosθ, cψ = cosψ and sφ = sinφ, sθ = sinθ, sψ = sinψ
Transformation matrix is used to calculate acceleration levels measured into body reference frame generated by the motion of reconstructed trajectory; considering sensor position coincident with the center of mass and that the body reference is not inertial,
In case sensor position may not considered coincident with the centre of mass, transportation acceleration term shall be inserted in equation (3) to consider angular velocity and angular acceleration of the body frame. It has also to be noted that the measured acceleration along X-axis is mainly driven by payload drag acceleration and so a good the correspondence with model acceleration may be obtained only using a 9 d.o.f model.
Dynamical Model of Commanded Parawing
Different approaches can be used to model the dynamics of a parawing system; the simplest model is a 6 d.o.f. model including inertial position components of the system mass centre as well as the three Euler orientation angles but complexity can be increased using a 9 d.o.f. model to consider relative payload canopy attitude [9].
Since dynamical model of Safe UAV parawing needed to be used to analyse test data an reconstruct descent trajectory a dedicated 8 d.o.f. dynamical model was implemented, using the classic intrinsic equations of motions of the center of mass of the parawing/payload system in the NED non-rotating Earth reference system. The system of equations of the equivalent rigid body motion is completed by two control equations for deflection of the brakes (σ is the asymmetric brake deflection and ε the symmetric brake deflection).
Since the canopy is a very light structure that is distant from the centre of mass of the parawing/payload system, the expected motion is strongly influenced also by the so-called apparent mass effect generated by fluid resistance to the motion of a body inside it. The additional forces needed to accelerate the fluid result in an apparent larger mass, impacting the transient response of the system to disturbances and control input. The effect has been modelled by imposing time constants for the control lag during the imposed manoeuvres for asymmetric and symmetric canopy deflections (τσ and τε).
The considered system of equations is reported in the following [10].
Where V is the airspeed velocity, γ is the flight path angle in NED reference, ψ is the azimuth angle of the velocity vector in the N-E plane, x is the downrange distance, y is the cross-range distance, h is the altitude above the ground, σ is the pseudo-bank angle, wx, wy and wz are the x, y and vertical components of the wind at the current position and altitude. The coordinate frame is chosen such that the origin coincides with the projection of the test's drop point on the N-E plane. W is the weight of the system (including mass of the payload and the canopy) and D and L are lift and drag forces acting on the canopy, neglecting line drag and payload drag.
The last two equations (10) an (11) represent the effect of two control inputs for the model, the first is essentially a commanded pseudo bank rate (expressing a coordinated turn rate) and represents the effect of the asymmetric deflection, while the second represents the variation of commanded change in the longitudinal control by the symmetric wing deflection and is essentially a change in CL and CD coefficients , causing a slight change in L/D ratio and mainly a variation in descent velocity.
The aerodynamic forces L and D are calculated using equation (12) and (13) [10] where S is the canopy area and the dynamic pressure is obtained considering constant air density (equal to the standard value at ground level ρ0 = 1.225 kg/m^3) and model calculated descent velocity V, CL and CD are obtained by the sum of a constant trim value and the variation due to the symmetric deflection ε
For the drop tests the CL and CD values have been considered constant and equal to the trimmed value at take-off since no longitudinal control was implemented during the descent. Expected CL and CD values have been evaluated using aerodynamic coefficients for low aspect ratio wings, whose lift curve slope may be approximated considering lifting line theory as: [11]
a'2D is the corrected form of two-dimensional lift curve slope for low aspect ratio wings,
Where [11]
and a2D is supposed to be equal to 6.89/rad as in 18% thick Clark-Y airfoil.
AR is aspect ratio of the parawing (for Safe UAV AR = 1.99), τ is a factor depending on the AR and can be calculated as in [11] to be close to 0.07.
Considering the anhedral angle ζ
Where b is span of the parawing and R is anhedral radius of parawing canopy, the resulting lift expression is a function of a and the difference between actual attach angle and zero lift angle
And k1 can be written as
The drag coefficient can be calculated as in [11] with the expression:
Where CD0 is the parasite drag contribution and δ is a small factor for non-elliptic wind loading and can be calculated as in [11] to be close to 0.01.
For the selected parawing the following coefficients have been therefore considered: AR = 1.99, τ = 0.07, δ = 0.01 a = 2.45, k1 = 0.68, CD0 = 0.089 (similar parawing in [11]), = 6.2°. The resulting estimated values for CL and CD and for L/D ratio are reported in Figure 11.
In the test campaigns the parawing has been trimmed to fly at an angle of attach close to 5° by properly regulating the suspension chords with actuators set in the default position, achieving a L/D ratio close to the expected maximum value in order to generate long gliding paths.
CL and CD values considered in the model are CL = 0.5 and CD = 0.15 and have been afterward verified simulating the descent of the parawing in the test drops and checking the overall flight profile using elaborated IMU sensors data.
Model Simulation of a Drop Test Descent
Test number 6 has been selected to be simulated with the dynamical model since negligible wind was measured at ground level, allowing to disregard wind contribution in the dynamic's equations. Furthermore, from video footage the wing after entering a spin after the drop experienced a phase of almost stable flight, so few seconds after the glide the wing was commanded in a right turn and following in a left turn. First turn's command was transmitted for 2.5 s while the right turn was slightly longer, just below 3 s The module of acceleration and angular velocities measured during the descent are reported in Figure 12.
The profile shows the unstable flight condition followed by the almost stable glide; three seconds after stable flight condition was reached, the wing was commanded in a right turn and afterwards in a left turn as may be noted in the plot of wx angular velocity.
Payload roll, pitch and yaw profiles have been reconstructed integrating the angular velocities obtained though equation (1) by measured rates. Pitch and roll values are reported in Figure 13.
In order to reproduce the flight profile, the commanded pseudo bank angle has been set to be equal to the reconstructed roll at payload level as shown in Figure 11; the assumption, based on the constructive geometry of the flying system, is introducing an error in the commanded angle due to the presence of payload oscillations, but final results show that the contribution can be disregarded for the considered short descent path (overall descent time is around 20 s).
Minor tuning of the wing aerodynamic coefficients was needed to produce a matching trajectory (CL = 0.53 and CD = 0.17).
The reconstructed trajectory profile for the descent is reported in Figure 14 where the commanded turns have been respectively plotted in green and red.
Calculated airspeed and flight path angle are reported in Figure 15. It may be noted the beginning of the descent is characterized by a "nose down" highly accelerated motion needed to reach the glide velocity, inducing a high amplitude payload pitch oscillation.
The considered 6 d.o.f. dynamical model of the parawing system has been therefore used to reproduce the descent trajectory of one of the UAV drop tests, qualitatively matching the recorded profile and the descent timeline. Although a simplified approach is used considering only the centre of mass motion and disregarding payload relative motion, information obtained by IMU data elaboration allow the preliminary tuning of the aerodynamic coefficients of the wing model.
Conclusion
Although the Safe UAV project is only in the beginning of its test activity, results achieved so far are promising for the realization of an autonomous parawing system.
The first prototype of the active parawing system has been realized and successfully tested in a series of drops from an UAV at 60 m altitude; limitations in system controllability have emerged when manually commanding turn manoeuvres due to the imposition of an excessive brake pull sometimes resulting in undesired spin motion.
Some of the test flight have anyhow resulted in smoother descent trajectories and have been used to provide angular velocity inputs to the dynamical model, allowing to reconstruct the descent trajectory, to conduct a preliminary tuning of aerodynamic coefficients and to achieve a better understanding of descent dynamics.
In the next upcoming campaign a bigger (3 m2) wing will be used in order to limit sinking during canopy inflation and reduce instability during turns. Redundancy in the GPS system will also be provided: Acquired trajectory data will allow an extensive tuning of parameters in the dynamical model with the use of predictor corrector methods usually implemented in trajectory reconstruction.
Once the dynamical model will be fully validated, it will be used for the final design of the emergency system for the octocopter drone and eventually scaled up for future tests on heavier payloads.
Acknowledgements
The project is developed under coordination and funding by Department of Industrial Engineering of the University of Padova.
Conflict of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.