
International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 6, Issue 1
Original Article
DOI: 10.35840/2631-5009/7549
On the Resolution of a Weak Fermi Paradox
ZN Osmanov1,2*
Figures
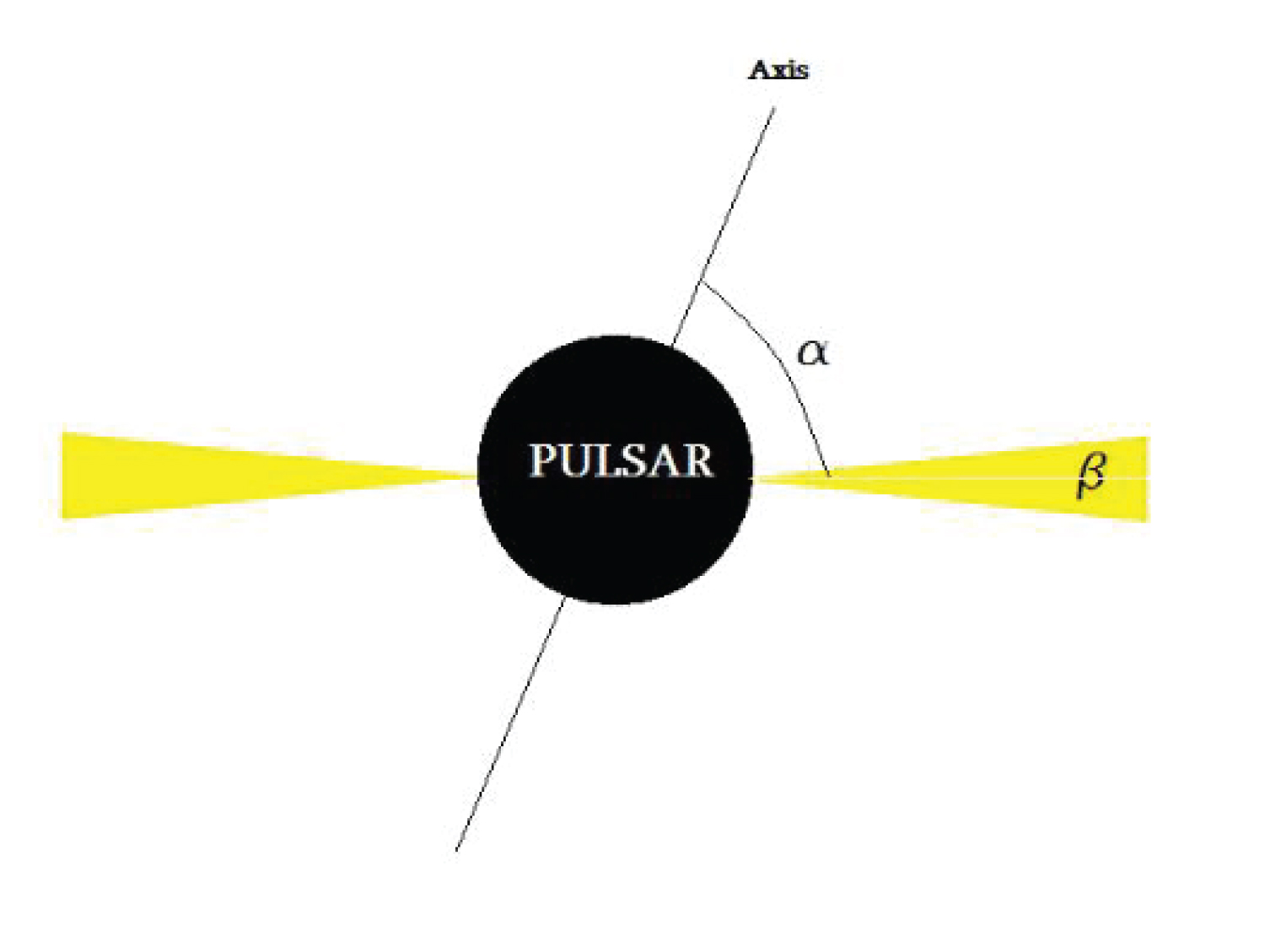
Figure 1: Here we schematically show the pulsar....
Here we schematically show the pulsar, its axis of rotation, and two emission channels (yellow) with an opening angle β.
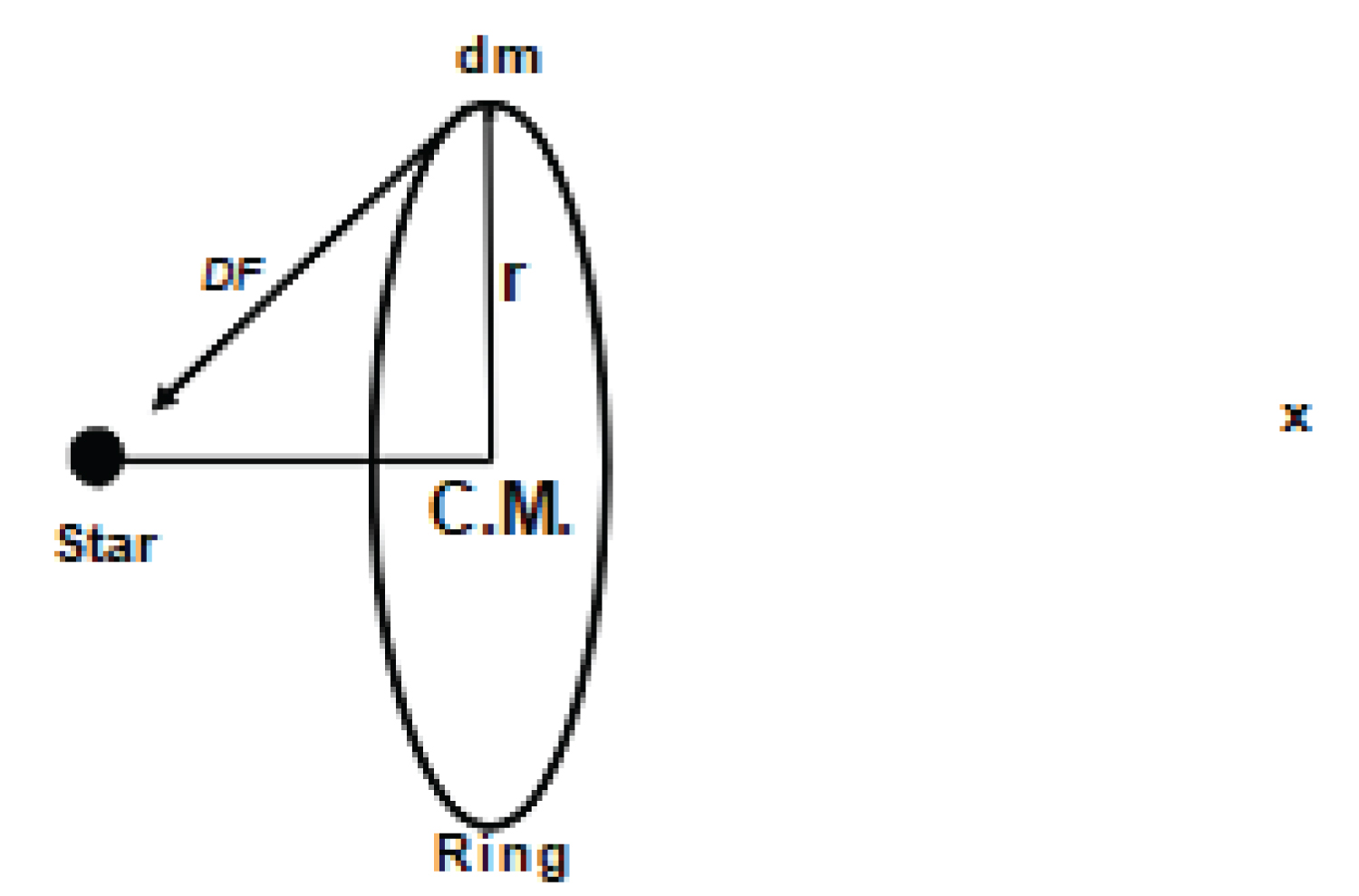
Figure 2: Here we show the out-of-plane displaced.....
Here we show the out-of-plane displaced ring with respect to the star (either a pulsar or a main sequence star).
Tables
Table 1: Here we present the variability time-scales for main sequence stars.
Table 2: Here we show the values of χ for main sequence stars derived in the framework of the spectral variability method.
Table 3: Here we show the values of χ for main sequence stars derived in the framework of the radial velocity method.
References
- Armstrong S, Sandberg A (2013) Eternity in six hours: Intergalactic spreading of intelligent life and sharpening the Fermi paradox. Acta Astronautica 89: 1-13.
- Lineweaver CH, Fenner Y, Gibson BK (2004) The galactic habitable zone and the age distribution of complex life in the milky way. Science 303: 59.
- Yu C (2015) The dark forest rule: One solution to the fermi paradox. JBIS 68: 142-144.
- Gertz J (2017) Nodes: A proposed solution to the fermi paradox. JBIS 70: 454.
- Cirkovic M (2018) The great silence: Science and philosophy of fermi's paradox. Oxford University Press, Oxford, UK.
- Dyson FJ (1960) Search for articial stellar sources of infrared radiation. Science 131: 1667-1668.
- Kardashev NS (1964) Transmission of information by extraterrestrial civilizations. Soviet Astronomy, 8: 217.
- Jugaku J, Nishimura S (2002) Bioastronomy 2002: Life among the stars. In: Norris R, Stootman F Proceedings of the IAU Symposium 213, San Francisco, USA, 437.
- Timofeev MY, Kardashev NS, Promyslov VG (2000) A search of the IRAS database for evidence of dyson spheres. Acta Astronautica Journal 46: 655-659.
- Carrigan RA (2009) IRAS-Based whole-sky upper limit on dyson spheres. The Astrophysical Journal 698: 2075-2086.
- Boyajian TS, LaCourse DM, Rappaport SA, Fabrycky D, Fischer DA, et al. (2016) Planet Hunters IX. KIC 8462852 - where?s the flux? Monthly Notices of the Royal Astronomical Society 457: 3988.
- Wyatt MC, van Lieshout R, Kennedy GM, Boyajian TS (2018) Modelling the KIC8462852 light curves: Compatibility of the dips and secular dimming with an exocomet interpretation. Monthly Notices of the Royal Astronomical Society 473: 5286-5307.
- Zackrisson E, Korn AJ, Wehrhahn A, Reiter J (2018) SETI with gaia: The observational signatures of nearly complete dyson spheres. The Astrophysical Journal 862: 21.
- Griffith RL, Wright JT, Maldonaldo J, Povich MS, Sigurdsson S, et al. (2015) The G In-frared search for extraterrestrial civilizations with large energy supplies III the reddest extended sources in wise. The Astrophysical Journal 217: 25.
- Lacki BC (2019) Sunscreen: Photometric signatures of galaxies partially cloaked in dyson spheres. Publications of the Astronomical Society of the Pacific 131: 024102.
- Melkikh AV, Mahecha DS (2017) On the broader sense of life and evolution: Its mechanisms, origin and probability across the universe. Journal of Astrobiology and Outreach 5: 162.
- Cirkovic MM, Bradbury RJ (2006) Galactic gradients, post biological evolution and the apparent failure of SETI. New Astronomy 11: 628-639.
- Cirkovic MM (2008) The temporal aspect of the drake equation and SETI. Astrobiology 4: 225-231.
- Bradbury RJ, Cirkovic MM, Dvorsky G (2011) Dysonian approach to SETI: A Fruitful Middle Ground? JBIS 64: 156-165.
- Osmanov Z (2016) On the search for articialdyson-like structures around pulsars. International Journal of Astrobiology 15: 127.
- Osmanov Z (2018) Are the Dyson rings around pulsars detectable?. International Journal of Astrobiology 17: 112-115.
- Haliki E (2019) Broadcast network model of pulsars as beacons of extraterrestrial civilizations. Inter-national Journal of Astrobiology 18: 455.
- Osmanov Z, Berezhiani VI (2018) On the possibility of the dyson spheres observable beyond the in-frared spectrum. International Journal of Astrobiology 17: 356.
- Wright JT (2020) Dyson spheres. Serbian Astronomical Journal 200: 1-18.
- Foucher F, Hickman-Lewis K, Westall F, Brack A (2017) A statistical approach to illustrate the challenge of astrobiology for public outreach. Life 7: 40.
- Ruderman MA, Sutherland PG (1975) Theory of pulsars - polar caps, sparks, and coherent microwave radiation. The Astrophysical Journal 196: 51-72.
- Los JH, Zakharchenko KV, Katsnelson MI, Fasolino A (2015) Melting temperature of graphene. Physical Review B 91: 045415.
- Sandberg A (1999) The physics of information processing super objects: Daily life among the jupiter brains. Journal of Evolution and Technology 5: 1-34.
- Cai W, Moore AL, Zhu Y, Li X, Chen S, et al. (2010) Thermal transport in suspended and supported monolayer graphene grown by chemical vapour deposition. Nano Letters 10: 1645.
- Carroll BW, Ostlie DA (2010) An introduction to modern astrophysics and cosmology. Cambridge University Press, Cambridge, UK.
- Taylor JH, Manchester RN (1977) Galactic distribution and evolution of pulsars. The Astrophysical Journal 215: 885-896.
- Hatzes AP (2016) The radial velocity method for the detection of exoplanets. Astrophysics and Space Science Library 428: 3.
- McInnes CR (2003) Non-Linear dynamics of ring world systems. JBIS 56: 308.
- Osmanov Z, Berezhiani VI (2019) On the possibility of the dyson spheres observable beyond the infrared spectrum. Journal of the British Interplanetary Society 72: 254.
- Demircan O, Kahraman G (1991) Stellar mass-luminosity and mass-radius relations. Astro-physics and Space Science 181: 313-322.
- Ke TT, Huang H, Lin DNC (2012) Rapid mid-infrared variability in protostellar disks. The Astrophysical Journal 745: 9.
- Muzerolle J, Flaherty K, Balog Z, Furlan E, Smith PS, et al. (2009) Evidence for dynamical changes in a transitional protoplanetary disk with mid-infrared variability. The Astrophysical Journal Letters 704: 15-19.
- Reach WT, Lisse C, Hippel TV, Mullally F (2009) The dust cloud around the white dwarf G 29-38. II. Spectrum from 5 to 40 m and Mid-Infrared photometric variability. The Astrophysical Journal 693: 697-712.
Author Details
ZN Osmanov1,2*
1School of Physics, Free University of Tbilisi, 0183, Tbilisi, Georgia
2Georgian National Astrophysical Observatory, Abastumani, 0301, Georgia
Corresponding author
ZN Osmanov, School of Physics, Free University of Tbilisi, 0183, Tbilisi; E Kharadze Georgian National Astrophysical Observatory, Abastumani, 0301, Georgia.
Accepted: May 04, 2021 | Published Online: May 06, 2021
Citation: Osmanov ZN (2021) On the Resolution of a Weak Fermi Paradox. Int J Astronaut Aeronautical Eng 6:049.
Copyright: © 2021 Osmanov ZN. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this paper we consider the Fermi's paradox (FP) and propose a possible resolution in the context of super-advanced alien civilizations. In this sense it can be regarded as to be the weak Fermi paradox (WFP). By assuming that super advanced extraterrestrials (ET) exist and are capable of constructing a huge ring-like megastructure around a pulsar or a main sequence star (MSS) to consume its emitted energy, we consider the stability problem of the ring, studying the out of plane dynamics. It has been shown that for normal pulsars the oscillation timescale, thus the timescale of the spectral variability is of the order of several days, whereas for MSS it can vary from minutes up to hundreds of years. We have shown that by means of the high resolving power and sensitivity, the European Southern Observatory's Very Large Telescope can detect either cold (T = 300 K) or hot (T = 4000 K) megastructures throughout the whole galaxy even for very small oscillation amplitudes of rings. As it is shown the observed variability can have characteristics similar to those of some other variables, which can be considered as one of the resolutions of the WFP.
Subject Headings
Fermi's paradox, Pulsar ring, Dyson sphere, SETI, Extraterrestrial, ESO's VLT, Life-detection
Introduction
In 1950 discussing the problem of extraterrestrial intelligence the physicist Enrico Fermi asked "where are they?". The scientific background of this question and consequently the Fermi's Paradox (FP) is following: There are approximately 2 × 1011 stars in our local galaxy, if only a tiny fraction, 10-9, [1] of these worlds develop intelligence, there would be approximately 200 ETs. On average, the terrestrial planets in the Milky Way are older than Earth by (0.9-2.7) billion years [2]. Therefore, if the intelligent beings exist, they should be more advanced than we are, but then the natural question arises: Where are they?. If the answer to this question is not trivial (we do not see them because they do not exist), then the problem is very fundamental and serious.
There have been proposed a series of possible solutions to the FP. In particular, Yu [3] suggests a solution based on an assumption that civilizations in the universe compete for limited resources and therefore, in the framework of this paradigm, the Universe is a dark forest, where any civilization is a hunter and any life-form exhibiting its existence must be terminated. In the context of communication by using the so-called nodes presented in [4], the author concludes that we are blind to the signals used by ETs because the corresponding beams are very narrow. Apart from the mentioned works, there is a number of other approaches to the problem of FP, which are analysed in detail [5] and it is argued that to resolve the problem one needs a new spirit of open mindedness towards original, speculative and even crazy leaps.
In 1960, Dyson has been proposed a very original idea in the framework of the Search for Extraterrestrial Intelligence (SETI). In particular, assuming that if an extraterrestrial intelligence exists and has reached a super technological level, capable of consuming the whole energy of their host star, it can build a spherical megastructure surrounding the central object [6]. Theoretical reasonability of Dyson's approach was based on two values: Our civilization's total power of energy consumption, 4 × 1019 ergs s-1 and the bolometric luminosity of the Sun-like stars, 4 × 1033 ergs s-1. Then, by assuming that 1% of annual increase in industry is maintained, one can straightforwardly show that in approximately 3000 years the civilization might reach the mentioned level of technology - Level-II in Kardashev's scale [7]. Based on these assumptions Dyson [6] theorizes that for the purpose of harnessing the whole energy of the star, the civilization has to construct a thin spherical shell.
Dyson sphere (DS) around this object. Then it is clear that the megastructure's surface located in the habitable zone (HZ) should be visible in the infrared spectral band and therefore might be detected by infrared telescopes.
In a historical perspective, the search for the DS candidates is relatively new challenge. The last two decades are somewhat prospective, because of several attempts to identify on the sky signatures of DSs [8,9]. An interesting work has been done by Carrigan [10], who analysing the data of The Infrared Astronomical Satellite, has identified 16 interesting candidates. A fascinating discovery was announced by Boyajian, et al. [11]: They have detected a variable object KIC8462852 (Tabby's star) with anomalously high flux dips, which cannot be explained by massive planet shading. Although, as it turned out, the anomalous behaviour of flux should be caused by exocomets [12], the discovery of the Tabby's star has stimulated a further study in this eld and in a certain sense, it has revived the Dysonian SETI. Recently, by taking into account the observational data of the Gaia mission, Zackrisson, et al. [13] emphasised peculiarity of the object TYC 6111-1162-1, which, according to the authors, deserves further investigation. The search for even more advanced, Level-III civilizations (capable of harnessing almost the whole energy of the galaxy) [7] has been performed by Griffith, et al. [14], who scrutinly studied the data of the Wide-field Infrared Survey Explorer (WISE), and have shown that among 105 galaxies 100 deserve a certain attention. A special case of galaxies partially cloaked by DSs was considered by Lacki [15] where the author has examined the corresponding observational pattern of such galaxies.
On the other hand, despite some attempts the SETI project in its broad sense (Dysonian SETI is only one particular branch) has failed and there is a serious scientific discussion about it (Melkikh & Mahecha 2017 [16]; Cirkovic & Bradbury 2006 [17]; Cirkovic 2008 [18]; Bradbury, et al. 2011 [19]) where it is argued that conventional methods and approaches must be widened. In this context, recently the original idea has been developed by Osmanov [20,21] where the problem of Dysonian SETI was presented in a rather exotic way.
In particular, the author has considered the possibility of colonising a nearby zone of a pulsar to utilize the whole radiated energy. Since the pulsars have narrow emission channels (see Figure 1), instead of a sphere, one should use a ring-like structure, requiring at least two orders of magnitude less material than for DSs [20]. In [21] the problem has been studied in the light of an observational pattern of these megastructures and their possible detection by ground based facilities. It is worth noting that pulsars as possible sites for advanced ET activities deserve more and more attention. In particular, Haliki [22] has considered pulsars as possible beacons used by ETs for communication.
Another interesting feature, although for DSs has been considered in [23] where we have studied the possible oscillation of the megastructure, leading to potentially detectable spectral variability1. In the recent study by Wright [24] it is shown that to maintain stability of the monolithic DS the elastic modulus of the material the megastructure is made of, should exceed the elastic modulus of the strongest material Graphen by many orders of magnitude, which indicates that monolithic spherical shells around stars are unrealistic. Therefore, in the present paper we consider the rings/incomplete DSs nearby pulsars and stars and study their variability in the context of the WFP.
1 I am grateful to Prof. J. Wright for making aware of an incorrect conclusion in (Osmanov & Berezhiani 2018), emphasising that the fully complete DS will not lead to pressure difference. Although, not completely closed DS or a ring, will inevitably lead to the spectral variability.The paper is organised in the following way: In Section 4, we develop a main approach, and in Section 5 we summarize our results.
Main Approach
We do not consider the problem of a non-trivial connection of probability of the existence of intelligent life-forms and the number of biosignatures [25]. In the framework of the paper we assume that if ETs have reached a level of super advanced civilization (Level-II), they might be able to "colonise" a nearby zone of either a pulsar or a star and construct a huge megastructure around them, which should be visible in the infrared or optical spectral band.
If the DS is complete, it will be in the so-called neutral equilibrium. In particular, from the Gauss law, it is clear that the gravitational net force acting on the megastructure equals zero. The star's radiation in turn, is spherically symmetric, the momentum transferred by the emission is symmetric as well and therefore, the radiation pressure net force is zero. On the other hand, non-spherical structures might lead to non-zero net force difference and consequently to the spectral variability. We consider here an original idea of Niven rings and calculate the corresponding emission pattern.
McInnes (2003) has considered a point mass and a thin solid ring to study non-linear dynamics of the latter. The author examined two different regimes, the so-called in-plane and out-of-plane motion of the ring. In the former case he has shown that the process is unstable. Studying the ring-like megastructure around pulsars Osmanov (2016) has shown that pulsar's efficient radiation pressure cannot stabilise the process, but restoring the equilibrium position requires power, small compared to the total power received from the central object.
In Figure 2 we schematically show the out-of-plane displaced ring. x represents the displacement of the C.M. (the centre of mass) from the central object's position. The overall stability in out-of-plane motion is provided by the x component of the gravitational force between the star (either pulsar, or a normal star) and the ring for small amplitude oscillations reducing to the following expression where G is the gravitational constant, Mst represents the star's mass and M is the mass of the ring. Then, one can straightforwardly show that the equation of motion is described by
with x = ξ /R and ω = (GMst/R3)1/2.
Megastructures around pulsars
As a first example we examine pulsars, studying possible observational signatures.
By taking into account that the total effective area of the ring is Aef = 8 π R2 sin (β/2), one can straightforwardly derive from energy balance the radius of the ring for a given black body temperature, T, where Lp is the bolometric luminosity of a pulsar, normalised by the typical value of normal pulsars, σ ≈ 5.67 10-5erg/(cm2K4) is the Stefan-Boltzmann's constant and temperature is normalised by the value corresponding to the HZ. We have also used the typical value of the opening angle, β ≈ 32° [26].
As it is clear from Eq. (12), the radius of the ring is much smaller than the radii of typical DSs ≈ 1AU. Therefore, an amount of material required for constructing the ring will be much less than for building the standard DS. On the other hand, one can assume that a reasonable tendency should be to decrease the total mass of the megastructure. In OB, we have examined Graphene as a typical example of a super strong material having a very high melting temperature 4510 K [27] and therefore, it can be located much closer to the host star than other materials. In fact, we assume that if our civilization can produce super light and super strong materials, the same job will not be a problem for alien Level-II civilizations. From Eq. (4) one can straightforwardly show that for T = 4000 K the radii of the rings will be of the order of 2 × 10-4 AU, which is by four orders of magnitude less than normal DS radii. In this case the megastructure's spectrum will peak at the wavelength, 725 nm, which in turn, means that it can be seen not only in far infrared, but also in the optical band. In this paper we consider only two typical temperatures: The normal temperature (300 K) and the maximum possible temperature (4000 K) as more or less two extreme cases.
On the other hand, as we have discussed in OB, some sector of the inner free space of the ring should be maintained relatively cold. If the megastructure is used for habitation, the temperature should be around 300 K and for providing high performance computing processes [28] the temperature should be of the order of 10 K. By taking into account that the typical values of modern cooling engines have the coefficient of performance (COP) of the order of 5, the engine to compensate the flux to the cold area, must process the energy (normalised by the total luminosity of the pulsar) to the hot reservoir, where we assumed ΔT = (4000-300) K= 3700 K, h ≈ 100 cm, is the thermal conductivity normalised by the corresponding value for Graphene (Cai, et al. 2010 [29]), S is the area inside the free space requiring cooling and we have considered the value equal to the total surface area of the Earth, 5.1 × 108 km2. In case the megastructure is used for high performance computing, one can see from the above equation that Pe will be still much less than the pulsar's luminosity. Therefore, from the point of view of laws of physics the process of cooling is quite realistic.
By combining Eqs. (3,4) the oscillation period writes as
Where Mp = 1.5 × Ms represents the pulsar's mass and Ms ≈ 2 × 1033 g is the Solar mass.
Such a periodic motion will inevitably lead to a variable character of an observational pattern. In particular, by means of the Doppler effect, the observed wavelength is given by [30].
Where by s we represent the original wavelength emitted by the ring, is an angle of velocity direction measured in an observer's frame of reference,
v denotes the corresponding velocity and c is the speed of light. It is clear that oscillation is non-relativistic, which for the maximum wavelength difference leads to
Where multiplier 2 comes from motion of the ring in different directions, vm = ω A denotes the maximum velocity and A = χ R is the amplitude of small oscillations (χ < < 1). A technical problem for observing such megastructures is to achieve high values of the resolving power, RP, of modern spectrographs. As we have already mentioned, the spectral band, in which these rings might be detected, is either in infrared (for T = 300 K) or far infrared-optical interval (for T = 4000 K). Up to now the European Southern Observatory's (ESO) Very Large Telescope (VLT) has the highest resolving power RP ≤ Δ λ/λs = 25000 for λ ≈ 9.6m (which corresponds to the blackbody radiation with T = 300 K)2. On the other hand, it is clear that spectral variations will be detected if the following relation Δλ/λs ≤ RP is satisfied. This imposes a certain constraint on pulsar luminosities which potentially might be observed.
2 www.eso.org/public/teles-instr/paranal-observatory/vlt/
By taking into account that ring's luminosity behaves with pulsar's rotation period as L ~ P-3 (Osmanov 2016) and since the upper limit of the average value of periods is of the order of 2 sec [31], one can estimate the minimum value of χm ~ 3 × 10-2, which will still allow to detect the variability.
For hot rings (T = 4000 K) the intensity peaks at λ ≈ 725 nm and the corresponding limit of the resolving power of the VLT facility is by one order of magnitude higher, RP = 190000, which reduces the minimum value of the spatial amplitude by one order of magnitude, χm ~ 3 × 10-4. Therefore, for hot rings the spectral variation might be detected for even smaller amplitude scales.
Generally speaking, if the observational pattern of the megastructure is characterised by absorption lines, then by using the so-called radial velocity method [32] it is possible to measure radial velocity by precision of the order of vm ~ m/s. For this case, one can obtain the constraint on potentially detected luminosities, which for T = 300 K and the same class of pulsars leads to the minimum value of the oscillation amplitude χm ≈ 5 × 10-6 and for T = 4000 K the corresponding value is of the order of χm ≈ 4 × 10-7.
McInnes (2003) [33] has shown that the ring is unstable with in-plane displacements with the corresponding timescale, ω = (2R3/(GMc))1/2, where R is the ring radius and Mc is the central object's mass. This in turn, means, that the characteristic velocity of the ring becomes of the order of vm ~ δR/τ where δR is the initial displacement of the ring from the equilibrium position. On the other hand, in the Lunar laser ranging experiment3 the distance is measured with the precision of the order of η ~ 10-10. Then, if one assumes that the precision of the super advanced civilization controlling the distance is not less than, one can straightforwardly obtain v ~ η (GMc)/(2Rc))1/2, which for typical pulsars leads to a value in the interval 10-3-10-2 cm/sec, being beyond the sensitivity of the modern facilities. It is worth noting that it would be possible to detect such megastructures if the measurement precision will be reduced by the factor of 104-5, which although is possible but less probable: If our civilization can measure distances with the precision 10-10, one can naturally assume that a super-advanced alien civilization might have even higher precision measurements.
3 The corresponding data is available from the Paris Observatory Lunar Analysis Center: http://polac.obspm.fr/llrdatae.htmlOsmanov (2018) has demonstrated the possibility of the VLT to distinguish the structure of the ring in the HZ and it has been shown that in the nearby zone of the Solar system (on a distance ~ 0.2kpc) for approximately 64 pulsars the megastructures might be observed in detail. By using the method of spectral variability, not only nearby pulsars, but very distant objects, located almost at the edge of our galaxy, might be monitored as well. In particular, the flux sensitivity of the VLT instruments is approximately Flux ≈ 3 × 1018 ergs s-1, which means that the maximum distance from which the radiation of the ring still might be detectable is given by
which is of the same order of magnitude as diameter of Milky Way.
Megastructures around MSS
In this subsection we examine the megastructures around MSS and outline the major results presented in [34]. We consider the ring like constructions. Then the radius of the ring for the Solar-type stars is given by
Where the stellar bolometric luminosity, Lst, is normalised by the solar luminosity, Ls ≈ 3.83 × 1033 ergs s-1. For the hot Dyson megastructure (T = 4000 K) the corresponding scale is of the order of 0.007AU.
Consequently, likewise the previous case, the variability timescale is expressed as follows,
We consider a wide range of main sequence stars with masses 0.1 Ms < Mst < 120 Ms, characterized by the following approximate luminosity-mass relation (Demircan & Kahraman 1991) [35].
Where α1 ≈ 1.03 and α2 ≈ 3.42. In Table 1 we show the variability time-scales for different classes of stars. As it is clear, the time-scale might become anomalously short, of the order of minutes and hours.
By taking the aforementioned equations into account, one can obtain the constraint on dimensionless spatial amplitude.
It is evident that for cold Dyson megastructures, more promising objects are M-type stars, but even for them the minimum value of the dimensionless amplitude is of the order of 0.1. For hot rings, the corresponding estimate leads to the value, 0.001 (See Table 2).
The radial velocity method still might be very efficient. In particular, the corresponding constraint in this case writes as
Which even for Solar type stars and cold megastructures leads to very small value χmin ≈ 3.72 × 10-5.
The hot Dyson rings with T = 4000 K lead to even smaller lower threshold, 2.79 × 106 (See Table 3).
Considering the in-plane instability of the ring for the wide range of stars, 0.1 Ms < Mst < 120 Ms and by taking into account Eqs. (12-14) one can straightforwardly show that the velocity amplitude of in-plane oscillations are of the order of 10-5-10-4, which is even smaller than in case of pulsars, implying that the modern facilities are not sensitive enough to detect the corresponding motion of megastructures.
We analyse the obtained results separately for pulsars and stars. As a first example we consider pulsars. From Eq. (6) it is evident that depending on temperature the timescales of variability might be several days or even less. On the other hand, modern observations in mid-infrared spectrum reveal the similar timescale variability from some astrophysical objects (Ke, et al. 2012 [36]; Muzerolle, et al. 2009 [37]; Reach, et al. 2009) [38]. Therefore, if the spectral features of the rings around pulsars are indistinguishable from conventional astrophysical objects, the former might be "hidden" and only very high spatial resolution can distinguish the internal structure of an observed object. At this moment the highest resolution, provided by the ESO's VLT instruments guarantee monitoring of only 64 pulsars in the nearby zone of the Solar system.
By analysing MSS, from Eq. (13) one can conclude that in case of cold Dyson megastructures (T = 300 K) the corresponding variability timescale might vary from days to almost a year (K and M stars), up to several years (G, F and A stars) and hundreds of years or higher (B and O stars). To identify Dyson megastructure candidates by detecting variability one should analyse the overall spectral picture. In particular, the long period stars belong to the spectral class F, M, S or C, but F stars cannot be considered as candidates since they are very hot (T = 7000 K). M stars have temperatures corresponding to hot DSs (2400-4700) K but are unrealistically luminous like S and C stars. On the other hand, as it is clear from Eq. (13), for stars with M > 7 Ms the variability timescale becomes more than 100 years and therefore, to discover them the observation time should be that large. This might be one of the resolutions of the FP - we do not have enough time to detect such objects, the technological artefacts of highly advanced civlizations.
Studying the hot megastructures, one can see that starting from M up to A type stars the timescale varies from several minutes to approximately a day. For B type stars the corresponding value varies from a day up to several months and for O type stars the variability timescale interval might be from months to years. One should emphasize that the ZZ Ceti stars are characterised by the variability timescale of the order of several minutes [30], but these stars have extremely high temperatures 104 K. The stars of spectral class B are characterised by variability timescales of the order of several hours, but still the temperature is very high. The similar inconsistency occurs with variability timescales from days to a year. Therefore, in order to find real candidates one should focus on anomalous spectral behaviour of variables.
In the framework of the paper we have assumed that the techno signatures of Level-I civilization should not be easily detectable because of the relatively small energy consumption. The existence of Level-III civilization is possible, but less probable, than Level-II, therefore, the paper is focused on the latter.
We have analysed the observational features of megastructures nearby stars and pulsars. In case of stars, if the megastructures are complete DSs then as we have already discussed, it will not be characterised by variability and therefore, cannot be detected. On the other hand, the incomplete megastructures - rings, will exhibit the strong variability in out of plane dynamics, but the emission characteristics of such rings, will be somehow "hidden" in the overall emission background of the sky and to discover a candidate one has to search for techno signatures by searching for anomalous variable "stars". It is also clear that to consume the whole energy of a star, one should construct the complete DS, requiring enormous material. Therefore, one should naturally assume the possibility of colonising pulsars - the advantage could be the usage of much less material. However, it is worth noting that the construction of megastructures around pulsars requires colonization and thus - migration. Summarizing, one can conclude that the techno signatures are either non-detectable (complete DSs around stars) or hidden in the sky's back grount (rings nearby stars or pulsars).
Conclusion
By considering the out-of-plane dynamics of the ring we have estimated the oscillation period of the megastructure. For reasonable parameters of stars and pulsars it has been shown that the typical timescale of oscillations and thus the timescales of variability might vary from minutes (hot megastructures around M stars or pulsars) to days (cold rings around M stars or pulsars) up to hundreds of years (cold megastructures around B and O type stars).
Two methods of detecting the techno signatures have been examined: The spectral variability and radial velocity method. We have studied as relatively cold (T = 300 K) as well as hot (T = 4000 K) megastructures. It was shown that by ESO's VLT instruments the variable character of spectra can be detected even for small oscillations χ ~ (0.001-0.01) (for pulsars) and χ ~ (0.001-0.1) (for stars). By considering the radial velocity method the results are following: χ ~ (10-7-10-6) (for pulsars) and χ ~ (10-6-10-4) (for stars).
It has been shown that rings might be spectrally indistinguishable from some variables - thus, they might be hidden, which in turn is one of the resolutions of the WFP. On the other hand, a super-advanced civilization might control the oscillation amplitude - making it extremely small, shifting the variability in an undetected "area". In any case, even if the megastructures are detectable, they should reveal anomalous character of their variability, which is the main reason why we cannot see them: We look for aliens in wrong "areas".

