International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 6, Issue 2
Original Article
DOI: 10.35840/2631-5009/7557
POD-Galerkin Based Reduced Order Modelling for Flow-Structure Interactions
Jiaxin Dong, Derek Ingham, Lin Ma* and Mohamed Pourkashanian
Figures
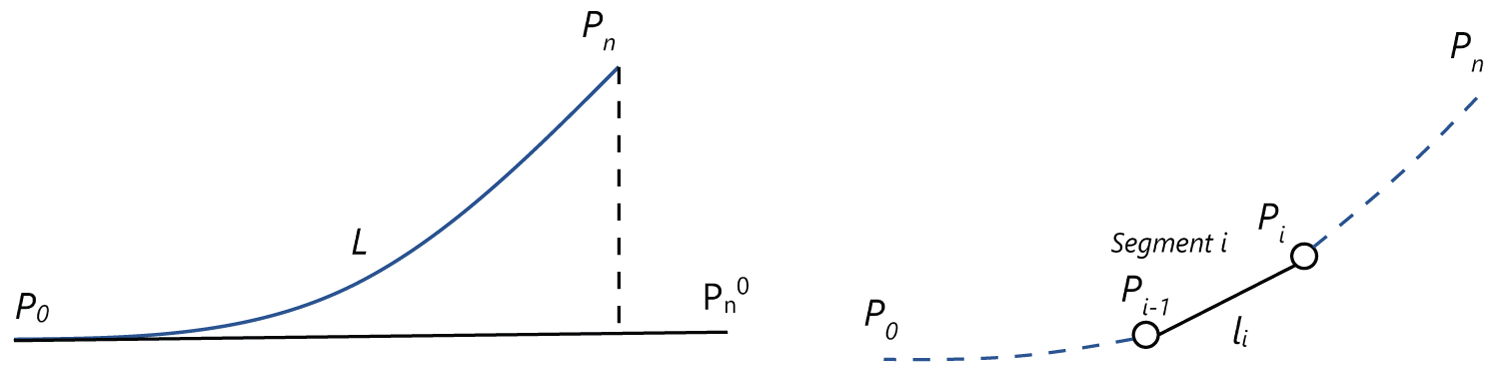
Figure 2: The finite segment method and....
The finite segment method and its notation, reproduced from [30].
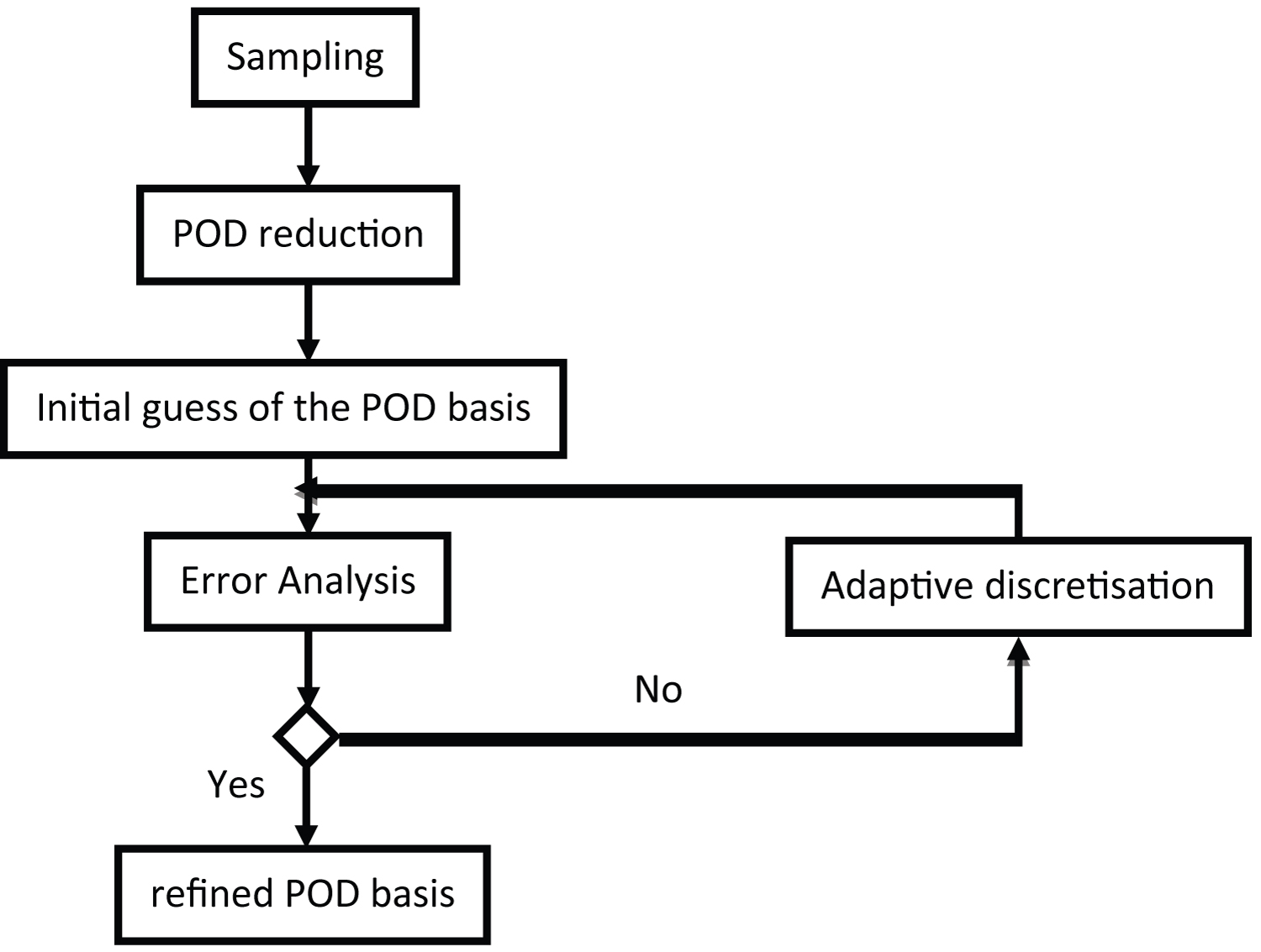
Figure 4: Solution scheme of the adaptive....
Solution scheme of the adaptive discretisation part for the proposed model.

Figure 5: A typical example of an adaptive....
A typical example of an adaptive discretisation at different time steps.

Figure 6: Schematic of the mesh used in the case....
Schematic of the mesh used in the case of the flow-induced vibration of the NACA 0015 aerofoil.
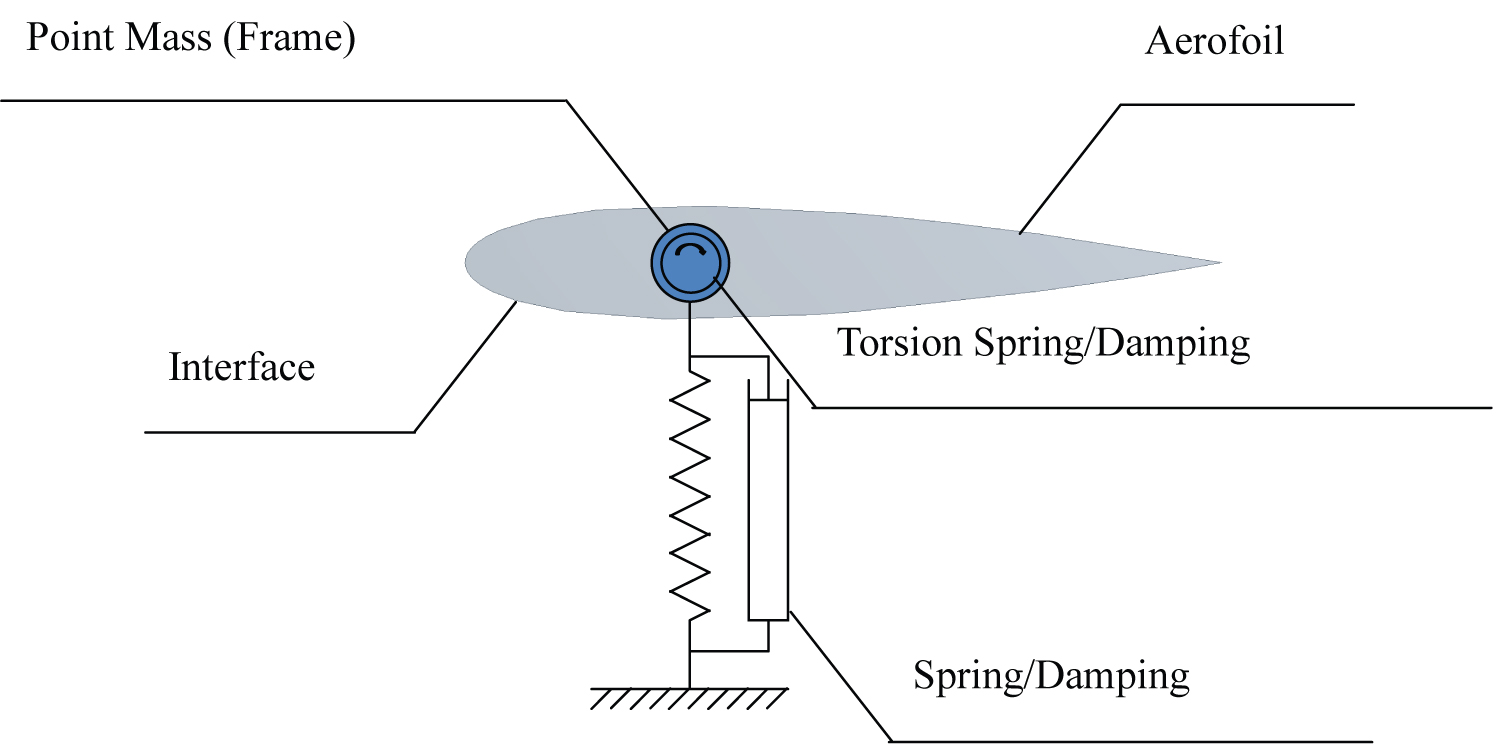
Figure 7: Structural model of the flow-induced...
Structural model of the flow-induced vibration of the NACA 0015 aerofoil.
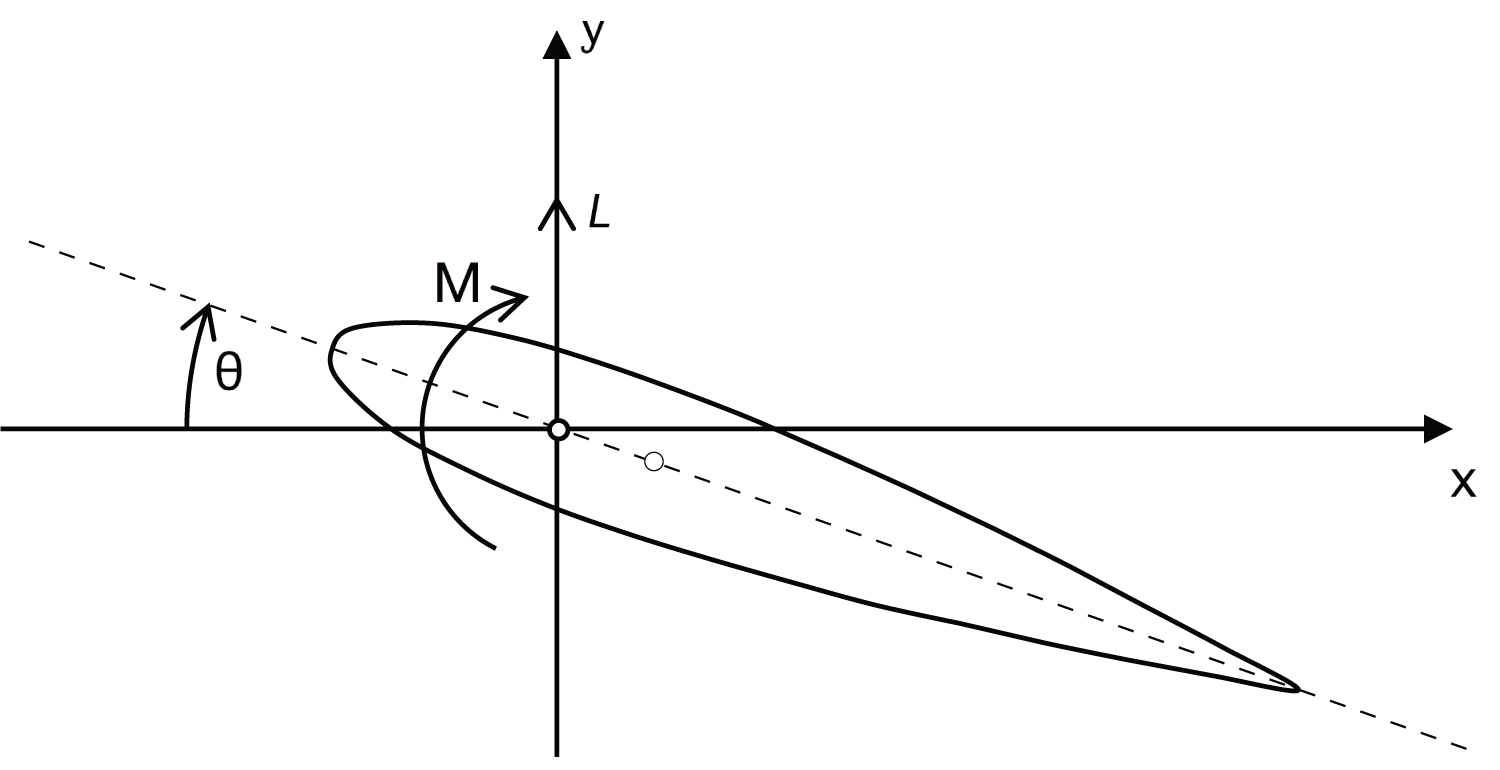
Figure 8: Schematic of a 2-D pitching and plunging....
Schematic of a 2-D pitching and plunging aerofoil.
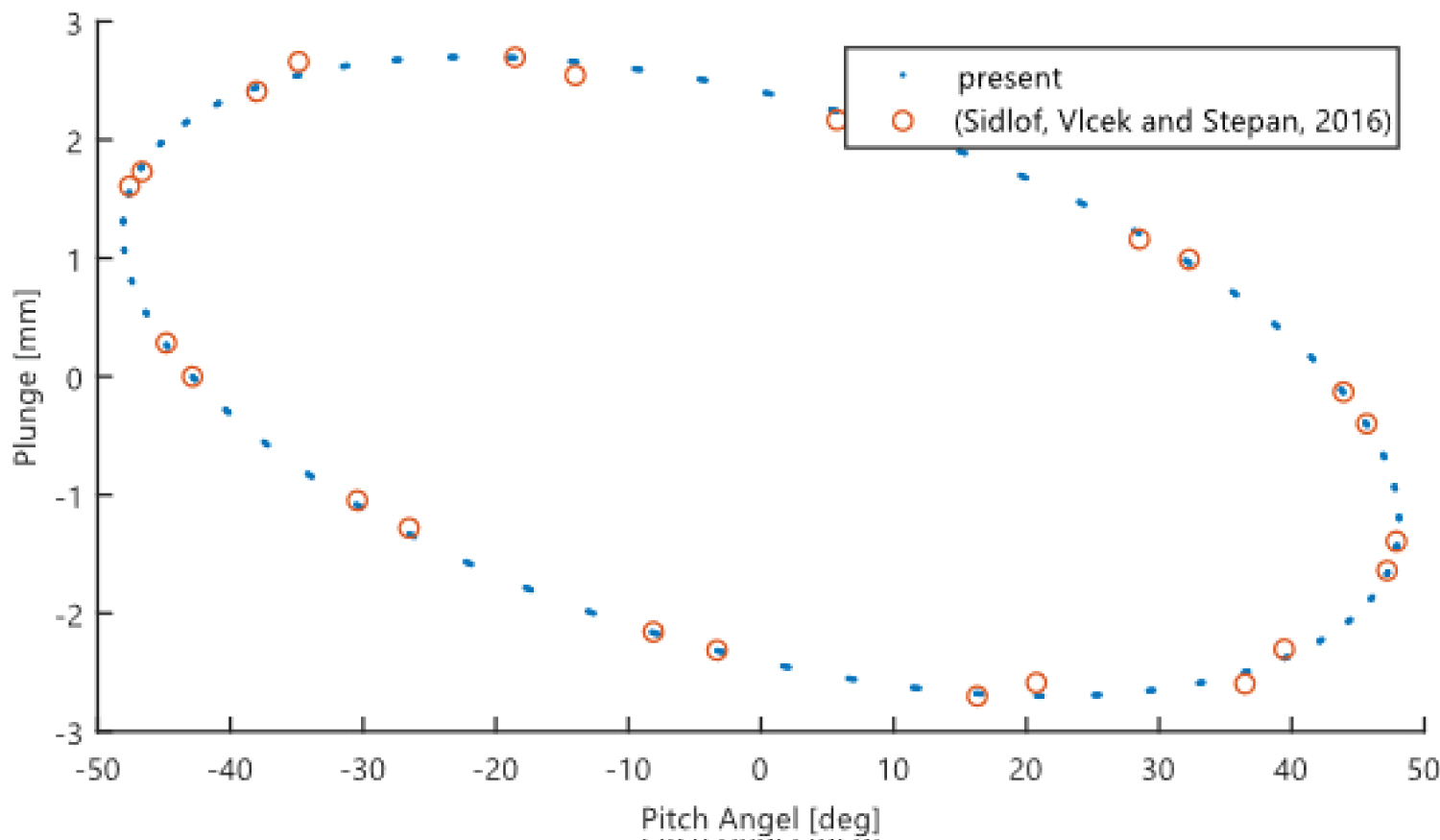
Figure 9: Comparison of the phase between the pitch...
Comparison of the phase between the pitch angle and plunge of the NACA 0015 aerofoil limit cycle oscillation (Re = 173,000).
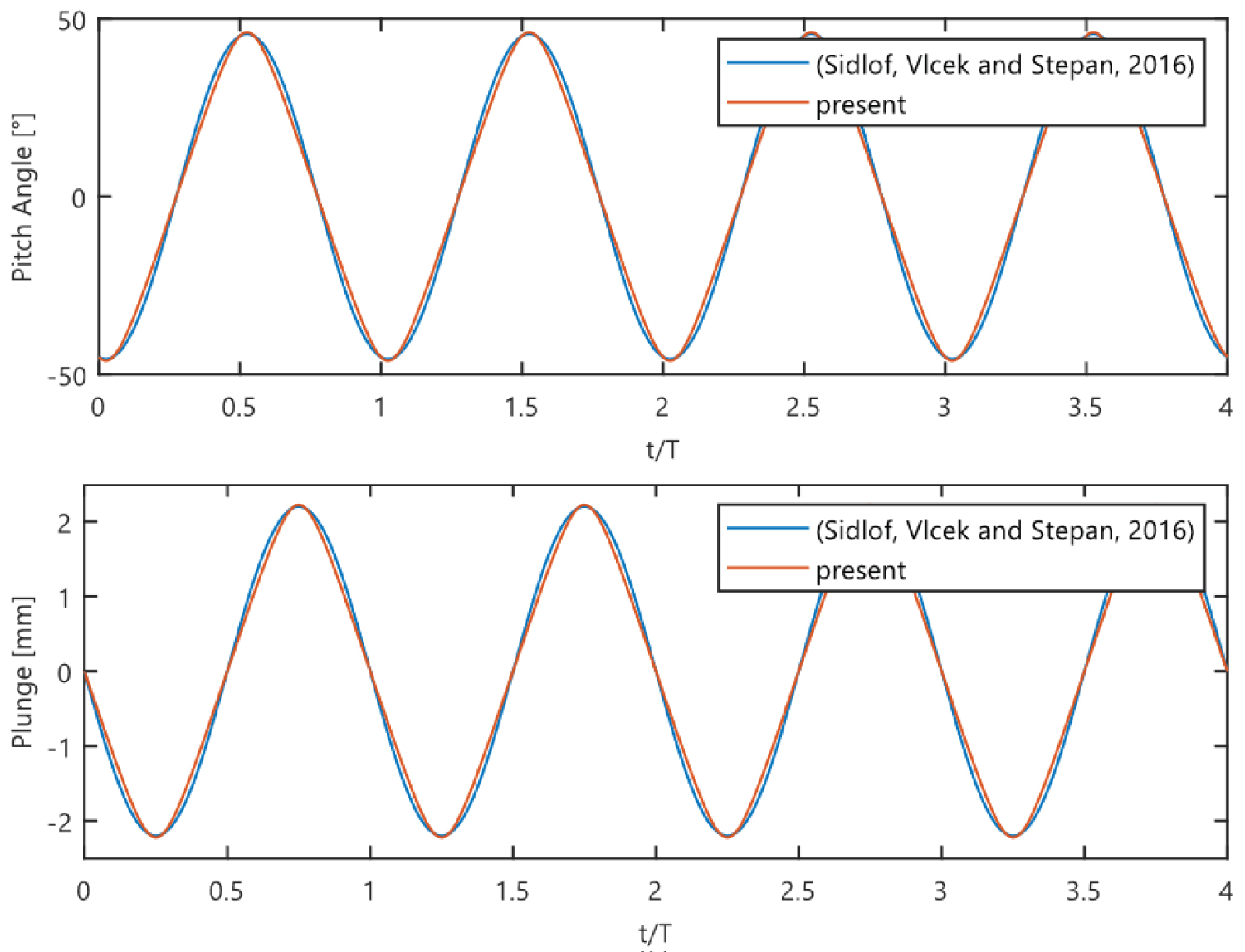
Figure 10: Time history of the pitch and plunge of the...
Time history of the pitch and plunge of the NACA 0015 aerofoil limit cycle oscillation over normalised periods (Re = 173,000).
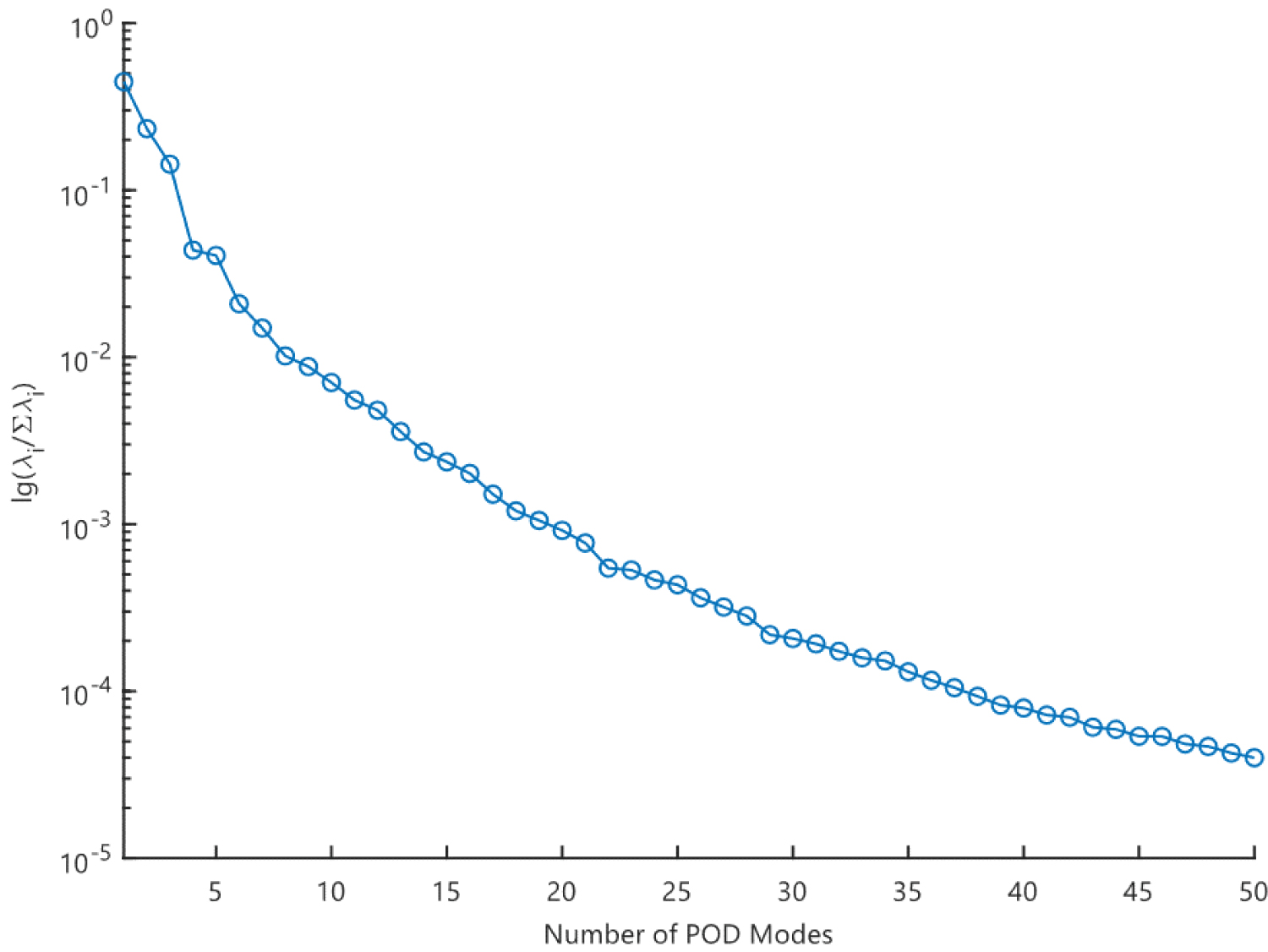
Figure 11: The energy spectrum of the POD modes...
The energy spectrum of the POD modes in the case of the limit cycle oscillation at the reynolds number Re = 173,000.
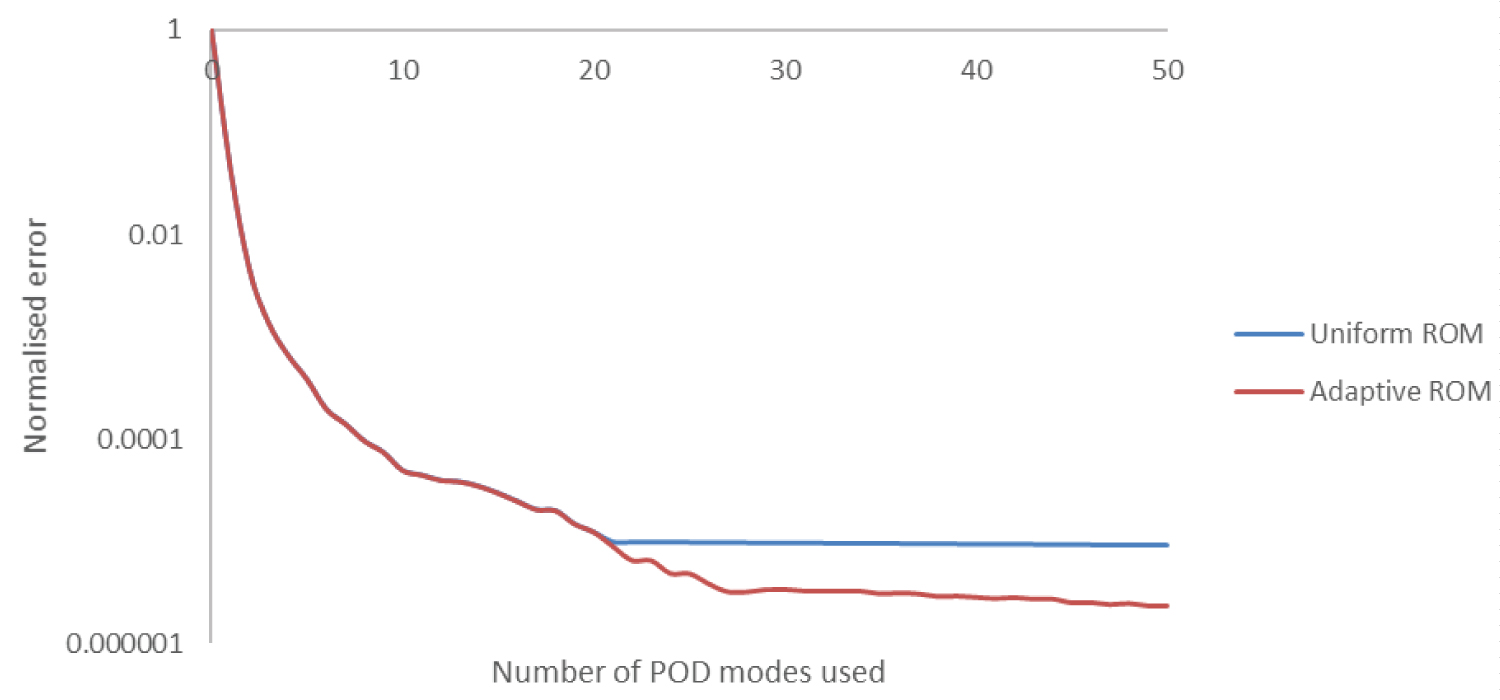
Figure 12: Decay of the normalized error for the...
Decay of the normalized error for the POD basis using the adaptive and uniform grid discretisation for the flow passing a pitching and plunging aerofoil at a reynolds number Re = 173,000.
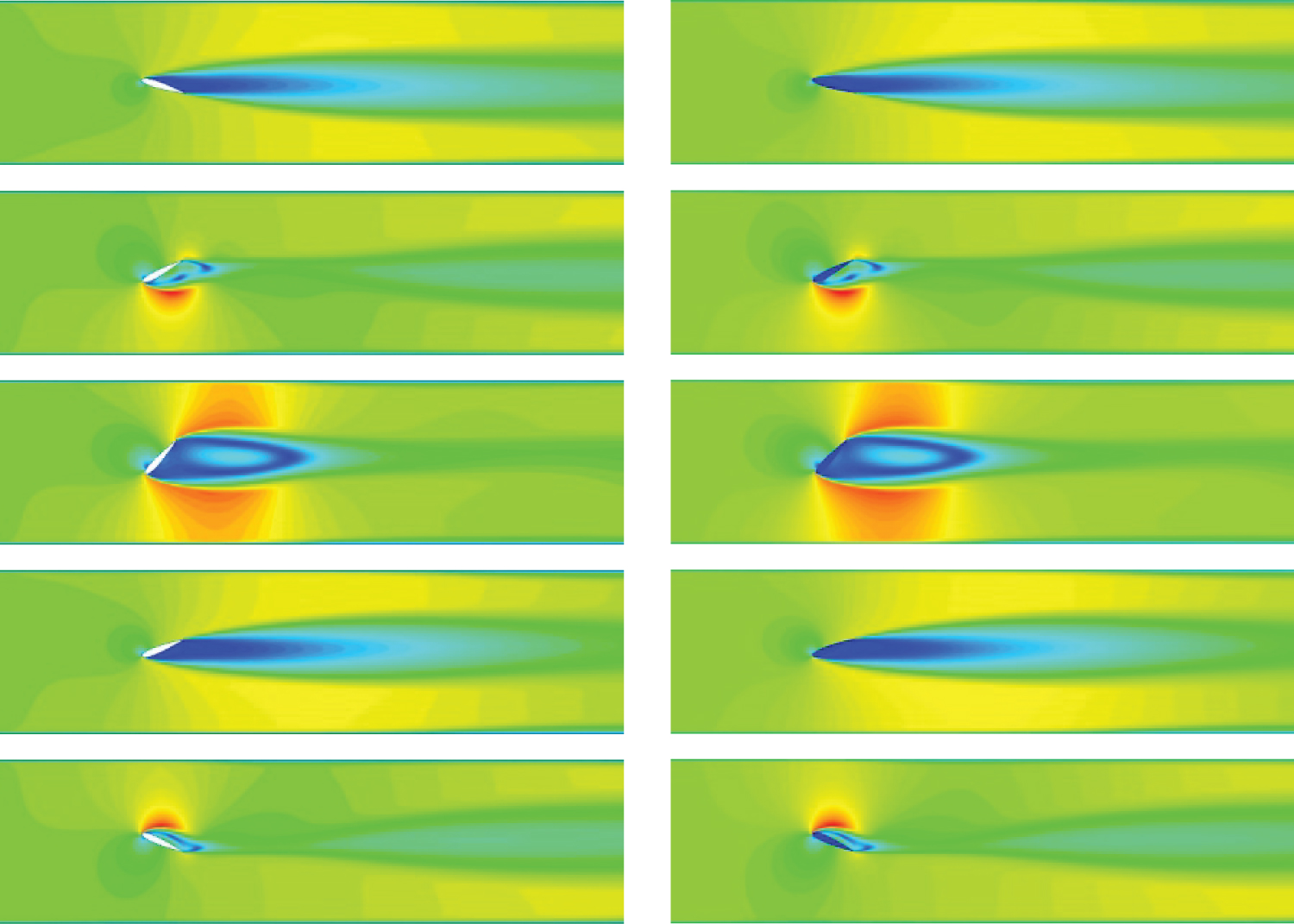
Figure 13: Proposed solution for a two-dimensional...
Proposed solution for a two-dimensional pitching and plunging aerofoil in the case of the limit cycle oscillation (Re = 173,000) at different snapshots. Left: Numerical solution; Right: Reconstructed flowfield using the new proposed ROM.
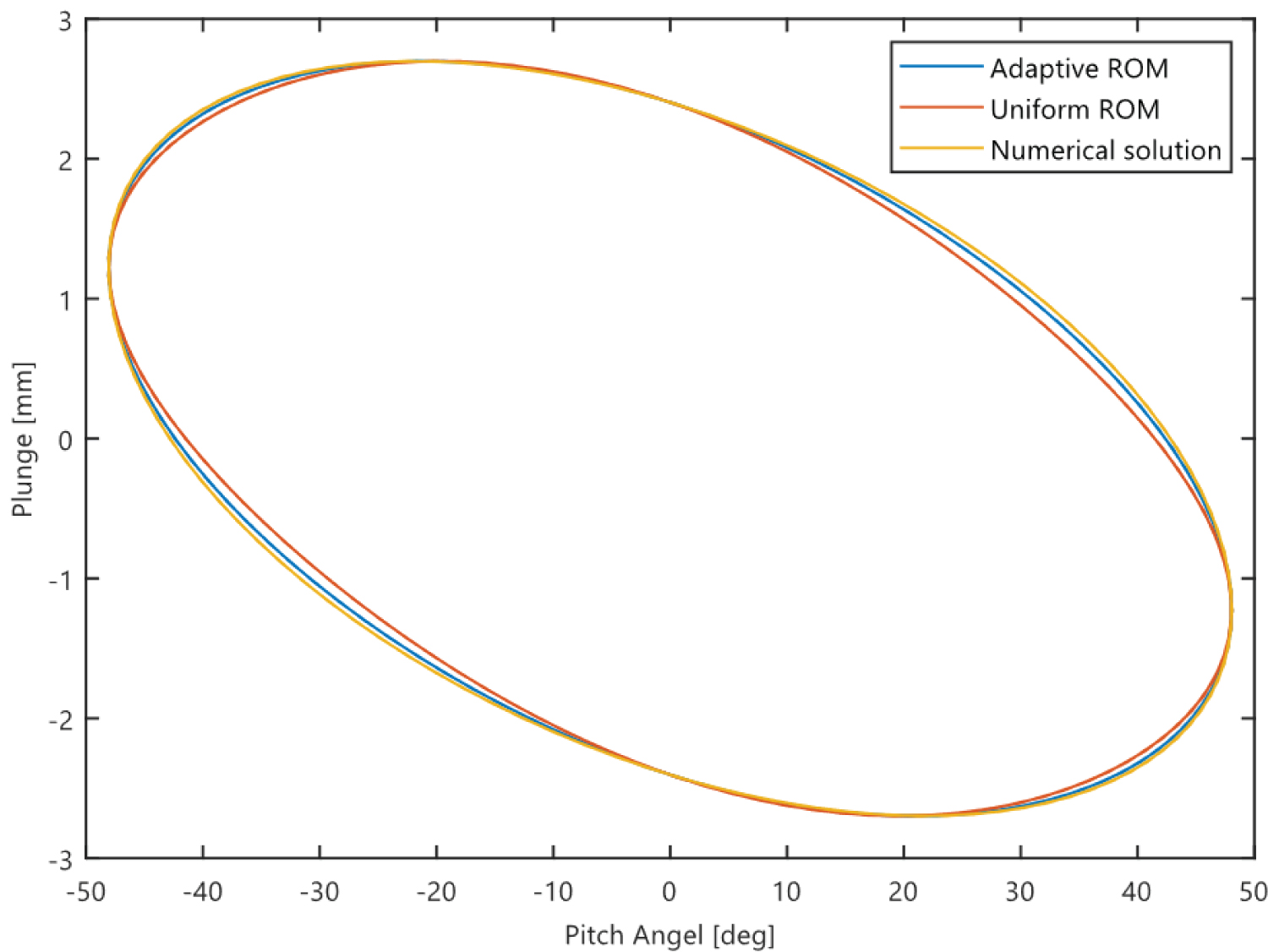
Figure 14: A comparison of the POD-Galerkin results...
A comparison of the POD-Galerkin results using the adaptive and uniform grid discretisaton for the flow passing a pitching and plunging aerofoil in the case of a limit damping oscillation at the reynolds number Re = 173,000.
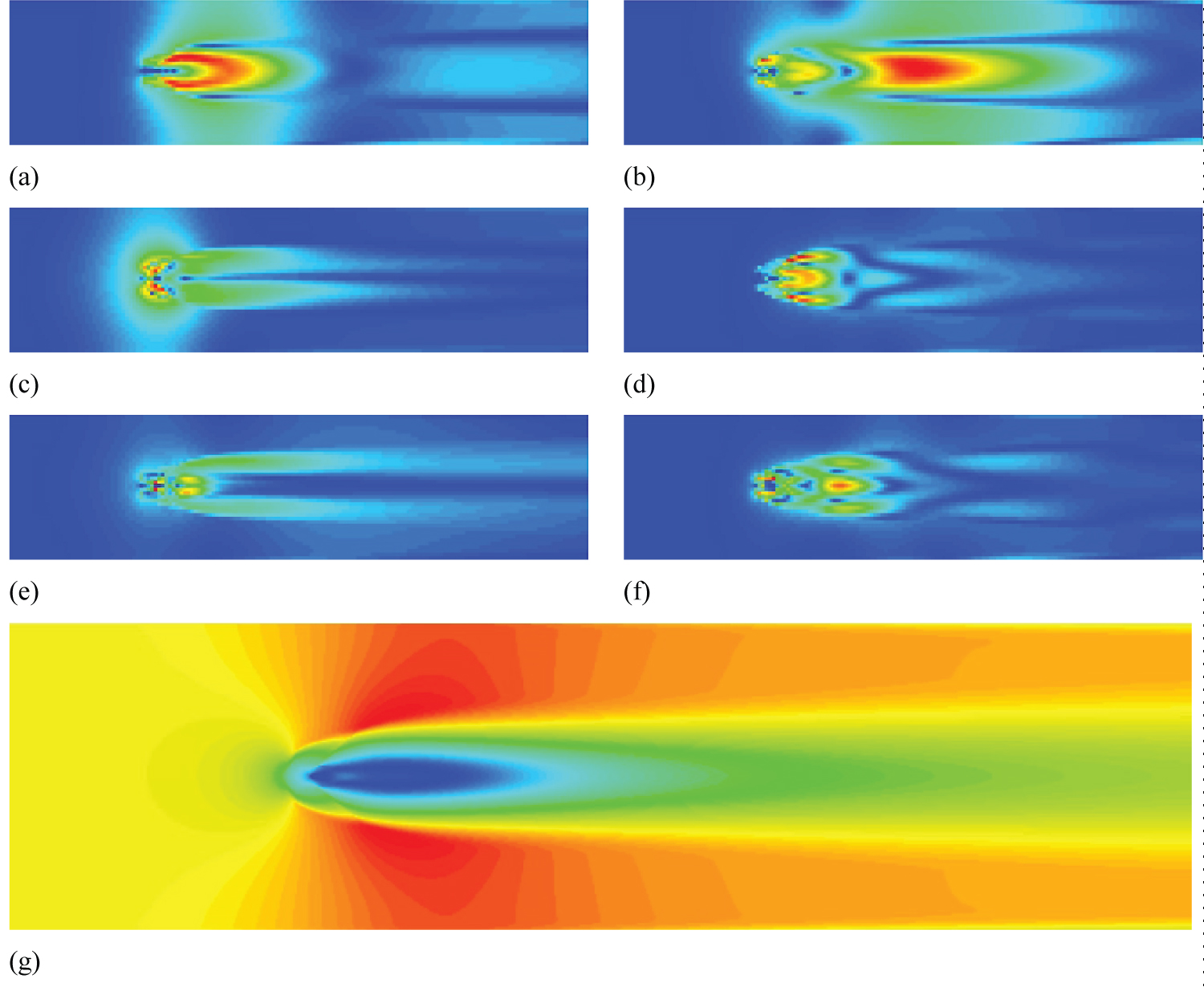
Figure 15: Vorticity contours of the first 6 POD....
Vorticity contours of the first 6 POD modes and the mean flow for a two-dimensional pitching and plunging aerofoil in the case of the limit cycle oscillation (Re = 173,000) (a) - (f): First six POD modes, (g): Voriticy contours of the mean flow.
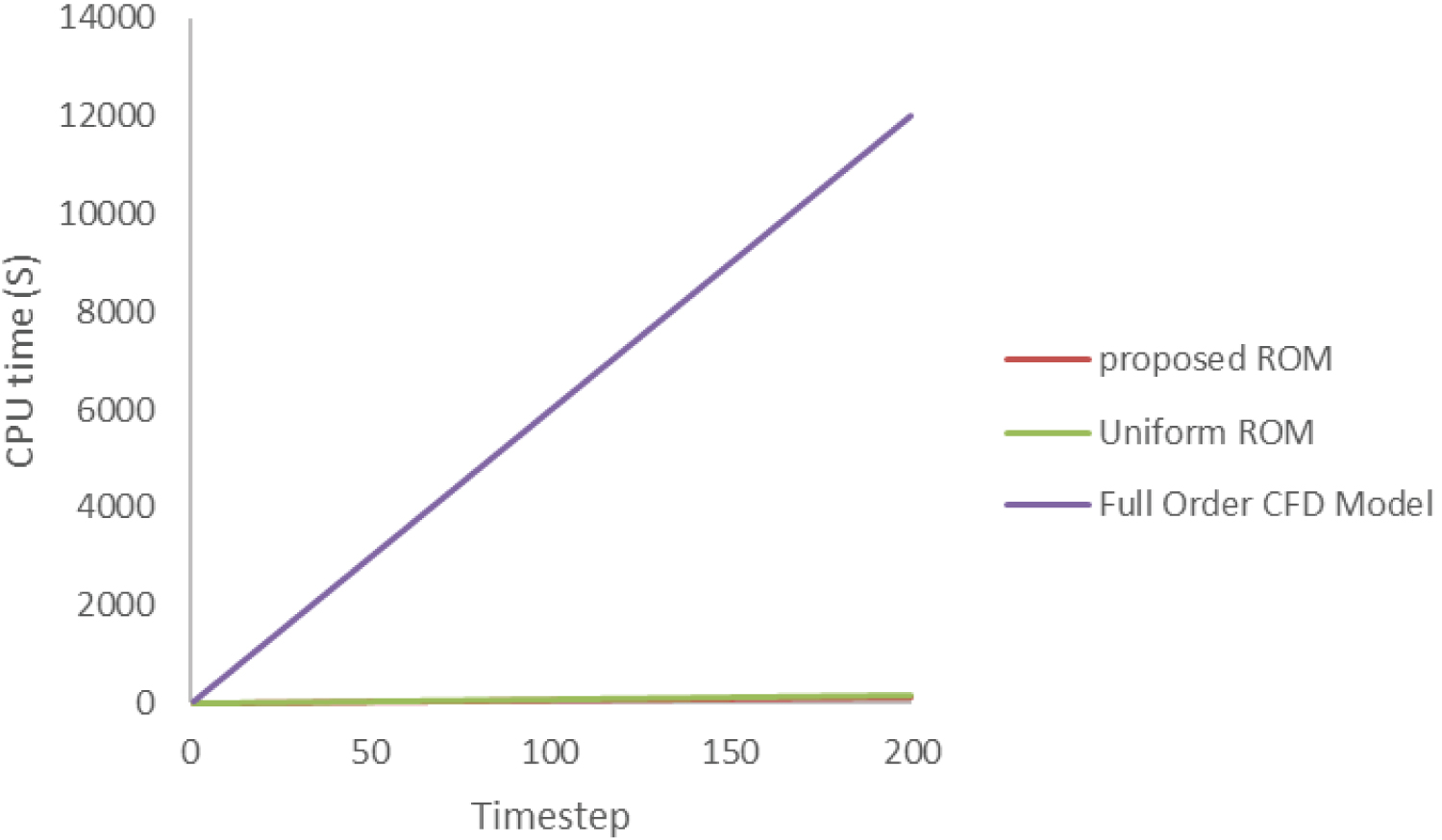
Figure 16: Comparison of the online CPU time history...
Comparison of the online CPU time history on the the two-dimensional pitching and plunging aerofoil in the case of the limit cycle oscillation between the full-order CFD solution and the ROMs.
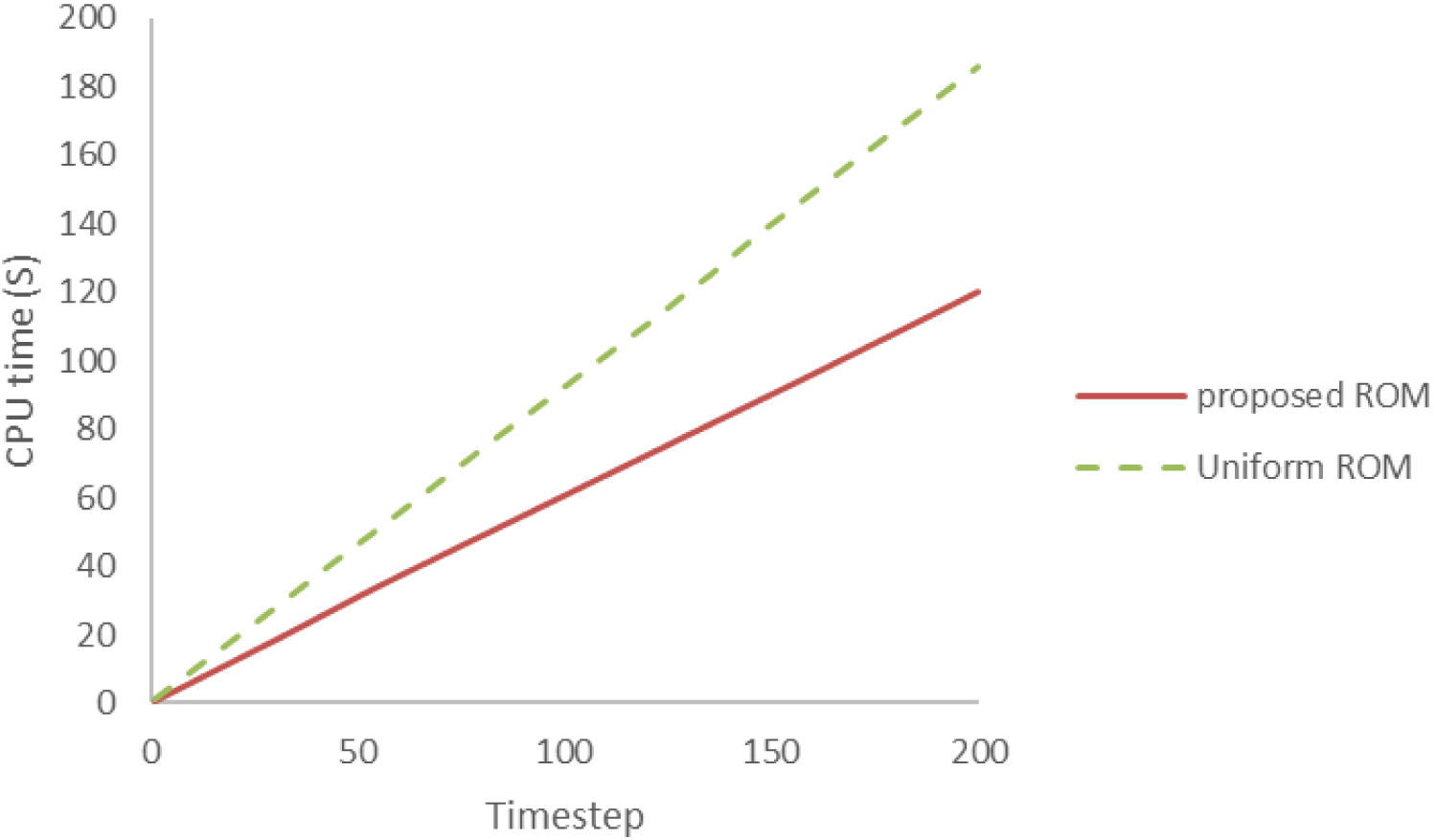
Figure 17: CPU time history for the ROMs on a...
CPU time history for the ROMs on a two-dimensional pitching and plunging aerofoil in the case of the limit cycle oscillation.
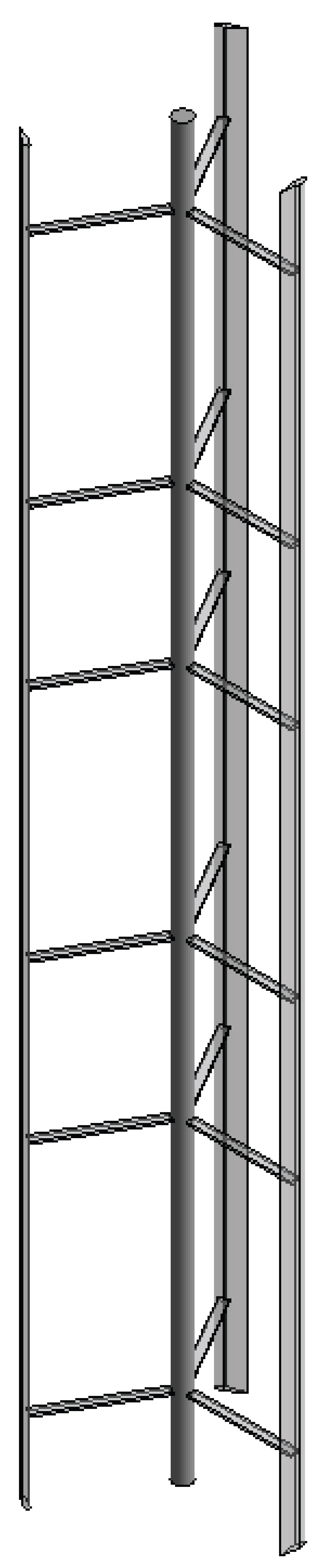
Figure 18: Geometry description of the 1.2 kW Windspire...
Geometry description of the 1.2 kW Windspire VAWT.
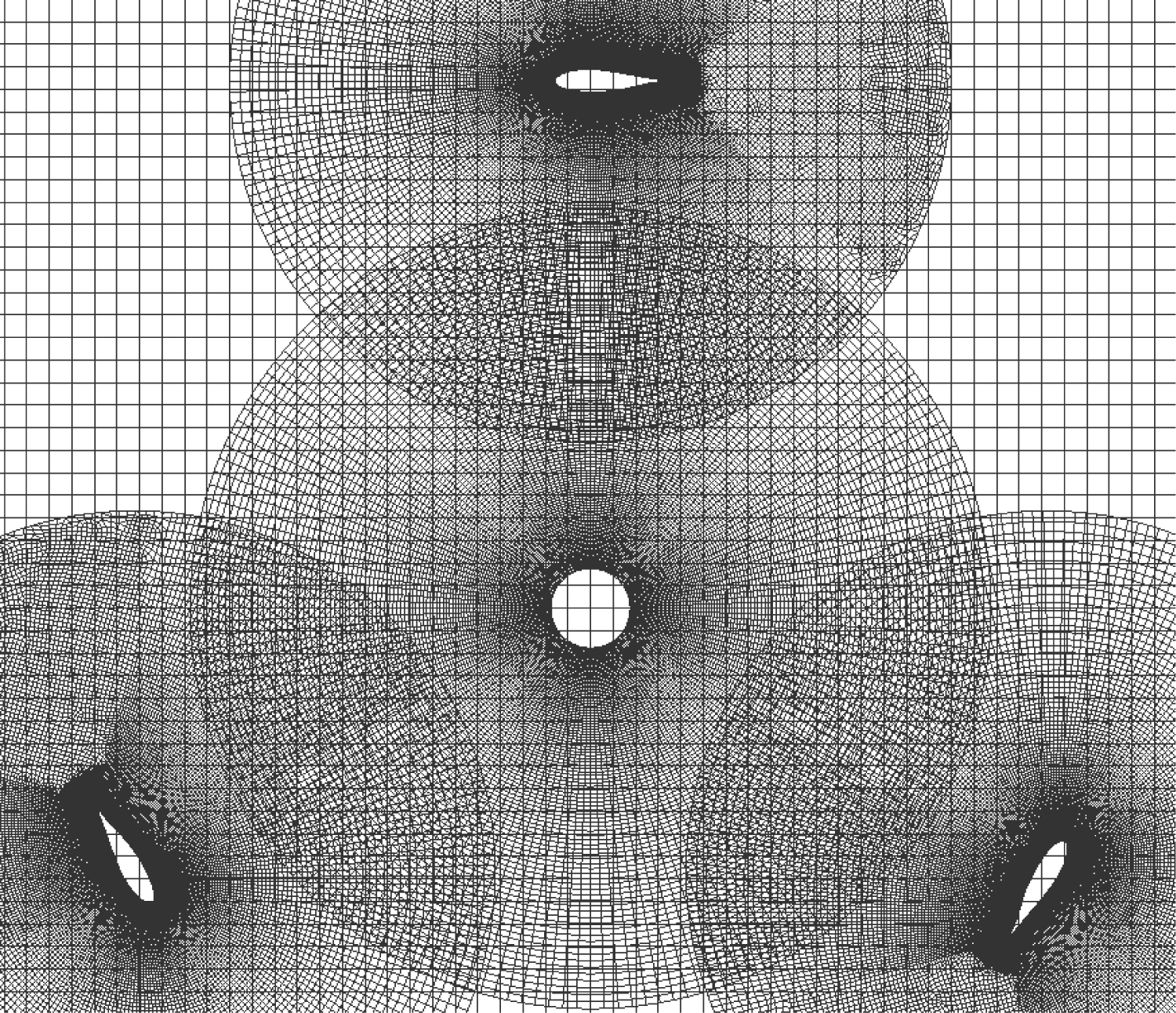
Figure 19: 2D cross section of computational mesh along...
2D cross section of computational mesh along the rotor axis. 4 overset mesh regions have been applied on the background mesh.
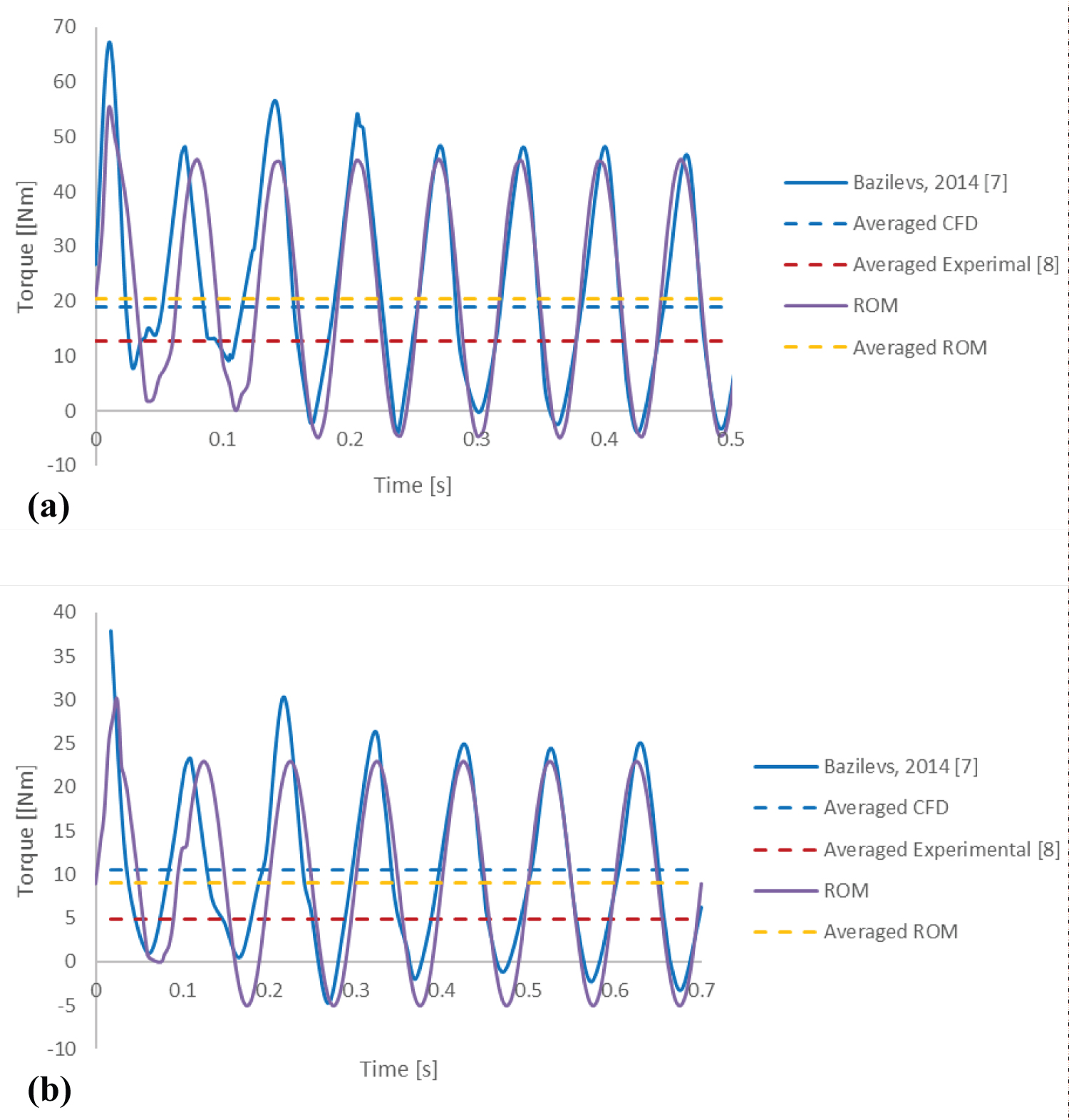
Figure 21: Time history of the aerodynamic torque...
Time history of the aerodynamic torque for the aerodynamic simulations: a) 8.0 m/s; b) 6.0 m/s.
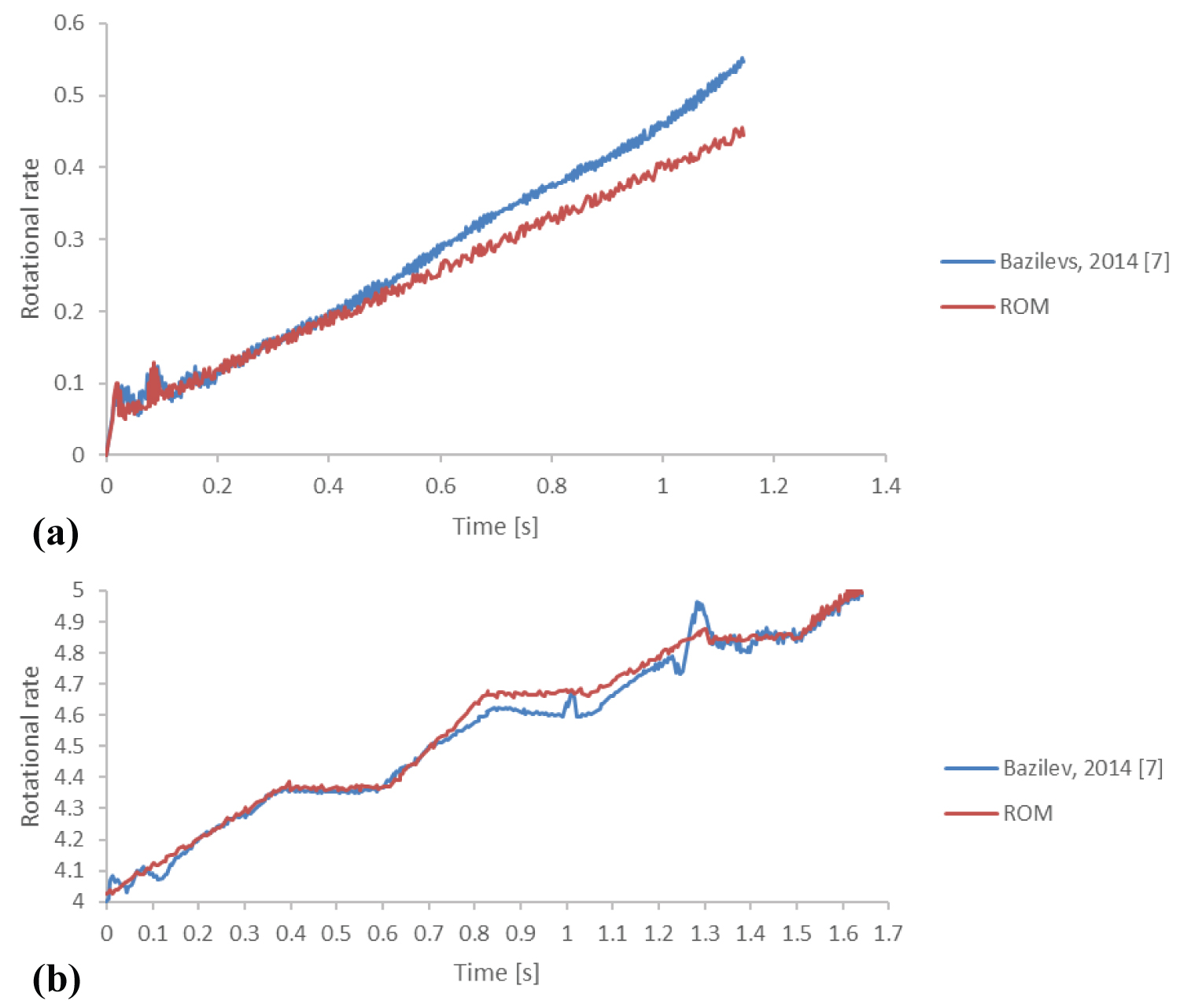
Figure 22: Time history of the rotor speed...
Time history of the rotor speed: a) Starting from 0 rad/s; b) Starting from 4 rad/s.
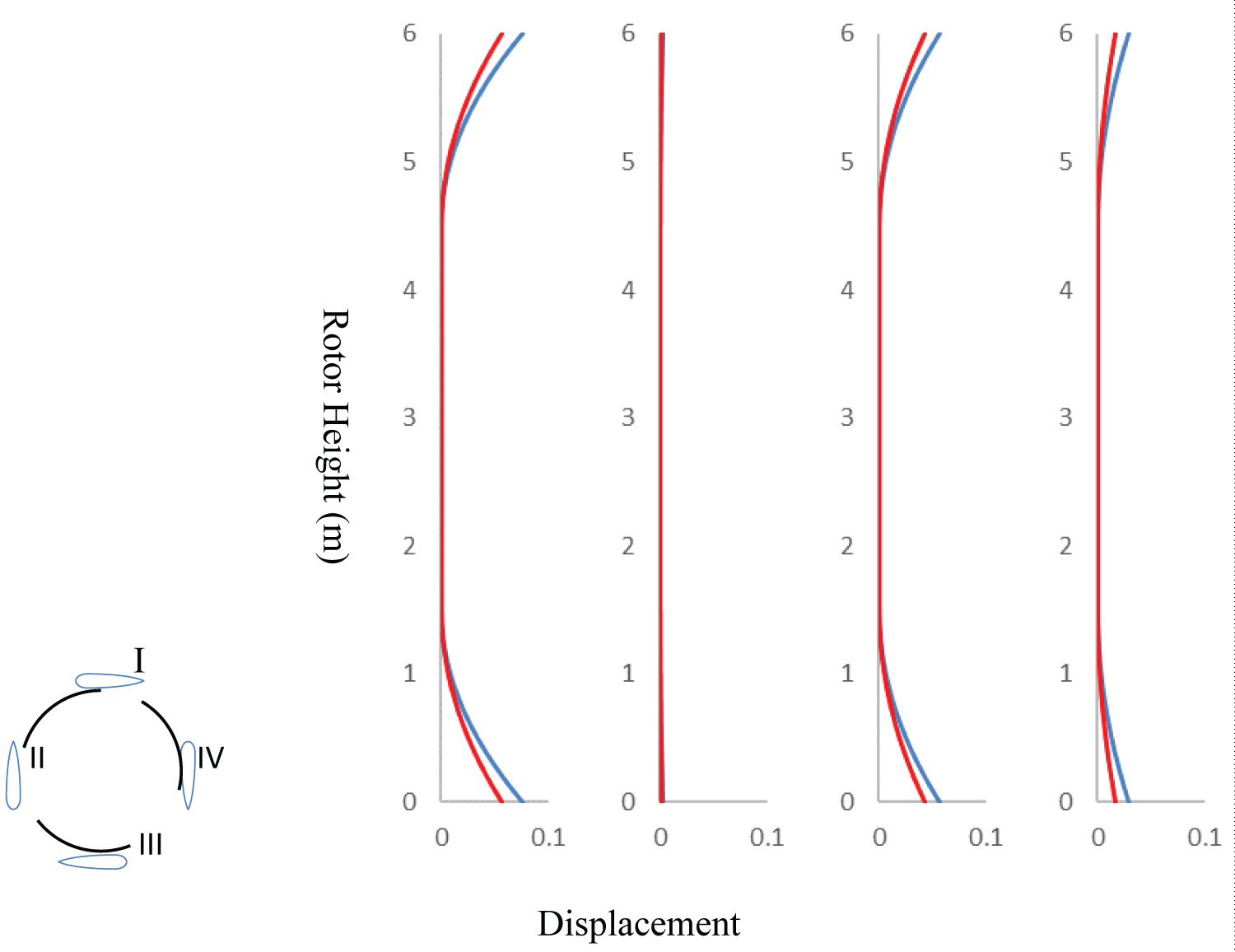
Figure 23: Time history of the blade bending displacement...
Time history of the blade bending displacement on one VAWT blade at different time snapshots during one operating period, inlet velocity 8.0 m/s (blue) and 6.0 m/s (red).
Tables
Table 1: Properties employed in the aerofoil model for the flow-induced vibration of the NACA 0015 aerofoil.
Table 2: Geometric and material properties of the 1.2 kW Windspire VAWT.
References
- Hansen MOL, Sørensen JN, Voutsinas S, Sørensen N, Madsen HA (2006) State of the art in wind turbine aerodynamics and aeroelasticity. Prog Aerosp Sci 42: 285-330.
- Liberge E, Hamdouni A (2010) Reduced order modelling method via proper orthogonal decomposition (POD) for flow around an oscillating cylinder. J Fluids Struct 26: 292-311.
- Camphouse RC, James HM, Ryan FS, Mark NG, Ausseur JM, et al. (2008) A snapshot decomposition method for reduced order modeling and boundary feedback control. 4th Flow Control Conf no 1-15.
- Lucia DJ, Beran PS, Silva WA (2004) Reduced-order modeling: New approaches for computational physics. Prog Aerosp Sci 40: 51-117.
- John L, Lumley JL (1970) Stochastic tools in turbulence. New York, London: Academic Press.
- Ali M, Pandey A, Gregory J (2016) Dynamic mode decomposition of fast pressure sensitive paint data. Sensors 16: 862.
- Halawa AM, Elhadidi B, Yoshida S (2017) POD & MLSM application on DU96-W180 wind turbine airfoil 04: 36-43.
- Gallardo D, Bevilacqua R, Sahni O (2014) Data-based hybrid reduced order modeling for vortex-induced nonlinear fluid-structure interaction at low reynolds numbers. J Fluids Struct 44: 115-128.
- Sabetghadam F, Jafarpour A (2012) $α$ regularization of the POD-Galerkin dynamical systems of the Kuramoto-Sivashinsky equation. Appl Math Comput 218: 6012-6026.
- Carlberg K, Farhat C, Cortial J, Amsallem D (2013) The GNAT method for nonlinear model reduction: Effective implementation and application to computational fluid dynamics and turbulent flows. J Comput Phys 242: 623-647.
- Sirisup S, Karniadakis GE (2005) Stability and accuracy of periodic flow solutions obtained by a POD-penalty method. Phys D Nonlinear Phenom 202: 218-237.
- Östh J, Noack BR, Krajnovic S, Barros D, Borée J (2014) On the need for a nonlinear subscale turbulence term in POD models as exemplified for a high-Reynolds-number flow over an Ahmed body. J Fluid Mech 747: 518-544.
- Xiao D, Yang P, Fang F, Xiang J, Pain CC, et al. (2016) Non-intrusive reduced order modelling of fluid-structure interactions. Comput Methods Appl Mech Eng 303: 35-54.
- Liberge E, Benaouicha M, Hamdouni A (2007) Proper orthogonal decomposition investigation in fluid structure interaction. Eur J Comput Mech 16: 401-418.
- Carlberg K, Bou-Mosleh C, Farhat C (2011) Efficient non-linear model reduction via a least-squares Petrov-Galerkin projection and compressive tensor approximations. Int J Numer. Methods Eng 86: 155-181.
- Chu Y, Serpas M, Hahn J (2011) State-preserving nonlinear model reduction procedure. Chem Eng Sci 66: 3907-3913.
- Aubry N, Holmes P, Lumley JL, Stone E (1988) The dynamics of coherent structures in the wall region of a turbulent boundary layer. J Fluid Mech 192: 115-173.
- Sirisup S, Karniadakis GE (2004) A spectral viscosity method for correcting the long-term behavior of POD models. J Comput Phys 194: 92-116.
- Noack BR, Afanasiev K, Morzyński M, Tadmor G, Thiele F (2003) A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. J Fluid Mech 497: S0022112003006694.
- Connelly JD, Huston RL (1994) The dynamics of flexible multibody systems: A finite segment approach-I Theoretical aspects. Comput & Struct 50: 255-258.
- Luo QZ, Wu YM, Li QS, Tang J, Liu GD (2004) A finite segment model for shear lag analysis. Eng Struct 26: 2113-2124.
- Hamper MB, Recuero AM, Escalona JL, Shabana AA (2012) Use of finite element and finite segment methods in modeling rail flexibility: A comparative study. J Comput Nonlinear Dyn 7: 041007.
- Connelly JD, Huston RL (1994) The dynamics of flexible multibody systems: A finite segment approach-II example problems. Comput Struct 50: 259-262.
- Bakr EM, Shabana AA (1987) Timoshenko beams and flexible multibody system dynamics. J Sound Vib 116: 89-107.
- Klein L, Gude J, Wenz F, Lutz T, Krämer E (2018) Advanced computational fluid dynamics (CFD)-multi-body simulation (MBS) coupling to assess low-frequency emissions from wind turbines. Wind Energy Sci 3: 713-728.
- Carrarini A (2003) Coupled multibody-aerodynamic simulation of high-speed trains manoeuvres. In: Virtual Nonlinear Multibody Systems. Springer, 411-418.
- Beyer F, Arnold M, Cheng PW (2013) Analysis of floating offshore wind turbine hydrodynamics using coupled CFD and multibody methods.
- Sirovich L (1987) Turbulence and the dynamics of coherent structures. III Dynamics and scaling. Q Appl Math 45: 583-590.
- Holmes P, Lumley JL, Berkooz G (1996) Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge: Cambridge University Press.
- Adamiec-Wójcik I, Wojciech S (2018) Application of the finite segment method to stabilisation of the force in a riser connection with a wellhead. Nonlinear Dyn 93: 1853-1874.
- Finkel RA, Bentley JL (1974) Quad trees a data structure for retrieval on composite keys. Acta Inform 4: 1-9.
- Björck Å (1994) Numerics of gram-schmidt orthogonalization. Linear Algebra Appl 197-198: 297-316.
- Šidlof P, Vlcek V, Štepán M (2016) Experimental investigation of flow-induced vibration of a pitch-plunge NACA 0015 airfoil under deep dynamic stall. J Fluids Struct 67: 48-59.
- Heinz JC, Sørensen NN, Zahle F (2016) Fluid-structure interaction computations for geometrically resolved rotor simulations using CFD. Wind Energy 19: 2205-2221.
- Bourguet R, Braza M, Dervieux A (2011) Reduced-order modeling of transonic flows around an airfoil submitted to small deformations. J Comput Phys 230: 159-184.
- Zanforlin S, Letizia S (2015) Improving the performance of wind turbines in urban environment by integrating the action of a diffuser with the aerodynamics of the rooftops. Energy Procedia 82: 774-781.
- Bazilevs Y, Korobenko A, Deng X, Yan J, Kinzel M, et al. (2014) Fluid-structure interaction modeling of vertical-axis wind turbines. J Appl Mech 81: 081006.
- Dabiri JO (2011) Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J Renew Sustain Energy 3: 4.
- Wind N, Renewable N, Van Dam J, Meadors M (2003) Wind turbine generator system power performance test report for the mariah windspire 1-kW wind turbine. 2: 1-44.
Author Details
Jiaxin Dong, Derek Ingham, Lin Ma* and Mohamed Pourkashanian
Energy 2050, Mechanical Engineering, University of Sheffield, Sheffield, UK
Corresponding author
Lin Ma, Energy 2050, Mechanical Engineering, University of Sheffield, Sheffield, UK
Accepted: November 22, 2021 | Published Online: November 24, 2021
Citation: Dong J, Ingham D, Ma L, Pourkashanian M (2021) POD-Galerkin Based Reduced Order Modelling for Flow-Structure Interactions. Int J Astronaut Aeronautical Eng 6:057.
Copyright: © 2021 Dong J, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Fluid-structure interactions, especially full rotor simulations for wind turbines, are still computationally inefficient. Although the Proper Orthogonal Decomposition (POD) - Galerkin based Reduced Order Modelling (ROM) has become a popular tool to solve many fluid dynamics problems, most studies are limited to fluid flows in a fixed or infinite domain. The ROM, with either spatially or temporally adaptive snapshots, are still lacking in research, and in this paper, a POD-Galerkin based ROM for a FSI problem is proposed. The aim is to reduce the complexity of the costly solution techniques for solving the governing non-linear unsteady partial differential equations that govern the aerodynamic flows over fluid-solid systems with moving interfaces. This novel POD-based ROM is applied to several cases of plunging-pitching aerofoils as well as fluid-structure interaction simulations of a 3D vertical axis wind turbine full rotor simulation. For both applications, this model is shown to be very effective when performed with the proposed snapshot grids, thus reducing the computational cost while maintaining the same level of accuracy.
Keywords
Reduced order modelling, Proper orthogonal decomposition, Fluid-structure interaction, VAWT
Introduction
Cost and complexity are still identified as the main obstacles when conducting numerical wind turbine fluid-structure interaction research [1]. One alternative to reduce the computational cost is to construct a reduced order model (ROM) of the aeroelastic system [2].
Reduced-order models (ROMs) are mainly aimed at capturing the detailed knowledge of the physical behaviour of the flow field via simple, robust, and convenient models. The nature of the aerodynamic flows yield non-linear unsteady partial differential equations whose computation requires numerical algorithms to be implemented on massive parallel super-computers, which is a very complicated and time consuming task [2]. Thus, the essential need arises for other effective tools to reduce the original complicated system of equations into a simple lower-dimensional model that characterises the physical process and captures its behaviour with a much lower computational cost. The computation of a ROM may be performed by either numerical simulations or measured experimental data. These models have been successfully applied in various topics, such as the steady analysis and design of inviscid flows past aerofoils, thermal chemical processing, and dynamical models [3]. The major contributions in the literature of reduced-order modelling are currently focused on unsteady aerodynamics.
Since wind turbines experience large unsteady pressure loads when exposed to the flow field, special care must be taken to design these components, such that they are capable of withstanding loads of this magnitude. These lead to a growing topic of research on reduced order modelling. The principle of the Reduced Order Modelling approaches is to replace computationally inefficient full order models of the aeroelastic system by a relatively small number of solutions generated by a high-fidelity model. The ROM seeks to simplify the problem by identifying important modes of the fluid system and the coupled system, based on the contribution of important modes [4]. The use of ROMs in a predictive setting raises some fundamental questions regarding the numerical properties, such as consistency, stability and convergence. One of these examples is the POD/Galerkin projection approach. Although it is a well-developed tool for model reduction, it is highly sensitive to any small changes in the state due to its inherent limitations. In addition, the implementation of this approach is limited, although it is capable of solving nonlinear systems, but often requires careful tuning in order to produce satisfactory results.
The Proper Orthogonal Decomposition (POD) approach for aerodynamics was first proposed by Lumley [5] in 1970 for the study of coherent structures in turbulent flows. The attractiveness of the POD method lies in the fact that it is a linear procedure and efficient in the design of robust feedback controllers leading to better-controlled airflow over aerofoils. Afterwards, much computational and experimental work has been performed by using this method to validate its effectiveness [6-8].
The reduced order modelling method has been applied to fluid-structure interaction problems. However, most studies are limited to fluid flows in a fixed or infinite domain. The implementation of the POD-Galerkin projection is not straightforward when there are moving solid boundaries or structures in the fluid flow, which is the case in many applications, including wind turbines. Actuation modes, Eulerian-Lagrangian dynamic mesh adaptation methods have been proposed to allow the transition between the moving/deforming near field to the stationary far field. The POD-Galerkin reduced order modelling approach has been applied to simulate Fluid-Structure Interaction problems [9-14]. Liberge, et al. [2,14] introduced a modified POD-Galerkin reduced order modelling of the Navier-Stokes equation for an oscillating cylinder. Xiao, et al. [13] proposed a different method to this topic by implementing non-intrusive functions to stabilise the solutions of the POD model. For unsteady flow problems, Sirisup & Karniadakis proposed a modified POD model by introducing penalty functions [11]. Most of these work focus on the FSI problem with a moving fluid structure interface and therefore the deformation of the solid domain is still lacking of research via the reduced order modelling approach [15-19].
In this paper, the Finite Segment Method (FSM) borrowed from the multi-body system [20] is coupled with the reduced order modelling approach to decompose the solid domain which shadows the merit of ROM methods. The finite segment method (FSM) has been used to model the shear deformation of various multi-body simulations (MBS) problems [21-24]. Luo, et al. [21] applied the FSM method to work out the shear deformation of box girders. In addition, FSM provides a good capability to couple multiple CFD solutions [25-27]. Klein, et al. coupled the CFD and the FSM methods to investigate a 5 MW wind turbine. Two individual solvers were run simultaneously and exchange results at discrete positions [25]. This method solves all geometries of the rotor, the pressure profile and all aerodynamic loads can be directly solved during simulations.
The objective of this paper is to present a new POD-Galerkin based ROM for the aerodynamical simulation with a moving and/or deforming fluid structure interface. This is achieved by coupling the POD-Galerkin based ROM and a proposed spatial and/or refinement strategy. This model is verified in a two-dimensional pitching and plunging aerofoil problem. In addition, to challenge its adaptability in 3D problem, a FSI investigation on a VAWT was chosen as a typical numerical application of this problem to demonstrate the capability of the new POD-Galerkin ROM at several different flow conditions.
Methodology
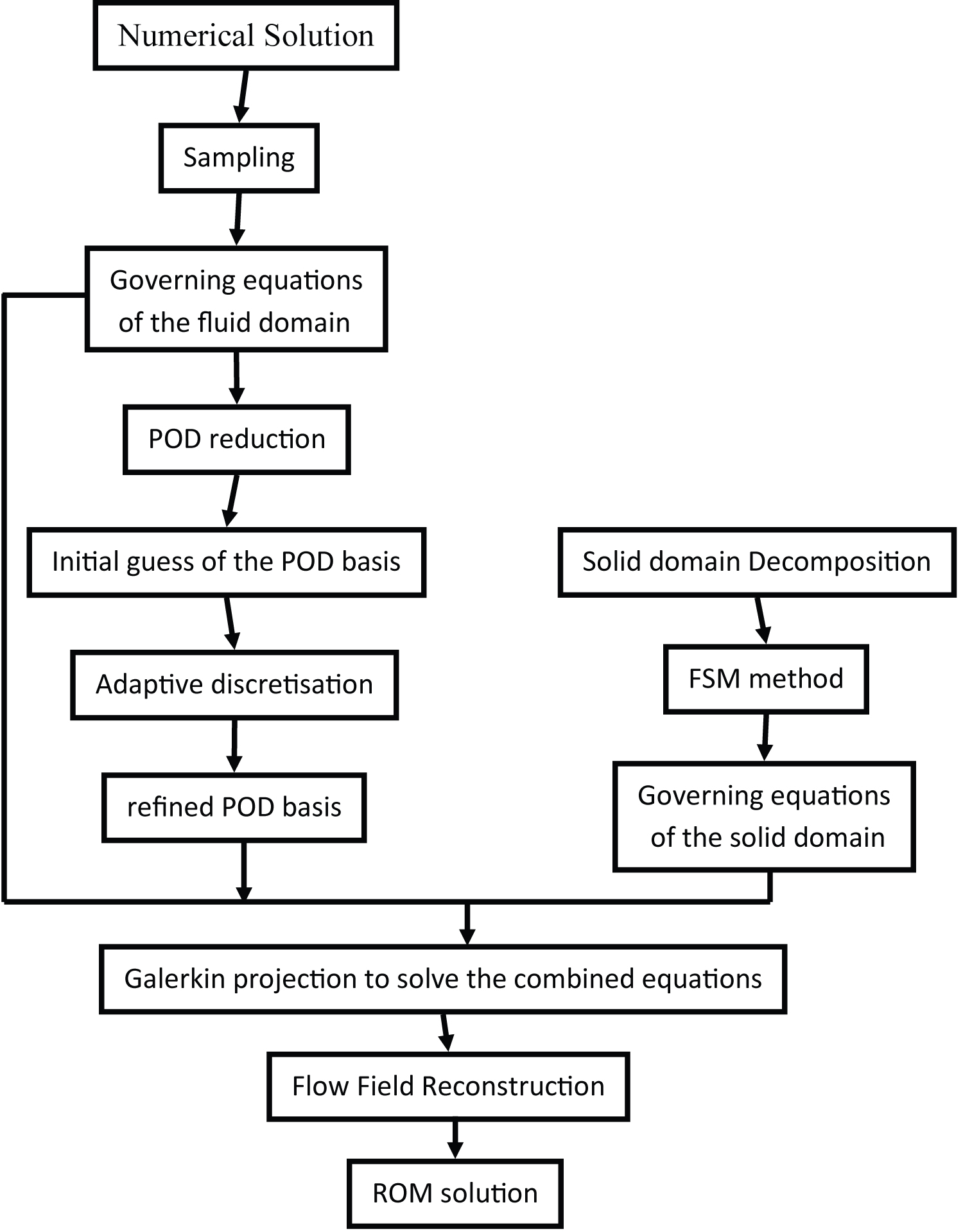
The overall solving process consists of three parts: using the POD-Galerkin method to decompose the governing PDE equations in terms of the temporal-dependent variables, namely the velocity or the motion of the domain. The solution scheme of the proposed method is illustrated in Figure 1. Since the motion of the solid domain needs to be calculated at each time step (as what the usual FSI simulation does), this undermines the computational efficiency of the ROM method. An additional decomposition method is introduced to work out the motion of the solid domain, that is, the Finite Segment method borrowed from the multibody system. Lastly, since the accuracy of the ROM method is highly depended on the base grid and the projection, the adaptive discretisation method is proposed to balance the accuracy and the cost.
Reduced order modelling
To start, some important definitions are introduced. The inner product is a generalisation of the dot product and follows the same basic rules as the dot product. In fluid dynamics, the inner product is defined as follows: in the space , for two vector field and defined in , the definition of the inner product is given by:
Mathematically, the function g can be any function. In this chapter, for the incompressible flow, and are represented by the velocity flow fields and , and the function g is directly defined as the energy. For instance, the inner product of the two velocity flow fields and , are defined in a two-dimensional domain and this yields the following:
Where and are the velocity components of in the x-direction and y-direction, respectively, namely, in a two-dimensional analysis. The induced norm of a vector u is then defined as:
Considering the reduced order model is based on the velocity flow field the time averaged of the velocity flow field is defined as:
The velocity is decomposed as follows:
Where, is the time-independent steady base flow and is the fluctuating velocity flow field. The goal is to present the fluctuating velocity flow field by the Proper Orthogonal Decomposition (POD) approach:
Where is the POD orthogonal basis and the temporal dependency is described by the amplitudes of .
To further reduce the computational cost, the method of snapshots [28], a discretisation of the POD procedure in the temporal domain, is implemented. Namely, M snapshots that are given at the discrete times as follows:
Similarly, the time averaged of the velocity flow field and the fluctuational velocity flow field are defined as:
The discrete form of the matrix R, which is a M × M matrix yields following:
Similar to the continuous case, the method of snapshots solves the following eigenvalue problem:
Where and are the eigenvectors and eigenvalues, respectively. Thus, the POD modes ui and the coefficients are computed as:
Considering an incompressible fluid in a rigid domain Ω, with the density and viscosity the coupled approach can be applied to the governing Navier-Stokes equation [29] is given as follows:
Where u is the velocity vector, p is the pressure. Using the POD method, the velocity flow field can be decomposed on the truncated POD modes at N modes as follows:
Where a0 = 1, is the mean velocity flow field; when i > 1, ai (t) are the temporal coefficients, and are the corresponding POD modes. An ordinary equation governing the temporal coefficients ai (t) is obtained by substituting the velocity flow field decomposition (Equation (2.15)) into the governing Navier-Stokes equation (Equation (2.14)) and projecting onto the subspace spanned by the POD modes , namely the Galerkin Projection:
Where denotes the inner product defined on the subspace. Due to the orthogonality and the free divergence of the POD modes , Equation (2.16) becomes:
Where
It should be noted that the incompressibility of the POD modes can be used to express in a boundary integral form as follows:
Where n is the outward norm of the domain considered for the boundary . The coefficient which contains the pressure term p.
Solid domain decomposition
The traditional POD-Galerkin ROM is capable of solving FSI problems when the solid domains are treated as fluid domains [2]. The method for decoupling the solid domain is borrowed from the Finite Segment Method used for the dynamic analysis of a slender system, in which a continuous system is replaced by a system of rigid bodies that reflect the inertial features of the system modelled, as schematically shown in Figure 1 [30]. The segments are connected by means of joints consisting of massless and nondimensional spring-damping elements that represent the stiffness characteristics of the link. Therefore, the governing partial differential equations for the dynamics are replaced by the equations of motion derived from the Lagrange equations.
When the longitudinal flexibility is omitted, the length of a deformed body along its curvature is constant and it is the sum of the lengths of each segment. Figure 2 shows the deformation of a test beam case modelled as a combination of 2 rigid segments. The deformation of the testing beam is realised as rigid body motion problems on the corresponding rigid segments. The position of any of the points lying on the interface between the fluid and solid domain depends on the width profile of the segment and the orientation of the axes of the reference coordinate system with respect to the axes of the inertial frame of reference. The deforming solid domain is therefore decoupled as a system of rigid bodies that can be pre-calculated.
Adaptive snapshot subspaces
The traditional uniform POD-Galerkin reduced order model does not represent a relatively accurate flow field in the case of a dramatic velocity change or thin solid bodies. Therefore, it is necessary to perform a local "refinement" strategy to improve its accuracy. The adaptive grid refinement process is illustrated in Figure 2. In this study, an adaptive grid discretisation based on a two-dimensional refinement strategy in which an internal node has exactly four children. The strategy is implemented using a quad-tree data structure which was first introduced by Finkel and Bentley [31], it can be implemented automatically and/or manually. The adaptive discretisation approach employed is initiated on a fixed grid, and at each iteration an inner node is introduced, which has four child grids when the velocity difference exceeds its threshold given by the user. The adaptive discretisation process is illustrated in Figure 3.
At the beginning of the adaptive refinement process, the initial POD grid is applied on the entire domain, i.e. the subspace is computed by means of the snapshot data basis. At the beginning of the simulation, this subspace is used to reduce the size of the nonlinear equation governing matrix, as illustrated in Figure 3a. From then on, in a loop over all grids, the differences are detected. If the accumulated difference is larger than a user defined tolerance value, the grid subspace affiliation is changed from the initial to a local-refined sub-domain, as illustrated in Figure 3b and Figure 3c. It should be noted that, at each time step after the same number of iteration loops, the number and size distribution of the subspace grid are determined by the baseline flow field. In addition, the process can be suppressed manually by adding local refinement to the region of interest, for example, the region near the aerofoils and tower in the vertical axis wind turbine (VAWT) simulations.
To minimise this additional drawback, the second grids update strategy is proposed. In each update, the new subspace in constructed by using only the relevant grids of the initial subspace or the subspace at the previous iteration loop. However, the extracted grids are orthonormalized, and the Gram-Schmidt algorithm is added to the adaptive solver [32].
Results
The proposed POD-Galerkin method is evaluated and validated via several testing cases, namely a two-dimensional oscillating aerofoil and a three-dimensional VAWT simulation. The proposed method is compared to both the corresponding full order CFD solution and the experimental results if approachable.
Oscillating aerofoil
A two-dimensional pitching and plunging aerofoil is studied as the application of the proposed POD-Galerkin model in this paper, but other motions can also be easily applied by the use of a similar approach. The numerical solution is based on the aerofoil oscillation experiments performed by Šidlof, Viček and Štěpán [33]. The CFD snapshots are pre-calculated to build the ROM.
The CFD snapshots are modelled according to Šidlof, Viček and Štěpán [33]. The flow-induced vibration of a NACA 0015 aerofoil freely moves normal to the direction of inlet. For more detailed information, please refer to Šidlof, Viček and Štěpán [33]. The NACA 0015 aerofoil, with a chord length c = 59.5 mm and a span 76.6 mm, is fixed in an 80 × 210 mm test section of a wind tunnel. The aerofoil rotates around the miniature ball bearings located at 1/3 of the chord, with the restoring moment is realized by a spiral torsion spring inside the aerofoil profile. The parameters employed in the model are summarised in Table 1, and these are the same values as those used in the experimental investigation.
Figure 4 illustrates the computational domain used in the CFD modelling. The fluidic model consists of 854,625 nodes and 879,632 elements. The mesh is split into two parts: background fluid domain and the overset domain near to the aerofoil. The time-step size is 5 × 10-5 second and the number of nonlinear iterations per time step is 1500. A loose coupling strategy was applied to couple both the fluidic and structural domains at each time step. The aerofoil is assumed as a rigid body, and the corresponding rigidity is modelled in the structural solver.
The structural model used in this study is a 2D aerofoil, and the vertical guide is modelled as a point mass at the rotational centre of the aerofoil. The aerofoil is attached to a linear spring-damping system which fits the linear stiffness and damping ratio employed in the experiment. The point mass and the aerofoil are then connected using a torsional spring-damping system which fits the experimental torsion stiffness and damping ratio. The structural model of the aerofoil is illustrated in Figure 4 and Figure 5.
The governing motion equation of the solid domain is determined by the structural model. A simple, linear, 2-D spring model coupled to the fluid dynamics model is employed, as shown in Figure 6 and the aerofoil modelled is free to translate along the y-axis. The fluid dynamics model generates the lift and moment coefficients that are introduced into the structural model that in turn determines the incremental motion of the aerofoil. This process is then executed in a stepwise fashion for each time increment. The previous time increment fluid dynamics model is used to compute the next time increment aerofoil position and then the aerodynamics of that position are calculated.
The proposed POD-Galerkin approach is applied to model the two-dimensional flow-induced pitching and plunging aerofoil in the cases of limit cycle oscillating at different Reynolds numbers. The amplitudes stabilize at the limit cycle oscillations due to the structural and/or aerodynamic nonlinearities. The accuracy and computational cost of the model in the case of a limit cycle oscillation is investigated. Accuracy and order reduction are discussed with respect to the full-order numerical model and the traditional POD strategy with uniform grids.
The model is established using ANSYS FLUENT coupled with the Transient Structure modules using the k-ω SST turbulence model. This two-equation model is suitable for modelling the boundary layers as well as the far field flows, and therefore it has been used extensively in studies involving wind turbine blades and aeroelastic problems with reasonable results [7,34].
The case of limit cycle oscillations are chosen at the Reynolds number 173,000, defined by the incoming velocity of 44.7 m/s, the chord length of the NACA 0015 aerofoil is 59.5 mm. The aerofoil starts to oscillate at the initial displacement of 3.3 mm, and the initial pitch angle of 0°. The two-way fluid-structure interaction strategy is selected to simulate the motion of the aerofoil.
The accuracy of the numerical model has been validated by comparing the new predicted results to the experimental data. The presentation of the pitch angle against the plunge at a Reynolds number 173,000 is presented in Figure 6. The phase trajectory rotates counter clockwise which increases the plunge amplitude, decreases the pitch amplitude and decreases the phase difference. In addition, the time history of the plunge and pitch angle for the limit cycle oscillation is shown in Figure 7 and Figure 8. The time history is plotted after convergence to the limit cycle. It has been shown that the accuracy of the numerical case is preserved to be almost the same as the experimental data, where the average error in both the pitch and plunge solutions are underestimated by about 5% in comparison to the experimental data. However, the frequency and phase are almost identical to the experimental data for both cases. The error in the amplitude is due to only two dimensions being considered in the numerical solution, and although the third dimension is negligible, it still has an effect on some of the results. Therefore, both limit cycle cases may be considered to be sufficiently accurate to construct the reduced order models.
Reduced-order modelling: The proposed POD-Galerkin ROM procedure was executed by implementing a MATLAB® subroutine and the results obtained are discussed. The reduced order model is built using a pre-calculated numerical solution.
The proposed ROM modes are computed from 400 snapshots of the simulation data that covers four complete periods of oscillation. The domain is uniformly discretised in 160 × 40, 320 × 80, 640 × 160, and 1280 × 320 grids in the x- and y-direction, respectively. Then, three different proposed ROM models based on firstly on the created uniform grids, namely 160 × 40 - adaptive, 320 × 80 - adaptive, 640 × 160 - adaptive, are built. For each case, overall computational cost, maximum velocity difference, weighted difference between the rebuilt velocity flow field and the analytical solution are summarised. For each case, the energy percentage of the POD mode decreases monotonically. The first ten dominiant POD modes, which cover more than 99.5% of the overall kinematic energy, are selected to perform the following calculation. The maximum difference of the velocity profile within each grid no larger than the 1/100 of the inlet velocity is selected as the threshold of the adaptibe discretisation. The flow field patterns of the limit cycle oscillation at a Reynolds number 173,000 are chosen to demonstrate the vorticity contours of each POD modes, and the mean flow of the limit cycle oscillation (LCO), as shown in Figure 9. Seleted POD modes associated with the velocity are qualitatively presented. These modes do not present the flow structures but can provide good information about the sparce correlations for example [35]. The symmetric/anti-symmetic patterns about the wake line have been previously reported [19]. Compared to the flow pattern obtained from the POD modes of the uniform ROM approach, the proposed ROM presents much more detail in the region with large velocity deviance, such as in the vicinity of the aerofoil, which provides the capability of predicting much more accurate results.
To further show the capacity of the model more clearly, the flow structure at the same time steps have been investigated: the velocity flow field computed by the numerical approach and the proposed POD-Galerkin ROM models. Five different time step snapshot of the limit cycle oscillation at the Reynolds number 173,000 are selected as an example. With this decomposed solid domain, the dynamics for this prescribed large solid motion problem and the corresponding adapted discretisation are shown in Figure 10. The accuracy of the adaptive reduced order model is preserved to be almost the same in comparison to the numerical solution after five iteration.
The reconstructed dynamic system of the most dominant modes, i.e. the first ten modes, are achieved by the adaptive projection onto these modes, and it is compared to the ROM using the same quality of uniform grids to quantify the performance of the proposed POD-Galerkin ROM. The phase portrait of the case of the limit cycle oscillation at the Reynolds number 173,000 is plotted in Figure 11, where a comparision is made between the numerical solution and the Galerkin-based ROM with and without the proposed method. The presentation of the plunge profile against the pitch angle is plotted after convergence onto the limit cycle. The phase trajectory rotates counter clockwise which increases the plunge amplitude, decreases the pitch amplitude and decreases the phase difference.
Compared to the uniform ROM approach, the proposed ROM more accurately predicts results for both limit cycle oscillation cases. Figure 12 shows the normalised error between the benchmarked numerical solution and the ROM method via the uniform approach and the proposed method. The shape, frequency and amplitudes are much closer to the experimental and numerical solution [33]. The proposed adaptive discretisation concentrates on the vicinity of the aerofoil, as well as in the wake region to minimise the velocity variance within the reduced order modelling process, and it varies at different time steps. The accuracies of the adaptive reduced order model are observed to be almost the same in comparison to the numerical solution after five iterations. In contrast, the reconstructed flow fields using the uniform ROM are not perfectly accurate due to the large motion of the aerofoil.
Figure 13 shows the online and offline CPU time required to compute up to 200 timesteps with varying mesh size. The computational cost of the full order CFD simulation is compared against those of a uniform discretisation and the proposed ROMs. It shows that the cost of the ROM models remains static with an increasing resolution of the mesh, and that significant CPU speed-ups are obtained when using the mesh with the largest number of nodes. The CPU costs were reduced by a factor of about 100 compared to the cost of the high-fidelity model. The offline CPU time listed here includes the time for assembling and solving the matrix for the full model and projecting the POD solution onto the full space, as shown in Figure 14. It can be seen that the proposed ROM is much more computationally efficient than the traditional uniform ROM, and this is because the decrease in terms of mesh density speeds the computational speed of the ROMs, since it involves assembling and solving different dimensional matrices.
The proposed ROM more accurately predicts the results for the limit cycle oscillation cases compared to the uniform ROM with the same level of grid. The reconstructed ROM solutions are compared to the existing numerical results as well as the experimental data. The results show a relatively good agreement with the CFD solution regarding the velocity and displacement fluctuations. Compared to the accuracy and the computational cost between the ROM approach and the numerical method, the proposed ROM shows a very good potential for use in fluid-structure interaction simulations (FSI) problems.
FSI modelling of windspire VAWT
In the previous application, the solid domain is considered as a rigid body, and this shadows the advantage of the proposed ROM to deal with FSI problems with flexible bodies. The proposed ROM is implemented in a 3D simulation to further challenge its capability and stability. The computations in this section are performed for a well investigated 1.2 kW Windspire design, which is a three-bladed Darrieus VAWT [36], as shown in Figure 15. The results of the FSI simulations are compared to [37] at realistic working conditions conducted by the NREL and the caltech field laboratory for optimized wind energy [38,39] (Figure 16 and Figure 17).
The blades and struts are made of aluminium, and the tower is made of steel. Pivotal structural properties, thickness t, radius r, Young's modulus E, Poisson's ratio ν, density ρ and mass m, are summarised in Table 2. In this chapter, the Tower is assumed to be rigid, and the deformations of other parts are investigated during the FSI simulation Figure 18.
A 50 m × 20 m × 30 m box grid is used for the simulation of the flow around the Windspire VAWT. Similar to [37], 15 metres separate the VAWT centre from the inlet at the upstream boundary and 35 m from the downstream outlet boundaries. The computational mesh is shown in Figure 19 and Figure 20. The computational domain is split into two parts: The background mesh with structural meshes and the overset mesh with a refined mesh near the VAWT of interest. The tower and the struts are modelled as rigid bodies and the blade of the VAWT is modelled as a flexible body. A uniform wind velocity profile is prescribed at the inlet. Mesh and time size sensitivity studies are carried out to determine the appropriate cell sizes and time step. 200 snapshots over 4 periods of revolution are used to build the ROM, and the VAWT is modelled as a system of 40 rigid bodies. Each blade is represented by a chain of 13 rigid segments. Two typical aerodynamic simulations are selected to challenge the capacity on the aeroelasticity and aerodynamics of the proposed ROM method regarding aerodynamic accuracy. The settings of these two simulations are wind speed of 8.0 m/s and rotor speed of 32.7 rad/s, and wind speed of 6.0 m/s and rotor speed of 20.6 rad/s, respectively, following [37]. For both cases, the time history of six cycles of the torque as well as the averaged value computed from the ROM are compared to the corresponding experimental [38] and numerical [37] results.
The first six dominating POD modes are selected to build the ROM code. These six dominant modes cover more than 99.9% of the overall kinematic energy, and therefore are selected to perform the following calculations. The time history of the aerodynamics for both cases is plotted in Figure 13. The pure aerodynamic ROM computation shows good agreement with the CFD simulation, despite the ROM results slightly overestimating the averaged torque. On the first few cycles, the ROM codes fail to show a consistent accuracy against the full-order solution. This may be due to it highly relying on the baseline model, and therefore cannot accurately predict the results when the full-order model is still fluctuating.
Furthermore, an FSI investigation, particularly focused on the self-starting of the VAWT, is performed in this paper. The inflow wind speed is fixed at 11.4 m/s, and rotor starts spinning at 0 rad/s and 4 rad/s. Figure 14 shows the comparison of the rotation rate obtained from the reduced-order model to that obtained from the CFD simulations performed by Bazilevs [7]. For both cases (shown in Figure 14), the proposed ROM shows good agreement in CFD simulation. The rotor naturally accelerates for both the 0 rad/s and 4 rad/s cases. The plateau regions are accurately predicted in the 4 rad/s cases. This is verified by the field test and articles that focus on the FSI of the VAWT (Figure 21).
Compared to the experimental data, both the ROM and CFD simulations overestimate the torque and the rotational rate of the aerodynamic and FSI simulations. One explanation may that it is due to the simplified models that are constructed in the ROM codes. The flexible VAWT blade is modelled as a chain of rigid bodies and the equivalent loads are applied uniformly distributed on each of the segments. Although this method successfully predicts the starting behaviour, the over prediction is still required to be minimised in the future work. This explanation has been validated in the following deformation discussion (Figure 22).
Figure 12 shows the bending displacement contour under constant inlet velocity 8.0 m/s and 6.0 m/s conditions at four evenly distributed snapshots during one cycle. It is apparent that a large deflection occurs in the vicinity of the free ends of the blade. The bending displacement in the middle region of the blade is around zero as there are several additional struts in this particular VAWT model. For both cases, the central part of the blade has the minimum deformation as this part of the blade is supported by struts, and this trend has been validated at all instantaneous time snapshots during one cycle. In addition, an increase in the tip speed ratio leads to an increased deformation as shown in Figure 12 and the ROM codes overestimate the deformation compared to the full-order numerical results, this is due to the assumption of the modelling the flexible blades as a chain of a small number of rigid bodies. This has been validated by a further investigation on the impact of the number of rigid bodies, as the number increases, the rigidity behaviour is closer to that of the actual flexible body Figure 23.
Conclusion
A POD-Galerkin ROM has been employed to predict the flow field in VAWT fluid-structure interaction problems. The method is borrowed from the immersed boundary technique used in this paper, where the effect of the moving boundary is represented by extra terms added to the governing Navier-Stokes equation. An alternative method borrowed from Finite Segment Method is implemented to decouple a function that describes the solid domain. This novel POD-based ROM is applied to some cases of plunging-pitching aerofoils. For the applications whose solid domain are either stationary or moving, this model is shown to be effective when performed with the proposed snapshot grids, thus reducing the computational cost while maintaining the same level of accuracy Compared to the uniform POD-Galerkin approach, the proposed POD-Galerkin reduced order models is more accurate close to the aerofoil due to its adaptive grid discretisation. In addition, the proposed POD-based ROM is applied successfully to the 3D case of the well investigated Windspire VAWT in terms of both the aerodynamic and aeroelastic modelling of the deformed and/or discontinuous solid domain. It is observed that the pure aerodynamic ROM computations and the FSI ROM simulations produced good agreement with the field-test data and/or full CFD simulations at various wind and initial conditions.
In conclusion, the new proposed reduced-order model shows a very promising application in computing the fluid-structure interactions and the aerodynamics of VAWTs over a large range of different operational conditions. This reduced order modelling method can be very successfully applied to a large variety of aerodynamic and aeroelasticity problems, especially those with a moving/deforming fluid-structure interface. The proposed method has been validated in both 2D and 3D simulations with various Reynolds number. The key advantage of these models are that there is a very substantial reduction in the computational time and effort and this can be realised as the typical 3D full FSI simulations of a complete wind turbine is computationally prohibitively expensive.