International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 7, Issue 1
Research Article
DOI: 10.35840/2631-5009/7561
Stability Analysis in Rotational Systems Using the Tumbling Coefficient
Danny Hernán Zambrano Carrera1* and Hans Ingo Weber2
Table of Content
Figures
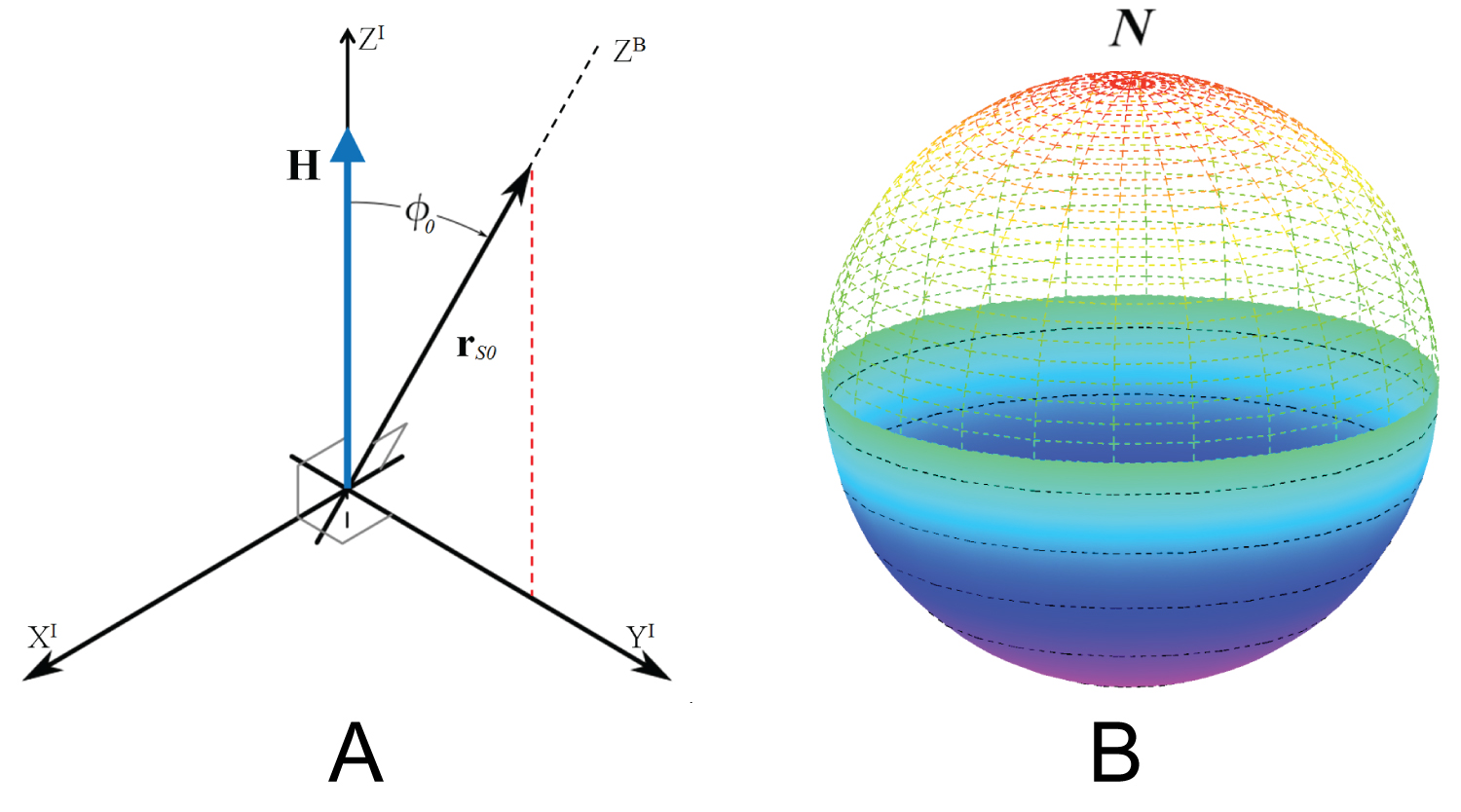
Figure 1: Hemispheres on the unit sphere...
Hemispheres on the unit sphere and inertial frame in initial condition, where H points to the north.
References
- Weber HI (2019) Raciocinando Dinâmica de rotação . Amazon, Rio de Janeiro, Brazil.
- Sidi MJ (1997) Spacecraft dynamics and control, A practical engineering approach. Israel Aircraft Industries Ltd. and Tel Aviv University, Cambridge University Press, UK.
- Wiesel WE (1977) Spacecraft attitude determination and control. (2 nd Edn), McGraw-Hill, US.
- Doroshin A (2014) Homoclinic solutions and motion chaotization in attitude dynamics of a multi-spin spacecraft. Communications in Nonlinear Science and Numerical Simulation 19: 2528-2552.
- Mueller A (2010) Approximation of finite rigid body motions from velocity fields. ZAMM Journal of applied mathematics and mechanics: Zeitschrift fu¨r angewandte Mathematik und Mechanik 90: 514-521.
- Carrera DHZ (2010) Unrestricted rigid body motion possibilities. Ph.D Thesis in Applied Mechanics, Pontifícia Universidade Católica de Rio de Janeiro, Brazil.
- Chen HK, Lee CI (2004) Anti-control of chaos in rigid body motion . Chaos, Solutions & Fractals 21: 957-965.
- JH Challis (2020) Quaternions as a solution to determining the angular kinematics of human movement. BMC Biomedical Engineering.
- Schutte AD, Udwadia FE (2009) A new formulation for rotational dynamics . 15 th International Workshop on Dynamics and Control. CIMNE. Barcelona.
- https://web.stanford.edu/class/me331b/documents/MomofInertLab.pdf
- Carrera DHZ, Weber HI (2012) Necessary conditions for tumbling in the rotational motion. AIP Conference Proceedings 1493: 1096-1102.
- Strogatz S (2001) Nonlinear dynamics and chaos: With applications to physics, biology, chemistry, and engineering. Advanced Book Program. Westview Press.
- Leine RI, Capobianco G, Bartelt P, Christen M, Caviezel A (2021) Stability of rigid body motion through an extended intermediate axis theorem: application to rockfall simulation. Multibody System Dynamics 52: 431-455.
- Chernousko FL (1990) Evolution to rigid body motions due to dissipative torques. In: W. Schiehlen, Nonlinear Dynamics and Engineering Systems. Springer Verlag, 51-57.
- Magnus K (1971) Springer-Verlag, Berlin Heidelberg.
- Rimrott FPJ, Pan R (1990) Attitude stability of a tethered satellite in locked rotation. Ing arch 60: 419-430.
Author Details
Danny Hernán Zambrano Carrera1* and Hans Ingo Weber2
1National Institute for Space Research - INPE, São José dos Campos, Brazil
2Pontifical Catholic University of Rio de Janeiro - PUC-Rio, Rio de Janeiro, Brazil
Corresponding author
Danny Hernán Zambrano Carrera, National Institute for Space Research - INPE, São José dos Campos, Brazil.
Accepted: August 09, 2022 | Published Online: August 11, 2022
Citation: Carrera DHZ, Weber HI (2022) Stability Analysis in Rotational Systems Using the Tumbling Coefficient. Int J Astronaut Aeronautical Eng 7:061
Copyright: © 2022 Carrera DHZ, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The goal of this work is the investigation of the necessary conditions for the existence of tumbling in rotational motion of rigid bodies. For this purpose, we choose a methodology to simplify the study of rotational motions with great amplitude, for example free bodies in the space, allowing an extension of the analysis to non-conservative systems. The developed method can be easily applied to orbital motion of a satellite in outer space, where the angular velocities are continuously monitored, and actuators are activated to seek for rotational stability. For any rotational motion, the projection of the angular velocity along the principal axes of inertia must be known, defining completely the initial condition of motion. In this paper coordinate systems are established in order to allow a simple analytical work on the equations of motion. As a result of the methodology used in this work it is proposed the definition of a parameter, calling it tumbling coefficient, to measure the intensity of the tumbling and also the amplitude of the motion, even passing the limits of stability in the concept of Lyapunov. In the motion of bodies in space only when this tumbling coefficient has a positive value, the no tumbling condition is guaranteed. The tumbling is inherent for a rotation around the axis of intermediate moment of inertia but can also occur by action of external impulses when the conical movement characteristic of the stable attitude is de-characterized. Another relevant result of this work associates for different initial conditions of motion the areas of stability and instability in the Magnus Triangle representation. In the study of non-conservative systems for an oblate body, a sufficient condition to investigate damped motion is given by the tumbling coefficient, and this condition is satisfied by viscous torques. This paper seeks to highlight the physical understanding of phenomena and the influence of various parameters that are important in the process.
Keywords
Attitude dynamics, Spin stabilization, Satellite, Tumbling, Nonlinear dynamics, Quaternion, Stability
Introduction
All classical literature in Mechanics spends some time describing the motion of free bodies in space: there is a good number of analytical possibilities to investigate this problem. Nevertheless, there are so many aspects to handle, that it always will be possible to have a new look of some particular situation. The general motivation of this analysis is to search the limits of stable operation of a free body spinning in space with unequal principal moments of inertia spinning in space after suffering the impact of some external perturbation.
The ideal initial condition will find the body spinning about one of the axes of principal moments of inertia. if it is the intermediate axis of inertia it will be naturally unstable, but for the other two possibilities the stability will depend on the impact itself [1]. This known behavior will allow to validate the results.
Our analysis will consider the unitary vector rs directed along the spin axis which, for no perturbations, is aligned with the angular momentum vector H calculated for the center of mass. But a misalignment between both vectors may exist due to, for example, a remaining rotation after the satellite separation from the launcher or an external perturbation [2,3]. For a moment free condition, this means that the vector rs starts rotating around the vector H. To visualize the motion we consider a sphere (Figure 1) divided in two hemispheres [4,5], where H points to the north. The tumbling of the satellite occurs if rs keep changing hemispheres [6].
An appropriate choice of reference frames will make all the investigation easier [1]. Coordinates for the inertial frame (SI) consider its z axis aligned with the angular momentum vector H and the body frame (SB) will have its z axis directed along the rs vector, which points according to one of the principal moments of inertia (depending on the geometry being investigated). The x and y axes of (SB) will be directed along the other principal directions of the body. The full position of (SI) is then established with its x axis orthogonal to the plane defined by the vectors H and rs (Figure 1).
The initial condition at t = 0 can be established just after a positive impact along the XI axis injects momentum and displaces H to a φ0 position from ZB aligned with the axis of principal inertia rs the identification of its intensity will be given by angle φ0. But it can also be at an arbitrary instant when the attitude and the angular speed are known. We will see that for the stability analysis the initial attitude must be defined, and it will also be needed to draw trajectories in space for the body’s motion [3].
Angular momentum in inertial frame, spin vector in body frame and at t = 0 in inertial frame, the normalized inertia tensor [7] for the center of mass in principal axes body frame are:
Angular velocity, director cosine attitude matrix and angular momentum in body frame are the next equations (3), while an index 0 will define the variables at the initial condition:
The deviation between spin axis and angular momentum axis defines the misalignment of the spin axis and is a measure for the impact [6]. It is obtained from the scalar product between these vectors, as shown by Equation (4).
Using Tait-Bryan (Cardan) sequential rotations [2] an equivalent rotation matrix BTI to the attitude matrix can be defined using the angles α, β e γ. According to the rotation sequence
Results
A negative α0 angle is necessary for the described impact.
There is a second solution for (5) to be considered if the body is tumbling and it is achieved for
and corresponds to angles .
Considering the initial condition (0 state)
It is possible to relate the initial position of the gamma angle with the attitude matrix in (3). According to Equations (3) and (4) the initial attitude is defined in Tait-Bryan angles:
The simulations done for this problem used attitude quaternions q = [ q1 q2 q3 λ ]T motivated by the frequent crossing of stability borders [8]. The initial conditions (Equation 9) are transformed to quaternions, the procedure for relate the quaternion components of the sequential rotations (Tait-Bryan) is explained in [9] and [6]. Integration of the quaternion equation result in rotation matrices along the time, allowing the visualization of the motion.
Normalized Equations
Beside the above-mentioned parameters, there is still the kinetic energy to be considered, which will be constant together with the angular momentum if we admit the system conservative and torque free. Considering only rotation, the kinetic energy can be related to the angular momentum using Equation (3):
Which suggests us to introduce a parameter K as follows:
K represents how the perturbation distributes between kinetic energy and the square of the angular momentum [10]: when the satellite is spinning without perturbation around the chosen axis of one of the principal moments of inertia K = 1 [11]. The imposed perturbation will increase or decrease K. It also will depend only on the geometry of the satellite and of the angular velocity components in the body frame [3], as we can see in the Equation (11).
The range of values for K depend on the geometry [6,10]. We investigate three geometries:
The oblate (flattened) body: 1 > µ1 > µ2 also 1 < K < 1/µ2;
The intermediate body: µ1 > 1 > µ2 also 1/µ1 < K < 1/µ2;
The prolate (stretched) body: µ1 > µ2 > 1 also 1/µ1 < K < 1.
We introduce an equivalent angular velocity ν for the normalization process [11,12] based on the square of the length of the angular momentum vector (Equation 12) and introduce non-dimensional components of the angular velocity:
In this way we get two equations for the problem, representing the conservation of kinetic energy and of angular momentum:
If we introduce , , then the possible solutions are obtained by the intersection of a sphere with an ellipsoid:
Necessary Conditions for Tumbling
Tumbling occurs when the spin vector rs crosses from one hemisphere [11], defined according to H, to the other (Figure 1). The component rz = 0 at this moment. Considering Equations (1), (2) and (3):
We see that the spin velocity becomes zero at this instant and the body is in the border condition to tumble. Also in (Equation (15)) r = 0 and only two parameters (p e q) must be considered to evaluate the start of the tumbling condition. An ellipse crosses a circle in 4 points (with same center) when a semi-major axis of ellipse is outside the circle and semi-minor is inside the circle. That means in Equation (15) that we look for an intersection between a circle and an ellipse [11]. There are two possible solutions for this intersection:
Both conditions will be attended introducing the tumbling coefficient in Equation (18). The acronym of this coefficient is derived from the word in Portuguese language "Capotamento" meaning tumbling.
This necessary condition will also be sufficient for the tumbling, occurring always when the tumbling coefficient is negative. A positive coefficient will be a guarantee that no tumbling can occur, and the motion is stable.
Some Simulations
The same body will be used for three different geometries (Figure 2), changing the spin axis form the principal axis of largest moment of inertia to the smallest. Therefore we start with an oblate body (largest inertia in z) µ1 = 0.9 µ2 = 0.5, then take the x axis for spin (it will be the new z axis) and get µ1 = 1/0.9 = 1.11 µ2 = 0.5/0.9 = 0.56 for the intermediate body an finally µ1 = 2 µ2 = 1.8 for the prolate body.
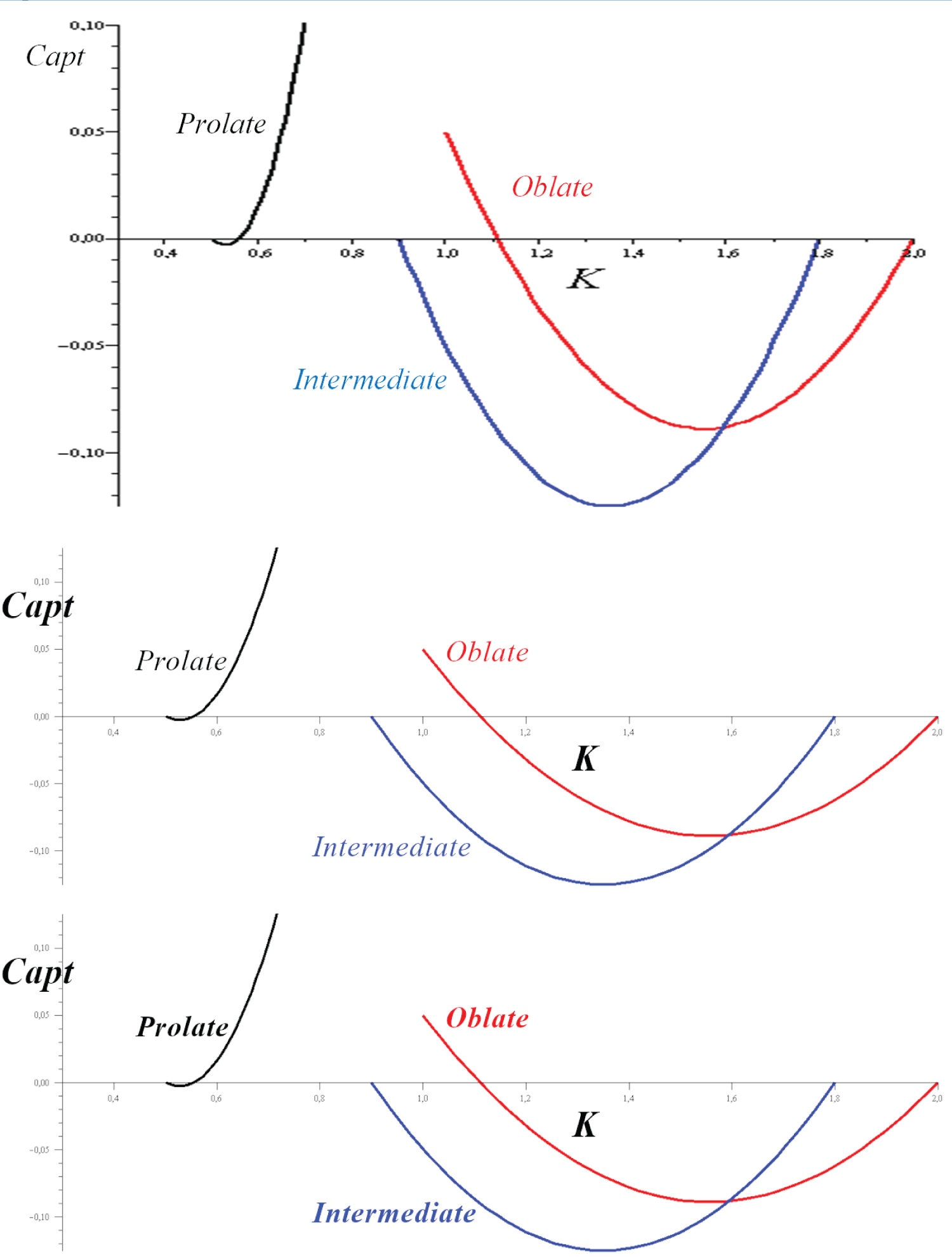
Figure 3 shows the tumbling coefficient for these cases, depending on the value of K. In this figure, it's observed that for the oblate body the Capt starts at a positive value, and remains positive for small impacts (K is close to 1), as the impact increases the Capt value decreases and becomes negative (K > 1.11), the rotational motion becomes unstable.
For the prolate body the Capt starts at positive value K = 1 (values close to 1 do not appear in the Figure 3 but they do exist), as the impact increases the K value decreases and the Capt value decreases also, for strong impact the rotational motion becomes unstable (K < 0.56).
In the case of intermediate body the Capt value is always negative. These results are consistent and expected as indicated in the introduction of this paper.
The intermediate case (which we know unstable [1,13]) can be investigated directly from the tumbling coefficient (Equation (18)) when we substitute the K value from Equation (14);
and with help of Equation (13) transform the inequality condition in:
For a body in the intermediate axis rotation condition, µ1 > 1 > µ2, Equations (18) and (20) will always be satisfied and tumbling is inherent.
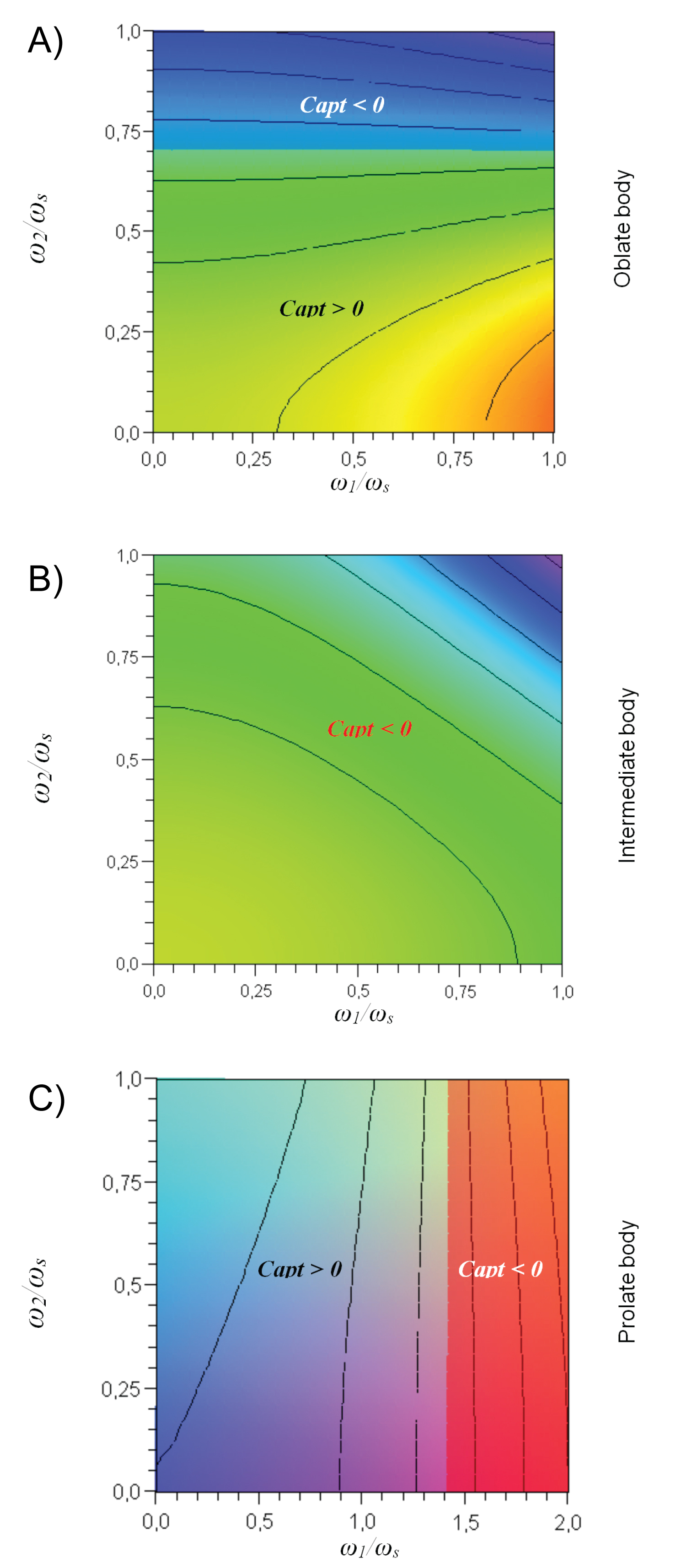
Using Equation (20) it is possible, for each geometry, to draw a stability map in the plot considering the referred representation of ω1/ωs with ω2/ωs looking for the Capt = 0 line.
Figure 4 shows the stability map [12] for these cases, depending on the geometries of bodies. It is possible to verify that the stability limits of the tumbling motion, in each body, depend only on one relation between angular velocities, the stability limits depend only on ω2/ωs in the oblate body, and depend only on ω1/ωs in the prolate body; this is because, according to the geometry of the body, one component of the Equation (20) maintains a constant sign for all possible values. This fact is useful to simplify the analysis, particularly in the analysis of a non-conservative motion, as shown later.
Analyzing Figure 4 in detail, it is possible to observe the lines with the same Capt value in the stability maps [12] (Capt is constant on this lines). In the oblate body (upper frame) these lines become horizontal when passing through zero (Capt = 0), and divide two areas of blue and green colors. In the prolate body (bottom frame) these lines become vertical when passing through zero (Capt = 0), and divide two areas of orange and celestial colors. In the intermediate body (middle frame) there exists only one area, that is, the entire area has negative values of Capt, the lines show the place for one constant Capt and divide its gradient in colors.
To calculate the tumbling condition for a certain geometry it is enough to start at a certain instant of time knowing the onboard measured angular velocity which will be ω0 = [ω10, ω20, ωs0]T in the body frame (SB). From Equation (11) we will obtain K. If the system is conservative the simulation will be simple since we use principal moments of inertia. Using Euler’s law for the body frame [14]:
Substituting the J matrix in Equation (22) we obtain the differential equation for the angular velocity, which will is:
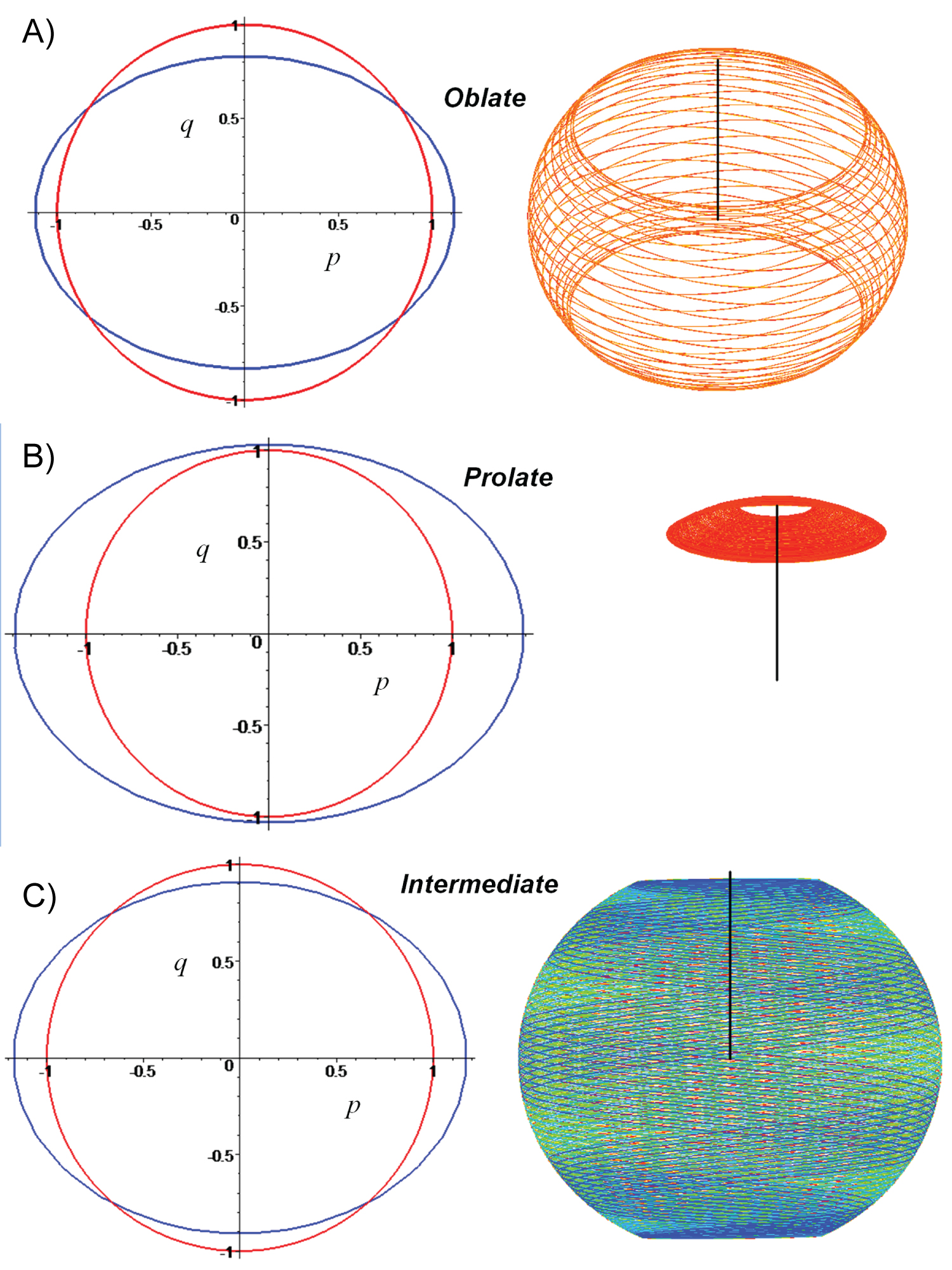
Figure 5 present the situation of the intersection between circle and ellipse in Equation (15) with r = 0, the value of K and the motion of spin axis in the inertial frame. To obtain the attitude we use the initial quaternion given by Equation (9) with:
And finally, the quaternion equation using the vector product formulation whit the antisymmetric matrix replacing the vector product [1], can be written as:
Which will give us the DCM (Direction Cosine Matrix [2]) to position the body in the inertial frame according to Figure 1. A certain impact with known value misaligns the vectors H and r, also removes the stability of the spin motion. Some examples are shown in Figure 5. One initial velocity is chosen arbitrarily for simulating the motion, to the three different aforementioned geometries.
Considering a initial velocity ω0 = [1.2 2.2 1]T.
In the oblate body (µ1 = 0.9 µ2 = 0.5) is obtained:
K = 1.4 and Capt = -0.078, therefore, tumbling occurs, and the motion is unstable.
Results to the prolate body (µ1 = 2 µ2 = 1.8):
K = 0.56 and Capt = 0.001, then, non tumbling occurs, and the motion is stable.
And finally, for the intermediate body (µ1 = 1.11 µ2 = 0.56):
K = 1.24 and Capt = -0.117, as expected, the motion is unstable.
To identify the occurrence of tumbling with the definition of only one parameter is useful and simple. The numerical results are consistent with the reasoning developed in this work. Thus, the stability or instability of the motion can be predicted by observing only one parameter.
Stability Chards Using Magnus Triangle
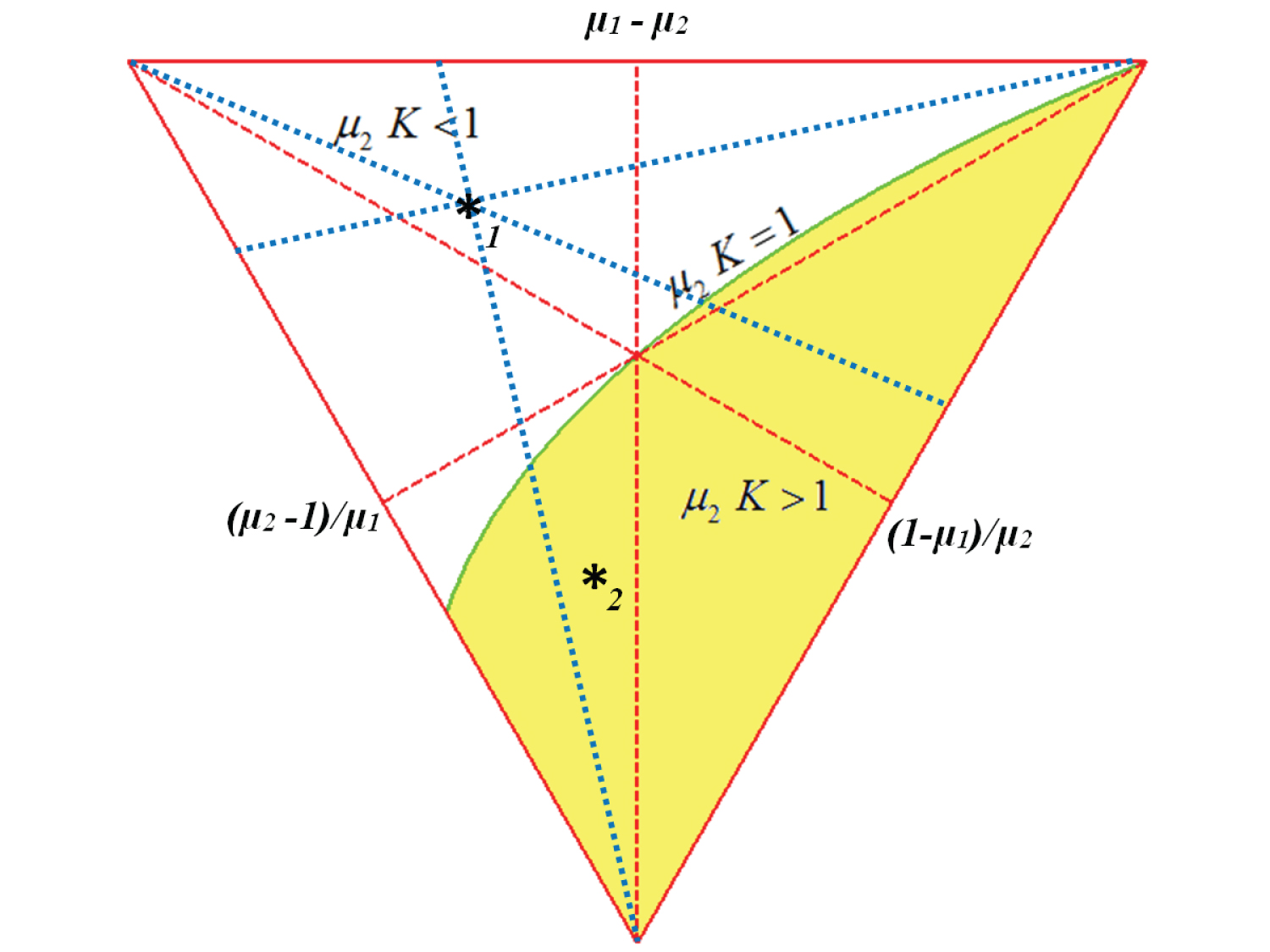
Magnus triangle is a practical way to represent rigid bodies of different geometries inside of the closed area of a triangle [15]. Each side represents relations of moments of inertia and if two of these values are known the lines connecting this points to the opposite vertex will cross defining the body. The third relation will be obtained connecting the third vertex to this crossing and looking for the value at the third triangle side.
The inequality Equation (18) will be explored for different body geometries using the triangle. The initial condition is given, and we may look how bodies will behave. Then, the regions where µ1 K > 1 and µ2 K < 1 (or µ1 K < 1 and µ2 K > 1) are identified according to a positive or negative tumbling coefficient Capt as stable or unstable.
In Figure 6, only one variable was considered (µ2 K), a curved line can be observed for the value µ2 K = 1, dividing the triangle area in two, one white and another yellow. There are 2 dots, the dot 1 that defines an oblate body and the dot 2 that defines a prolate body.
Also shown in this Figure 6 is the way to locate the points (or bodies), defining a line that starts from the vertex and reaches the opposite side of the triangle at the correspondent variable value.
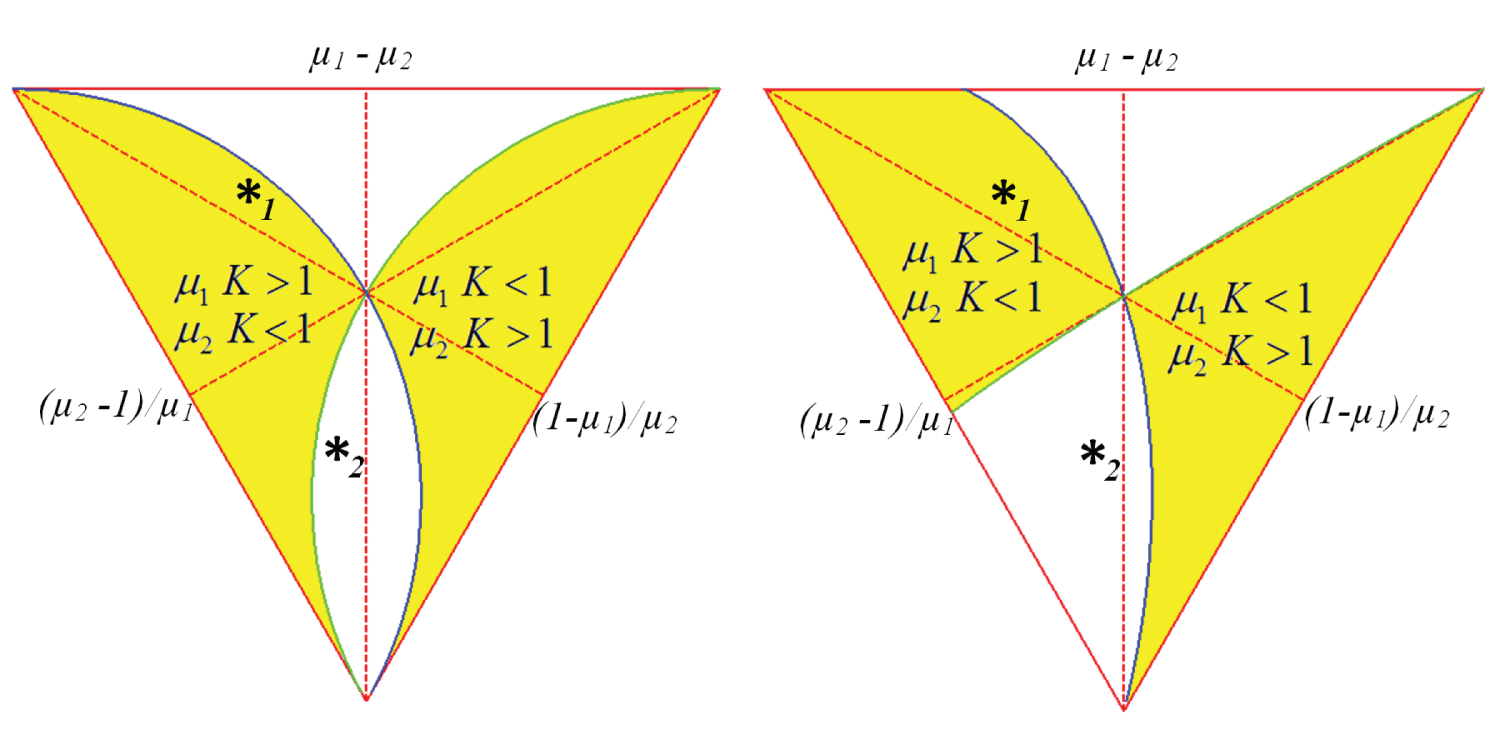
In Figure 6, Figure 7 and Figure 8, the triangle is divided in 6 areas by its barycentric lines [15], the two upper areas belonging to an oblate body (for example the dot 1), the two lower areas belonging to a prolate body (for example the dot 2), and the intermediate areas (like the butterfly) belong to an intermediate body.
With an initial condition ω0 = [0.5 0.5 1]T Figure 7 shows these regions. When Capt < 0 there is instability, and the region is colored grey. Two dots are highlighted in the triangle: it is the same body, once with a spin axis which turns it oblate µ1 = 0.9 and µ2 = 0.5 (dot 1), the other changes the spin axis and it rotates as an prolate body µ1 = 2 and µ2 = 1,8 (dot 2). We can notice that the body in the first condition is much nearer to the stability border [16].
Figure 8 compares two initial conditions:
ω0 = [1 1 1]T (left) and
ω0 = [0.2 1.5 1]T (right).
The curved lines correspond to µ1 K = 1 and µ2 K = 1.
In the last figure, the diagram loses the symmetry, which depends on the components of the angular velocity orthogonal to the spin axis. In this case, the velocity components on the x and y axes are different.
Non-Conservative Motion of an Oblate Body
The conservative analysis done up to now will be extended considering the non-conservative motion of an oblate body, which could represent a satellite. The idea is to use the tumbling coefficient as a stability parameter, in the sequence of the motion the same analysis is repeated, and the coefficients are compared.
Oblate body
The oblate body presents 1 > µ1 > µ2 and, as can be seen from Figure 3, also 1 < K < 1/µ2 (in the range of abscissa of Figure 3), i.e., µ2 < µ2 K < 1. Therefore, in Equation (18), the positive or negative value of Capt will be defined by the part we call C:
But we also know that Capt will be positive in the range 1 > K > 1/µ1 (Figure 3). The non-dimensional K is time dependent in the non-conservative case [6].
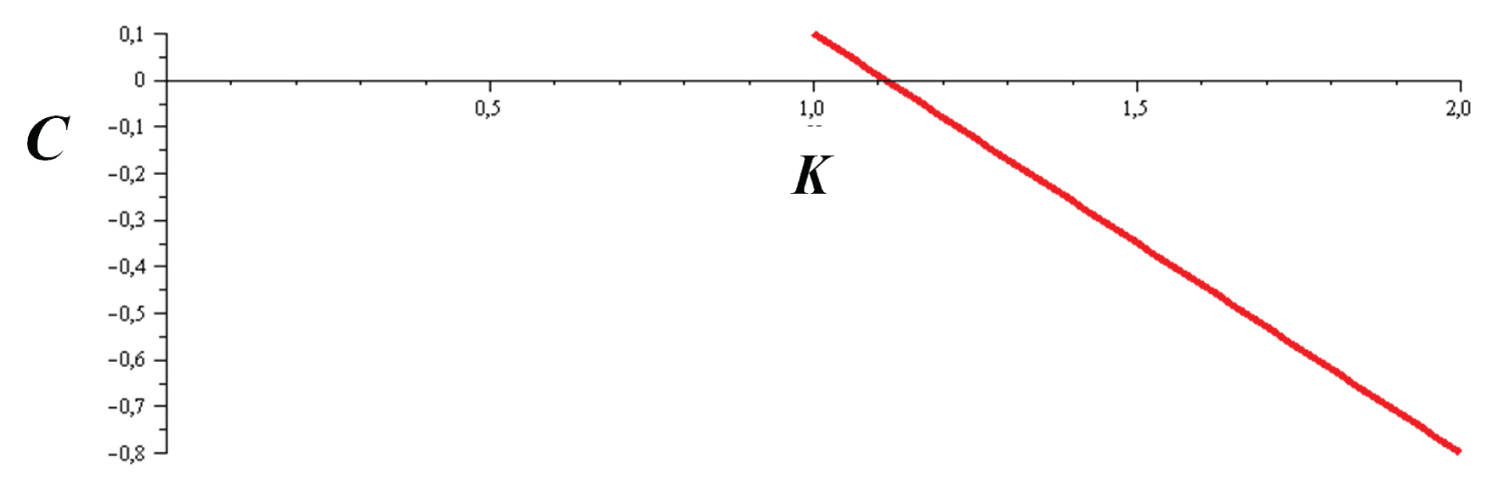
Parameter C has a linear dependence of K (Equation 26). The development of motion towards stability needs a C that always increases (which means that K is tending to the limit K = 1). In other words, the temporal derivative of C has to be positive to leave the instability region. We can see this well in the Figure 9.
Using the definition of K given by Equation (11), now kinematic energy and angular momentum depend on time, the equation can be derived, so:
To guarantee a positive result for increasing values of C we need
The derivatives can be calculated using the definitions (matrix J is diagonal):
Replacing the derivatives in (28):
Any applied torque on this oblate body (spinning on the axis of largest inertia) should obey this inequality to improve stability. A control law is possible trying to maximize de rate of change of C.
One could look for the resulting motion due to viscous damping. Using the torque as
To simplify the analysis, the coefficients on all degrees of freedom will be considered equal [14]: (a = a1 = a2 = as) and has to be negative for a damping condition, then:
Then,
This inequality is always satisfied when there is a misalignment of vectors ω e H. The loss of energy of the oblate body will lead to a stabilization around the spin axis of largest moment of inertia.
Prolate body
The prolate body presents µ1 > µ2 > 1 and, as can be seen from Figure 3, also 1/µ1 < K < 1 (in the range of abscissa of Figure 3), i.e., 1 < µ1 K < µ1. Therefore, in Equation (18), the positive or negative value of Capt will be defined by the part we call B:
But we also know that Capt will be positive in the range 1/µ2 > K > 1 (Figure 3). The non-dimensional K is time dependent in the non-conservative case.
Parameter B has a linear dependence of K (Equation 36). The development of motion towards stability needs a B that always increases (which means that K is tending to the limit K = 1). In other words, the temporal derivative of B has to be positive to leave the instability region.
Using the definition of K given by Equation (11), now kinematic energy and angular momentum depend on time, the equation can be derived, so:
To guarantee a positive result for increasing values of B we need
The derivatives can be calculated using the definitions (matrix J is diagonal) in Equation 29 and 30. Replacing the derivatives in (38):
Any applied torque on this oblate body (spinning on the axis of largest inertia) should obey this inequality to improve stability. A control law is possible trying to maximize de rate of change of B.
One could look for the resulting motion due to viscous damping. Using the torque as
To simplify the analysis, the coefficients on all degrees of freedom will be considered equal [14]: (a = a1 = a2 = as) and has to be negative for a damping condition, then:
Then,
This inequality is never satisfied when there is a misalignment of vectors ω e H. The loss of energy of the prolate body will lead to a destabilization around the spin axis of largest moment of inertia. The motion should stabilize on another axis of rotation.
Intermediate body
The intermediate body presents µ1 > 1 > µ2 and, as can be seen from Figure 3, also 1/µ1 < K < 1/µ2 (in the range of abscissa of Figure 3), i.e., 1 < µ1 K and µ2 K < 1.
The result indicates that the body will tend to remain unstable [13]. Similar to the prolate body, the motion can stabilize on another axis of rotation.
Conclusion
The main purpose of this work, investigating the border of the tumbling motion of a body rotating in space, was achieved by an adequate definition of the coordinate systems, simplifying the mathematical analysis and diminishing the variables for the initial condition of the equations. The definition of a tumbling coefficient reduced the stability analysis to one parameter: if its value is positive the satellite does not tumble, otherwise it tumbles.
The tumbling condition does not depend on a specific attitude and will be defined through angular velocities. The inertial frame will be conveniently defined at any moment considered for initial condition and the angular velocity starts the tumbling analysis.
The normalized equations of motion describing any rotational behavior of the body will allow establishing the necessary conditions for an unstable behavior. These are necessary and sufficient conditions for the tumbling occurrence. Analytical expressions defining stability are established and stable and unstable regions for the consequent rotations are identified. This work provides useful tools to predict whether the rotational motion will remain stable or become unstable.
The analysis was verified by numerical results for different inertial configurations showing that the use of a single parameter is sufficient to predict tumbling.
Magnus stability triangle is a valuable tool to synthesize the stability conditions for bodies of any geometry. Stability areas are defined, borders are analytically established and conditions that favor stability are identified.
In the analysis of the non-conservative motion of an oblate body, the tumbling coefficient can be reduced to one relevant variable. Its derivative in time will result in a sufficient condition for tumbling and may help establishing the required maneuver to stabilize the motion. The amplitude of the resulting motion will be inversely proportional to this variable. Using this criterion for a damped motion, it is possible to show that there is always convergence to a rotational stability around the axis of larger inertia.