
International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 5, Issue 1
Original Article
DOI: 10.35840/2631-5017/2520
Final Element of Periodic Table is Element N 137
AV Morozkin1* and R Nirmala2
Figures
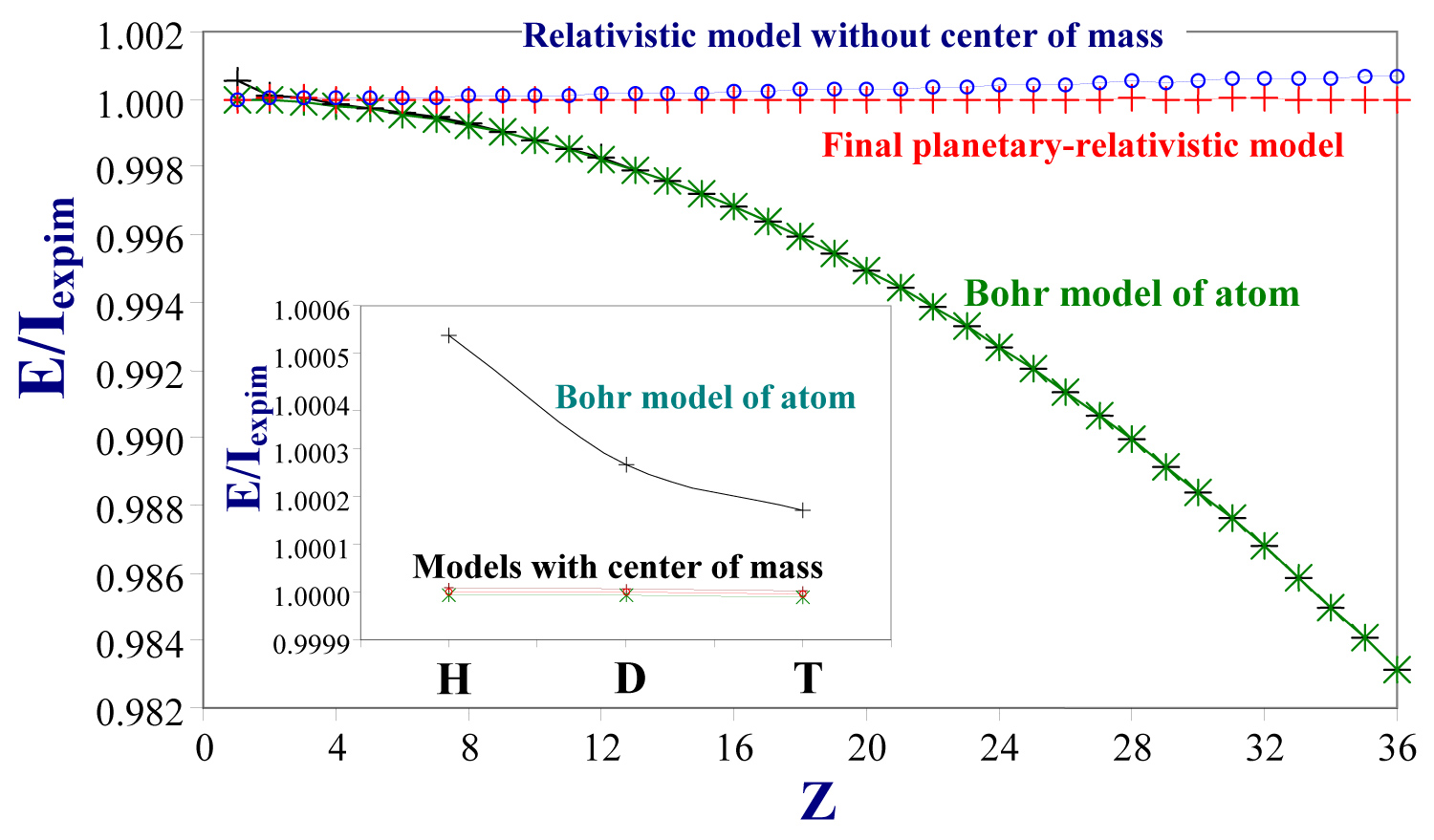
Figure 1: Accordance of the different models of single-electron....
Accordance of the different models of single-electron ions with experimental data: The E/Iexperim ratio vs element number Z. Inset in Figure: The E/Iexperim ratio for hydrogen (H), deuterium (D) and tritium (T). (E the calculated energy of 'electron-atomic nucleus' bond in the different models of single-electron ions and Iexperim the experimental ionization potential [2-6]).

Figure 2: Deviation of planetary-relativistic model from.....
Deviation of planetary-relativistic model from the experimental data: ΔE/E0 ratio vs. element number Z (here ΔE = E - Iexperim, E0 = mee4/[8ε02h2]). Inset in Figure: ΔE/E0 vs Z10/3.
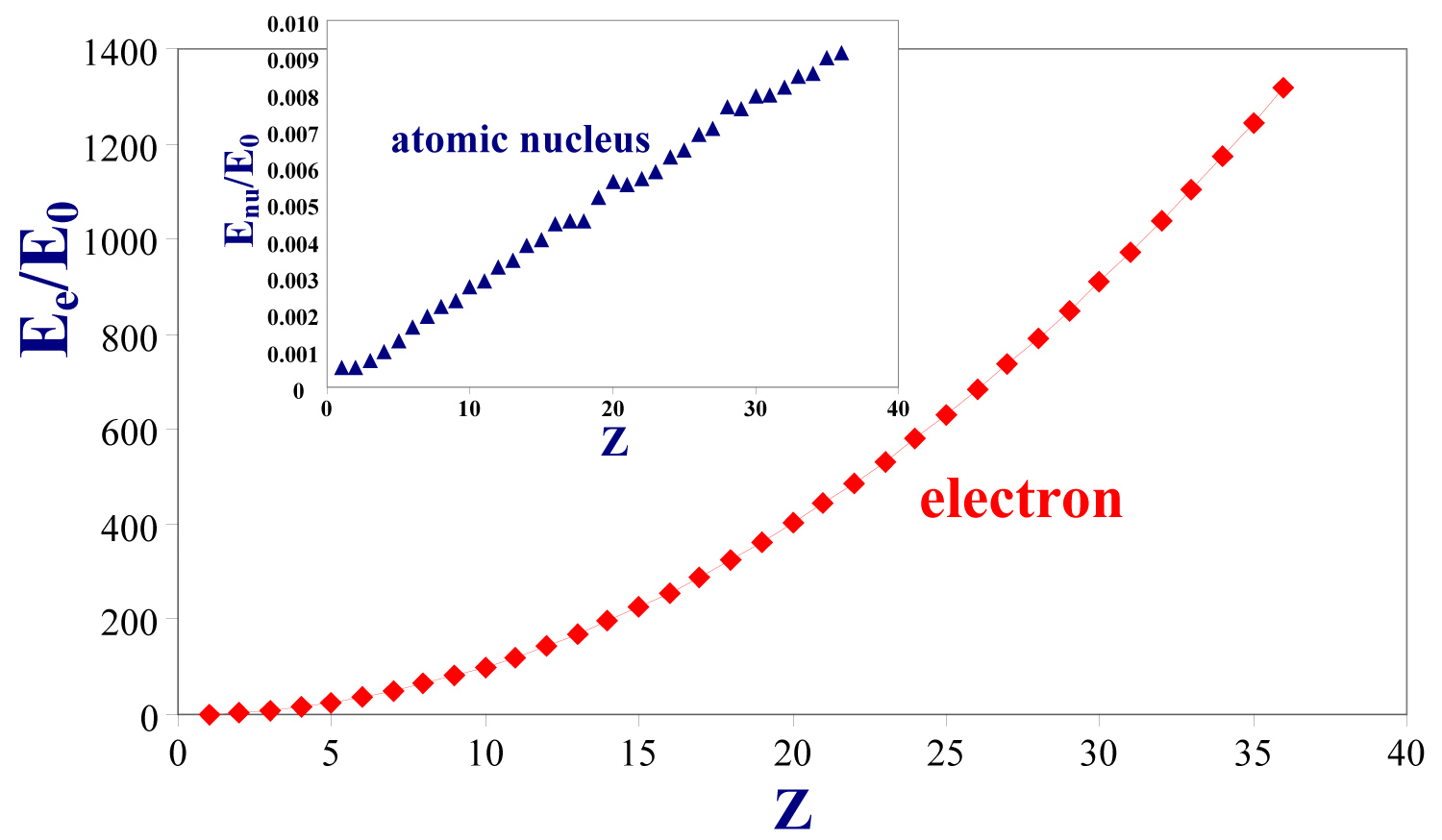
Figure 3: The electron and atomic nucleus energy in the...
The electron and atomic nucleus energy in the final planetary-relativistic model: Ee/E0 and Enu/E0 ratios vs. Z (E0 = mee4/[8 ε02h2]).
References
- BM Yavorsky, AA Detlaf (1977) The physica. Nauka, Moscow.
- B Edlen (1964) Atomic spectra. In: S Flugge, Encyclopedia of Physics. Springer, Berlin, 27: 79-220.
- CE Moore (1970) Ionization potentials and ionization limits derived from optical spectra. Nat Bur Stand, NBS 34, USA.
- RL Kelly (1982) Atomic and ionic spectrum lines below 2000A: Hydrogen through argon. Oak Ridge, Tennessee, USA.
- AA Radtsig, BM Smirnov (1986) The parameters of atoms and atomic ions. M Energoizdat.
- M Energoatomizdat (1991) Physical data. In: IS Grigor'ev, EZ Meilihov, Moscow, 411-420.
Author Details
AV Morozkin1* and R Nirmala2
1Department of Chemistry, Moscow Lomonosov State University, Russia
2Department of Physics, Indian Institute of Technology Madras, India
Corresponding author
AV Morozkin, Department of Chemistry, Moscow Lomonosov State University, Leninskie Gory, House 1, Building 3, Moscow, GSP-2, 119991, Russia.
Accepted: September 17, 2020 | Published Online: September 19, 2020
Citation: Morozkin AV, Nirmala R (2020) Final Element of Periodic Table is Element N 137. Int J At Nucl Phys 5:020.
Copyright: © 2020 Morozkin AV, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
This work reports the model of single-electron ion with average ionisation potential accuracy of 0.00116%. This model confirms the thesis about final/last element of Periodic Table with N 137 and it permits to construct the full variant of Periodic Table.
Keywords
Single-electron ion, Ionization potential, Periodic table
Introduction
The well-known Bohr model of the atom [1] is basic model for explanation of electronic shell structure. Bohr model shows that the final/last element of the Periodic Table is N 137 from the confition ve < c (here ve the speed of electron and c the light speed). However the ionization potentials of the singe-electron atom/ions from H to Kr35+ [2-6] show systematic deviation from Bohr model of atom (Figure 1). This deviation reaches value of 1.6885% for Kr35+ with average accuracy of ± 0.5764% and minimal deviation of 0.020% for Li2+ ion (Table 1).
The planetary model of atom based on well-known Rutherford and Kepler planetary models [1] has better agreement with experiment than Bohr model of atom for the ionization potentials of H, D and T (inset in Figure 1), but this model shows deviation from the experimental data in case of single-electron ions with Z bigger than 1.
The models with such deviations from experimental data does not permit to do conclusion concerning final element of the Periodic Table and the problems for final element of Periodic Table and full variant of the Periodic Table remains unclear.
The relativistic models of the single-electron ion (atom) (Table 1) based on well-known Einstein special relativity [1] permits to improve the Bohr atom and planetary models. These relativistic models improve the accordance of calculated and experimental data for Z bigger than 1 (Table 1 and Figure 1).
However, the resulting deviation of the experimental data obtained from planetary-relativistic model shows presence the additional component in the interaction of 'electron-atomic nucleus' (Figure 2). This empirical component proportional to the ~ Z10/3 may be due to e.g. some asymmetry of the electric charge of the atomic nucleus ore magnetic 'electron - atomic nucleus' interaction.
Anyway, the final planetary-relativistic model with this empirical component (Table 1) has the best agreement with experimental data (Figure 1). Moreover, the deviations of this model from experiment are close to the experimental estimated standard deviation (ESD). Formally, the electron full energy and atomic nucleus full energy in this model may be calculated (Figure 3).
The details of the Bohr model of atom, planetary, relativistic, planetary relativistic and final planetary-relativistic models are summarized in Table 1. The resulting expression of final planetary-relativistic model is: E = me0M0c2×[(1 - v2/c2)1/2 - 1]/[me0 + M0], here v = (Z + A×Z7/3)e2/(2e0hn) and A = -2.81×10-6 (deviation for H% is 0.000181%, for Ar35+ is 0.000189%, maximum deviation of 0.00364% for Li2+ and average deviation of 0.00116% is obtained).
Final model gives the full energy of 'electron- atomic nucleus' system with good accuracy. The calculated v and ve speeds (electron speed ve and sum of electron and atomic nucleus speeds v) reach values of v ≈ ve = 0.997753204×c at Z = 137 and they should be bigger than c speed at Z = 138. Even if atomic nucleus with Z > 137 will stable, the every free electron should fall down on atomic nucleus with well-known reaction of 'p + e ® n + n' [1] that shifts the element number to equal of 137 or less.
So, the ve (v) less than c is condition of the stable electronic shell and the final possible element of Periodic Table with stable atomic nucleus is N 137.
The full variant of the Periodic Table may be constructed using this condition and well-known rules of filling of the electronic shell [1] (Table 2).
The g-elements from 121 to 137 are essentially new elements with orbital quantum number l = 4. Perhaps, they will demonstrate the magnetic properties, like 3d and 4f elements [6] and they may be interesting for science and technology. Meanwhile, the final 137 element will has the full electronic shell 1s2 2s22p6 3s23p6 4s23d104p6 5s24d105p66s24f145d106p6 7s25f146d107p6 8s2 5g17.
On one hand these are evident results and electron speed close to light speed is evident factor of heavy element synthesis, on the other hand this full variant of Periodic Table permit to estimate the perspectives of new elements for materials and technology. E.g. from empirical rule the stable element N 106 should have the melting temperature about 4380 K (for comparison: The Cr, Mo and W elements from this group have the melting temperature of 2130, 2890 and 3680 K [6], respectively).
Acknowledgements
Thanks to Prof BM Bulychev and Prof SG Ionov (Department of Chemistry, Moscow Lomonosov State University, Russia) for useful discussion.

