International Journal of Atomic and Nuclear Physics
(ISSN: 2631-5017)
Volume 6, Issue 1
Original Article
DOI: 10.35840/2631-5017/2526
Study on Vibrational-Gamma Soft Properties in 124Te Nucleus
I Hossain1*, IM Ahmed2, Hewa Y Abdullah3, MA Saeed4, MO Alzanbaqi1 and Fadhil I Sharrad5,6
Table of Content
Figures
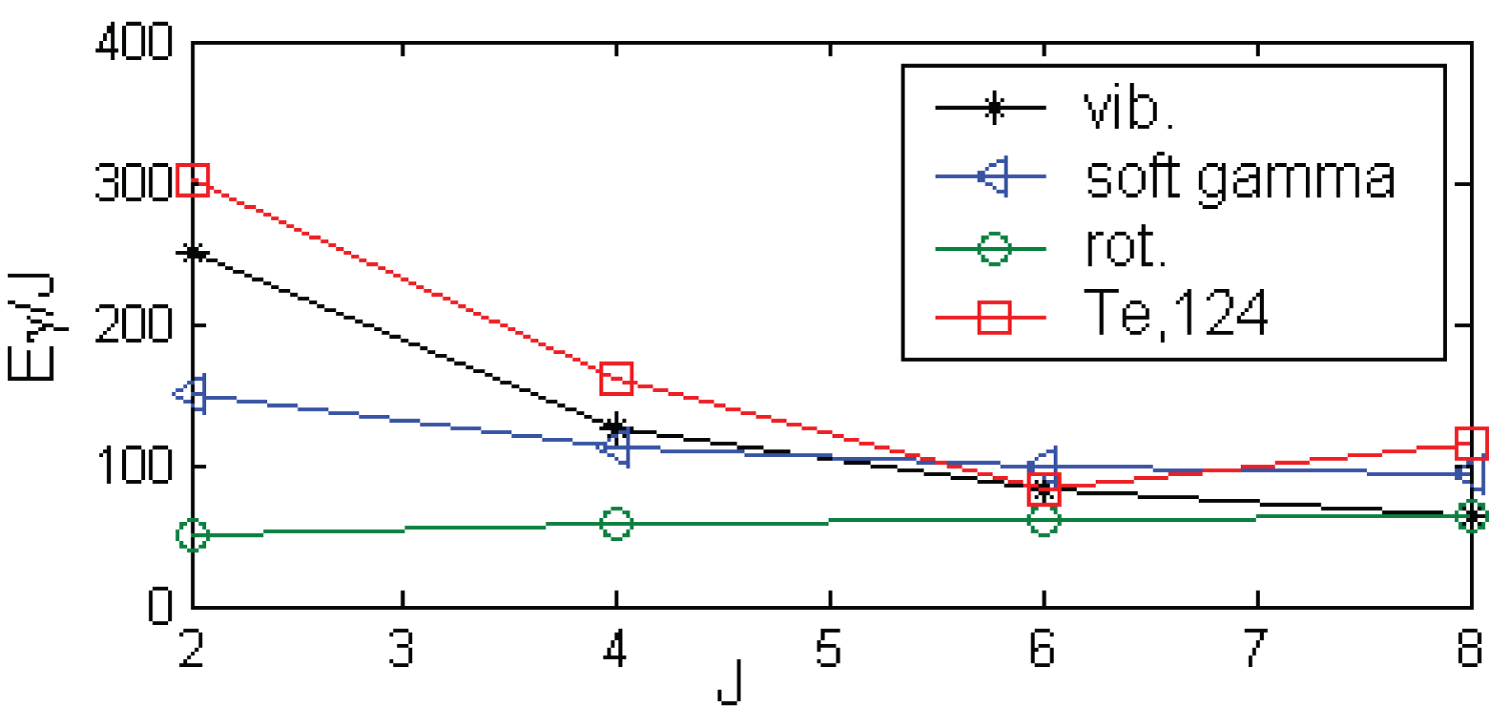
Figure 1: The E-GOS plots of 124Te related....
The E-GOS plots of 124Te related to the typical limit of rotator, vibrator and gamma soft.
Tables
Table 2: The r(2/J + J) Vs. J of 124Te nucleus for yrast level.
Table 3: The boson number and parameters in (keV) of different type of models.
Table 4: Comparative data of experiment and theoretical models in yrasts state (keV).
References
- Iachello F, Aritma A (1997) The interacting boson model. Cambridge University Press, UK.
- Kotila J, Suhonen J, Delion DS (2003) Low-lying collective states in 98-106Ru isotopes studied using a microscopic anharmonic vibrator approach. Phys Rev C 68: 054322.
- Bohr A, Mottelson BR (1998) Nuclear deformations. Nuclear Structure, World Scientific Publishing, Volume 2, 748.
- Ganev H, Garistov VP, Georgieva AI (2004) Description of the ground and octupole bands in the symplectic extension of the interacting vector boson model. Phys Rev C 69: 014305.
- Doma SB, EL-Gendy HS (2012) Some deformation properties of the even-even ytterbium, hafnium and tungsten nuclei. Int J Mod Phys E 21: 1250077.
- Hossain I, Abdullah HY, Ahmed IM, Sharrad FI (2021) Nuclear gamma soft character in 128Ba. EJA Phys 3: 16-20.
- Hossain I, Ahmed IM, Abdullah HY, Saeed MA, Sharrad FI (2020) Sharrad study on nuclear structure of even-even 124Te-128Ba nuclei for N = 72. 1st International Conference on Advances in Material Science.
- Hicks SF, Vanhoy JR, Burkett PG, Champine BR, Etzkorn SJ, et al. (2017) Lifetimes in 124Te: Examining critical-point symmetry in the Te nuclei. Phys Rev C 95: 034322.
- Ghita DG, Cata-Danil G, Bucurescu D, Cata-Danil I (2008) 124Te and the E(5) critical point symmetry. Int J Mod Phys E 17: 1453-1466.
- Ahmed IM (2013) The U(5)-O(6) properties of 102Pd, 106 Cd, 124Te and 128Xe nuclei. Int J Mod Phys E 22: 1350074.
- Sabri H, Jahangiri Z, Mohammadi MA (2016) Investigation of shape coexistence in 118-128Te isotopes. Nucl Phys A 946: 11-28.
- Dan-Yang P (2014) Effects of relativistic kinematics in heavy ion elastic scattering. Chin Phys C 38: 024104.
- Hossain I, Ahmed IM, Sharrad FI, Abdullah HY, Salman AD, et al. (2015) Yrast states and B(E2) values of even 100-102Ru isotopes using Interacting Boson Model (IBM-1). Chang Maj J Sci 42: 996-1004.
- Sharrad FI, Hossain I, Ahmed IM, Abdullah HY, Ahmad ST, et al. (2015) U(5) symmetry of even 96,98Ru isotopes under the framework of Interacting Boson Model (IBM-1). Braz J Phys 45: 340-346.
- Zhang DL, Mu CF (2019) Description of the critical point symmetry in 124Te by IBM- 2. Chinese Physics C 43: 024104.
- Jalili Majarshin A, Luo YA, Pan F, Fortune HT, Draayer JP (2021) Nuclear structure and band mixing in 194Pt. Physical Review C 103: 024317.
- Jalili Majarshin A, Jafarizadeh MA (2017) Photo scattering and absorption cross section in framework of the sdfp-interacting boson model. Nuclear Physics A 968: 287-325.
- Leupold S (2018) The nucleon as a test case to calculate vector-isovector form factors at low energies. Eur Phys J A 54: 1-14.
- Jalili Majiarshin A, Sabri H, Rezaei M (2018) Exactly solvable model in quadrupole-octupole coupled states. Nuclear Physics A 971: 168-199.
- Isacker PV (1987) The interacting boson model. Cambridge University Press, UK.
- Scharff-Goldhaber G, Weneser J (1955) System of even-even nuclei. Phys Rev 98: 212.
- Bohr AN, Mottelson BR (1953) Collective and individual-particle aspects of nuclear structure. Kongel. Dan. Vidensk. Selsk., Mat.-Fys. Medd 27: 1-174.
- Iachello F, Abrahams K, Allart K, Dieperink AEL (1981) Nuclear structure. Plenum Press, USA.
- Bonatsos D, Daskalovannis C, Drenska SB, Karoussos N, Minkov N, et al. (2000) ?I = 1 staggering in octupole bands of light actinides: “Beat” patterns. Phys Rev C 62: 024301.
- Katakura J, Wu ZD (2008) Nuclear data sheets for A = 124. Nucl Data Sheets 109: 1655-1877.
- Hossain I, Sharrad FI, Saeed MA, Abdullah HY, Mansour SA (2016) B(E2) values of Te isotopes with even N(68-74) by means of interacting boson model-1. Maejo International Journal of Science and Technology 10: 95-103.
Author Details
I Hossain1*, IM Ahmed2, Hewa Y Abdullah3, MA Saeed4, MO Alzanbaqi1 and Fadhil I Sharrad5,6
1Department of Physics, Rabigh College of Science & Arts, King Abdulaziz University, Saudi Arabia
2Department of Physics, College of Education, Mosul University, Iraq
3Physics Education Department, Faculty of Education, Tishk International University, Iraq
4Department of Physics, Division of Science & Technology, University of Education, Pakistan
5Department of Physics, College of Education, Kerbala University, Iraq
6College of Health and Medical Technology, Al-Ayen University, Iraq
Corresponding author
I Hossain, Department of Physics, Rabigh College of Science & Arts, King Abdulaziz University, 21911 Rabigh, Saudi Arabia.
Accepted: November 11, 2021 | Published Online: November 13, 2021
Citation: Hossain I, Ahmed IM, Abdullah HY, Saeed MA, Alzanbaqi MO, et al. (2021) Study on Vibrational-Gamma Soft Properties in 124Te Nucleus. Int J At Nucl Phys 6:026.
Copyright: © 2021 Hossain I, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We explained aspects of vibrational soft symmetry in 124Te nucleus using different types of models such as Bohr-Mottelson Model (BM), Interacting Vector Boson Model (IVBM), Interacting Boson Model (IBM-1), and Doma-El-Gendy (D-G) relation. The factor and energy level of this nucleus have been studied and confirmed that 124Te nucleus is vibrational to gamma soft aspects. A graph of 124Te nucleus has been investigated with the ordinary plots of rotational, gamma soft and vibrational limits. The known measured data of the yrast states of this nucleus are compared with four types of models BM, IVBM, IBM-1, and D-G. The theoretical calculations of these models are excellent with measured data.
Keywords
124Te, BM, IBM-1, D-G, IVBM
Introduction
The study of tellurium isotopes is very important for nuclear physicist during the last two decades. The tellurium isotope with 72 numbers of neutrons is very much interesting to study the nuclear collectivity based on experimental and theoretical aspects. Because it is an even-even nucleus and easily produced E2 transitions where the low-lying excitation levels are 2+, 4+ , 6+ and 8+ states etc . This type of nucleus could be fruitfully described nuclear collective aspects using IBM-1 model [1]. According to his model there is no discrepancy between protons and neutrons and the collective states are defined by bosons number NB. There are two bosons: d- (L = 2) and S- (L= 0) bosons. The collective states have three types of deformed symmetries: rotational SU(3), vibration U(5), and gamma-soft O(6) [2]. Bohr-Mottelson found discrete revolving energy of a nucleus depends on the function of [3]. Genev, et al. developed ground and octuplet band of nuclei by IVBM [4]. A novel technique for revolving energy subjected to and was developed by Doma and El-Gendy [5].
We have studied the gamma soft character in 128Ba [6,7]. The neutron-rich 128Ba nucleus gives valuable information on the double nuclear shell closer to 132Sn and raises the possibility to study the 124Te nucleus. The 124Te nucleus consists of 52 protons and 72 neutrons existed near to closed shell 132Sn. The configuration of 124Te nucleus is πg (proton particles) and υh (10 neutron holes). This configuration is excellent to study E2 gamma rays transition on the 124Te nucleus by theoretically and experimentally. It gives valuable information on the yrast band for deformed nuclei.
Recently, the Doppler-shift attenuation method has been used to measure life time of 124Te [8]. Ghita, et al. studied the low-lying states and critical symmetry in 124Te nucleus by gamma ray spectroscopy [9]. The collective properties of vibrator-γ-soft energy of this nucleus were investigated by Ahmed using IBM-1 [10]. The shape coexistence in 118-128Te was studied by Habri, et al. [11]. The B (E2) data of Pd102-112 and Ru96-102 nuclei were examined [12-14]. Several vibrational-gamma soft properties IBM calculations have been reported that dealt with the IBM and IVBM models [15-19]. The aim of the present work is to interpret the collective behavior of yrast state of 124Te nucleus by D-G, IBM-1, BM, and IVBM models. The nucleus with neutron number N = 72 should be transitional nuclei that are expected to play an important role in shape evolution as well as shape coexistence and are hence worth pursuing.
Materials and Methods
The details methodologies are explained in ref. [6]. For the three limits, Hamiltonian and eigen-values [20]:
U(5):
With
K1= 1/12 a1
K4 = -1/10 a1+ 1/7 a3- 3/70 a4
K5 = -1/14 a3 + 1/14 a4
O(6):
with
K3= 1/4 a0
K4 = 1/2 a3
K5 = a1 -1/10 a3
SU(3):
with
K2 = 1/2 a2
K5 = a1 – 3/8 a2
K5, K4, K3, K2, K1 are strength parameters.
For the three limits, and are given [21,22]:
Vibrator: when (4)
-soft: when (5)
Rotor: when (6)
The details calculation of eigenvalues for U (5) - O (6) limits of yrast states [6,23], coefficient A, B, C in BM model [6,24], , parameter of ground state band in IVBM [4,6] and the coefficient A, D, C in Doma - El-Gendy equation [5,6] depends on and according to given in references.
Outcomes and Discussion
The first excited levels and the relations of of 124Te nucleus were explored vibration to gamma soft aspects are given in Table 1. The first excitation energy and give the information of vibrator, gamma-soft and rotational symmetry of a nucleus.
Table 1 gives detailed evidence of the first excited levels, and the ratio of the first 4+ to the first 2+ states of 124Te nucleus. The value of the first 2+ and 4+ level is 602.73 keV and 1247.65 KeV respectively. In Table 1 the ratio of is 2.07 is signature of vibrational to gamma soft limit for the mention nucleus. The E-GOS curve of the measured gamma energy/J [25] is drawn to vibrator, gamma-soft and rotator limit in Figure 1. It is shown that the measured value of yrast level in 124Te of 2+ levels rapidly decreases up to 6+ level and then slowly increases up to 8+ levels. The measured data is close to vibrator limit up to 6+ and then near to gamma soft limit up to 8+ levels. It clearly indicates that the yrast band of 124Te nucleus is variable aspects.
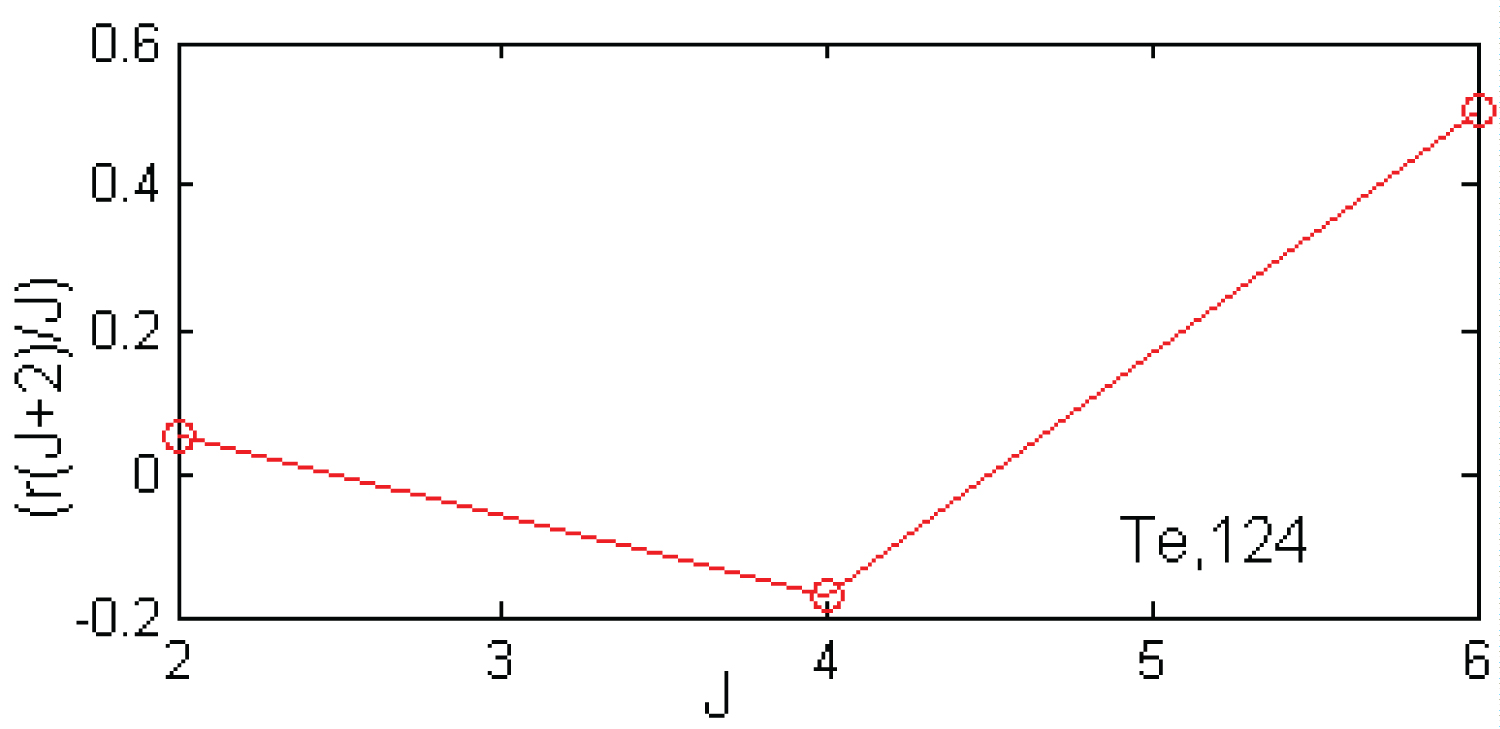
Table 2 displays the value of r (1 + 2/J) at J = 2, 4 and 6 are 0.054, -0.169 and 0.504 respectively and Figure 2 exhibits factor r(1 + 2/J) of 124Te are 0.169 ≤ r ≤ 0.504 which are the vibration-gamma-soft property. The yrast bands of the 124Te nucleus are calculated using BM, IVBM, IBM-1, and D-G methods. The best parameters and bosons numbers are given in Table 3. The boson number is 6. The values of in are 100.45; and do not satisfy the estimated parameters of this nucleus. Therefore this nucleus is not a purely rotational.
The experimental data [25] and calculated energies of the yrast level of 124Te nucleus using different type of models are listed in Table 4. The calculated data are consistent with the reference of the 124Te nucleus. The employed model reproduces the observed normal and intruder bands. Furthermore, the calculated energy spectra indicate that the mixing between the normal and intruder bands is apparent. In general, the approach is somewhat schematic and is considered on purely phenomenological grounds. Yet, such a study is still meaningful because a more realistic E2 transition approach would require this system. In addition the measured values of E2 transition rates of this nucleus were compared with the IBM-1 model [26]. We found the IBM-1 model for B(E2) is analytically deduced in U(5) limit for a few ground-state transitions in even 124Te nucleus.
Conclusions
We studied the properties of the 124Te nucleus using measured data and four different types of models: BM, IVBM, IBM-1, D-G. The first excitation of measured data is 602 keV and the ratio of is 2.07 in 124Te nucleus indicate a vibration to gamma soft property. The yrast level of 124Te nucleus in IBM-1, BM, IVBM, and D-G are consistent with the measured values. The factor r (J + 2/J) of 124Te at 2+, 4+ and 6+ is 0.054, -0.169 and 0.504 respectively. The low lying states of this nucleus are not pure rotator. The calculated energy spectra indicate that the mixing between the normal and intruder bands is apparent. This study confirmed vibrational soft aspects of the 124Te nucleus. These results are comparable with the experimental results and extremely useful for compiling nuclear data table.