
International Journal of Earth Science and Geophysics
(ISSN: 2631-5033)
Volume 1, Issue 1
Research Article
DOI: 10.35840/2631-5033/1802
Modeling and Analysis of Main Magnetic Field of the Earth for the Period 2010-2015
Andrei V Vorobev* and Gulnara R Shakirova
Table of Content
Figures

Figure 1: Model of inner GMF full vector...
Model of inner GMF full vector distribution for Epoch 2010.

Figure 2: Model of inner GMF full vector...
Model of inner GMF full vector distribution for Epoch 2015.
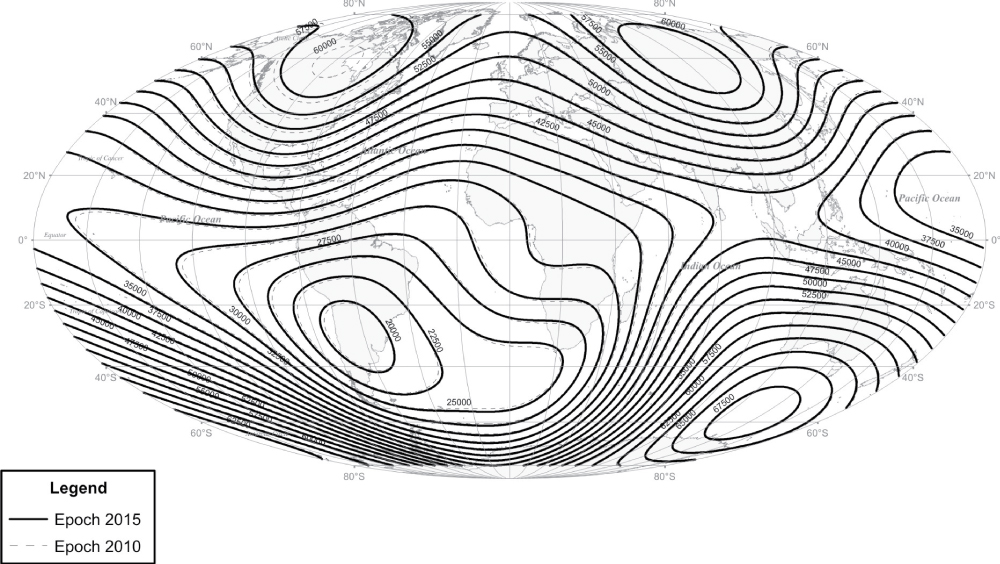
Figure 3: Comparison of inner GMF full vector...
Comparison of inner GMF full vector distribution for Epochs 2010 and 2015.
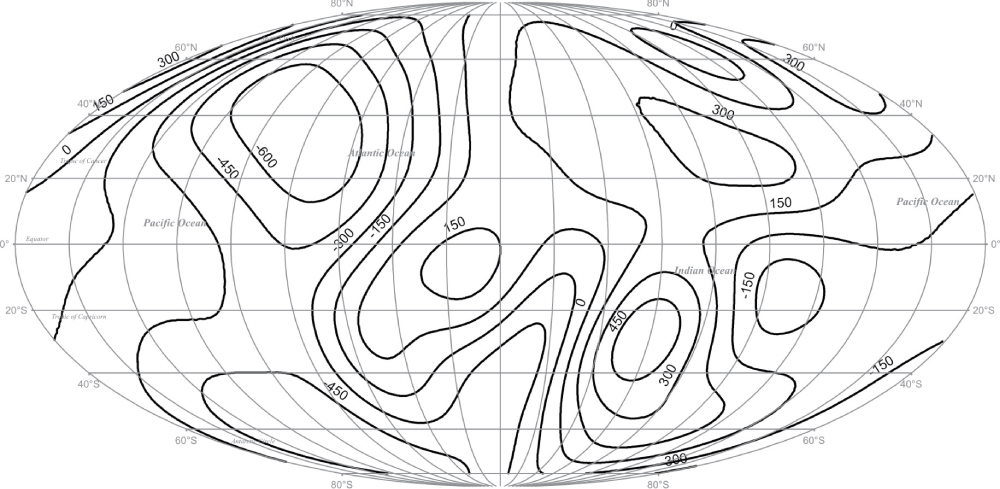
Figure 4(a-c): Analysis of the increments of inner...
Analysis of the increments of inner GMF for 2010-2015.
Tables
Table 1: Matrix of coefficients gmn,t0, nT (Epoch 2010).
Table 2: Matrix of coefficients hmn,t0, nT (Epoch 2010).
Table 3: Matrix of coefficients gmn,t0, nT (Epoch 2015).
Table 4: Matrix of coefficients hmn,t0, nT (Epoch 2015).
Table 5: Matrix of coefficients gmn, nT/year (Epoch 2010).
Table 6: Matrix of coefficients hmn, nT/year (Epoch 2010).
Table 7: Matrix of coefficients gmn, nT/year (Epoch 2015).
Table 8: Matrix of coefficients hmn, nT/year (Epoch 2015).
Table 9: Calculated values of geomagnetic dipole parameters.
References
- Lyakhov AN, Yu I Zecer, Fuller-Rowell T (2006) Possible consequences of geomagnetic reversal for the Earth's upper atmosphere. Reports of the Academy of Sciences 409: 1-3.
- Standard GOST 25645.127-85 (1985) The Earth's magnetosphere. Model of magnetic field of magnetosphere currents, Standards Publishing House, Moscow.
- Standard GOST 25645.126-85 (1985) Geomagnetic field. Model of field of intraterrestrial sources, Standards Publishing House, Moscow.
- Vorobev AV, Shakirova GR (2014) Pseudostorm effect: computer modelling, calculation and experiment analyzes. Proceedings of the 14th SGEM GeoConference on Informatics, Geoinformatics and Remote Sensing, Albena, Bulgaria 1: 745-752.
- Vorobev AV, Milovzorov GV, Milovzorov DG (2013) Methodics of geomagnetic pseudostorm parameters description. Vestnik IzhGTU 1: 103-107.
- Vorobev AV (2014) Approach to complex assess the effect of the geomagnetic pseudostorms: Patent for invention No. 2526234.
- Vorobev AV, Milovzorov GV, Shakirova GR, Kilmetov EA (2014) Research and analysis of geomagnetic pseudostorm while air flights. Vestnik USATU 18: 132-141.
- Vorobev AV (2013) Modelling and research of geomagnetic pseudostorm effect. Geoinformatika 1: 29-36.
- Vorobev AV (2014) Analysis and research of special geomagnetic variations, Contemporary problems of science and education.
- Vorobev AV (2012) Problems of digital geomagnetic observatories development. LAP Lambert Academic Publishing G mbh & Co. KG, Berlin, 133.
Author Details
Andrei V Vorobev* and Gulnara R Shakirova
Department of Computer Science and Robotics, Ufa State Aviation Techical University, Ufa, Russia
Corresponding author
Andrei V Vorobev, Department of Computer Science and Robotics, Ufa State Aviation Techical University, K. Marx Str, Ufa, Russia, Tel: +7-917-345-22-99, E-mail: gimslab@yandex.ru
Accepted: November 27, 2015 | Published Online: November 30, 2015
Citation: Vorobev AV, Shakirova GR (2015) Modeling and Analysis of Main Magnetic Field of the Earth for the Period 2010-2015. Int J Earth Sci Geophys 1:002.
Copyright: © 2015 Vorobev AV, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The paper deals with research, modelling and analysis of internal geomagnetic field parameters, which considered as the geomagnetic field induced by internal (intraterrestrial) sources. The calculation was based on the set of final coefficients for World Magnetic Model for Epoch 2010/2015 and Epoch 2015/2020. Comparative analysis of geomagnetic field parameters for Epoch 2010/2015 and Epoch 2015/2020 was given to represent the reversal of inner geomagnetic field, changes of geomagnetic dipole and shifts of magnetic poles.
The aim of research is to analyze the redistribution of geomagnetic field full vector, the changing of geomagnetic dipole parameters and dynamics the Earth's magnetic poles shifting during this period. To achieve this goal the authors suggest a set of mathematical, algorithmic and methodological tools and models for the solution of the problem of calculating of main geomagnetic field parameters (here main field is considered as the geomagnetic field induced by intraterrestrial sources.). The suggested mathematical models and software is based on the matrices of spherical harmonic coefficients for calculating the parameters of the geomagnetic field for the periods 2010-2015 and 2015-2020 respectively. Changes in the main field for one year, or so-called secular variations, are also represented by the series of spherical harmonics. The basis of representation in the mathematical models is a Gauss series, which is suggested as an international standard normal state of the geomagnetic field. The authors also suggest a program GEOmagnetic_v1.0, which allows to generate estimates of the state parameters of the geomagnetic field and perform their geospatial binding in automatic mode with acceptable accuracy.
Keywords
Geomagnetic variations, Geomagnetic field, Inner (intraterrestrial) sources
Introduction
In modern world scientists and specialists in various spheres pay great attention to study dynamics of parameters of geomagnetic field (GMF) in common and GMF of inner (intraterrestrial) sources and geomagnetic dipole in particular. This interest is mainly concerned with acute problem of research and forecast of geomagnetic reversal (geomagnetic poles shift) and modeling its possible consequences [1].
GMF is well-known as the magnetic force field that surrounds the Earth. To simplify the description of the GMF it can be defined as a large bar magnet placed at the center of the Earth, with its south end oriented toward the north magnetic pole. The main goal of the Earth's magnetic field is to deflect most of the solar wind. Otherwise the charged particles of the solar wind would strip away the ozone layer of the Earth and all the systems and objects at the planet would be subjected to the influence of harmful ultraviolet radiation [1].
GMF is shaped somewhat like a comet, which tail stretches for hundreds of thousands of kilometers in the direction opposite to the Sun and accumulates magnetic energy [2]. This area is called the magnetosphere and its shape is formed in response to the dynamic pressure of the solar wind.
At any point on the Earth's surface the geomagnetic field is a combination of several magnetic fields generated by various sources. These fields are superimposed on and interact with each other [3].
GMF is not stable and changes with periodicities from about 0.3 second to hundreds of years. These changes are often referred to as geomagnetic variations, which can arise from both sources external to the Earth or internal to the Earth. For example, sometimes the energy in magnetosphere tail is released in explosions. They heat up plasma, and cause powerful electric currents. At this moment the magnetosphere is filled to capacity with hot plasma, while its electric currents embrace the entire near-Earth space. These phenomena are referred to as magnetic storms [3].
Traditionally the full vector of the Earth's magnetic field intensity in any geographical point with spatiotemporal coordinates (latitude, longitude, altitude, year) is defined as a sum of two components [2,3]:
where B1 is an intensity vector of GMF of inner (intraterrestrial) sources; B2 is a regular component of intensity vector of GMF of magnetosphere currents, which is calculated in solar-magnetosphere coordinate system.
Magnetic field of inner (intraterrestrial) sources consists of two fields: electric currents field in the core (the main ("core") field), which is ~98% of the whole field, and rocks magnetism field, which is ~2% of the whole field. Thus, with altitude raise the crust field decreases much quicker, then the main field, and from the altitude ~100 km its value can be neglected [2].
At the same time magnetosphere currents magnetic field defines a regular component of geomagnetosphere. This field depends on parameters of interplanetary medium. It demonstrates the well-known compression of the Earth's magnetosphere on the sunlit side due to the interaction with the solar wind, asymmetry "day-night" (the field on the night side of the Earth is weakened), diurnal, season, yearly and other variations of geomagnetic field [3].
Mathematical Models and Algorithms for Calculation of Inner Geomagnetic Field Parameters
Solving the problem of B1 parameters analytical estimation, it is helpful to represent the main field model by spherical harmonic series, depending on geographical coordinates.
The scalar potential of intraterrestrial sources GMF induction U [nT•km] in the point with spherical coordinates r, θ, λ is defined by the expression (1):
where n is a degree of spherical harmonics (m ∈ [0,12]), m is an order of spherical harmonics (n ∈ [0,12]), r is a distance from the Earth's center to observation point (geocentric distance), [km]; λ is a longitude from Greenwich meridian, [degrees]; θ is a polar angle (collatitude, θ = (π/2)-φ', [degrees], where φ' is a latitude in spherical coordinates, [degrees]); RE is an average radius of the Earth, RE = 6371.03 km; gmn (t), hn (t) are spherical harmonic coefficients, [nT], which depend on time period; Pmn are Schmidt semi-normalized associated Legendre functions of degree n and order m [4-6].
In geophysical literature the expression (1) is widely known as a Gaussian and generally recognized as an international standard for undisturbed GMF [7,8].
The amount of performed spherical harmonic analysis is very important. However, a problem of spherical harmonic optimal length definition is still acute. Values of higher orders for elements gnm and hnm were calculated by G. Phanzelau (up to 15th order) and V. Kolosov and E. Kropachev (up to 23rd order). The main conclusion about these values is that there is sharp decrease of all coefficients for 6-8 orders and then their slow decrease with some oscillations. There are no coefficients (up to 23rd order) with sharp increase, which could point on magnetic field local sources (Table 1 and Table 2).
Analyses of calculation results with great amount of elements prove hypothesis of Gauss about convergence of spherical harmonic, which represents a geomagnetic potential. As usual in spherical harmonic analyses the harmonics are limited by 8-10 elements. But for sufficiently homogeneous and highly accurate data (for example, as like as in satellite imaging) the harmonics series can be extended up to 12 and 13 harmonics. Coefficients of harmonics with higher orders by their values are compared with or less than error of coefficients definition. For example, for series of 11-13 harmonics an error of GMF calculation on the Earth surface is less than ~2%.
Due to the main field temporal variations the coefficients of harmonic series (spherical harmonic coefficients) are periodically (once in 5 years) recalculated with the new data, which are obtained from satellites and magnetic observatorie (Table 3 and Table 4).
The change of main field for one year (or secular variation) is also represented by spherical harmonics series (Table 5 and Table 6 for Epoch 2010 and Table 7 and Table 8 for Epoch 2015).
Schmidt semi-normalized associated Legendre functions Pnm from expression (1) in general can be defined as an orthogonal polynomial, which is represented as follows (2):
where εm is a normalization factor (εm = 2 for m ≥ 1 and εm = 1 for m = 0); n is a degree of spherical harmonics; m is an order of spherical harmonics.
It is important to mention here, that in a number of scientific problems some geospatial data (for example, positions of satellites in space) are represented in geographical (geodesic) coordinates φ, λ, h, which are based on the Earth's surface approximation by spheroid. In these problems the Earth's ellipticity is neglected with no difference between spherical and geodesic coordinates. But in accurate calculations the Earth's pole compression should be taken into account.
So, values r and φ' with the compression taken into account are defined by the expressions (3) and (4) [9]:
where φ is a geographical (geodesic) latitude of the point, [degrees]; h is an altitude (elevation), [degrees]; a is a semi-major axis of Earth's ellipsoid; b is a semi-minor axis of Earth's ellipsoid.
The longitudes λ in spherical and geodesic coordinates are identical. So the components X', Y', Z' of induction vector of intraterrestrial sources GMF in nT are defined as follows:
So, in the point with coordinates φ, λ, h the orthogonal components of induction vector (in geodesic coordinate systems) are defined by the expressions (5)-(8), and the module of GMF induction vector is defined by the expression (9):
where |H| is a horizontal component of GMF induction vector B1 (B1 projection on horizontal plane XY).
Field value Y in expression (6) for the point with θ = 0 is calculated via linear interpolation. Angle elements of geomagnetic dipole are defined as follows:
where D is a magnetic declination - the angle between geographic and magnetic meridians (positive to the east); I is a magnetic dip - the angle between horizontal plane XY and a vector B0 (positive to the east).
Geomagnetic elements for the appropriate year t are to be calculated with spherical harmonic coefficients gnm(t) and hnm(t), which are recalculated (actualized) according to the expressions (11) and (12):
where t is a current year, t0 is a year of the known spherical harmonic coefficients gnm(t), hnm(t); gnm and hnm are the spherical harmonic coefficients amendments, which are connected with secular variations of GMF (Table 5 and Table 6 for Epoch 2010 and Table 7 and Table 8 for Epoch 2015).
Dipole geomagnetic field corresponds to the field, which is represented by the first element of spherical harmonics in (1). The components of dipole element are defined by the following expressions:
The coordinates of magnetic dipole poles (geomagnetic poles) and magnetic moment M [Tl•m3] are defined by the expressions (16), (17) and (18):
where Φ0 and Λ0 are geographical latitude and longitude of geomagnetic pole, [degrees].
Figure 1 and Figure 2 represent methodic and algorithm of calculation of parameters of GMF and geomagnetic dipole, which are adapted for programming formalization. Detailed description of methodic and algorithm is given in previous papers [10].
Programming instrumental complex GEOmagnetic_v1.0 (Certificate of official computer program registration No. 2013610905) was developed on the basis of the methodic and algorithm to increase an efficiency of GMF parameters calculation. This complex provides operations for generating calculated data about GMF and their geospatial link in automated mode with error, which is acceptable according to Russian Federation standard [3] "Geomagnetic field. Inner field model" [3].
Modeling, Visualization and Analysis of GMF Parameters for 2010-2015
Figure 1 and Figure 2 represent an example of visualization of GMF parameters calculation results (as a set of isolines). Values of the parameters were obtained via programming instrumental complex for Epochs 2010 and 2015. Isolines in the figures are represented with step of 1000 nT (1 μT) to allow making judgments about their relative displacement.
Integration of programming instrumental complex with modern GIS technologies [11-13] provides a possibility of clear representation of inner GMF full vector parameters change dynamics for 2010-2015 (Figure 3). On the figure dashed and solid lines define a distribution of parameters of inner GMF full vector at 2010 and 2015. Isolines step is 2500 nT (2.5 μT).
Figure 4 represents a visualization of ΔB1 parameter, which is defined according to expression (15) and provides a basis for judgments about global reversal of inner GMF:
where B1_2015 and B1_2010 are values of inner GMF vector at 2010 and 2015.
According to the analysis of figure 3 and figure 4 it is obvious, that for 2010-2015 a reversal of inner GMF in the Western Hemisphere is appeared as weakening (ΔB1_min = -730.1 nT) and in the Eastern Hemisphere - as strengthening (ΔB1_max = 567.2 nT). Maxima and minima of weakening and strengthening are observed on North-Western and South-Eastern regions of the planet.
Table 9 represents results of calculation of geomagnetic dipole magnetic moment. Also the table represents the coordinate of its North Pole according to expressions (12)-(14).
Analysis of table 9 proved, that for the last five years magnetic moment of geomagnetic dipole decreased by 2.218•1013 T•m3 (~0.286 %). Thereby North magnetic pole shifted from the point -80.015° N, 72.219° E to the point -80.312° N, -72.621° E. It is ~33.93 km in southern geographical direction.
Conclusion
So, calculation, modeling and analysis of inner GMF parameters for 2010-2015 proved, that:
• for this period a reversal of inner GMF in the Western Hemisphere appeared as weakening (ΔB1_min = -730.1 nT) and in the Eastern Hemisphere - as strengthening (ΔB1_max = 567.2 nT);
• for the last five years magnetic moment of geomagnetic dipole decreased by 2.218•1013 T•m3 (~0.286 %);
• North magnetic pole shifted from the point -80.015° N, 72.219° E to the point -80.312° N, -72.621° E. It is ~33.93 km in southern geographical direction.
Acknowledgments
The reported study was supported by RFBR, research projects No. 14-07-00260-a, 14-07-31344-mol-a, 15-17-20002-d_s, 15-07-02731_a, and the grant of President of Russian Federation for the young scientists support MK-5340.2015.9.

