
International Journal of Earth Science and Geophysics
(ISSN: 2631-5033)
Volume 7, Issue 1
Research Article
DOI: 10.35840/2631-5033/1844
Comparison of Ocean Tide Loading Models Using Strain Data Measured in the Sopronbánfalva Geodynamic Observatory, Hungary
Gyula Mentes*
Table of Content
Figures
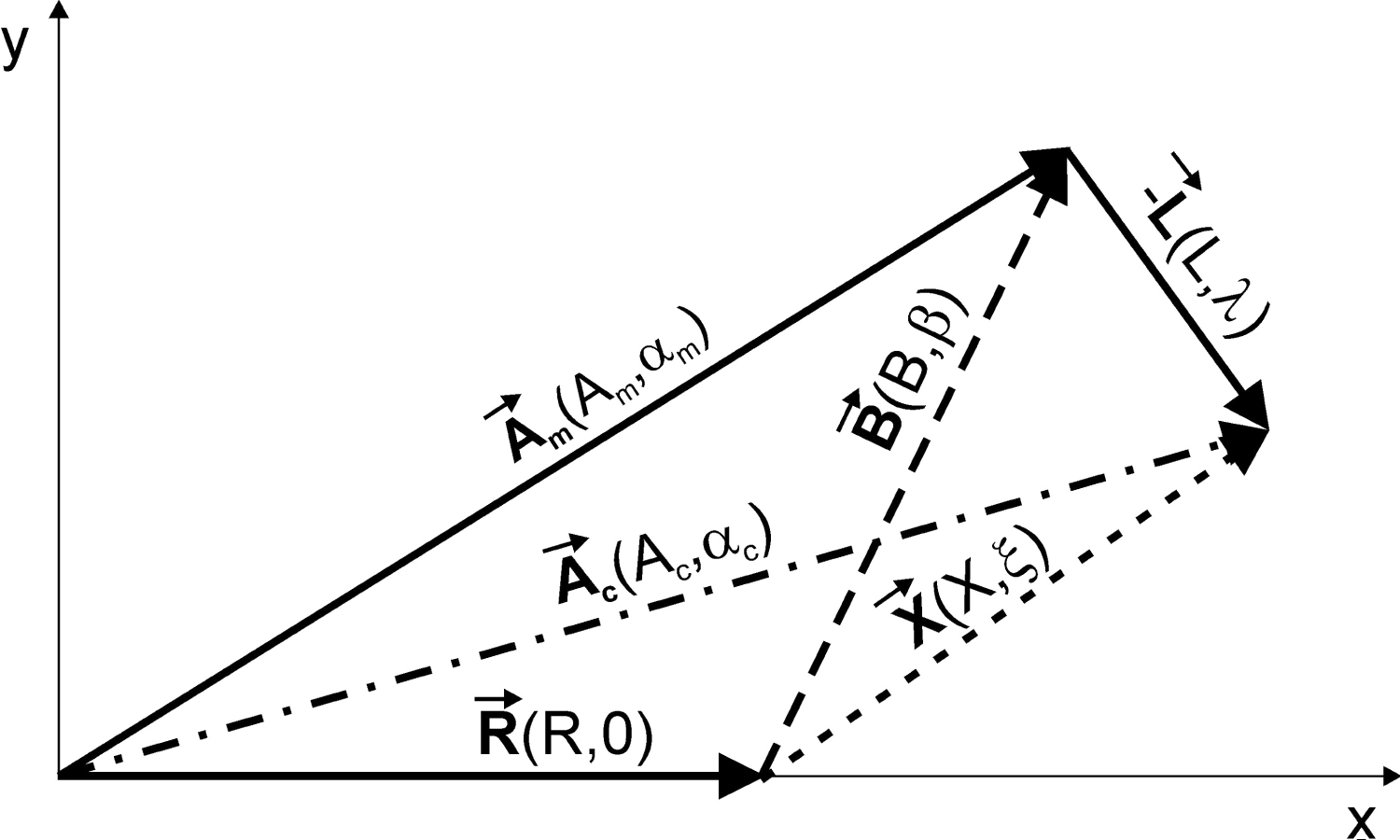
Figure 1: Outline of tidal ocean loading correction....
Outline of tidal ocean loading correction. Theoretical tidal vector , observed tidal vector , observed residual vector , ocean loading vector , corrected tidal vector and remaining residual vector . The vectors are defined by their amplitudes (R, Am, B, L, Ac and X) and phases (0, αm, β, λ, αc and ξ).
Tables
Table 1: Tidal results calculated from strain data corrected for temperature and barometric pressure.
Table 2: Results of correction of the O1 wave for ocean tide loading derived from 10 ocean loading models with different Earth models calculated by SPOTL routines. The observed values, not corrected for ocean tide loading, are in Table 1.
Table 3: Results of correction of the K1 wave for ocean tide loading derived from 10 ocean loading models with different Earth models calculated by SPOTL routines. The observed values, not corrected for ocean tide loading, are in Table 1.
Table 4: Results of correction of the M2 wave for ocean tide loading derived from 10 ocean loading models with different Earth models calculated by SPOTL routines. The observed values, not corrected for ocean tide loading, are in Table 1.
Table 5: Results of correction of the O1, K1, M2 waves for ocean tide loading derived from three ocean loading models with different Earth models calculated by the ocean load provider service. L amplitude of the ocean tide load, λ phase of the ocean tide load, Ac corrected strain amplitude, αc phase of the corrected strain, X amplitude of the remaining residual, ξ phase of the remaining residual, ηc corrected amplitude factor. The observed values, not corrected for ocean tide loading, are in Table 1.
References
- Farrell W (1972) Deformation of the earth by surface load. Rev Geophys Space Phys 10: 761-797.
- Jentzsch G (1997) Earth tides and ocean tidal loading. In: Wilhelm H, Zürn W, Wenzel H-G, Tidal phenomena, lecture notes in earth sciences. Springer, Berlin Heidelberg, 66: 145-167.
- Ducarme B (2009) Limitations of high precision tidal prediction. Bull Inf Marées Terr 145: 11663-11677.
- Agnew DC (2015) Earth tides. In: G Schubert, Treatise on Geophysics. (2nd edn), 3: 151-178.
- Bos MS, Penna NT, Baker TF, Clarke PJ (2015) Ocean tide loading displacements in western Europe: 2. GPS-observed anelastic dispersion in the asthenosphere. J Geophys Res Solid Earth 120: 6540-6557.
- Llubes M, Mazzega P (1997) Testing recent global ocean tide models with loading gravimetric data. Prog Oceanog 40: 369-383.
- Baker TF, Bos MS (2003) Validating earth and ocean tide models using tidal gravity measurements. Geophys J Int 152: 468-485.
- Boy JP, Llubes M, Hinderer J, Florsch N (2003) A comparison of tidal ocean loading models using superconducting gravimeter data. Journal of Geophysical Research 108.
- Boy JP, Lyard F (2008) High-frequency non-tidal ocean loading effects on surface gravity measurements. Geophys J Int 175: 35-45.
- Sun HP, Ducarm B, House X, Leslie V, Jianqiao X, et al. (2005) Adaptability of the ocean and Earth tidal models based on global observations of the superconductive gravimeters. Science in China Ser D Earth Sciences 48: 1859-1869.
- Sun HP, Hsu HT, Chen W, Chen XD, Zhou JC, et al. (2006) Study of the earth's gravity tide and ocean loading characteristics in Hongkong area. Chinese Journal of Geophysics 49: 657-670.
- Lysaker DI, Breili K, Pettersen BR (2008) The gravitational effect of ocean tide loading at high latitude coastal stations in Norway. J Geod 82: 569-583.
- Arnoso J, Benavent M, Montesinos FG (2011) [en línea]. Updating gravimetric tide parameters and ocean tide loading corrections at the observing sites Cueva de los Verdes and Timanfaya of the Geodynamics Laboratory of Lanzarote. In: 25 years of scientific activity at the Lanzarote Geodynamic Laboratory. House of the Volcanoes - Cabildo de Lanzarote. 1-20.
- Hábel B, Meurers B (2014) A new tidal analysis of superconducting gravity observations in Western and Central Europe. Contrib Geophys Geod 44: 1-24.
- Amoruso A, Crescentini L (2016) Nonlinear and minor ocean tides in the Bay of Biscay from the strain tides observed by two geodetic laser strainmeters at Canfranc (Spain). J Geophys Res Oceans 121: 4873-4887.
- Amoruso A, Crescentini L (2020) Parameters of the earth's free core nutation from diurnal strain tides. Scientific Reports 10: 9756.
- Hinderer J, Riccardi U, Rosat S, Boy J, Hector B, et al. (2020) A study of the solid earth tides, ocean and atmospheric loadings using an 8-year record (2010-2018) from superconducting gravimeter OSG-060 at Djougou (Benin, West Africa). J Geodyn 134: 101692.
- Lambert A, Pagiatakis SD, Billyard AP, Dragert H (1998) Improved ocean tide loading corrections for gravity and displacement: Canada and northern United States. J Geophys Res 103: 30231-30244.
- Thomas ID, King MA, Clarke PJ (2007) A comparison of GPS, VLBI and model estimates of ocean tide loading displacements. J Geod 81: 359-368.
- Penna NT, Bos MS, Baker TF, Scherneck HG (2008) Assessing the accuracy of predicted ocean tide loading displacement values. Journal of Geodesy 82: 893-907.
- Penna NT, Clarke PJ, Bos MS, Baker TF (2015) Ocean tide loading displacements in western Europe: 1. Validation of kinematic GPS estimates. J Geophys Res Solid Earth 120: 6523-6539.
- Vergnolle, Bouin MN, Morel L, Masson F, Durand S, et al. (2008) GPS estimates of ocean tide loading in NW-France: determination of ocean tide loading constituents and comparison with a recent ocean tide model. Geophys J Int 173: 444-458.
- Hwang Ch, Huang JF (2013) Numerical modeling of displacements due to ocean tide loading: Case study at GPS stations in Taiwan and western Pacific. Journal of the Chinese Institute of Engineers 36: 1017-1028.
- Li Z, Jiang W, Ding W, Deng L, Peng L (2014) Estimates of minor ocean tide loading displacement and its impact on continuous GPS coordinate time series. Sensors 14: 5552-5572.
- Kalita JZ, Rzepecka Z (2015) Impact of ocean tides loading on precise point positioning based on FES2004 model. Artificial Satellites 50: 77-89.
- Amoruso A, Crescentini L (2009) The geodetic laser interferometers at Gran Sasso, Italy: Recent modifications and correction for local effects. Journal of Geodynamics 48: 120-125.
- Amoruso A, Botta V, Crescentini L (2012) Free core resonance parameters from strain data: Sensitivity analysis and results from the Gran Sasso (Italy) extensometers. Geophys J Int 189: 923-936.
- d'Oreye N, Zürn W (2006) Quarter-diurnal tides observed with a long-base water-tube tiltmeter in the Grand Duchy of Luxembourg. Journal of Geodynamics 41: 175-182.
- Boy JP, Longuevergne L, Boudin F, Jacob T, Lyard F, et al. (2009) Modelling atmospheric and induced non-tidal oceanic loading contributions to surface gravity and tilt measurements. J Geodyn 48: 182-188.
- Florsch N, Llubes M, Wöppelmann G, Longuevergne L, Boy JP (2009) Oceanic loading monitored by ground-based tiltmeters at Cherbourg (France). J Geodyn 48: 211-218.
- Mentes G (2008) Observation of recent tectonic movements by extensometers in the Pannonian Basin. J Geodyn 45: 169-177.
- Mentes G (2010) Quartz tube extensometer for observation of Earth tides and local tectonic deformations at the Sopronbánfalva Geodynamic Observatory, Hungary. Rev Sci Instrum 81: 074501.
- Van Camp M, Vauterin P (2005) Tsoft: Graphical and interactive software for the analysis of time series and earth tides. Computers & Geosciences 31: 631-640.
- Wenzel HG (1996) The nanogal Software: Earth tide data processing package Eterna 3.30. Bull Inf Marées Terr 124: 9425-9439.
- Wahr JM (1981) Body tides on an elliptical, rotating, elastic and oceanless Earth. Geophys J R Astr Soc 64: 677-703.
- Dehant V (1987) Tidal parameters for an unelastic Earth. Phys Earth Planet Inter 49: 97-116.
- Hartmann T, Wenzel HG (1995) Catalogue HW95 of the tide generating potential. Bull Inf Marées Terr 123: 9278-9301.
- Agnew DC (2013) SPOTL: Some programs for ocean-tide loading. Institute of Geophysics and Planetary Physics, Scripps Institution for Oceanography, University of California, USA Technical Report.
- Bos MS, Scherneck HG (2013) Computation of green's functions for ocean tide loading. In: G Xu, Sciences of Geodesy - ii. Springer, Berlin Heidelberg, 1-52.
- Harkrider DG (1970) Surface waves in multilayered elastic media Part II. Higher mode spectra and spectral ratios from point sources in plane layered Earth model. Bull Seismol Soc Am 60: 1937-1987.
- Savcenko R, Bosch W (2012) EOT11a - empirical ocean tide model from multi-mission satellite altimetry. DGFI Report No. 89.
- Taguchi E, Stammer D, Zahel W (2014) Inferring deep ocean tidal energy dissipation from the global high-resolution data-assimilative HAMTIDE model. J Geophys Res Oceans 119: 4573-4592.
- Egbert GD, Erofeeva YS (2002) Efficient inverse modeling of barotropic ocean tides. Journal of Atmospheric and Oceanic Technology 19: 183-204.
- Cheng Y, Andersen OB (2010) Improvement in global ocean tide model in shallow water regions. OSTST Meeting, Lisbon, 18-22.
- Eanes RJ (1994) Diurnal and semidiurnal tides from TOPEX/POSEIDON altimetry. Eos Transactions American Geophysical Union 75: 108.
- Lyard F, Lefevre F, Letellier T, Francis O (2004) Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn 56: 394-415.
- Le Provost C, Lyard F, Molines J, Genco ML, Rabilloud F (1998) A hydrodynamic ocean tide model improved by assimilating a satellite altimeter-derived data set. J Geophys Res 103: 5513-5529.
- Schwiderski EW (1980) On charting global ocean tides. Rev Geophys 18: 243-268.
- Carrère L, Lyard F, Cancet M, Guillot A, Roblou L (2013) FES 2012: A new global tidal model taking advantage of nearly 20 years of altimetry. Proc '20 Years of Progress in Radar Altimetry' 24-29 September 2012, Venice, Italy.
- Carrère L, Lyard F, Cancet M (2015) FES2014, A new tidal model on the global ocean with enhanced accuracy in shallow seas and in the arctic region. EGU General Assembly, Vienna, Austria, 12-17.
- Carrère L, Lyard F, Cancet M, Guillot A, Picot N (2016) Finite Element Solution FES2014, a new tidal model - Validation results and perspectives for improvements. Presentation to ESA Living Planet Conference, Prague.
- Ray RD (1999) A global ocean tide Model from TOPEX/POSEIDON Altimetry: GOT99.2. NASA Technical Memorandum 209478.
- Kustowski B, Ekström G, Dziewonski AM (2008) Anisotropic shear-wave velocity structure of the Earth's mantle: A global model. J Geophys Res 113.
- Neumeyer, J del Pino J, Dierks O, Sun HP, P flugH (2005) Improvement of ocean loading correction on gravity data with additional tide gauge measurements. J Geodyn 40: 104-111.
Author Details
Gyula Mentes*
Geodetic and Geophysical Institute, Research Centre for Astronomy and Earth Sciences, Hungary
Corresponding author
Gyula Mentes, Geodetic and Geophysical Institute, Research Centre for Astronomy and Earth Sciences, Csatkai E. u. 6-8, 9400 Sopron, Hungary, Tel: +36-99-508382.
Accepted: March 16, 2021 | Published Online: March 18, 2021
Citation: Mentes G (2021) Comparison of Ocean Tide Loading Models Using Strain Data Measured in the Sopronbánfalva Geodynamic Observatory, Hungary. Int J Earth Sci Geophys 7:044.
Copyright: © 2021 Mentes G. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Tidal strain observations carried out in the Sopronbánfalva Geodynamic Observatory (SGO) in Hungary are used to test thirteen different ocean tide loading models for diurnal and semi-diurnal tidal harmonic constituents O1, K1 and M2. Strain data with one minute sampling rate were corrected for temperature and barometric pressure and decimated to one hour sampling rate. Strain data, corrected in this way, were subjected to correction for ocean load. In the case of the diurnal tidal constituents O1 and K1 the measured amplitude factors of nearly 0.5 became close to the theoretical as a result of the correction, while in the case of the M2 semi diurnal wave the measured amplitude factor of almost 1 hardly changed due to correction. It was only found a negligible difference between the individual global ocean tide loading models mainly due to using different Earth models and Green functions. The effect of the diurnal (O1 and K1) and the semidiurnal (M2) ocean tide loading components is in the same order of magnitude at the SGO. The large residual vectors after the correction suggest that local effects need further investigation.
Keywords
Earth tide, Extensometer, Tidal parameters, Ocean tide loading, Strain
Introduction
Ocean tide surface loading causes both radial and tangential displacements of the Earth surface and changes of gravity. This latter comprises effects resulting from radial displacement in the Earth's gravity field, the internal redistribution of mass, and the direct gravitational attraction of the tidal water mass [1-5].
Various authors have been dealing with testing and comparison of recent global ocean tide models on the basis of gravimetric [6-17], displacement (GPS) [18-25], extensometric [15,16,26,27] and tilt measurements [28-30].
In this paper, the efficiency of ocean loading corrections are compared using thirteen different ocean tide loading models for the diurnal and semi-diurnal tidal harmonic constituents O1, K1 and M2 on the basis of strain data observed in the SGO in 2017.
Measurement Site and Instrument
Extensometric measurements were carried out in the SGO which is located on the Hungarian-Austrian border in the Sopron Mountains. The coordinates of the observatory are: Latitude 47°40'55'' N; longitude 16°33'32" E; the altitude is 280 m a.s.l. The yearly mean temperature in the gallery is 10.4 ℃ and the yearly and daily temperature variations are less than 0.5 ℃ and 0.05 ℃, respectively. The instrument is a 22 m long quartz-tube extensometer with capacitive transducer. The azimuth of the extensometer is 116°, and its scale factor is 2.093 ± 0.032 nm mV-1. Observation site and construction of the extensometer and its calibration are described in detail by Mentes [31,32].
Data Processing
Strain, temperature and barometric pressure data recorded with a sampling rate of one minute were used for correction by the T-soft program [33]. Data series were despiked and ungapped. The long-term constituent of the strain and temperature data were approximated by fitting a polynomial of 9th order to the raw data series and were subtracted from strain and temperature data, respectively. Theoretical tide was subtracted from the remaining strain data and then strain data were corrected for the temperature and barometric pressure by simple linear regression method and after the correction the theoretical tide was added back. During the correction procedure time lags between strain and temperature and barometric pressure data were taking into consideration. Then the data were low-pass filtered and decimated to one hour sampling and processed by ETERNA 3.40 Earth tide data processing program package [34] using the Wahr-Dehant Earth model [35,36] and the HW95 tidal potential catalogue [37].
For the ocean tide load prediction the SPOTL routines [38] and the ocean load provider service [39] were used. The name of the SPOTL codes are: gr.mmmmmm.www.pnn,c[e|m], The mmmmmm string denotes the Earth model. The SPOTL uses three different Earth models, which are denoted namely the Gutenberg-Bullen Model A average Earth (gbaver) and two extreme models of the Earth's crust and mantle structure [40], one oceanic (gbocen) and one continental shield (gbcont). www denotes: Who computed the function: the source code is wef for W.E. Farrell [1], who computed and tabulated all Green functions. pnn denotes: 01 coarse grid; 02 fine grid (about 20 m for the innermost range) running to much closer to the center (about 100 m). The ce suffix denotes a reference frame with the center of mass of solid Earth and the cm a reference frame with the common center of mass of the load and the Earth.
For ocean load correction of strain data ten ocean tide models have been used with SPOTL, supplemented by the local model osu.mediterranean.2011: EOT11a [41], HAMTIDE11a [42], OSU.TPXO72atlas, OSU.TPXO72, TPX070 [43], DTU10 [44], CSR4.0 [45], FES2004 [46], FES95.2.1 [47], SCHW1 [48] and three other models were chosen from the Free Ocean Tide Loading Provider created by Scherneck and Bos (http://holt.oso.chalmers.se/loading/): FES2012 [49], FES2014b [50,51], GOT00.2 [52].
Without external forces the common centre of mass of oceans and the solid Earth will remain fixed in space. Since the ocean tides cause water mass displacements, its centre of mass moves periodically and it is compensated by an opposite motion of the centre of mass of the solid Earth. Accordingly, in these three cases the ocean load was calculated relative to the fixed common mass center of the ocean and the solid Earth and the moving center of mass of the solid Earth. In both cases the calculations were carried out using elastic [1] and visco-elastic Earth model STW105 [53].
The ocean loading correction (see Figure 1) was carried out according to Neumeyer, et al. [54]. The L amplitude and λ phase of the ocean tide load vectors were determined from the above-mentioned different ocean tide loading models and were subtracted from the observed strain tidal vectors in case of the O1, K1 and M2 tidal waves to obtain the corrected tidal strain vectors . The remaining residual X depends on the accuracy of the instrument calibration, the local effects, such as the cavity effect, the inaccurately corrected temperature, air pressure and on the accuracy of the ocean tide model.
Results and Discussion
Results of the tidal evaluation of the measured strain data in case of the tidal constituents O1, K1 and M2 without ocean tide loading corrections are shown in Table 1. In the SGO the obtained amplitude factors for the diurnal waves (O1, K1,) are about 0.5, half of the theoretical value, while for the semidiurnal wave M2 it is about 1. Table 2, Table 3, Table 4 and Table 5 show the amplitudes (L) and phases (λ) of the ocean tide load, the amplitudes (Ac) and phases (αc) of strain corrected for the ocean tide load, the amplitudes (X) and phases (ξ) of the residues and the corrected amplitude factors (ηc) in case of different Earth and global ocean tide loading models.
Table 2 shows the O1 tidal constituents corrected for ocean tide loading with SPOTL in case of different Earth models and 10 global ocean tide models. The uncorrected amplitude factor is 0.5323 (see Table 1), while the corrected amplitude factors (average: 1.025 ± 0.001) are somewhat higher than one in the case of solid Earth model with the center of mass (ce suffix denotes the reference frame with the center of mass of solid Earth) and somewhat lower (average: 0.928 ± 0.003) in the case of the Earth model with the common center of mass of the load and the Earth (cm suffix denotes the reference frame with the common center of mass of the load and the Earth). Similar results were obtained for K1 (see Table 3) for which the uncorrected amplitude factor was 0.5283. The corrected average amplitude factors are 1.026 ± 0.001 (ce) and 0.966 ± 0.002 (cm). The measured amplitude factor for M2 is 1.0036 (see Table 1), while the corrected average values (see Table 4) are 1.059 ± 0.004 (ce) and 1.039 ± 0.007 (cm). In both cases the corrected values are higher than the measured value, but similarly to O1 and K1 the corrected values are higher in case of reference frame with the center of Earth (ce) than in the case of common center of load mass and the center of Earth.
Table 5 shows the results of correction of the O1, K1, M2 waves for ocean tide loading derived from three ocean loading models (FS2012, FS214b and GOT00.2) with different Earth models calculated by the ocean load provider service. In case of the elastic and visco-elastic Earth models almost identical corrected amplitude factors (ηc) were obtained for O1, K1 and M2 waves but these were somewhat higher when motion correction was applied in case of the diurnal waves (O1 and K1), while for the semidiurnal wave M2 the opposite values were obtained.
Comparing the residues in Table 2, Table 3, Table 4 and Table 5, it can be seen that the amplitudes (X) of the residual vectors changed only slightly compared to the measured ones (B), while the phase angles decreased significantly. Large residues remaining after the correction suggest that local effects (e.g. cavity) affect the measurement site, which requires further study. The amplitudes (L) of the ocean load vectors are in the same order of magnitude for the diurnal (O1, K1) and semidiurnal (M2) waves at the site of the SGO.
Conclusions
Strain measurement was used to test thirteen global ocean tide loading models. Tidal parameters corrected for ocean tide loading were calculated. All models provided virtually the same result. In the case of the diurnal tidal constituents O1 and K1 the measured amplitude factors of nearly 0.5 became close to 1 as a result of the correction, while in the case of the M2 semi diurnal wave, the measured amplitude factor of almost 1 hardly changed due to correction. It was only found a negligible difference between the individual tide loading models mainly due to the use of different Earth models, and Green functions. The effect of the diurnal (O1 and K1) and the semidiurnal (M2) ocean tide loading components is in the same order of magnitude at the SGO. The large residual vectors after the correction suggest that local effects need further investigation.
Acknowledgments
This work was funded by the Hungarian National Research Fund (OTKA) under project K 109060. Special thanks to Tibor Molnár for his careful maintenance of the instruments.

