International Journal of Earth Science and Geophysics
(ISSN: 2631-5033)
Volume 7, Issue 2
Research Article
DOI: 10.35840/2631-5033/1850
Computing Oil Saturation of Fractured Sandstone Reservoir
Bin Zhao1*, Guangyou Zhu2, Yanjun Shang3 and Peng Shao3,4
Table of Content
- Abstract
- Keywords
- Introduction
- Determining Physical and Mechanical Parameters of Fractured Sandstone Reservoir
- Determining Ground Stresses in Fractured Sandstone Reservoir
- Anisotropy of Effective Porosity in Fractured Sandstone Reservoir
- Anisotropy of Physical Property of Fractured Sandstone Reservoir
- Engineering Application Example
- Conclusions
Figures

Figure 1: Diagram of coring from fractured....
Diagram of coring from fractured sandstone reservoir.
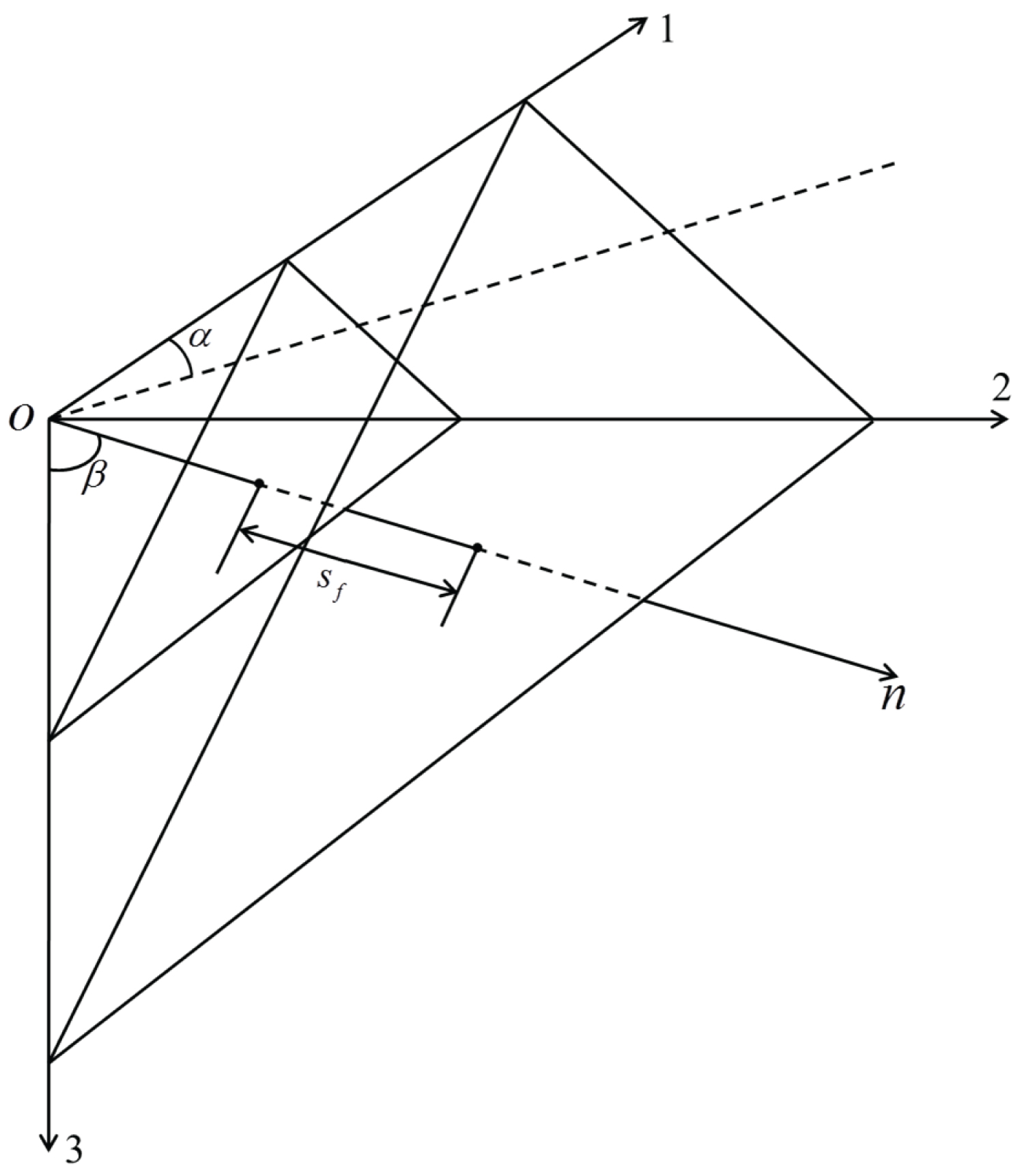
Figure 3: Diagram of dip, dip angle and....
Diagram of dip, dip angle and fracture spacing of fracture surface principal ground stress space.
References
- Taillet E, Lataste JF, Rivard P, Denis A (2014) Non-destructive evaluation of cracks in massive concrete using normal dc resistivity logging. NDT&E International 63: 11-20.
- Taillet E, Lataste JF, Rivard P, Denis A (2015) Characterization of discontinuities inside massive concrete structures with normal dc resistivity logging. J Appl Geophysics 120: 69-80.
- Müller C, Siegesmund S, Blum P (2010) Evaluation of the representative elementary volume (REV) of a fractured geothermal sandstone reservoir. Environ Earth Sci 61: 1713-1724.
- Moran JH, Gianzer S (1979) Effects of formation anisotropy on resistivity-logging measurements. Geophysics 44: 1266-1286.
- Chen MJ, Kang YL, You LJ, Shi YJ, Zhang HT (2014) The response of electrical parameters of saturated tight sandstone to effective stress changes. Progress in Geophysics 29: 1128-1132.
- Yin S, Fan ZY, Zhao W (2017) Sensitivity of conventional well-logging series to fractures in tight sandstone reservoirs with coal. Natural Gas Technology and Economy 11: 9-12.
- Liu ZY, Zhang CG, Tang J, Xiao CW (2018) Influence of fracture on rock resistivity and its application in saturation calculation. Lithologic Reservoirs 30: 120-128.
- Tang H, Yu B, Yang D, Wang B, Li WW (2013) A resistivity calibration method for fracture carbonate reservoir. World Well Logging Technology 2013: 62-63.
- Xiao CW, Xin Y, Gao JF, Wu XN, Xu JB (2008) Log evaluation of Epimetamorphic sandstone reservoirs with low porosity and fractures in Silurian in North Tarim Basin. Well Logging Technology 32: 529-533.
- Dürrast H, Rasolofosaon PNJ, Siegesmund S (2002) P-wave velocity and permeability distribution of sandstones from a fractured tight gas reservoir. Geophysics 67: 241-253.
- Li ZM, Zhang JZ (1997) Geostress and oil and gas exploration and development. Petroleum Industry Press, Beijing, China.
- Ma JH, Sun JM (2002) Calculation of formation stress using logging data. Well Logging Technology 26: 347-351.
- Xu ZL (2016) Elastic Mechanics. Higher Education Press, Beijing, China.
- Chen X, Yang Q, Li DJ (2016) Study on the mechanical effect of anisotropic damage of rock fracture network. Science Press, Beijing, China.
- Hong YM (2008) Logging principle and comprehensive interpretation. China University of Petroleum Press, Beijing, China.
- Liu GQ, Li CX (2019) Petrophysical characteristics and logging evaluation method of continental tight oil. Science Press, Beijing, China.
Author Details
Bin Zhao1*, Guangyou Zhu2, Yanjun Shang3 and Peng Shao3,4
1Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, Korla, China
2Research Institute Exploration and Development, China National Petroleum Corporation, Beijing, China
3Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing, China
4University of Chinese Academy of Sciences, Beijing, China
Corresponding author
Bin Zhao, Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina, 841000, Korla, China.
Accepted: August 10, 2021 | Published Online: August 12, 2021
Citation: Zhao B, Zhu G, Shang Y, ShaoP (2021) Computing Oil Saturation of Fractured Sandstone Reservoir. Int J Earth Sci Geophys 7:050.
Copyright: © 2021 Zhao B, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Physical and mechanical properties of fractured sandstone reservoir present as significant anisotropy. Resistivity logging is used to evaluate oil bearing property of sandstone reservoir in production practices. Obvious deviation of resistivity value emerges in resistivity logging of fractured sandstone reservoir, which induces adverse effect on accurate evaluation of oil bearing property of reservoir. Cores in three directions along principal ground stresses were obtained with directional coring technique. Young's moduli of intact rock, Poisson's ratios of rock with fracture, and normal stiffness of fracture surface were gained through experiments of rock mechanics. Fracture spacing was determined by core observation and electrical imaging logging. Considering occurrence and mechanical properties of fracture, computing formulas of effective porosity in fractured sandstone reservoir were derived based on poroelasticity. Lithology coefficient and porosity index along three directions of principal ground stress were determined through experiments base on Archie's formula. Finally, oil saturation of fractured sandstone reservoir was computed. A practical example was given to show application of the new method provided in this study. Results indicate that effective porosity and oil saturation in fractured sandstone reservoir have remarkable anisotropy. The new method shown in this study can be used to improve computing accuracy of oil saturation.
Keywords
Fractured sandstone reservoir, Resistivity, Effective porosity, Anisotropy, Oil saturation
Introduction
Oil saturation is the basic data to judge reservoir quality and adjust development scheme. Mechanical and electrical properties of fractured sandstone reservoir have remarkable anisotropic feature. Resistivity logging is used to evaluate petroliferous property of fractured sandstone reservoir in practical production process. However, resistivity in fractured sandstone reservoir shows a significant deviation, which induces errors of petroliferous property evaluation. Fracture, a type of discontinues, which cause relatively greater differences of Young's modulus, Poisson ratio, effective porosity and permeability along different directions in reservoir. And ultimately induce the anisotropy of petroliferous property. Many scholars have researched the fractures and influence of fracture on logging data. Normal electrical probe was used to detect damage zones and discontinues, to diagnose internal structure, and to characterizes centimeter or millimeter cracks in concrete [1,2]. Permeability of fractured reservoir is not merely the function of geometry of fractures, which more dependent on stress state of reservoir [3]. Effects of anisotropy of reservoir on resistivity were investigated [4]. Electrical parameters of 71 tight sandstone samples under different effective stress were determined [5]. Cracks in coal bed markedly affect parameters of resistivity logging series [6]. A normalized resistivity formula of rock was introduced to compute gas saturation of fractured tight sandstone reservoir, which improved the double-porosity model [7]. Artificial fractures were produced in three rock samples to imitate tectonic fractures. Resistivities of fracture with different aperture were determined, which were used to fit formula between resistivity of fracture and resistivity of original core [8]. Effects of fractures on seepage capability of reservoir were studied of fractured sandstone reservoir in Tarim basin [9]. Occurrence of fracture has remarkable effects on P wave propagation [10]. A method used to compute oil saturation of fractured sandstone reservoir is needed. This study described the method considering effects of fractures on petroliferous property. In principal ground stress space, anisotropy of mechanical and electrical properties was obtained through experiments and analytical derivation. Young's modulus, Poisson ratio, effective porosity of intact rock, and normal stiffness of fracture were determined by rock mechanics experiments. Resistivity of rock mass cored from reservoirs was investigated with rock physical experiments. Ultimately, a formula based on Archie's formula was derived, which reflected the anisotropy of oil saturation in fractured sandstone reservoir. The method can be adopted to reduce logging cost and assess petroliferous property of fractured sandstone reservoir.
Determining Physical and Mechanical Parameters of Fractured Sandstone Reservoir
Determining Young's modulus and Poisson's ratio of fractured sandstone
Large size cores were taken out from deep strata by directional coring method,and small size samples conducted rock mechanical experiment drilled from them, as shown in Figure 1. Young's moduli in three principal ground stress directions, , , , were determined by triaxial compressive experiments in which rock samples without fracture were used. Six Poisson's ratios (i, j = 1, 2, 3) were determined through rock samples with fracture.
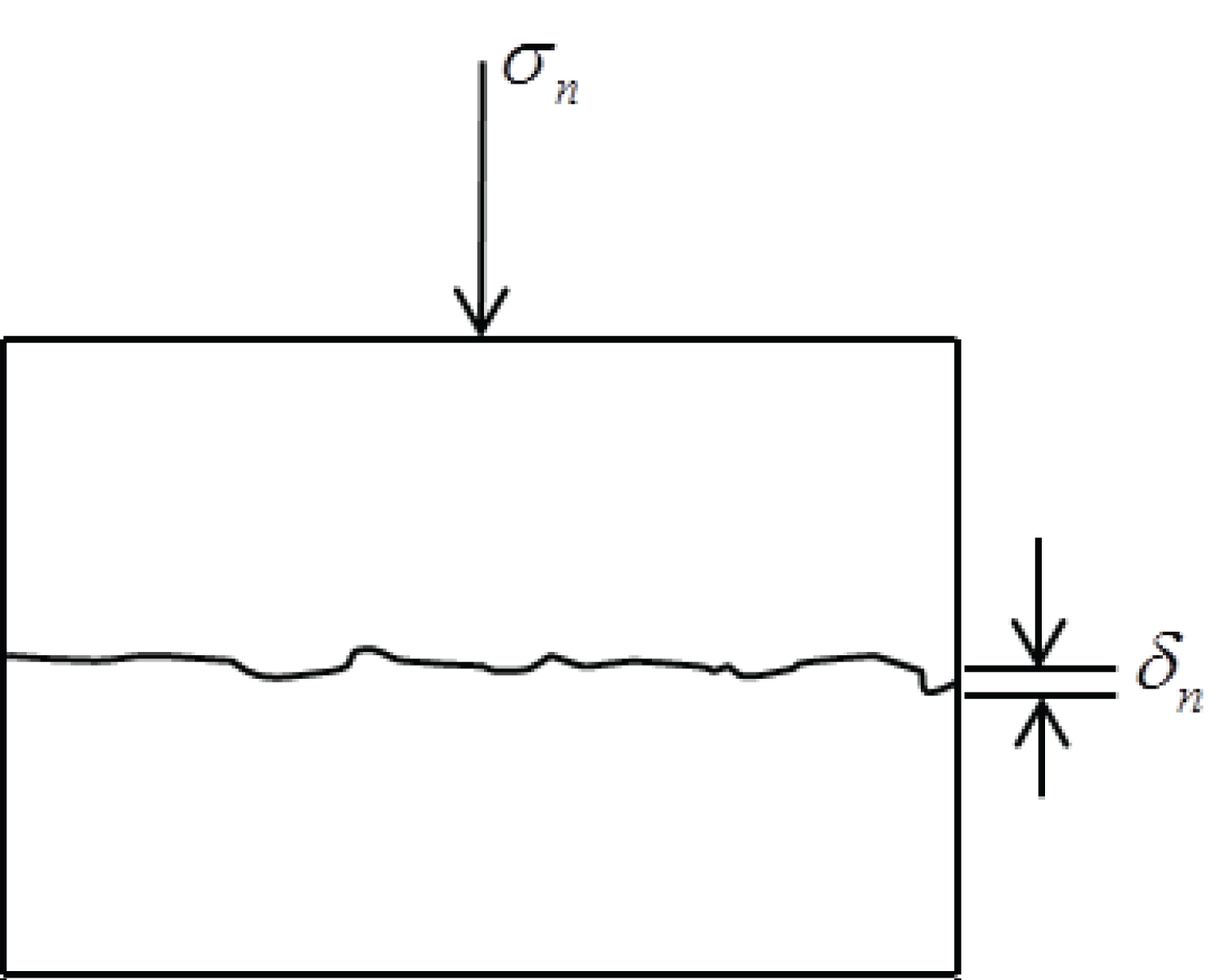
Determining normal stiffness of fracture
Rock samples with fracture were chosen to conduct the experiments used to determine the normal stiffness of fracture in sandstone reservoir. As shown in Figure 2, was acted in direction of perpendicular to fracture surface, and closure displacements of fracture were monitored in loading process. Normal stiffness was obtained through definition formula .
Determining Ground Stresses in Fractured Sandstone Reservoir
Orientation of principal ground stresses can be obtained by analyzing collapse orientation or induced fractures of borehole wall. Magnitude of the minimum principal ground stress was obtained from fracture pressure values of hydraulic fracturing. Vertical ground stress can be calculated with Eq. (1).
Where is vertical ground stress, MPa; is density of formation rock, g/cm3; g is gravitational acceleration, 9.8 m/s2; is thickness of formation, m.
Maximum principal ground stress and minimum principal ground stress can be obtained with Eq. 2 and Eq. 3. [11,12]
Where is the maximum principal ground stress, MPa; is the minimum principal ground stress, MPa; is pore pressure of reservoir, MPa; E is Young's modulus of rock, MPa; is Poisson's ratio, dimensionless; is vertical stress, MPa; α is Biot coefficient; is strain in the direction of maximum principal stress, dimensionless; is strain in the direction of minimum principal stress, dimensionless.
Anisotropy of Effective Porosity in Fractured Sandstone Reservoir
Principal ground stress space can be determined by the directions of three principal ground stresses, as shown in Figure 3. 1, 2, 3 axes represent maximum principal ground stress, intermediate principal ground stress, and minimum principal ground stress, respectively. Included angle between dip of fracture surface and direction of maximum principal ground stress is α. Dip angle of fracture surface is β. Fracture spacing is .
Young's modulus of rock mass can be calculated with Young's modulus of matrix, normal stiffness of fracture surface, and fracture spacing. The calculation expression is as follow [13,14].
Where is Young's modulus of rock mass in i direction, MPa; is Young's modulus of intact rock in i direction, MPa; is normal stiffness of fracture surface, N/m; is fracture spacing, m.
Dip and dip angle of fracture are α and β, respectively. Direction cosines of normal direction areas follow
According to elastic theory of porous media and Terzaghi principle, strain in three directions of principal ground stresses can be derived as Eq. (6)
Where is strain in i direction, dimensionless; , , are stresses in i, j, k direction, respectively, MPa; E is Young's modulus of fractured sandstone, MPa; is Poisson's ratio of fractured sandstone, dimensionless; is pore pressure of fractured sandstone reservoir, MPa.
Effective porosity in three directions of ground stresses were derived with definition of effective porosity and Eq. (4)-Eq. (6). The effective porosity in three directions of ground stresses are as follow
Where is effective porosity in direction of maximum principal ground stress, dimensionless; is effective porosity in direction of intermediate principal ground stress, dimensionless; is effective porosity in direction of minimum principal ground stress, dimensionless; is initial effective porosity of fractured sandstone reservoir, dimensionless; is Young's modulus of intact sandstone in the direction of maximum principal ground stress, MPa; is Young's modulus of intact sandstone in the direction of immediate principal ground stress, MPa; is Young's modulus of intact sandstone in the direction of minimum principal ground stress, MPa; α is included angle between dip direction of fracture and maximum principal ground stress, º; β is dip angle of fracture surface, º; is normal stiffness of fracture surface, MPa•m-1; is fracture spacing, m; (i, j = 1, 2, 3)represents compressive strain in direction j generated by tensile stress in direction i, dimensionless; is pore pressure of fractured sandstone reservoir, dimensionless; is maximum principal stress, MPa; is intermediate principal stress, MPa; is minimum principal stress, MPa; Arranging vertical stress , maximum horizontal principal ground stress , minimum horizontal principal ground stress arrange in order of magnitude, and assigning maximum value to , intermediate value to , minimum value to .
Anisotropy of Physical Property of Fractured Sandstone Reservoir
Anisotropy of effective porosity of fractured sandstone reservoir
Resistivity of fractured sandstone reservoir in three directions of principal ground stresses was obtained through Archie's formula [15,16].
where, is resistivity of fractured sandstone reservoir in three directions of principal ground stresses saturated by water, ; is lithology factor in three directions of principal ground stresses, dimensionless; is porosity index in three directions of principal ground stresses, dimensionless; is effective porosity in three directions of principal ground stresses, dimensionless; is resistivity of formation water, . Lithology coefficient and porosity index can be determined through experiments. Using Young's moduli , , of intact sandstone, Poisson's ratio of fractured sandstone in reservoir, normal stiffness of fracture surface , and fracture spacing , effective porosity , lithology index and porosity index of fractured sandstone reservoir can be calculated. in three directions of principal ground stresses were gained with Eq. (10). Cores in three directions of principal ground stresses were adopted to determine the resistivity of formation water. Resistivity at different effective porosity were determined, and curve of were plotted through least square method. Lithology coefficient and porosity index in three directions of principal ground stresses can be obtained by the curve.
Anisotropy of oil saturation of fractured sandstone reservoir
Oil saturation of fractured sandstone reservoir in three directions of principal ground stresses can be computed by Eq. (11).
Where is resistivity of fractured sandstone reservoir in three directions of principal ground stresses saturated by water, ; is resistivity of petroliferous fractured sandstone reservoir in three directions of principal ground stresses, ; is experimental fitting parameters, dimensionless; is experimental fitting parameters, dimensionless. Resistivity of fractured sandstone with different water saturation were calculated. curve used to calculated oil saturation at different effective porosity was fitted out with least square method.
Engineering Application Example
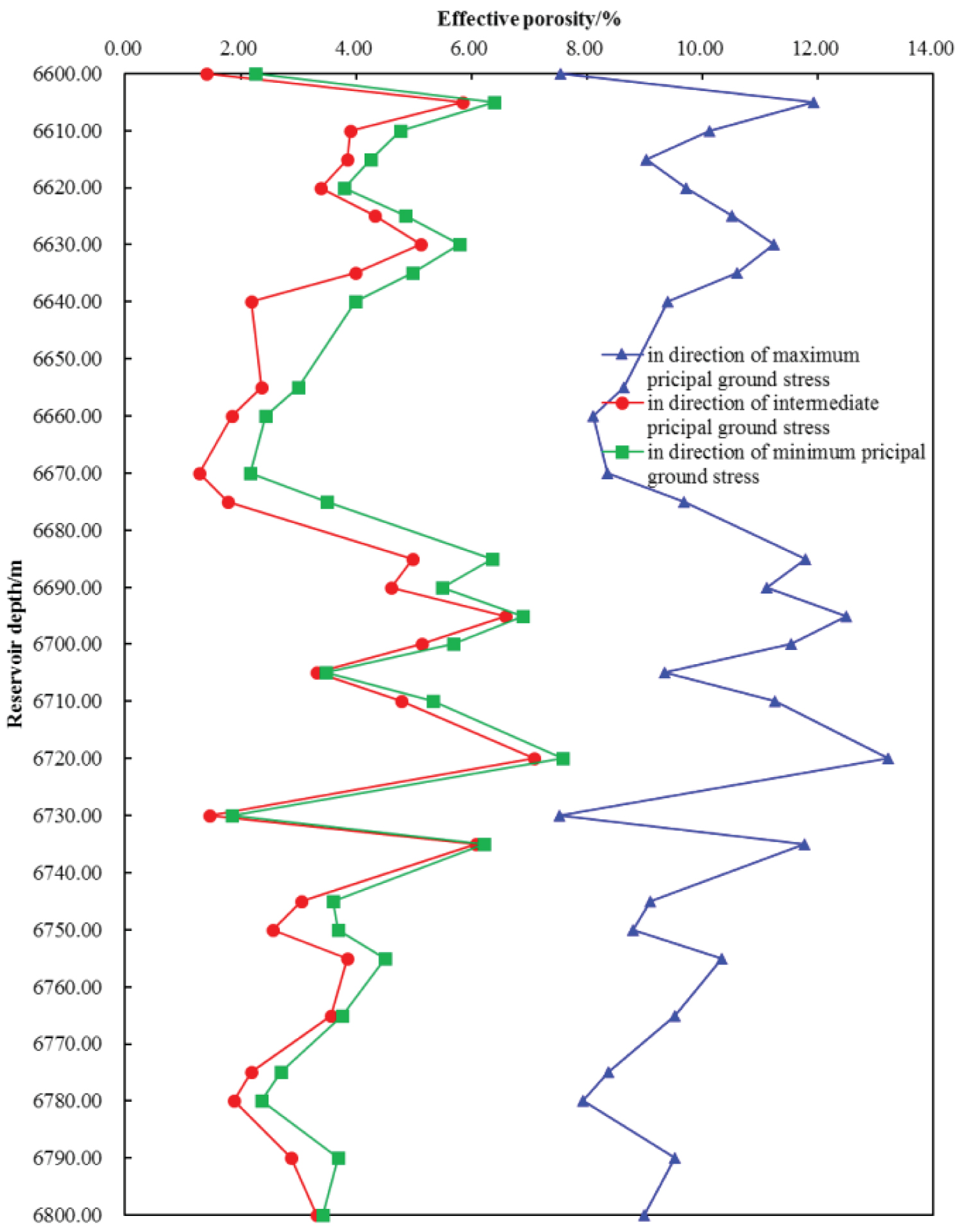
Taking representative oil-bearing rock (big sample) and coring small samples along three directions of principal ground stresses in big sample. Washing off crude oil with organic solvent and saturating these small samples with formation water, then flooding small samples with kerosene. Monitoring water saturation ( ) and corresponding resistivity . Plotting ( ) curve and fitting with least square method, determining parameters , () with curve. As shown in Figure 4, formation with a set of tectonic fracture at depth range from 6600 m to 6800 m, effective porosity in three directions of principal ground stresses have significant anisotropy. And corresponding oil saturation also have conspicuous anisotropy in three directions of principal ground stresses, as shown in Figure 5.
Conclusions
Fractures in sandstone reservoir have significant effects on physical, mechanical, and electrical properties of rock mass in reservoir. In this study, analytical and experimental approaches were used to compute oil saturation of fractured sandstone reservoir. Fractures can induce conspicuous anisotropy in physical, mechanical, and electrical properties in sandstone reservoir, which finally affects the accuracy of petroliferous property evaluation. Normal stiffness of fracture is an important factor to affect the electrical property of reservoir. Analytical derivation was conducted in space of principal ground stress, considering a set of tectonic fracture. Engineering example indicates that effective porosity and oil saturation along three directions of principal ground stress have remarkable anisotropy. The method provided in this paper can be used to compute oil saturation in fractured sandstone reservoir.