
International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 1, Issue 1
Research Article
DOI: 10.35840/2631-5068/6501
A New Technique for Measuring the Chemical Potential of Magnons Confined in Nanostructures
Chidubem A. Nwokoye1,2, Edward Della Torre1*, Lawrence H. Bennett1, Abid Siddique1 and Frank A. Narducci2
Table of Content
Figures
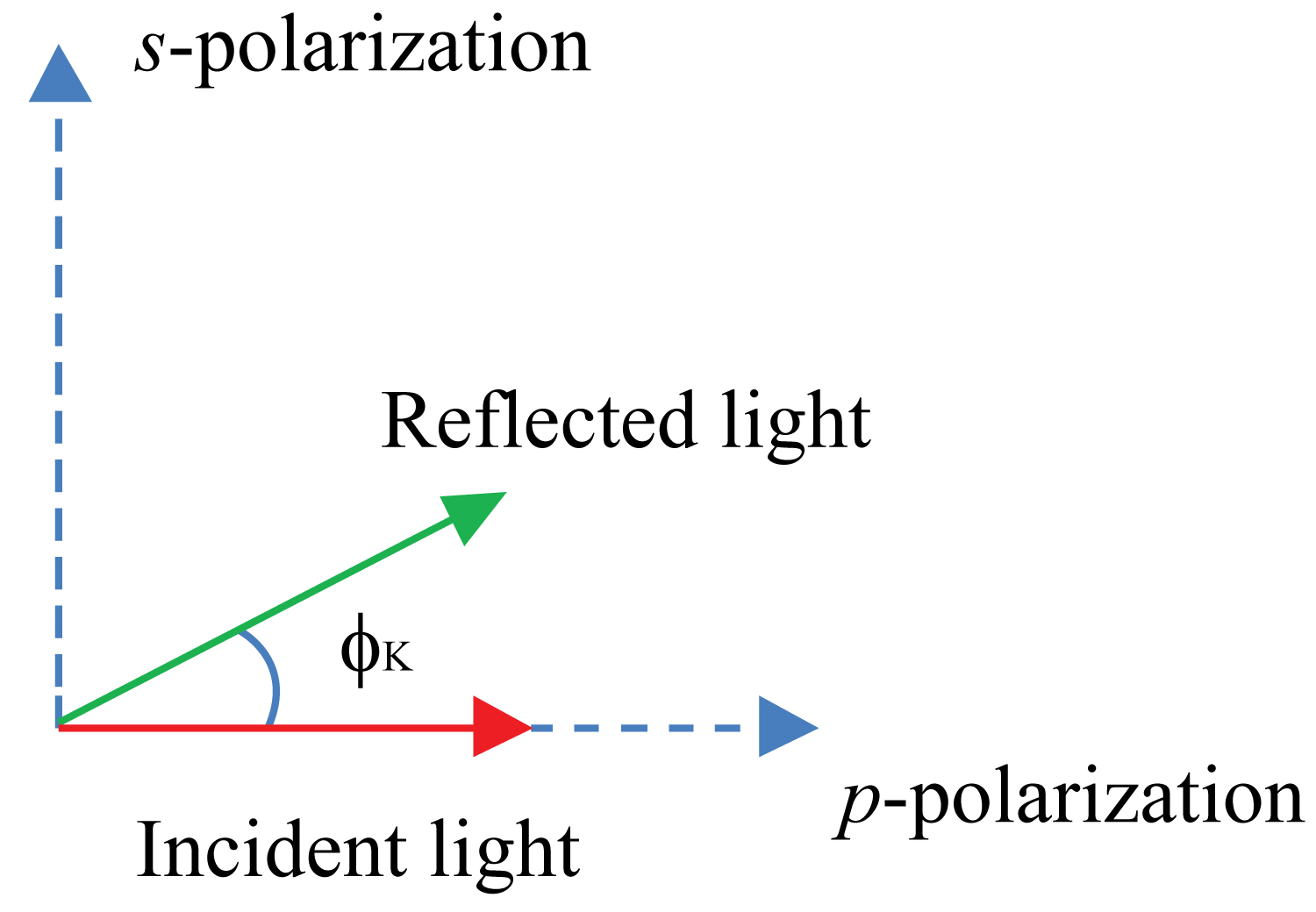
Figure 1: Polarization of incident...
Polarization of incident and reflected light depicting Kerr rotation effect in magnetic materials. The p-axis represents polarization in the plane of scattering and s-axis represents polarization perpendicular to the plane of scattering.
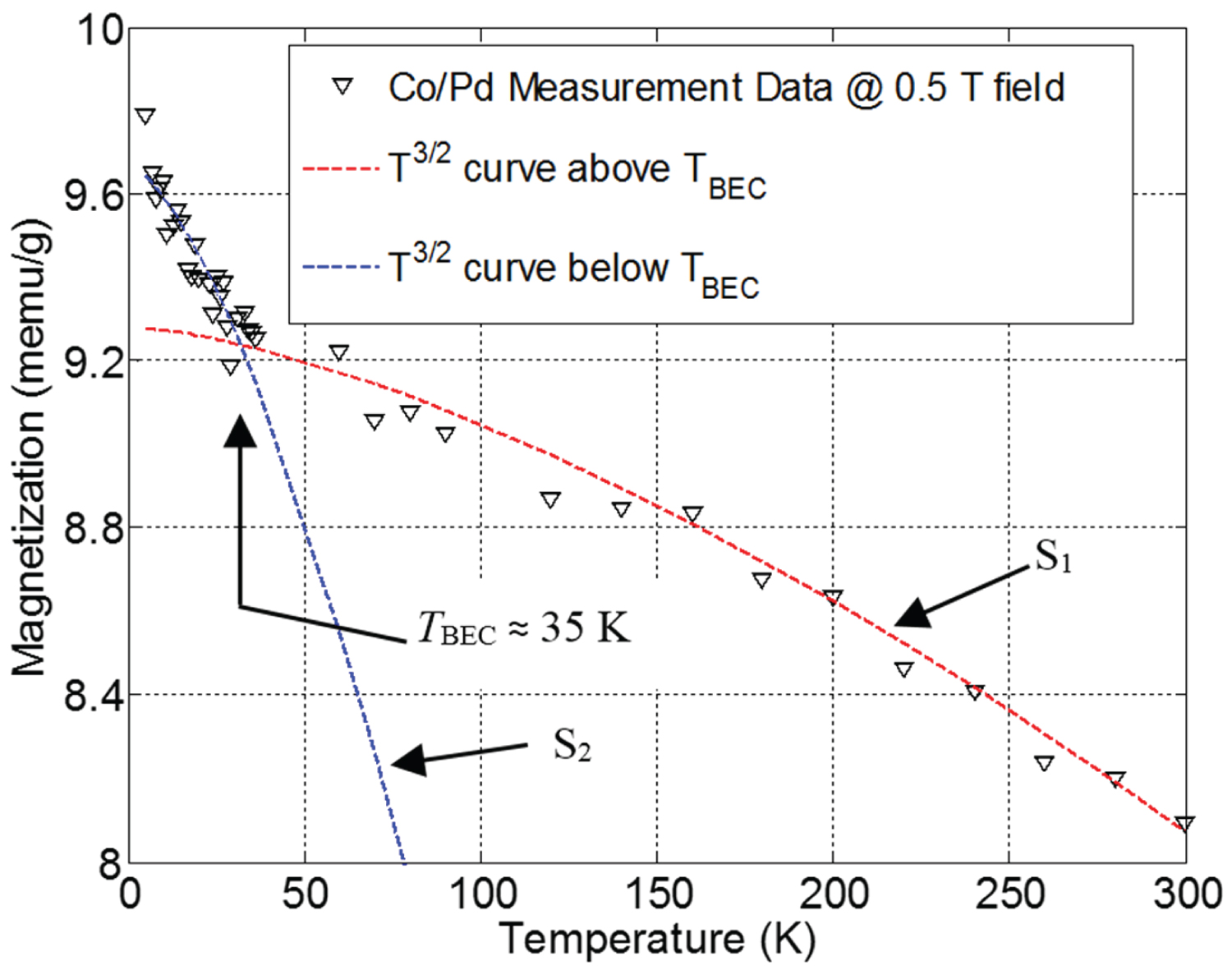
Figure 2: SQUID measurement of...
SQUID measurement of Co/Pd multilayered film temperature response for saturation magnetization. With permission from Nwokoye, et al. [24].
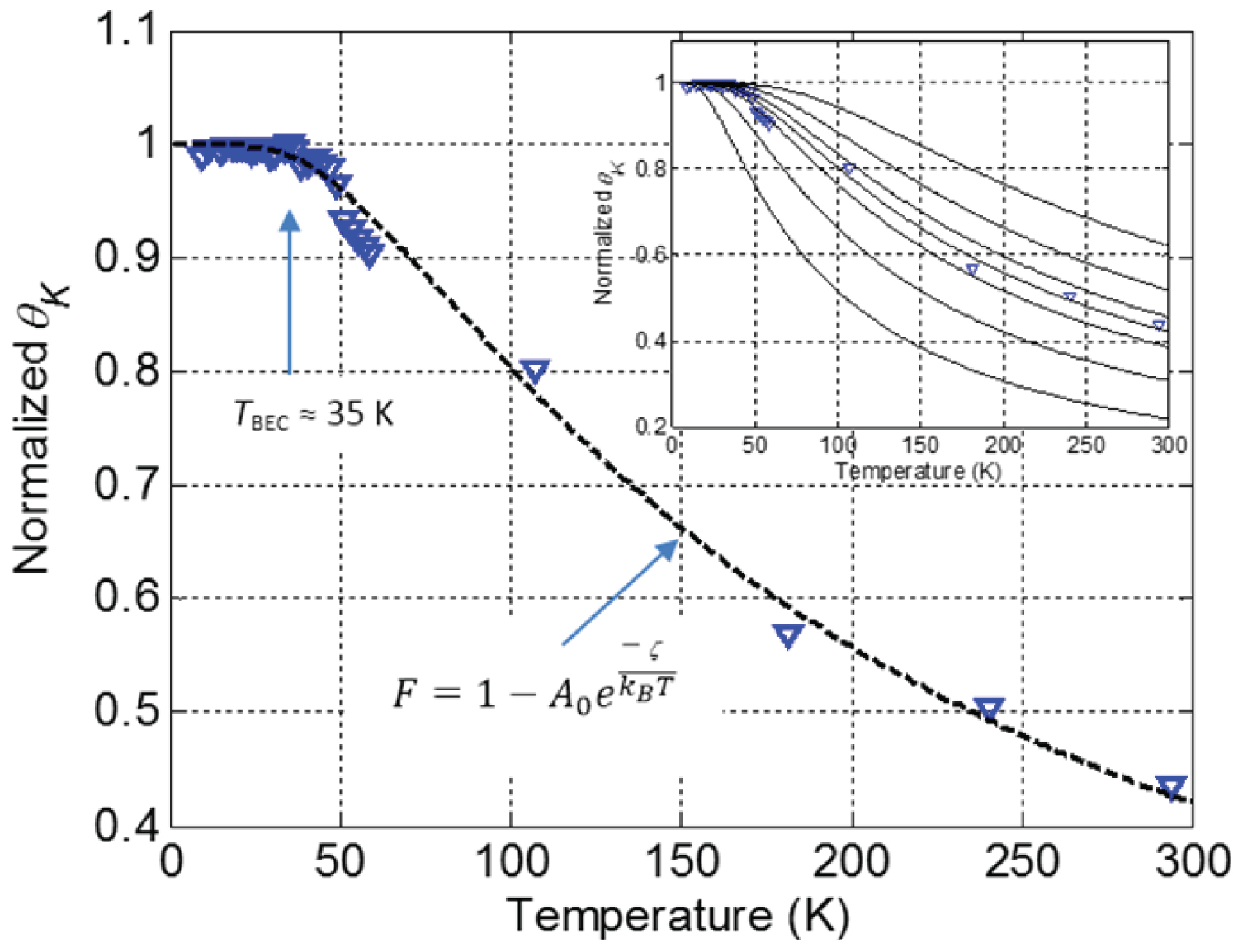
Figure 3: Co/Pd thin film temperature...
Co/Pd thin film temperature response of normalized Kerr rotation angle at saturation field. The triangles represent the measured data normalized to approximately 0.31°. The dash line is from a curve fit employing Equation (16). Inset shows plot of measured data and curves of Equation 16 with a range of constant values for . With permission from Nwokoye, et al. [24].
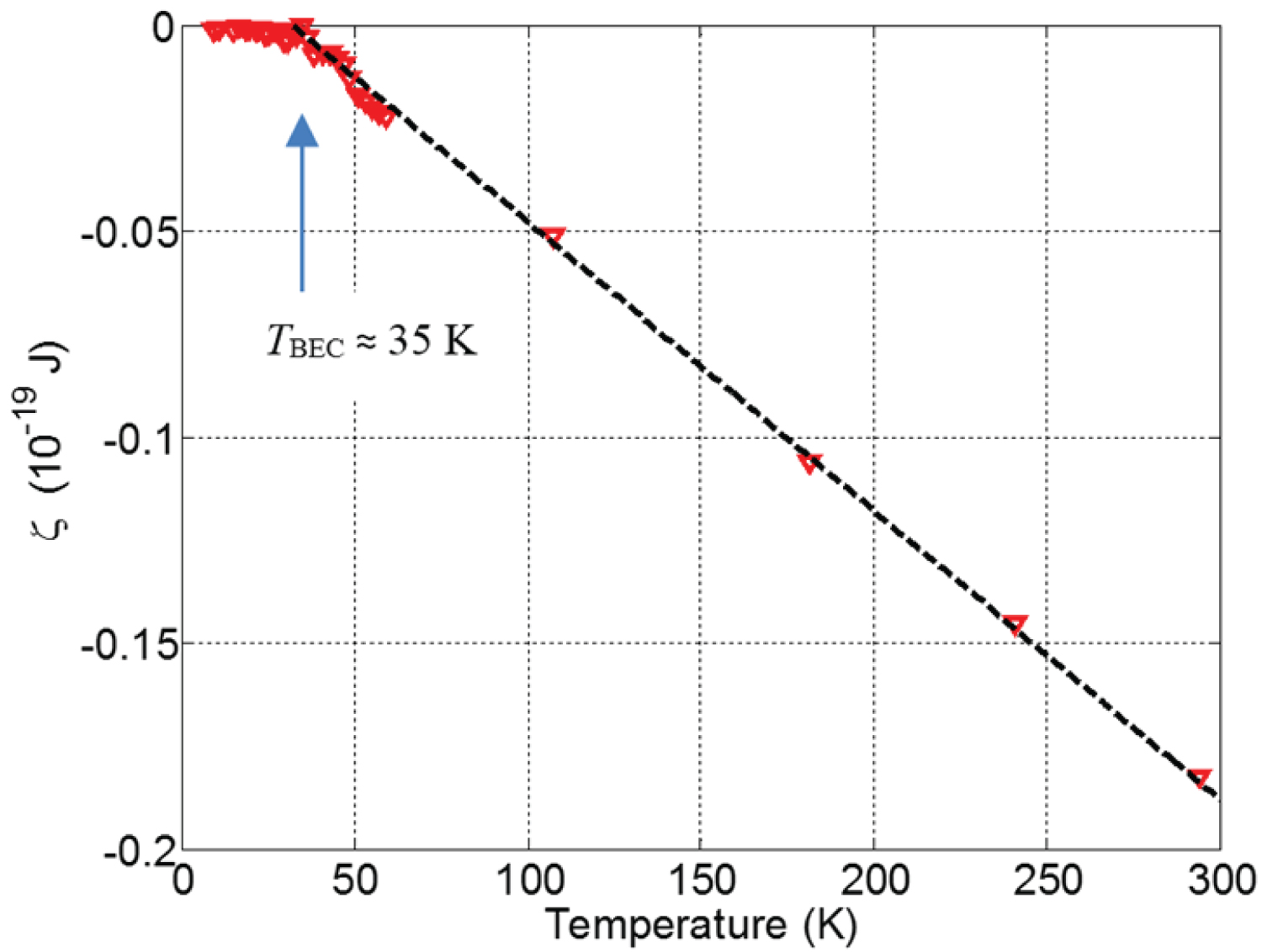
Figure 4: Temperature variation of chemical...
Temperature variation of chemical potential of magnons, in units of 10-19 J (extracted from Kerr rotation plot in figure 3 using Equation (17)). The dash line is a linear fit above .
References
- Bennett LH, Della Torre E (2008) The chemical potential of magnons in quasi-equilibrium. Physica B 403: 324-329.
- Topp J, Heitmann D, Kostylev MP, Grundler D (2010) Making a Reconfigurable Artificial Crystal by Ordering Bistable Magnetic Nanowires. Phys Rev Lett 104: 207205.
- Wang ZK, Zhang VL, Lim HS, Ng SC, Kuok MH, et al. (2010) Nanostructured magnonic crystals with size-tunable bandgaps. ACS Nano 4: 643-648.
- Tacchi S, Duerr G, Klos JW, Madami M, Neusser S, et al. (2012) Forbidden band gaps in the spin-wave spectrum of a two-dimensional bicomponent magnonic crystal. Phys Rev Lett 109: 137202.
- Liu XM, Ding J, Adeyeye AO (2012) Magnetization dynamics and reversal mechanism of Fe filled Ni80Fe20 antidot nanostructures. Appl Phys Lett 100: 242411.
- Duerr G, Huber R, Grundler D (2012) Enhanced functionality in magnonics by domain walls and inhomogeneous spin configurations. J Phys Condens Matter 24: 024218.
- Zhang VL, Lim HS, Lin CS, Wang ZK, Ng SC, et al. (2011) Ferromagnetic and antiferromagnetic spin-wave dispersions in a dipole-exchange coupled bi-component magnonic crystal. Appl Phys Lett 99: 143118.
- Livesey KL, Ding J, Anderson NR, Camley RE, Adeyeye AO, et al. (2013) Resonant frequencies of a binary magnetic nanowire," Phys Rev B 87: 064424.
- Pascu O, Caicedo JM, López-García M, Canalejas V, Blanco Á, et al. (2011) Ultrathin conformal coating for complex magneto-photonic structures. Nanoscale 3: 4811-4816.
- Morrish AH (2001) The Physical Principles of Magnetism. IEEE Press, Piscataway, 299.
- Bose SN (1924) PlancksGesetz und lichtquantenhypothese. ZeitschriftfürPhysik 26: 178-181.
- Landau LD, Lifshitz EM (1958) Statist Phys London, UK Pergamon 153-154.
- C. Kittel (1963) Quantum Theory of Solids, Wiley, New York 143: 672.
- Holstein T, Primakoff H (1940) Field Dependence of the Intrinsic Domain Magnetization of a Ferromagnet. Phys Rev 58: 1098.
- Della Torre E, Bennett LH, Watson RE (2005) Extension of the BLOCH T(3/2) law to magnetic nanostructures: Bose-Einstein condensation. Phys Rev Lett 94: 147210.
- Kerr J (1877) XLIII. On rotation of the plane of polarization by reflection from the pole of a magnet. Philos Mag 3: 321-343.
- Saini SM, Singh N, Nautiyal T, Auluck S (2007) Reflectance and magneto-optical Kerr rotation in DyP. Indian J Pure Appl Phys 45: 66-68.
- Hunt RP (1967) Magneto-Optical Scattering from Thin Solid Films. J Appl Phys 38: 1652-1671.
- Chun-Yeol You, Sung-Chul Shin (1996) Derivation of simplified analytic formulae for magneto-optical Kerr effects. Appl Phys Lett 69: 1315.
- Postava K, Maziewski A, Stupakiewicz A, Wawro A, Baczewski LT, et al. (2006) Transverse magneto-optical Kerr effect measured using phase modulation. Journal of the European Optical Society-Rapid Publications 1: 06017.
- Sato K (1981) Measurement of Magneto-Optical Kerr Effect Using Piezo-Birefringent Modulator. Jpn J Appl Phys 20: 2403-2409.
- Nwokoye CA, Bennett LH, Della Torre E, Siddique A, Narducci FA, et al. (2015) Low Temperature Magneto-Optical Kerr Effect Experimental System with a Cryogen-Free Sample Environment.
- Della Torre E, Bennett LH (2001) Temperature Variation of Magnetic Aftereffect. IEEE Trans Magn 37: 1118-1122.
- Nwokoye CA, Bennett LH, Della Torre E, Siddique A, Narducci FA, et al. (2015) Low-Temperature Magneto-Optical Phase Transition in Nanostructured Co/Pd Multilayered Material.
- Bennett LH, Della Torre E (2014) Bose-Einstein Condensation of Confined Magnons in Nanostructures. J Mod Phys 5: 693-705.
- Paduan-Filho A (2012) Bose-Einstein Condensation of Magnons in NiCl2-4SC(NH2)2. Braz J Phys 42: 292.
- Nikuni T, Oshikawa M, Oosawa A, Tanaka H (2000) Bose-Einstein condensation of dilute magnons in TlCuCl3. Phys Rev Lett 84: 5868-5871.
- Bennett LH, Della Torre E, Johnson PR, Watson RE (2007) A phase diagram for the Bose-Einstein condensation of magnons. J Appl Phys 101: 09G103.
Author Details
Chidubem A. Nwokoye1,2, Edward Della Torre1*, Lawrence H. Bennett1, Abid Siddique1 and Frank A. Narducci2
1Institute for Magnetic Research, Department of Electrical and Computer Engineering, The George Washington University, Washington, DC 20052, USA
2Naval Air Systems Command, Avionics, Sensors and E*Warfare Department, Patuxent River, MD 20670, USA
Corresponding author
Edward Della Torre, Institute for Magnetic Research, Department of Electrical and Computer Engineering, The George Washington University, Washington, DC 20052, USA, E-mail: edt@gwu.edu
Accepted: September 12, 2015 | Published Online: September 14, 2015
Citation: Nwokoye CA, Torre ED, Bennett LH, Siddique A, Narducci FA (2015) A New Technique for Measuring the Chemical Potential of Magnons Confined in Nanostructures. Int J Magnetics Electromagnetism 1:001.
Copyright: © 2015 Nwokoye CA. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The chemical potential provides an in-depth insight into the temperature variation of magnons and other quantum mechanical features. Here we present a novel magneto-optical technique to measure the chemical potential of magnons influenced by photon-magnon interactions. Our result shows the required negative chemical potential of magnons of Co/Pd in quasi-equilibrium above the observed Bose-Einstein condensation phase-transition temperature. The technique generates a single curve, contrasting with multiple curves obtained in a non-magneto-optical technique.
Introduction
Magnons confined in nanostructures display a variety of interesting phenomena, including a Bose-Einstein condensation (BEC) at a critical temperature, non-Arrhenius behavior of the magnetic aftereffect decay rate, and the shape of the magnetization behavior as a function of temperature.
Magnons are known to be the dominant factor to the magnetization dynamics in nanostructures. The thermal magnetic aftereffect provides a valuable measurement tool to probe specific relaxation processes caused by various mechanisms such as the crystallographic phase transition caused by distortion in the crystal lattice structure, defects, interstitials, and pinning. The energy barrier and chemical potential of magnons are known to be vital parameters that control this non-equilibrium process [1]. The barrier energy, also a function of applied magnetic field, increases greatly from the demagnetized state to the saturated state, while the chemical potential determines how many magnons are available; it is a function of the magnetic state and temperature and plays an important role in magnetic aftereffect predominantly in the demagnetized state. Variation in the magnon chemical potential produces anon-Arrhenius behavior of the temperature dependence of the magnetic aftereffect decay rate coefficient.
Recent research advances show a high potential for the development of novel micro and nano magnetic devices for sensor [2-5] memory [6-8] and optical applications [9]. The physics of magnons and their interaction with various external stimuli (photons and temperature) will lead to the development and realization of novel sensors, and quantum computing processors.
In this paper, we present a novel technique for measuring the chemical potential of confined magnons in a ferromagnetic nanostructured material. Below, we first describe the dependency between magnon population, chemical potential, and magnetization along with the theory and experiment of the magneto-optical Kerr effect (MOKE). We conclude with explanations of magnetization and MOKE experimental results and their relationship with chemical potential.
Chemical Potential of Magnons
Magnonsat temperatures below the temperature of magnetic ordering can be considered as a gas of weakly interacting bosons, having an integer spin value. When confined in a small nanoparticle e.g., an iron sphere with a diameter on the order of 1-10 nm, the allowed magnon wave vectors ki are quantized, giving a discrete spectrum with an energy gap between the lowest and next to lowest allowed states [10]. If the magnons are in equilibrium at temperature T, then the number in a state 'i' is given by the Bose-Einstein distribution function.
The electronic spin in this model reverses by creating or annihilating magnons. When the rate of creation of magnons is the almost the same as the annihilation rate, the magnetization of the system is almost constant with time. This static magnetization behavior of the system is in quasi-equilibrium since the population density of the various states is essentially constant in the measurement time window, and thus can be determined using thermodynamic methods.
To find the most probable state, one has to add to the energy state a constant (Lagrange multiplier), namely the chemical potential . Since magnons are bosons, the Bose-Einstein distribution [11] in Equation (1-2) can be used to describe the population of magnons
Defining , equation (1) becomes
Where is the Boltzmann's constant, N is the total number of magnons, and B is the fugacity. The chemical potential is zero below Bose-Einstein Condensation (BEC) temperature and negative above [12]. Since the energies are usually taken to be positive, then as the temperature T increases, the statistics approach the classical statistics described by the Maxwell-Boltzmann distribution due to the fugacity component. In terms of magnon wavelengths, the classical limit arises when the typical wavelength is far smaller than the average distance between magnons, such that there is negligible overlap of their wave functions.
The low energy effective Hamiltonian for describing magnons in the presence of a magnetic field is given by [13]
Where J is the exchange energy The spin components, , are not independent, but are connected by the identity where S is the magnitude of spin projection vector. After applying Holstein-Primakoff transformation [14] to spin-wave variables, the Hamiltonian becomes
Where the bilinear term relates to the internal energy of unit volume of the magnon in thermal equilibrium at temperature T. The dispersion relation is expressed in . The higher-order term describes the magnon-magnon interactions and it may be neglected when the excitation is low.
Magnetization measurement is one of many ways to test whether the number of magnons is conserved at a given temperature. The saturation magnetization, (T), at temperature T is defined by the magnetization in a field strong enough to align all the spins in the material at a given temperature T, but not so large as to suppress the generation of magnons by raising the energy barrier to the creation of a magnon greater than . It is assumed that the decrease in magnetization with increasing temperature is due to an increase in the number of magnons. Kittel [13] has shown that the total spin S for the whole system containing N spins is given in by the relation
Where is the z-component of the spin operator and is the occupation number operator for the magnon state k Therefore, the saturation magnetization per unit volume is given as the
Using the relation and , the fractional decrease in magnetization, at temperature T is derived [15] to be
Where the BEC threshold temperature and S is is the magnons spin value. As discussed in [15], the summation term is a correction to the law and accounts for BEC of magnons and negative chemical potential of magnons observed in some metallic ferromagnets.
Magnetization is known to be proportional to magneto-optical parameters of magnetic materials. The next section in this letter provides background and experimental investigation of this relationship.
Magneto-Optical Kerr Effect
The magneto-optical Kerr effect, MOKE, describes a rotation change in the polarization plane of linearly polarized incident light reflected from the surface of a magnetic material. The rotation is directly related to the surface magnetization of the material [16]. Figure 1 depicts the context-level diagram of the Kerr effect.
As a linearly polarized light reflects from the surface of a magnetic material, it experiences the following [17]: (1) Rotation of the polarization plane, described by Kerr rotation angle (2) Phase difference between the electric field components perpendicular and parallel to the plane of the incident light as described by the Kerr ellipticity .
These quantities make up the complex Kerr angle, given as
The MOKE effect can be observed in three configuration modes namely: polar, longitudinal, and transverse modes [18,19]. In polar and longitudinal Kerr effects, the reflected light experiences both Kerr rotation and Kerr ellipticity, while in transverse Kerr effect, the reflected light only experiences change in intensity. Recently, the two common experimental design setups for MOKE systems that measure the complex Kerr angle are the standard differential intensity and photoelastic modulation (PEM) designs [20,21]. Experiments reported in this letter utilized the PEM-based MOKE design.
Experiment
A multilayer film with nominal composition (0.3 nm Co/1 nm Pd) [15] was grown (molecular beam epitaxy) on silicon dioxide substrate using electron beam evaporation and designed to exhibit large perpendicular magnetic anisotropy. Polar Kerr rotation was examined on the sample at 632.8 nm with a low-temperature MOKE experimental system. The experimental system consists of an automated photoelastic modulator (PEM) based MOKE system and a closed cycle refrigeration system. Details of the experimental setup and procedures are described in [22].The MOKE system measures the Kerr rotation and Kerr ellipticity from the detected and laser intensities which correspond to the fundamental frequency, and of the PEM modulation frequency. The Kerr rotation and Kerr ellipticity are directly proportional to the detected and laser intensities respectively (as shown in Equations (14,15)). The data processing software on the computer computes the intensity ratios. The magneto-optical properties ( and ) are directly proportional to the intensity and the coefficients in Equations (14,15) can be determined by calibration procedure in [21].
The polar Kerr rotation angle of the Co/Pd sample was measured while sweeping the magnetic field (4.3 kOe to -4.3 kOe) from positive to negative saturation and back again to produce a hysteresis loop of versus applied magnetic field. The hysteresis loops at different sample temperatures (9 K to room temperature) were measured and recorded for data processing.
Results and Discussion
Measuring the chemical potential of magnons in a ferromagnetic material is important and aids to reflect the growth of the magnon density in the material. Objections that have been raised about the idea that an open system could have a nonzero chemical potential has been addressed in [1]. Work by Della Torre, et al. [23], addresses that there is a negative chemical potential of magnons, and that it can be determined from magnetic aftereffect experiments. A result discussed here presents an alternate method for determining the chemical potential.
Magnetization curves of a ferromagnetic nanostructured Co/Pd multilayered film from the work by Nwokoye, et al. [24] shows a subtle upturn in magnetization around the vicinity of 35 ± 4 K. The measurement was performed with a low-temperature SQUID magnetometer. As shown in Figure 2, the data points fit two curves with different slopes (S1 and S2) that intersect at the upturn point that is attributed to the magnon BEC temperature. It is noticeable that S1 is lesser than S2 due to the contribution of the chemical potential of magnons at temperatures above the BEC temperature and agrees with the model prediction in Equation (12) (The physical explanation is presented in [15]). Also, Bennett, et al. [1] discusses that BEC is always in an open system and exhibits metastability that can be treated as a thermodynamic equilibrium for a finite time window. The observed upturn signature has also been recorded in some metallic ferromagnetic nanomaterials within the 10 to 50 K [25] and in some ladder compounds [1,26]. This observation reinforces the presence of a phase transition attributed to magnons BEC.
Thereafter, the recorded data from a MOKE experiment of the same sample exhibited a plateauing of the Kerr rotation angle (at sample saturation) below 35 ± 3 K and decreases with higher temperatures. The Kerr rotation angle temperature response is depicted in Figure 3 [24]. This observation provides insight into the temperature variation of magnon-photon interactions in the Co/Pd material below and above the magnon BEC temperature.
After an in-depth review of the normalized Kerr rotation angle temperature response, we noticed that the shape of the measured data best fits the response produced by the exponential function model
Where is a constant, is the Boltzmann's constant, T is the temperature, and is the chemical potential. The exponential function sharply approaches unity below the magnon BEC temperature at approximately 35 K. We iteratively adjusted constant values for and to obtain a curve that best fits the measured data. The function describes how the measured normalized Kerr rotation angle depends on temperature, thus can be approximated by Equation (16) (i.e. ). In order to investigate the temperature variation of the chemical potential, we performed a one-step transformation of Equation (16) to solve for to be
After plugging the measured data values for F (Equation (17), assuming ), we find that the sharply approaches zero below the and varies linearly with temperature above temperature.
The extracted chemical potential of confined magnons (shown in Figure 4) in the Co/Pd sample has a negative value with temperature above the identified magnon BEC temperature. After obtaining the chemical potential variation with temperature, a clearer picture of the magnon-photon interactions is feasible. As the temperature decreases from room temperature, the increase in Kerr rotation angle (which is directly proportional to reflected laser intensity in Equation (15)) arises from an increase in magnetization (from Figure 2) and a decrease in absorption of incident laser. Hence, less population of excited magnons (high energy magnons) interacts with photons from incident laser. After the temperature drops below the magnon BEC temperature (35 ± 4 K), large amounts of the confined magnons begin to populate the lowest energy state and this causes the observe plateauing of the Kerr rotation angle as a result of less population of excited magnons.
Our findings provide analternative experimental technique, using Equation (17), for measuring the chemical potential of confined magnons in a ferromagnetic film via Kerr rotation angle measurement.
Conclusions
A new technique to measure the chemical potential of confined magnons in Co/Pd is reported. The Kerr rotation angle fits the response produced by an exponential function in Equation (16). The technique utilizes a one-step transformation process in Equation (17) of the Kerr rotation angle temperature response measurement from a MOKE system to extract the chemical potential. This produces a single curve which contrasts with the multiple curves obtained in the previous technique [23]. Results in Figure 4 shows the required negative chemical potential of magnons of Co/Pd in quasi-equilibrium for temperatures above the BEC temperature and a constant zero value for temperatures below the BEC temperature. Our finding is in agreement with the temperature variation of the negative chemical potential of magnons reported in previous research [1,28].
Acknowledgements
The research at The George Washington University was supported in part by the Naval Air Systems Command's NISE Section 219 funds. The author will like to thank members of the IMR group for their valuable discussion during the course of the research.

