
International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 6, Issue 1
Research Article
DOI: 10.35840/2631-5068/6528
Fractal Density Matrix for the Case of Time Dependent Radio Frequency Pulses Defined in the First Rotating Frame
Dennis J Sorce*
Figures

Figure 1: (a,b,c) Dotted Line is the Numerical....
(a,b,c) Dotted Line is the Numerical Solution Bloch equations for a Sin-Cos Pulse. The Full Line is the Profile form the Density Matrix with an alpha of 1 for Mx, My and Mz for Figure 1a, Figure 1b and Figure 1c respectively. As can be seen the agreement is excellent.
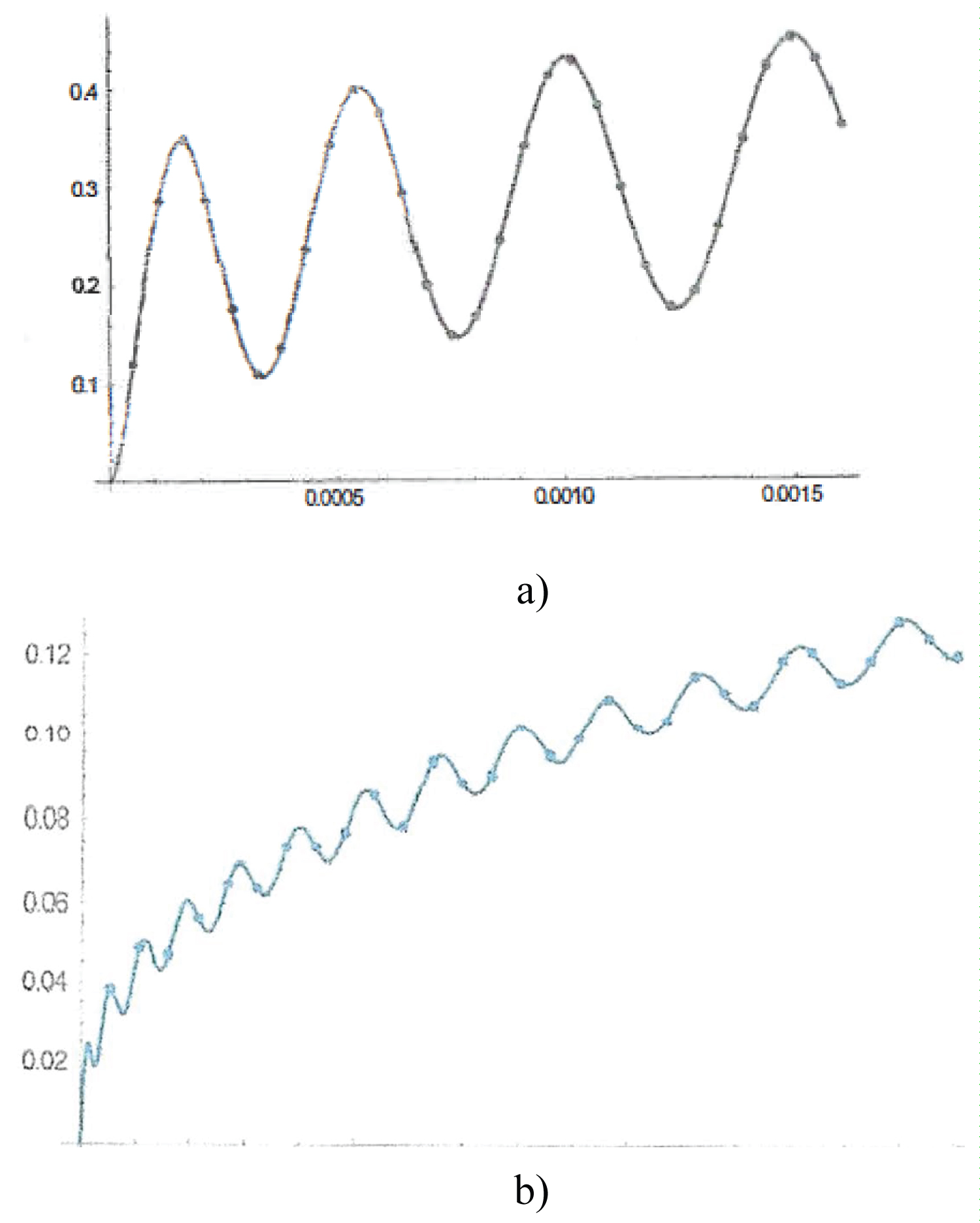
Figure 2: (a,b) Dotted Line is the Numerical Solution.....
(a,b) Dotted Line is the Numerical Solution Bloch equations for a Sin-Cos Pulse. The Full Line is the Profile form the Density Matrix with an alpha of 0.9 for My for Figure 2a, Dotted Line is the Profile form the Density Matrix with an alpha of 0.6 for My Figure 2b respectively. As can be seen the agreement is excellent.
References
- A Haase (1990) Snapshot flash MRI - Applications to T1, T2 and chemical-shift imaging. Magn Reson Med 13: 77-89.
- MR Bendall, M Garwood, K Ugurbil, DT Pegg (1987) Adiabatic refocusing pulse which compensates for variable RF power and off-resonance effects. Magn Reason Med 4: 493-499.
- T Liimatainen, S Mangia, W Ling, J Ellermann, DJ Sorce, et al. (2011) Relaxation dispersion in MRI induced by fictitious magnetic fields. J Magn Reson 209: 269-276.
- S Michaeli, H Grohn, O Grohn, DJ Sorce, R Kauppinen, et al. (2005) Exchange-influenced T2rho contrast in human brain images measured with adiabatic radio-frequency pulses. Magn Reason Med 53: 823-829.
- S Michaeli, G Oz, DJ Sorce, M Garwood, K Ugurbil, et al. (2007) Assessment of brain iron and neural integrity in patients with parkinson's disease using novel MRI contrasts. Mov Disord 22: 334-340.
- RL Magin, C Ingo (2012) Entropy and information in a fractional order model of anomalous diffusion. IFAC Proceedings Volumes 45: 428-433.
- RL Magin, W Li, MP Velasco, J Trujillo, DA Reiter, et al. (2010) Anomalous NMR relaxation in cartilage matrix components and native cartilage: Fractional-order models. J Magn Reson 210: 184-191.
- R Magin, X Feng, D Baleanu (2008) Solving the fractional order bloch equation. Concepts Mag Reson 34A: 16-23.
- AG Palmer III, CD Kroenke, JP Loria (2001) Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol 339: 204-238.
- A Abragam (1991) Principles of nuclear magnetism. Clarendon Press, Oxford.
- AE Sitnitsky (2008) Anomalous diffusion in disordered media from NMR relaxation. arXiv:0709.03412, 1-26.
- J Dong (2010) Applications of density matrix in the fractional quantum mechanics. arXiv: 1012.4958v1.
- N Laskin (2008) Principles of fractional quantum mechanics. arXiv:0811.1169v1.
- MI Kettunen, A Sierra, MJ Narvainen, PK Valonen, S Yla-Herttuala, et al. (2007) Low spin-lock field T1 relaxation in the rotating frame as a sensitive MR imaging marker for gene therapy treatment response in rat glioma. Radiology 243: 796-803.
- L Minati, WP Weglarz (2007) Physical foundations, models, and methods of diffusion magnetic resonance imaging of the brain: A review. Concepts Magn Reson Part A 30A: 278-307.
- R Kimmich (2002) Strange kinetics, porous media, and NMR. Chemical Physics 284: 253-285.
- R Metzler, J Klafter (2000) The random walk's guide to anomalous diffusion: A fractional dynamics approach. Physics reports 339: 1-77.
- D Abergel, AG Palmer (2003) On the use of the stochastic liouville equation in nuclear magnetic resonance: Application to R1rho relaxation in the presence of exchange. Concepts Magn Reson 19A: 134-148.
- W Chen (2006) Time-space fabric underlying anomalous diffusion. Chaos, Solitons and Fractals 28: 923-929.
- C Slichter (1996) Principles of magnetic resonance. Springer-Verlag, New York, USA.
- J Blicharski (1972) Nuclear magnetic relaxation in rotating frame. Acta Phys Pol A 41: 223-236.
- M Fisher, A Majumdar, E Zuiderweg (1998) Protein NMR relaxation: Theory, applications and outlook. Progr NMR Spectr 33: 207-272.
- DJ Sorce, S Mangia, T Liimatainen, M Garwood, S Michaeli (2014) Exchange-induced relaxation in the presence of a fictitious field. J Magn Reson 245: 12-16.
- AC Redfield (1965) The theory of relaxation processes. Adv Magn Reson 1: 1-32.
- M Goldman (2001) Formal theory of spin-lattice relaxation. J Magn Reson 149: 160-187.
- T Liimatainen, DJ Sorce, RO'Connell, M Garwood, S Michaeli (2010) MRI contrast from Relaxation along a Fictitious Field (RAFF). Magn Reson Med 64: 983-994.
Author Details
Dennis J Sorce*
Retired, Center for Magnetic Resonance Research, Minneapolis, USA
Corresponding author
Dennis J Sorce, Retired, Center for Magnetic Resonance Research, Minneapolis, MN 55455, USA, Tel: 410-628-2461.
Accepted: December 04, 2020 | Published Online: December 06, 2020
Citation: Sorce DJ (2020) Fractal Density Matrix for the Case of Time Dependent Radio Frequency Pulses Defined in the First Rotating Frame. Int J Magnetics Electromagnetism 6:028
Copyright: © 2020 Sorce DJ. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We treat in this effort the problem of time evolution during a time dependent radio-frequency pulse in the First Rotating Frame (FRF) with Fractal Time Derivatives for the Representation of the Schroedinger Equation and Fractal Density Matrix for Like Spins ½. The resultant time evolutions during a Sin-Cos Pulse are compared with the Time Dependence during the Fractal Bloch equations without relaxation solved using Standard Runge Kutta methods. The results are found to be identical. The dependence of the Magnetization on the Fractal Coefficient is Explored and Documented.
Introduction
The ability to model spin systems time evolution occurring during radiofrequency (RF) irradiation has increased importance to the expanding use of shaped RF pulses [1,2]. There is currently a need to model the time-evolution of spins which make use of both amplitude and frequency modulation [2,3]. There is also a pressing need to be able to characterize the Magnetization resulting from nuclei in heterogeneous environments such as Brain Tissue [4,5]. There has appeared in recent years a respectable literature concerning the so-called Fractional Bloch Equations [6-8]. There have been a handful of reports of investigation of Fractal Bloch equations [6-8]. In this effort we extend the theoretical treatment using Fractal Time Derivatives to the case of a Fractal Density Matrix for spin ½ nuclei.
In this paper we first outline the theoretical development of the formalism behind the proposed Fractal Density Matrices for spin ½, and then, in the Schroedinger Picture, apply it to obtain magnetization profiles valid in the First Rotating frame (FRF) for various values of the fractal coefficient which we compare with the Profiles obtained through numerical solution of the Bloch equations without relaxation defined in the FRF [9-13]. We find for the values tested complete agreement between the two.
The results are taken and interpreted to mean that the definition of the Fractal Density Matrices are valid and may prove useful in the characterization of Biological Tissues using NMR and MRI methods [4,7,14,15].
Fractal treatments of physical systems became very popular in the 70's and 80's due to the pioneering efforts of Mandelbrot [16-18]. Fractional Calculus is a branch of Mathematics that dates back to the era of Leibnitz the Diplomat, Mathematician and Philosopher [17]. Leibnitz was the co-inventor of the Calculus although he championed a development of the Calculus based on limit arguments while Newton used an infinitesimal point of view. As the name implies the Fractional Calculus is a generalization of the integer based development that is standard in most textbook treatments, in which the order of the derivative or the integral can be a real number usually specified over a given interval on the real line [17].
There is already a substantial literature on the use of the fractional calculus in deriving so called Fractional Bloch [6,7]. The Magin group and W. Chen [19] has been particularly active in this regard.
Theory
We start the development by writing down Radio-Frequency Hamiltonian that can be used to characterize the time evolution of a spin ½ system of nuclei which is valid in the so-called First Rotating Frame (FRF) [20,21]. In this Hamiltonian we neglect any dissipative terms such as Dipolar or Quadrupolar interactions [12,22-25].
Here the spin angular momenta are defined from the Pauli Matrices adopting the following standard representation as [20,22]:
So we define the spin angular momentum, setting the reduced Planck constant to 1 as:
The radio frequency terms ω1(t), Δω(t) are respectively the amplitude of the RF along the x axis in the FRF while the latter is the frequency offset in the FRF along z [21].
If one uses the matrix representation stated in Eqs 2 and 3, one can write down for the RF Hamiltonian the following:
One then is naturally led to writing down a simple Schroedinger equation for the wavefunction of the spin ½ particle using this Hamiltonian as:
Here the simple wavefunction has two components labeled as 1 and 2, so in component form writing out the resultant system of first order differential equations with time dependent coefficients as:
We next apply the definition of the so-called Fractal Time Derivative of a well behaved arbitrary function u as defined in:
It can be shown that this is equivalent to the transformation:
So applying the Fractal Derivative Transform in Eq(8) to the system of equations for the wavefunction Eqs(7), we immediately obtain a proposed system of equations whose solution yields wavefunctions with a dependence on the Fractal Coefficient. The result is:
This system of equations can be easily solved numerically for any combination of RF functions using standard platforms such as Mathematica 11.1 using the NDSolve Function [19].
In Figure 1 we show the sample numerical solution of these equations in the time domain for the specified conditions.
We next move onto apply the textbook definition of the density matrix elements for a spin ½ particle using these numerically solved wavefunctions. We assert the following form:
So, we can then easily define the density matrix in matrix form as:
We next choose to write the equation for the Time Evolution of the Magnetization in the FRF under the Radio Frequency Hamiltonian using the Schroedinger Picture in Quantum Mechanics [20,25] as:
We next note that we compare the time profiles for the magnetization given in Eqs(12) with the numerical solution of the system of Bloch equations without relaxation with the RF on x as:
We choose to test the Magnetization Profiles generated from the numerical solution of these equations under a Sin/Cos RF Pulse [3,26].
We take the definition:
We use the assignment 625.0 Hz as used in applications [3,26].
In Figure 1 we compare the Magnetization Profiles for the Cartesian Magnetization from the numerical solution of the Bloch Equations in the FRF with the Magnetization Profiles from the Fractal Density Matrix. As can be seen for an alpha of 1 the two sets of plots are identical. We take this as a first indication that the formalism presented here has a measure of validity. In Figure 2 we compare the solution of the Bloch equations in the FRF for a fractal coefficient of 0.9 and 0.6 with the Profiles from the Fractal Density Matrix Trace. As can be seen the agreement is very good and gratifying. Further word would be required to explore the general applicability of these density matrix relations for the case of alpha between zero and 1 to modeling magnetization resulting from spin ½ nuclei in tissue.

