
International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 7, Issue 1
Research Article
DOI: 10.35840/2631-5068/6534
Signal Noise Ratio and Magnetic Density in Digital Magnetic Recording System: Analytical and Numerical Investigation
Joseph D NOULA TEFOUET* and David YEMELE
Table of Content
Figures
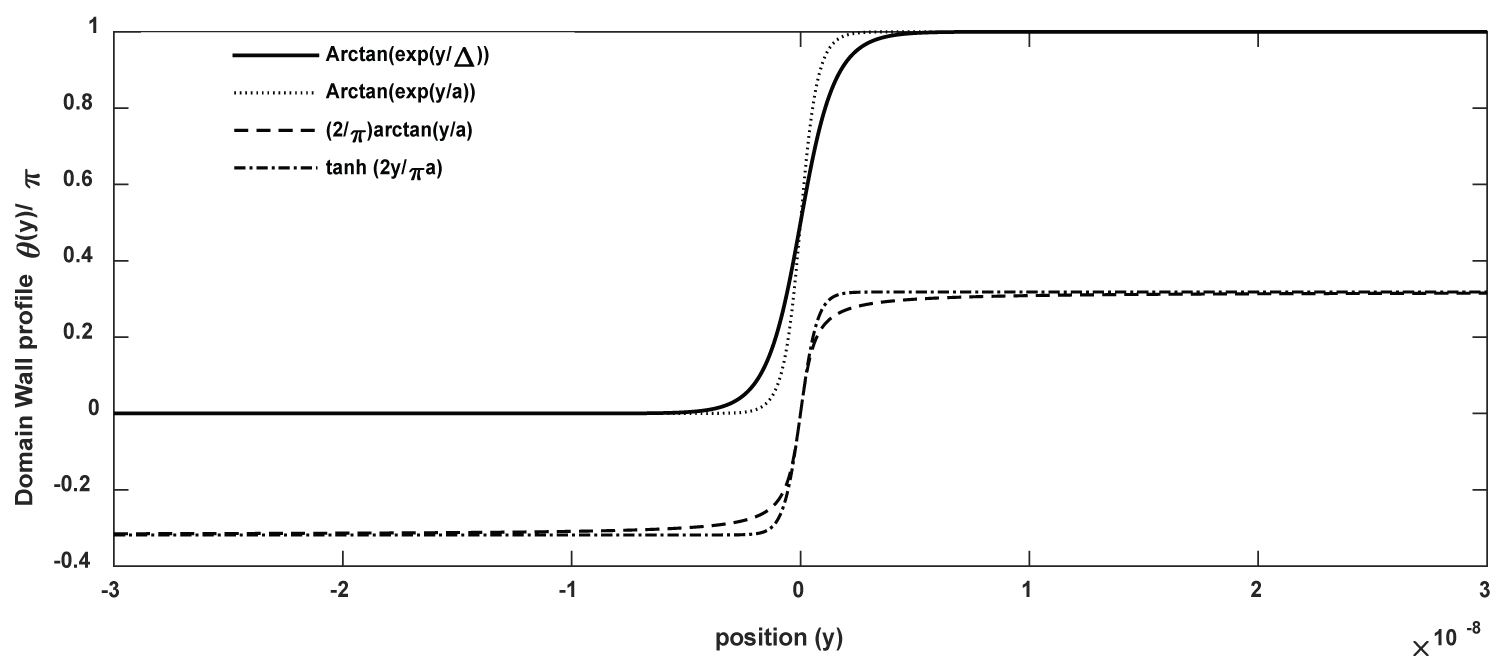
Figure 1: Comparative graph of some magnetic....
Comparative graph of some magnetic domain wall profiles. The value of used is considered as inter atomic distance.

Figure 2: Domain Wall representation in longitudinal.....
Domain Wall representation in longitudinal recording media: (a) Infinitely sharp transition in the horizontal magnetization; and (b) Zig zag domain wall structure representing the source of transition noise.

Figure 3: Variation of domain wall width versus....
Variation of domain wall width versus anisotropic constant K due to first and second anisotropy directions (Variation of K1 when K2 remains constant, and vice versa).
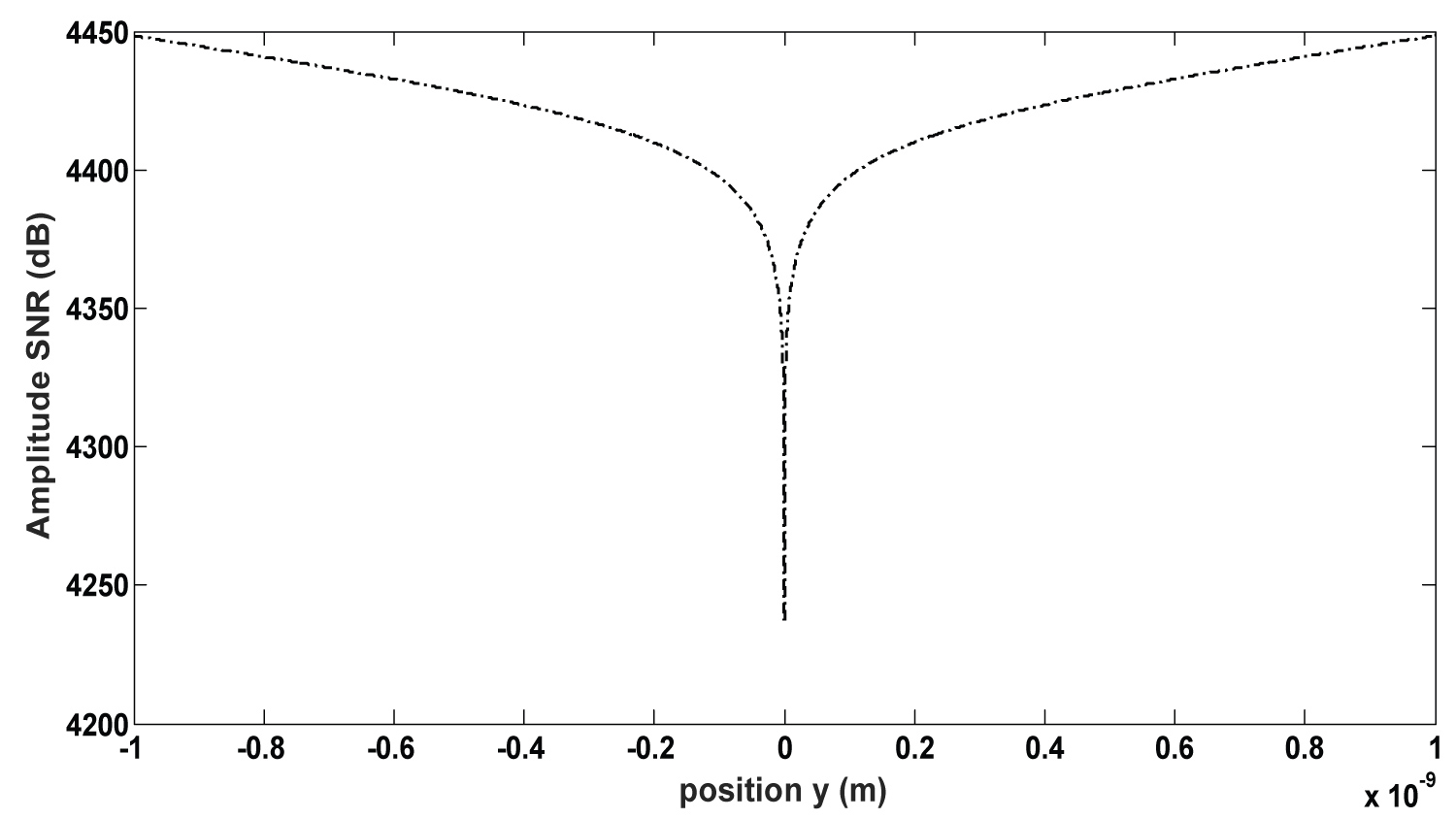
Figure 4: Illustration of SNR (dB) versus the....
Illustration of SNR (dB) versus the position media. The values are computed arbitrary, with Head-media separation , the transition width parameter , the media thickness and the gap length (From [54]).
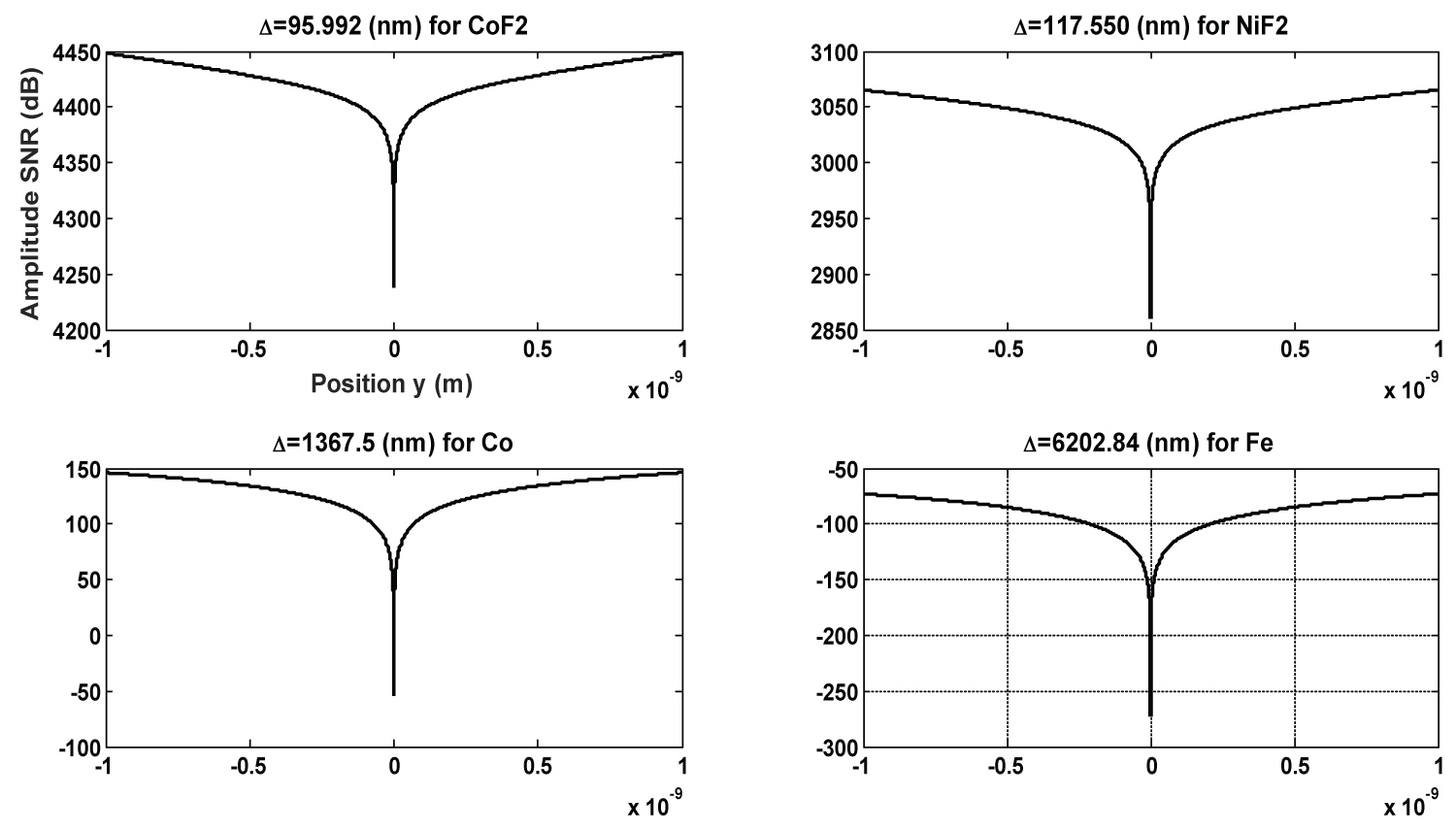
Figure 5: Comparative graph of SNR versus position....
Comparative graph of SNR versus position (y) according to different values of domain wall width for CoF2, NiF2 compounds, Cobalt (Co) and Iron (Fe) single metal.
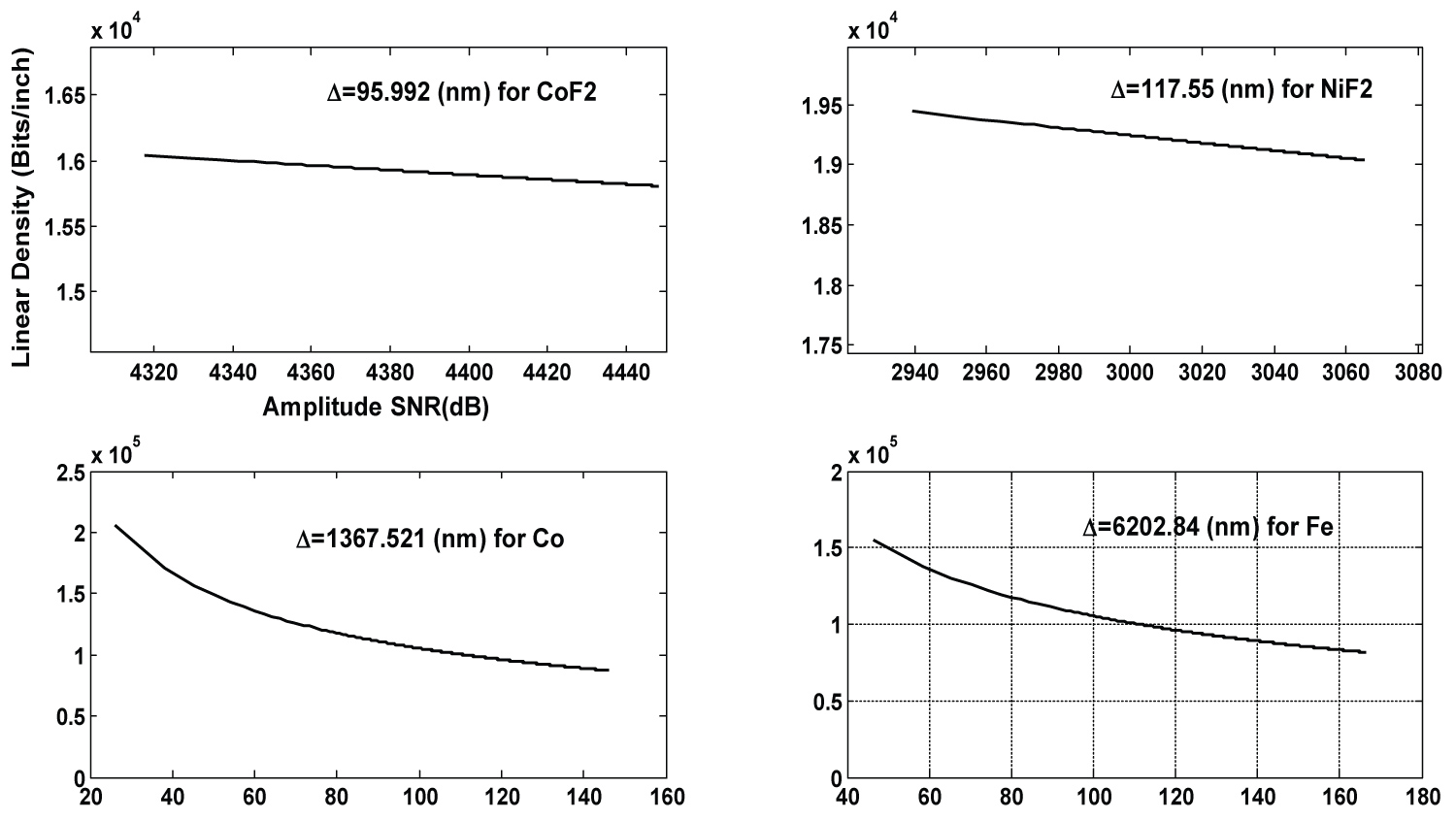
Figure 6: Comparative graph of linear density....
Comparative graph of linear density (LD) versus signal noise ratio (SNR) according to different values of domain wall width for CoF2, NiF2 compounds, Iron (Fe) and Cobalt (Co) single metal (note that DW width is the factor taking into consideration all crystal parameters due to each compound or metal).
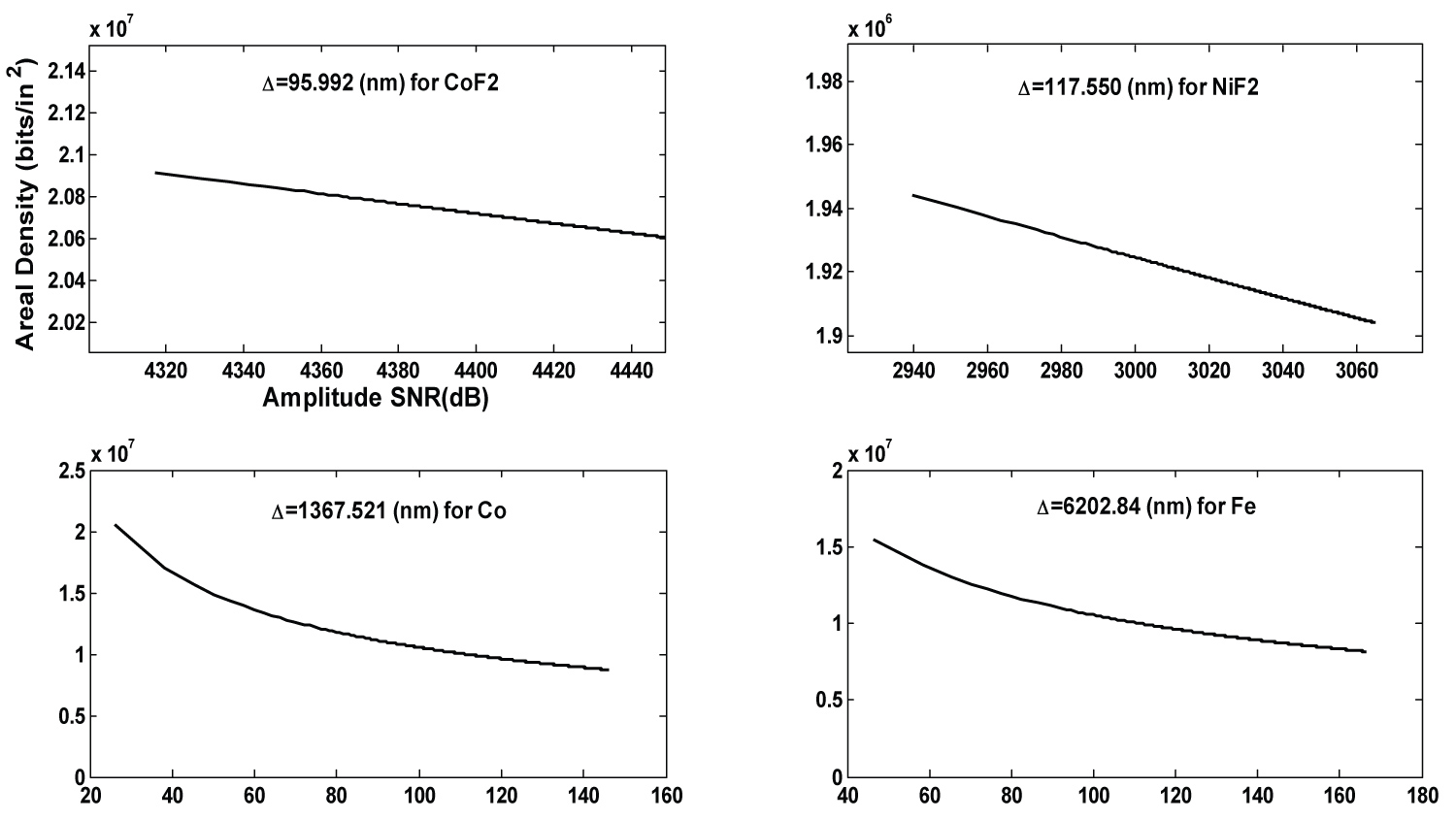
Figure 7: Area density (AD) versus SNR graph...
Area density (AD) versus SNR graph, using experimental values of read-write recording head parameters (the materials here are basic compound and metal used in fabrication of magnetic recording media).

Figure 8: Comparison of linear density (LD)...
Comparison of linear density (LD) versus signal-noise-ratio (SNR) graph for present Arctanexp and Tanh transition profile. The graphs are plot with the same magnetic recording head key parameters for both profile and curve.
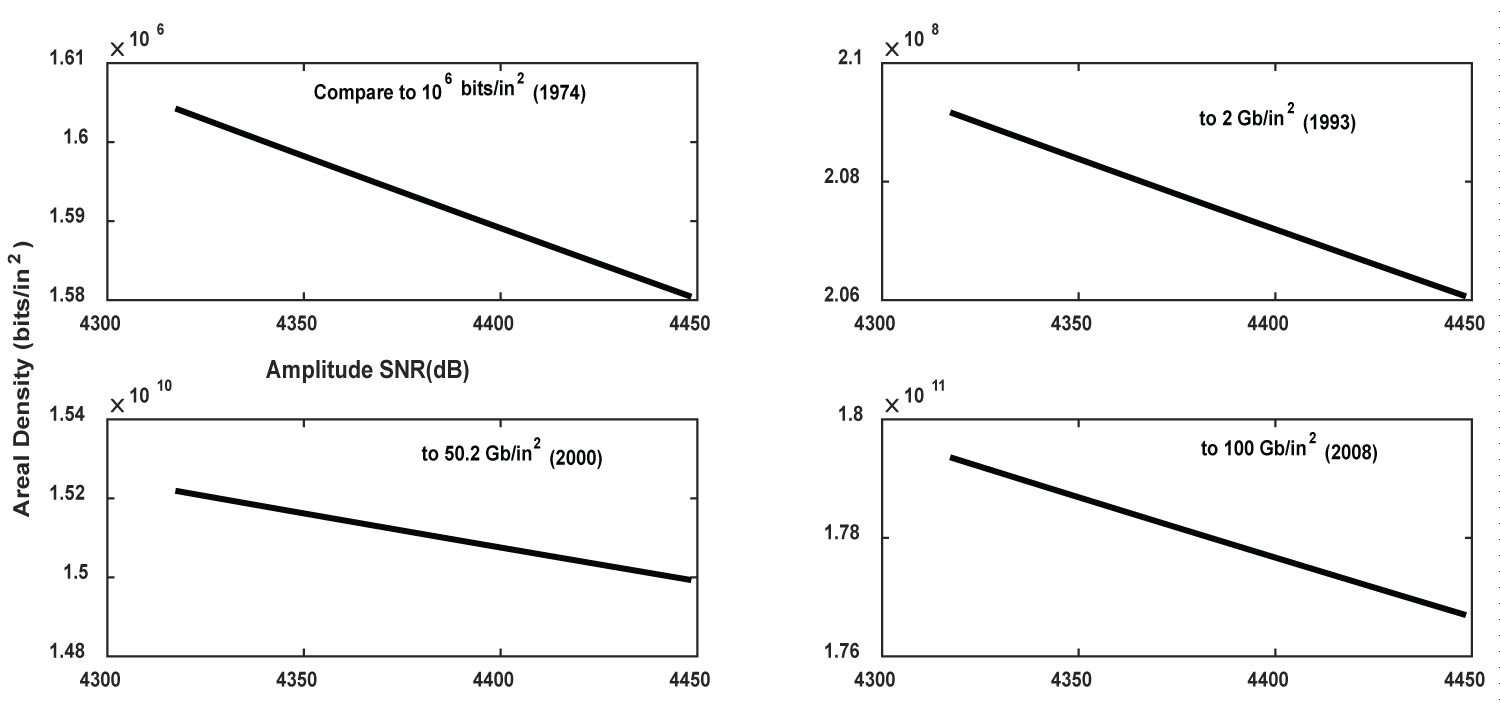
Figure 9: Area density (AD) versus SNR graph ...
Area density (AD) versus SNR graph, using experimental values of read-write recording head parameters compare with the old transition profile and density values obtain at this period with those old profile. (The materials here are basic compound and metal used in fabrication of magnetic recording media).
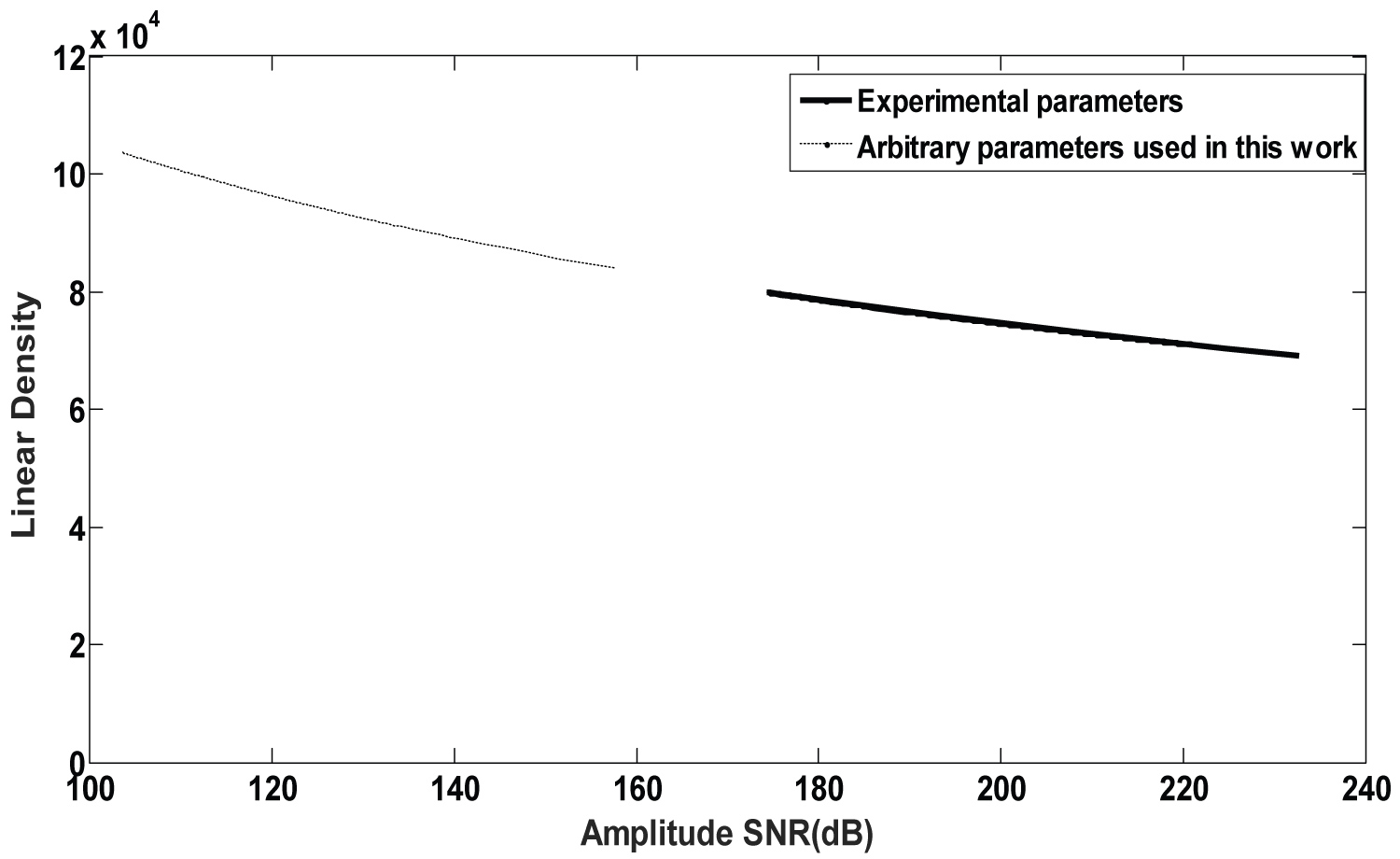
Figure 10: LD versus SNR graph, using experimental...
LD versus SNR graph, using experimental values of read-write recording head parameters used in this work and compare with arbitrary parameters values.
Tables
Table 1: Experimental crystal parameters values for two useful compound in manufacturing magnetic recording media.
Table 2: Experimental crystal parameters values for two magnetic metals used to made magnetic recording media.
Table 3: Prediction of Areal density and Track Density during the magnetic recording density evolution with Grain Density or particles density conjecture.
References
- Parkin SSP, Hayashi M, Thomas L (2008) Magnetic domain-wall racetrack memory. Science 320: 190-194.
- Fukami S, Suzuki T, Nagahara K, Ohshima N, Ozaki Y, et al. (2009) Low-current perpendicular domain wall motion cell for scalable high speed MRAM. 2009 Symposium on VLSI Technology, 230-231.
- Steven L (2016) Déplacement de paroi de domaine par transfert de spin dans des jonctions tunnel magnétiques: Application au memristor spintronique. Matériaux, Université Paris Saclay (COmUE), Français.
- Chanthbouala A, Matsumoto R, Grollier J, Cros V, Anane A, et al. (2011) Vertical-current-induced domain-wall motion in MgO-based magnetic tunnel junctions with low current densities. Nature Physics 7: 626-630.
- Middelhoek S (1963) Domain walls in thin Ni [single bond] Fe films. Journal of Applied Physics 34: 1054.
- Neel ML (1968) Parois dans les films minces. Journal de Physique Colloque 29: C2-87-C2-94.
- Thiaville A, Nakatani Y (2006) Domain-wall dynamics in nanowires and nanostrips. Spin Dynamics in Confined Magnetic Structures III 101: 161-205.
- Korde VB, Patil NM (2019) Domain imaging in Fe-doped KNbO3 single crystal via trinocular microscopy and scanning electron microscopy. Materials Chemistry and Physics 226: 230-234.
- Middleton BK (1996) Recording and reproducing processes. In: CD Mee, ED Daniel, Magnetic recording handbook. (2nd edn), 147.
- Howell TD, McCown DP, Tang YS, Hense KR, Gee RL (1990) Error rate performance of experimental gigabit per square inch recording components. IEEE Trans Magn 26: 2298-2302.
- Moon J (1991) Discrete-time modeling of transition-noise-dominant channels and study of detection performance. IEEE Trans Magn 27: 4573-4578.
- Baugh R, Murdock E, Natarajan B (1983) Measurement of noise in magnetic media. IEEE Trans Magn 19: 1722-1724.
- Belk N, George P, Mowry G (1985) Noise in high performance thin-film longitudinal magnetic recording media. IEEE Trans Magn 21: 1350-1355.
- Pierre H (1999) Effets et matériaux magnétostrictifs. Engineering Techniques.
- Jacob F (2010) Handbook of modern sensors: Physics, designs, and applications. (4th edn), USA, Springer, 73.
- Florez M, Simão JP, Antoun RS (2019) Improvement in adhesion of cellulose fibers to the thermoplastic starch matrix by plasma treatment modification. Composites Part B: Engineering 163: 207-216.
- Rani E, Valeria LS, Anastasia M (2017) Smart composites: Mechanics and design (composite materials). CRC Press.
- Tyunina M, Yao LD, Chvostova D, Kocourek T, Jelinek M, et al. (2015) Effect of epitaxy on interband transitions in ferroelectric KNbO3. New J Phys 17: 043048.
- Korde VB, Patil NM (2019) Synthesis, structural, dielectric and domain properties of Al-doped KNbO3 single crystal. Journal of Materials Science: Materials in Electronics 30: 6910-6919.
- Nuraje N, Su K (2013) Perovskite ferroelectric nanomaterials. Nanoscale 5: 8752-8780.
- Mallinson JC (1974) On extremely high density digital recording. IEEE Trans Magn 10: 368-373.
- Bertram HN (1994) Theory of magnetic recording. Cambridge University Press, 100.
- Middleton BK (1996) Recording and reproducing processes. In: CD Mee, ED Daniel, Magnetic recording handbook. (2nd edn), 30.
- Aleksandar K, Jose MF Moura (1997) Statistical Study of zig-zag transition boundaries in longitudinal digital magnetic recording. IEEE Trans Magn 33: 4482-4491.
- Freiser MJ (1979) On the zigzag form of charged domain walls. IBM J Res Dev 23: 330-338.
- Muller M, Murdock E (1987) Williams-Comstock type model for sawtooth transitions in thin film media. IEEE Trans Magn 23: 2368-2370.
- Zhang XY, Suhl H, George PK (1988) Relationship between the transition width and the zigzag wavelength. J Appl Phys 63: 3257-3259.
- Middleton BK, Miles JJ, Noyau RH (1988) The digital recording properties of thin film media having sawtooth magnetization transitions. IEEE Trans Magn 24: 3099-3101.
- Arnoldussen TC, Tong HC (1986) Zigzag transition profiles, noise, and correlation statistics in highly oriented longitudinal media. IEEE Trans Magn 22: 889-891.
- Tang YS, Osse L (1987) Zig-zag domains and metal film disk noise. IEEE Trans Magn 23: 2371-2373.
- Middleton BK, Miles JJ (1991) Sawtooth magnetization transitions and the digital recording properties of thin film recording media. 1990 Eighth International Conference on Video, Audio and Data Recording, 20-25.
- Middleton BK, Miles JJ (1991) Recorded magnetization distributions in thin film media. IEEE Trans Magn 27: 4954-4959.
- Aleksandar K, Jose MF Moura (1995) Triangle zig-zag transition modeling. Tech Rep, Data Storage Syst Center, Carnegie Mellon University, USA.
- Minnaja N, Nobile M (1972) Stability conditions for saw-tooth walls between head-on domains. AIP Conf Proc 10: 1001-1005.
- Semenov V, Factorivich A, Gikas M (1991) The effect of coercive squareness S* on transition noise in thin metal media. Proc Jap Mag Society of Japan 15: 251-256.
- Mougin A, Cormier M, Adam JP, Metaxas PJ, Ferré J (2007) Domain wall mobility, stability and walker breakdown in magnetic nanowires. Euro Physics Letters 78: 57007.
- Galkina EG, Ivanov BA, Savelev S, Nori F (2008) Chirality tunneling and quantum dynamics for domain walls in mesoscopic ferromagnets. Physical Review B 77: 34425.
- Webster JG (1999) Wiley encyclopedia of electrical and electronics engineering. John Wiley & Sons.
- Morrish AH (1965) The physical principles of magnetism. Wiley, New York, USA.
- Varvaro G, Casoli F (2016) Ultrahigh density magnetic recording: Storage materials and media designs. Taylor and Francis Group, LLC 2: 59-60.
- Xinzhi X, Neal Bertram H (1997) Analysis of transition noise in thin film media. Center for magnetic recording research, University of California San Diego, USA.
- Neal Bertram H, Hong Z, Roy G (1998) Signal to noise ratio scaling and density limit estimates in longitudinal magnetic recording. IEEE Trans on Magn 34: 1845-1847.
- Neal Bertram H (2005) Introduction to magnetic recording from medium grains and head poles to system error rate and high density limits, 199.
- Wang SX, Taratorin AM (1999) Magnetic information storage technology. Academic Press, USA.
- O'Handley RC (2000) Modern magnetic materials: Principles and spplications. John Wiley Pr Sons, Bnc, New York, USA.
- Middleton BK (1996) Recording and reproducing processes. In: CD Mee, ED Daniel, Magnetic recording handbook. (2nd edn), 87.
- Karlqvist (1954) Calculation of the magnetic field in the ferromagnetic layer of a magnetic drum. Trans R Inst Technol, Stockholm 86: 3.
- Robert IP (1974) Digital magnetic recording theory. IEEE Trans on Magn 10: 502-508.
- Boris S, Neal Bertram H (1994) Transition noise analysis of thin film magnetic recording media. IEEE Trans on Magn 30: 2808-2817.
- Neal Bertram H (1994) Theory of magnetic recording. Cambridge University Press, 131, 148, 153.
- Neal Bertram H (1986) Fundamentals of the magnetic recording process. IEEE Trans on Magn 74: 1503.
- Aziz MM (1999) Signal and noise properties of longitudinal thin-film disk media. Degree of Doctor of Philosophy, Faculty of Science and Engineering, University of Manchester 3: 86-88.
- Zhan Y, Shtrikam S, Bertram HN (1997) Playback pulse shape and spectra for shielded MR heads. IEEE Trans on Magn 33: 1093-1103.
- Middleton BK, Miles JJ, Aziz M (1998) High-density recording on magnetic thin film disk media. Journal of Magnetism and Magnetic Materials 188: 248-259.
- Neal Bertram H, Xiaodong C (1993) General analysis of noise in recorded transitions in thin film recording media. IEEE Trans on Magn 29: 201-208.
- I de PR Moreira, Dovesi R, Roetti C, Saunders VR, Orlando R (2000) Ab initio study of MF2 (M= Mn, Fe, Co, Ni) rutile-type compounds using the periodic unrestricted Hartree-Forck approach. Phy Rev B 62: 7816.
- Weissmann M, Maria Llois A, Kiwi M (2001) Calculation of the interface exchange coupling constants between Fe and FeF2-like fluorides. Journal of Magnetism and Magnetic Materials 234: 19-24.
- Patrick B (1993) Physical origines and theoretical models of magnetic anisotropy. Institut d'Electronique Fondamentale, Université Paris-Sud, France.
- Cullity BD, Graham CD (2009) Introduction to magnetic materials. (2nd edn), IEEE PRESS, 227.
- Cinthia AC, Karel V (2018) Electronic structure and magnetic anisotropies of antiferromagnetic transition-metal difluorides. Phy Rev B 97: 235111.
- Zhao GP, Zhao L, Shen LC, Zou J, Qiu L (2019) Coercivity mechanisms in nanostructured permanent magnets. Chin Phys B 28: 077505.
- Zhao GP, Wang XL (2006) Nucleation, pinning, and coercivity in magnetic nanosystems: An analytical micromagnetic approach. Physical Review B 74: 012409.
- Zhao GP, Ong CK, Feng YP, Lim HS, Ding J (1999) Remanence enhancement of single-phased isotropic nanostructured permanent magnets. Journal of Magnetism and Magnetic Materials 192: 543-552.
- Weng XJ, Zhao GP, Tang H, Shen LC, Xiao Y (2020) Thickness dependent coercivity mechanism and hysteresis loops in hard/soft magnets. Rare Met 39: 22-27.
- Stout JW, Reed SA (1954) The crystal structure of MnF2, FeF2, CoF2, NiF2, and ZnF2, contribution from the institute for the study of metals. University of Chicago, USA.
- Endo Y, Kitakami O, Okamoto S, Shimada Y (2000) Determination of first and second magnetic anisotropy constants of magnetic recording media. Applied Physics Letters 77: 1689.
- Lubarda VA (2003) On the effective lattice parameter of binary alloys. Mechanics of Materials 35: 53-68.
- Díaz-Ortiz A, Drautz R, Fähnle M, Dosch H, Sanchez JM (2006) Structure and magnetism in bcc-based iron-cobalt alloys. Phy Rev B 73: 224208.
- Steiner MM, Albers RC, Sham LJ (1992) Quasiparticle properties of Fe, Co, and Ni. Phys Rev B Condens Matter 45: 13272-13284.
- Bertram HN, Williams M (2000) SNR and density limit estimates: A comparison of longitudinal and perpendicular recording. IEEE Trans On Mag 36: 4-9.
- Richter HJ (1999) Recent advances in the recording physics of thin-film media. J Phys D: Appl Phys 32: 147-168.
- Futamoto M, Kugiya F (1993) Development of technologies for 2Gb/in2 areal density recording. Electronics and Communications in Japan (Part 2), 76.
- Weller D, Doerner MF (2000) Extremely high-density longitudinal magnetic recording media. Annu Rev Mater Sci 30: 611-644.
- Argumedo AJ, Berman D, Biskeborn RG, Cherubini G, Cideciyan RD, et al. (2008) Scaling tape recording areal densities to 100Gb/in2. IBM J Res and Dev, 52.
Author Details
Joseph D NOULA TEFOUET* and David YEMELE
Research Unit of Mechanics and Modeling of Physics Systems, Dschang School of Science and Technology (DSST), Faculty of Science, University of Dschang, Cameroon
Corresponding author
Joseph D NOULA TEFOUET, Research Unit of Mechanics and Modeling of Physics Systems (RU-2MSP), Dschang School of Science and Technology (DSST), Faculty of Science, University of Dschang, Po Box 067, Dschang, Cameroon, Tel: +237-678-93-38-09.
Accepted: May 12, 2021 | Published Online: May 14, 2021
Citation: TEFOUET JDN, YEMELE D (2021) Signal Noise Ratio and Magnetic Density in Digital Magnetic Recording System: Analytical and Numerical Investigation. Int J Magnetics Electromagnetism 7:034.
Copyright: © 2021 TEFOUET JDN, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this work the analysis of noise especially the transition jitter noise is used to evaluate the areal density which are consider as one of the most important characteristics in magnetic recording systems. This is possible through the analytical evaluation of the signal noise ratio (SNR) using kink soliton as domain wall profile and assuming that, the transition noise are the dominant noise in recording media. The intrinsic parameters and experimental values for magnetic recording media especially the domain wall width are chosen to emphasize the impact of noise in a certain simple materials and compounds materials used to manufacture recording media. The comparative study on evolution of areal density is done to reinforce the fact that noise can governed the magnetic density, where the values of 180 Gb/inch2 is attaint for kink soliton profile here compare to 100 Gb/inch2 obtain in 2008. The study is complete with numerical investigation of areal density where the value about 1.8 × 1011 bits/inch2 can be attaint when SNR is about 4300 dB, this results are obtain with a basic compound CoF2 having a domain wall width of 95.992 nm just to strengthen the work.
Keywords
Domain wall, Recording media, Signal noise ratio, Linear density, Areal density
Introduction
It is not a secret that magnetic recording systems are best devices to store and recall information. Then, it becomes important to have a good knowledge on properties of magnetic materials that made up many class of recording system. The most important property no doubt is the one possess by magnetic materials to orientate naturally its magnetization. This magnetization orientation is according to a certain direction said easy anisotropic axes; allowing the formation of regions called domains where that magnetization is constant. Note that, two consecutive magnetic regions are separated by the transition region called domain wall. In other word the region separating the consecutive domains, where the direction of magnetization changes are called magnetic domain wall (DW). Study of magnetic domain walls is remaining at the forefront of the recoding memory activity and attracts a lot of attention from engineering and physical communities.
From domain walls an application point of view, their use is very promising with regard to magnetic memories and many other fields of engineering [1,2]. It is one of the driving forces of the memristor spintronics, artificial neuron network and for carrying out neuromorphic tasks [3]. Domain walls are therefore at the center of several studies and it is for this reason it has been widely studied in the literature for about thirty years [1,4-7]. It should be noted that there are mainly two types of domain wall: The Bloch wall where the magnetization rotate in three directions of space, and the so-called Néel wall where the rotation of magnetic moments occur in a single plane. The type of wall encountered depends both on the material used and on its structure. It depends in particular on the privileged direction of the magnetization as we said above. This is called an easy magnetization axis, which can have different sources, such as the crystallographic structure of the material (crystalline anisotropy), or even its shape (form anisotropy). The thickness of the domain wall is very often a function of the competition that exists between these two energies. In a domain wall there exist competitions, one of them is between the exchange and the anisotropy energy where the first tend to increase the thickness of domain wall and the second tend to reduce that thickness, then the competition can determine the domain wall width. Here we see that the type of material, the shape and the crystal structure play a major role in the development of support which can offer us several advantageous domains and domain walls. This is part of what is done in the work of [8] which presents a correlation between the magnetization easy axis, the magnetic domains and thin film stacks.
These studies are in part motivated by a new field of applied physics (spintronics) offering a great promise for creating the new (Racetrack) and next generation of data storage, logic devices combining spin dependent effects with conventional charge based electronics. Most of these devices work or function with perturbations and disturbances where the most relevant perturbation is noise. Noise in continuous magnetic thin-film media is mainly due to the random fluctuations in the micro and macroscopic properties of the magnetic layer [9]. Noise in recording medium comes from three predominant sources: The playback amplifier (electronics noises), the playback head (head noises), and the recording medium (medium noises). The last one arises from transition, particulate and modulation. Transition noise has two principal components the transition jitter and the transition width fluctuations: They both occur in the writing process whenever a transition in the writing current polarity takes place. Transition jitter is a fluctuation of a transition's position, this effect results in a shift of the pulse position at the output of the reading head. According to [10,11] the transition noise could account for as much as 90 percent of the total noise power in recording systems.
Another opinion [12,13] conclude that the noise is concentrated in the transition regions and the increase of the noise voltage spectrum with reduced bit spacing is due to the increase of the fluctuations in the transition regions where the transition free zones are reduced to a minimum, this reinforce the idea that domain wall should look with particular attention. One important observation did by Belk, et al. [13], is the way concerning the physical representation of the transition noise and they stipulate that, the physical basis of transition noise is the irregular zig-zag domain structures. As transition noise is the dominant noise in the magnetic recording media, this work will concentrate on transition noise modes particularly the position jitter. The magnetic domains structure and that of domain walls would be responsible for the magnetic behavior of ferromagnetic materials like Iron, Nickel, Cobalt and their alloys [14]. This domain structure would also be responsible for the magnetic behavior of ferrimagnetic materials and even composite materials such as NdFeB which is an alloy used in neodymium magnets [15]. A composite material also called a composition material is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a material with properties unlike the individual elements. Within the finished structure, the individual elements remain separate and distinct, distinguishing composites from mixtures and solid solutions [16,17]. These composite materials have brought significant advances in the field of engineering in general but much more in magnetism and materials science. For illustrative purposes, Ferroelectric materials are used in the formation of thin films, single crystals, and bulk ceramics for different applications [18]. In view of importance of this type of material in the manufacture of magnetic tapes, it is more than urgent to work on obtaining composite materials that can make it possible to have small wall widths and thus reach high density and also minimize noise (especially transition noise). Fortunately, excellent work is already underway to produce this type of composite material for us. This is the case of Potassium niobate KNbO3 (KN) well-known as lead-free ferroelectric material with high-quality, which has recently been developed into excellent work led by V. B. Korde and collaborators [8,19]. It must be said that according to [8], Potassium niobate (KN; chemical formula: KNbO3) is a ferroelectric perovskite oxide which has enormous potential in various applications. For proof, according to [20] the perspectives concerning the future direction of ferroelectric nanomaterial's research and its potential application is renewable energy. In view of all the above, we note that crystals, compounds, materials in general and particularly composite materials have a very important role both in the field of micro magnetism and engineering with numerous applications.
In this work the kink soliton profile, is used to find analytical results concerning the magnetic digital density through the calculation of the jitter position and signal-to-noise ratio (SNR). Knowing that the digital density can be governed by the SNR of recording system [21] and using that SNR, we obtain the analytical linear density (LD) of storage media. Most results in this work are compared with the previous results [22] where researchers use old DW profile. Then, using numerical simulation and by help of experimental values parameters used in recording system, we can valid the uses of this magnetic transition shape or magnetic domain walls (DW). These comparative works aim at a good application in magnetic recording systems. This work emphasis then the fact that, by carefully choosing the crystals or materials for the fabrication of recording media and the use of a soliton profile preferably the profile, it possible to obtain the much reduced domain wall widths which give the possibility of having a satisfactory signal-to-noise ratio and a marked improvement in storage density.
The paper is organized as follows. In Sec.4, this work describes the model by presenting the predominant source of noise (transition noise) and showing the real impact of crystallographic direction on DW width. In Sec.5, the analytical and numerical investigation of signal noise ratio are well done while in Sec.6, the analysis of some intrinsic magnetic recording parameters are exploited to emphasis the necessity of researchers to look carefully materials use in fabrication of media. Sec.7 is consecrated to magnetic linear or areal density when considering noise as key phenomenon this is by the aids of the numerical simulation. The next section allows us to give a constructive discussion which brings out the main observation of this work. Final part of the paper is devoted to concluding remarks with some opening axes of futures researches work.
Model Description and Transition Noise in Magnetic Recording Media
The basic constituents for magnetic recording are a head system to write the signal, a magnetic medium to store and a playback system to detect and reproduce the recorded signal. As domain wall, transition noise and linear density are the main objectives of this work, it is very simple to focus all our effort on the magnetic medium.
It has long been observed that most of the noise in thin film magnetic recording media occurs in the transitional regions between two oppositely magnetized magnetization patterns in the media. Domain wall plays an important and major role in physics of magnet in general but in the magnetic recording devices in particular. Knowing the fact that several domain wall profiles exist, it is imperative for an optimization of the results to choose the right profile. It should be able at least to have a small width or good stability if used in racetracks. [22,23] presented the most popular profiles namely: ; and where a is the transition length (Figure 1).
The source of this noise lies in the irregularity of the transition boundary, where the importance of choosing appropriate DW for the recording media. The Figure 2a above shows the infinitely sharp transition in the horizontal magnetization and Figure 2b the zig-zag structure of domain wall which certainly be the source of transition noise.
Several works present this irregularity as a zigzag wall and due to this zigzag nature of domain wall in thin film disks, the transition center defined as the average transition center across data track, becomes also uncertain. This uncertainty, usually called transition position jitter, will lead to transition noise. The zig-zag boundary itself is a realization of a random process, which is why the observed media noise is random. In the past, there have been many studies of zig-zag wall shapes. Several zig-zag models have been suggested [24]. These models cluster in two groups: Deterministic and stochastic models. Examples of deterministic models are described in [25-28]. While deterministic models are useful in understanding the physical mechanisms involved in the recording process, they cannot explain the random character of noise. The stochastic models [29-33] model the zig-zag transition line as a random process, thus accounting for the random character of media noise. Hence, simplified modeling assuming zigzag walls can give reasonable models of transition shape as well as noise [25,26,34,35].
For the simplicity of this problem we consider that the average profile described by the zigzag wall is of a well known shape and represented by a soliton profile. The shape of domain wall used in this work is the kink soliton profile given by [36]
Where y0 is the domain wall center corresponding to the position coordinate y in recording media, ∆ is the domain wall width or the transition parameter and can be express as , where J, a and φ represent respectively the exchange coupling constant, lattice spacing and azimuthal angle which in general describes the chirality of the soliton solution [37]. The domain wall width of 180° Bloch wall is most commonly defined in the literature by ; where A and K are the exchange constant and the anisotropy energy respectively.
Notice that we assume that the magnetization pasted on the media has the same profile as DW and for the simplicity , with K1 refer to the strength of longitudinal anisotropy while K2 the strength of the transverse anisotropy.
Let us note that transition length or width domain wall is a key parameter for the study of domain wall. The ∆ parameter is needed to specify the transition characteristics: A small value of ∆ corresponds to a rapid transition, and this favors high-density recording [38]. In this work, we are going to shows that through this profile it is possible to have the signal noise ratio (SNR) and evaluate the linear density of the recording media.
For that, the transition length ∆ and more others experimental parameters values should be used to confirm the veracity of this work. The importance of ∆ is well view when plotting the domain wall width versus anisotropy constant Ki. In Figure 3, it is observed that the DW may decreases rapidly as the anisotropy in the first direction increases and tend to stabilize as K1 approaches a certain limit value.
In this work the focal object is the magnetic recording medium as we said where the quantities as magnetic domain, the magnetic domain wall, the magnetization and probably noises coexist together. The recording media is assumed to have an easy axis along Z (with K1 as anisotropy constant) and a hard axis along Y (with K2 as anisotropy constant in that direction). Many researchers assumed that recording media are isotropic and used a uniformly and single anisotropy constant Ku. This consideration does not reflect the reality, because to make a magnetic material with uniform anisotropy is not easy. We realize that when anisotropy in the first direction K1 (due to Z axis) increases while that of second direction (K2) remain constant, the DW width decrease rapidly and its value range remain very small compare to the second case. When doing the inverse (e.g. increasing K2 when K1 remain constant), we also obtain the low decreasing of DW width but the decreasing appear slowly and the range of DW width value is large compare to the first case. The most remark in that Figure 3 shows that, in the first case, (e.g. increasing K1 when K2 remain constant) the DW width value is smaller than in the second case (e.g. increasing K2 when K1 remain constant) which is favorable for the formation of many magnetic domain in a smaller recording medium area and issue the higher the magnetic recording density this is possible and good for perpendicular magnetic anisotropy (PMA). Highly by all this, we realize that, when manufacturing a recording medium the choice of crystallographic axis are predominant, also the selection of easy and hard direction of magnetization are very important in the aim of having the most denser particle (PMA), the reducing magnetic Domain Wall width and prevent the media from large transition noise. The decrease of DW width needs a normal value of K2, which is possible in practical contrary to the second case (e.g. increasing K2 when K1 remain constant). Here the decrease of DW width needs a very low value of K1 which is not possible in practical. Observations of Figure 3 are in good agreement with results tabulated by A. H. Morris1965, presenting an experimental values of different anisotropy constants due to different crystallographic axes of some materials as Fe, Co and Ni [39]. The most remark that can be made here first is that, magnetic anisotropy sets an axis not a direction; secondly the anisotropy constant depends strongly on the type of magnetic material, its crystallographic structure as well as the density of particle in the unit volume. Looking the exchange parameter, we observe that the DW width strongly depends on the anisotropy plane parameters. We then conclude that the increase of anisotropy constant in y-direction favorites the decrease of DW width thus impacts on DW width parameter and transition noise. From this observation, it is necessary to consider anisotropy at least in two directions of recording material since the width of transition DW limits the maximum linear density possible in media, it is useful for our recording medium to have a very high anisotropy constant in the direction of medium (y-direction), so that the most efforts should be done to make that DW as thin as possible because, "The lower the width DW, the higher the linear or areal density" [28,40]. The previous observation comes as to make a fixation or an emphasis on the fact that domain wall in particular its width is a key element for the theory, this as to conclude this part. Also as introduction to the next two sections which is devoted to SNR and density. These SNR and density are also significant quantities in the evaluation of the performance of a recording system. Finally this affirmation comes as if to mark the close link that could exist between the domain wall width and the density.
Signal Noise Ratio: Analytical and Numerical Investigation
As we said early, the principle focused in this theory is to use a particular kink soliton DW profile instead of others and then look if this DW shape is good for improving or to ameliorate as far as possible the recording density through the calculation of SNR. From all previous observations it is clearly that the higher density depends drastically from DW. Magnetic recording system cannot function as perfect system but there exist some undesirable effect and the most relevant are noises were the principals are medium noise, electronic noise and head noise. Hence it is clearly that the evaluation of recording system is not possible without an evaluation of perturbations. Adding to the fact that, signal-noise-ratio (SNR) can govern the magnetic density; it can also be used to evaluate the performance of the recording system. Knowing that "the small the size of information, the more the noise in the signal" and using certain theoretical consideration as, in reality, signal always coexists with noise, the transition noise is the dominant noise or the most perturbation in the recording media theory [41]. It is then necessary to use transition shape and transition noise (SNR) to determine and evaluate the density of recording media system. From the definition of SNR (the ratio of single pulse peak signal power over integrated transition noise power) a correlation exists between the voltage and noise as two principal elements in the determination of digital density. Mallinson (1974) proposed an extraordinary two expressions giving linear density (LD) and areal density (AD) versus SNR. Bertram, et al. (1998) [42] proposed a general expression of SNR for transition shape. However Bertram (2005) [43] stipulated the general relation for SNR corresponding to all transition shape. That SNR Expression is given in the form of
Where , and are respectively the output voltage, the square peak voltage and the jitter transition noise. The simple form of Eq. (2) can be given by the following expression [40,42]
Where B is the bit length, is the half pulse width of output voltage .
The jitter transition noise due to the position is given by
It should be noted that B is mostly time proportional to the transition width e.g. . In a magnetic thin film medium, the magnetic DW does not have rigorous and smooth form but has a certain distortion and rough aspect. Therefore, it is not possible to represent carefully by a single point the center of the magnetic transition. We then consider the average transition center over all the media cross track as the transition center as in [44]. The position of the transition center becomes unpredictable and this creates the transition noise called the transition position jitter. According to [45] the more irregular transitions in thin-film media are referred to as zigzag or sawtooth transitions. Noise in thin-film media is due primarily to the formation of zigzag transitions between bits. In addition to the fact that fluctuations or variation concentrated in the transition domain are another source of noise in magnetic thin film recording media [41]. It therefore becomes necessary to see even important to envision a study not of the noise alone, but also by taking into account the domain or then the domain wall. From all the above, we note that the search for an interconnection or a correlation between domain wall, signal to noise ratio and density becomes essential in the good realization and good conduct of this work. Because a vector spin cannot rotate, and occupy the same position, it would have a smaller shift in term of position; all this will contribute and reinforce the existence of position jitter. It should be noted that the output voltage used here is the same replay voltage obtained by the Karlqvist method [46,47]. Now the SNR relation which takes into account V (y), and can be given by
At this step the remaining problem is only to obtain the jitter transition noise where their components are presented bellow. and
In this part of work we have consider the output voltage as [48],
Where N is the number of turn coil, the width track of recording media, the media thickness, E the efficiency of the head, the saturation remanent magnetization and y is the position (coordinate in magnetic media).
The magnetic field is the horizontal component of the head field and can be expressing as [36]:
Where represent the head-medium separation, d the empty space between the poles and the media while g is the gap length (distance between magnetic poles of read write head). As mention above, assuming that the magnetization paste on the media has the Kink soliton form indicate that
The terms F, G and H in are results of the integral of [V (y)]2 over the recording media, g is the distance between the magnetic poles of read write head also called gap length and y represent the position on the recording media. This enables us to represent the intrinsic SNR versus position, where results are very close to the reality and more accurate. The most observation is the break point which occurs near , representing the center of transition and which is in agreement with previous results of [49] and [50]. In those previous works, they present the schematic illustration of full noise spectrum density (PSD) versus normalized wave number , or Normalize voltage versus density for square wave recording . [51] Represent the measure of the fundamental voltage component versus frequency, where the thickness loss is very important for the short wavelength, while this do not appear in the present work. At the starting transition, the SNR amplitude decreases at a constant rate and it is not fair to represent the measure of the fundamental normalize voltage versus density. Since in this case, the thickness loss is very important for short wavelengths. This results fall on to the predictions of AZIZ (1999), in his PhD thesis come out with a result to reinforce our own, by plotting an intrinsic SNR (dB) for a transition versus density where B is the magnetic bit length [52,53]. In Figure 4, we observe that the total transition noise or transition jitter noise is mostly concentrated at the center of transition, where the break point occurs at domain wall middle. Otherwise, the probability for which that noise can disturb the information present in magnetic domain is very small this also; confirm the fact that total transition jitter noise is concentrated at the transition center. Because of the jitter relation components (), we realize that the term affecting the transition jitter is the square of the first derivative of output voltage. This "square of first derivative" predicts the behavior of the "roll-off" curve and shows very well the zero of the curve. It should be noted that similar results were obtained [50], as they work in spectral domain. We can then conclude that the transition kink soliton shape can be valid for use in magnetic digital recording systems.
With this graph the discontinuity point is closer to the transition centre than when the same graph is plotted with other transition shape. We also observe that, the gap loss in [51] is just slight and far away from the center; which is not fair when made devices to become small in size yet. But, by looking our plot of SNR versus position we observe that the gap loss is most important and this help devices maker to produce smaller recording systems in term of size. Remember that, we allowed the other sources of noise and consider only the transition noise (transition jitter noise) in the system. Finally the SNR can be written as seen below and, by the help of this we can express the linear density (LD) or the area density (AD) of the system using the actual profile as in relation (5). The strength of that SNR is given in (dB) when applying the 20 log function. This is for good appreciation of behavior and best quantization of the SNR of the system in term of amplitude.
Intrinsic Recording Magnetic Media Parameters Values
In the purpose of this work, we find and obtain experimental values of read-write magnetic recording head parameters, made by engineers and present in many scientific reviews. As [54] thin polycrystalline film recording media form the basis of high density digital disk systems for this intrinsic parameter should be look carefully. In this work we have reported some parameters in Table 1 of compounds and Table 2 for single crystal metal. The most examples of parameters used in this study are the lattice distance a, the exchange interaction J and the anisotropy constant K where the experimental values are well done in [55-60].
Note that these three parameters are very essential when made or manufacturing the magnetic recording media, because they are intrinsic characteristics of the natural material used to fabric media. It should be noted with force that, recently there are very advanced composite materials such as Nd2Fe14B and many others which are presented with their magnetic properties by G. P. Zhao, et al. in their excellent works [61,62]. These new compounds are both rare-earth permanent magnets (Rare earth) and composite materials which integrate all the magnetic properties and make it possible to obtain domain wall widths with a fairly fine range. As an example the Nd2Fe14B which could have a wall width of 4.2 nm [63], would be a major advance in the field.
We could note here that, we used simple compounds just to start the study and get an idea of how compounds behave compare to single crystal, but only in the work that we are already doing and therefore the results will be proposed in the very near future we will use the properties of new materials like Nd2Fe14B, Pr2Fe14B and many more materials which are well presented in some best works [61-64].
Thus the experimental values for CoF2 compound, NiF2 crystal parameters with first and second magnetic anisotropy constants of the crystal formed by the compound [65] are given bellow:
The material selection for the ferromagnetic old (HDD) and new (Racetrack) recording systems plays a large role in determining the manipulation of magnetization or the dynamics of domain wall motion creation and movement. For Hard type (cobalt), they have ability to manipulate domain walls and its width. For Soft type like Crystalline Cobalt Iron (CoFe), the uses of advantage of crystallographic anisotropic direction to control the Domain Wall width and predict the preferred direction of propagation of DW when making ferromagnetic nanowire for recording media.
For single metals like Iron (Fe), Cobalt (Co) or Nickel (Ni) which constitute the most useful metal in forming compound and in manufacturing industry of magnetic recording media, parameters used of fabrication of magnetic recording media with single atom are reported in Table 2 [58,66-68].
To reinforce the fact that, for the manufacturing magnetic recording media, compound materials are best for, we draw comparative graphs for fundamental quantities of recoding systems like, signal to noise ratio (SNR) versus position Figure 5. In those comparative graphs, we emphasize and highlight the fact that DW width (∆) is the key parameter when evaluating the performances of the storage media, and work with that ∆ to evaluate the appropriate material or compound used to manufacture the recording media. The choice of variation of ∆ used in those comparative graphs, is not fortuitous because, by looking the DW width it is obvious to see that, the quantity depend mostly to the parameters which can characterize a compound, metal or a single crystal. Recall that those crystal parameters are: Lattice distance a, Exchange interaction J and anisotropy constant Ki.
Linear and Areal Density
As we said early the noise in magnetic recording media can affect the recording density. It is for that John C. Mallinson in 1974 Propose the relation between the SNR and Density as [21]
Where n and N are respectively number of particle per unit volume (e.g. for standard tape particles per cubic inch) and number of track per distance (track density for standard tape is about 100 tracks per inch, here 1 inch = 2.54 Cm) [21]. The numbers n and N used in numerical simulation can affect the behavior of LD as the number of particle per unit volume is directly proportional to linear density mean while the number of track per distance is inversely proportional to magnetic linear density. To appreciate this result, we plot the signal-noise-ratio (SNR) versus linear density (LD) in Figure 6 and realize that our results are in good agreement with previous results [69] as the total noise affects the LD. Also [70] really conclude that the medium noise power increases with increasing linear density and this result confirm the validity of this work. The smaller the noise, the lower the linear density or the smaller the signal, the higher the density.
The same comparative study can be done with areal density by plotting SNR against AD then, Figure 7 illustrate very well the fact that the high density can be attained but for that achievement the noises should be reduces.
To justify the choice of the present DW model and reinforce the fact that most researchers consider this model as the preferable one. For that we compare in Figure 8 the linear density of magnetic digital recording system obtained by the present Arctanexp model and the Tanh model where the LD is plotted against SNR. The simple conclusion is that, at the same SNR amplitude, the LD of the DW model used here is greater than LD obtained with Tanh model.
Concerning prediction of areal density (AD), there are many researchers who give prediction on the recording density of some prototype with different track density and grain or particles density. The Table 3 gives a few areal density (AD) and track density (N) during evolution period of magnetic recording systems. Note that the grain density propose in the Table 3 [21,71-73] are just a simple conjecture.
With this Table 3, we realize that evolution or the growing of digital density is also due to amelioration of track density (N) consequently the improvement on number of particle per unit volume or the grain density (n). For that, we plot Figure 9 with the characteristics of the same compound (CoF2), areal density using different track density and corresponding grain density. The diagram sketch just to show or compare the range of (AD) obtain with the Arctanexp(y/∆) transition shape that is transition used in this work with the old results obtain with the aids of other transition shape. By the observation of this graph, it is clearly that the DW transition used in this work is appropriate for the recording systems and offer the possibilities to achieve the high magnetic recording density.
Finally, we incorporate all the experimental read write head parameters in the model presented in this work, and compare the linear density versus SNR graph with an arbitrary parameters and final results are presented in Figure 10. All this reinforce, agree and confirm the rights of adopting this Arctanexp model as magnetic domain wall profile that can be used in magnetic recording systems, prove the necessity of choosing an appropriate material or compound when making magnetic recording media and also proof that with well chosen material it is possible to have reasonable AD or LD with accommodate and acceptable noise.
Discussion
Looking carefully Figure 3 we observe that in the first direction (K1 varied when K2 remain constant) the values range of DW width is smaller than when chosen the second direction (K2 varied when K1 remain constant); the range is . This tell us that it is preferable and benefit to adopt the first direction as crystallographic axis or when selected the type of recording materials.
Follow this, Figure 4 for its part confirms our predictions and proposals because the signal to noise ratio is low at the center of the wall, thus signifying the high noise rate. This result is somewhat satisfactory in the sense that this signal-to-noise ratio increases as one moves away from the center of the wall, thus demonstrating that the noise rate decreases when one approaches the magnetic domain which should welcome a data. So, therefore we can be convinced of the fact that in the magnetic domain, noise will not be able to disturb too much the information written on the media.
The look at Figure 5 is not insignificant because the noise is even smaller if we are in the presence of a composite material than of a simple crystal. Since this same graph already shows us that the materials compounds already offer a very small magnetic domain wall width thus giving the possibility of having a high storage density. This therefore reveals that it would be desirable to have more advanced composite materials for the manufacture of recording media because this type of material will have to offer a high signal to noise ratio and therefore a low disturbance rate due to noise, in addition they will offer walls of low width thus giving the possibility of reaching high density.
The next part deals with the storage density (linear or areal) as it shows that the density is proportional to the noise (the more the noise is, the more the density increases). It is therefore not a reason to absolutely seek high densities, but to seek the noise margin that cannot alter the information while remaining within an acceptable proportion reached by the density. This challenge is indeed ours because Figure 6 and Figure7 show us the linear and areal density as a function of the signal to noise ratio. This comparison carried out for two compounds and two simple materials gives us to see that the storage density can reach large proportions while the noise remains moderately low. The confirmation of this is clearly visible with the COF2 where areal density can reach while the signal to noise ratio remains low (signifying a low rate of disturbance).
The whole study is confirmed when a comparative study is made between an old transition profile (Tanh) and the soliton kink profile (Arctanexp) used in this work. The observation in this comparison is startling because even if we look at the past, the densities opted with this profile are far superior to those obtained at the time and with other transition models. For example in 2008 [74] researchers could reach while with the approach developed here we could at that time reach . This observation therefore reinforces our study and gives us reasons to believe that the improvement of composite materials used in the manufacture of read write heads, mastery and knowledge of attenuation and noise control factors will allow us to develop in the very near future more efficient recording and storage systems with very large storage capacities.
Conclusions
The aim of this work was to obtain the linear and areal density, by considering the magnetic recording media as continuous medium where exist noises and the most predominant are transition noise jitter. Using the signal noise ratio relation, we prove that, using the domain wall (DW) kink soliton transition in recording systems it is possible to improve de linear and areal density. For that, we have made a certain comparison of key parameters of recording systems using the signal-noise-ratio (SNR) of the system and used the experimental parameters values taken in the literature to agree the model shape. The important verification that should be made is asking what type of material or compound are good for optimization of our recording media and systems. In other word, which materials can be used to manufacture Racetrack memory considers as the promising recording systems? The answers of these questions are one of most challenges for many researchers in magnetic recording systems since the Racetrack memory are now the focal point of many works.

