International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 7, Issue 1
Research Article
DOI: 10.35840/2631-5068/6537
Coherence Amplification in Off-Diagonal Density Matrix Elements
Dennis J Sorce*
References
- Kevin A, Gregg J (2009) Finite-time destruction of entanglement and non-locality by environmental influences. Foundations of Physics, arXiv:0903.0009.
- Hornberger K (2009) Introduction to decoherence theory. In: Buchleitner A, Viviescas C, Tiersch M, Lecture Notes in Physics, Entanglement and Decoherence Berlin, Springer-Verlag 768: 221-276.
- Heinz-Peter B, Francesco P (2010) The theory of open quantum systems. (4th edn), Oxford University Press, New York, USA.
- Maximilian S (2008) Decoherence. Quantum Physics, Springer-Verlag, New York, USA.
- Michael AN, Isaac LC (2019) Quantum computation and quantum information. (8th edn), Cambridge University Press, New York, USA.
- Anatole A (1986) Principles of nuclear magnetism. Oxford University Press, New York, USA.
- Brian C (1997) Nuclear magnetic resonance and relaxation. Cambridge University Press, New York, USA.
- Maurice G (1988) Quantum description of high-resolution NMR in liquids. Oxford University Press, New York, USA.
- Michael M (1988) Coherence and NMR. John Wiley and Sons, New York, USA.
- Michael G, Lance De L (2001) The return of the frequency sweep: Designing adiabatic pulses for contemporary NMR. J Magn Reson 153: 155-177.
- Wolfram Research Mathematica, V12 Urbana, USA.
Author Details
Dennis J Sorce*
Retired, Center for Magnetic Resonance Research, Minneapolis, USA
Corresponding author
Dennis J Sorce, Retired, Center for Magnetic Resonance Research, Minneapolis, MN 55455, USA, Tel: 410-628-2461.
Accepted: August 07, 2021 | Published Online: August 09, 2021
Citation: Sorce DJ (2021) Coherence Amplification in Off-Diagonal Density Matrix Elements. Int J Magnetics Electromagnetism 7:037.
Copyright: © 2021 Sorce DJ. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We demonstrate coherence amplification in off-diagonal density matrix elements for a decoherence model for spin ½ particles with applied radio-frequency pulse without relaxation. The method of coherence amplification developed may be of general utility in applications in NMR/MRI.
Introduction
The manifestation of coherence phenomena is a hallmark of quantum mechanics, differentiating it from classical phenomenon due to the property of superposition in quantum reality due to the linearity of the Schroedinger equation [1-4].
Methods of possible amplification of coherence as quantitated by the absolute value of off-diagonal density matrix elements, may be of use in applications such as quantum computing [5] and MRI tissue contrast [6,7].
In the Letter, we develop a Possible Methodology of Coherence Enhancement. It is easily implemented and may have value in Venues of NMR/MRI [8].
Formalism Development
We base our Treatment on the Following Expression often used in Formalism of Coherence [1,9].
Here, is the time-dependent Density Matrix. is a Time Dependent Radio-Frequency Hamiltonian, defined as:
are Spin ½ Angular Momentum Operators [8] . The Radio-Frequency terms and are respectively, Amplitude and Frequency Offset Variable defined in Appendix I.
Here, is Boltzmann's Constant.
T is Temperature in Kelvins.
h is Planck's Constant Divided by 2 .
is a Time Constant Characterizing the Decoherence.
For the Specific Cases Treated here, to Explore a Model of Coherence Enhancement Effects, we specialize to the HS1 Adiabatic Pulse as detailed by Garwood, et al. [10] [see Appendix II].
If one substitutes Eq (2) into Eq (1), one obtains after "straightforward but tedious algebra":
Where:
And:
is the 2 by 2 Identity Matrix.
For Clarity and Completeness, we Explicitly Define the Following Terms:
We adopt the Standard Definition of the Spin-1/2 Cartesian Spin Angular Momentum Operators
As:
Where, Eqs (7b) are the Pauli Matrices [9].
If one substitutes Eqs (5,6,7a-b) into Eq (4) one finds after manipulations the following set of four first order differential equations in time for the four matrix elements of the defined Density Matrix. We note that the derived system of equations below were numerically verified versus Eq(9) below:
We note that for ease of manipulation and coding, one can rewrite Eqs (1) as:
Using a Numerical Platform such as Mathematica [11] one can readily Numerically Solve the four Differential equations Eqs (8 a,b,c,d) to obtain the Time-Dependent Matrix Elements .
Results
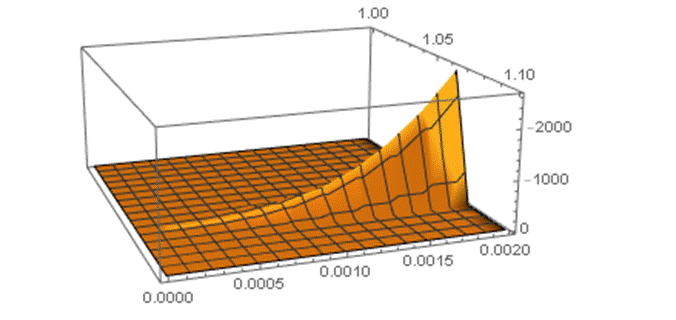
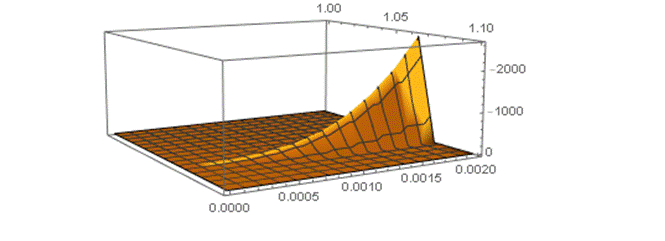
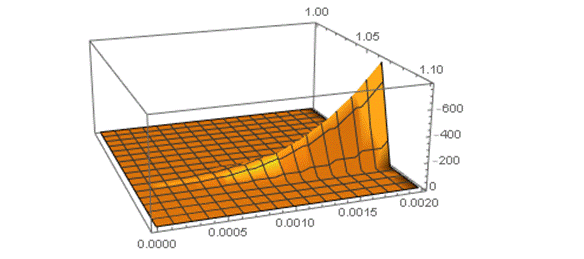
In Figure 1a, Figure 1b, Figure 1c and Figure 1d we see plotted the dependence in Three-Dimensional Figures of the Four Density Matrix elements which are numerical solutions of Eqs [8a,b,c,d]. We note that the density matrix elements are considered dimensionless [4,6,8,9]. One can readily see there are Maxima at over the domain considered.
In Summary, the Key Results of this effort, is the finding of Maxima for the dependence of Density Matrix element which indicate amplification of the coherences and populations for spin ½ nuclei which are solutions of the system of Eqs [8a,b,c,d] that incorporate Decoherence effects at . The system of Eqs [8] are to the knowledge of the author unique to the Magnetic Resonance literature.
Such Enhancement may prove to be of utility in Biomedical Applications in NMR/MRI, because the spin angular momenta can be expressed as sums and differences of the spin-1/2 Density Matrix elements which can be shown to exhibit pronounced amplification that are proportional to the Magnetization.