International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 7, Issue 2
Research Article
DOI: 10.35840/2631-5068/6538
Magnetic Monopole Interaction with a Magnetic Sphere
R Alarki and D Palaniappan*
Table of Content
- Abstract
- Introduction
- Mathematical Setting for a Magnetic Sphere in an External Magnetic Field
- Exact Solution for a Monopole-magnetic Sphere Interaction Problem
- Particular Locally Generated Magnetostatic Fields
- The Magnetic Interaction Force
- MFM Tip Modeling and Numerical Force Calculations
- Conclusion
Figures
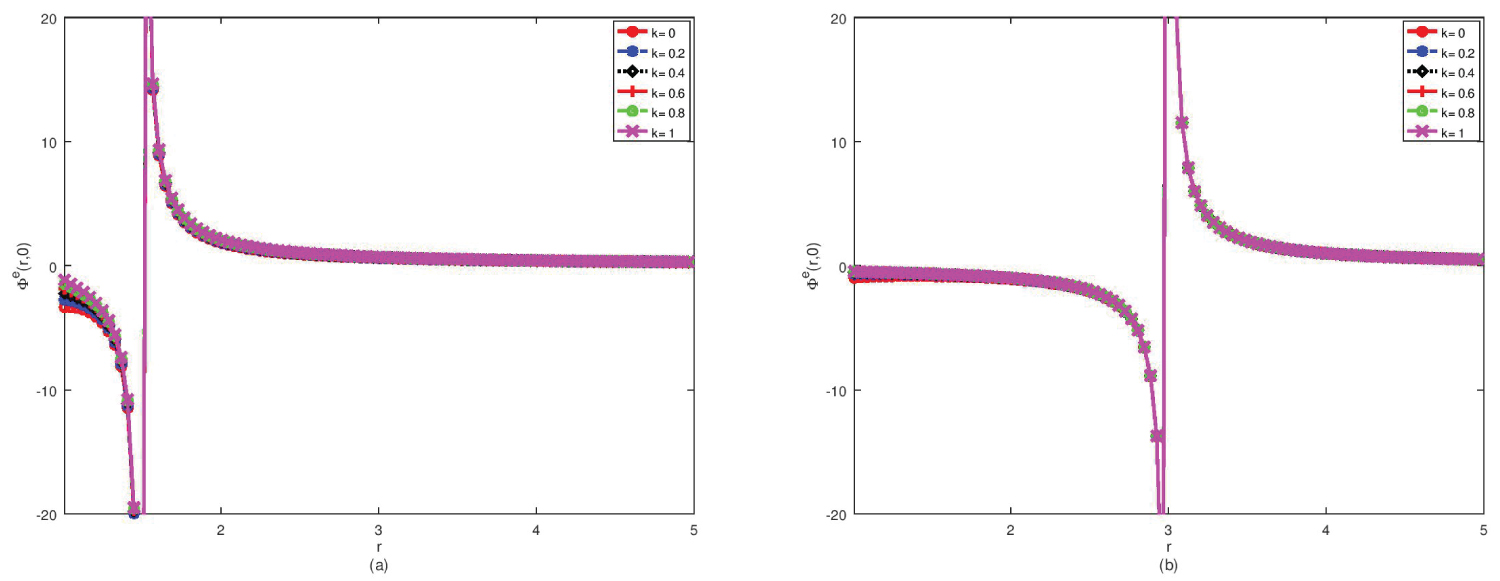
Figure 2: Axis potential Φe(r, 0) outside....
Axis potential Φe(r, 0) outside the magnetic sphere due to a pole at (0, 0, c), c > 0 versus r for various values of the permeability parameter k: a) c = 1.5; b) c = 3.0.

Figure 3: Potential contour plots for....
Potential contour plots for a magnetic sphere in a constant magnetic field for various of k: a) k = 0; b) k = 0.25; c) k = 0.5; d) k = 0.75; e) k = 0.95; f) k = 1.5.
Figure 4: Potential contour plots for....
Potential contour plots for a magnetic sphere in a linear magnetic eld for various of k: a) k = 0; b) k = 0.25; c) k = 0.5; d) k = 0.75; e) k = 0.95; f) k = 1.5.

Figure 5: Normalized force component....
Normalized force component due to a magnetic pole at (0, 0, c), c > 0: a) Force versus location ratio for fixed k; b) Normalized Approximate force versus .
Tables
Table 1: Numerical values of the MFM tip-sphere interaction force for typical PtCo and Alnico 5 magnets.
References
- Varon M, Beleggia M, Kasoma T, Harrison RJ, Dunin-Borkpwski RE, et al. (2013) Dipolar magnetism in ordered and disordered low-dimensional nanoparticle assemblies. Scientific Reports 3: 1234.
- Lin QG (2007) Comment on "London model for the levitation force between a horizontally oriented point magnetic dipole and superconducting sphere". Phys Rev B 75: 016501.
- Palaniappan D (2009) Magnetic interaction force and a couple on a superconducting sphere in an arbitrary dipole field. J Supercond Nov Magn 22: 471-477.
- Levin ML (1964) The solution of a problem in quasi-stationary electrodynamics by the method of images. Sov. Phys Tech Phys 9: 312.
- Yang ZJ (1998) Interaction between a magnetic dipole and a superconducting sphere. Solid State Comm 107: 745.
- Overton WC, van Hulsteyn DB, Flynn ER (1993) Theoretical and experimental verification of the properties of superconductor surface imaging. IEEE Trans Appl Supercond 3: 1930.
- van Hulsteyn DB, Petschek AG, Flynn ER, Overton WC (1995) Superconductor imaging surface magnetometry. Rev Sci Instrum 66: 3777.
- Coffey MW (2000) Levitation force between a point magnetic dipole and superconducting sphere. J Supercond Nov Magn 13: 381-388.
- Coffey MW (2002) Levitation force between a horizontally oriented point magnetic dipole and a superconducting sphere. J Supercond Nov Magn 15: 257.
- Palaniappan D (2007) Comment on "London model for the levitation force between a horizontally oriented point magnetic dipole and superconducting sphere". Phys Rev B 75: 016502.
- Trombley C, Palaniappan D (2016) Interaction of a straight line current with a superconducting sphere: Theoretical results. J Supercond 29: 89-100.
- Stratton JA (1941) Electromagnetic theory. McGraw-Hill Book Co, London.
- Jackson JD (1999) Classical electrodynamics. (3rd edn), Wiley, London, 19.
- Griffiths DJ (1999) Introduction to electrodynamics. (3rd edn), Addison-Wesley, USA.
- Lindell IV (1992) Electrostatic image theory for the dielectric sphere. Radio Sci 27: 1.
- Norris WT (1995) Charge images in a dielectric sphere. IEE Proc Sci Meas Technol 142: 142-150.
- Cai W, Deng S, Jacobs D (2007) Extending the fast multipole method to charges inside or outside a dielectric sphere. J Comput Phys 223: 846-864.
- Ma M, Gan Z, Xu z (2017) Ion structure near a core-shell dielectric nanoparticle. Phys Rev Lett 118: 076102.
- Holehouse A, Pappu RV (2018) Collapse transitions of proteins and the interplay among backbone, sidechain, and solvent interactions. Ann Rv Biophysics 47: 19-39.
- Meier QN, Fechner M, Nozaki T, Sahashi M, Salman Z, et al. (2019) Search for the magnetic monopole at a magnetoelectric surface. Phys Rev X 9: 011011.
- Aad G, Abbott B, Abbott DC, Abdinov O, Abed Abud A, et al. (2020) Search for magnetic monopoles and stable high-electric-charge objects in 13 Tev proton-proton collisions with the ATLAS detector. Phys Rev Lett 124: 031802.
- Ray MW, Ruokokoski E, Tiurev K, Mottonen M, Hall DS (2015) Observation of isolated monopoles in a quantum field. Science 348: 544-547.
- Aartsen MG, Abbasi R, Ackermann M, Adams J, Aguilar JA, et al. (2014) Search for non-relativistic magnetic monopoles with IceCube. Eur Phys J C 74: 2938.
- Dirac PAM (1931) Quantised singularities in the electromagnetic field. Proc R Soc A 133: 60.
- Hug HJ, Jung Th, Gunterodt HJ, Thomas H (1991) Theoretical estimates of forces acting on a magnetic force microscope tip over a high temperature superconductor. Physica C 175: 357-362.
- Alarki R (2017) Calculation of laplace and helmholtz potentials in two-phase problems. MS Thesis, TAMUCC.
- Bussemer P (1993) Comment on "Image theory for electrostatic and magnetostatic problems involving a material sphere" by Ismo V Lindell [Am J Phys 61: 39{44 (1993)]. Am J Phys 62: 657.
- Dassios G, Sten JC (2012) On the neumann function and the method of images in spherical and ellipsoidal geometry. Math Meth Appl Sci 35: 482.
- Neumann C (1883) Hydrodynamische untersuchungen. Leipzig, Appendix, 281.
- Gradshteyn IS, Ryzhik IM (2015) Table of integrals, series, and products. Academic Press.
- Abromowitz M, Stegun IA (1964) Handbook of mathematical functions. Applied Mathematics.
- Lin YC, Baumketner A, Deng SZ, Xu ZL, Jacobs D, et al. (2009) An Image-based reaction field method for electrostatic interactions in molecular dynamics simulations of aqueous solutions. J Chem Phys 131: 154103.
- Rahman HI, Tang T (2018) Electric potential of a point charge in multilayered dielectrics evaluated from Hankel transform. J Eng Math 110: 63.
- Pendry JB, Schuring D, Smith DR (2006) Controlling electromagnetic fields. Science 312: 1780-1782.
- Leonhardt U (2011) To invisibility and beyond. Nature 471: 292-293.
- Ishikawa A, Tanaka T, Kawata S (2005) Negative magnetic permeability in the visible light region. Phys Rev Lett 95: 237401.
- Urman YM, Bugrova NA, Lapin NI (2010) On levitation of diamagnetic bodies in a magnetic field. Tech Phys 55: 1257-1265.
- Schonenberger C, Alvarado SF (1990) Understanding magnetic force microscopy. Z Phys B 80: 373-383.
- Haberle T, Haering F, Pfeifer H, Han L, Kuerbanjiang B, et al. (2012) Towards quantitative magnetic force microscopy: Theory and experiment. New J Phys 14: 043044.
Author Details
R Alarki and D Palaniappan*
Department of Mathematics & Statistics, Texas A&M University, USA
Corresponding author
D Palaniappan, Department of Mathematics & Statistics, Texas A&M University, Corpus Christi, TX 78412-5025, USA.
Accepted: October 25, 2021 | Published Online: October 27, 2021
Citation: Alarki R, Palaniappan D (2021) Magnetic Monopole Interaction with a Magnetic Sphere. Int J Magnetics Electromagnetism 7:038.
Copyright: © 2021 Alarki R, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The two-phase problem of a magnetic sphere of radius a with permeability constant μi (interior phase) interacting with a monopole/magnetic source located at (0, 0, c), c > a, in the host medium with permeability μe (exterior phase) is addressed in this paper. By considering the Maxwell-Maxwell (MM) framework, exact results for the scalar magnetostatic potentials in the regions exterior and interior to the magnetic sphere are presented in various forms. The constructed potentials in infinite series and closed forms satisfy a set of mixed boundary conditions on the sphere and provide image system interpretations similar to those in electrostatics. An alternative form of the solution reveals a new interpretation that the image system can also be expressed as a distribution of magnetic dipoles between the sphere center and the Kelvin's inverse point. The non-dimensional permeability parameter , 0 ≤ k ≤ 1, influences the magnetostatic potentials significantly and yields magnetically conducting, superconducting, and planar interface results in the limiting cases. Graphical illustration of the computed exterior axis potential is positive beyond the location of the magnetic source and is negative between the sphere and the monopole location indicating a stronger interaction in the close proximity of the magnetic sphere. The magnetic interaction force on the magnetic sphere, a key physical quantity, is calculated in a quadrature form. The dependence of the force on k and the monopole-sphere separation ratio c/a are illustrated. The integral in the force as well as the other integrals in the scalar magnetostatic potentials can be evaluated numerically. Direct numerical/graphical analysis of the magnetic force indicates that the interaction force is attractive (positive) or repulsive (negative) according to the permeability parameter or , respectively. An approximate expression for the force is proposed which exactly captures the actual force characteristics qualitatively. By modeling the tip of a Magnetic Force Microscope (MFM) as a monopole and the sphere as a magnetic material, force measurements are made, using the theoretical results presented herein, for Cobalt-Platinum (PtCo) and Alnico 6 (Alcomax) magnetic materials. Our estimates predict forces as high as 10-12 N for PtCo magnets and 10-11 N for Alcomax types of magnetic materials. Larger force estimates are attainable by altering the tip-to-sphere separation and other parameters as well.
Introduction
The interactions among magnetic microspheres and assemblies of spherical nanoparticles are often approximated by magneto- static dipolar fields and the forces [1]. The principal knowledge of magnetostatic potentials (MP), magnetic interaction energy (MIE) and the magnetic forces (MF) on the magnetized bodies are crucial to engineer new and novel magnetic materials and devices. Quantification of interactions of magnetic particles in a foreign host medium is essential to recognize the potential of these materials and structures. Mathematical calculations and approximations of the magnetostatic fields and the existing forces involving magnets of various types and shapes can be very handy in practical realization of such physical systems. In the present contribution, the fundamental classic problem dealing with the interaction of a point magnetic source/monopole with a magnetic spherical boundary is addressed.
The magnetic field calculations involving perfectly superconducting (single phase with vanishing normal component of the magnetic field at the surface) magnets placed in a surrounding medium have been performed in many studies (see for instance, [2-7]). Exact results for the magnetostatic scalar potentials, interactions, levitation forces and moments on the magnets are available for a spherical superconductor [8-10] in the homogeneous case. A typical physical problem reduces to a Neumann boundary value problem for the Laplace equation for which closed form analytical solutions are tractable via spherical harmonic methods [2,8,9] or using analogous hydrodynamical approach [3,11]. For permanent magnets and materials with dissimilar magnetic permeability constants compared to that of the surrounding host medium the magnetic field calculations are more challenging due to 'heterogeneity'. A mathematically equivalent problem of the latter situation exists in the context of electrostatics where a dielectric spherical inclusion embedded in another medium of infinite extent [12-14]. It should be pointed out that there is now an extensive literature available on this latter problem [12,15,16], among others, and it continues to grow [17-19]. New elegant proposals emerge for ways to obtain results that have applications in the fields such as quantum dots and molecular interactions at the atomic levels. Molecular interactions are attractive or repulsive forces between molecules and between non-bonded atoms. Majority of these investigations and calculations have focused on situations for which electrostatic assumptions and approximations can be applied. For accurate magnetostatic field computations the knowledge of physical quantities such as interaction forces and energy are crucial in addition to the calculation of scalar magnetostatic potentials. Therefore, in this article, we derive analytical results for the problem of a magnetic sphere of radius a with permeability μi placed in a host medium of magnetic permeability μe. The field in the surrounding medium (that is, outside the spherical inclusion) is assumed to be generated by a magnetic monopole (magnetic source) and we determine the interaction force characteristics due to the monopole via finding the scalar potentials in the regions outside and inside the sphere.
An isolated magnetic monopole/source has not been fully realised in experiments as done for a dipole. However, it is one of the simplest of all poles and the results can be used in the discussion of more complicated magnetic sources. Several recent studies [20-23] demonstrate the efforts in search and generation of magnetic monopoles in a variety of settings. The monopole relevance in electromagnetic theory was particularly emphasized in the novel work of Dirac [24]. The monopole is often used as a building block for magnetic dipoles of any desired orientation. A straight-forward directional derivative of a magnetic source yields a magnetic dipole. Indeed, multipole and spherical harmonic expansions are all based on the analytic expression for the fundamental solution of the Laplace equation, which is a source. A uniform magnetostatic field can be realised as one of the leading terms in the multipole expansion of a monopole and can be induced with two opposite sources. For example, consider a magnetic source of strength -m located at ε and another source at -ε with strength m. By a direct calculation it can be shown that by taking the limit m → ∞ and ε → ∞ but fixing (H is a constant) one can generate a uniform magnetic field. Moreover, as discussed in [25] the Magnetic Force Microscopy (MFM) tip can be modeled by a magnetic monopole. MFM is a special mode of operation of the non-contact scanning force microscope. The origin of the magnetic forces, image contrast, and the influence of tip magnetic field on the sample magnetization are topics that have strong theoretical foundations. Forces of the order of 10-9 N have been predicted for tip-half-space high temperature superconducting (HTSC) models [25] with Cobalt-platinum and Alcomax magnetic materials. Dipole-sphere superconducting (SC) configurations with Nd-Fe-B magnets have yielded a force of 10-12 N [3]. We show here that the monopole-magnetic sphere model for Cobalt-Platinum and Alnico 5 materials generate tip forces whose magnitudes lie between the HTSC and SC estimates and are measurable by an MFM.
Mathematical treatment of two-phase models generally require solutions of demanding vector partial differential equations. Additionally, the initial and boundary constraints arising due to physical considerations impose further challenges. In magnetostatics context a two-phase structure consists of two regions, one exterior and the other interior to a bounding surface, with different permeabilities. In our current situation for an isolated magnetic sphere placed in an external host medium we employ Maxwell's equations for the magnetic induction fields in both regions (exterior and interior to the magnetic sphere), sometimes referred to as MM model in classical magnetostatics. Further, the fields are assumed to be independent of time in the entire domain. We transform the vector boundary value problem (BVP) into a scalar BVP via the scalar potential transformations in the two regions. This in turn yields a mixed BVP for the scalar magnetostatic potentials along with the boundary conditions on the magnetic sphere of Dirichlet and Neumann type. The solutions of the mixed BVP for the Laplace equations (harmonic functions) can be constructed by using spherical harmonics expansion (in series form) and summation of the infinite series technique (in closed form). Indeed, the scalar harmonic potentials provide the basis functions for the study of monopole-sphere interactions. The magnetic induction field components can then be found via a straightforward differentiation of the scalar potentials. Each term of the multipole expansion of the magnetic source solution yields locally generated magnetostatic fields that can be analyzed. The magnetic interaction force acting on the magnetic sphere due to a monopole can be computed using the scalar potential expressions.
The paper is organized as follows. First, we provide the mathematical setting of the underlying magnetostatic physical model as a mathematical mixed boundary-value problem for the scalar magnetic potential functions in section 3. Maxwell's equations in simplified forms in the two regions (r > a and r < a), and the scalar functional representations of the magnetic induction fields are also given in this section. In section 4, analytic solutions for the monopole-sphere interaction problem are provided in infinite series form. The summation details of the series leading to closed form expressions for the potentials are given in this section. The interpretation of the image system, equivalent expressions for the scalar magnetostatic potentials, limiting cases, and axis potential illustrations are also carried out in the same section. Particular locally generated magneto-static fields extracted from the series solutions are discussed in section 5. The derivation of an important physical quantity namely, the interaction force acting on the magnetic sphere is provided in section 6 along with several features. As will be seen later, the force is expressed in integral form from which all the special cases can be deduced quickly. An equivalent expression for the force in an infinite series form is also provided. Numerical results for the force via graphical illustrations, the effect of the permeability and monopole-sphere separation parameters, and approximate expressions for the force are elucidated in the latter section. Application of our results in MFM tip modeling and numerical results for some magnetic materials are documented in section 7. Finally, section 8 summarizes our important findings and outlines some immediate promising applications.
Mathematical Setting for a Magnetic Sphere in an External Magnetic Field
Consider a magnetic sphere of radius a with permeability μi embedded into an external magnetic field acting in a medium with permeability μe. The magnetic vector fields inside and outside the sphere are denoted by Hi and He, respectively with the corresponding magnetic induction fields Bi and Be. The two fields are related by Bi = μiHi and Be = μeHe in the respective regions, where μ0 is he magnetic permeability in vacuum. Let (r, θ, φ) be the spherical coordinates corresponding to the Cartesian counterpart (x, y, z) with the origin at sphere (r = a) center. The unit vectors in spherical and Cartesian frames are designated by < ˆer, ˆeθ, ˆeφ > and < ˆex, ˆey, ˆez >, respectively. Assuming the Maxwell-Maxwell (MM) model in the regions r < a and r > a, the field equations in the simplified from are given by [13,14].
The first of these follow from Maxwell equations for the respective H fields and the last ones are the incompressibility (solenoidal) conditions of the magnetic induction vector fields. Determination of He and Hi (or, equivalently, the B fields) in the two regions subject to the bounding surface constraints require solving the aforementioned vector harmonic equations with suitable boundary conditions. The resulting procedure is a complicated affair and so one seeks a scalar function formulation of the problem. We note that since the magnetic fields in the two phases are irrotational (the first equations of (1) and (2)) in the two regions, there exist scalar functions Φi and Φe such that
in the respective regions, where Φi(r, θ, φ) and Φe(r, θ, φ) are known as the magnetic scalar potentialsa [13,14]. Using the relation between B and H fields and applying the incompressibility condition of magnetic induction to (3) and (4) one gets
aPhysically, the magnetic scalar potential is not the real potential by which charges nay interact magnetic field. Also, magnetic scalar potential is only valid in the region of no current. The use of scalar potentials is the mathematical trick to turn the problem of magnetostatic field analogous to electric potential.
in the interior (r < a) and exterior (r > a) regions, respectively. Therefore, the vector equations (1) and (2) reduce to solving the scalar Laplace equations (5) and (6) for the magnetic scalar potential functions subject to the field boundary conditions. For a magnetic sphere placed in an external host medium, the appropriate boundary conditions are that the radial and transverse components are continuous across the surface of the spherical boundary. In terms of the scalar potentials these conditions become
Thus, the two phase physical problem of a magnetic sphere of radius a embedded in an external magnetic field reduces to solving the mathematical mixed boundary value problem (mixed BVP) for the Laplace equations, in the respective phases, stated in (5)-(8). The analytical/numerical solution of such a mathematical boundary value problem will yield the corresponding magnetostatic potentials prevailing in the two regions. The magnetic induction fields in the domains r < a and r > a are then determined using (3) and (4), after straightforward differentiation. Below we address the magnetic monopole-sphere interaction problem and provide analytical solutions for the scalar potentials Φe(r, θ, φ) and Φi(r, θ, φ) and record the related consequences. As mentioned in the introduction the solution to source-sphere problem has been discussed in various electrostatic and two-phase environments [15-17,26]. However, the details of its magnetostatics counterpart has been largely ignored, Here we provide the derivation in the magnetostatics context and recast the solutions in various forms suitable for further calculation and manipulation purposes.
Exact Solution for a Monopole-magnetic Sphere Interaction Problem
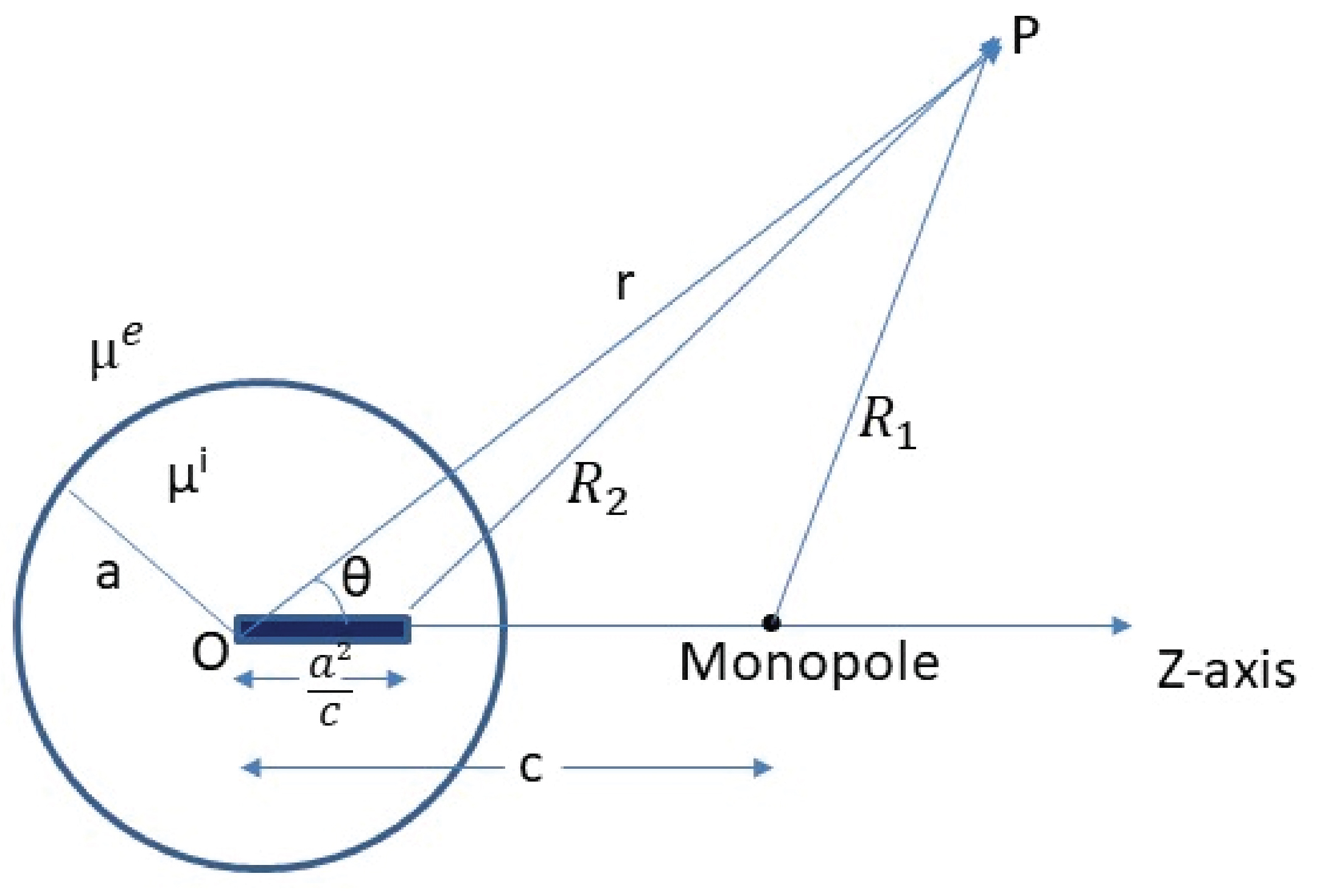
Now consider a magnetic source (monopole) outside a spherical boundary of radius a located at a distance c > a from the center of the sphere. The monopole-magnetic sphere configuration is shown in Figure 1. The magnetic material inside the sphere has a magnetic permeability constant μi and the host medium on the magnetic source side has a magnetic permeability constant μe. The monopole of strength m is positioned on the z-axis with coordinates (0, 0, c). Let Φ0(r, θ, φ) denote the scalar magnetic potential for the field generated by the magnetic source alone. Due to rotational symmetry of the system, the potential function Φ0 is independent of the coordinate φ, so we have for the monopole field
where Expanding Φ0(r, θ) for c > r in terms of spherical harmonics [14] we obtain
where Pn are the Legendre polynomials of degree n. The linearity property of the Laplace equation together with the orthogonality of Legendre polynomials allows one to write the modified potentials in the two regions r > a and r < a, respectively in the form
and
Note that equations (11) and (12) are the representations of solutions via multipole expansion method. The application of boundary conditions (7) and (8) on the sphere r = a stated in the previous section leads to
where the parameter k defined by
is the nondimensional magnetic permeability parameter with 0 ≤ k ≤ 1. For k = 0, the above coefficients reduce to that of Dirichlet problem and when k = 1 the constant Bn yields the multipole coefficient for the Neummann boundary value problem for a superconducting sphere (in Meissner state [2]). Now the analytic solutions for the scalar magnetostatic potentials in the two regions due to a monopole in the presence of the magnetic sphere r = a for arbitrary k are now given by
for the exterior region and
for the interior phase of the magnetic sphere, where the infinite series expansion of Φ0 is given in (10). The expansion for Φ0 in (10) is valid for r < c, but in equation (16) this function appears for r > a, which contains the range r > c. It should be reminded that the expansion for Φ0 is different in that region although it is not needed for the boundary conditions. The interpretation of the terms in the infinite series given in (16) and (17) leads to the image system for the magnetic sphere under the influence of a magnetic monopole. First, note that the term in the series solutions with n = 1 represents the magnetic sphere placed in a constant external magnetic field (uniform magnetic field) by defining the constant [12,14]. The image in the exterior field in this case is a single magnetic dipole located at the sphere center (0, 0, 0). The second term with n = 2 gives the result for a magnetic sphere embedded in a linear field (also known as quadrupole field) consisting of an image quadrupole at the center of the sphere. We return to these two particular (locally generated) fields in the next section. It should be pointed out that the higher order fields and the respective images can be extracted in a similar fashion from the series solutions given in (16) and (17).
Next, we proceed to the closed form analytic solutions for the monopole-magnetic sphere interaction problem. The magnetostatic potential expressions (due to an initial magnetic source) given in (16) and (17) can be cast into closed form exact solutions (see [17,26,27] for details). By using the representation of the potential due to an initial source Φ0 in closed and infinite series forms given in (9) and (10) it is possible to determine the sums of the infinite series in (16) and (17). The final results for the scalar potentials in the two regions read
for the exterior phase and
for the interior phase, where With these closed form ions for the monopole-sphere interaction problem the image system in the exterior phase for the magnetostatic problem at hand can be interpreted as follows. It consists of
• a monopole of strength at the inverse point (the second term on the R.H.S of (18))
• a line distribution of monopole poles extending from the center of the sphere (0, 0, 0) to the inverse point with line density (the integral term).
A similar interpretation of the image system for the interior region can be stated in terms of monopole and monopole distributions. As said earlier, the image system in the electrostatics context for a dielectric sphere due to an external electric charge (an equivalent mathematical boundary-value problem) has been presented in many studies (see [15-17,28], for instance). Actually, the results (using a different scheme) were originally presented by Carl Neumann in 1883 as an appendix in his book [29] for the corresponding magnetostatic problem. Our mathematical solutions given in (16)-(19) agree with all the solutions derived previously [15-17,29] in various circumstances.
The integrals in (18) and (19) can be evaluated in terms of hypergeometric functions [30,31], but we shall not discuss the details here. Instead, we focus on possible other representations suitable for magnetostatic environment calculations. We illustrate our ideas for the integral in the region r > a (exterior phase) as it is required for the force calculations later. The equivalent ideas can be utilized for the interior potential as well. One can write the integral in (18) in the form
The first term in (20) can be evaluated in terms of elementary functions as
for and R2 is defined as before (see just after equation (19)). With this result the magnetostatic potential in the exterior region Φe can be alternatively written in the form
The second term in (21) corresponds to the Kelvin's image (as in the electrostatics case) and the second and third terms together represent Neumann images (superconducting case) with strengths now depend on k. The last term with an integral arises due to the continuity of the magnetic potentials across the spherical surface and vanishes for the extreme values when k = 0 (the coefficient reduces to zero) and k = 1 (the integrand becomes zero). In the simulation of molecular interactions [17,32] the exterior potential needs different approximations to maximize the computational efficiency. Although the integral in (21) can be evaluated in terms of slowly convergent special functions, establishing the convergence is tedious in general circumstances. For points farther from the spherical boundary, the contribution from the integral term may be small and can be neglected. In these situations the second and third terms may provide good approximation to the perturbed scalar potential outside the magnetic sphere.
Another interesting and useful form for the exterior potential can be derived via the following approach. Note that the expression for Φe given in (18) may also be written as
The two terms in the square bracket in (22) can be recast in the form (using integration by parts)
Note that the explicit R2 contribution in (22) can be extracted from (23) by performing the integration. With this representation, the images system for exterior potential may also be interpreted as the distribution of ‘magnetic dipoles' between the center of the sphere (0, 0, 0) and the Kelvin's inverse point with the line density Surprisingly, such an interpretation of the image system for the source-sphere problem does not seem to have been discussed in the literature. It should be noted that the three closed form expressions for the exterior potentials provided in (18), (21) and (23) are equivalent. The representation given in (18) may be generally seen in the electrostatics literature [15-17] and yields the corresponding planar interface result via a direct limiting process (see below). The form given in (21) (derived using a manipulation of (18)) demonstrates the extraction of additional terms from the integral as needed. The new representation for the exterior potential expression provided in (23) can be conveniently employed in the calculation of axis potentials and resulting forces acting on the magnetic sphere (see section 6). Additionally, it serves as a useful expression in deducing various limiting cases as shown below. The potential expression Φi(r, θ) in the interior phase (r < a) is the same as given in equation (19).
Magnetically conducting (insulated) case k → 0: When k → 0 equation (23) reduces to (after integration)
This is the potential expression for an insulated sphere in a monopole field. The image system in this case consists of a monopole at the Kelvin's image point and another pole at the origin (sphere center). For purely conducting case the limit k → 0 in (18) or (21) yields the image monopole at the Kelvin's inverse point. It should be remembered that care must be taken when we take the limit k approaches zero since the integrals in (18) and (21) become improper integrals in this case. These solution correspond to the well-known solutions for a classical Dirichlet problem involving an isolated sphere solved in electrostatics [12,14]. The interior field is zero in this case.
• Superconducting sphere limit k = 1: In this limit, (23) becomes
which represents the solution for the Neumann problem involving a superconducting sphere in a source field. After performing the integration in (25), the result can be shown to be equivalent to the form given in [2]. Here again, the interior potential field is zero. The Neumann problem has an hydrodynamics analogue as discussed in [3,10,11].
• Planar interface separating two phases: In the limit a → ∞ and c → ∞ such that c - a → h we see from (18) that integral contains the factor which tends to zero as a approaches infinity. The resulting expressions can be written in the form (using Cartesian coordinates)
for the upper half (z > 0) and the lower-half (z < 0) of the plane regions, respectively. The above solutions correspond to the two-phase magnetic media separated by a planar interface. Here z = 0 is the plane and (0, 0, h) is the location of the initial source. The electrostatic analogue of this result is also discussed recently in [33].
We emphasize that the equivalent forms of the exterior potential can be employed depending on the purpose. For instance, the systematic derivation of the monopole-magnetic sphere solution leads to the potential expression given in (18).
The equivalent forms given in (21) and (23) can be used if one wishes to derive approximations and special cases. The form (23) for the exterior potential is especially suited for the derivation of the interaction force in a much simpler manner.
It is also of interest to calculate the exterior potential on the z-axis where the initial source is located. The expression (21) for the exterior potential on the z-axis (r = z, θ = 0) reduces to
Alternatively, one obtains from (23)
The plots of the exterior potential evaluated on the axis, plotted versus the distance r using (29), are shown in Figure 2 for two different monopole locations. The radius a of the magnetic sphere is taken to be unity while the permeability parameter k is varied. It is seen that the exterior potential on the axis is negative between the sphere and the location of the monopole while it is positive in the region after the source location as seen in Figure 2a and Figure 2b. This implies that the image (or perturbed) terms in the potential expression dominates when the initial monopole is positioned in the close proximity of the magnetic sphere whereas the image contribution is less significant when the magnetic source is away from the sphere. Note that the scalar potential represents the magnetostatic potential energy, a concept similar to that in electrostatics. The magnetostatic (or electrostatic) potential energy is mutually shared by the initial monopole (charge) and the image charges. This may be the reason that the effect of k is a little noticeable on the axis potential.
Particular Locally Generated Magnetostatic Fields
Electromagnetic cloak is a novel phenomena observed in theoretical and experimental studies involving point charges [34,35]. This is based on the understanding that the local field due to a off-centered point charge located near the sphere is that of the constant electrostatic field [34]. The results for such locally generated fields can be achieved by expanding the off-centered charge about the sphere center in a Taylor series leading to a multipole expansion. As mentioned briefly in section 4 (see after equation (17)), each term in the multipole expansion in the neighborhood of the charge/monopole generates local magnetostatic fields around the spherical inclusion. The first and second terms yield locally generated fields due to constant and linear magnetic induction. Thus the analytic solutions for the monopole-magnetic sphere interaction problem derived in the previous section can also be used to study a these local fields induced by the monopole in the vicinity of the magnetic sphere. These solutions may lead to approximate forces for MFM applications as well (see Section 6). In this section, we provide details of the solutions for two locally generated magnetostatic fields (i) Constant magnetic induction; and (ii) Linear magnetic induction fields. Note that the two fields correspond to n = 1 and n = 2 in the infinite series solutions for the monopole-sphere problem given in (16) and (17). It should be emphasized that the constant field solution may also be obtained using two opposite monopole solutions in the presence of a magnetic sphere as illustrated in the introduction. We proceed to demonstrate the locally generated fields solutions via (16) and (17).
Constant magnetic induction
By taking n = 1 in (16) and (17) and defining the constant we obtain
for the exterior phase
for the interior phase of the magnetic sphere. Here the Legendre polynomial P1(μ) = cos θ. This well-known result corresponds to a constant magnetic induction of strength H applied along the z-direction in the presence of a magnetic sphere [2,14]. The image system in the exterior phase for constant magnetic induction consists of a dipole of strength located at the center of the sphere. Note that the strength of the image dipole depends on the permeability parameter k and the radius a. For the sign of the dipole is negative, and for the sign is positive. For the image dipole vanishes. In this case the magnetic permeabilities of the exterior and interior phases coincide. Thus, there is a dipole reversal in the case of a uniform magnetic field applied in the presence of a magnetic sphere.
The potential contour plots for a magnetized sphere placed in a constant external magnetic field are portrayed in Figure 3 for various values of the permeability parameter k. When k = 0, the situation refers to that of a Dirichlet problem for a sphere in electrostatics [13,14]. The potential contours coming from positive infinity go around the sphere and reach negative infinity (see Figure 3a). For k > 0, the contours in exterior and the interior phases exist as seen from Figure 3b, Figure 3c, Figure 3d, Figure 3e and Figure 3f. Two patterns are seen according to k is less than or greater than 0.5. For k < 0.5, the potential contours in the external phase go around the sphere as in the case of k = 0, (Figure 3b and Figure 3c). However, when k > 0.5, the contours in the exterior region bend towards the magnetic sphere and then move away after hitting the spherical surface as shown in Figure 3d, Figure 3e and Figure 3f. The interior contours get denser for k ≥ 0.5. These features are probably due to the dipole reversal in the image solution for the potential expressions. We remark that when k > 1 (Figure 3f), the situation corresponds to negative interior magnetic permeability μi < 0 [36].
Linear magnetic induction
The second term with n = 2 in (16) and (17) leads to the solution for a linear magnetic induction field (also termed as quadrupole field). The magnetic induction vector B0 for this field in the absence of the spherical inclusion has Cartesian components given by
and the corresponding the magnetic scalar potential is
where from (10). The particular solutions for the boundary value problem in this case become
in the exterior phase of the magnetic sphere and
in the interior phase of the spherical inclusion. The Legendre polynomial P2 is given by
In the quadrupole local field, the image system in the exterior phase consists of a magnetic quadrupole of strength located at the center of the sphere. The direction of the quadrupole changes according to and : and vanishes when . Thus, there is a quadrupole reversal for the linear magnetic induction field in the presence of a magnetic sphere.
The potential contours in the exterior and interior phases are plotted in Figure 4, for various k. It is seen that here are 4 different divisions of contours symmetrical about the two coordinate axes in the xy-plane. When k = 0, the contour plots reproduce those in the context of electrostatics as shown in Figure 4a. As k increases from zero, the potential contours start appearing in both phases as can be seen in Figure 4b, Figure 4c, Figure 4d, Figure 4e and Figure 4f. The contours are also symmetrical in the interior phase and have 4 divisions when k > 0. The potential contours get increasingly closer in the region r < a. It appears that the contours cross at the center of the magnetic sphere. This scenario seems to exist for all k > 0. When k > 1, the potential contours show different patterns as shown in Figure 4f and this may be due to the negative permeability of the interior phase [36].
We remark that there are five other combination of x, y, z that lead to linear magnetic induction fields. Their linear combination can be written as
Note that each term in (34) is a solution of Laplace equation. The analytic solutions for these magnetic linear fields can be obtained in a similar way as explained in the preceding paragraphs using a general spherical harmonic expansion [14]. Our particular solutions presented here provides the key idea for the general linear (quadrupole) fields. It is worth a while to point out that the image system in each case will have a quadrupole at the sphere center whose strength depends on the radius a and the permeability parameter k.
Solutions to other locally generated higher order fields can be derived using the infinite series solutions (16) and (17) in a similar fashion. Their local interactions with the magnetized sphere can be analyzed with the corresponding analytical results. In the next section, we focus on the calculation of the interaction force acting on the magnetic sphere in a monopole field.
The Magnetic Interaction Force
It is of great practical interest to determine the force acting on a magnetic sphere placed in the field of a magnetic pole. In the context of superconductivity such forces are termed as levitation forces [3,12,14]. The levitation force exerted on the superconducting sphere due to poles and dipoles have been calculated by many researchers [2,8,9]. We will show later (see below equation (37)) that the superconducting limit (single phase) due to a monopole-sphere configuration is a special case of our result provided in this paper. The force on a sphere due to a circular current loop [2] and their stability [37] are determined in the Meissner state. Recently, Trombley and Palaniappan [11] determined the force acting on the superconducting sphere placed in the field of a straight line current. They found that the expression for the force can be expressed in an integral form involving a logarithmic function. It is also stated that the integral can be evaluated in terms of special functions. In the following, we calculate the interaction force acting on the magnetic sphere due to a magnetic monopole. As will be seen, the force for this configuration can be expressed as a quadrature. Various force representations allow interpretation of qualitative features and approximations as well. In a later section we demonstrate the relevance of our theoretical results in MFM tip modeling using physical units.
Interaction force on a magnetic sphere due to a magnetic monopole
The magnetic interaction force acting on the magnetic sphere of radius a due to the field generated by a magnetic pole can be found from Newton's third law as the inverse of the (more easily calculated) force that the sphere exerts on the monopole. For the magnetic pole located at (0, 0, c), using the approach adopted in [2,26], one can calculate the force from
where, μ0 is the vacuum permeability. The expression Φe - Φ0 can be extracted from the analytic solution (21) or (23), and the suffix outside the square bracket indicates evaluation of quantities at the initial source location point (0, 0, c). Using (23) (or equivalently (21)) in (35), and evaluating the gradient of the indicated function at the initial source point, one obtains
As seen from (36) the force due to a monopole located in the vicinity of a magnetic sphere is expressed as a quadrature. The interaction force has its component along the z-axis on which the initial monopole is situated. It is clear from the above expression that the force depends on the magnetic permeability ratio k (0 ≤ k ≤ 1), the radius a and the center to monopole distance c. The integral in (36) can be evaluated in terms of the slowly convergent hypergeometric functions [30,31] for all . It may be useful to write the expression for the interaction force, after using integration by parts twice, in the form
The first term inside the square brackets is the force acting on a superconducting sphere due to a monopole [2]. The first two terms together (without the factor (1 - k)) represent the force on a magnetically conducting sphere (corresponding to equation (24)), an electrostatic analogue. Observe that the integral term vanishes for k = 0 (electrical case) and k = 1 (ideal superconducting situation). It can be shown that the integral in (37) can be evaluated in terms of elementary functions for k = 0.25, 0.75 and so on.
In order to highlight some qualitative features of the magnetic interaction force we use the normalized form of (37) with a normalization factor of The normalized force component versus the non-dimensional magnetic source-sphere separation c/a is plotted in Figure 5a for various values of the dimensionless permeability parameter k. It is seen that the magnitude of the force is positive in the interval and is negative when The two scenarios in the general case indicate the attractive and repulsive nature of the interaction force with respect to c/a. Since and we see from Figure 5a that the force is
• positive (attractive) for or that is when the exterior magnetic permeability is less than the permeability inside the magnetic sphere r = a
• negative (repulsive) for or that is when the magnetic permeability in the exterior region is greater than that of the interior permeability of the magnetic sphere
Furthermore, the interaction force approaches zero as the source-sphere separation c/a increases for all k. Therefore, the interacting is stronger when the monopole is closer and weaker when it is away from the magnetic sphere.
Numerical evaluation indicates that the contribution from the integral term in (37) to the overall normalized force is too little and can be neglected for practically large source-sphere separations. For a very close separation the situation is that of a monopole-planar interface for which the force can be evaluated using (26) without using the integral. Therefore, for all reasonable source-sphere separations, one may approximate the interaction force by
The approximate force given in (38), normalized by is plotted versus c/a and is displayed in Figure 5b. It is clear that, qualitatively, the trend is very similar to the exact expression plotted in Figure 5a illustrating that the expression given in (38) can provide a very good approximation for the magnetic interaction force due to a magnetic monopole in the presence of a magnetic sphere.
It is also of interest to provide another approximation for the interaction force using the infinite series solution for the magnetostatic potential given in (16) and the locally generated magnetic fields results presented in section 5. Application of the force formula (35) to (16) yields the following expression for the force in an infinite series form:
The infinite series form of the magnetic interaction force given above in (39) is equivalent to the closed form expression (37). Taking the first two terms of the series in (39) results in an approximation
Note that the first term in the square brackets in (40) is due to the locally generated constant magnetic induction field discussed in the subsection 5.1 (with as defined there). The second term corresponds to the linear magnetic induction field described in the subsection 5.2 (with ). The exterior potential expressions (30) and (32) when substituted into the force formula (35) yields the first and second terms in (40), respectively. Thus, the interaction force can also be approximated by dipole and quadrupole solutions induced by locally generated magnetic fields due to a magnetic source. Higher order multipole contributions may be added from the infinite series in (39) to obtain improved approximations. We return to (40) in our quantitative discussion of the force in the next section.
MFM Tip Modeling and Numerical Force Calculations
Let us now turn our attention on the MFM tip modeling using our monopole-magnetic sphere results in order to enunciate the physical relevance. MFM is one of the most preferred analytical tool whenever the near surface magnetic field variation of a magnetic sample is of interest [38,39]. High resolution results can be achieved with tip radius ranging from 10-100 nm for sufficiently strong magnetic field variations. As pointed out in [25,38], the MFM tip can be treated as a monopole under certain conditions. Therefore, we model the MFM tip simply by a magnetic charge m (monopole) in the vicinity of a magnetic sphere of radius a. The correct size of the charge is taken to be and is chosen in such a way that m has the same units as the flux as explained in [25]. Here M is the magnetization in A/m and r0 is the tip radius in nm. Then the approximate expression for the magnetic interaction force component given in (38) can be recast in the form
where is the MFM tip to sphere radius separation ratio. To predict a magnetic tip yielding forces high enough to be measured by a MFM we select two hard magnetic materials of types Cobalt-Platinum Pt76.7CO23.3 and Alnico 5 (Alcomax) Fe51Al8Ni14Co24Cu3 with high values of spontaneous magnetizations [25]. The former type has M = 5.13 × 105 A/m and the latter category has the magnetization M as high as 10.5×105 A/m (see [25]) with the vacuum permeability μ0 = 4π10-7 N/A2. The tip radius is chosen to be r0 = 100 nm, while = 0.1 and x = 1.5 in our computations. For this set of input data the computed numerical values of the force (in Newton), calculated using (41), for k = 0, 0.2, 0.4, 0.6, 0.8, 1 are provided in Table 1.
First, the numerical values of the approximate interaction force given in Table 1 are in complete agreement with the qualitative features discussed in section 6. Next, if the tip is located at a distance of 1.5a then the the force for Alnico 5 type magnetic materials is higher than that of the PtCo type magnets with the radii ratio For intermediate values of the non-dimensional permeability ratio k, that is for 0 < k < 1, our results predict forces as large as 10-12N and 10-11N in the case of PtCo and Alnico 5 type hard magnetic materials, respectively (see Table 1). Our estimated values for the force lie between those for HTSC models [25] and dipole-superconducting configuration with Nd-Fe-B magnets [3].
Using the MFM tip modeling discussed above the multipole approximated force component expression (40), in physical units, can be put in the form
For k = 0.2 the magnetic interaction force using the approximation given in (42) yields a force of 5.9080 × 10-12N and 2.4750 × 10-11N for PtCo and Alnico 5 type hard magnetic materials, respectively. Comparison with those given in Table 1 (see the second row in the table corresponding to k = 0.2) implies that the expression (42), which is based on dipole and quadrupole solutions for the locally generated fields, can be a crude approximation for the force due to MFM tip-magnetic sphere configurations for these hard materials. Addition of higher order multipole contributions may lead to an improved approximation using (42). Also, the precision using (42) (in comparison with (41)) may be improved for larger tip-sphere separations. In all cases our monopole tip model yields forces measurable by a Magnetic Force Microscope.
Conclusion
Theoretical results for the interaction between a magnetic monopole and a magnetic sphere have been presented in this paper. Under the framework of Maxwell-Maxwell theory, the two-phase mathematical boundary value problem with mixed conditions at the spherical inclusion is modeled and solved with the use of the scalar magnetic potentials Φe(r, θ) and Φi(r, θ) in the exterior (r > a, with magnetic permeability μe) and in the interior (r < a, with magnetic permeability μi) regions, respectively. An alternative form of the analytical solution given here (equation (23)) allows a new interpretation of the image system as a distribution of dipoles between the sphere center and the Kelvin's inverse point. The two key non-dimensional parameters, among others, are the permeability parameter and the monopole-sphere separation ratio The magnetic interaction force, an important physical quantity, acting on the spherical inclusion is found as a quadrature involving these parameters. It is demonstrated that an alternative form for the force, obtained via integration by parts, leads to an expression that contains electrostatic and superconducting forces along with a integral term and is convenient for numerical evaluations. Smaller contribution of the latter integral term allows an approximate analytic expression for the interaction force that is qualitatively very similar to the exact expression. In general, the magnetic force is positive (attractive) or negative (repulsive) according to or respectively. Weak and strong interactions are predicted for larger and closer momopole-sphere separations.
By treating the Magnetic Force Microscope tip as a monopole and the sphere as a magnetic material of a given type, the force measurements in physical units are recorded. Our theoretical results predict forces as high as 10-12 N for PtCo (Cobalt-Platinum) and 10-11 for Alnico 5 (Alcomax) types of magnetic materials for the tip radius of 100 nm and a tip-to-sphere separation ratio of 1.5 when 0 < k < 1. These estimates are smaller than the calculated values for a monopole-half-space high temperature superconductors (HTSC) [25], but higher than that of a dipole-superconductor sphere models [3]. Higher magnitude force measurements are possible for closer tip-to-sphere separations. The predicted forces are high enough and fairly reasonable to be measured by a MFM. The estimates provided here can also be utilized for a direct comparison with existing [25] and future experimental data.
The point monopole (magnetic source) interaction with a magnetic sphere results determined here provides the fundamental solutions (Green's functions) for the Laplace equation in the two regions with mixed-type boundary conditions. By linear superposition, the magnetic fields and the interaction forces can then be constructed for extended sources in the presence of spherical inclusions. Hence, the work reported here has provided necessary extension of the results for the superconducting sphere [2,3,10,11] that are fundamental to the advancement of MFM models and designs. Further, the our theoretical results have clearly laid necessary groundwork for modeling the tip as higher order multipoles (dipoles, quadrupoles, etc.) and predicting interactions and forces. Adopting the current approach to those physical problems may lead to significant contributions towards improved understanding of MFM point tip modeling with a variety of magnetic materials.