International Journal of Metallurgy and Metal Physics
(ISSN: 2631-5076)
Volume 5, Issue 4
Research Article
DOI: 10.35840/2631-5076/9261
Experimental Verification and Application of Computational Thermodynamic, Kinetic, and Solidification Modeling to Gas Atomized Al Powder
Bryer C Sousa1*, Victor K Champagne Jr2, Aaron T Nardi2 and Danielle L Cote1
Figures
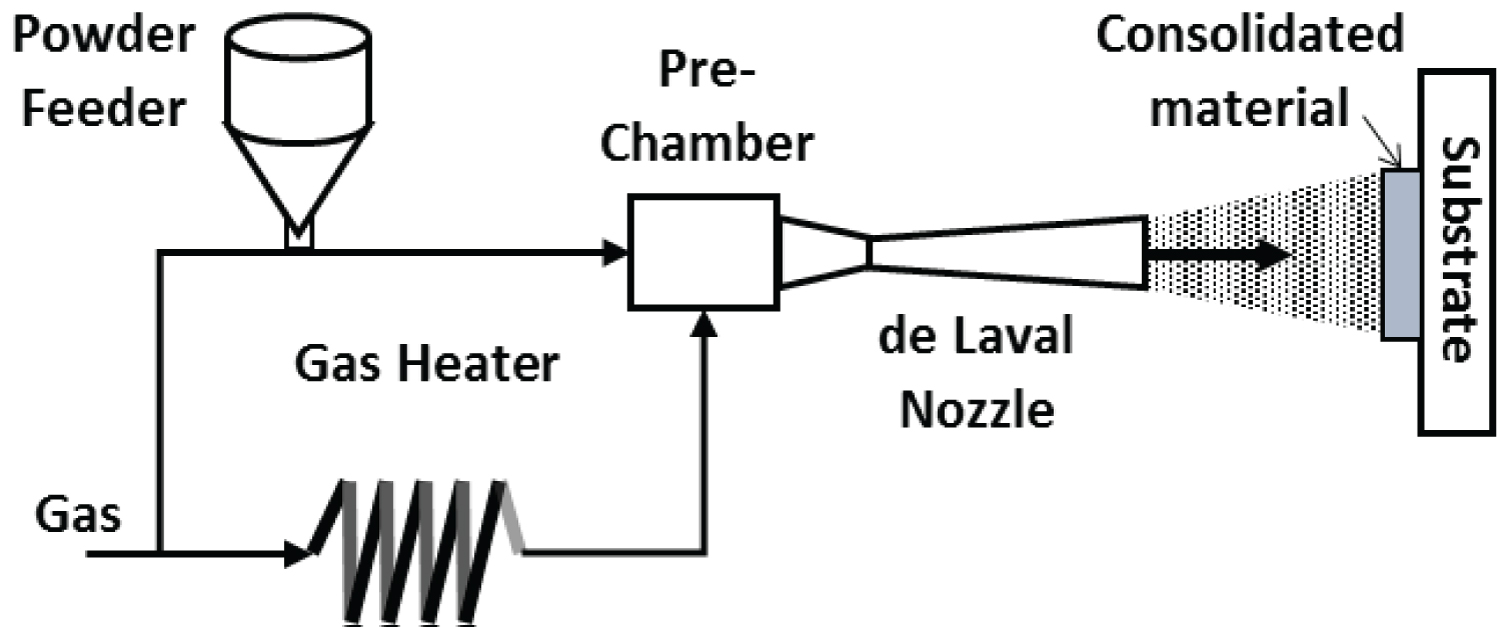
Figure 1: Schematic of a common configuration....
Schematic of a common configuration of the cold spray process [7].
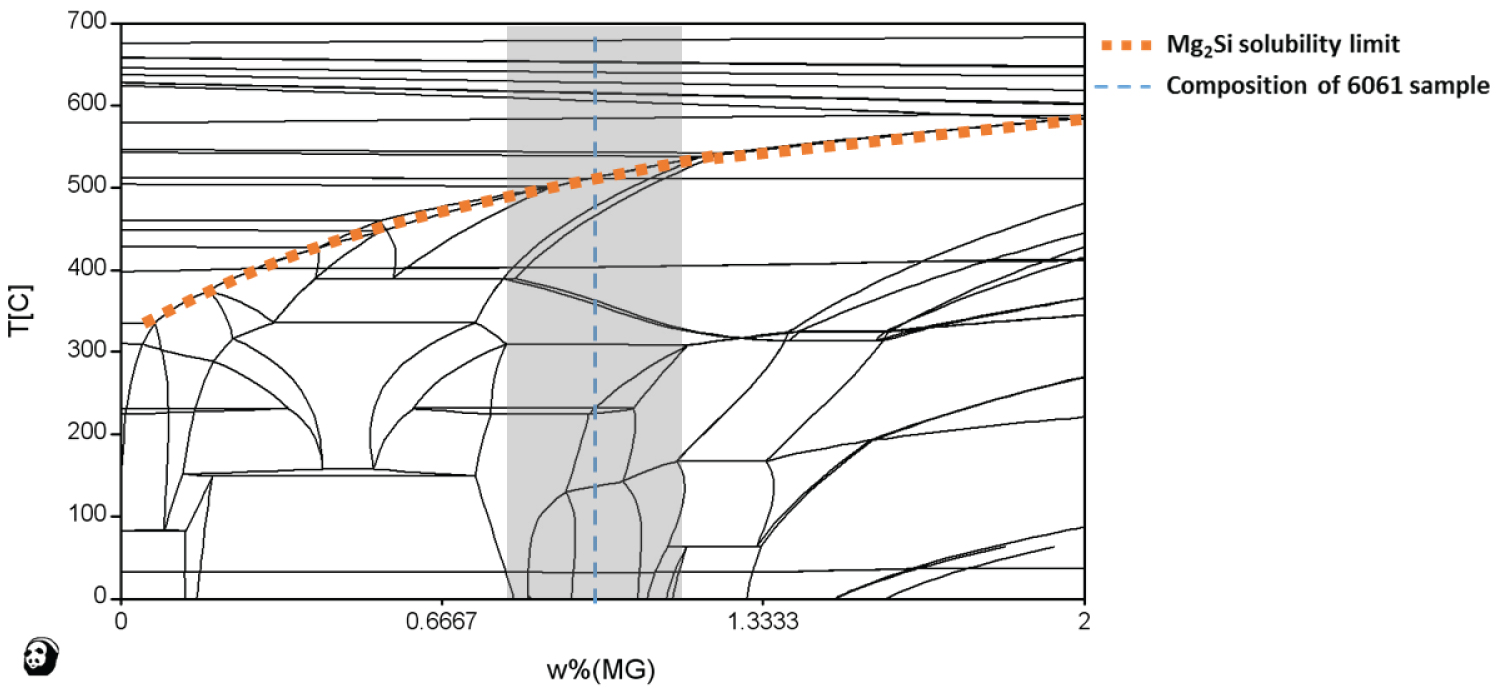
Figure 3: Isopleth of Al 6061 created in Pandat....
Isopleth of Al 6061 created in Pandat software showing thermodynamically predicted equilibrium phases. The blue vertical dashed line represents the experimentally measured Mg in a batch of Al 6061 powder used in the experiments, 1.0 wt%. The shaded area represents the allowable range of Mg in Al 6061, 0.8-1.2 wt%. The orange horizontal dashed line represents the solubility limit of Mg2Si in the alloy.

Figure 4: Equilibrium phase fractions in Al 6061....
Equilibrium phase fractions in Al 6061 as a function of temperature at the composition given by the blue vertical dashed line from Figure 3 (1.0 wt% Mg). Phases with phase fractions not exceeding 0.25 wt% are not shown.

Figure 5: STEM image of a gas atomized Al 6061 powder....
STEM image of a gas atomized Al 6061 powder particle showing different precipitates that have formed at the grain boundaries during solidification.
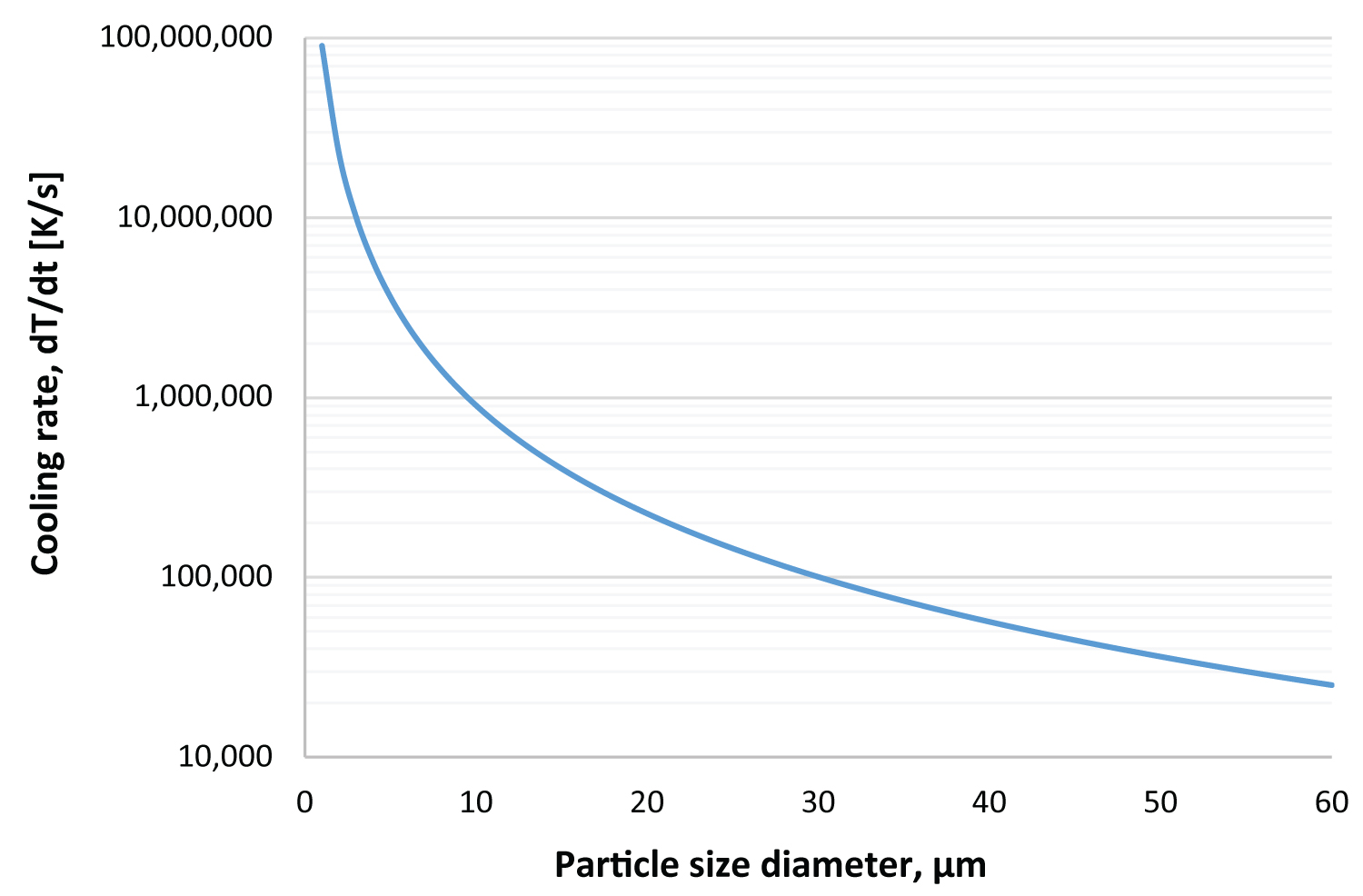
Figure 6: Cooling curve resulting from the simplified....
Cooling curve resulting from the simplified solidification model given by Equation 2 for Al 6061 in argon atomizing gas.

Figure 7: SEM of etched and unmounted Al 6061 powder...
SEM of etched and unmounted Al 6061 powder particles visually showing the relationship between particle size, microstructural feature size, and cooling rate.
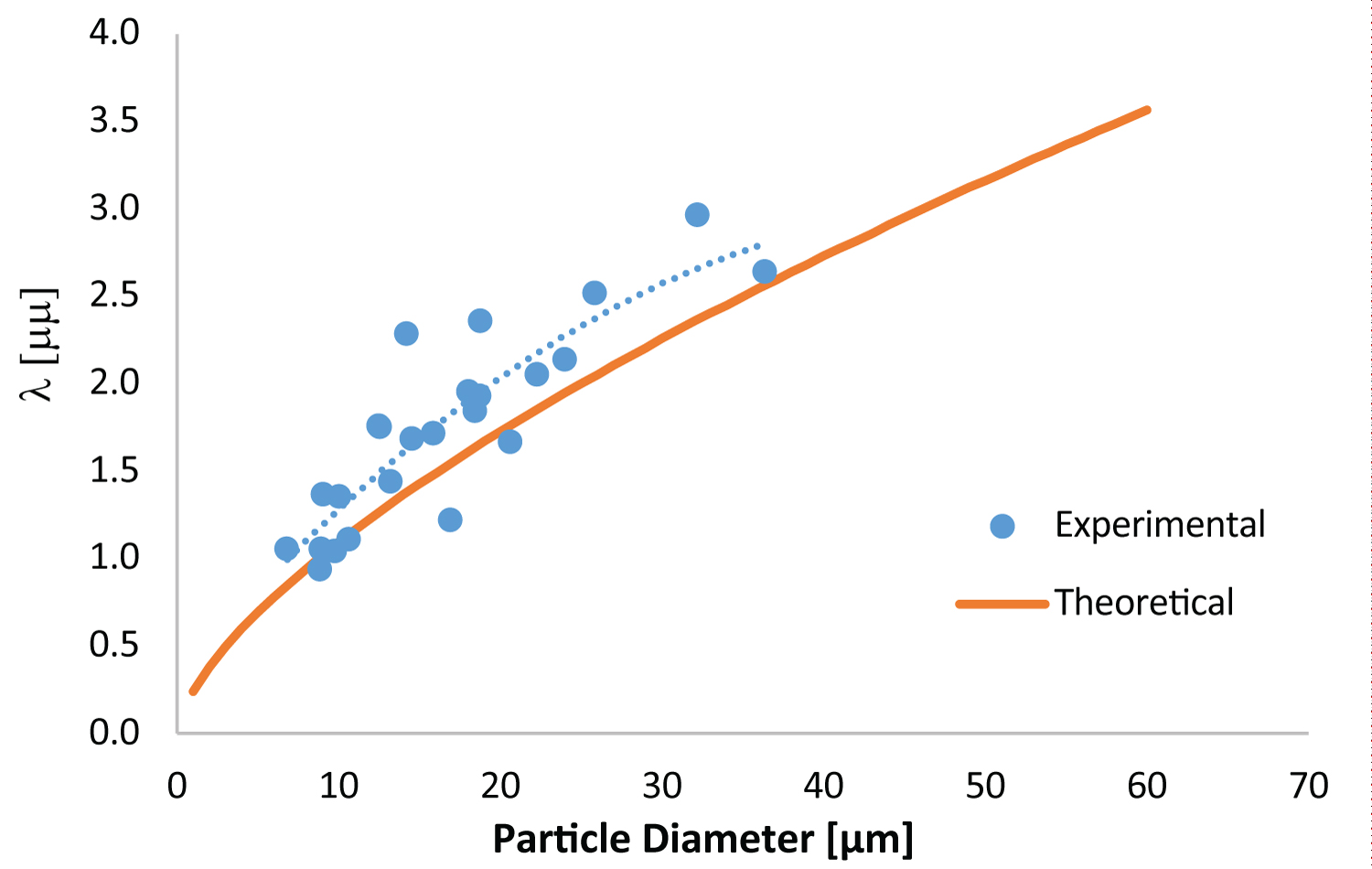
Figure 8: Theoretical and experimental relationship...
Theoretical and experimental relationship between feature size and powder particle diameter.
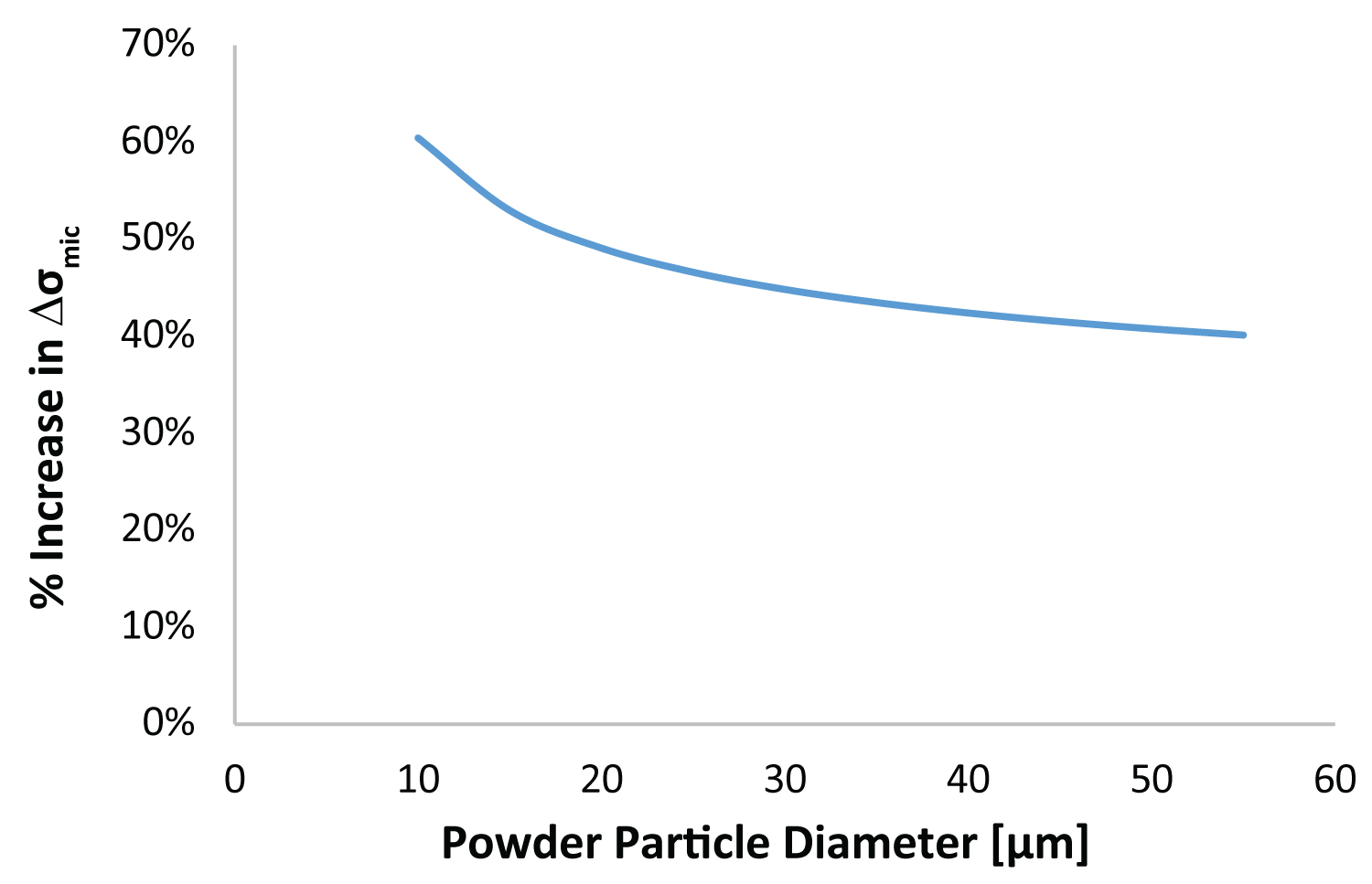
Figure 9: The increase in the intrinsic strength...
The increase in the intrinsic strength predictions of the powder particles due to microstructural feature size, as calculated in the Hall-Petch relationship in Equation 5.
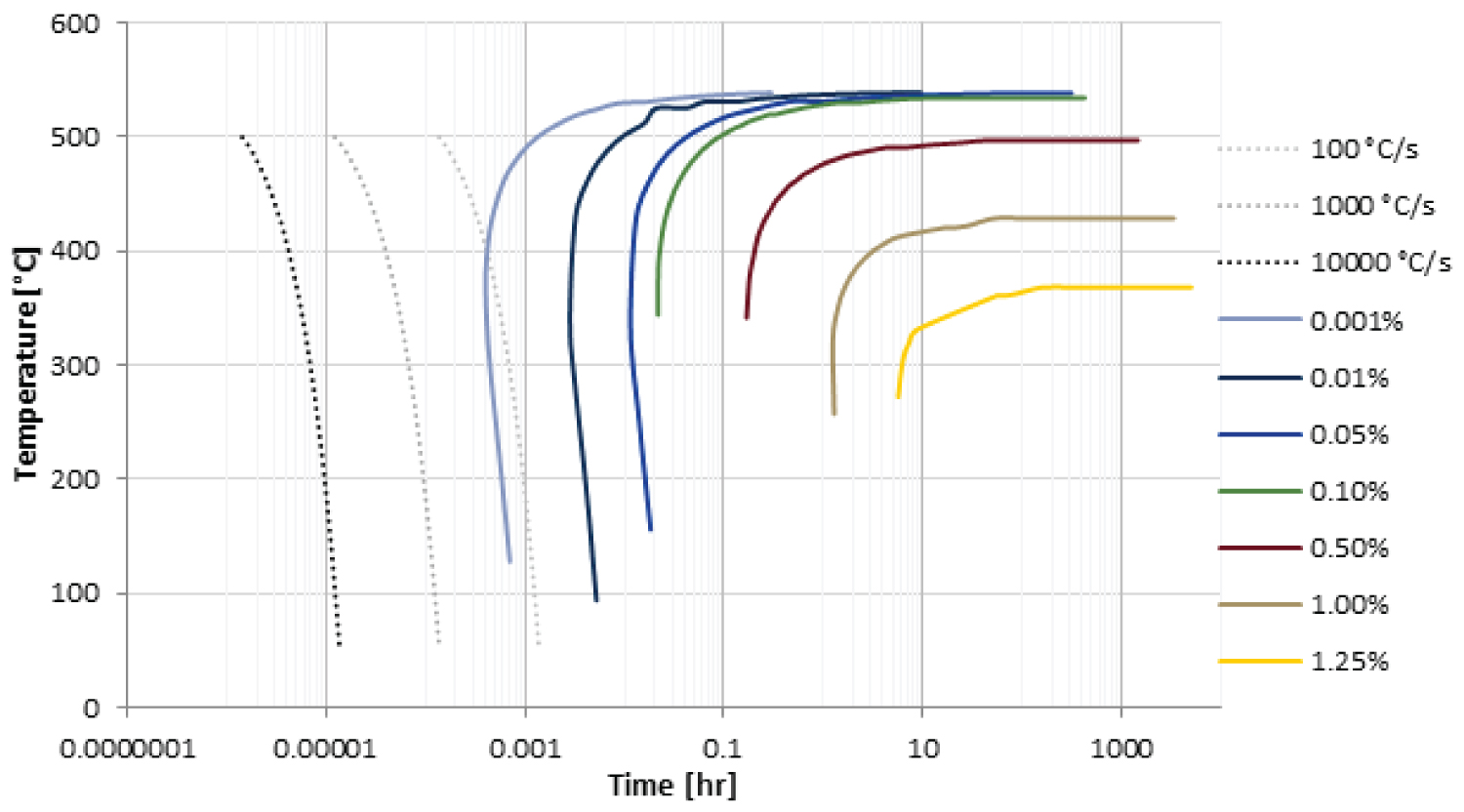
Figure 10: Continuous cooling transformation curves...
Continuous cooling transformation curves for the formation of Mg2Si in Al 6061 given in mass percent of the predicted equilibrium amount. Powder solidification models for the powders used in this study show cooling rates around 1 × 104 to 1 × 105 ℃/s, which would result in no Mg2Si phase forming during solidification.
References
- Champagne VK (2007) The cold spray materials deposition process: Fundamentals and applications. Woodhead Publishing Limited, Fl, Boca Raton, USA.
- Dykhuizen RC, Smith MF (1998) Gas dynamic principles of cold spray. Journal of Thermal Spray Technology 7: 205-212.
- Irissou E, Legoux JG, Ryabinin AN, Jodoin B, Moreau C (2008) Review on cold spray process and technology: Part I-Intellectual property. Journal of Thermal Spray Technology 17: 495-516.
- Stoltenhoff T, Kreye H, Richter HJ (2002) An analysis of the cold spray process and its coatings. Journal of Thermal Spray Technology 11: 542-550.
- Champagne VK, Leyman PF, Helfritch DJ (2008) Magnesium repair by cold spray. Plating and Surface Finishing 95: 34.
- Champagne VK (2013) Innovations in DOD cold spray applications. The Defense Manufacturing Conference And Expo, Fl, Orlando, USA.
- Belsito D, Mcnally B, Bassett L, Champagne VK, Sisson RD (2013) Through-process modeling for cold spray alloy optimization. Proceedings MS&T.
- Allison J, Collins P, Spanos G (2011) From processing to properties: Through-process modeling of aluminum sheet fabrication. In: Proceedings of the 1st world congress on Integrated Computational Materials Engineering (ICME). John Wiley & Sons, Inc, Hoboken, NJ, USA, 9-17.
- Crumbach M, Goerdeler M, Gottstein G, Neumann L, Aretz H, et al. (2004) Through- process texture modelling of aluminium alloys. Modelling and Simulation in Materials Science and Engineering 12: S1-S18.
- Engler O, Lochte L, Hirsch J (2007) Through-process simulation of texture and properties during the thermomechanical processing of aluminium sheets. Acta Materialia 55: 5449-5463.
- Dørum C, Laukli HI, Hopperstad OS (2009) Through-process numerical simulations of the structural behaviour of Al-Si die-castings. Computational Materials Science 46: 100-111.
- Champagne VK, Helfritch DJ, Dinavahi SPG, Leyman PF (2011) Theoretical and experimental particle velocity in cold spray. Journal of Thermal Spray Technology 20: 425-431.
- Bassett L (2014) Simulating particle impact to predict the mechanical properties of cold sprayed alloys. The Minerals Metals And Materials Society, San Diego, USA.
- Zheng BL, Lin YJ, Zhou YZ, Lavernia EJ (2009) Gas atomization of amorphous aluminum powder: Part II. Experimental investigation. Metallurgical and Materials Transactions B 40: 995-1004.
- Zheng BL, Lin YJ, Zhou YZ, Lavernia EJ (2009) Gas atomization of amorphous aluminum: Part I. Thermal behavior calculations. Metallurgical and Materials Transactions B 40: 768-778.
- Su YH, Tsao CYA (1997) Modeling of solidification of molten metal droplet during atomization. Metallurgical and Materials Transactions B 28: 1249-1255.
- German RM (1994) Powder metallurgy science. Metal Powder Industries Federation, Princeton, USA.
- Boettinger WJ, Bendersky L, Early JG (1986) An analysis of the microstructure of rapidly solidified Al-8 Wt Pct Fe Powder. Metallurgical Transactions A 17: 781-790.
- Couper MJ (1984) Microstructure of rapidly solidified aluminium alloy powders.
- Sakaguchi Y, Harada T, Kuji T (1994) Microstructural studies of Nd-Fe-B powders produced by gas atomization. Materials Science and Engineering: A 181-182: 1232-1236.
- Osório WR, Spinelli JE, Afonso CRM, Peixoto LC, Garcia A (2012) Electrochemical corrosion behavior of gas atomized Al-Ni alloy powders. Electrochimica Acta 69: 371-378.
- He SW, Liu Y, Guo S (2009) Cooling rate calculation of non-equilibrium aluminum alloy powders prepared by gas atomization. Rare Metal Materials and Engineering 38: 353-356.
- Baricco M, Bosco E, Olivetti E, Palumbo M, Rizzi P, et al. (2004) Rapid solidification of alloys. International Journal of Materials & Product Technology 20: 358-376.
- Saunders N (2004) The modelling of stable and metastable phase formation in multi- component al-alloys. Proceedings of the 9th International Conference on Aluminium Alloys, 96-106.
- Yu J, Li X (2011) Modelling of the precipitated phases and properties of Al-Zn-Mg-Cu alloys. Journal of Phase Equilibria and Diffusion 32: 350-360.
- Army US (2007) Military apecification: MIL-DTL-32262 Detail Specification Armor Plate, Aluminum Alloy, Unweldable Applique 6061.
Author Details
Bryer C Sousa1*, Victor K Champagne Jr2, Aaron T Nardi2 and Danielle L Cote1
1Worcester Polytechnic Institute, USA
2US Army Research Laboratory, Aberdeen Proving Ground, USA
Corresponding author
Bryer C Sousa, Worcester Polytechnic Institute, 100 Institute Road, Worcester, MA 01609, USA.
Accepted: October 21, 2020 | Published Online: October 23, 2020
Citation: Sousa BC, Champagne VK, Nardi AT, Cote DL (2020) Experimental Verification and Application of Computational Thermodynamic, Kinetic, and Solidification Modeling to Gas Atomized Al Powder. Int J Metall Met Phys 5:061
Copyright: © 2020 Sousa BC, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In the majority of powder consolidation techniques, powder properties are disregarded due to particle melting during processing. In the solid-state cold spray process, however, powder particles significantly affect the mechanical properties of the consolidated material. Therefore, it is essential to fully characterize the powder properties in order to better predict properties of the cold sprayed deposit. An additive strength model is used to predict the powder particles' strength and hardness as a function of diameter. It is based on thermodynamic, kinetic, and solidification principles and considers contributions to the overall particle strength by solid solution strengthening, microstructural feature size, and precipitation/dispersion strengthening. This additive model quantifies the first two stages of the cold spray through-process model (TPM).
The stages of the TPM are Powder Production, Powder Preparation, Cold Spray Parameters, Particle Impact, and Post-Processing. This paper focuses on the modeling and experimental works on the Powder Production stage of the TPM, in particular the strength contribution from microstructural feature size. For as-received gas atomized Al 6061 powder the increase to the intrinsic strength of the material due to the particles' microstructural feature size is between 60% and 40% for 10 um to 55 um particles, respectively. This paper compares theoretical predictions with experimental findings for the purpose of verification.
Introduction
The cold spray process is an important repair technology for military applications because of its ability to produce lightweight alloys that have high strength, durability, and toughness while maintaining low porosity [1]. In order to maximize the benefits and broaden the variety of applications of the cold spray process, a through-process model (TPM) was developed to allow for the prediction of cold sprayed material properties as a function of the material used and processing parameters. Synergy between modeling and experimental results was crucial in developing this model and is discussed in the following sections.
Cold spray process
The cold spray process is a material-deposition technique resulting in the consolidation of powder particles onto a suitable substrate, thus forming a coating or near net shaped part. A schematic of the process is shown in Figure 1. Powder particles, typically between 5 and 100 um in diameter, are injected into a heated inert gas stream. The carrier gas is accelerated to supersonic velocities through a de Laval nozzle. The particles are then ejected from the nozzle onto a substrate at high velocities, plastically deform upon impact and adhere to the substrate. As this process continues, deposited layers additively create a consolidated material [1-4].
An important military application of the cold spray process is to repair high cost magnesium and aluminum aerospace parts. Examples can be found in [5]. Cold spray is used for dimensional restoration of worn or corroded parts and is accomplished by spraying directly onto a part and building up the required thickness without the concern of forming a heat affected zone, as is formed with welding and/or other thermal spray techniques. Additionally, bulk materials and even near net shaped parts, have been produced by the cold spray process by spraying directly onto a mold. Shaped charged liners, projectile bodies, sputter targets, and donor tubes for the explosive cladding process have been produced in this manner [6,7] (Figure 1).
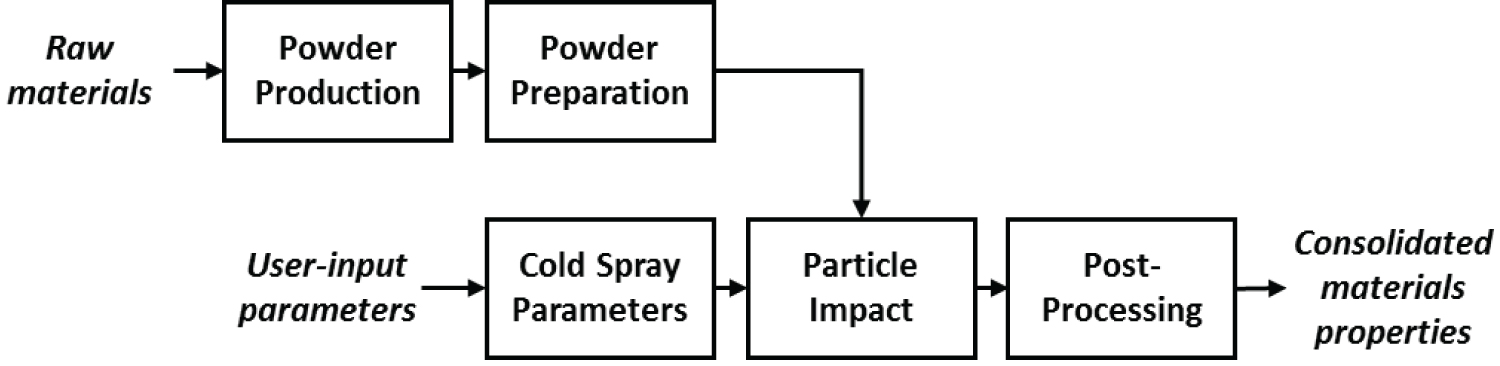
Through-process model
Through-process models have been used to model metal processing techniques, specifically for Al sheet fabrication and die castings [8-11]. In order to completely model and predict the properties of the cold sprayed deposit, property predictions of the feedstock powder are needed, as well as the effects of processing and particle-substrate impact parameters. Each of these stages were modeled independently, then integrated into a TPM. This holistic approach allows for the properties of the cold sprayed deposit to be predicted based on starting material and process parameters. Conversely, if there are mechanical property specifications, the model can be used to suggest starting material and process parameters to produce materials with the desired properties. The TPM is represented schematically in Figure 2.
The top row of steps involves modeling the powder material used as feedstock in the cold spray process. Cold spray is a solid state process in which a significant amount of plastic deformation and grain refinement can occur and the microstructure of the feedstock powder largely determines the microstructure in the deposit [7], fortifying the importance of the powder models.
The first of the powder stages of the TPM, Powder Production, predicts the microstructure and mechanical properties, yield strength and hardness, of the powder particles as a function of particle diameter; specifically, for aluminum powders produced by the gas atomization process. The Powder Preparation stage accounts for any pre-treatments which the powder undergoes after atomization and before being sprayed. The Cold Spray Parameters stage considers processing parameters such as gas temperature, pressure, flow rates, and composition [12]. These parameters, in addition to the powder properties, will be received as input into the Particle Impact stage. In this stage, ABAQUS/Explicit axisymmetric and three-dimensional models were used to predict system behavior upon particle impact based on processing parameters, such as impact velocity, particle temperature, and substrate temperature [13]. The final stage of the TPM is an optional Post-Processing step, considering effects of heat treatment and/or thermochemical surface treatments on the cold sprayed deposit.
Models have been developed for powders produced by gas atomization [14-16]. Development of cold spray process and particle impact models is ongoing and is included in the TPM. Modeling the pre-processing procedures of powders, as well as post-processing treatment models of cold sprayed materials are lacking. Further, there is a current disconnect among existing models of various stages shown in Figure 2. Development of these models and integration of all five models is the goal of the cold spray TPM.
To integrate the powder stages into the Particle Impact model, represented by the schematic in Figure 2, an additive strength model is employed. Contributions to the overall powder particle strength as a function of particle size diameter is quantified by the equation,
Where , is the intrinsic strength of the material, is the contribution from solid solution strengthening, is the contribution from microstructural feature size, and is the dispersion and precipitation strengthening contribution.
Powder properties are especially important in modeling the solid-state cold spray process because, unlike other powder consolidation techniques where the powder particles are melted, the powder properties directly influence the deposited material properties. This paper focuses on the modeling and experimental work on the Powder Production stage in order to quantify the microstructure for the TPM. This stage is vital to the accurate predictions of the cold sprayed deposit properties. Specifically, the phases and microstructural grain size were computationally predicted and experimentally verified.
Materials and Methods
Thermodynamic models
The first step in modeling the microstructure of the powder particles was to determine the equilibrium phases present. Commercially available thermodynamic software, Thermo-Calc, was used to predict these phases using the CALPHAD (calculation of phase diagrams) approach. This approach utilizes the minimization of Gibbs free energy to yield the most thermodynamically stable phases, which are those present under equilibrium conditions. Results are depicted in the form of isopleths, and further quantification of the isopleths can be made, producing phase fractions of equilibrium phases present as a function of temperature and composition.
The results of these predictive models were compared to experimental characterization using scanning electron microscopy (SEM), transmission electron microscopy (TEM), and energy dispersive spectroscopy (EDS), discussed in the Thermodynamic Model Results section.
Solidification model
Due to the small size and therefore extremely rapid solidification rates of powder particles, standard solidification models were not used. Particle cooling rate has a significant effect on the microstructure of the powder particles [17-20]. This subsequently determines the powder particles' material and mechanical properties and is therefore important as input into kinetic models, discussed below, which consider time-dependency. A rudimentary model to determine the cooling rate of the powder particles during formation via gas atomization was created.
The majority of Al powders used in the cold spray processing performed at the Army Research Laboratory and their affiliates were formed by the gas atomization process, including the powders studied in this work. In gas atomization, a metal melt contacts a high velocity gas stream resulting in the breakup of the melt into small particles. The particles solidify as they travel through the atomization chamber and are collected as solidified powder particles [21].
A simplified heat transfer model for powder particle solidification during the gas atomization process was presented by He, et al. [22], making the assumptions of Newtonian heat flow and neglecting the negligible heat loss to radiation and internal conduction. The Biot number for the powder particles was calculated for various diameters and were all < < 0.1, validating the assumption of negligible internal thermal conduction. The resulting equation is formed upon the assumption that the relative velocity between particle and atomizing gas approaches zero,
Regarding the determination of the thermophysical properties, Equation 2, the molten droplet properties were calculated using JMatPro software as a function of temperature. The thermal conductivity of the argon gas was generated using GRANTA CES EduPack software.
The relationship between secondary dendrite arm spacing and cooling rate has been established by the following equation, and has been experimentally verified for numerous alloy systems, referenced in [14],
Where is the secondary dendrite arm spacing, and n are alloy system-dependent constants, T is the droplet temperature, t is time; is therefore the cooling rate of the droplet. In the case of powder particles, the microstructure may yield grains, cellular units, dendrites, or an amorphous structure depending on composition, particle size, and cooling rate. In this work, and in Equation 3, the secondary dendrite arm spacing refers to these "features." as a function of initial cooling rate of the melt data was available from JMatPro. Data for Al 6061 was plotted and fit to a power law curve to determine the constants and n to be 100.99 and 0.33, respectively.
With this data, feature size can be experimentally measured in particles that contain and exhibit grains, cells, or dendrites to experimentally calculate cooling rates. Not all particles, however, form these features. Particles that solidify at very rapid cooling rates form amorphous particles, also noted by [15,17,23]. Since particle cooling rate is directly proportional to particle size, with smaller particles cooling more rapidly, the smallest particles are those which form amorphously. Dendrites only form with relatively slow cooling rates, and after a recalescence stage. These are the particles for which feature size can be measured, and these "slow" cooling rates can be estimated.
As previously mentioned, the cooling rate of each powder particle affects its resulting microstructure. Finer microstructural sizes result from more rapidly cooling particles. Since cooling rate is a direct function of powder size, the microstructural feature size also varies with powder particle size, though the dependency of microstructural feature size is stronger on cooling rate than powder size due to varying degrees of undercooling [20]. Despite the variation in undercooling between particles of equal size adding a degree of variability in actual cooling rate and powder particle size, there is still a strong relationship between powder particle size and microstructural feature size.
Combining Equations 2 and 3, an equation for microstructural feature size as a function of powder particle size can be determined,
To quantify the contribution of this microstructural feature size to the strength of the powder particles from Equation 1, the Hall-Petch relationship is used,
Where and are the yield strength and intrinsic yield strength of the material, respectively, and k is a material constant.
The relationship of microstructural feature size, powder particle size, and cooling rate is verified experimentally in the Solidification Model Results section. The additional contribution terms in Equation 1, solid solution strengthening, and precipitation/dispersion strengthening, are only calculated after the Powder Preparation stage and are therefore not quantified in this paper.
Kinetic models
The thermodynamic models presented earlier predict equilibrium conditions, which do not likely represent all of the actual phases present in the powder particles upon solidification due to their extremely high cooling rates, calculated in the previous section. Therefore, kinetic consideration must be given.
Sente Software's JMatPro and Thermo-Calc's software TC-PRISMA were used to perform the kinetic calculations, and are widely used in the field [24,25]. Calculations include the fraction of secondary phases formed during solidification, displayed as continuous cooling transformation (CCT) curves.
Experimental
Gas atomized aluminum alloy 6061 powder was characterized in order to verify results from the predictive models. The composition is shown in Table 1 as determined by direct current plasma emission spectroscopy. A thin foil from an approximately 20 um size powder particle was prepared by a FEI 200 TEM focused ion beam (FIB) and viewed in an FEI Technai F30 transmission electron microscope. EDAX Sapphire EDS with a Si(Li) detector was used to verify the composition of phases observed in the microstructure. A sampling of loose powder was mounted onto copper tape, dipped into a 0.5% hydrofluoric acid and distilled water solution and viewed in a JSM-7000FX SEM to allow for measurements of particle and microstructural feature size.
Results
Thermodynamic models
An isopleth of Al 6061 is shown in Figure 3. Due to the large number of equilibrium phases present, the phase names are not shown on the isopleth in this paper, but each line represents a phase boundary. The blue dashed vertical line at 1.0 wt% Mg represents the amount of magnesium in the Al 6061 sample, given in Table 1. The shaded region in Figure 3 between 0.8 wt% Mg and 1.2 wt% Mg represents the allowable range of Mg in Al 6061 according to military specification [26]. It was noted that despite an alloying having a composition within the specification range, several different phases may actually be present, depending on the composition of the particular batch of alloys received. Finally, the orange horizontal dashed line represents the solubility limit of Mg2Si in the alloy.
Using the same thermodynamic principles, diagrams showing equilibrium phase fractions as a function of temperature were created for Al 6061, as shown in Figure 4. An FCC matrix is the primary phase and is out of viewing range over the majority of the temperature range due to the scale of the diagram. The major secondary phases predicted are Mg2Si, Al7Cu2Fe, and alpha (Al47(Fe,Mn,Cr)11Si5).
A STEM image of an Al 6061 powder particle is shown in Figure 5. Individual grains within the powder particle are observed, which are outlined by precipitates at the grain boundaries. Three secondary phases were found and analyzed by XEDS. The darkest phase contained Mg and Si, represented by the solid arrow in Figure 5. The white and light gray phases were Fe-containing, indicated by the dashed arrows. These phases correspond to the major secondary phases that are predicted by the thermodynamic models, shown in Figure 4: Mg2Si and Fe-containing phases, α (Al47(Fe,Mn,Cr)11Si5) and Al7Cu2Fe. The composition from XEDS of the Fe-containing phases does not perfectly correlate with the stoichiometry predicted by the thermodynamic models.
Additional analysis of the Mg2Si phase revealed a 2:1 Mg:Si stoichiometry without the equilibrium Mg2Si crystal structure. This work will be presented separately. The phases present in the gas atomized powder may be meta-stable phases formed by the rapid cooling rate. This verifies the need for the time-dependent kinetic models.
Solidification models
In this work, Al 6061 particles between 10 um and 50 um diameters were studied. Using Equation 2, depicted in Figure 6, cooling rates between 1.0 × 106 ℃/s and 3.5 × 104 ℃/s were predicted. These rates are in good agreement with gas atomization cooling rate predictions [15,17,23].
The loose powder was viewed in the SEM in order to verify the results of the solidification model. Based on the powder particle size of the powders shown in Figure 7, cooling rates were calculated using Equation 2, as shown in Figure 6. The individual powder particles are shown along the calculated cooling rate gradient. The experimentally calculated cooling rates agree with predicted cooling rates for gas atomized particles [15,17,23]. As the experimentally calculated cooling rate increases to the left, the microstructural feature size decreases until amorphous powder particles are observed at very high cooling rates.
Equation 4 of the solidification model was verified quantitatively by experimentally measuring microstructural feature size and particle size. Figure 8 shows the comparison between the theoretical calculation and the experimental results for Al 6061.
The percent increase of intrinsic strength of the powder particles due to the contribution of microstructural feature size is calculated by the Hall-Petch relationship given in Equation 5. This is graphically represented in Figure 9. This contribution is included in the second term of the additive strength model in Equation 1.
Kinetic models
Figure 10 contains continuous cooling transformation (CCT) curves for the formation of Mg2Si in Al 6061, created in JMatPro. Solidification models, discussed in the previous section, approximated the cooling rate of the majority of Al 6061 powder particles used in the cold spray process to be 3.5 × 104 to 1 × 106 ℃/s. According to the CCT curves for the equilibrium Mg2Si phase, this phase would not form during solidification of these powders. However, cooling rate depends on powder particle size. Larger powder particles have a slower cooling rate, resulting in the formation of additional phases and a higher amount of these phases. This result is not at all evident when observing only the equilibrium isopleth and shows the necessity of kinetic considerations.
Discussion
This paper focused on the modeling and experimental verification on the Powder Production stage of the TPM. Specifically, the phases and microstructural grain size were computationally predicted and experimentally verified. This data is an important and necessary input to the subsequent stages of the TPM.
The equilibrium isopleth given in Figure 3 can be used to observe the variation in phases formed as a function of alteration in chemical composition. This data shows the potential variation in equilibrium phases present in different samples of the same material despite all being within the allowable specification range of composition, as indicated by the shaded region. Also, composition of the alloy can be varied to produce desired or avoid deleterious secondary phases. Finally, these isopleths can be used to determine the alloy's potential for precipitation hardening.
These isopleths are used to determine initial predictions of phases present in the alloy under investigation. The thermodynamically predicted phases in Al 6061 in Figure 4 were inconsistent with the experimental TEM of the powder, leading to kinetic consideration. While thermodynamic models can be very accurate for traditional cast alloys, the extremely high cooling rates predicted by Equation 2, plotted in Figure 6, do not allow the equilibrium phases to form during the solidification of the powder particles during gas atomization. This is evident in the cooling curves in Figure 10, where the cooling rates of the powder particles used in cold spray are between 3 × 104 to 1 × 106 ℃/s. These rates are even higher, or further to the left, of the plotted cooling rates, indicating that they will never intersect the stable Mg2Si cooling curves, therefore this phase is absent in the as-atomized powder.
Phases predicted by the thermodynamic and kinetic models contribute to the initial strength of the powder particles. Depending on the coherency of the predicted secondary phases, various yield strength models are used calculate this contribution. This is captured by the last term in the additive strength model in Equation 1. This work is discussed in a separate paper.
Figure 8 shows the relationship between microstructural feature size and powder particle diameter for Al 6061, given by Equation 4. The experimental results show good agreement with the predicted values. This data is important in determining the mechanical properties of the powder particles since the microstructural feature size has a direct correlation with material strength, as given by the Hall-Petch relationship in Equation 5. This strength contribution depends on particle diameter; smaller particles have finer microstructural feature sizes which increase the Hall-Petch strength contribution as shown in Figure 9. For Al 6061 it is predicted that cold sprayed particles within the range of 10 um to 55 um contribute an additional 60% to 40% of the material intrinsic strength to the powder particles' intrinsic as-received strength, respectively.
The data for the additive strength model is used as a starting point for the model integration, combined with the next stage of the TPM, Powder Preparation, and used as input into the Particle Impact Model. Effects of heat treatment, degassing, etc. alter the results from the first stage and are considered in the Powder Preparation stage.
Acknowledgements
The authors thank the U.S. Army Research Laboratory for their funding through contract #W911NF-10-2-0098. Also, they would like to acknowledge contribution from Mr. Le Zhou and Prof. Yongho Sohn for transmission electron microscopy carried out at Materials Characterization Facility of University of Central Florida, Orlando, FL, USA. The authors declare that they have no conflict of interest.