
International Journal of Metallurgy and Metal Physics
(ISSN: 2631-5076)
Volume 5, Issue 4
Research Article
DOI: 10.35840/2631-5076/9262
Modeling Fusion Welds: A Multi-Scale Submodeling Approach
EA Bonifaz*
Figures
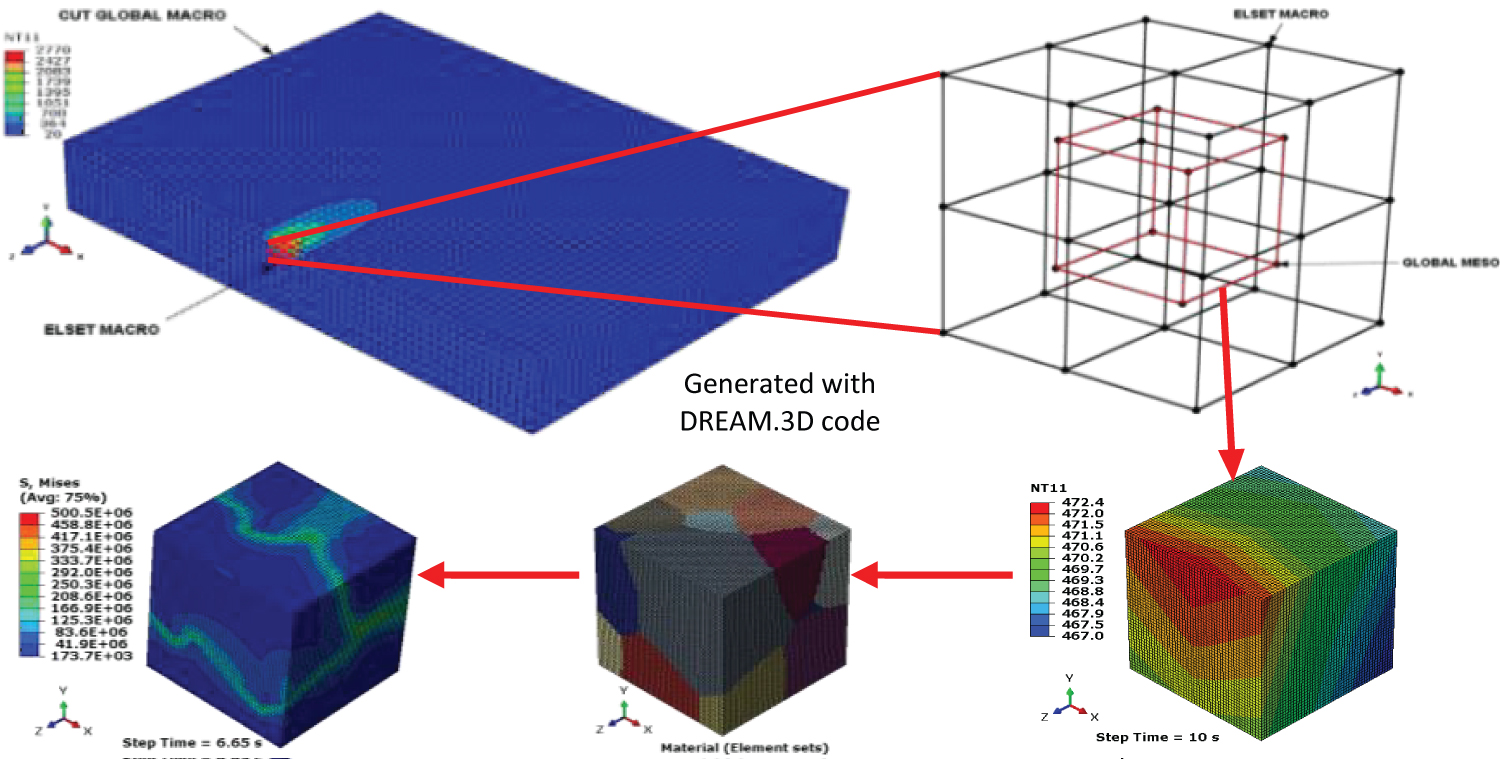
Figure 1: The multi-scale mesh strategy applied....
The multi-scale mesh strategy applied in an initial coarse macro global model. The zoomed-in volume illustrates the finite element submodeling technique. The RVE-finite element polycrystalline meshes constructed by using the coupling DREAM.3D-ABAQUS.
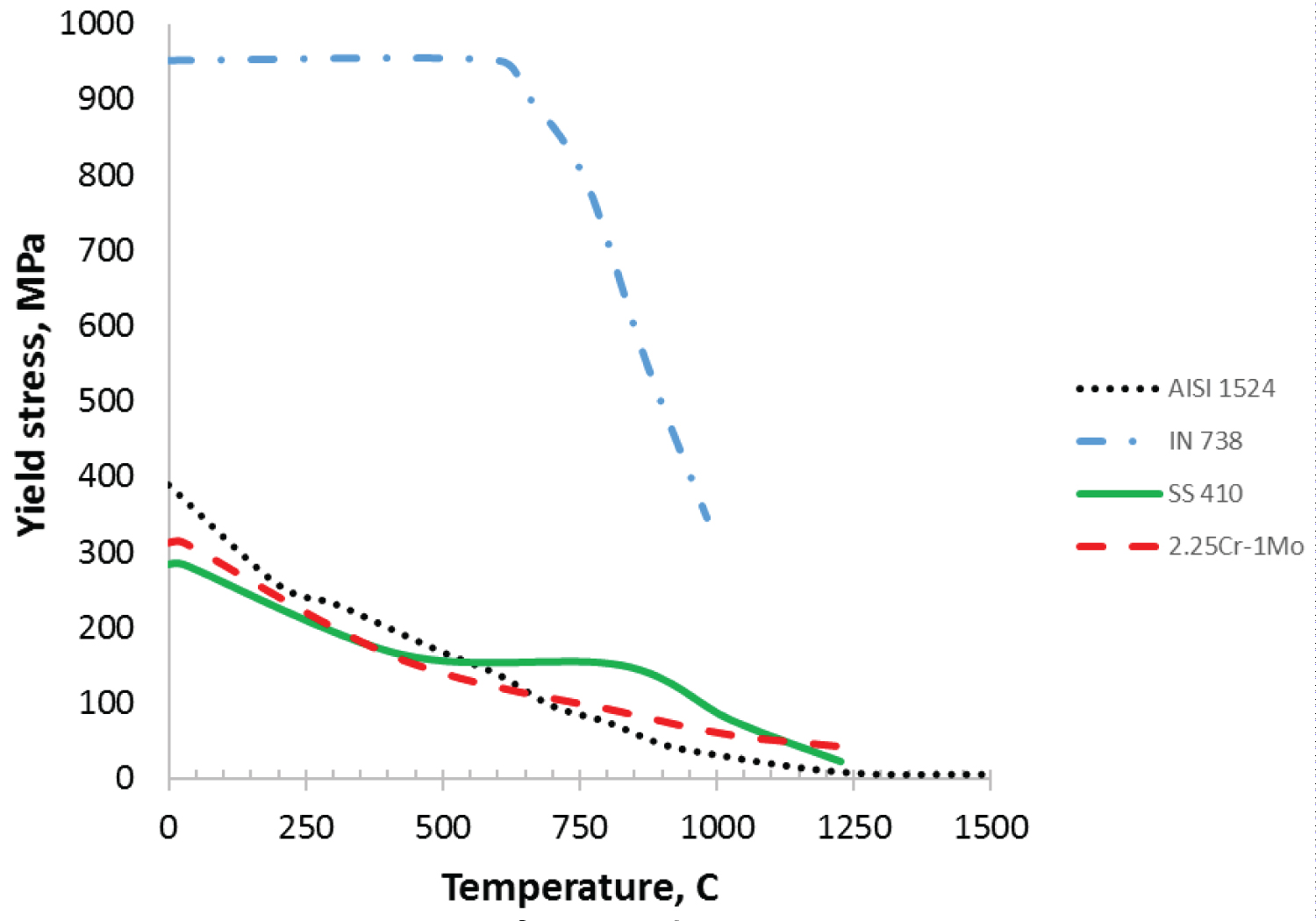
Figure 2: Temperature dependent yield stress of.....
Temperature dependent yield stress of AISI-SAE 1524 steel, IN-738 LC alloy, SS 410 steel in annealed condition, and 2.25Cr-1Mo steel.
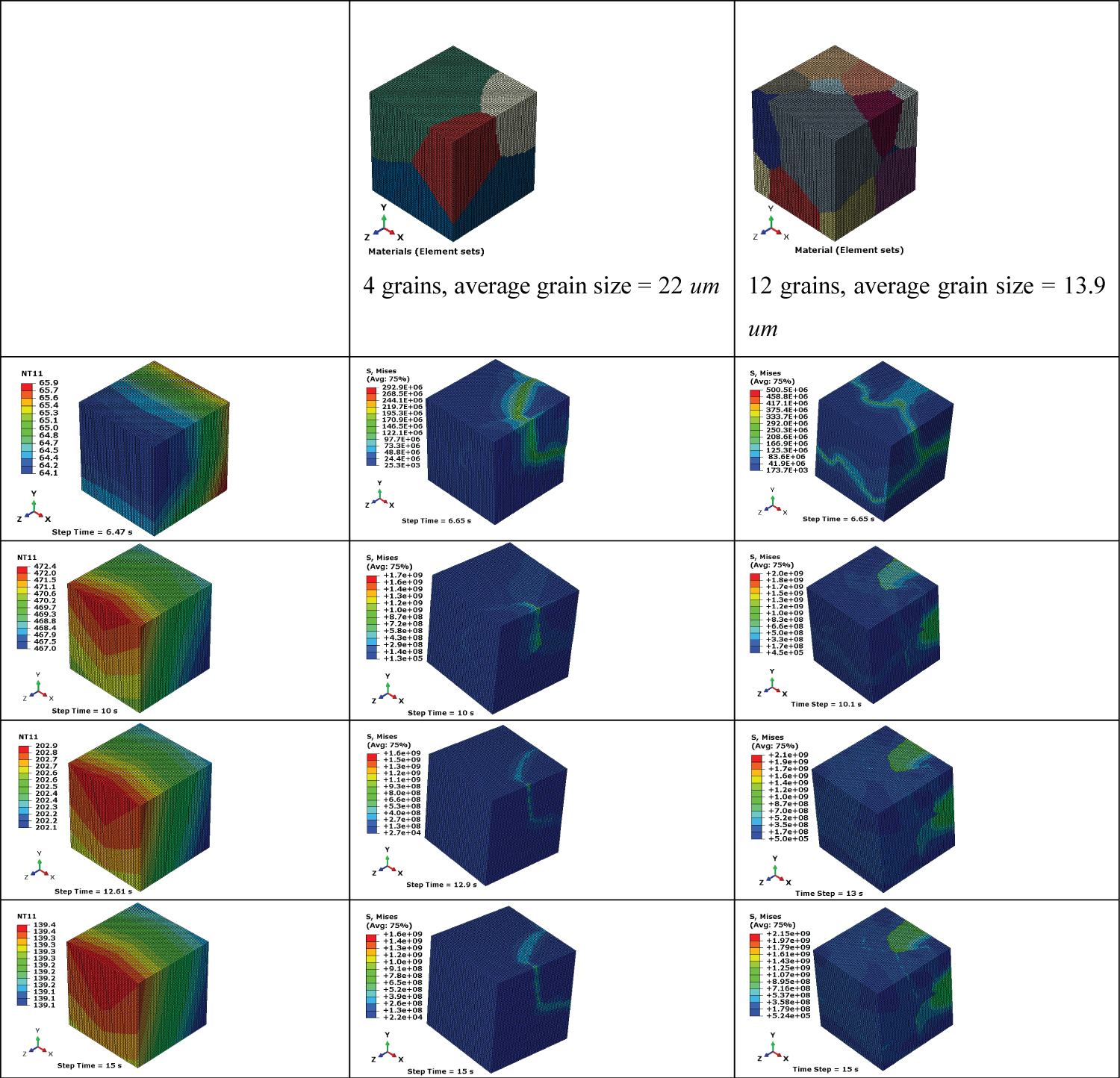
Figure 3: Temperature distribution and micro-residual....
Temperature distribution and micro-residual stress distribution at documented step times in two random polycrystalline aggregate of 4 and 12 grains generated using the coupling DREAM.3D-ABAQUS. The units of Mises residual stresses are in Pascal.
Tables
Table 1: Mechanical properties of AISI-SAE 1524 steel, IN-738 LC alloy, SS 410 and 2.25Cr-1Mo steels.
References
- EA Bonifaz (2013) Submodeling simulations in fusion welds. Journal of Multiscale Modelling 4: 1250014.
- EA Bonifaz (2014) Submodeling simulations in fusion welds: Part II. Journal of Multiscale Modelling 5: 1350008.
- EA Bonifaz, A Czekanski (2014) Multiscale simulations in a butt fusion weld. International Journal of Aerospace and Lightweight Structures 4: 273-280.
- EA Bonifaz, JM Conde, A Czekanski (2019) Determination of secondary dendrite arm spacing for IN-738LC gas-tungsten-arc-welds. Journal of Multiscale Modelling 10: 1850012.
- EA Bonifaz, NL Richards (2008) The plastic deformation of non-homogeneous polycrystals. International Journal of Plasticity 24: 289-301.
- S Kou (2003) Welding metallurgy. (2nd edn), Wiley, New York, USA.
- T Debroy, SA David (1995) Physical processes in fusion welding. Reviews of Modern Physics 67: 85-112.
- RG Thiessen, IM Richardson (2006) A physically based model for microstructure development in a macroscopic heat-affected zone: Grain growth and recrystallization. Metall Mater Trans B 37: 655-633.
- GW Krutz, LJ Segerlind (1978) Finite element analysis of welded structures. Welding Journal 57: 211s-216s.
- SB Brown, H Song (1992) Implications of three-dimensional numerical simulations of welding of large structures. Welding Journal 71: 55s-62s.
- VA Lubarda, MS Schneider, DH Kalantar, BA Remington, MA Meyers (2004) Void growth by dislocation emission. Acta Materialia 52: 1397-1408.
- AF Norman, R Ducharme, A Mackwood, P Kapadia, PB Prangnell (1998) Application of thermal modelling to laser beam weldingof aluminum alloys. Sci Technol Welding Joining 3: 260-266.
- JA Goldak, AP Chakravarti, M Bibby (1984) A new finite element model for welding heat sources. Metallurgical Transactions B 15: 299-305.
- J Goldak, M Bibby, J Moore, R House, B Patel (1986) Computer modeling of heat flows in welds. Metallurgical Transactions B 17: 587-600.
- EA Bonifaz (2000) Finite element analysis of heat flow in single pass arc welds. Welding Journal 79: 121s-125s.
- EA Bonifaz (2007) Thermo-mechanical modeling of single fusion welds. Canadian Welding Association Journal, 13-20.
- A Paul, T Debroy (1988) Free surface flow and heat transfer in conduction mode laser welding. Metallurgical Transactions B 19: 851-858.
- P Tekriwal, J Mazumder (1998) Finite element analysis of three-dimensional transient heat transfer in GMA welding. Welding Journal 7: 151s-156s.
- EA Bonifaz (2018) Thermo-mechanical analysis in SAE-AISI 1524 carbon steel gas tungsten arc welds. Int J Computational Materials Science and Surface Engineering 7: 269-287.
- EA Bonifaz (2019) Modelling of thermal transport in wire?+?arc additive manufacturing process. In: JMF Rodrigues, PJS Cardoso, J Monteiro, R Lam, VV Krzhizhanovskaya, et al. Computational Science - ICCS 2019, Springer, Cham, 11539: 647-659.
- EA Bonifaz, NL Richards (2010) Stress-strain evolution in cast IN-738 superalloy single fusion weld. International Journal of Applied Mechanics 2: 807-826.
- EA Bonifaz, NL Richards (2009) Modeling cast IN-738 superalloy gas tungsten arc welds. Acta Materialia 57: 1785-1794.
- EA Bonifaz (2014) Finite element modeling to simulate the elasto-plastic behavior of polycrystalline in 718. Journal of Multiscale Modelling 5: 1350011.
- M Shenoy, J Zhang, DL Mc Dowell (2007) Estimating fatigue sensitivity to polycrystalline Ni-base superalloy microstructures using a computational approach. Fatigue and fracture of engineering materials and structures 30: 889-904.
- T Mukherjee, JS Zuback, W Zhang, T DebRoy (2018) Residual stresses and distortion in additively manufactured compositionally graded and dissimilar joints. Computational Materials Science 143: 325-337.
- MA Groeber, MA Jackson (2014) DREAM.3D: A digital representation environment for the analysis of microstructure in 3D. Integrating Materials and Manufacturing Innovation 3: 1-17.
- (2018) Finite element software. ABAQUS 6.14.2, Simulia ABAQUS® Inc.
Author Details
EA Bonifaz*
Mechanical Engineering Department, Universidad San Francisco de Quito, Ecuador
Corresponding author
EA Bonifaz, Mechanical Engineering Department, Universidad San Francisco de Quito, Cumbayá, 170901, Quito, Ecuador.
Accepted: December 12, 2020 | Published Online: December 14, 2020
Citation: Bonifaz EA (2020) Modeling Fusion Welds: A Multi-Scale Submodeling Approach. Int J Metall Met Phys 5:062
Copyright: © 2020 Bonifaz EA. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The technological properties of fusion welds are formed due to the simultaneous effects of different physical phenomena which occur on different length scales. In the multi-scaled modelling method designed to make microstructure modelling more tractable, a fine meso sub-mesh resides in each element of a coarse macroscopic global mesh. Of the same manner, a fine micro sub-mesh resides in each element of a coarse mesoscopic global mesh. In this work, a transient non-linear multi-scale finite element heat flow-mechanical model to determine micro-residual stresses was developed. Thermal cycles calculated to predict macro, meso and micro-residual stresses, were imposed as load conditions. The numerical procedure was developed in a three-dimensional domain using the coupling DREAM.3D-ABAQUS, and the construction of ABAQUS user-defined subroutines. A non-standard domain decomposition method based on the concept of Representative Volume Elements (RVEs) was used to include the polycrystalline nature of the specimen. The micro-submodel developed to identify temperature, strain and stress contours at different step times, requires the meso temperature gradient information as prescribed driven (load) boundary conditions. A strong dependence of micro residual stresses on grain size is clearly observed.
Keywords
Welding, Sub-modeling, Micro residual stresses, Thermal gradients, Digital microstructures codes
Introduction
Material properties are dependent upon the microstructural characteristics of the part. Developing an accurate and sufficient representation of the microstructure obtained in fusion welds is critical to precisely estimate material properties. Since the material properties of welded parts are an important function of the welding processing parameters, a fundamental understanding of how welded components behave in load-bearing applications depends on understanding the evolution of thermal cycles and residual stresses during component fabrication. A few researches have been conducted to simulate the thermal cycles, thermal gradients, stress formation, and part distortion at the micro level [1-4]. One of the reasons is that the technological properties of fusion welds are formed due to the simultaneous effects of different physical phenomena that occur on different length and time scales. Length scales for processes and materials are generally classified as nanoscale (< 100 nm), microscale (100 nm to 100 µm) and mesoscale (> 100 µm). The length can be an external dimension of a component, or the internal dimension of a material such as the crystalline grain size.
The characterization of mechanical and physical properties, on meso, micro, and nanoscales, is crucial for a fundamental understanding of materials behavior to assess other characteristics of materials in the actual service (i.e., elastic-plastic deformation, residual stresses, time-dependent creep and relaxation properties, fracture toughness, fatigue, yield strength, etc.). Even though, differences between the mechanical and physical properties of macro scale materials and those of meso and microscale materials are great, the data related to the properties of micro and meso scale materials are lack of. So, the mechanical and physical properties of micro and mesoscale materials should be studied vigorously. In particular, the understanding mechanics and physics of materials at the micro-scale are essential because material can no longer be considered homogeneous when the process size dimensions approach the material grain size [5]. The interaction of the residual stresses with localized stress concentrations and crack-like defects must also be taken into account to predict component reliability in load bearing and thermomechanical applications.
The residuals stress profiles and their magnitudes are difficult to quantify [6]. Although residual stresses and plastic strains have been studied for many decades, accurate calculation and measurement of these still remains a major issue. Differences in calculated and measured residual stresses are attributed to lack of an accurate stress-strain constitutive relation, experimental errors, and the use of Finite Element (FE) bulk coarse grids [6,7]. The more textured the material, or the higher the inter granular stress (micro stress), or when there are chemistry changes, the less likely for measured and simulations to agree. An explanation is that traditional welding simulations do not consider the polycrystalline nature of the specimen in the FE mesh step. Thus the uncertainties in the numerical calculations procedures include the inaccuracies in the calculation of thermal cycles as well as the approximations in the assumed stress-strain relation, particularly when important solid-state transformations take place [6,7]. Computational models [8-18] however can provide a detailed description of the residual stress distribution and microstructure development in weldments, though a prerequisite for the calculations is the detailed and accurate time-temperature history obtained from numerical simulations.
Modeling the influence of the entire thermal cycle of the welding process with a physically based multi-scale model for the material can provide new understanding of the microstructure and distortion evolution due to the welding process [1,2]. The multi-scale analysis framework covers micromechanical stress and failure analysis, as well as thermal analysis, of extended microstructural regions. Actual investigations aim to integrate dendritic morphology evolution with micro-residual stresses and dislocation evolution into a fluid-thermal-metallurgical-mechanical multi-scale approach. In this work, the sub-modeling technique (a separate analysis that can be used to any number of levels) was used to mesh a local part of the model with a refined mesh based on interpolation of the solution from an initial, relatively coarse, macro global model (see Figure 1). The meso-sub-model is the global model for the subsequent micro sub-model. The strategy used to calculate temperature gradients, plastic strains and residual stresses at the macro, meso and micro-scale level, is very flexible to be used to any number of levels [1-3]. The multi-scale submodeling approach can be used to capture weld pool features at the macro-meso scale level, and micro residual stress and secondary dendrite arm spacing features at the micro-scale level. The major advantage of this model, in addition to the ability to calculate macroscopic parameters such as temperatures, plastic strains, residual stresses, etc., is the possibility of predicting the distribution and evolution of even microscopically small crystal defects such as dislocations.
The main objective of this research was to initiate the development of microstructural models to identify fusion welding process parameters for preserving the single crystal nature of gas turbine blades during repair procedures. Representative Volume Elements (RVEs) generated with the digital microstructure code DREAM.3D were included in the analysis to represent the polycrystalline aggregate. Of similar manner, by using the calculated numerical thermal results, microstructure evolution using the phase field method could be easily predicted at these sub-level scales.
The Model
The welding conditions chosen to solve the 3-D transient nonlinear heat conduction (Eq. 1) and equilibrium (Eq. 2) governing differential equations are documented in our previous work [19].
Here, ρ is the density, cp is the specific heat, k is the thermal conductivity, T is temperature, t is time, and Q the internal heat source term. In the present research, Q is zero and the latent heat was not considered.
Here, is the stress tensor.
The thermal gradients calculated with the thermal model already described in our previous related research [19-22], were imposed as load conditions to calculate micro residual stresses based on the proposed multi-scale strategy. Details of the thermo-mechanical analysis can be found in the above mentioned works. Following the literature recommendations [23,24], a cubic box with an edge size (Lo) is used to represent the polycrystalline aggregate with
Where <dgr> is the average grain size, and ngr is the number of grains.
Two random polycrystalline Representative Volume Elements (RVEs) of edge size Lo = 50 um and number of grains 4 and 12 each were generated with the code DREAM.3D. By using the Eq. 3, the dimensions of the average grain size in the virtual specimens are 22 and 13.9 um respectively. The von Mises yield criterion was used in the model. The use of the von Mises equivalent quantities implies plastic isotropy of the material. Mises stresses and equivalent plastic strains identify the yield condition for a multiaxial stress state; that is one in which more than one direct stress exists. To observe the strong dependence of micro residual stress on grain size in specimens subjected to similar thermal gradient initial conditions, four materials with the mechanical properties described in Table 1 and Figure 2 were included into the finite element analysis. The mechanical properties of SS 410 steel in annealed condition, and 2.25Cr-1Mo steel were obtained from Mukherjee, et. al. [25], while the mechanical properties of AISI-SAE 1524 steel and IN-738 LC alloy were obtained from Bonifaz [19]. In the 4 grains aggregate, each grain was assigned the mechanical properties of a unique material, while in the 12 grains aggregate, randomly groups of three grains were assigned the mechanical properties of a unique material. The calculations were performed with ABAQUS® code using an 8 node C3D8 representative finite element mesh.
Results and Discussions
It is known that dendrite secondary arm spacing belongs to the micron-scale and that the cooling rate belongs to the macro-scale [22], so, a connection between scales is yet unclear. The present research is an effort to clarify the link between solidification grains substructures with micro residual stresses and cooling rate. By performing three-dimensional transient non-linear thermo-mechanical simulations, thermal histories, thermal cycles, strains and stresses that occur during the welding process at the sub-level scale were numerically investigated. The multi-scale submodeling approach was used to capture weld pool features at the macro-meso scale level, and micro-residual stress features at the micro-scale level. Figure 3 shows temperature distribution and Mises stress distribution at documented step times in two virtual specimens of 4 and 12 grains generated using the coupling DREAM.3D-ABAQUS [26,27]. At similar thermal gradients, differences in micro residual values are clearly observed. Higher Mises values are found in the polycrystalline aggregate composed of 12 grains (grain size 13.9 um). Results demonstrate that materials display strong size effects when the characteristic length scale associated with non-uniform plastic deformation is on the order of microns.
Conclusions
1. A 3D transient non-linear multi-scale finite element heat flow-mechanical model to determine micro-residual stresses was developed.
2. A strong dependence of micro-residual stresses on grain size is clearly observed.
3. The micro-submodel developed to identify temperature, strain and stress contours at different step times, requires the meso temperature gradient information as prescribed driven (load) boundary conditions.
4. With the present sub-modeling strategy, the development of a physics-based model for simulating initiation and propagation of cracks in weld samples, starting at the microstructural length scale, can be easily achieved.

