
International Journal of Optics and Photonic Engineering
(ISSN: 2631-5092)
Volume 6, Issue 1
Research Article
DOI: 10.35840/2631-5092/4535
Electronic Properties of Wurtzite GaN, InN and their Ternary Alloys InxGa1-XN (0 < X < 1): A Comparative Study Using Different Methods
A. Said1, Y. Oussaifi1*, N. Bouarissa2 and M. Said1
Table of Content
Figures
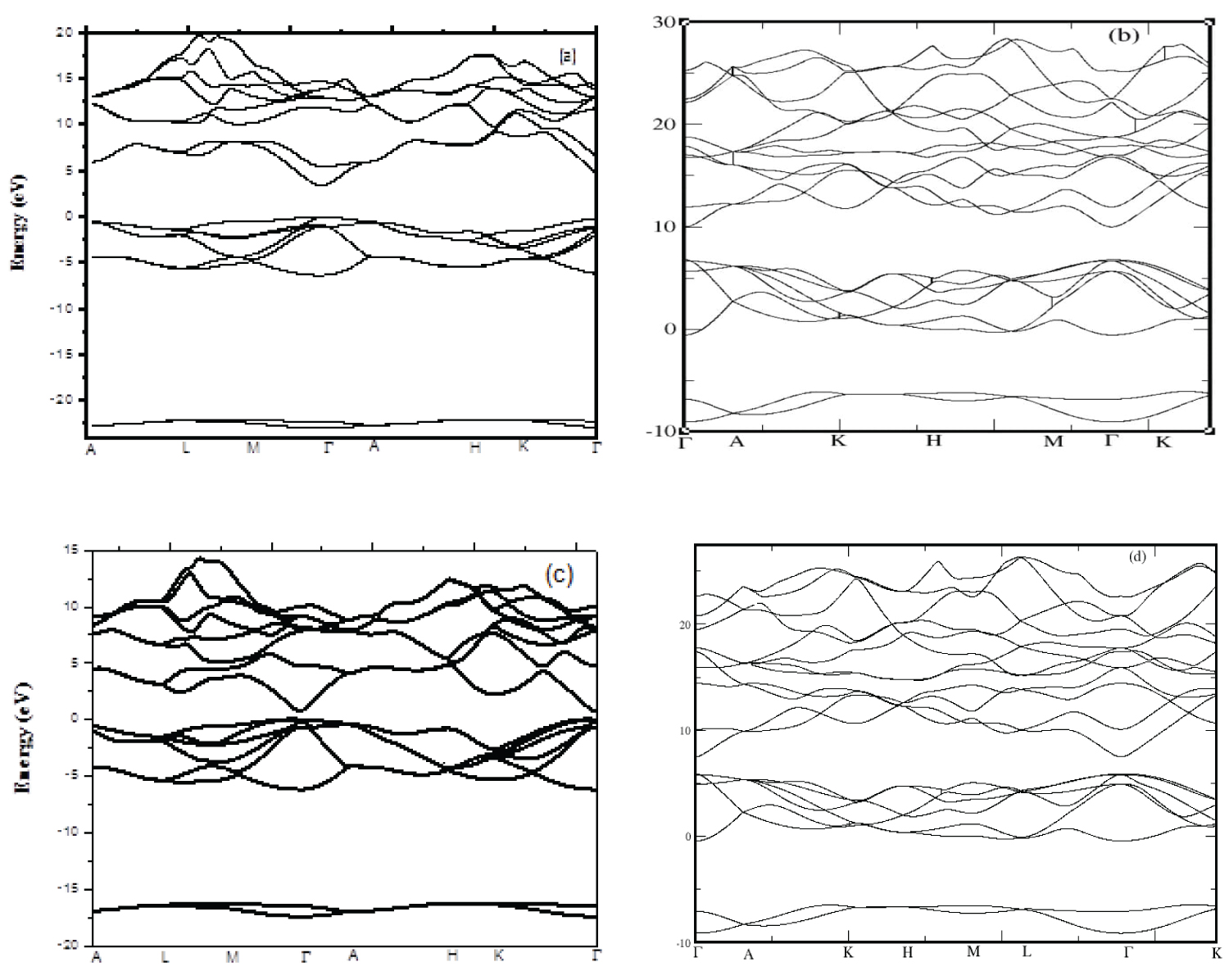
Figure 1: (a and b) Band structure of wurtzite....
(a and b) Band structure of wurtzite GaN (a) using EPM within VCA method; (b) using DFT (HSE) method along the high symmetry lines of the first Brillouin zone; (c and d) Band structure of wurtzite InN (c) using EPM within VCA method; (d) using DFT (HSE) method along the high symmetry lines of the first Brillouin zone.
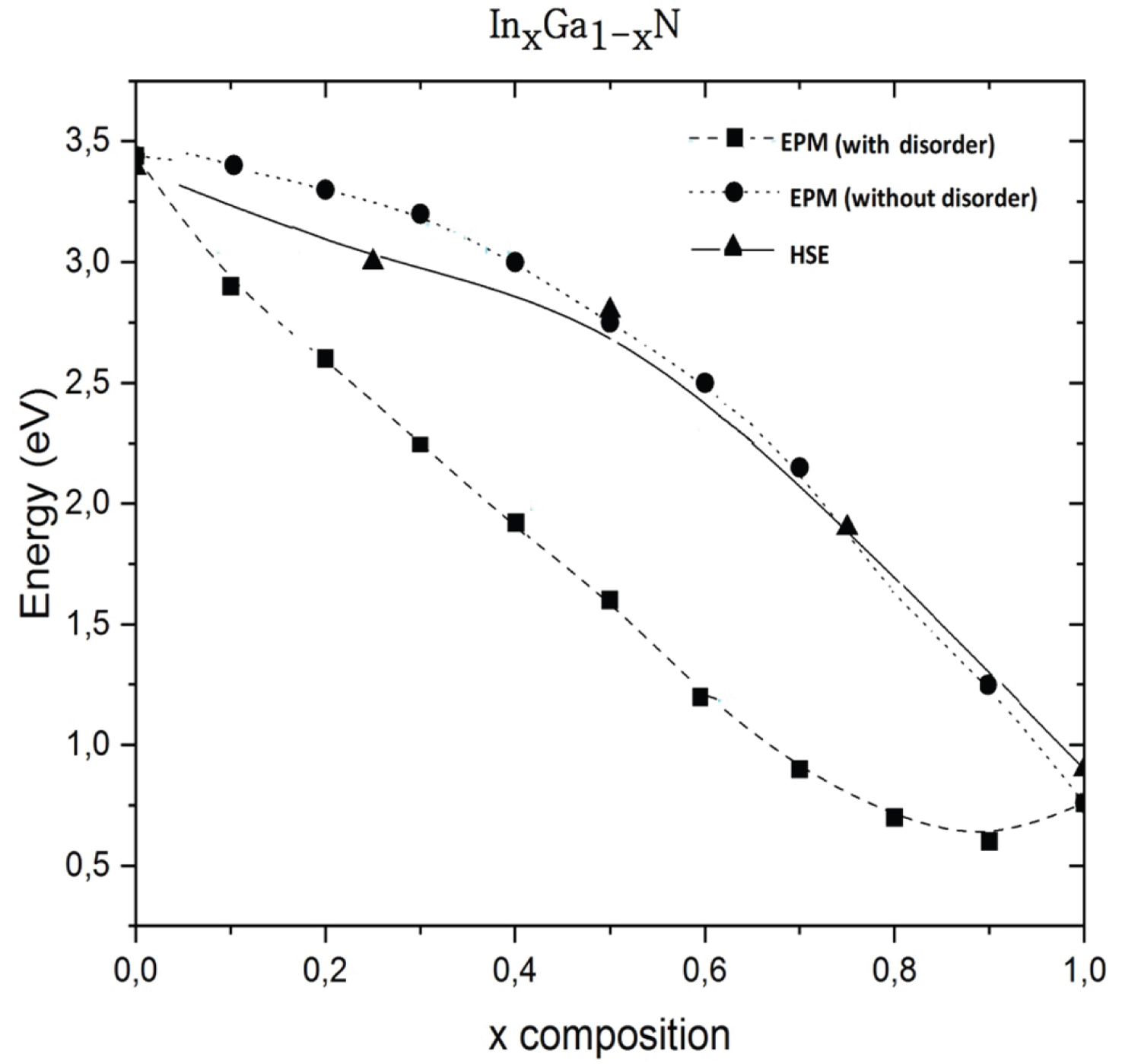
Figure 2: Energy gap as a function of x for.....
Energy gap as a function of x for wurtzite InxGa1-xN at Γ point calculated without disorder (standard VCA), with including the compositional disorder (improved-VCA) and with HSE.
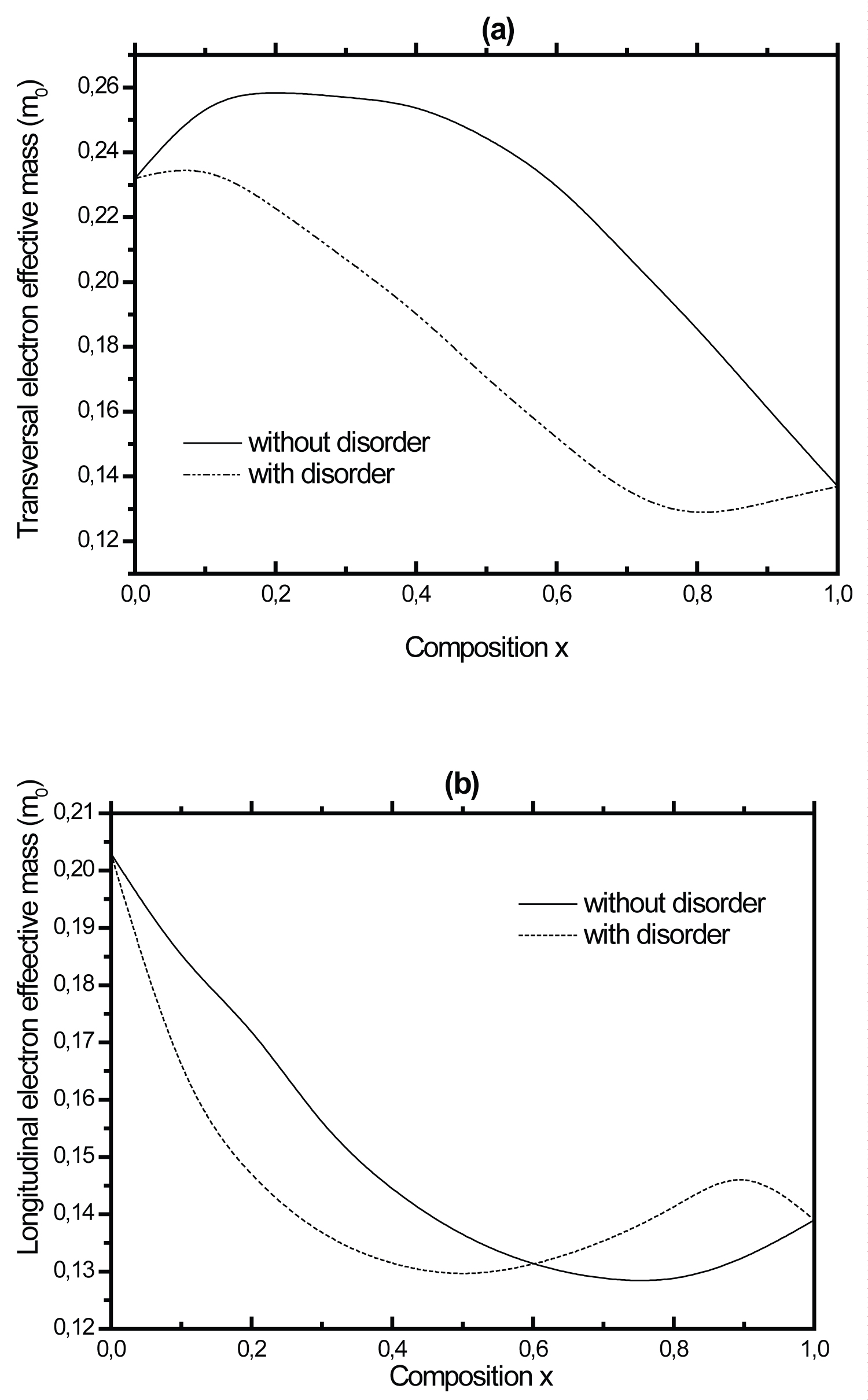
Figure 3: The transversal (a) and longitudinal....
The transversal (a) and longitudinal (b) electron effective masses of Γ valleys in wurtzite InxGa1-xN as a function of indium composition x. The solid and dashed lines correspond to calculations without and with disorder, respectively.
Tables
Table 1: The symmetric and antisymmetric form factors of wurtzite GaN and InN structures in (Ry).
Table 2: The lattice constants (a, c in Å and c/a) of wurtzite GaN and InN structure obtained with the HSE functional method in comparison to experimental and theoretical results from the literature.
Table 3: Comparison of eigen energies at Γ point of GaN and InN with experimental and theoretical results (in eV).
Table 4: Fundamental gap bowing parameter b (in eV) of ternary alloys of interest in the wurtzite structure.
Table 5: Effective electron masses of the conduction band minimum in wurtzite GaN and InN compared with experimental and theoretical results.
Table 6: Bowing factors of electron effective masses calculated at conduction band minima.
References
- Ponce FA, Bour DP (1997) Nitride-based semiconductors for blue and green light-emitting devices. Nature 386: 351-359.
- Orton JW, Foxon CT (1998) Group III nitride semiconductors for short wavelength light-emitting devices. Rep Prog Phys 61.
- Jain SC, Willander M, Narayan J, Van Overstraeten R (2000) III-nitrides: Growth, characterization and properties. J Appl Phys 87: 965-1006.
- Bouarissa N (2002) Electronic structure and lattice properties of zinc-blende InN under high pressure. Eur Phys J B 26: 153-158.
- Bouarissa N (2002) Electron and positron energy levels and deformation potentials in group-III Nitrides. Phys Stat Sol 231: 391-402.
- Vurgaftman I, Meyer JR (2003) Band parameters for nitrogen-containing semiconductors. J Appl Phys 94: 3675-3696.
- Saib S, Bouarissa N (2007) Structural phase transformations of GaN and InN under high pressure. Physica B: Condensed Matter 387: 377-382.
- Saib S, Bouarissa N, Rodríguez-Hernández P, Muñoz A (2008) First-principles study of high-pressure phonon dispersions of wurtzite, zinc-blende, and rocksalt AlN. J Appl Phys 103: 013506.
- Bouarissa N (2000) Composition dependence of positron states in zincblende Ga1-xInxN. Philos Mag B 80: 1743-1756.
- Kassali K, Bouarissa N (2000) Pseudopotential calculations of electronic properties of Ga1-xInxN alloys with zinc-blende structure. Solid State Electron 44: 501-507.
- Bouarissa N, Kassali K (2001) Mechanical properties and elastic constants of zinc-blende Ga1-xInxN Alloys. Phys Stat Sol (b) 228: 663-670.
- Lee SJ, Kwon TS, Nahm K, Kim CK (1990) Band structure of ternary compound semiconductors beyond the virtual crystal approximation. J Phys Cond Matter 2: 3253-3257.
- Bouarissa N (1998) Effects of compositional disorder upon electronic and lattice properties of GaxIn1-xAs. Phys Lett A 245: 285-291.
- Bouarissa N (2007) Pseudopotential calculations of Cd1-xZnxTe: Energy gaps and dielectric constants. Physica B 399: 126-131.
- Cohen ML, Chelikowsky JR (1988) Electronic structure and optical properties of semiconductors. Springer, Berlin.
- Heine V (1970) The pseudopotential concept. Solid State Physics 24: 1-36.
- Cohen ML, Heine V (1970) The fitting of pseudopotentials to experimental data and their subsequent application. Solid State Physics 24: 37-248.
- Oussaifi Y, Said A, Ben Fredj A, Debbichi L, Ceresoli D, et al. (2012) Effect of pressure on the energy band gaps of wurtzite GaN and AlN and electronic properties of their ternary alloys AlxGa1-xN. Physica B 407: 3604-3609.
- Schulz H, Thiemann KH (1977) Crystal structure refinement of AlN and GaN. Solid State Commun 23: 815-819.
- Rinke P, Winkelnkemper M, Qteish A, Bimberg D, Neugebauer J, et al. (2008) Consistent set of band parameters for the group-III nitrides AlN, GaN, and InN. Phys Rev B 77: 75202.
- Giannozzi PL, Baroni S, Bonini N, Calandra M, Car R, et al. (2009) QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J Phys Condens Matter 21: 395502.
- Monkhorst HJ, Pack JD (1976) Special points for Brillouin-zone integrations. Phys Rev B 13: 5188-5192.
- Perdew JP, Chevary JA, Vosko SH, Jackson KA, Pederson MR, et al. (1992) Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys Rev B Condens Matter 46: 6671-6687.
- Heyd J, Scuseria GE, Ernzerhof M (2003) Hybrid functionals based on a screened Coulomb potential. J Chem Phys 118: 8207.
- Dridi Z, Bouhafs B, Ruterana LP (2003) First-principles investigation of lattice constants and bowing parameters in wurtzite AlxGa1-xN, InxGa1-xN and InxAl1-xN alloys. Semicond Sci Technol 18: 850.
- Wright AF, Nelson JS (1995) Consistent structural properties for AlN, GaN, and InN. Phys Rev B Condens Matter 51: 7866-7869.
- Min BJ, Chan CT, Ho KM (1992) First-principles total-energy calculation of gallium nitride. Phys Rev B Condens Matter 45: 1159-1162.
- Huang MZ, Ching WY (1985) A minimal basis semi-ab initio approach to the band structures of semiconductors. J Phys Chem Solids 46: 977-995.
- Yeo YC, Chong TC, Li MF (1997) Electronic band structures and effective-mass parameters of wurtzite GaN and InN. J Appl Phys 83: 1429.
- Monemar B (1974) Fundamental energy gap of GaN from photoluminescence excitation spectra. Phys Rev B 10: 676-681.
- Yu Davydov V, Klochikhin AA, Emtsev VV, Smirnov AN, Goncharuk IN, et al. (2003) Photoluminescence and Raman study of hexagonal InN and In-rich InGaN alloys. Phys Status Solidi b 240: 425-428.
- Westra KL, Lawson RPW, Brett MJ (1988) The effects of oxygen contamination on the properties of reactively sputtered indium nitride films. J Vac Sci Technol A 6: 1730.
- Guo Q, Yoshida A (1994) Temperature dependence of band gap change in InN and AlN. Jpn J Appl Phys Part 1 33: 2453.
- Fritsch D, Schmidt H, Grundmann M (2003) Band-structure pseudopotential calculation of zinc-blende and wurtzite AlN, GaN, and InN. Phys Rev B 67: 235205.
- Arnaudov B, Paskova T, Paskov PP, Magnusson B, Valcheva E, et al. (2004) Energy position of near-band-edge emission spectra of InN epitaxial layers with different doping levels. Phys Rev B 69: 115216.
- Bagayoko D, Franklin L (2005) Density-functional theory band gap of wurtzite InN. J Appl Phys 97: 123708.
- Wu J, Walukiewicz W, Shan W, Yu KM, Ager JW, et al. (2002) Small band gap bowing in In1-xGaxN alloys III. Appl Phys Lett 80: 4741-4743.
- Wu J, Walukiewicz W, Shan W, Yu KM, Ager III JW, et al. (2002) Effects of the narrow band gap on the properties of InN. Phys Rev B 66: 201403.
- Kasic A, Schubert M, Saito Y, Nanishi Y, Wagner G (2002) Effective electron mass and phonon modes in n-type hexagonal InN. Phys Rev B 65: 1152061-1152067.
- Inishima T, Mamutin VV, Vekshin VA, Ivanov SV, Sakon T, et al. (2002) Physical properties of InN with the band gap energy of 1.1 eV. J Cryst Growth 481: 227-228.
- Bhuiyan AG, Hashimoto A, Yamamoto A (2003) Indium nitride (InN): A review on growth, characterization, and properties. J Appl Phys 94: 2779-2808.
- Davidov VY, Klochikhin AA, Emtsev VV, Ivanov SV, Vekshin VV, et al. (2002) Band gap of InN and In-Rich InxGa1-xN alloys (0.36 < x < 1). Phys Status Solidi B 230.
- Van Schilfgaarde M, Sher A, Chen AB (1997) Theory of AlN, GaN, InN and their alloys. J Cryst Growth 178: 8-31.
- Dridi Z, Bouhafs B, Ruterana P (2002) Pressure dependence of energy band gaps for AlxGa1-xN, InxGa1-xN and InxAl1-xN. New J Phys 4: 94.
- McCluskey MD, Van de Walle CG, Romano LT, Krusor B, Johnson NM (2003) Effect of composition on the band gap of strained InxGa1-xN alloys. J Appl Phys 93: 4340-4342.
- Osamura K, Naka S, Murakami Y (1975) Preparation and optical properties of Ga1-xInxN thin films. J Appl Phys 46: 3432.
- Nagatomo T, Kuboyama T, Minamino H, Omoto O (1989) L1334 properties of Ga1-xInxN films prepared by MOVPE. Jpn J Appl Phys 28.
- Nakamura S, Iwasa N, Nagahama S (1993) Cd-Doped InGaN Films Grown on GaN Films. Jpn J Appl Phys 32.
- Romano LT, Krusor BS, McCluskey MD, Bour DP (1998) Structural and optical properties of pseudomorphic InxGa1-xN alloys. Appl Phys Lett 73: 1757.
- Shan W, Walukiewicz W, Haller EE, Little BD, Song JJ, et al. (1998) Optical properties of InxGa1-xN alloys grown by metalorganic chemical vapor deposition. J Appl Phys 84: 4452.
- Wetzel C, Takeuchi T, Yamaguchi S, Katoh H, Amano H, et al. (1998) Optical band gap in Ga1-xInxN (0 < x < 0.2) on GaN by photoreflection spectroscopy. Appl Phys Lett 73: 1994-1996.
- Parker CA, Roberts JC, Bedair SM, Reed MJ, Liu SX, et al. (1999) Optical band gap dependence on composition and thickness of InxGa1-xN (0 < x < 0.25) grown on GaN. Appl Phys Lett 75.
- Wagner J, Ramakrishnan A, Behr D, Maier M, Herres N, et al. (1998) Composition dependence of the band gap energy of InxGal-xN layers on GaN (x=0.15) grown by metal-organic chemical vapor deposition. MRS Internet J Nitride Semicond Res 537.
- Agrawal BK, Agrawal S, Yadav PS, Kumar S (1997) Ab initio calculation of electronic properties of alloys. J Phys Cond Matter 9: 1763.
- Shan W, Little BD, Song JJ, Feng ZC, Schurman M, et al. (1996) Optical transitions in InxGa1-xN alloys grown by metalorganic chemical vapor deposition. Appl Phys Lett 69: 3315.
- Schenk HPD, Mierry P, Laügt M, Omnes F, Leroux M, et al. (1999) Indium incorporation above 800 ℃ during metalorganic vapor phase epitaxy of InGaN. Appl Phys Lett 75: 2587.
- Drechsler M, Hofmann DM, Meyer BK, Detchprohm T, Amano H, et al. (1995) Determination of the conduction band electron effective mass in hexagonal GaN. J Appl Phys 34.
- Nakwaski, Lodzimierz W (1995) Effective masses of electrons and heavy holes in GaAs, InAs, A1As and their ternary compounds. Physica B: Condensed Matter 210: 1-25.
- Bouarissa N (2006) Effective masses of electrons, heavy holes and positrons in quasi-binary (GaSb)1-x(InAs)x crystals. J Phys Chem Solids 67: 1440-1443.
- Witowski AM, Pakula K, Baranowski JM, Sadowski ML, Wyder P (1999) Electron effective mass in hexagonal GaN. Appl Phys Lett 75: 4154.
- Kim K, Lambrecht WRL, Segall B, Van Schilfgaarde M (1997) Effective masses and valence-band splittings in GaN and AlN. Phys Rev B 56: 7363-7375.
- Suzuki M, Uenoyama T, Yanase A (1995) First-principles calculations of effective-mass parameters of AlN and GaN. Phys Rev B Condens Matter 52: 8132-8139.
- Inushima T, Higashiwaki M, Matsui T (2003) Optical properties of Si-doped InN grown on sapphire (0001). Phys Rev B 68: 235204.
- Pugh SK, Dugdale DJ, Brand S, Abram RA (1999) Electronic structure calculations on nitride semiconductors. Semicond Sci Technol. 14: 23-31.
Author Details
A. Said1, Y. Oussaifi1*, N. Bouarissa2 and M. Said1
1Département de Physique, Faculté des Sciences de Monastir, Laboratoire de la Matière Condensée et des Nanosciences (LMCN), Monastir, Tunisia
2Laboratory of Materials Physics and its Applications, University of M'sila, M'sila, Algeria
Corresponding author
Y. Oussaifi, Département de Physique, Faculté des Sciences de Monastir, Laboratoire de la Matière Condensée et des Nanosciences (LMCN), Avenue de l'Environnement, 5019 Monastir, Tunisia, Tel: (+216)-92959996.
Accepted: June 12, 2021 | Published Online: June 14, 2021
Citation: Said A, Oussaifi Y, Bouarissa N, Said M (2021) Electronic Properties of Wurtzite GaN, InN and their Ternary Alloys InxGa1-XN (0 < X < 1): A Comparative Study Using Different Methods. Int J Opt Photonic Eng 6:035.
Copyright: © 2021 Said A, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We present a theoretical study of the electronic properties of GaN, InN and their ternary alloys InxGa1-xN in the wurtzite structure. Our results are obtained by means of two computational methods: The empirical pseudopotential method within the virtual crystal approximation and first-principles calculation based on density functional theory within the Heys, Scuseria and Ernzerhof hybrid functional for exchange-correlation energy. Our findings are compared with data available in the literature.
The alloy composition dependence of the energy band-gap at high-symmetry Γ point in the Brillouin zone and the longitudinal and transversal electron effective masses is examined and discussed. Comparison between the results obtained from the two used methods is made. The present investigation may be useful information for technological applications in the blue and green regions of the spectrum.
Keywords
Nitrides, Density-functional theory, Pseudopotential calculations, Lattice constants, Energy gaps, Electron effective masses, Bowing parameter, Wurtzite structure
Introduction
III-nitride semiconductor materials- (Al, Ga, In) N- have attracted much attention during the last decades [1-8]. This is mainly due to their superior properties with respect to conventional III-V semiconductors. The first motivation of these materials comes from their energy band gaps which can range from 0.7 to 6.2 eV and their strong bond strength. Thus, these materials can be used for violet, blue, and green light emitting devices and for high temperature transistors.
By alloying with the group III nitrides are of particular importance. This is due to the large difference between the energy band-gaps of III-nitrides parent compounds which makes them possible for the design of optoelectronic devices covering thus a wide spectral range [3,6,9-11]. The ternary alloys Ga1-xInxN (0 ˂ x ˂ 1) are those semiconductors formed from GaN and InN binary compounds. They are very promising materials for field emission device applications. They exhibit very important physical properties and cover a large domain of applications where they operate in the violet to orange regions of visible light [2,3,10]. GaN and InN binary compounds crystallize preferentially in the hexagonal wurtzite structure [11] and devices have so far been based on this semiconductor material.
In order to provide some information on the electronic properties of GaN and InN and their ternary alloys InxGa1-xN, which might be useful for the design and application of devices based on these semiconducting materials, the electronic properties of the materials of interest in the wurtzite structure have been investigated. The aim of this contribution is the study of the alloy composition dependence of the energy band gaps and electron effective masses in InxGa1-xN in the wurtzite structure. For that, two methods have been used, namely the empirical pseudopotential method (EPM) within a modified virtual crystal approximation (VCA) that takes into account of the compositional disorder effect and density functional theory (DFT) within the Heys, Scuseria and Ernzerhof (HSE) hybrid functional for exchange-correlation energy.
The organization of the present contribution is as follows. After a brief introduction in Section 1, the computational methods used in the present calculations namely the EPM within the VCA and the DFT within HSE are described in Section 2. In Section 3, we present and discuss the results of our study regarding the electronic properties of the materials of interest. We compare our findings with the available experimental data as well as with previous theoretical calculations. The summary and conclusions are given in Section 4.
Methods of Calculation
EPM within VCA
The present calculations are first performed using the EPM within a modified VCA that takes into account the effect of compositional disorder as described in more details in Refs. [12-14]. In the EPM, the crystal potential is represented by a linear superposition of atomic potentials, which are modified to obtain good fits to the experimental direct and indirect band gaps. Further details are presented by Cohen and Chelikowsky [15] and in the reviews by Heine and Cohen [16,17].
The pseudopotential form factors for wurtzite GaN and InN are obtained following the same approach as that used in Ref. [18]. Our results are depicted in Table 1. The wurtzite lattice constants of the alloy InxGa1-xN are determined using Vegard's law,
Where , and , are the lattice constants of the pure semiconductors GaN and InN respectively which are taken as the experimental values reported in the literature [19,20].
The hybrid DFT-HSE approach
We have performed DFT based calculations using the projector augmented wave (PAW) to describe the frozen core electrons and their interaction with valence electrons as implemented in the quantum espresso package [21].
The cutoff energy for all calculated systems is kept constant at 80 Ry for a plane wave basis set expansion. The valence states considered during the calculations are Ga (4s, 4p), In (5s, 5p) and N (2s, 2p). The simulation procedure has been iterated self-consistency with a grid of 4 × 4 × 2 k-points in the reciprocal space. We have employed the Monkhorst and Pack scheme [22] to generate G-centered K point sets. The mixing of a certain amount of non-local Hartree-Fock (HF) exchange interaction in the PBE scheme as described in Ref. [23], the so-called hybrid functional, has proven to improve the description of the electronic structure (including energy band gap). However, there are practical computational difficulties in this approach arising from the evaluation of the slowly decaying HF exchange with distance. To solve this problem Heyd, et al. [24] proposed a more tractable hybrid functional scheme for supercell calculation as follows in Eq. (2):
Where α represents the percentage of HF exchange included and µ is the controlling parameter for the range separation of the exchange interaction into short-range (SR) and long-range (LR) components, Ec is the correlation energy which remains unchanged relative to PBE functional and α = 1/4 is the HF mixing constant (determined analytically via perturbation theory). If µ = 0, HSE is equal to PBE and if µ→∞, HSE tends toward the pure PBE functional. The HSE form can be viewed as an adiabatic connection functional only for the short-range portion of exchange, whereas long-range exchange and correlation are treated at the PBE generalized-gradient approximation (GGA) level. The HSE functional has performed well in a number of previous studies. First, the effect of the screening parameter µ has been examined for a large number of enthalpies of formation. We have found that the values of α and µ are 0.25 and 0.20 Å-1. In the present calculations, we have used 16 atoms supercell to calculate the band structure parameters of InxGa1-xN alloys.
The results of lattice constants (a, c in Å and c/a), obtained by the HSE functional method in comparison to experimental and theoretical data, are listed in Table 2. We compare the lattice constants from various calculations for both GaN and InN.
Results and Discussion
Band structures of wurtzite GaN and InN
The calculated band structures of wurtzite GaN and InN semiconductor compounds using the EPM within the VCA and DFT (HSE) methods are shown in Figure 1a, Figure 1b and Figure 1c and Figure 1d respectively. Note that the overall features of these bands look like to be qualitatively similar. The valence band energies are bonding combinations of hybridized atomic sp3 orbitals. These bands appear to be less dispersive than the conduction bands. This is because they are more localized than the conduction bands. From the quantitative point of view, the difference between the presented electronic band structures lies in their calculated fundamental energy band gap. In this respect and in order to compare between the energy band gaps as obtained from the EPM and HSE and those of experiment and previous theoretical works, we report the direct band gaps at high symmetry Γ point in Table 3. Note that both binary compounds, GaN and InN exhibit a direct band gap (Γ-Γ). For GaN, our results yielded a fundamental energy band-gap of 3.44 and 3.39 eV using EPM and HSE approaches, respectively. These values agree well with the experimental ones of 3.44 eV reported in Ref. [29] and 3.50 eV reported in Ref. [30]. As regards InN, the fundamental energy band gap obtained by our calculations is 0.77 eV when using EPM and 0.9 eV when using the HSE approach. The former value lies in the experimental range of 0.65-0.8 eV reported in Ref. [26] and the latter is in excellent accord with that of 0.9 eV reported by Davydov, et al. [31]. Thus, both approaches give good results as compared to experiment. It should be worth mentioning that InN band gap was reported to be about 1.8-2.0 eV [32,33]. Early EPM calculations [34] basically reproduced the gap of 2.0 eV as reported by the early experiments. Nevertheless, later, measurements of the band gap of InN films, grown by molecular-beam epitaxy (MBE), reported values in the 0.7-1.0 eV range [35].
The high quality of the samples in these experiments was partly utilized to explain the large difference between the early and latter [36-39] experiments. The significant effect of the electron concentration on the band gap [40-42] could explain the 0.75-0.8 eV band gap. The full potential linearized augmented plane-wave [43,44] (FLAPW) calculations mostly reported negative values of the band gap, from -0.4 to -0.19 eV. The full potential linear muffin-tin orbital [44] (FP-LMTO) and atomic sphere approximation (ASA) approaches led to values between 0.2 and 0.43 eV.
Band gap of ternary alloys and bowing parameters
For a ternary alloy AxB1-xN, the fundamental gap is given as:
Where b is the band-gap bowing parameter.
Using HSE method and the EPM within the VCA (p = 0), we have calculated the band gap energies of wurtzite InxGa1-xN as a function of In concentration x in the range 0-1. The agreement with the experimental band gap eV for indium molar fraction x = 0.1 [45] is reached for the value of p = -0.458 (p is the disorder parameter that includes the effect of compositional disorder). The curves that fit best the calculated HSE and EPM under VCA data are plotted in Figure 2. Different behaviors are clearly observed. In fact, within the improved VCA, when x goes from 0 to 0.8, we note an habitual decrease of band gap energy versus indium concentration. Beyond x = 0.8, the curve shows a nonlinear variation. The best fit of our energy band gap data yielded the following equations,
Taking into account of the disorder effect, we note that the bowing parameter b depends strongly on the alloy composition x according to the following expression,
On the other hand, one can note that the band gap bowing parameter obtained from the EPM within the VCA is not far from that obtained from the HSE approach. The best fit of the data determined from both approaches show a quadratic behavior. The dependence of the bowing parameter on x can be explained by the fact that at high values of x, the compositional disorder has little effect on InN. Moreover, due to the large difference in electronegativity and atomic radius between indium and nitrogen, the dependence of band energies with interatomic distances can be non-linear even if the lattice constant changes linearly in accordance with Vegard's law. In Eqs. (4a) and (4c), one can see that the bowing factor for is negative in sign when using the VCA and HSE functional methods, in disagreement with the experimental values ranging from b ≈ 1 eV [46-48] to b ≈ 2.6-4.11 eV [48-53]. However, one should be careful in these experiments, the InN band gap was reported to be around 2 eV which is much larger than the one we calculated. On the other hand, our findings suggest that the ternary InxGa1-xN of interest is a direct band-gap semiconductor over all the composition range 0 < x < 1. This result agrees with that reported in Ref. [54]. Our results as regards the direct band-gap bowing parameters of the material system of interest are depicted in Table 4. The deviation parameters of the lattice constants and the inaccurate determination of the composition x which often disregards the strain influence [57] may cause the discrepancy between the band gap bowing parameters obtained from the linear and nonlinear situations.
Electron effective mass
The transport properties in semiconductors require the study of the electron effective mass [58,59]. The electron mass tensor is represented by a transverse mass m⊥ (with k lying in the kx-ky plane) and a longitudinal mass m∥ (with k parallel to kz). By adopting a parabolic relation of E versus the wave vector k, we can obtain at the conduction band minima (at the Γ point) as described in Ref. [59].
The calculated effective masses of electrons for GaN and InN in the wurtzite structure are listed in Table 5. Our calculated electron effective masses for wurtzite GaN (m⊥ and m∥) agree reasonably well with the experimental one of 0.22 quoted in Ref. [56]. However, they are larger than the ones obtained by using a self-consistent full-potential linearized augmented plane-wave method within the local-density-functional approximation, m⊥ = 0.18 and m∥ = 0.20 [30]. Our calculated values are better than those reported in Ref. [27] since they are closer to the experimental data than those of Ref. [27]. The electron effective masses for InN calculated from Γ to M and from Γ to A directions, respectively are m⊥ = 0.137 and m∥ = 0.139, roughly agree with the experiment [60], taking into account of the quality and other features of the samples; temperature, pressure, electron concentrations.
It should be mentioned that folds of energy bands appeared when we have adopted 16 atoms for the ternary alloy of interest using first-principles calculation based on DFT within HSE. Therefore we can't identify the positions of K points in the Brillouin zone, while we have determined the electron effective mass in the conduction band minima at the Γ valley from the band curvature obtained using EPM calculation for different indium composition for the ternary InGaN.
The variation of the electron effective mass versus x, evaluated in units of the free electron mass (mo), is displayed in Figure 3. The longitudinal electron effective mass for InGaN shows firstly a decreasing trend as x increases up to x = 0.9, then it increases. At Γ point, without taking into account the disorder effect, a nonlinear variation of the transversal and longitudinal electron effective masses is obtained according to the following expressions:
These results (improved VCA) show that the bowing parameter b of the effective mass m⊥ and m∥ respectively depends strongly on the indium composition x:
Unfortunately, the lack of both experimental and theoretical results in literature prevents the validation of our calculated bowing values which they were presented in Table 6 and are predictions that may serve for future studies.
Conclusion
In summary, we have investigated structural and electronic properties of wurtzite InxGa1-xN using the EPM under the VCA and a modified VCA and DFT within HSE hybrid functional for exchange-correlation energy. Lattice constants, band gap energies and electron effective masses at the Γ point have been calculated and compared with previously available data. Our results showed that the bowing parameter b of the energy gap depends strongly on the indium composition x. It is also found that b has a negative sign when using VCA and HSE functional methods. The electron effective masses m⊥ and m∥ at the Γ point for wurtzite structure have been calculated for the ternary alloy InxGa1-xN using EPM without taking into account the disorder effect. Our results show that the bowing parameter b of the effective mass depends strongly on the indium composition. Generally, a good accord was obtained between our results and data quoted in the literature for InN and GaN materials. Therefore, more experimental measurements and first-principles calculations are needed in order to obtain more accurate and reliable results for wurtzite InxGa1-xN.

