International Journal of Robotic Engineering
(ISSN: 2631-5106)
Volume 5, Issue 1
Research Article
DOI: 10.35840/2631-5106/4123
Linear Adaptive Fault Tolerant Control against Aircraft Actuator Failures for Wing Rock Suppression
Hamza Benchaita and Samir Ladaci*
Table of Content
Figures
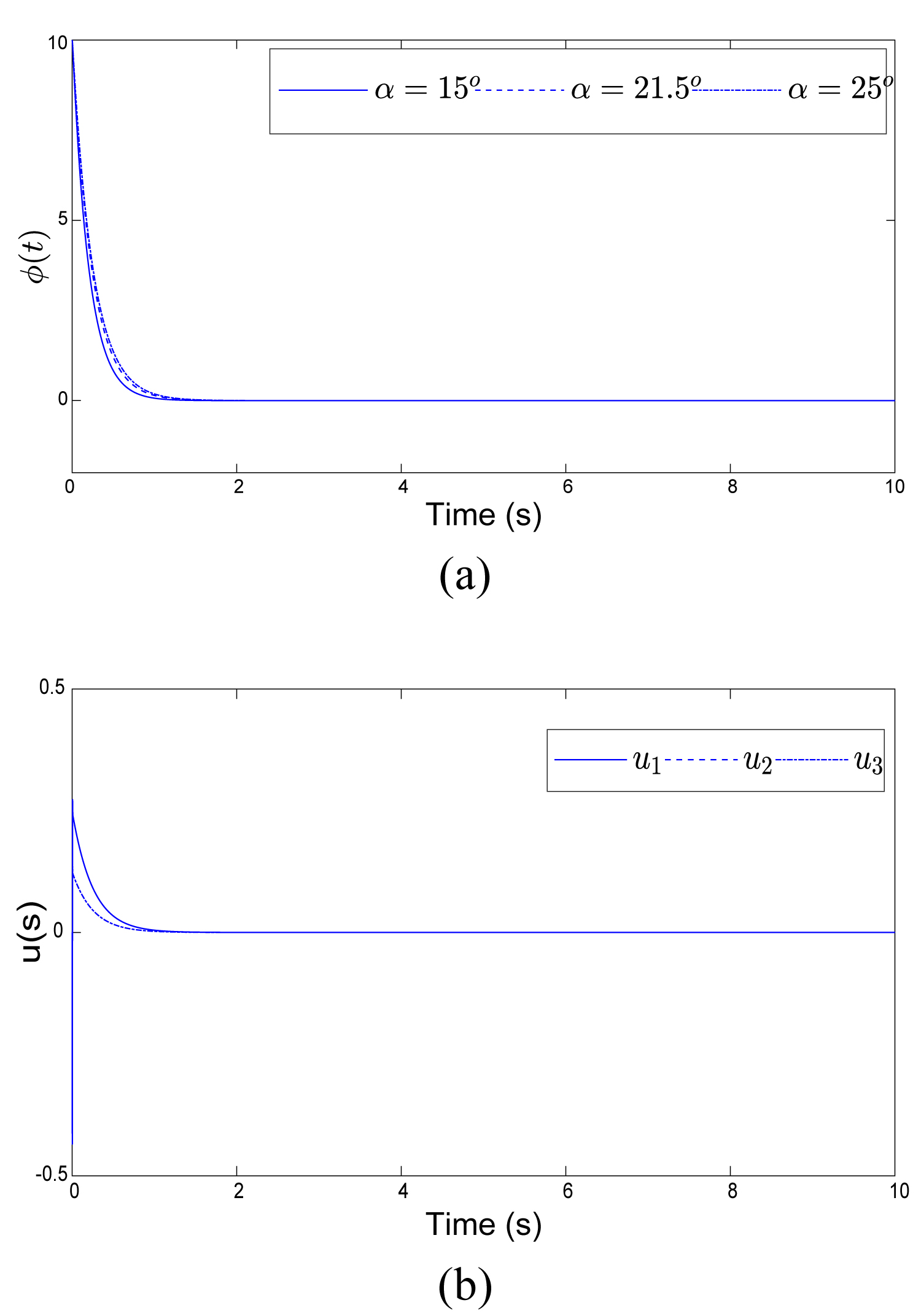
Figure 4: System response without failure....
System response without failure: a) Output ; b) Control input .
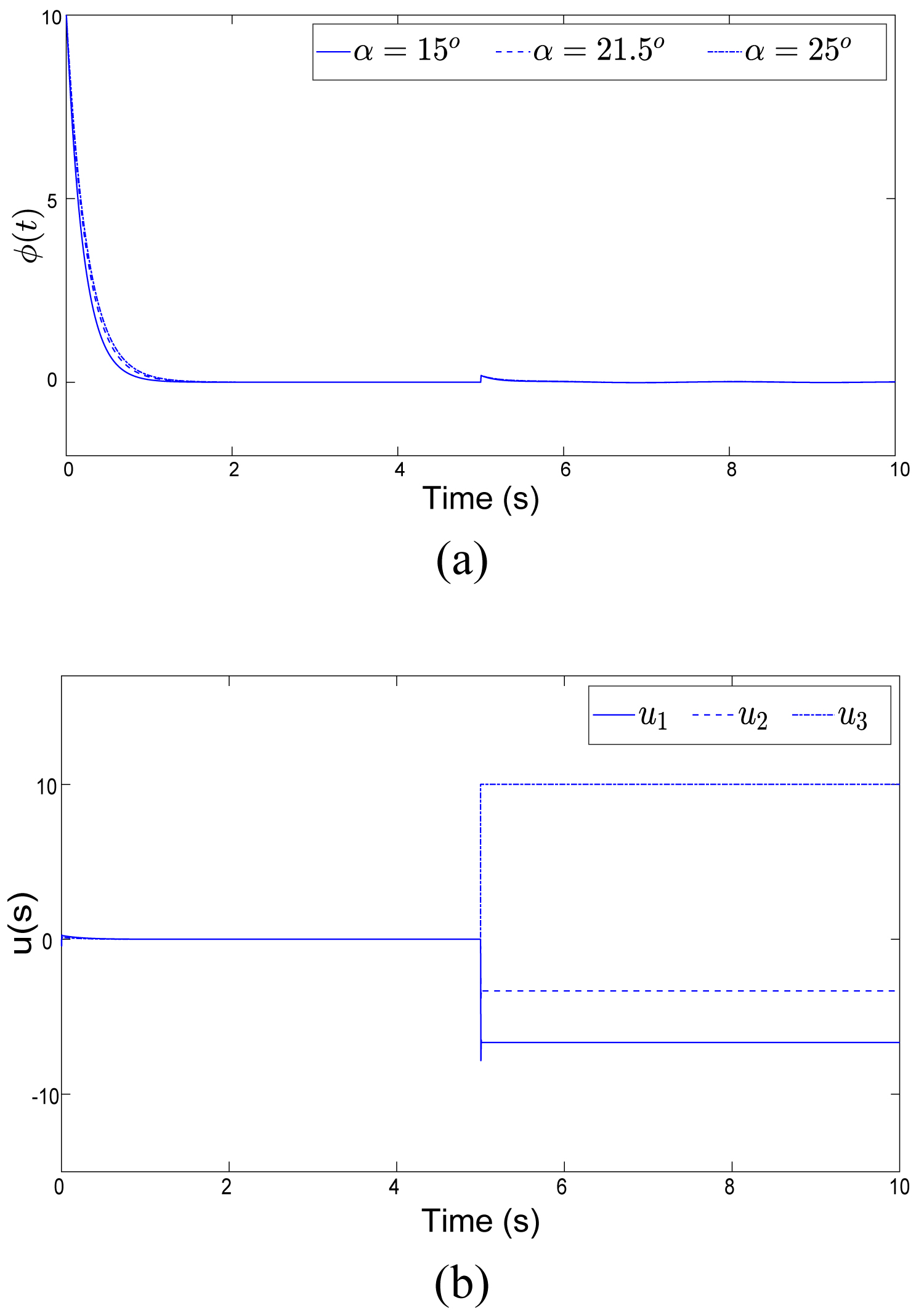
Figure 5: System response in the failure case 1....
System response in the failure case 1: a) Output ; b) Control input .
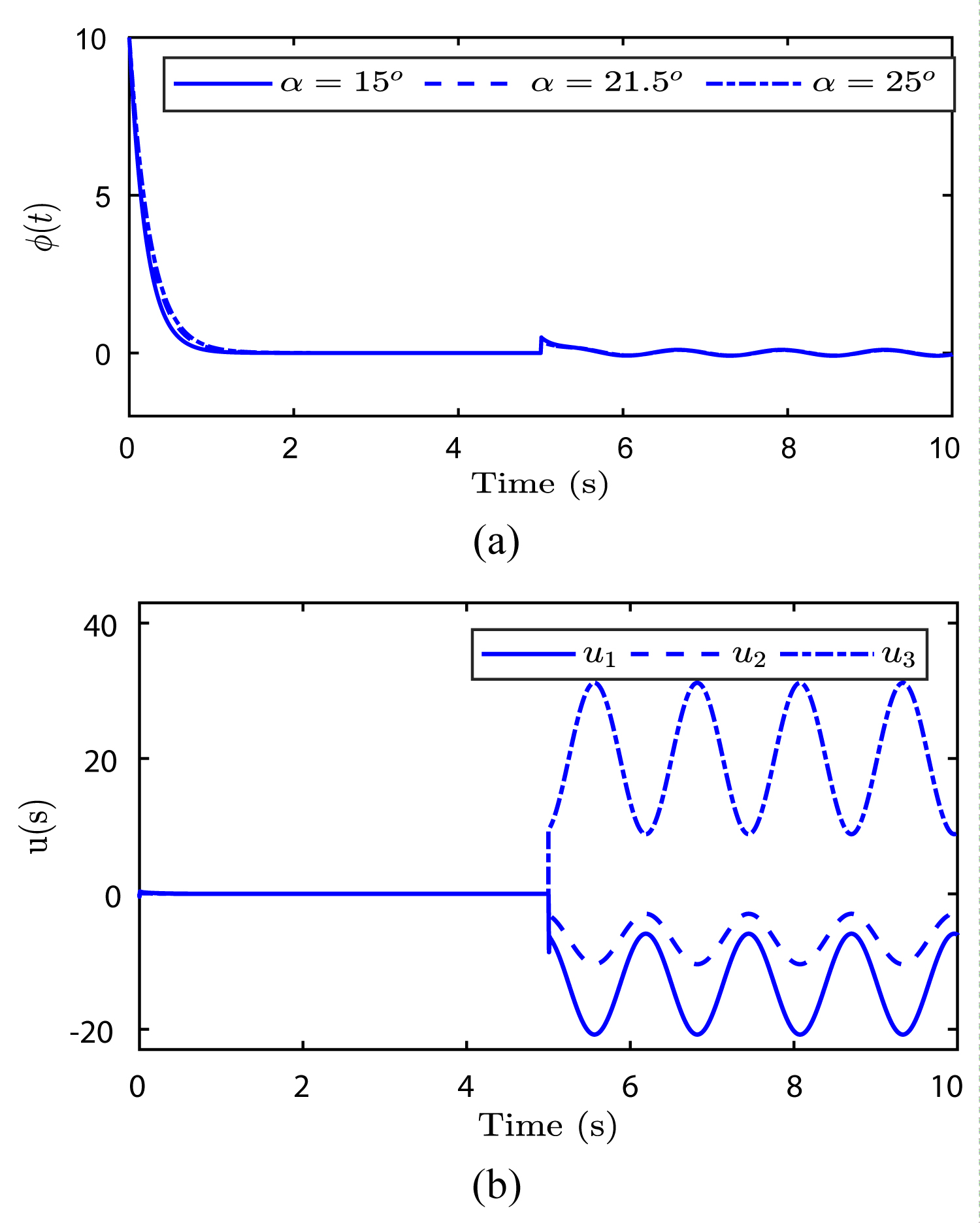
Figure 6: System response in the failure case 2...
System response in the failure case 2: a) Output ; b) Control input .

Figure 7: System response in the failure case 3...
System response in the failure case 3: a) Output ; b) Control input .
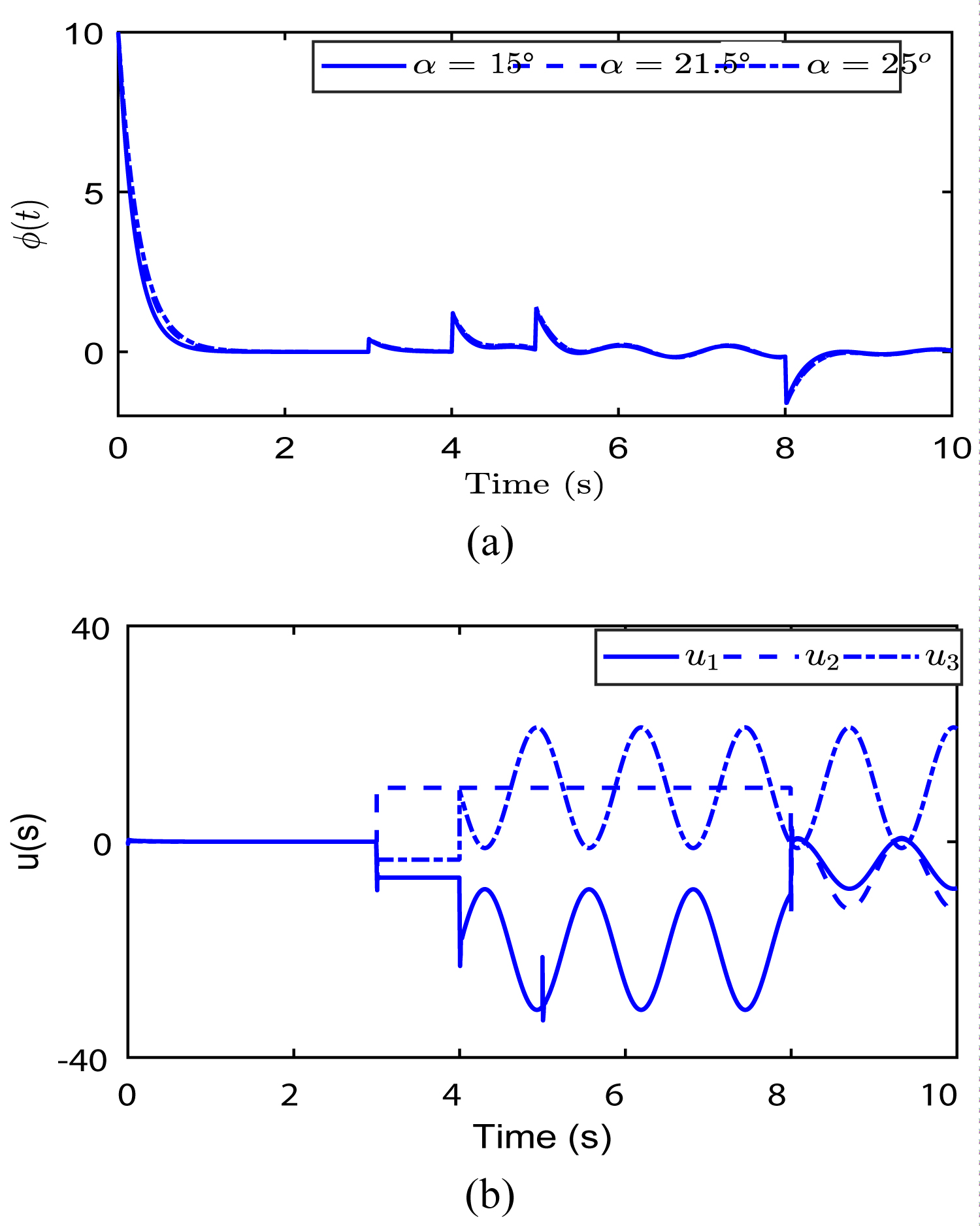
Figure 8: System response in the failure case 4....
System response in the failure case 4: a) Output ; b) Control input .
References
- AH Nayfeh, JM Elzebda, DT Mook (1989) Analytical study of the subsonic wing-rock phenomenon for slender delta wings. J Aircraft 26: 805-809.
- G Guglieri, F Quagliotti (2001) Analytical and experimental analysis of wing rock. Nonlinear Dynamics 24: 129-146.
- TH Go (1999) Aircraft wing rock dynamics and control. Ph.D. Thesis Department of Aeronautics and Astronautics, MIT, USA.
- G Guglieri, D Sartori (2013) Design of a sliding mode control for wing rock suppression in highly-swept wing aircraft. International Journal of Aerospace Sciences 2: 1-10.
- S Boulouma, S Labiod, H Boubertakh (2017) Linear adaptive actuator failure compensation for wing rock motion control. Aerospace Science and Technology 67: 155-168.
- R Ordonez, KM Passino (2000) Wing rock regulation with a time-varying angle of attack. 15th IEEE Int Symposium on Intelligent Control (ISIC 2000), Greece, 145-150.
- J Pietrucha, K Sibilski, AS Mroziewicz, M Zlocka, A Zyluk (2009) Comparative analysis of wing rock control. 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, 58.
- C Hsu, CE Lan (1985) Theory of wing rock. J Aircraft 22: 920-924.
- TR Sisk, NW Matheny (1979) Precision controllability of the F-15 airplane. NASA technical memorandum 72861.
- B Liebst (1998) The dynamics, prediction, and control of wing rock in high- performance aircraft. Philos Trans R Soc Lond A 356: 2257-2276.
- ZL Liu, CY Su, J Svoboda (2003) Control of wing rock using fuzzy PD controller. The 12th IEEE International Conference on Fuzzy Systems 1: 414-419.
- ZL Liu, CY Su, J Svoboda (2004) Control of wing rock phenomenon with a variable universe fuzzy controller. Proceeding of the 2004 American Control Conference, England, 04: 1719-1724.
- AG Sreenatha, MV Patki, SV Joshi (2000) Fuzzy logic control for wing-rock phenomenon. Mechanics Research Communications 27: 359-364.
- AG Sreenatha, JY Choi, PP Wong (2004) Design and implementation of fuzzy logic controller for wing rock. Int J of Control Automation and Systems 2: 494-500.
- HJ Rong, S Han, GS Zhao (2014) Adaptive fuzzy control of aircraft wing-rock motion. Applied Soft Computing 14: 181-193.
- ZL Liu (2005) Reinforcement adaptive fuzzy control of wing rock phenom- ena. IEE Control Theory Appl 152: 615-620.
- SV Joshi, AG Sreenatha, J Chandrasekhar (1998) Suppression of wing rock of slender delta wings using a single neuron controller. IEEE Trans Control Systems Tech 6: 671-677.
- CF Hsu, CM Lin, TY Chen (2005) Neural-network-identification-based adaptive control of wing rock motion. Control Theory Appl 155: 65-71.
- A Tewari (2000) Nonlinear optimal control of wing rock including yawing motion. AIAA Guidance, Navigation, and Control Conference and Exhibit, USA, 14-17.
- SP Shue, RK Agarwal, P Shi (2000) Nonlinear H∞ method for control of wing rock motions. J Guid Control Dyna 23: 60-68.
- EN Abdulwahab, C Hongquan (2008) Periodic motion suppression based of control of wing rock in aircraft lateral dynamics. Aerosp Sci Technol 12: 295-301.
- M Zribi, S Alshamali, M Al-Kendari (2013) Suppression of the wing-rock phenomenon using nonlinear controllers. Nonlinear Dynamics 71: 313-322.
- S Ladaci, A Charef (2006) On fractional adaptive control. Nonlinear Dynamics 43: 365-378.
- S Ladaci, S Chettah, K Khettab (2015) Direct fractional adaptive pole placement control for minimal phase systems. Sciences and Techniques of Automatic control and computer engineering, Tunisia, 21-23.
- S Ladaci, Y Bensafia (2016) Indirect fractional order pole assignment based adaptive control. Engineering Science and Technology an International Journal 19: 518-530.
- SN Singh, W Yim, WR Wells (1995) Direct adaptive and neural control of wing-rock motion of slender delta wings. AIAA J Guid Control Dyn 18: 25-30.
- E Capello, G Guglieri, D Sartori (2012) Performance evaluation of an L1 adaptive controller for wing-body rock suppression. J Guid Control Dyn 35: 1702-1708.
- MM Monahemi, M Krstic (1996) Control of wing rock motion using adaptive feedback linearization. J Guid Control Dyna 19: 905-912.
- BB Sharma, IN Kar (2008) Adaptive control of wing rock system in uncertain environment using contraction theory. American Control Conference, USA, 2963-2968.
- G Tao, SH Chen, XD Tang, SM Joshi (2004) Adaptive control of systems with actuator failures. IEEE Transactions on Automatic Control 50: 930-931.
- J Ioannou, P Sun (1996) Robust adaptice control. Prentice Hall, Upper Saddle River, USA.
- S Ladaci, A Charef, JJ Loiseau (2009) Robust fractional adaptive control based on the strictly positive realness condition. International Journal of Applied Mathematics and Computer Science 19: 69-76.
Author Details
Hamza Benchaita and Samir Ladaci*
Department of EEA, National Polytechnic School of Constantine, Algeria
Corresponding author
Samir Ladaci, Department of EEA, National Polytechnic School of Constantine, BP 75, A, Nouvelle ville RP, Constantine, Algeria.
Accepted: March 03, 2020 | Published Online: March 05, 2020
Citation: Benchaita H, Ladaci S (2020) Linear Adaptive Fault Tolerant Control against Aircraft Actuator Failures for Wing Rock Suppression. Int J Robot Eng 5:023.
Copyright: © 2020 Benchaita H, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this paper we consider the problem of the suppression of wing rock phenomenon in presence of actuator faults. The main aim of this work is the application of a linear adaptive actuator failure compensation control scheme for wing rock motion of a slender delta wing. First, the analytical nonlinear model that characterizes the phenomenon of wing rock is given, and its behavior for different angles of attack is presented. Then, an adaptive actuator failure compensation redundant control design is proposed, and applied for a rolling motion regulation in the presence of actuator faults. Finally, numerical simulations are conducted to show the effectiveness of the control scheme for wing rock suppression for different actuator failures scenarios.
Index Terms
Wing-rock motion, Actuator failures, Fault tol- erant control, Adaptive control
Introduction
Wing rock phenomenon is a self-induced rolling motion that can happen on both civilian or military aircrafts and can show by limit cycle oscillations in high speed regimes [1,2]. Many factors can cause these undesirable behavior even at low or high angles-of-attack (AOA) such as fluid flow past an aircraft; with many risks for the aircraft operating dynamics, maneuvering flexibility leading sometimes to loss of control [3].
The wing rock phenomenon is characterized by some aerodynamic parameters which are [4]:
1. Angle of Attack (AOA),
2. Angle of sweep,
3. Leading edge extensions,
4. Slender forebody.
Aircraft with highly swept wings operating with leading edge extensions are highly susceptible to suffer from this problem. Generally we remark an increase in amplitude up to a limit cycle, then a final state is usually stable and defined by large roll oscillations [5,6].
Many research works have focused on the analysis and modelization of this phenomenon in order to predict the magnitude and the frequency of the limit-cycle limitations [7,8], and since many mathematical and numerical models with different precision orders have been developed based on experimental simulations on benchmarks [9,10].
The problem of suppressing wing rock has a very rich state of the art. A great number of control solution have been proposed with more or less success, most of them are using simple second order models. Many authors have proposed fuzzy controllers to eliminate these oscillations. Among them, Liu, et al. proposed fuzzy PD controller [11] and a variable universe fuzzy controller [12] with a satisfactory performance at different AOA. Whereas, Sreenatha, et al. [13,14] tried out a forty-nine rule based FLC with the delta wing model in the wind tunnel with results indicating the effectiveness and robustness of the FLC. Other works used adaptive fuzzy controllers to improve the aircraft behavior like Rong, et al. [15] and Liu [16].
Another solution was the neural control proposed by Joshi, et al. [17] and Hsu, et al. [18] with a good ability to achieve favorable tracking performance for the wing rock motion for an aircraft operating at subsonic speeds and high angles of attack. In [19], Tewari used an optimal feedback controller, derived from the Hamilton Jacobi equations, to suppress wing- rock oscillations.
At meantime, some other researchers tried nonlinear control strategies like Shue and Agarwal [20] who introduced a nonlinear H∞ method for the control of wing rock motions. In [21], Abdulwahab and Hongquan achieved limit cycle prevention by adding a certain control function to the nonlinear dynamics of the wing-rock model; Zribi, et al. [22] introduced a state transformation such that the transformed dynamic model is in a form which is suitable for a variety of control designs. A feedback linearization control scheme and a sliding-mode control (SMC) scheme are then proposed to suppress wing rock oscillations.
One of the more efficient control techniques is adaptive control [23] which is more suitable in case of unknown or varying model parameters. According to the fact that the model is identified or not by the control algorithm there are direct [24] and indirect [25] adaptive control schemes.
Singh, et al. [26] and Capello, et al. [27] and proposed adaptive control strategies for the problem of wing rock suppression. Adaptive feedback linearization is proposed to suppress the wing rock by Monahemi and Krstic [28]. The work of Ordonez and Passino [6] considers the regulation of a wing- rock problem via nonadaptive as well as adaptive controllers for the case of time-varying AOA. In the case of model uncertainties, Sharma and Kar [29] used contraction theory in the development of an adaptive backstepping controller for the suppression control of the wingrock phenomenon.
However, most of these works only considered the failure free case even if the occurrence of such failures on an aircraft is very critical. Some authors have addressed this important problem particularly the actuators' failures like the works of Tao, et al. [30] and Boulouma, et al. [5] who developed an adaptive controller tolerant to actuators' failures.
In this paper we address the problem of wing rock suppression in presence of various actuator failures and propose a linear adaptive control design for this phenomenon model derived in [1]. And we show using numerical simulation that this adaptive controller is able to suppress the undesirable wing rocks rapidly and efficiently.
The reminder of this paper is organized as follows: Section II presents the wing-rock modelization and the control problem definition. The proposed robust adaptive control design is detailed in Section II-C. In Section III, simulations results are presented to illustrate the efficiency of the proposed robust adaptive control method. Concluding remarks are given in Section IV.
Problem Statement
Wing-rock dynamical model
In this paper, we consider the model proposed by Nayfeh, et al. [1] which is described by the following differential equation,
With,
We have = 0.354 and = 0.001.
The ai coefficients values depend on the incidence angle α. Table 1 give the values of ai parameters for some values of α.
Let us rewrite equation (1) in the state space form by taking
we get:
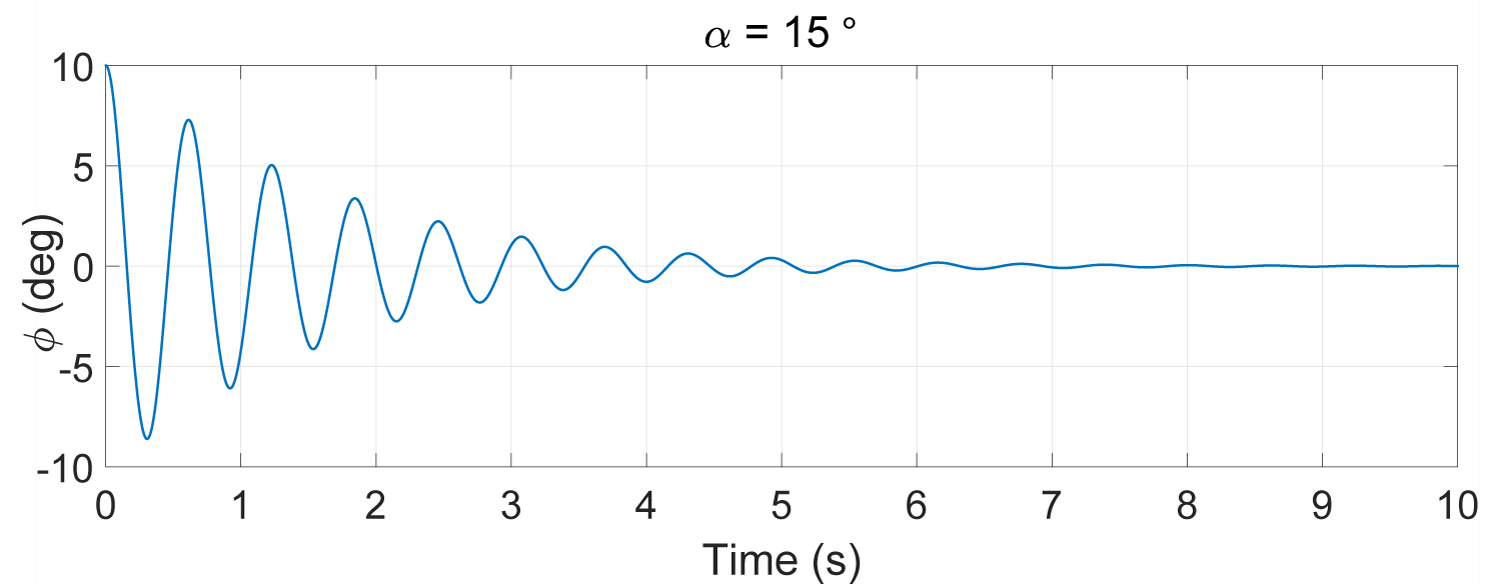
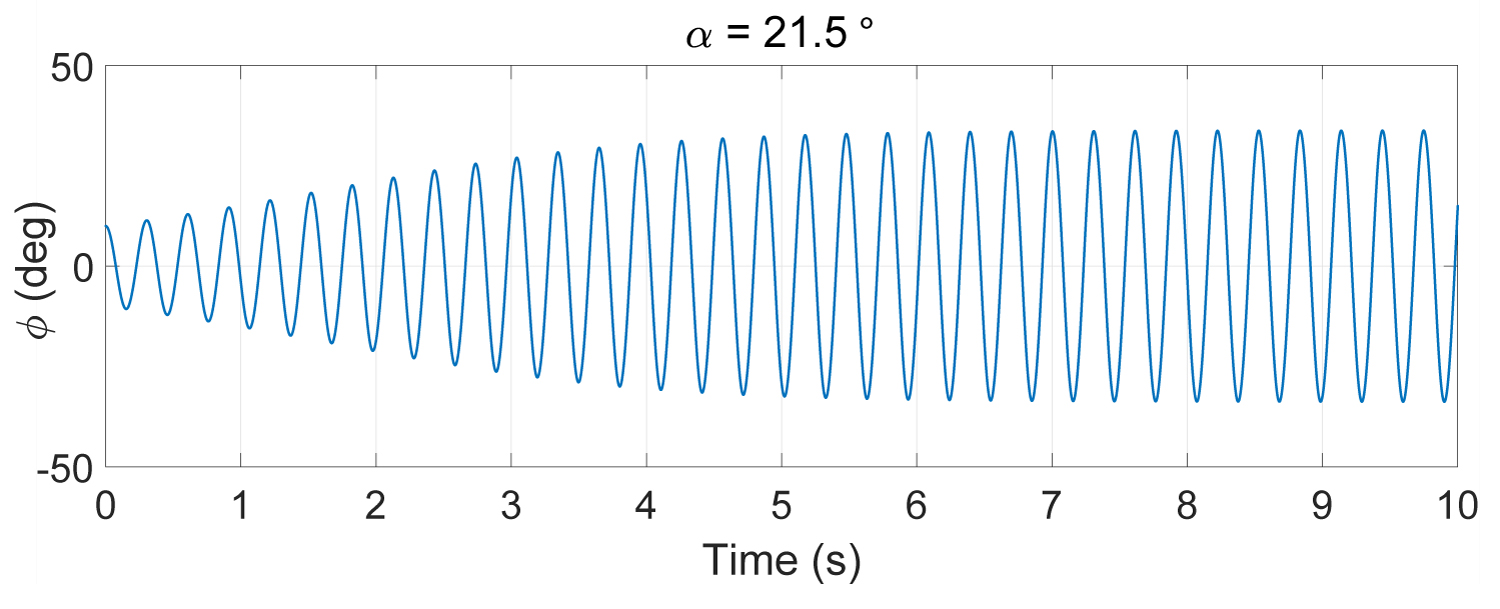
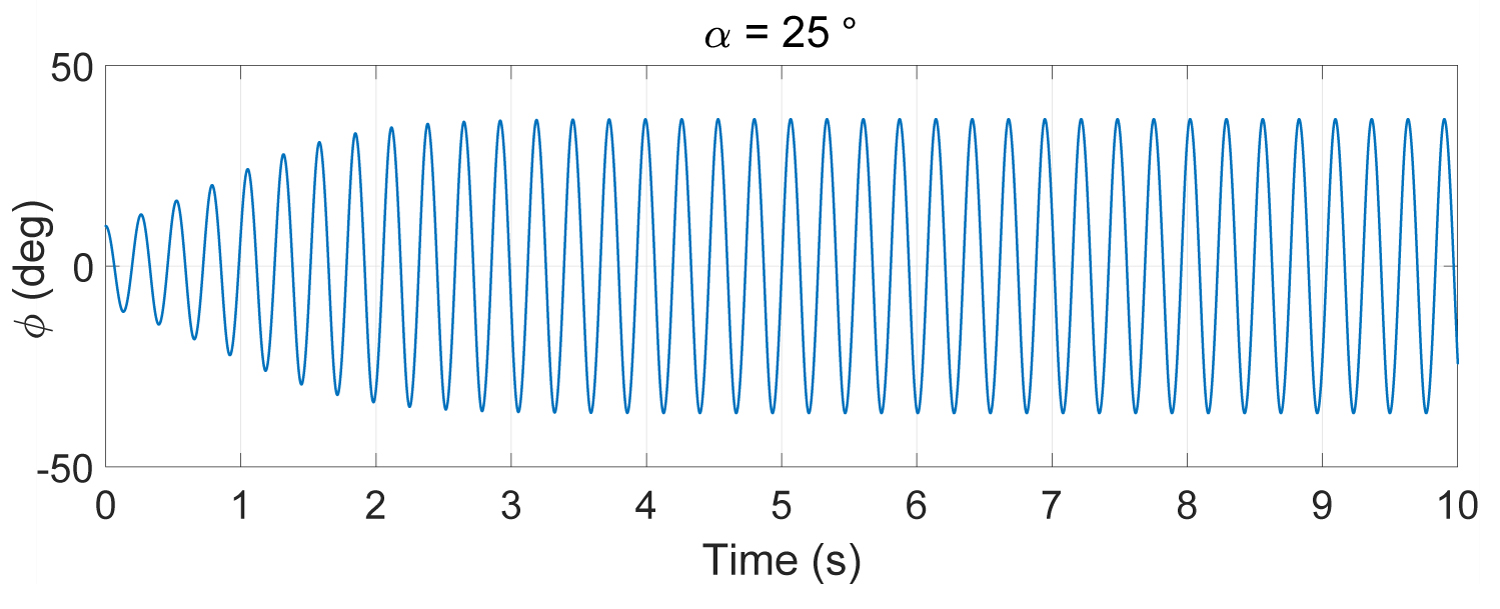
In [1] it is shown that the model is stable for the incidence angles α < 19.5 deg. for more important angles, it begins to oscillate and becomes unstable. We remark an augmentation of the oscillations magnitude until it reaches a limit-cycle.
Figure 1, Figure 2 and Figure 3 represent the open loop system response for the incidence angles α = 15°, α = 21.5° and α = 25° respectively.
In the simulation work, we consider three aileron segments δ as a control input and the roll angle as the system output. Introducing the control u = [u1, u2, u3] we can rewrite (2) as follows,
In order to design a fault tolerant control for the system stabilization, the actuators redundancy is necessary, thus, the control will be provided by the three aileron segments u = [u1, u2, u3]T.
Thus (3) becomes
Equation (4) can be rewritten in a compact form as,
With,
Actuators failures modelization
The actuators' defaults considered by Boulouma, et al. [5] are of two types:
Type 1 - Total loss of the actuator efficiency: At the instant , the input is no more influenced by the applied control law, which could be described by,
Where the constant value and the occurrence moment are unknown; this failure case is very frequent in the flight control systems (rudder, aileron, elevon rod). It is caracterized by the actuator blocking in some given position.
A more general case is the model of time varying parametric failure [30] modelized as,
With,
for unknown constant values and known signals
The actuator failure model given in (7) allows the approxima-tion of a great number of failure cases, by a judicious choice of the basic functions [30].
We can rewrite (7) as follows,
Where is the unknown failures values vector, and is the chosen basic functions vector.
Type 2 - Partial loss of efficiency: In this case the input remains partially influenced by the applied control law.
In case there two types of failures conjointly, we can rewrite the control law as follows:
Where with if the actuator has a failure and otherwise.
The aim of the proposed control is to design a control strategy that allows the estimation and the compensation the actuators' failures that occur in the system (1).
However it is mandatory for the controller to have a redundant actuators in order to be able to compensate the failures of one or multiple actuators, that means, these actuators do the same tasks.
In our problem, we suppose that the redundant actuators contribute proportionally to the system regulation (see [5,30]), which has the advantage to render the control design procedure from a MISO problem to a SISO one. So, we can define the control to be applied as follows
Robust adaptive control design
In this Section we will develop the proposed adaptive control law following the method proposed in [5]. From (3), we can write,
In case there are two types of failures (11), the equation (13) becomes,
Taking,
and
and replacing in (14), we get,
Our objective is to design a control law that forces the output to follow the reference signal (in our case ) and guarantees the closed loop stability of the nonlinear system in presence of disturbing terms that modelize the actuators failures which can occur during the system operation.
It is worth noticing that the control law design and stability analysis are detailed in [5]. We will give the resulting adaptive control law that satisfies the control objectives,
With the θ parameter updating and the unknown term given as follows,
With j = 1, 2, 3.
In order to ensure that the parameters' vector is bounded and to improve the robustness of the adaptive control laws (17) and (18) in presence of approximation errors, a supplementary term has been introduced as follows [31,32],
With j = 1,2,3.
In the next Section we will simulate the response of the system (5) by considering different cases of actuator failures.
Simulations Et Discussions
In order evaluate the tracking performance of the proposed adaptive control strategy by numerical simulation we will consider the aerodynamic parameters of the delta wing modelized by Nayfeh, et al. [1] for different angles of attack α. Four actuators are available on the aircraft and are perfectly redundant.
It is assumed that the model parameters are: c1 = 0.354, c2 = 0.001, and the coefficients ai are given in Table 1.
First, we will simulate the system response without any actuator failure with the initial conditions: (0) = 10°. The simulation result is shown in Figure 4. We observe that the adaptive controller stabilizes the system and eliminates the oscillations with a fast transitory response. We remark also that the system performance are not sensitive to the attack angle variations.
At the second stage we will simulate our regulator in presence of different actuator failure scenarios. Four cases are considered:
Failure scenario 1
The initial conditions are (0) = 10°. The first actuator remains intact: u1 (t) = v1 (t), and at the instant t = 3s, the second actuator is in fail situation to 50% amount: u2 (t) = 0.5v2 (t), and the third actuator is blocked in = 10 beginning from t = 5s.
Figure 5 shows that the adaptive controller handles perfectly the partial loss of efficiency of u2, and when u3 is blocked the control action redistributes the necessary effort in order to stabilize the system with the two still operating actuators. The moment of failure occurrence at t = 5s involves a small deviation of the angle which is quickly corrected by the controller.
Failure scenario 2
The initial conditions are (0) = 10°. The first actuator remains uninjured: u1(t) = v1(t), from the instant t = 3s the second one loses 50% of efficiency: u2 (t) = 0.5v2 (t), and from the moment t = 5s the third actuator becomes uncontrollable and begins to oscillate as u3 (t) = 20 + 5 sin(5t) - 10 cos(5t).
As we can see in Figure 6, the controller compensates the uncontrollable variations of the actuator u3 and succeeds to stabilize the system with very negligible oscillations around 0 caused by the failing actuator. The control effort is portioned on the two other actuators to eliminate this undesirable effect.
Failure scenario 3
The initial conditions are (0) = 10°. The first actuator remains uninjured: u1(t) = v1 (t), from the instant t = 3s the third actuator is blocked at = 15 then it retrieves its efficiency at the instant t = 8s: u3(t) = v3 (t), for t > 6s the second actuator is only 30% efficient: u2(t) = 0.3v2 (t).
As for the first scenario, we can remark from the Figure 7 that the controller is able to correct efficiently the bad behavior due to the blocked actuator with the remaining actuators even if partially efficient. The two observed deviations at instants t = 3s and t = 8s are caused by the blockage of u3 and the moment of its resumption respectively.
Failure scenario 4
The initial conditions are (0) = 10°, (0) = 0°/s. from the instant t = 5s, the first actuator becomes 70% efficient: u1(t) = 0.7v1 (t), and at the instant t = 3s the second one loses its efficiency and remains blocked at = 10 then it is reactivated at the instant t = 8s. And for t > 6s, the third actuator begins to oscillate following the form u3(t) = 10 + 5 sin (5t) - 10 cos (5t).
In presence of different types of failures, the controller remains efficient in terms of system stabilization and reference track- ing. Figure 8 shows more important deviations of the angle α at the actuators' failures' instants due to the fact the remaining actuator u1 is only partially efficient, but is able to stabilize the system.
Conclusion
In this paper, we introduce an adaptive fault tolerant control strategy to deal with wing rock oscillation due to the aircraft actuators failures. Considering four redundant actuators, we have applied our proposed control design to a system model defining this phenomenon for different attack angles.
Many scenarios of multiple actuators' failures have been simulated numerically to illustrate the efficiency of this robust adaptive controller. The simulation results show that the proposed adaptive control law is able to stabilize the aircraft even in case of actuator failure and system parameters variation.
However, this may lead to a large control signal, and this problem is to be addressed in future research work. In particular, the use of fractional order adaptive controllers to improve these encouraging results is being worked out.