International Journal of Robotic Engineering
(ISSN: 2631-5106)
Volume 5, Issue 1
Research Article
DOI: 10.35840/2631-5106/4124
Fractional Order Control for the Grasping by Coiling
Mircea Ivanescu1*, Mihaela Florescu2 and Cristian Vladu3
Table of Content
Figures

Figure 10: Circle criterion for continuum arm with.....
Circle criterion for continuum arm with high gravitational component.
References
- Deghami M, Moosavin S (2014) Dynamics modeling of a continuum robotic arm with a contact point in planar grasp. Journal of Robotics 308283.
- Robinson G, Davies JBC (1999) Continuum robots-A state of the art. IEEE Int Conf on Robotics and Automation, Detroit, USA, 2849-2854.
- Gravagne Ian A, Walker ID (2000) On the kinematics of remotely-actuated continuum robots. Proc 2000 IEEE Int Conf on Rob and Aut, San Francisco, 2544-2550.
- Gravagne IA, Walker ID (2000) Kinematic transformations for remotely-actuated planar continuum robots. Proc 2000 IEEE Int Conf on Rob and Aut, San Francisco, 19-26.
- Gravagne IA, Walker ID (2002) Uniform regulation of a multi-section continuum manipulators. Proc 2002 IEEE Int Conf on Rob and Aut, Washington, USA, 1519-1525.
- Gravagne I, Walker ID (2001) Manipulability and force ellipsoids for continuum robot manipulators. Proc 2001 IEEE/RSJ International Conference on Intelligent Robors and Systems, Maui, Hawaii, USA, 304-310.
- Chirikjian GS, Burdick JW (1990) An obstacle avoidance algorithm for hyper-redundant manipulators. Proc IEEE Int Conf on Rob and Aut, Cincinnati, Ohio, USA, 625-631.
- Mochiyama H, Kobayashi H (1999) The shape Jacobian of a manipulator with hyper degrees of freedom. Proc 1999 IEEE Int Conf on Robotics and Automation, Detroit, USA, 2837-2842.
- Jinglin L, Jing X (2011) Determining grasping configurations for a spatial continuum manipulator. 2011 IEEE/RSJ Int Conf on Intelligent Robots and Systems, San Francisco, USA, 4207-4213.
- Walker IM, Hannan M (1999) A novel elephant's trunk robot. AIM 99: 410-415.
- Jones B, Walker ID (2006) Practical kinematics for real-time implementation of continuum robots. IEEE Trans Robotics 22: 1087-1099.
- Kapadia A, Walker I, Dawson DM (2009) A model-based sliding mode controller for extensible continuum robots. Recent Advances in Signal Processing, Robotics and Automation, 103-120.
- Rucker DC, Webster RJIII, Chirikjian GS, Cowan NJ (2010) Equilibrium conformations of concentric-tube continuum robots. Int Journal of Robotic Research 29: 1263-1280.
- Popescu N, Popescu D, Ivanescu MA (2013) Spatial weight error control for a class of hyper- redundant robots. IEEE Trans on Robotics 29: 1043-1050.
- Ivanescu M, Popescu N, Popescu D (2015) The shape control of a tentacle arm. Robotica Cambridge Journal 33: 684-703.
- Ivanescu M, Popescu D, Popescu N (2015) A decoupled sliding mode control for a continuum arm. Adv Robotics, Special Issue: Continuum Robots and Manipulation 29: 831-845.
- Hammond IIIF, Kramer R, Wan Q, Howe D, Wood R (2014) Soft tactile sensor arrays for force feedback. IEEE Sensors Journal 14: 1443-1452.
- Diethelm K (2004) The analysis of fractional differential equations. Springer- Verlag, London.
- Petras I (2011) Fractional-order nonlinear systems, modeling, analysis and simulation. Higher Education Press, Springer-Verlag, London.
- Monje C, Chen YQ, Vinagre B, Hue D, Feliu V (2010) Fractional-order systems and controls. Springer Verlag London Limited.
- Norelys AC, Manuel DM, Javier AG (2014) Lyapunov functions for fractional order systems. Commun Nonlinear Sci Numer Simulat 19: 2951-2957.
- Khalil H (2003) Nonlinear Systems, Prentice Hall, New Jersey, USA.
- Li Y, Chen YQ, Podlubny I (2010) Stability of fractional order nonlinear systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput Math Appl 59: 1810-1821.
- Argarwal R, Hristova S, Regan DO (2015) Lyapunov functions and strict stability of Caputo fractional differential equations. Advances in Difference Equations 346: 2-20.
- Zhao Y, Wang Y, Liu Z (2015) Lyapunov function method for linear fractional order systems. Proc of the 34th Chinese Control Conference, 1457-1463.
- Dadras S, Soodeh D, Malek H, Chen Y (2017) A note on the lyapunov stability of fractional order nonlinear systems. In: Proc of the ASME Cleveland, Orlando, 123-129.
- Slotine JE, Weiping Li (1991) Applied nonlinear control. Prentice Hall, USA.
- Al-Saggaf UM, Mehedi IM, Rachid M, Maamar B (2017) Rotary flexible joint control by fractional order controllers. International Journal of Control, Automation and Systems 15: 2561-2569.
- Rhong L, X Peng, Zhang B (2018) A reduced-order fault detection filter design for polytopic uncertain continuous-time markovian jump systems with time-varying delays. International Journal of Control, Automation and Systems 16: 2021-2032.
- Khimani D, Patil M (2018) High performance super-twisting control for state delay systems. International Journal of Control, Automation and Systems 16: 2063-2073.
- Wu B, Wang CL, Hu YJ (2018) Stability analysis for time-delay systems with nonlinear disturbances via new generalized integral inequalities. International Journal of Control, Automation and Systems 16: 2772-2780.
- Heymann N, Podlubni I (2014) Physical interpretation of initial conditions for fractional differential with Riemann-Liouville fractional derivatives. Rheologica Acta 23: 45-63.
Author Details
Mircea Ivanescu1*, Mihaela Florescu2 and Cristian Vladu3
1Department of Mechatronics, University of Craiova, Romania
2Department of Mechanical Engineering, University of Craiova, Romania
3Department of Electrical Engineering, University of Craiova, Romania
Corresponding author
Mircea Ivanescu, Department of Mechatronics, University of Craiova, Romania.
Accepted: May 14, 2020 | Published Online: May 16, 2020
Citation: Ivanescu M, Florescu M, Vladu C (2020) Fractional Order Control for the Grasping by Coiling. Int J Robot Eng 5:024.
Copyright: © 2020 Ivanescu M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The paper studies the grasping control by coiling for a class of grippers with continuum arms. First, the fractional order model of continuum arm is proposed. The viscoelastic components are assimilated by the fractional Kevin-Voigt model and the fractional-order dynamics are inferred. A hybrid control technique with two control loops for position and force control, respectively, is proposed. The Lyapunov method for position control is applied. Sector-type constraints for input torque are implemented and frequential conditions, Popov Circle Criterion, that ensure asymptotic stability, are inferred. A conventional PD controller is proposed for the force control. Numerical simulations illustrate the performances of the control system.
Keywords
Continuum arm, Fractional-order model, Control
Introduction
In this paper, a class of arms with continuum elements that performs the grasping function by coiling is analysed. This function is often met in the animal world as octopus tentacle, the elephant's trunk or constrictor snakes. In robotic applications, this function is used to manipulate objects with geometric shapes that contain borders with concave areas (Figure 1), to objects with certain fragility and resistance to manipulate, etc. In this area of application, the architectures of continuum arm type play an important factor in determining the control laws. The specialized literature contains a large number of papers addressing the study of these models known as systems with distributed parameters. A summary of these results can be found in [1]. Among the pioneering works we can mention [2-4] which introduce the basic concepts of these models, the state equations. The dynamic models and the control laws for constrained motions are inferred in [5,6]. In [7] are discussed kinematic algorithms to avoid the obstacles of hyper-redundant manipulators. An extension of Jacobian based methods for infinite dimensional systems is presented in [8]. In [9] are studied the grasping configurations of continuum arms. Similarities of these systems with certain classes of biological models are analysed in [10]. Kinematic control for real time implementation is discussed in [11]. Sliding mode control techniques for hyper-redundant robots are studied in [12]. Architectures based on concentric tubes for the continuum arm are presented in [13]. Spatial weight error control for a class of hyper-redundant robots is treated in [14]. Shape control of the tentacle robots is presented in [15,16].
This paper studies the grasping control by coiling for a class of grippers with continuum arms. First, the fractional order model of continuum arm is proposed. The viscoelastic components are assimilated by the fractional Kevin-Voigt model and the fractional-order dynamics are inferred. A hybrid control technique with two control loops for position and force control, respectively, is proposed. The Lyapunov method for position control is applied. Sector-type constraints for input torque are implemented and frequential conditions that ensure asymptotic stability, similar to the Popov Circle Criterion for classical systems, are inferred. A conventional PD controller is proposed for the force control. Numerical simulations illustrate the performances of the control system.
The paper is structured as follows: Section 2 presents technological principles, section 3 treats the dynamic model, section 4 describes the control system, section 5 verifies the control techniques by numerical simulations, section 6 presents discussions and section 7 resumes the conclusions.
Technological Principles
The main component of the grasping system is the continuum arm that manipulates the object by exerting a sufficiently high pressure on the contact surface so that it can execute its displacement on a predetermined path. We denote this system as "Continuum Arm Grasping System (CAGS)". CAGS can achieve any position and orientation in 3-D space to surround the manipulated load on the surface of different geometric shapes. CAGS constitutes the terminal component of a conventional robot intended for current part handling functions. The present work is focused only on the control of the grasping operations.
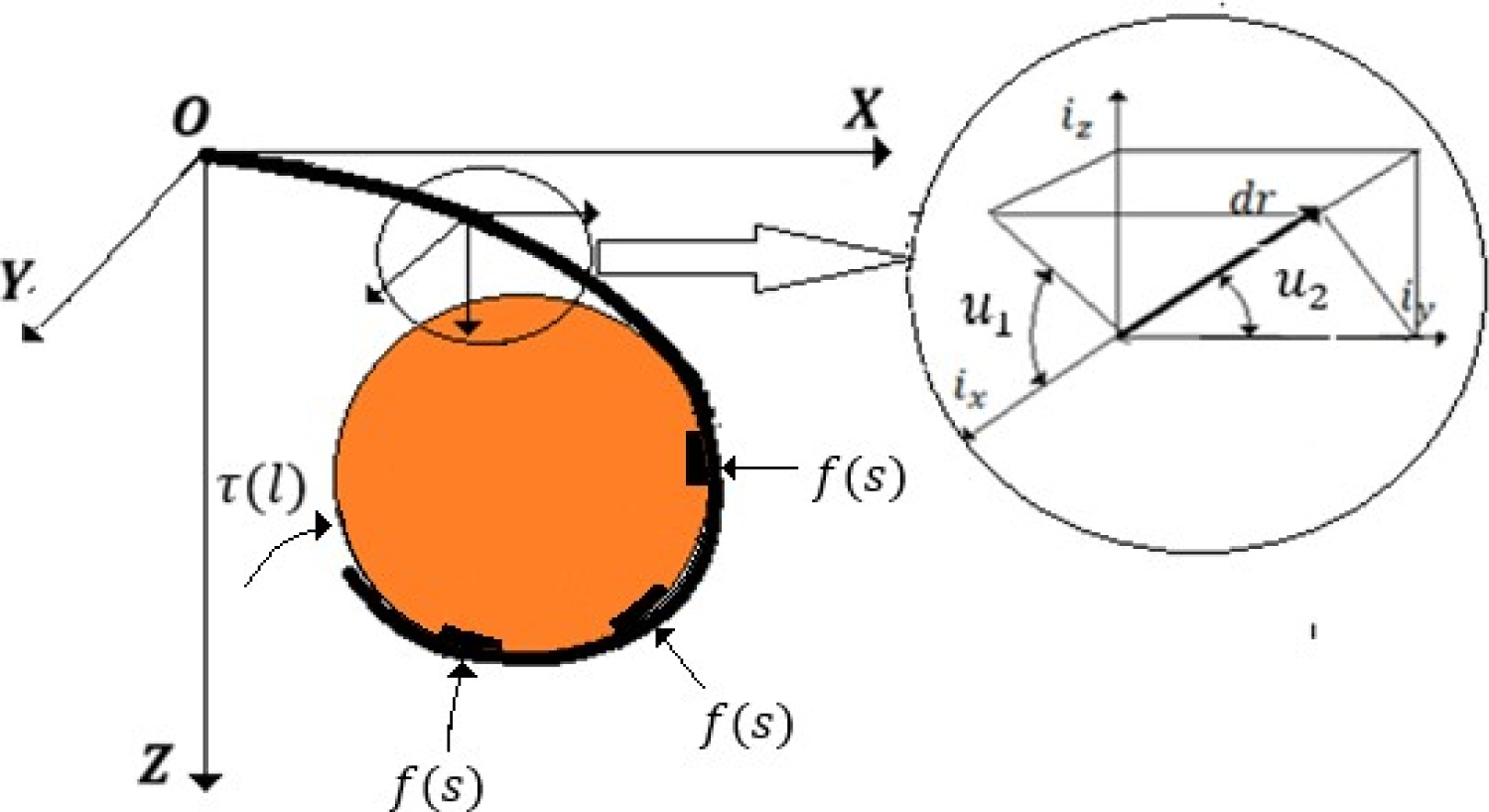
The main component of the CAGS mechanical structure is a long flexible backbone. It is surrounded by an elastic envelope and a viscoelastic solution fill the whole system ensuring a large flexibility (Figure 2). The actuation system consists of antagonistic Bowden cables with DC motor driving. The mechanical architecture is composed of several segments with independent Bowden cable driving system that allows a decoupled control strategy for each arm segment. The measuring system consists of two components: A measuring system of the geometric parameters of the orientation of the arm and one for measuring the compression forces during the grasping operation. The first system is achieved by measuring the lengths of the Bowden cables [16]. The second system is consisted by an array of Force Sensitive Resistors (FSR) (Figure 2). They are constructed of several thin flexible layers that varies in resistance as pressure is applied and released [17].
The backbone of the arm is defined by a 3-dimensional curve C and a length parameter s, , , where l is the length of the arm. The arm orientation is given by two angles , , defined by a right-handed orthonormal basis vector , where is parallel to a base coordinate frame, Figure 3.
Dynamic Model
The dynamic behaviour of the CAGS is determined by its structure with distributed mass and by the viscoelastic component characterized by the Kevin-Voigt fractional order model defined by the stress-strain relation
Where is the Caputo fractional derivative of order β. The dynamic model is derived by using Lagrange equations [5,14] for this class of hyper-redundant arms. We consider a light weight arm with following parameters: is inertial rotational density, E is equivalent elastic modulus and I is the moment of inertia. It is assumed that during the grasping operation, the arm is subjected to a disturbance, the moment m, distributed along the contact surface. In terms of the orientation variables this model can be rewritten as
Where
, , , , , , , , , , is the shortened notation for the Caputo fractional derivative. The initial conditions are
The boundary conditions are determined by the driving moments,
Where, . Technical constraints impose the sector constraints on the driving torques,
The nonlinear term is determined by the gravitational component and satisfies the constraints [14,15].
Where, is a positive constant. The system output is evaluated as a weighted average
Where and is an eigenfunction of the operator . The aim of the control problem is to ensure the movement to the target position represented by the curve ,
The evolution error will be
The dynamic model (2)-(3) becomes
Where
The fractional order model will be [18-21] .
The following fractional order model can be inferred from (9)-(12) (for simplification of notations the index i is eliminated starting from here),
Where
Grasping Control System
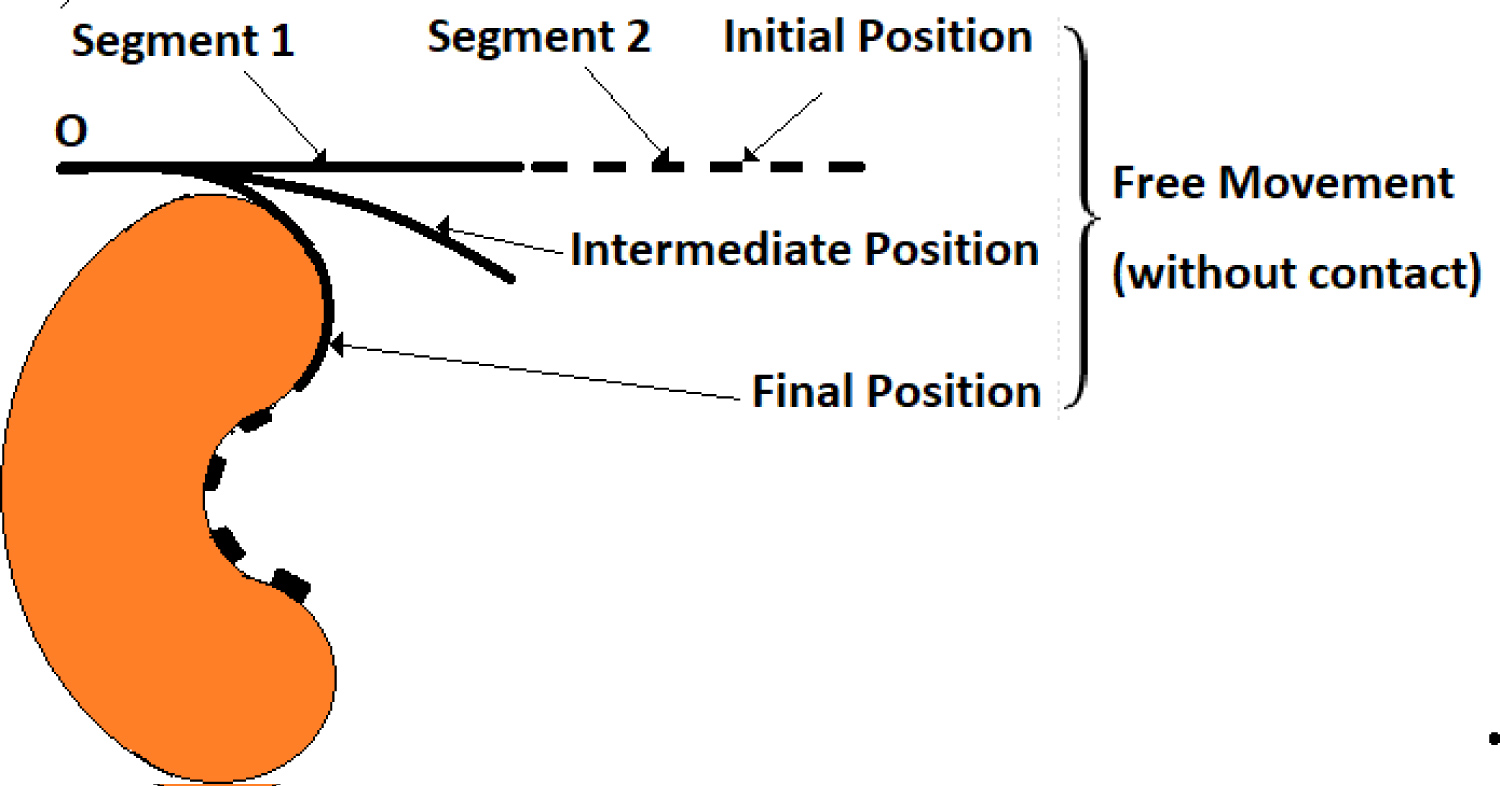
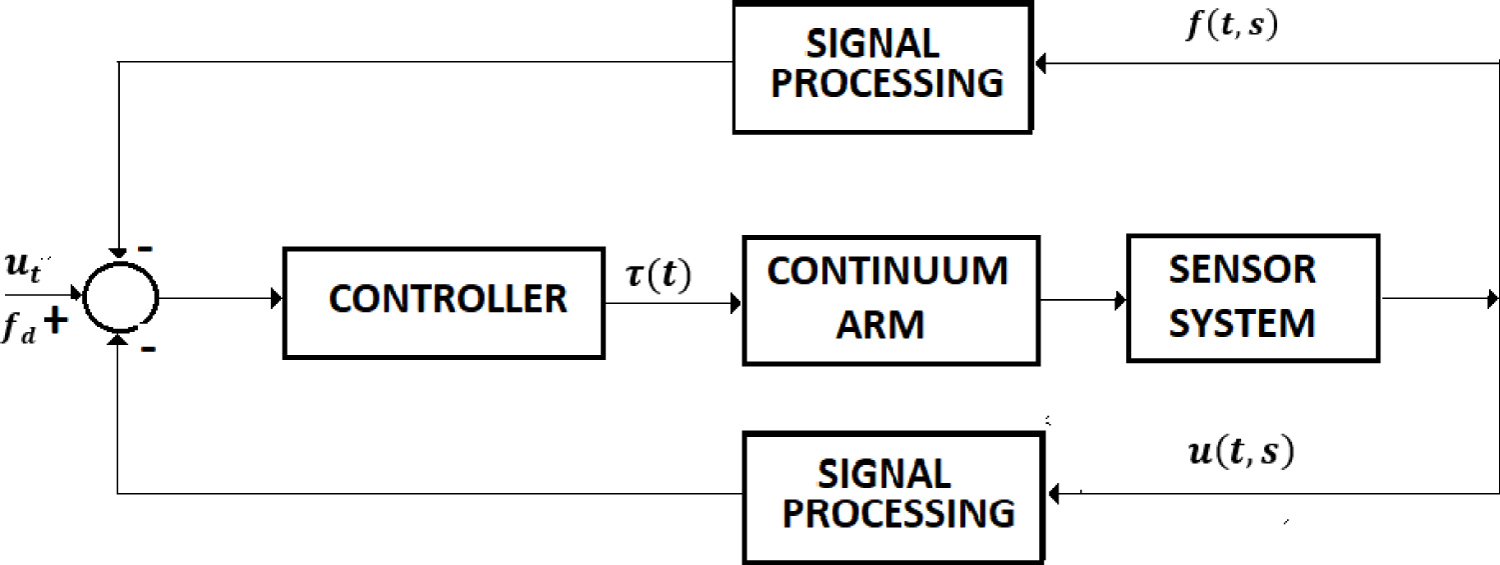
The control of the grasping operation is a hybrid control system, position-force control that comprises two phases. In the first phase, the free movement of the arm, without contact with the object, is controlled to the target position (Figure 4), in the second phase; the grasping operation is performed, the arm exerting on the object the needed compression force. The control system is shown in Figure 5.
Two cases will be analyzed: The control system for a free movement to a desired position and the control system for the control of the grasping compression forces.
Grasping position control
Dynamic model is rewritten in terms of error (13)-(18) as
Consider the control law
The force constraints (4) determine sector type restrictions on the gain k,
Where define the new sector parameters.
Algorithm 1. The dynamic system (19), with the control variable (20), (21) is asymptotically stable if:
a) is Hurwitz stable, where (22)
b)
c)
Where the following notations were used: , , P is a solution of Lyapunov equation, I is the unit matrix, and is a constant that satisfies the condition
Where, from (21) yields
The frequency inequality (23) can be interpreted in terms of the constraints (21), (26) as [22],
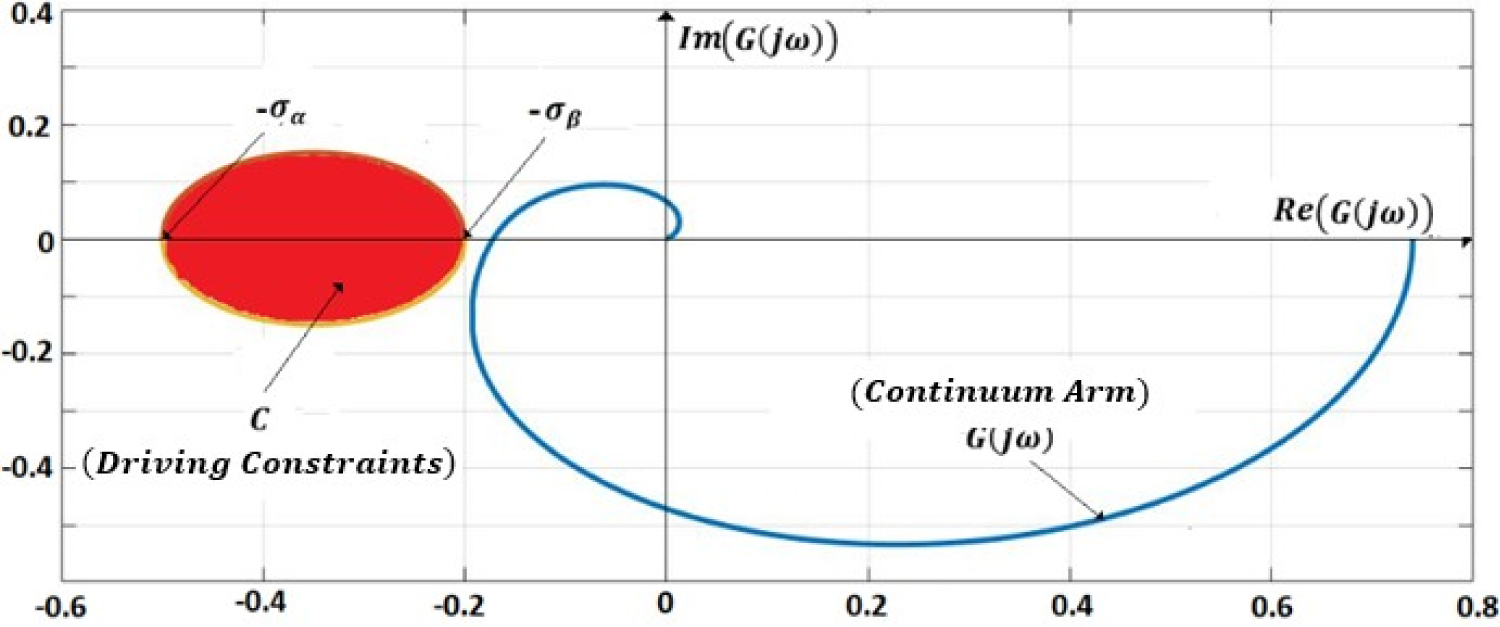
Consider that to be the circle in the complex plane (Figure 6) defined by the points and . In this case, the condition (26) can be defined as: all points of plot of must be outside the circle , or as the plot of does not intersect (Figure 6).
Because defines the frequency characteristics of the arm and represents the input constraints, the stability condition can be rewritten as:" the both domains must not intersect".
The relation (28) can be considered as an extension of the Popov's Circle Criterion for this class of fractional order models [22].
Convergence Algorithm Proof. The following Lyapunov function is used
Where, . This Lyapunov function verifies asymptotic stability conditions [19,23,24]. From [21- 26], the fractional derivative of (29) becomes
By evaluating this inequality along the solutions of (19), results
Considering (22), the relation (31) becomes
From (19), (21), (25), this inequality is rewritten as
Applying Yakubovici-Kalman-Popov (YKP) Lemma [22], yields
Substituting this result into (33), after simple calculations, considering the control law (19), it follows that
Grasping force control
Consider that the stress-strain relation of the Kevin-Voigt model (1) can be approximated by
Assume that is the measured distributed force, , is the desired, needed grasping force. The weighted average of the error is evaluated from (6) as
The force dynamics can be approximated from (1), (38), (40) using the same procedure as developed in (8),
Where are the equivalent coefficients obtained from (8).
Algorithm 2. The force control system is asymptotically stable with the following PD control law
Where are positive gains of the controller that satisfy the conditions:
Where are positive constants . that verify
Proof: The proof is simple and is obtained by Lyapunov conventional techniques [22,27].
Numerical Simulations
Consider a grasping control problem for a 2-D motion in a horizontal plane (Figure 7). The following parameters characterize the mechanical system: the length of the arm segment , the rotational inertial density , the bending stiffness , equivalent Kelvin-Voigt model coefficients: , . The fractional order model (12)-(15) will be
From (6), the constraints of the compression forces are assumed as
The system is fractional order stable but is not Hurwitz stable [28-30]. The matrix is selected to satisfy the condition (22) and the behaviour of the nonlinear model is characterized by . A control law (20) is applied with , , , , . The condition (24) is verified for , MATLAB/SIMULINK and techniques based on the Mittag-Leffler functions are used for the simulation [31,32]. A weighting eigenfunction is used. Initial position is and the target position is defined as
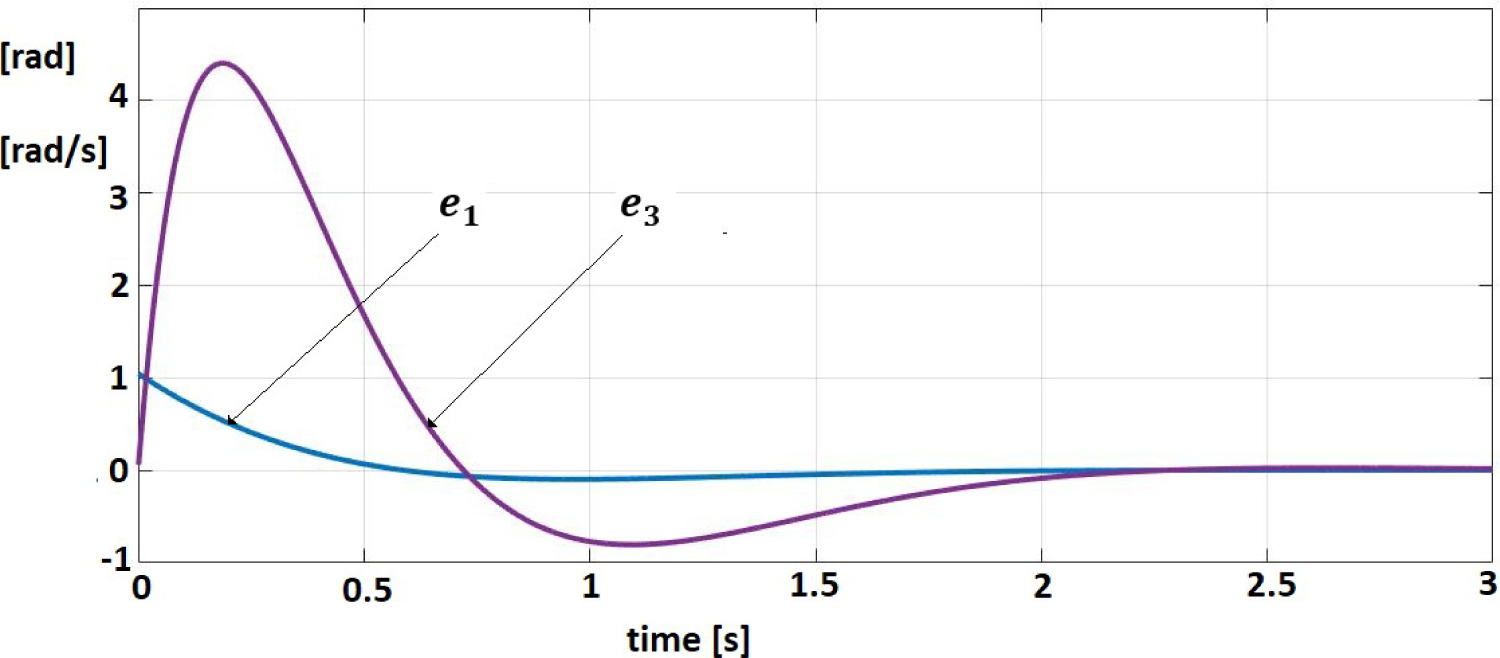
In Figure 8 are shown the error trajectories for position and velocity . The good quality of motion can be remarked from this imagine.
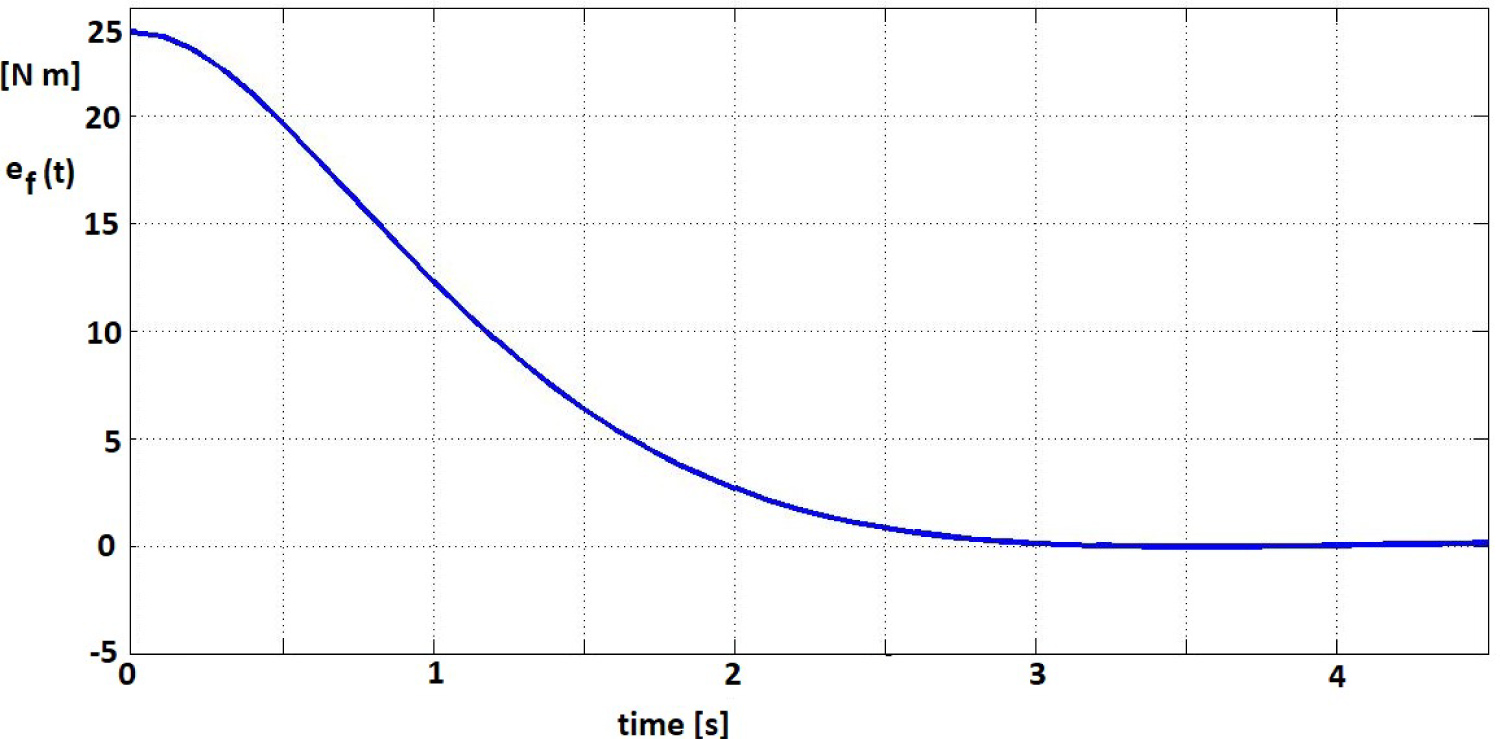
The grasping force control is obtained for with a spatial weighting average . A control law (42) with is used. The trajectory of the force error (39) is shown in Figure 9.
Discussion
The dynamic model of the continuum arm is associated with the light weight model, for which the gravitational component has a small influence. If this component increases, the stability conditions are getting worse.
In Figure 10 are shown two plots of the linear and nonlinear continuum arm models, respectively. We remark that the nonlinear component moves the plot of to the left, toward the circle C which leads to a decrease in stability. For high value of nonlinearity coefficient , when intersects the circle C, the system becomes unstable.
Conclusions
The paper studies the grasping control by coiling for a class of grippers with continuum arms. First, the fractional order model of continuum arm is proposed. The viscoelastic components are assimilated by the fractional Kevin-Voigt model and the fractional-order dynamics are inferred. A hybrid control technique with two control loops for position and force control, respectively, is proposed. The Lyapunov method for position control is applied. Sector-type constraints for input torque are implemented and frequential conditions that ensure asymptotic stability, similar to the Popov Circle Criterion for classical systems, are inferred. A conventional PD controller is proposed for the force control. Numerical simulations illustrate the performances of the control system.