International Journal of Astronautics and Aeronautical Engineering
(ISSN: 2631-5009)
Volume 3, Issue 2
Research Article
DOI: 10.35840/2631-5009/7520
Three-Dimensional Modelling and Simulation of the Ice Accretion Process on Aircraft Wings
S Chang1, H Tang1, H Wu2*, X Su1, A Lewis2 and C Ji2
Table of Content
Figures
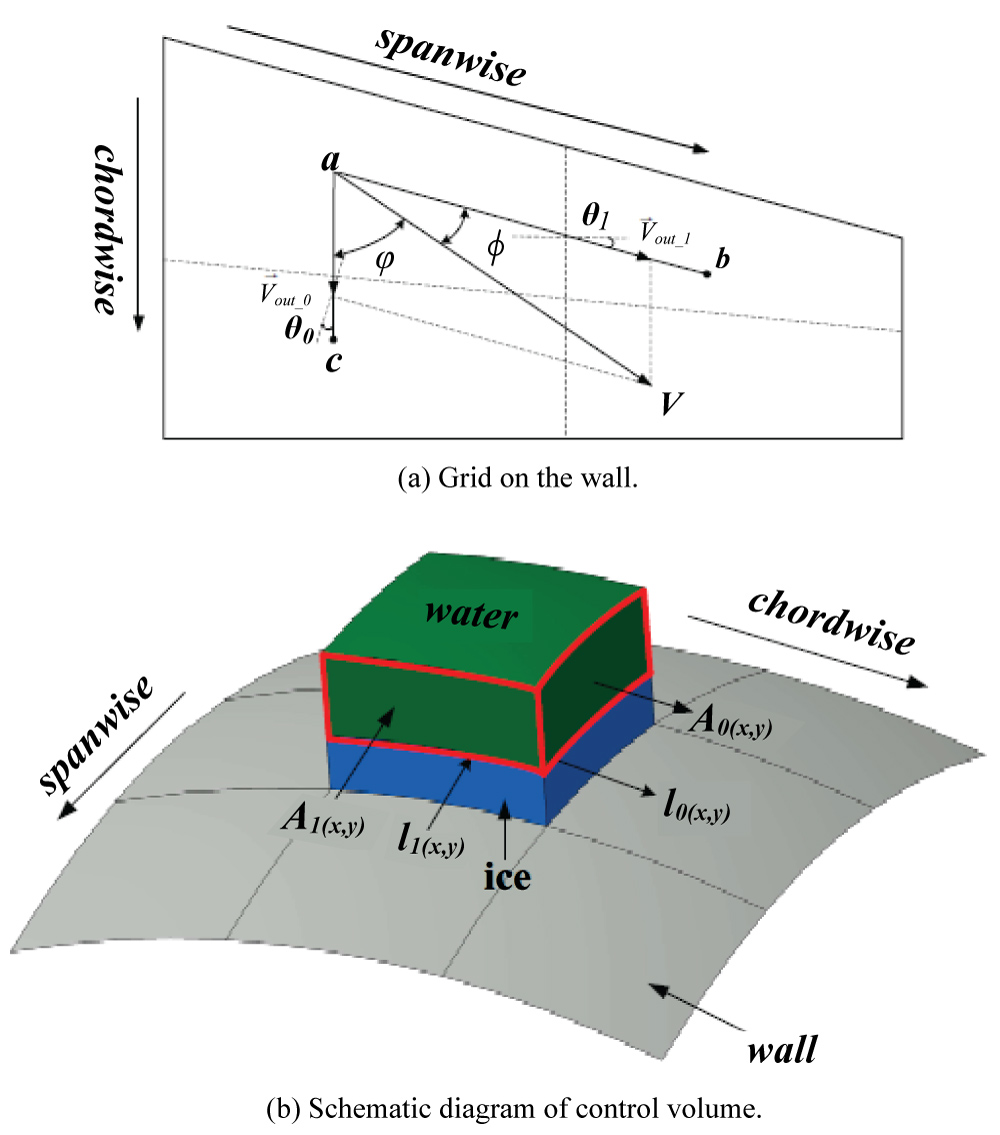
Figure 6: Components of runback water...
Components of runback water within the control volume. a) Grid on the wall; b) Schematic diagram of control volume.
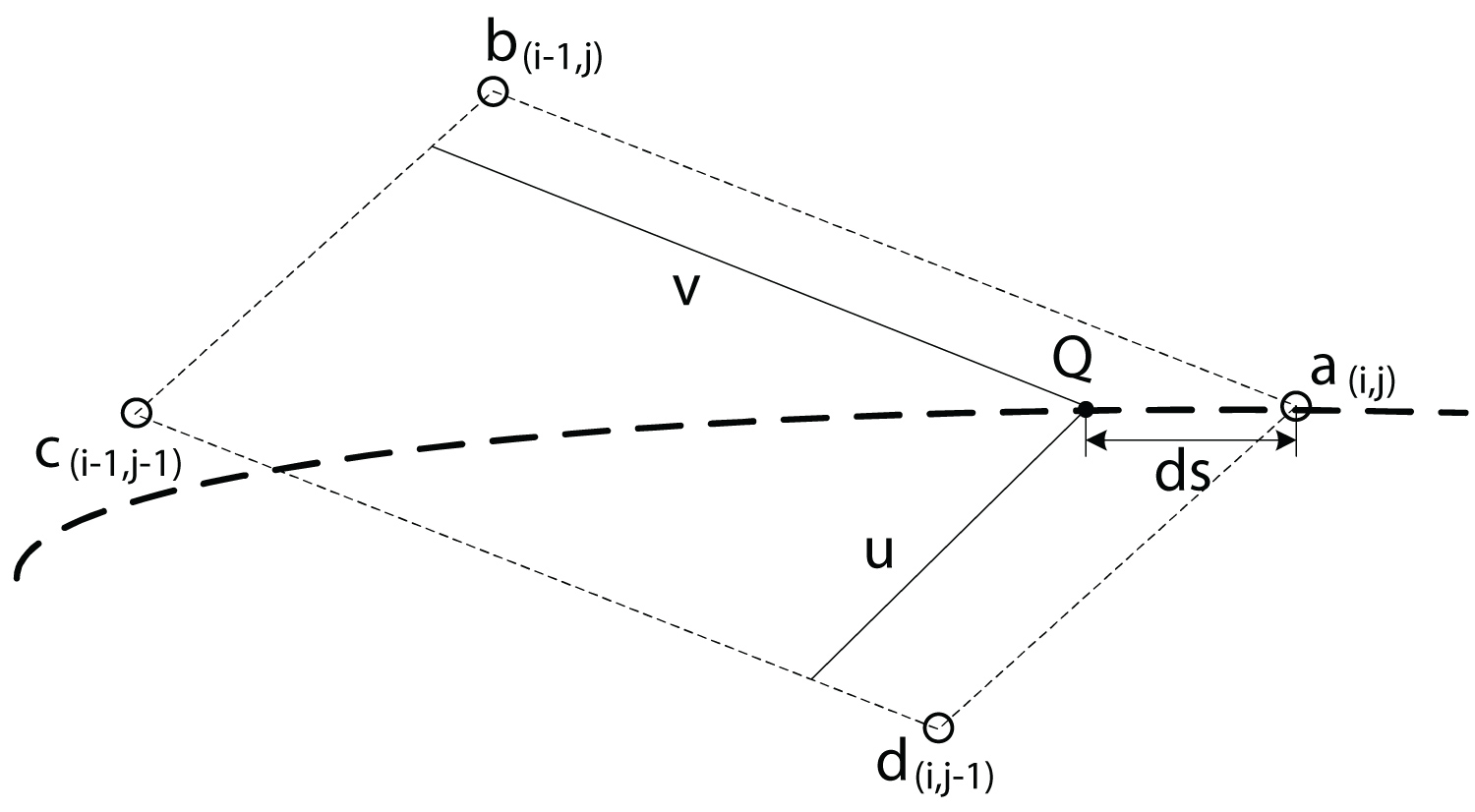
Figure 9: Velocity computation at...
Velocity computation at boundary layer edge using liner interpolation.
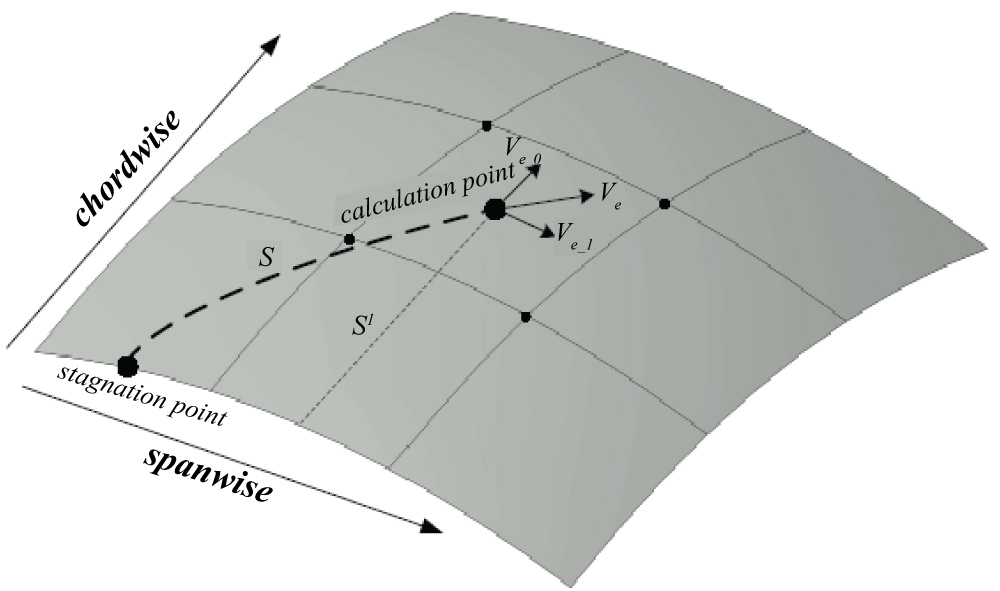
Figure 10: Schematic diagram of distance...
Schematic diagram of distance between calculation point and stagnation point.
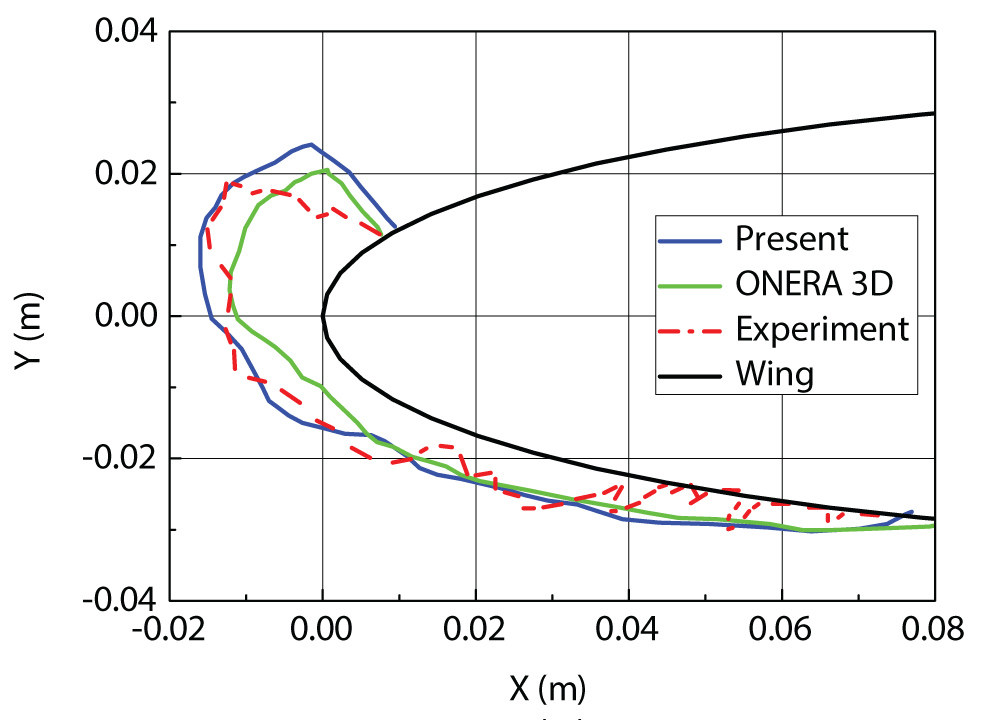
Figure 12: Comparison of ice shape...
Comparison of ice shape between present model and ONERA 3D as well as experimental data.
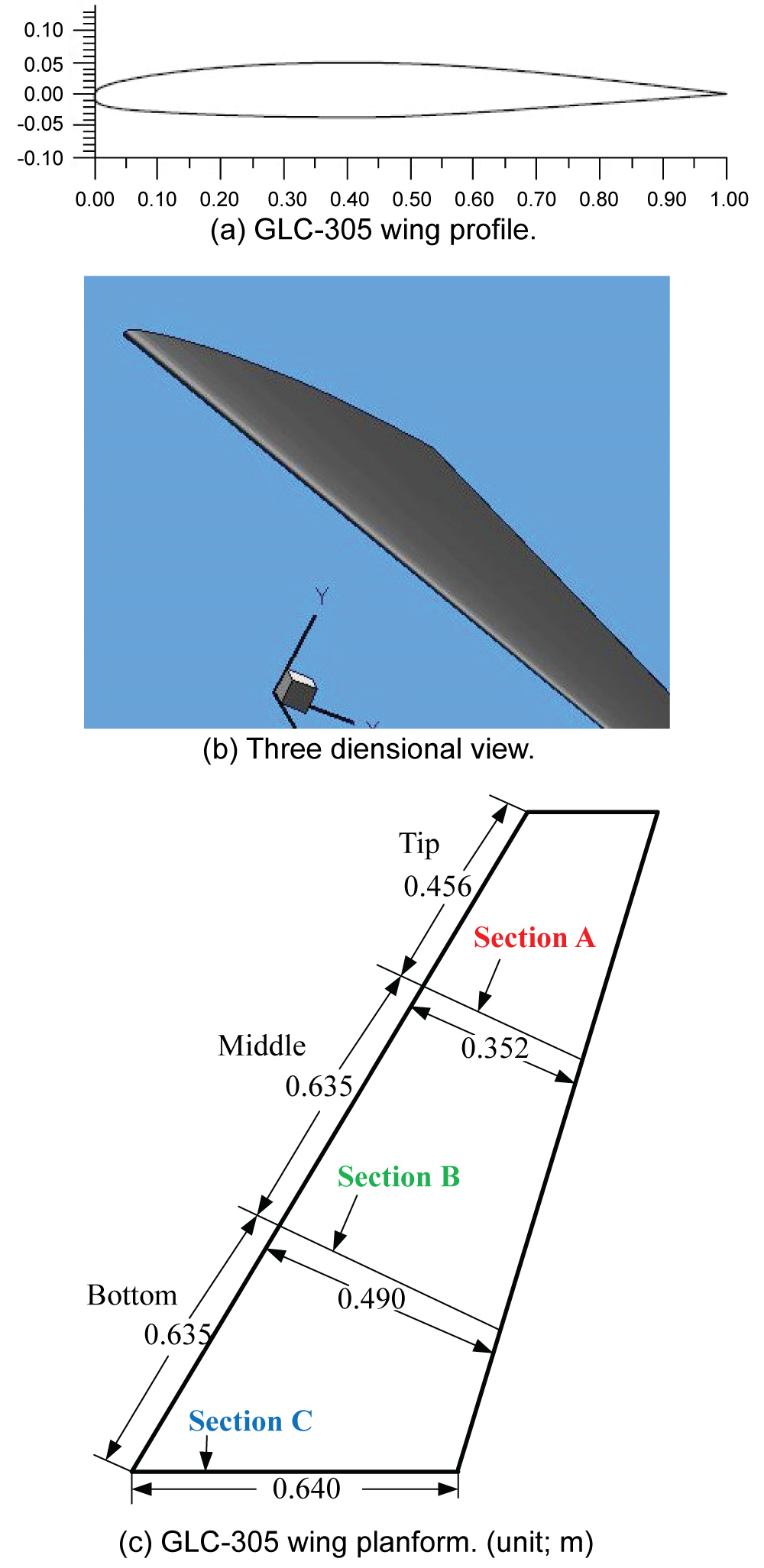
Figure 13: Computational modelling....
Computational modelling. a) GLC-305 wing profile; b) Three dimensional view; c) GLC-305 wing planform. (unit: m).
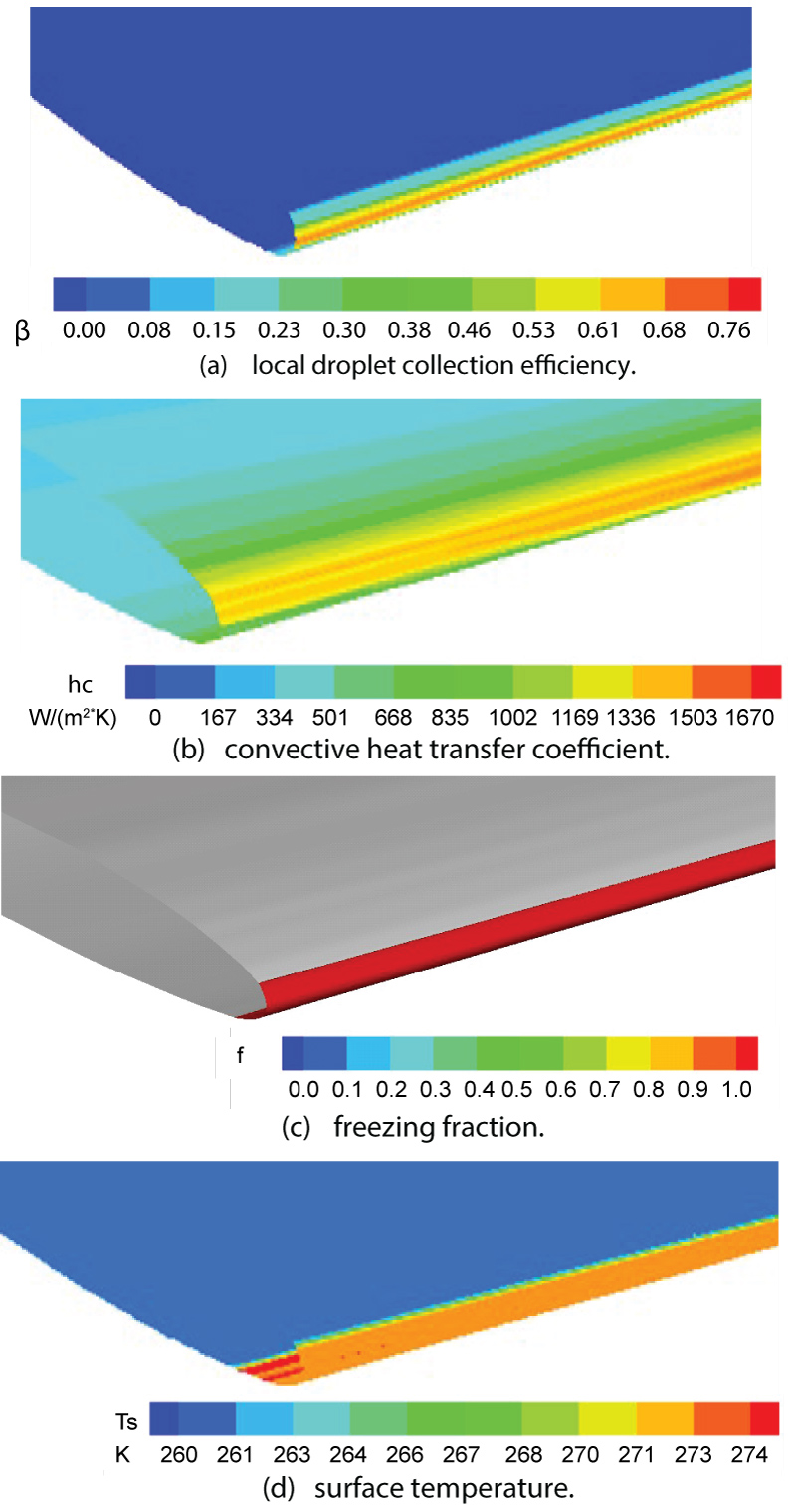
Figure 14: Four typical computational...
Four typical computational contour distribution for case I: a) Local droplet collection efficiency; b) Convective heat transfer coefficient; c) Freezing fraction; d) Surface temperature.
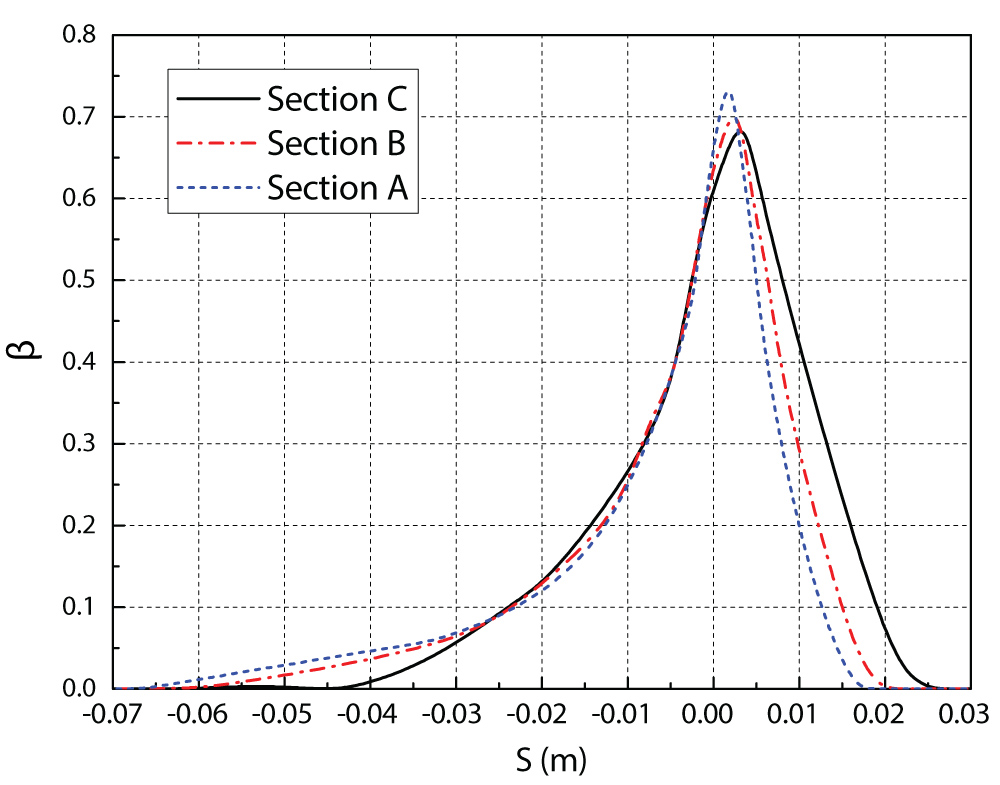
Figure 15: Case I: Comparison of...
Case I: Comparison of local droplet collection efficiency in Sections A, B and C.
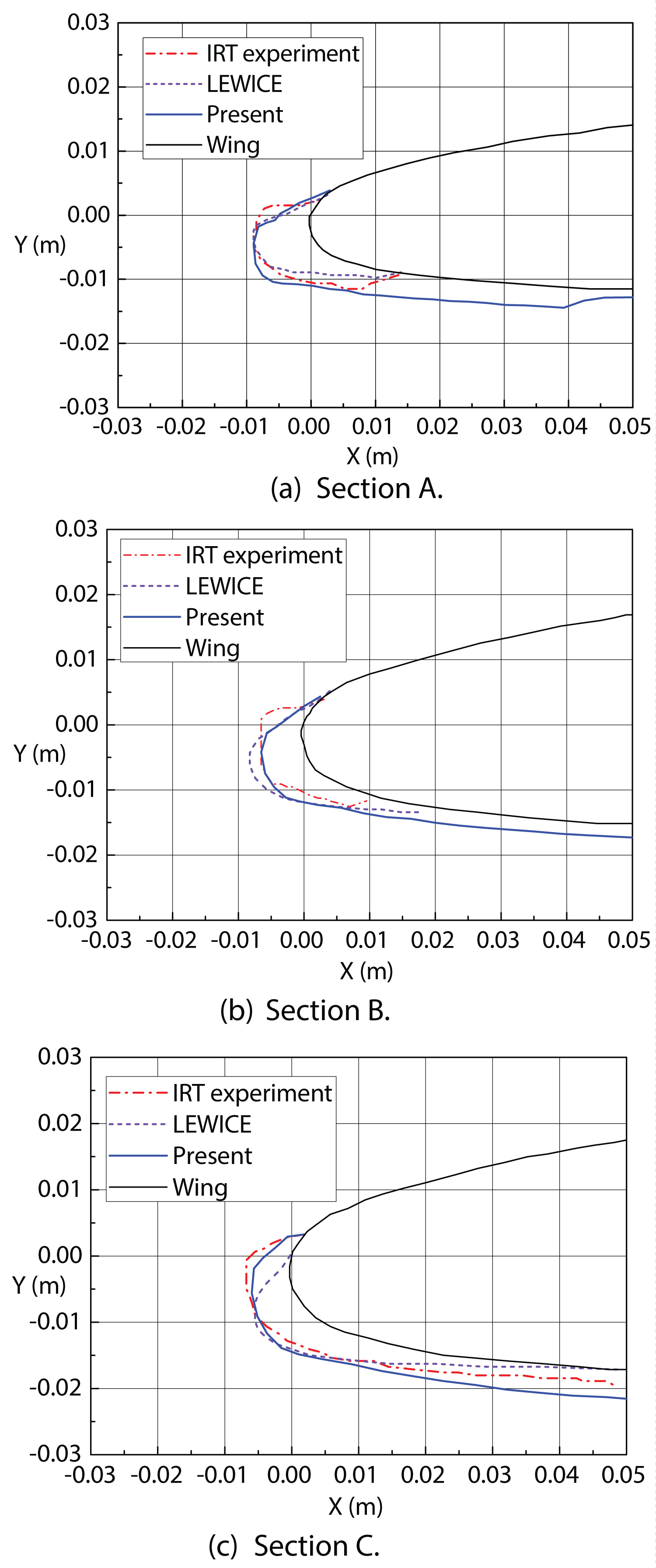
Figure 16: Comparison of the ice...
Comparison of the ice shapes obtained in the present study with experimental and LEWICE results (rime ice). a) Section A; b) Section B; c) Section C.
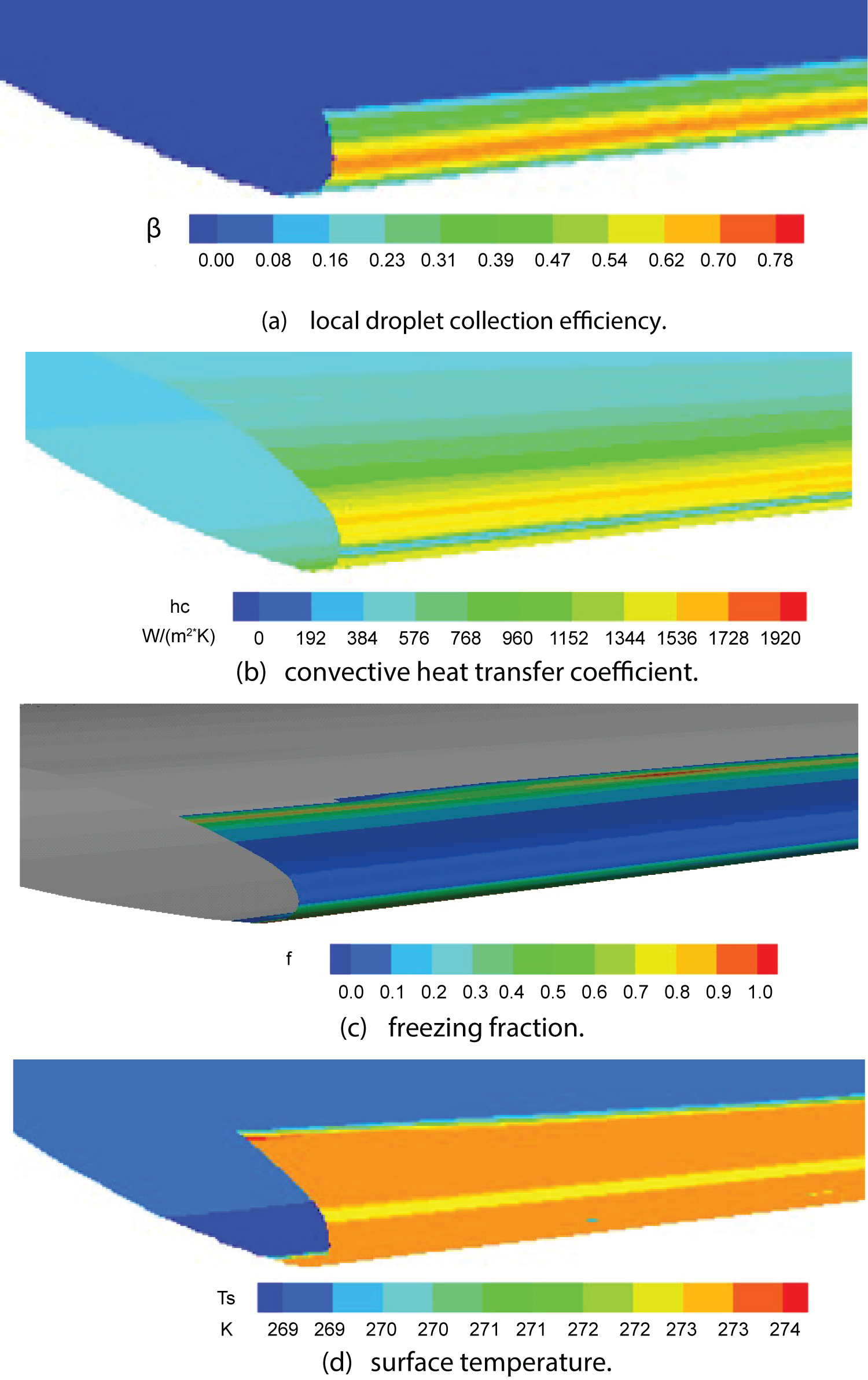
Figure 18: Four typical computational contour...
Four typical computational contour distribution for case II: a) Local droplet collection efficiency; b) Convective heat transfer coefficient; c) Freezing fraction; d) Surface temperature.
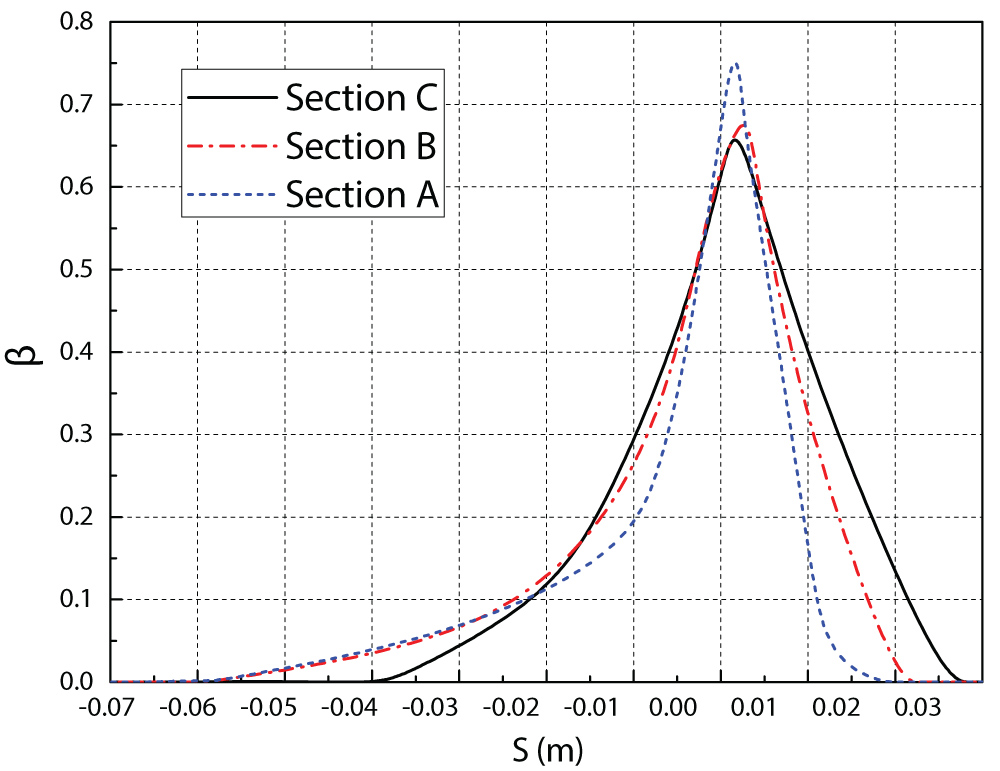
Figure 19: Case II: Comparison of local...
Case II: Comparison of local droplet collection efficiency in Sections A, B and C.
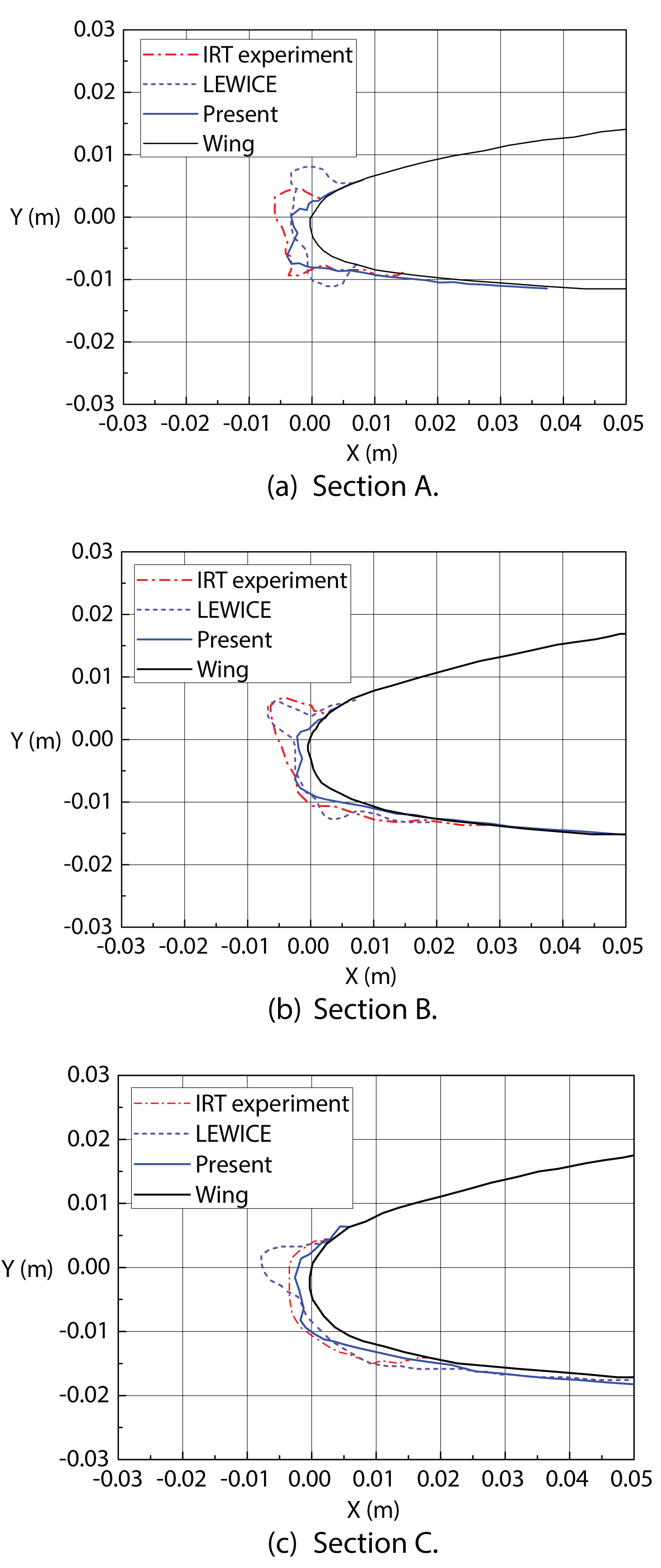
Figure 20: Comparison of the ice shapes...
Comparison of the ice shapes obtained in the present study with experimental and LEWICE results (glaze ice). a) Section A; b) Section B; c) Section C.
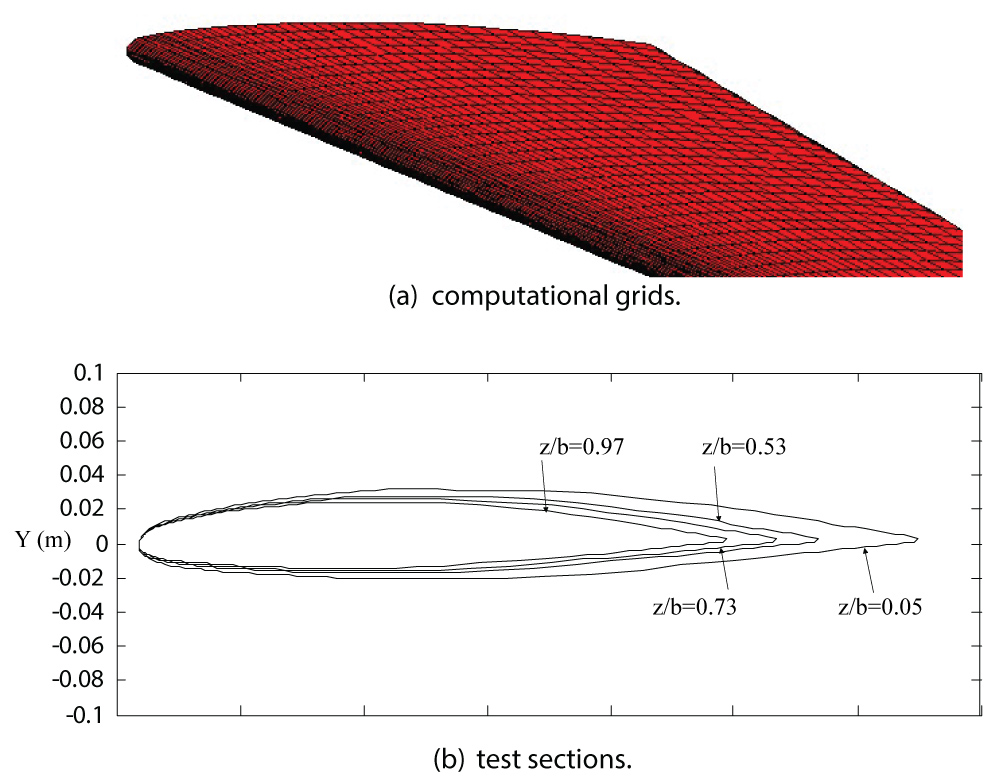
Figure 22: Computational grid and test...
Computational grid and test section over M6 wing: a) Computational grids; b) Test sections.
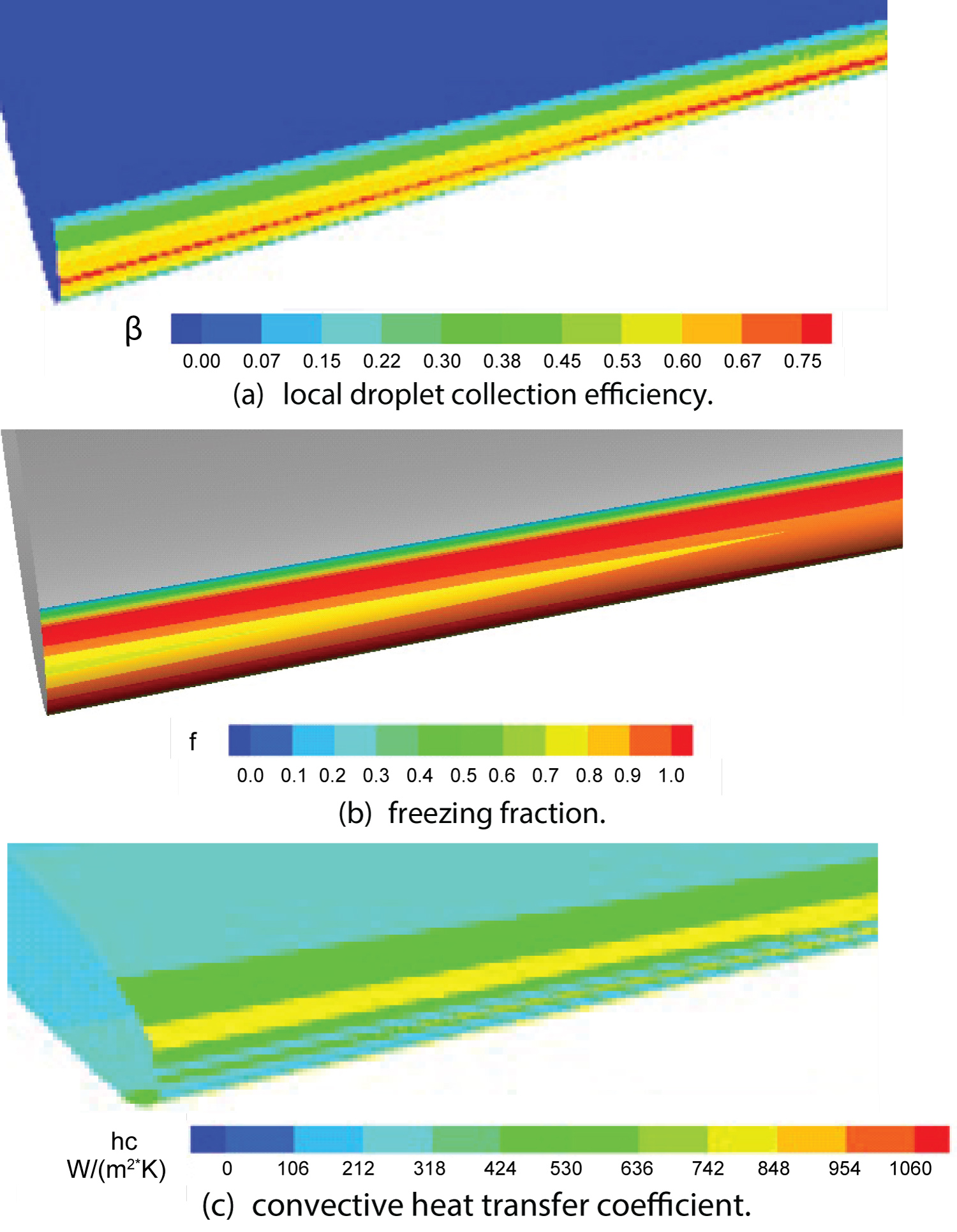
Figure 23: Calculated contour distributions...
Calculated contour distributions over M6 wing surface for Case IV: a) Local droplet collection efficiency; b) Freezing fraction; c) Convective heat transfer coefficient.
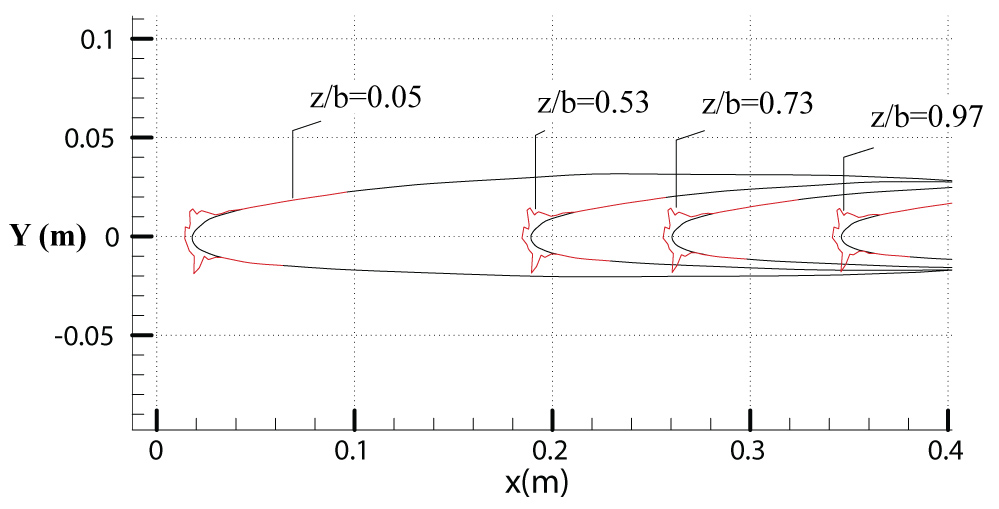
Figure 24: Ice shapes at four different...
Ice shapes at four different test sections over M6 wing for case III.
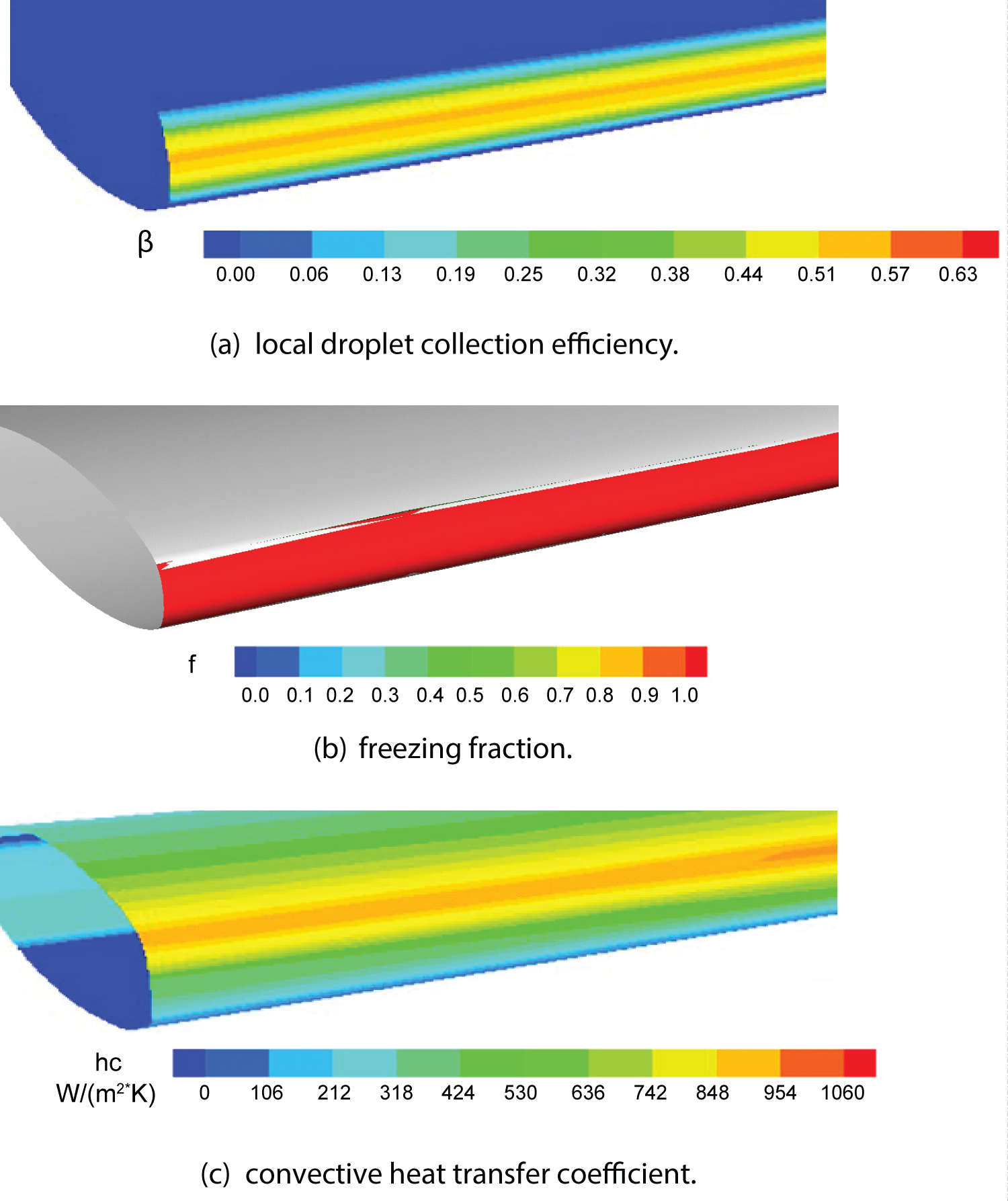
Figure 26: Calculated contour distributions...
Calculated contour distributions over M6 wing surface for Case III: a) Local droplet collection efficiency; b) Freezing fraction; c) Convective heat transfer coefficient.
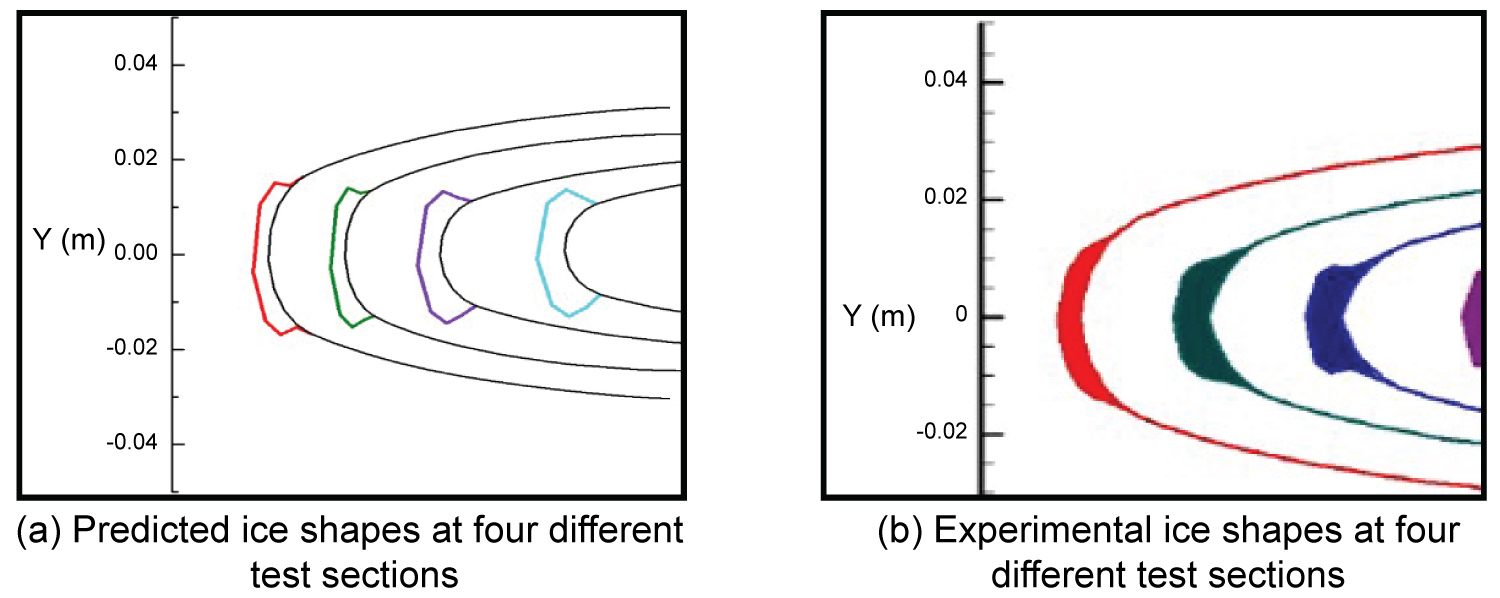
Figure 27: Comparison of the predicted...
Comparison of the predicted ice shapes of the present study a) With experimental data; b) Over M6 wing for case IV.
Tables
Table 1: Geometric and flow conditions for code validation calculation.
Table 2: Geometric and flow conditions of M6 wing.
References
- RW Gent, NP Dart, JT Cansdale (2000) Aircraft icing. Phil Trans R Soc Lond A 358: 2873-2911.
- SK Jung, S Shin, RS Myong, TH Cho (2011) An efficient CFD-based method for aircraft icing simulation using a reduced order model. J Mech Sci Tech 25: 703-711.
- Y Cao, Z Wu, Y Su, Z Xu (2015) Aircraft flight characteristics in icing conditions. Progress in Aerospace Sci 74: 62-80.
- M Mirzaei, MA Ardekani, M Doosttalab (2009) Numerical and experimental study of flow field characteristics of an iced airfoil. Aerosp Sci Technol 13: 267-276.
- CS Bidwell, D Pinella, P Garrison (1999) Ice accretion calculations for a commercial transport using the LEWICE3D, ICEGRID3D and CMARC Programs. NASA/TM-1999-208895.
- T Hedde, D Guffond (1995) ONERA three-dimensional icing model. AIAA Journal 33: 1038-1045.
- BL Messinger (1953) Equilibrium temperature of an unheated icing surface as a function of air speed. J Aeronau Sci 20: 29-42.
- GA Ruff, BM Berkowitz (1990) Users’ manual for the NASA Lewis ice accretion prediction code (LEWICE). NASA Technical Report 185129.
- CS Bidwell, MG Potapczuk (1993) Users manual for the NASA Lewis three-dimensional ice accretion code (LEWICE 3D). NASA Technical Repot 105974.
- P Tran, MT Brahimi, I Paraschivoiu (1994) Ice accretion on aircraft wings with thermodynamics effects. AIAA Paper 94-0605.
- Y Bourgault, Z Boutanios, WG Habashi (2000) Three-dimensional Eulerian approach to droplet impingement simulation using FENSAP0ICE, Part I: Model, algorithm, and validation. J of Aircraft 37: 95-103.
- H Beaugendre, F Morency, WG Habashi (2003) FENSAP-ICE’s three-dimensional in flight ice accretion module: ICE3D. J of Aircraft 40: 239-247.
- F Morency, H Beaugendre, GS Baruzzi, WG Habashi (2001) FENSAP-ICE: A comprehensive 3D simulation tool for in-flight icing. AIAA Paper.
- M Papadakis, HW Yeong, SC Wong, M Vargas, M Potapczuk (2005) Experimental investigation of ice accretion effects on a swept wing. Final report, DOT/FAA/AR-05/39.
- MG Potapczuk, M Papadakis, M Vargas (2003) LEWICE modeling of swept wing ice accretions. AIAA Paper.
- M Papadakis, HW Yeong, SC Wong, M Vargas, MG Potapczuk (2003) Aerodynamic performance of a swept wing with ice accretions. AIAA Paper.
- R Honsek (2005) Development of a three-dimensional Eulerian model of droplet-wall interaction mechanisms. MSc Thesis McGil University, Canada.
- H Beaugendre, F Morency, WG Habashi (2006) Development of a second generation in flight icing simulation code. J Fluids Eng 128: 378-387.
- AK Wynn, YH Cao (2010) Computation of aerodynamic performance about a swept wing with simulated rime ice accretion. International Conference on Mechanical and Electrical Technology (ICMET 2010), 50-54.
- WG Habashi (2010) Recent progress in unifying CFD and in-flight icing simulation. Tenth International Congress of Fluid Dynamics, ICFD10-EG-30I11, Egypt.
- MP Kinzel, RW Noack, CM Sarofeen, D Boger, RE Kreeger (2011) A CFD approach for prediction 3D ice accretion on aircraft. SAE Technical Paper 2011-38-0044.
- Y Cao, C Ma, Q Zhang, J Sheridan (2012) Numerical simulation of ice accretions on an aircraft wing. Aerosp Sci Technol 23: 296-304.
- D Pena, Y Hoarau, E Laurendeau (2016) A single step ice accretion model using level-set method. J Fluids and Structures 65: 278-294.
- SG Pouryoussefi, M Mirzaei, MM Nazemi, M Fouladi, A Doostmahmoudi (2016) Experimental study of ice accretion effects on aerodynamic performance of an NACA 23012 airfoil. Chinese Journal of Aeronautics 29: 585-595.
- X, Zhang, J Min, X Wu (2016) Model for aircraft icing with consideration of property variable rime ice. Int J Heat Mass Transfer 97: 185-190.
- X Zhang, X Wu, J Min (2017) Aircraft icing model considering both rime ice property variability and runback water effect. Int J Heat Mass Transfer 104: 510-516.
- Y Bourgault, WG Habashi, J Dompierre, GS Baruzzi (1999) A finite element method study of Eulerian droplets impingement models. Int J Numer Meth Fluids 29: 429-449.
- P Fu, M Farzaneh (2010) A CFD approach for modeling the rime-ice accretion process on a horizontal-axis wind turbine. J Wind Eng Industr Aerodynam 98: 181-188.
- L Zhou (1993) Theory and numerical modeling of turbulent gas-particle flows and combustion. Science Press and CRC Press.
- ANSYS FLUENT theory guide, release 14.5.
- G Fortin, JL Laforte, A Ilinca (2006) Heat and mass transfer during ice accretion on aircraft wings with an improved roughness model. Int J Therm Sci 45: 595-606.
- JE Dillingh, HWM Hoeijmakers (2004) Numerical simulation of airfoil ice accretion and thermal anti-icing systems (CD-Rom). ICAS.
- M Snellen, OJ Boelens, HWM Hoeijmakers (1997) A computational method for numerically simulating ice accretion. AIAA-1997-2206.
- X Yi (2007) Numerical computation of aircraft icing and study on icing test scaling law. China Aerodynamics Research and Development Center Graduate School.
Author Details
S Chang1, H Tang1, H Wu2*, X Su1, A Lewis2 and C Ji2
1School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, China
2School of Engineering and Technology, University of Hertfordshire, United Kingdom
Corresponding author
Dr. H Wu, School of Engineering and Technology, University of Hertfordshire, Hatfield, AL10 9AB, United Kingdom, Tel: +44(0)1707-284265, Fax: +44(0)1707-285086.
Accepted: November 26, 2018 | Published Online: November 28, 2018
Citation: Chang S, Tang H, Wu H, Su X, Lewis A, et al. (2018) Three-Dimensional Modelling and Simulation of the Ice Accretion Process on Aircraft Wings. Int J Astronaut Aeronautical Eng 3:020.
Copyright: © 2018 Chang S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this article, a new computational method for the three-dimensional (3D) ice accretion analysis on an aircraft wing is formulated and validated. The two-phase flow field is calculated based on Eulerian-Eulerian approach using standard k-ε dispersed turbulence model and second order upwind differencing with the aid of commercial software Fluent, and the corresponding local droplet collection efficiency, convective heat transfer coefficient, freezing fraction and surface temperature are obtained. The classical Messinger model is modified to be capable of describing 3D thermodynamic characteristics of ice accretion. Considering effects of runback water, which is along chordwise and spanwise direction, an extended Messinger method is employed for the prediction of the 3D ice accretion rates. Validation of the newly developed model is carried out through comparisons with available experimental ice shape and LEWICE codes over a GLC-305 wing under both rime and glaze icing conditions. Results show that good agreement is achieved between the current computational ice shapes and the compared results. Further calculations based on the proposed method over a M6 wing under different test conditions are numerically demonstrated.
Keywords
Ice accretion, Aircraft wing, Two-phase flow, Heat transfer, Eulerian-Eulerian approach
Nomenclature
A: Area [m2]; b = mass transfer coefficient [m s-1]; cpa: Specific heat of air [J Kg-1 K-1]; C1ε: Model constant [-]; C2ε: Model constant [-]; CD: Drag coefficient[-]; Cw: Specific heat of water [J Kg-1 K-1]; e: Saturation vapor pressure [Pa]; f: Freezing fraction [-]; : Correction factor; : Force vector [N m-3]; : Gravitational acceleration [m s-2]; hc: Heat transfer coefficient [W m-2 K-1]; hice: Ice thickness [m]; hq: Specific enthalpy of phase q [J Kg-1]; : Unit tensor [-]; k: Kinetic energy per unit mass [J Kg-1]; Le: Latent heat of evaporation [J Kg-1]; Lf: Latent heat of fusion [J Kg-1]; LWC: Liquid water content [g m-3]; m: mass [g]; : Mass low rate [kg s-1]; n: Total number of phases [-]; p: Pressure [Pa]; Pr: Prandtl number [-]; : Heat flux of phase q [W m-2]; Q: Flow rate of enthalpy [W]; r: Recovery factor [-]; Re: Reynolds number [-]; Rv: Gas constant [J mol-1 K-1]; : Interaction force between phase p and q [N m-3]; Δs: Area [m2]; S: Source term [W]; T: Temperature [K]; Trec: Recovery temperature [K]; Ts: Ice surface temperature [K]; ΔTw: Temperature rise due to kinetic energy of impinging liquid [K]; = Overall velocity vector [m s-1]; va: Viscosity coefficient of air [m s-2]; : Velocity vector of outflow water [m s-1]; Ve: Velocity at boundary layer edge [m s-1].
Greek Symbols
α: Volume fraction [-]; β: Local collection efficiency [-]; γ: Ice height [m]; ε: Turbulent dissipation [m2 s-3]; θ: Angle[°]; : Heat conduction coefficient [W m-1 K-1]; λq: Bulk viscosity of phase q [Pa s]; μ: Shear viscosity [Pa s]; ρ: Density [kg m-3]; σ: Surface tension [N m-1]; : Stress tensor [Pa]; Φ: Angle[°]; φ: Angle[°].
Subscripts
0: Along chordwise; 1: Along spanwise; c: Capture; conv: Convective; d: Droplet phase; e: Edge; evap: Evaporation; f: Freeze; g: Gas phase; i, j: Coordinate summation index; ice: ice; in: Inlet of a control volume; l: Lift; m: Mixture; out: Outlet of a control volume; pq, qp: Transfer between phase p and q; q: Phase q; s: Surface; ve: Water vapour at edge of the boundary layer; vm: Virtual mass; vs: Water vapour at the surface; wv: Water velocity term.
Introduction
Aircraft icing has long been recognized for over sixty years and continues to be an important flight safety issue in the aerospace community [1-3]. Ice accretion on an aircraft wing occurs when supercooled water droplets in the atmosphere impact on the surface of aircraft’s wings. The formation of ice on an aircraft wing results in a sharp increase in drag and a reduction in maximum lift [4]. Furthermore, ice accretion on aircraft wings also leads to a reduction in stall angle and increment in moment coefficient of the wing. This causes a deterioration in the aerodynamic performance of the aircraft. The simulation of ice accretion on aircraft wing is an iterative process that consists of the successive computation of airflow, water droplet trajectories, collection efficiency, and heat transfer balance to determine the shape of accreted ice. Ice accretion simulations have traditionally been based on 2D and quasi-3D inviscid codes (Panel method) or Euler flow to compute the airflow solution [5], on Lagrangian tracking techniques [6] for droplet impingement calculation, and on a 1D control volume analysis of the heat and mass transfer to predict ice shapes [7] for the last two decades. The best-known codes using this structures are ONERA [6], NASA’s LEWICE [8,9] and Bombardier Aerospace’s CANICE [10]. Modern CFD-based approach has proven to be an attractive method for determining the ice shapes on aircraft wings and open new possible uses for complex 3D icing prediction. FENSAP-ICE [11-13] is a fully 3D in-flight icing analysis tool, capable of computing a water droplet field solution via an Eulerian description of two phase flow and 3D ice shapes using partial differential equations on the aircraft’s surface. To the best of authors’ knowledge, only a small number of investigations have addressed the impact of ice shapes on iced 3D wings especially the lack of experimental data [14]. Efforts that devoted to 3D ice accretion simulation using CFD methods in the 56 open literature are summarized below. Potapczuk, et al. [15] and Papadakis, et al. [16] conducted a study that considered ways to simulate highly 3D ice accretion. Honsek [17], afterwards, developed an improved 3D Eulerian model to investigate the droplet-wall interactions and predicted collection efficiency distributions and velocity profiles in close agreement with experimental observation. However, their model was not able to communicate external disturbances into the computational domain due to a lack of a pressure equivalent source term in the equations governing droplet momentum. The numerical result of Beaugendre, et al. [18] for calculating ice shapes on simple or complex 3D geometries showed that the developed second-generation CFD-based in-flight icing simulation system was successful. Wynn and Cao [19] employed a one-equation Spalart-Allmaras turbulence model to simulate the 3D ice accretion on the aircraft swept wing under subsonic Mach number conditions. The evaluation of ice accretion on aerodynamic performance was also implemented. Their results presented that the effects of rime ice shape on the aerodynamic performance of lift coefficients was increased and drag coefficients was reduced with respect to the clean swept wing at different angels of attack. Habashi [20] demonstrated a recent progress in a 3D CFD-based platform, FENSAP-ICE, which has been extended to solve more complex geometrical systems and to bring more physics into in-flight icing simulation. Most recently, Kinzel, et al. [21] developed a new iced-aircraft modeling tool that is based on a multiscale-physics, unstructured finite-volume and can be applicable to general purpose aircraft icing applications. Their results displayed good validation for predicting ice shape on a variety of geometries. Cao, et al. [22] developed an approach to predict the ice accretions on a 2D airfoil and a 3D wing based on the Eularian two-phase flow. The ice accretions on a NACA0012 airfoil and a GLC-305 wing model under different icing conditions were evaluated. Pena, et al. [23] developed a new approach using the Level-Set framework in the NSMB (Navier-Stokes-multi-block) compressible solver for modelling the ice/air interface evolution through time during in flight icing. Single step icing was simulated on NACA 23012 and NACA 0012 airfoils and on the ONERA-M6 and the GLC-305 swept wings. The simulated results are in good agreement with existing data. Pouryoussefi, et al. [24] carried out an experimental study to investigate the effects of ice accretion on an NACA 23012 airfoil at a fixed Reynolds number in a wind tunnel for horn, runback, and spanwise ridge ice at different angles of attack. It was found that the ice accretion on the airfoil can contribute to formation of a flow separation bubble on the upper surface downstream from the leading edge. Zhang, et al. [25] developed a new one-dimensional model to describe the aircraft icing process based on the fundamental theory of solid-liquid phase change. It was stated that the model with consideration of property-variable rime ice can better describe the ice accretion process. Later on, a series of work by Zhang, et al. [26] further improved the one-dimensional model which can be divided into the dry and wet mode icing stages. Their results showed that the rime ice property variability and runback water influence the heat conductions in the ice layer and water film and consequently the ice accretion characteristics. Although many significant results in numerical models of ice accretion have been already obtained by now, the comprehension of the ice accretion mechanism on aircraft wing is still quite limited, especially for the cases of 3D, and there is still much room for improvement. From the mechanism research’s point of view, the purpose of the present study is to perform a systematic evaluation of the current computational capability to capture the ice accretion at three different sections over a GLC-305 wing under both rime and glaze icing conditions. In order to assess the newly developed model as an analysis tool for carrying out more studies to further elucidate the pertinent physical phenomena involved in the ice accretion, the computed results compare with available experimental data and LEWICE codes. Moreover, the proposed method has been implemented and successfully applied for 3D ice accretion computation over a M6 wing under different test conditions.
Mathematical Formulation
It has been well established that four fundamental elements must be taken into account concurrently for realistic simulation. They are the representation of the aerodynamic flow field characteristics on and around the body, the establishment of the water droplet trajectories with subsequent impingement characteristics, the thermodynamics of the ice growth process, and, lastly, the growing ice accretion. In the current study, an Eulerian formulation [2,27,28] is employed since the dispersed liquid can be treated as a continuum, which enabling the prediction of fully 3D impingement limits and collection efficiency distributions in an automatic fashion at all locations within the computational domain, irrespective of geometric intricacies or aerodynamic interference patterns. The Eulerian formulation of the flow field process yields a set of partial differential equations representing the continuity and momentum equations of the dispersed droplet phase.
Flow field determination
In this research the Eulerian multiphase model was adopted to simulate the air-droplet flow. The following major assumptions were made in the derivations of the governing equations: (i) The volume fraction of water in the atmosphere is very small, and the water droplets are distributed as the discrete phase in the airflow. Therefore, the water droplets can be considered to move with the airflow at the same velocity without affecting the velocity of the airflow; (ii) There is no heat transfer or evaporation in the process of droplets prior to impingement. Thus, the thermophysical properties of the droplets are assumed to be constant; (iii) Droplets sizes are small, hence assumed to be spherical; (iv) Droplets do not coalesce, bounce or splash upon impinging onto the wing surface; (v) The droplets distributed in the flow field can be regarded as pseudo fluid [29]. Other simplifications are described in the due course in the rest of the paper.
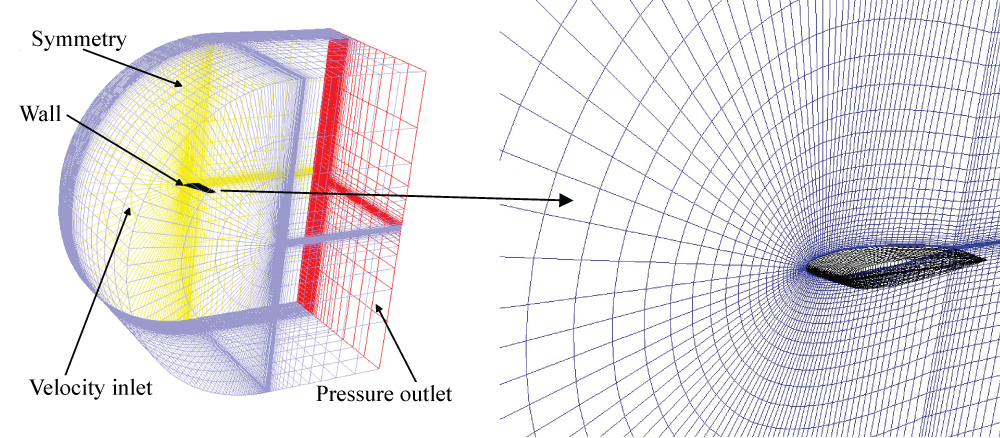
In the present numerical procedure, structured grid for the complete flow field was successfully generated for the wing as well as with fine grid near the wing surface in order to capture the flow information in the boundary layer. Figure 1 shows the grid distribution and boundary conditions of the present computational domain. The boundary conditions were set as velocity inlet, pressure outlet and symmetry, respectively.
The governing equations are basically the unsteady continuity, momentum and energy equations, which are given as:
■ Continuity equation:
Where t is the time and n is the total number of phases, αq, ρq and are the non-dimensional volume fraction, density and velocity of phase q , respectively. characterizes the mass transfer between phases p and q.
■ Momentum equation:
Based on the above mentioned assumptions, momentum equation can be simplified as
where p is the pressure shared by all phases, is the qth phase stress-strain tensor, is the gravitational acceleration and is an interactive force between the pth and the qth phase.
Details can be obtained from ANSYS FLUENT V14.5 [30].
■ Energy equation:
Where hq is the specific enthalpy of the phase q, is the heat flux, Sq is a source term that includes sources of enthalpy, Qpq is the intensity of heat exchange between phase p and phase q, and hpq is the interphase enthalpy. The heat exchange between phases must comply with the local balance conditions Qpq -Qqp and Qqq = 0.
Under in-flight icing conditions, the ratio between LWC of droplets and air mass is usually of the order of 10-3, leading to a droplet volume fraction αp of the order of 10-6. The air volume fraction αg can thus be considered constant and equal to 1. The air droplet flow is then viewed as a dilute gas-particle system, where only the effects of air on droplets are considered and where water droplets are treated as spherical particles. The dispersed turbulence model is adopted, as it is the appropriate model when the concentrations of the secondary phases are dilute.
■ Turbulence model:
Fully turbulent flow is assumed using the two-equation k-ε turbulence model, in which mixture properties and velocities are used to capture the physics of the turbulent flow. The two equations solved are as follows:
And
Where k denotes turbulent kinetic energy, and ε is the turbulent dissipation; ρm and are the mixture density and velocity, μt,m is turbulent viscosity, and Gk,m is the production of turbulence kinetic energy.
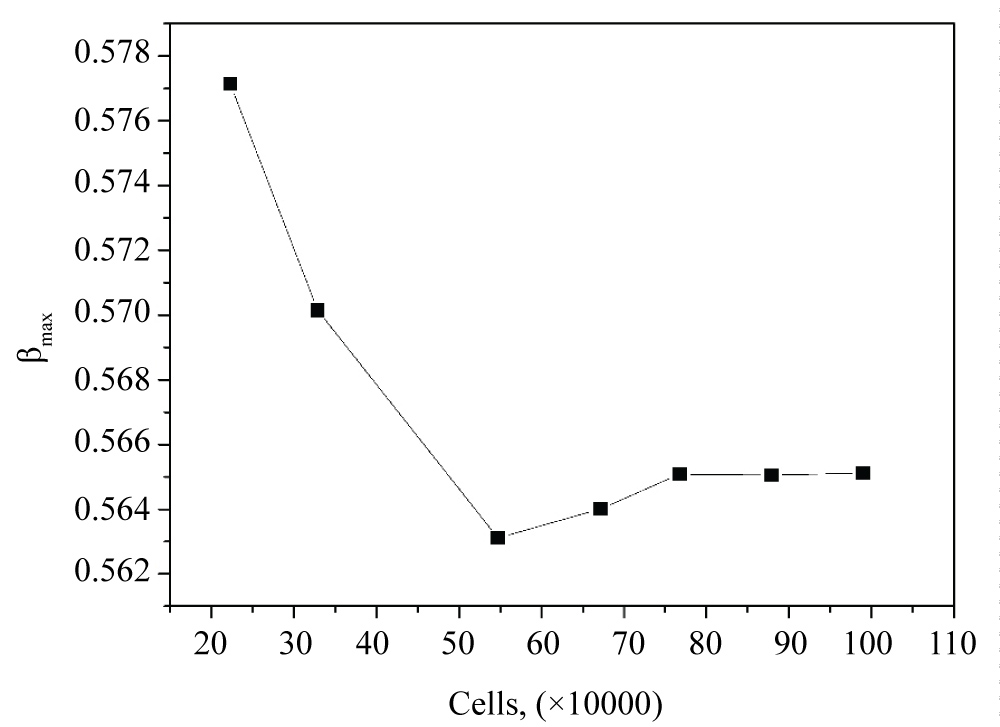
In the current study, the volume fraction was discretized using QUICK format while other governing equations were discretized with second order upwind format. The phase couple SIMPLE (PC-SIMPLE) scheme was applied in the numerical simulation. Prior to the actual numerical simulation, as shown in the Figure 2, a grid independence study for the current model was performed by using seven different grids with 220000, 330000, 550000, 570000, 770000, 880000, 990000 cells, respectively. The values of y+ on the wing are 57, 52, 44, 43, 35, 32, 27 respectively. Generally, the y+ is most suitable around 30 for the standard wall function method used on the wing, it was found that the maximum variety of predicted droplet collection efficiency was 0.05% as the grid increased from 770000 to 990000 cells. Therefore, a compromise between computation accuracy and computing capability led to the use of 770000 cells.
Droplet impingement
On the surface of the wing, the no-slip boundary condition was applied. In addition, for the liquid droplet flow field, a negative mass source term was added in near-wall grid through user defined function in order to allow this value is equal to the mass of the water droplet that impinged on the surface of the wing. Thus, the droplets will not accumulate on the surface of the wing, and therefore the droplets volume fraction distribution around the wing will not be affected. In the current study, for the continuity equation the negative source term would be , while for the momentum equation the negative source term would be .
Establishing representative water droplet trajectories is the second step in the process for simulating ice accretions which occur when an aircraft penetrates a cloud containing supercooled water droplets, freezing drizzle, or freezing rain. The Eulerian droplet impingement model is essentially a two-fluid model. The Eulerian droplet model provides local values for the collection efficiency β and the droplet impact velocity ud. When the numerical computation for air-droplet flow converges, the location of the impingement zones, where droplets accrete according to the collection efficiency β, can be obtained.
In order to obtain the distribution of droplets along the wing surface, as it is not uniformly distributed, the droplet collection efficiency β needs to be calculated.
Where and denote the local velocity of droplet and the unit surface normal vector of the ith phase. is the free stream velocity, αwi and represent the droplet volume fraction on the surface and on the far-field, respectively.
The mass flow rate that impinging on the surface may thus be expressed as:
Where Δs stands for the area of the panel. Since the normal velocity and apparent density of droplets on the wall boundary can be obtained, the droplet collection efficiency β and the mass flow rate can be determined.
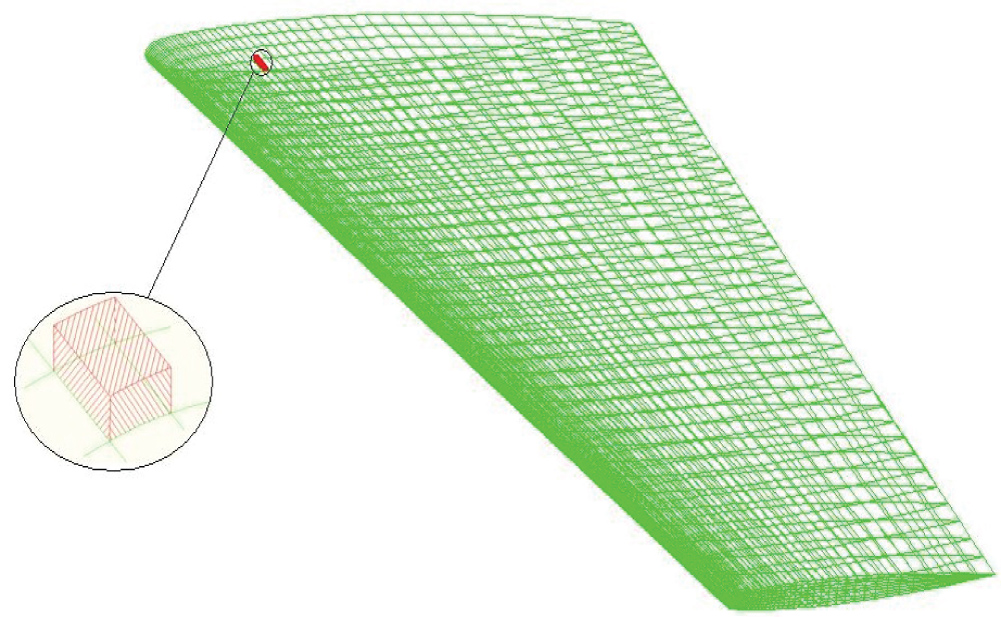
Thermodynamic analysis
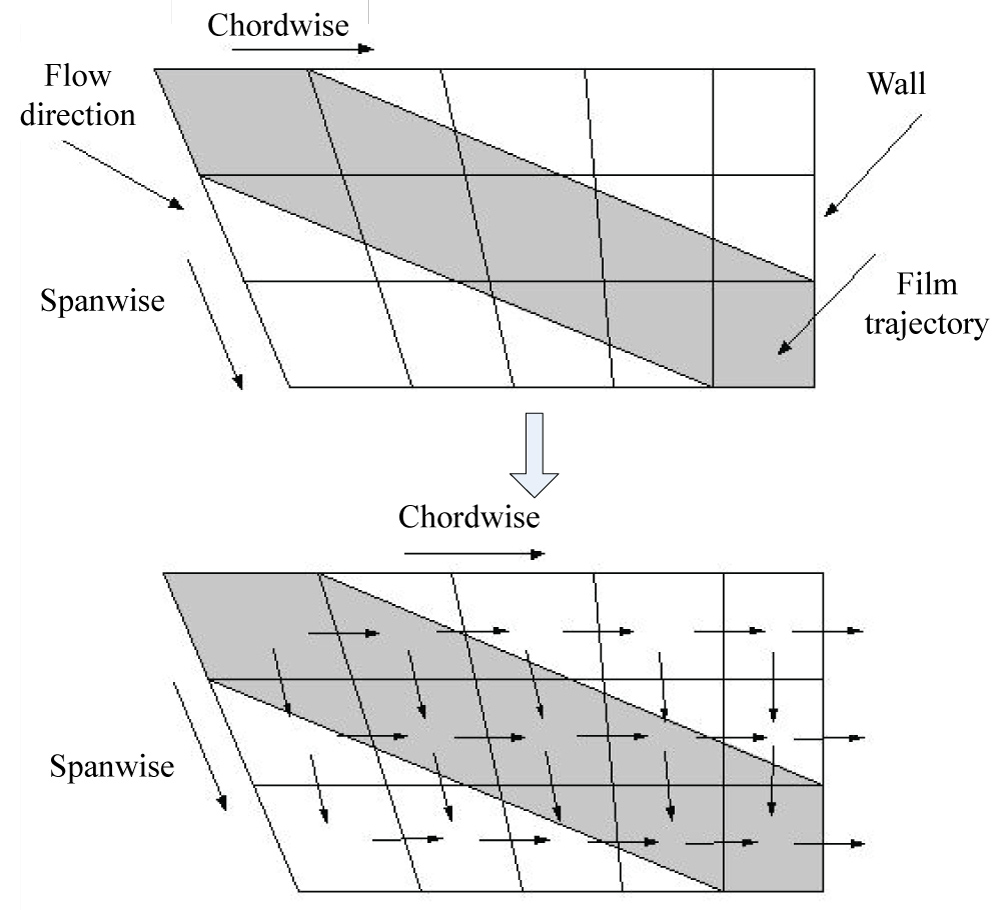
The grid distribution on the surface of the wing is shown in Figure 3. The heat and mass transfer model used in the current work is an improved approach based upon the Messinger’s model, which can be further applied to 3D flow. It is assumed that all flow backward, which decomposed the flow along the chordwise and spanwise direction, as shown in Figure 4. The water remains over the ice surface since the aerodynamic and gravitational forces are not large enough to break the surface tension of water.
Mass transfer analysis
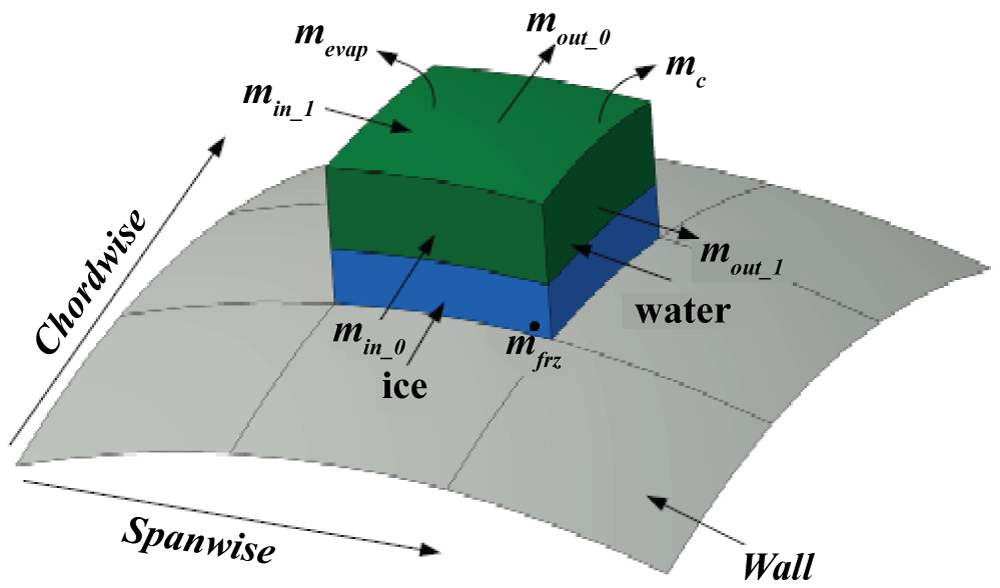
As shown in Figure 5, the mass balance equation in a control volume can be expressed in the following manner:
Where the subscripts i and j refer to coordinate summation indexes along spanwise and chordwise direction.
• , denotes the impinging water mass per unit time, and can be calculated by
• , denotes the evaporation water mass on the wing surface:
Where is the mass transfer coefficient, given by
Where hc is the convective heat transfer coefficient.
The total water flow out the control volume is expressed as:
Where and denote the mass flow out of the control volume along chordwise and spanwise direction. with
The above relationship is presented in more detail in Appendix A (Figure 6).
• Combine Eqs. (12) and (13), the mass flow out of the control volume along chordwise and spanwise direction can be calculated by
• The flow-in mass equals to the mass flow out of the previous control volume:
Where denote the mass flow in the control volume along chordwise and spanwise direction.
• The mass of icing water, , is expressed as follows:
Where is the freezing fraction, defined as:
Combine Eqs. (8), (12) and (19), resulting in:
It should be noted that closing the models requires the energy balance equations, which will be described in detail in below.
Heat transfer analysis
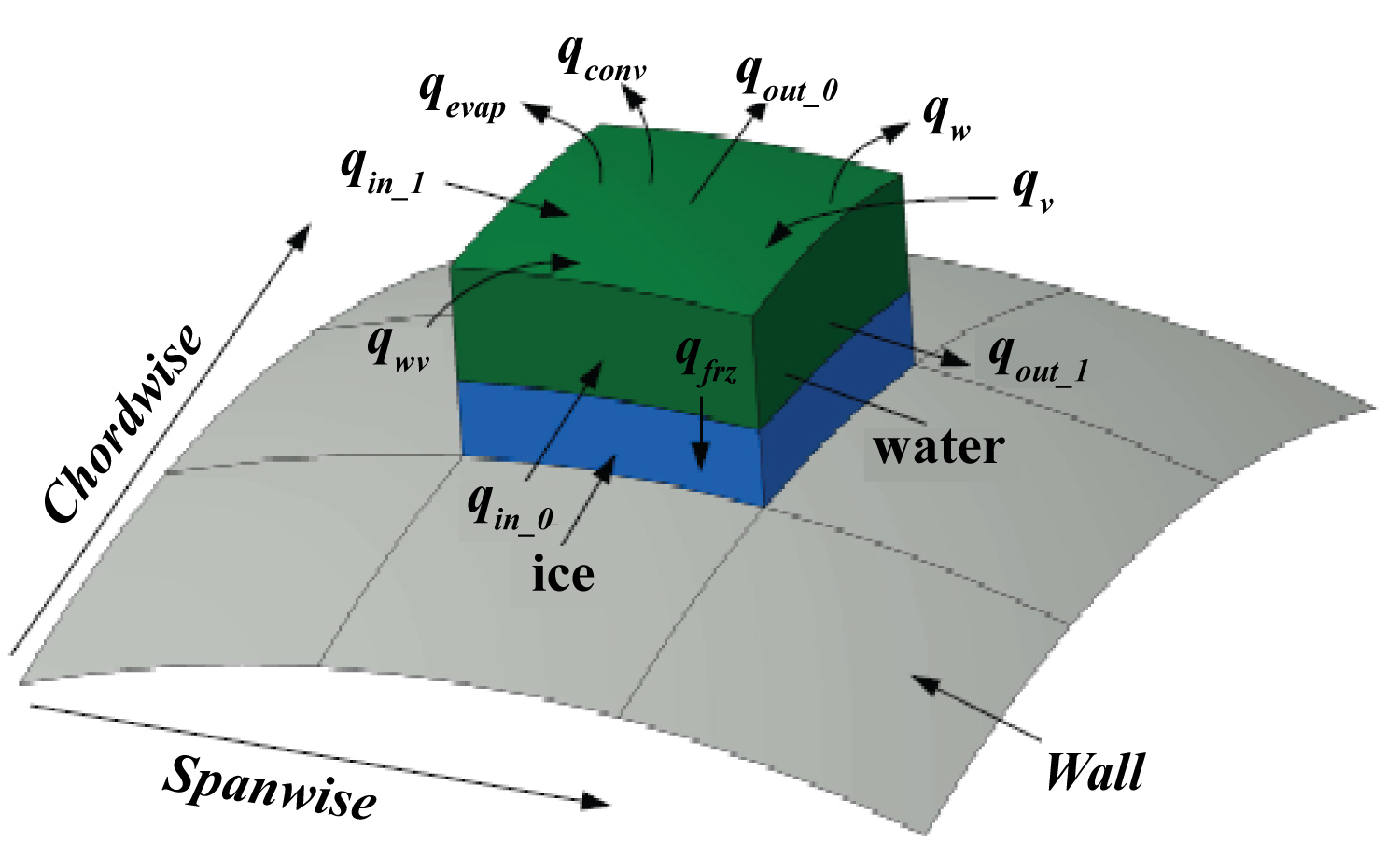
As the surface temperature of the wing is very low, it is assumed that the radiation effects can be neglected. The heat transfer within the control volume on the surface of the wing is shown in Figure 7.
The following equation is the energy conservation that applied on a control volume, where the rate at which energy enters the control volume is equal to the rate at which energy exits the control volume:
Where:
■ Convective heat transfer at the water surface:
Where denotes the surface temperature of wing.
The relation for Eq. (22) is shown in Appendix B (Figure 8, Figure 9 and Figure 10) [31-33].
■ Evaporative heat loss:
Where Le is the latent heat of evaporation.
Substituting Eq. (10) into Eq.(23) leads to
■ Viscous heating:
With
Where ΔT means the temperature rise caused by aerodynamic, and r is the recovery coefficient in boundary layer.
■ Cooling by incoming droplets:
Substituting Eq. (9) into Eq.(27) yields
■ Kinetic energy of impinging droplets:
With
Where ΔTw is the temperature rise due to the kinetic energy of impinging liquid.
Combining Eqs. (9), (29) and (30), resulting in:
■ Heat given off as the liquid water freezes into ice:
The term, Lf, is the latent heat of fusion. Indeed, it is known that water flow will also affect the heat balance. In the current study, the heat carried by the flow-in and the runback water along both directions, , will be considered for the sake of generality.
■ The heat carried by the flow-in water is:
Similarly,
■ The energy brought in by the runback water can be written as:
The final form of the energy equation within the control volume on the surface of the wing can be expressed as (see Appendix C):
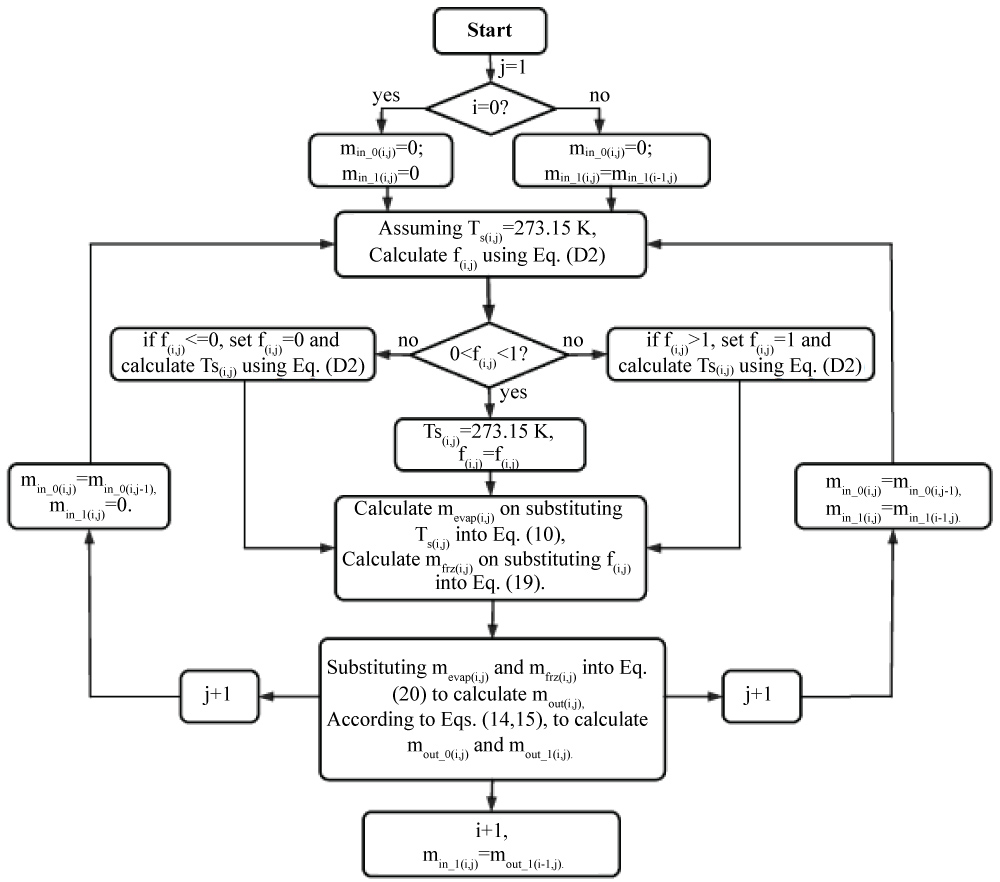
From this heat balance an estimate for the freezing fraction can be obtained by setting the temperature. If the freezing fraction greater than 1, then only rime ice will occur, setting the freezing fraction to 1 then allows an average temperature to be obtained. If the freezing fraction is found to be less than 0, then it is taken as identically 0 and the average temperature estimated. When the freezing fraction has a value between 0 and 1, that is when all the water does not freeze in the given control volume, the average temperature held at 0 ℃. A brief flowchart of the calculation procedure and the developed program is presented in Figure 11.
Ice accretion
The 3D partial differential equation is derived based on the Messinger model. It has been further improved to predict the ice accretion and water runback on the surface. In the 3D cases, ice accretion results are obtained using only one cycle of calculation (one shot ice accretion) since multi layers ice accretion simulation in 3D take a large computing time. In the present study only one-shot results are shown for 3D calculations. Thus, the effect of ice accretion on the airflow and droplets fields is neglected.
The ice volume can be determined by:
Where ρice is the density of ice.
The local ice thickness follows from
The displacement length is the average ice height.
Where n is normal vector.
The new coordinates for the panel are obtained from the relation:
Where x1 is the coordinate of the centre of the panel and x2 is the component of the unit normal vector for the panel. For the complicated 3D case, as a first step, the single time step calculations used for the current study could be capable of reproducing the overall characteristics of the ice shapes. Multiple time step calculation should be performed to try to improve the agreement between computation and experiment.
Results and Discussion
Prior to conducting the aimed computations, it is necessary to validate the computational model and the developed code. In the current work, two case studies are conducted to validate the developed model. The first case study (Case study I) is to compare the ice shape with the ONERA 3D results obtained from Hedee and Guffond [6]. For the second case study (Case study II), the numerical results are compared qualitatively with 3D experimental ice shape over a GLC-305 swept wing that have been created in the NASA Lewis Icing Research Tunnel (IRT) [16], and with those predicted results using LEWICE code [16].
Model validation - Case study 1
Figure 12 compares the ice shape predicted by the current model and ONERA 3D simulation results as well as the experimental data.
In the calculation, the environment temperature is 266.45 K, which is typical glaze ice condition. When supercooled droplet impacting on the wing, it will not freeze completely, the droplet will flow within a thin film which make the ice shape complicated. In this simulation, the angle of attack is 4 degree, it can be observed that the predicted ice shapes are mainly on the lower surface. Both the ONERA 3D model and the current model demonstrated similar ice shapes compared with experimental data.
Model validation - Case study II
For the purpose of comparison, two test case conditions, case I (rime ice) and case II (glaze ice), were selected for the numerical simulations, as summarized in Table 1. Figure 11a and Figure 11b show the dimensionless standard airfoil model of GLC-305 swept wing and 3D simulation modelling, respectively. Comparisons were performed in terms of the ice shapes obtained in three sections, namely Section A, B and C depicted in Figure 13c. Through all this section, the ice shapes are plotted in meters.
Case 1: Rime ice:
Figure 14 represents four typical contour plots of distributions of the local droplet collection efficiency, convective heat transfer coefficient, freezing fraction, and surface temperature for case I along the length of the wing, respectively. Figure 14a shows the contour local droplet collection efficiency plot. The results in Figure 14a clearly show that the local droplet collection efficiency reaches a peak value at the leading edge of the wing, and then decreases gradually to zero along the chordwise direction. It is also noted that the peak value of local droplet collection efficiency increases slightly along spanwise of the wing. A comparison of the calculations of local droplet collection efficiency in Sections A, B and C for case I is presented in Figure 15. As it is expected, similar trends in the variation of local droplet collection efficiency is obtained for each of the three 433 sections. The plot shows the local collection efficiency increases to a peak value near the stagnation point and then decreases sharply toward the end. As can be seen from Figure 15, the computed peak value of local droplet collection efficiency is 0.73 in Section A,0.7 in Section B and 0.68 in Section C. This implied that the local collection efficiency over the wing surface increases with the decrease of chord length.
It is recognised that the heat transfer plays a very important role in ice accretion. Figure 14b presents the distribution of the convective heat transfer coefficient. This parameter is used to measure the heat exchange between the surface and the airstream. From Figure 14b, it can be observed that the trend of convective heat transfer coefficient is similar to that of local droplet collection efficiency. That is, peak value obtained near the leading edge, and then starts to decrease along chordwise direction. In addition, the peak value increases along spanwise of the wing. Unlike the local droplet collection efficiency distribution, the convective heat transfer coefficient shows a relatively small gradient on the surface of the wing. Furthermore, at the stagnation point, the convective heat transfer coefficient does not reach peak value. This is due to the smaller flow velocity within the boundary of the region. The decreasing mixing intensity of the airflow could weaken the heat transfer. At downstream, the air speed increases, this can enhance the heat convection, thus the convective heat transfer coefficient increases accordingly. Afterwards, the convective heat transfer coefficient decreases with the decrease of air speed.
Figure 14c presents distribution of the freezing fraction. This parameter plays an important role in determining whether the ice shape is rime ice or glaze ice. For example, if the freezing fraction equals to 1, liquid droplet freezes immediately upon impingement and ice accretion on the surface will be rime ice. Otherwise, when the freezing fraction is smaller than 1, liquid droplet impinges the surface without freezing at the point but runback, which forms a film moving afterward and leads to glaze ice. It is clearly seen from Figure 14c that impinging liquid freezes upon impact. According to this, for case I, rime ice could be accreted. Figure 14d gives the distribution of surface temperature. As can be seen from Figure 14d, the surface temperature is lower than that of the icing temperature although the temperature at the leading edge is higher than ambient temperature. Thus, incoming droplet freezes upon impact and forms rime ice on the upwind surface.
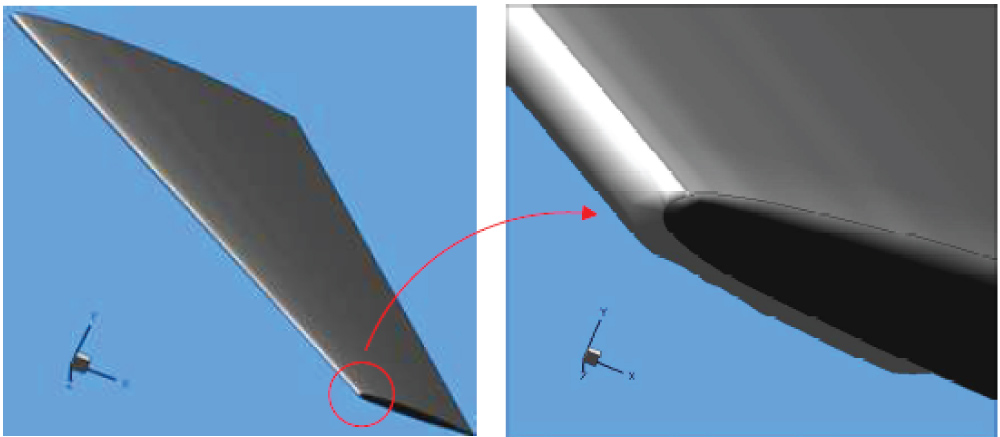
Figure 16a, Figure 16b and Figure 16c compare the ice shapes obtained for Sections A, B and C in the current study with those measured experimentally, as well as the LEWICE codes. As can be observed, for all three sections, the predicted ice shape of the current study agree well with the experimental one and LEWICE codes at the ice limits on the upper surface. Besides, the maximum ice thickness and ice shape in the stagnation area also agree well with other results. But it should be noted that on the lower surface, the current calculations predict a much larger extension compared to others. This could mainly be due to the fact that less freezing fraction at the end edge of lower surface, as shown in Figure 14c. On the other hand, in Sections A and C, both predicted and measured ice thickness is similar, showing good agreement. However, predicted ice thickness in Sections B of the current study is smaller than those obtained by LEWICE, but more closer to the experimental data. The ice shapes observed in Figure 16a, Figure 16b, Figure 16c show typical rime ice shapes, which are consistent with the analysis of Figure 14. Figure 17 exhibits the computed 3D ice accretions along the wing surface and the enlarged ice shape at the tip area of the wing.
Case II: Glaze ice:
For the purpose of comparison, the overall features of ice accretion for case II are numerically simulated using the same numerical scheme as in case I. Figure 18 illustrates the distributions of the local droplet collection efficiency, convective heat transfer coefficient, freezing fraction, and surface temperature for case II along the length of the wing, respectively. Similar to that of case I, it can be seen from Figure 18a that the local droplet collection efficiency reaches a peak value at the leading edge of the wing, and then decreases gradually to zero along the chord wise. The peak value of the local droplet collection efficiency increases slightly along spanwise of the wing. A close look at the values of local droplet collection efficiency, it is found that the local droplet collection efficiency for case II are slightly bigger than those for case I. This could be due to the higher flight speed and larger droplet diameter for case II. Distribution of convective heat transfer coefficient for case II in Figure 18b shows similar trend with that of case I. It will not be repeated here for the sake of briefness. At the stagnation vicinity, the convective heat transfer coefficients are smaller due to the lower air speed. The computed freezing fraction distribution in Figure 18c displays a remarkable difference with that of case I. Compared to case I, in Figure 18c, it can be observed that the freezing fraction along chord wise of the wing shows a wide range but smaller value for case II. This indicates a typical glaze ice characteristics, that is, the impinging droplets does not freeze totally right upon its impact but part of them forms liquid film and runback downstream along the wing surface, icing later somewhere downstream. Computational contour distribution for surface temperature is displayed in Figure 18d. It also shows different behaviour with case I that the surface temperature for case II is higher. The reason could be that the droplets do not freeze immediately upon impingement.
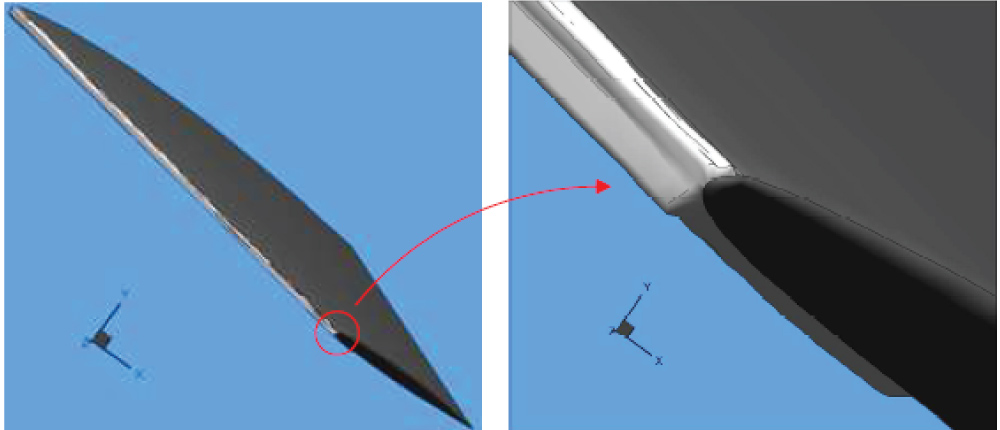
Figure 19 shows the local droplet collection efficiency profiles at Sections A, B and C. Again, according to the curves presented in Figure 19, the highest local collection efficiency of 0.75 is predicted to occur in Section A. In this case, Figure 20a, Figure 20b and Figure 20c compare the ice shapes in Sections A, B and C obtained in the current study with experimental data as well as LEWICE codes. The calculation demonstrates a horn shape, which is typical of glaze ice. In the case of Section A, as shown in Figure 20a, the developed code predicts the experimental shape at lower horn well, while predict a smaller than experimental one at upper horn but with same horn direction. The results of the current model agree better with the experimental shape compared to LEWICE codes. In the case presented in Figure 20b, a fairly similar shape to the experimental shape is found at lower horn in the current study. It is the ice shape predicted by LEWICE codes that agrees very well with the experimental shape. As can be observed in Figure 20c, predicted ice shapes for Section C in the current study is close to the experiments, while LEWICE codes could not predict the ice shape well at upper horn. Figure 21 shows the computational 3D ice shape for case II and the enlarged ice shape at the tip area of the wing. The validation study indicates that the newly developed Eulerian formulation can be capable of predicting ice shapes over the wing.
Ice accretion prediction over M6 wing
The validation performed and discussed above show that the numerical method and code is accurate with satisfaction, thus, in this section, an ice shape over a M6 wing is considered. Two different geometric and flow conditions (Case III and Case IV) corresponding to M6 wing are presented in Table 2. The computational grid employed is depicted in Figure 22a, and four different test sections, z/b = 0.05, 0.53, 0.73 and 0.97, are selected for computation, as shown in Figure 22b. Under the operating conditions studied (case III) in Table 2, it is expected that the high temperature (260 K) combined with high LWC (1.0 g/m3 587) could yield typical glaze ice conditions.
Figure 23a, Figure 23b, Figure 23c illustrate the calculated distribution of the local droplet collection efficiency, freezing fraction and convective heat transfer coefficient over M6 wing surface. The distribution of calculated freezing fraction presented in Figure 23b shows that the droplets do not freeze completely upon impact at stagnation vicinity. It can be also noted that at downstream, freezing fraction equals to 1, which indicates the droplets freeze upon impact. As a consequence, a layer of liquid film is formed at the leading edge. The runback water will pile up and freeze at the observed location. The ice shape obtained at four selected sections by the current study, as depicted in Figure 24, are typical glaze as expected. The 3D ice profile predicted by the current model is shown in Figure 25. For the purpose of further validation, the computed results for case IV are validated against available experimental results of [34]. Compared to the test conditions for case III, both the temperature (253.15 K) and LWC (0.5 g/m3) are lower, therefore, rime ice is expected under this operating condition for case IV. Figure 26a shows the local droplet collection efficiency increases gradually from wing root to wing tip. It should also be noted that high freezing fraction exists at the leading edge of the wing, as shown in Figure 26c. Figure 27 presents the comparison of ice shape between the current predicted results and available experimental data of Yi's work [32] at four different test sections. It is clearly seen that, for case IV, rime ice is accreted on the surface of the wing. Figure 28 shows the predicted ice accretion along the M6 wing surface for case IV.
Conclusions
A newly developed computational model is employed for the calculation of 3D ice accretion and compared with ONERA 3D predicted results. On the other hand, based on the developed model, the 3D ice accretion at three different sections, namely Section A, B and C, on GLC-305 wing under both rime (Case I) and glaze (Case II) icing conditions and comparing these results with available experimental data as well as LEWICE codes. In general, the current model provides a reasonably good prediction of the ice shape when compared to the other results. A close look at the comparison between current model and LEWICE codes show that for the Case I, the predicted ice shape of the current study agreeing well with the experimental one and LEWICE codes at the ice limits on the upper surface, while on the lower surface, the current calculations predict higher compared to others. On the other hand, in Sections A and C, both predicted and measured ice thickness is similar, showing good agreement. However, predicted ice thickness in Sections B and C of the current study is smaller than those obtained by LEWICE. While for the Case II, the results of the current model agree better with the experimental shape in Section A compared to LEWICE codes. In the case presented in Section B, it is the ice shape predicted by LEWICE codes that agrees well with the experimental shape. Predicted ice shapes for Section C in the current study is close to the experiments, while LEWICE codes cannot predict the ice shape well at upper horn. And finally, further calculation and validation based on the proposed method for ice shape prediction over a M6 wing under different icing conditions are numerically demonstrated.
Acknowledgements
The authors would like to acknowledge the financial support from the National Natural Science Foundation of China (Grant No.11372026 and Grant No. 11072019) and University of Hertfordshire, United Kingdom.