
International Journal of Earth Science and Geophysics
(ISSN: 2631-5033)
Volume 2, Issue 1
Review Article
DOI: 10.35840/2631-5033/1806
Relationship between the Aspect Ratio of a Collapsed Caldera and the Regional Stress Field - Their Evaluations Using a Single Small Spherical Magma Chamber Model in an Anisotropic Stress Field
Shigekazu Kusumoto1* and Toshiyasu Nagao2
Table of Content
Figures
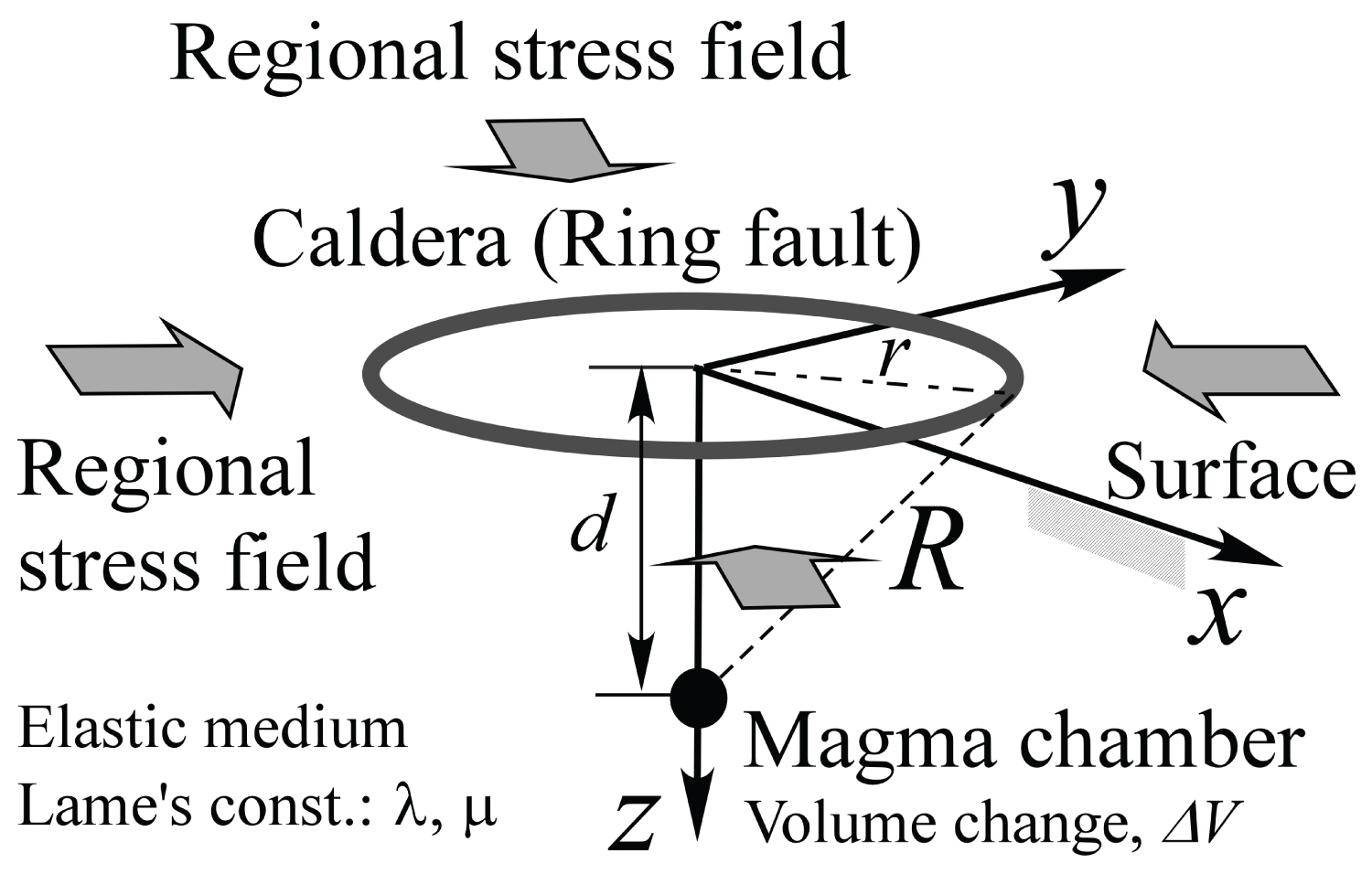
Figure 1: Model of small spherical magma chamber...
Model of small spherical magma chamber (point source model), with depth to center d, in an anisotropic regional stress field. Here, r is the horizontal distance from the surface point directly above the magma chamber to the periphery of the caldera (ring-fault).
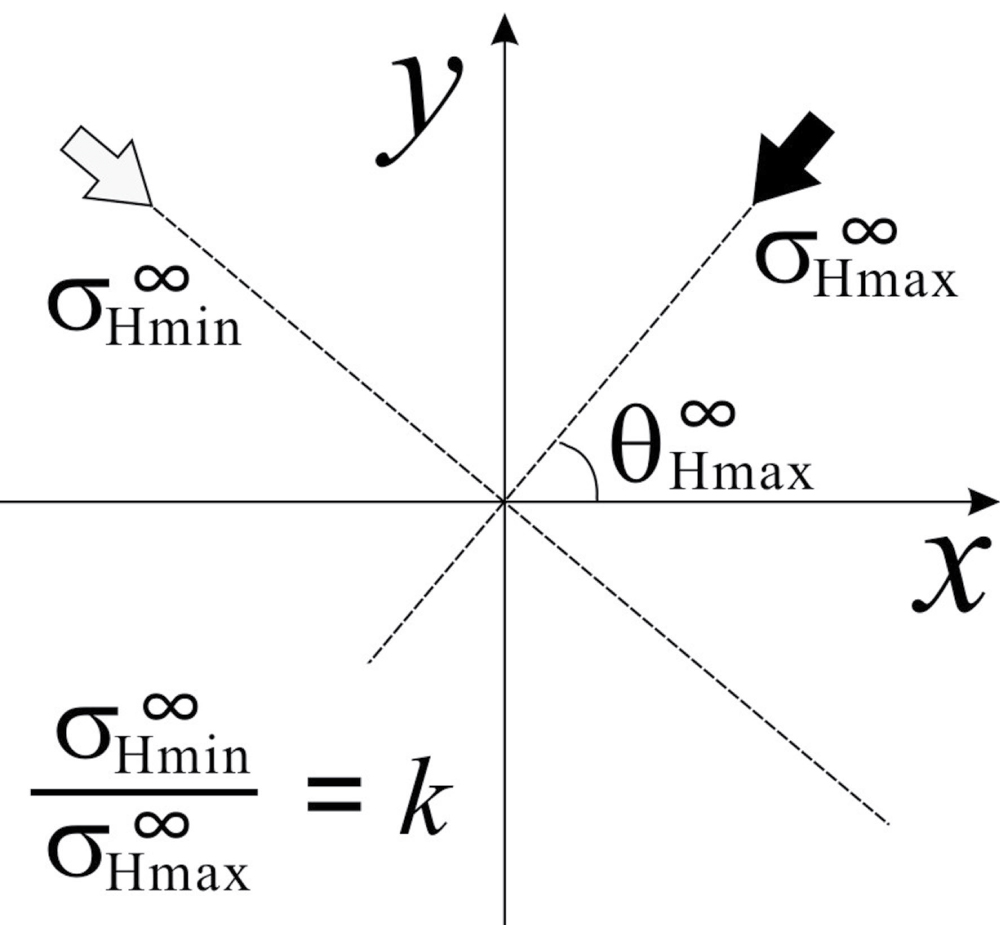
Figure 2: Relationship between the x-y coordinate system...
Relationship between the x-y coordinate system and the regional stress field (σ∞Hmax, σ∞Hmin, θ∞Hmax). σ∞Hmax, and σ∞Hmin are the maximum principal stress and minimum principal stress, respectively. θ∞Hmax is the angle of σ∞Hmax measured counterclockwise from the x-axis.
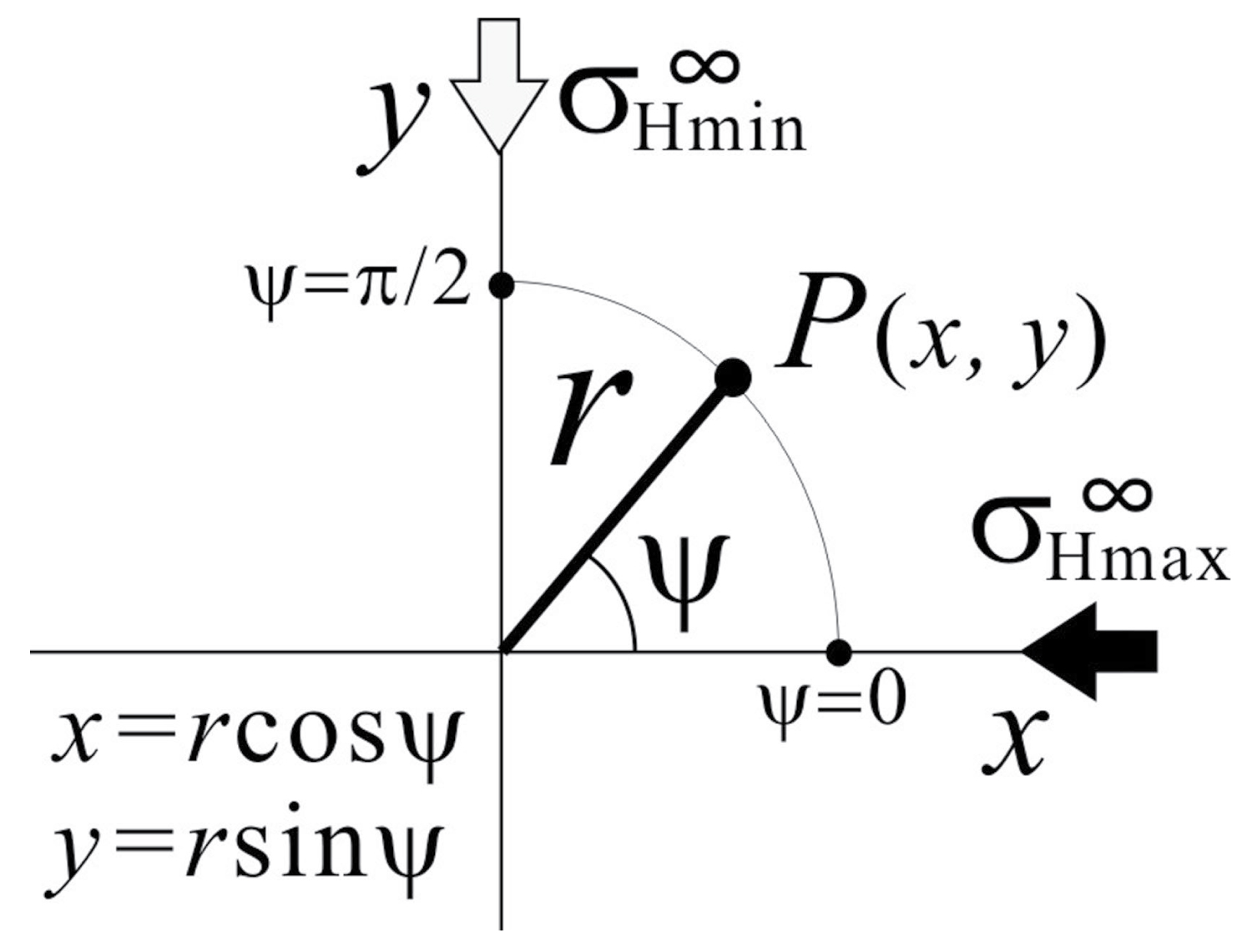
Figure 3: Relationship between the x-y coordinate system...
Relationship between the x-y coordinate system and the polar coordinate system. In order to facilitate mathematical treatment, the direction of the maximum principal stress of the regional stress field corresponds to the x-axis, so that θ∞Hmax = 0°.
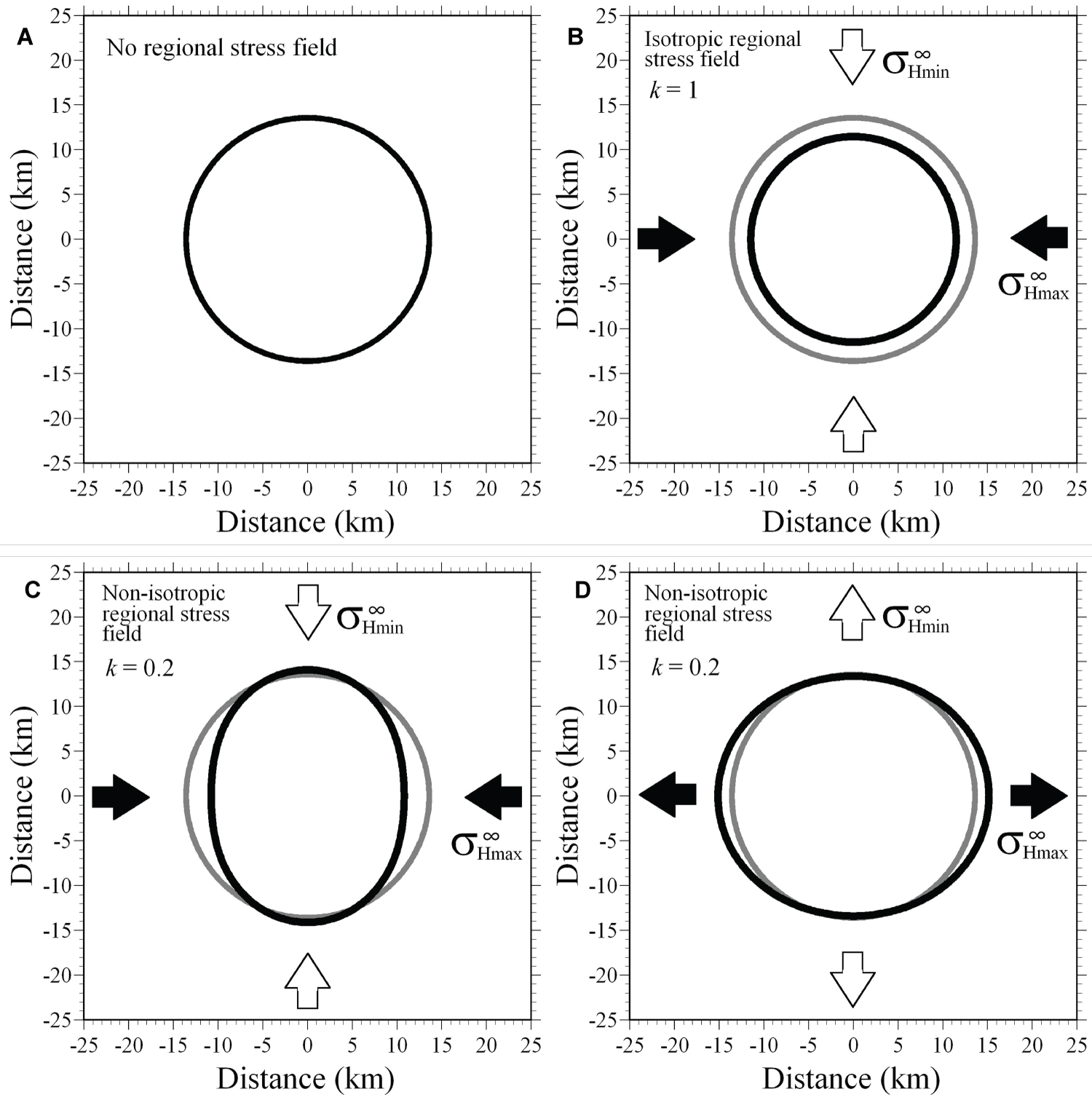
Figure 4: Caldera morphology under some regional stress...
Caldera morphology under some regional stress field (solid black shape). The solid gray circles in (b) - (d) indicate the caldera morphology when there is no regional stress; (a) Caldera morphology when there is no regional stress. Under this condition, the caldera is circular; (b) Caldera morphology under an isotropic homogeneous regional stress field of 25 MPa. Although the caldera is circular, its radius is smaller than the caldera formed when there was no regional stress; (c) Caldera morphology under an anisotropic homogeneous regional stress field with a stress ratio, k, of σ∞Hmin to σ∞Hmax of 0.2 and σ∞Hmax = 25 MPa. The caldera is elongated in the direction of the minimum compressional stress axis; (d) Caldera morphology under an anisotropic homogeneous regional stress field with a stress ratio, k, of σ∞Hmin to σ∞Hmax of 0.2 and σ∞Hmax = -10 MPa. The caldera is elongated in the direction of the maximum tension axis.
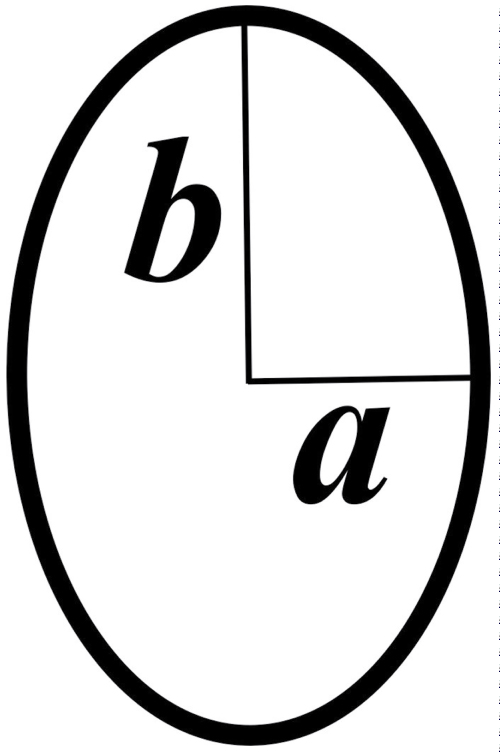
Figure 5: Definition of the aspect ratio. The aspect ratio...
Definition of the aspect ratio. The aspect ratio is the ratio (b/a) of the lengths of the major axis b and minor axis a of a caldera.
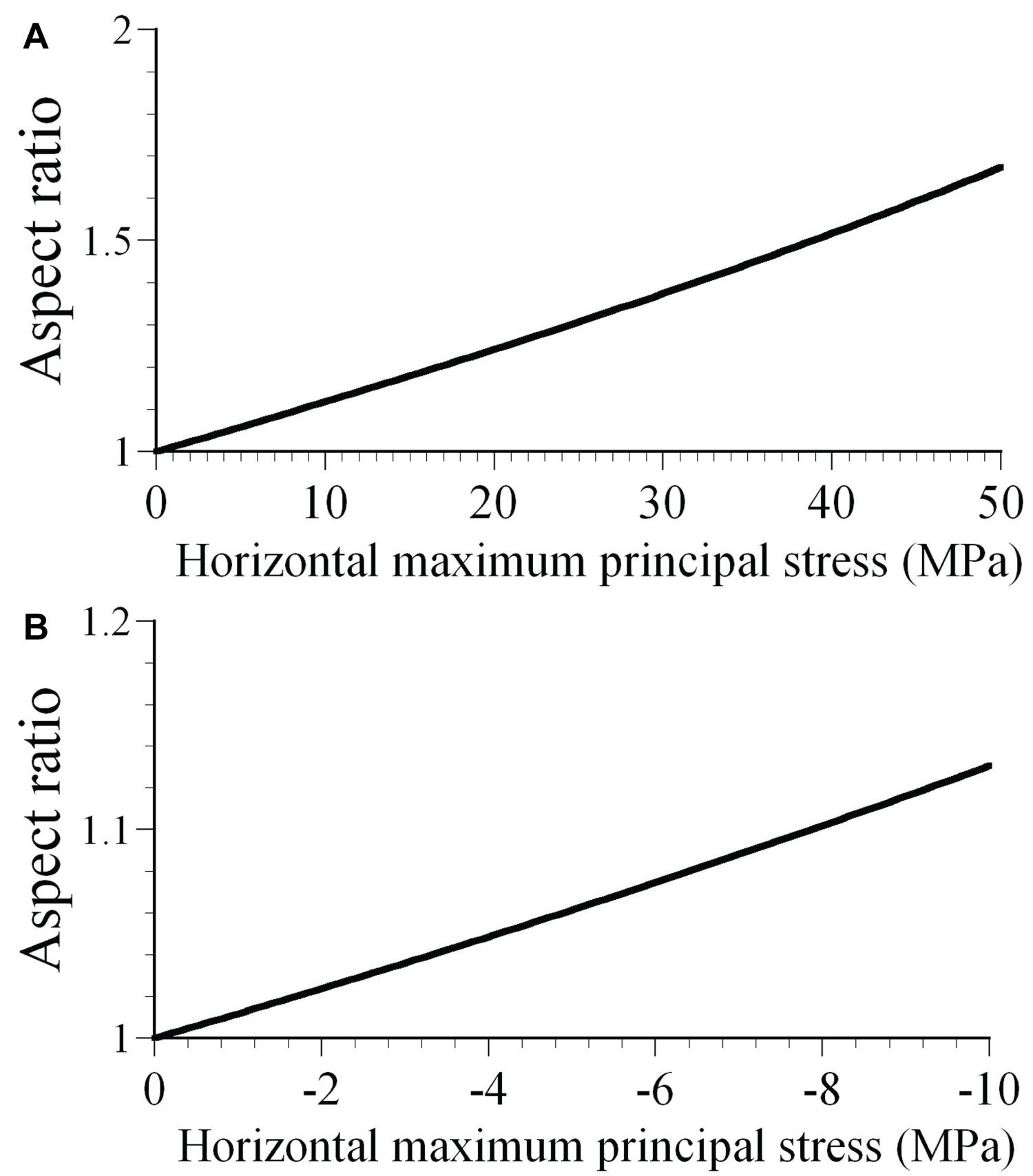
Figure 6: (a) Variations of the aspect ratio of the caldera...
(a) Variations of the aspect ratio of the caldera morphology caused by changes in the horizontal maximum principal stress (compressional stress field: positive stress). Stress ratio is constant at k = 0.2; (b) Variations of the aspect ratio of the caldera morphology caused by changes in the horizontal maximum principal stress (extensional stress field: negative stress). Stress ratio is constant at k = 0.2.
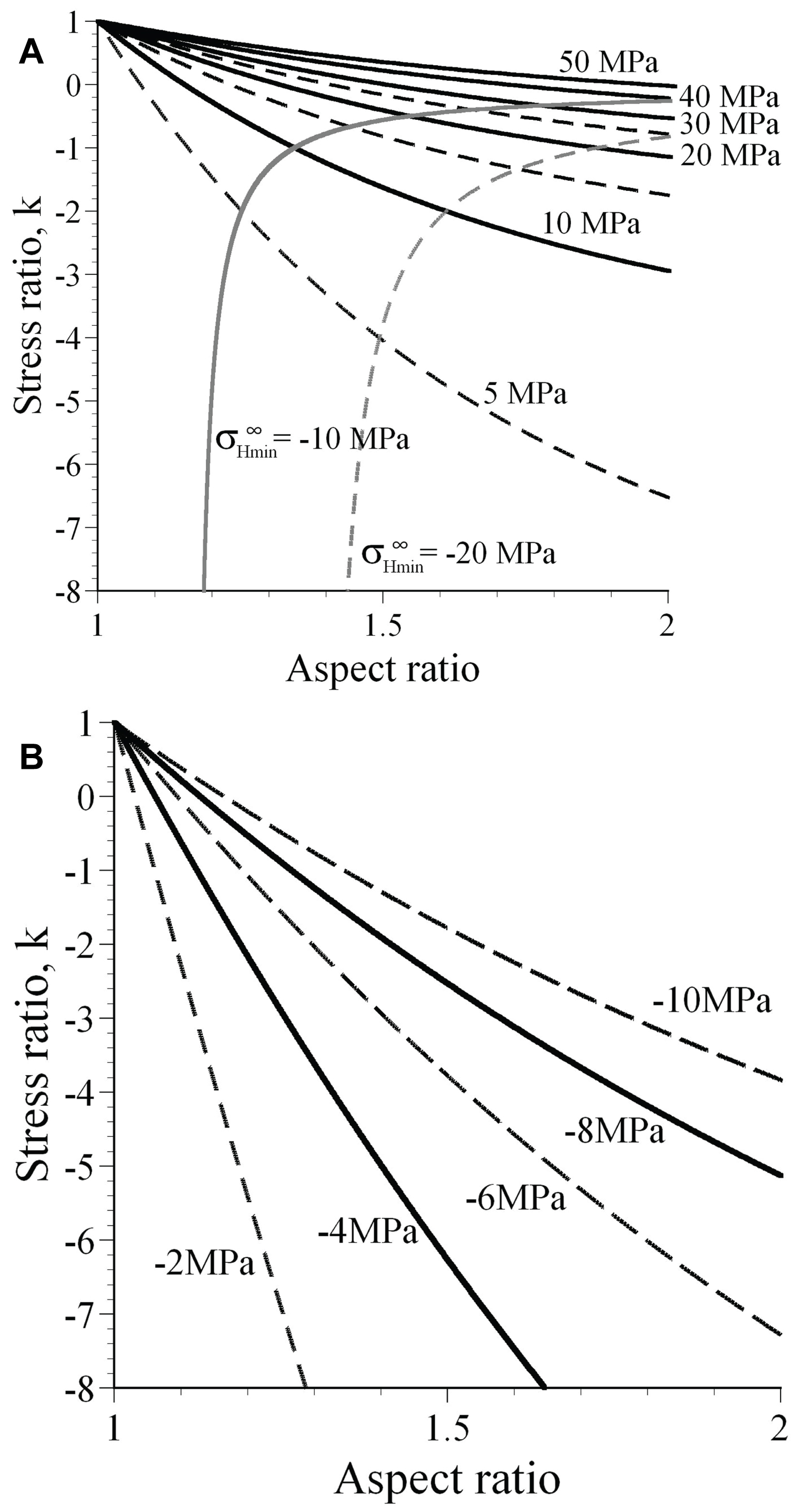
Figure 7: Relationship between the aspect ratio of the...
Relationship between the aspect ratio of the caldera and stress ratio, k. (a) Relationship between the aspect ratio and the stress ratio, k, with the horizontal maximum principal stress varying from 5 to 50 MPa. Compressional stress is positive. The solid gray line and dashed gray line indicate σ∞Hmin = -10 MPa and σ∞Hmin = -20 MPa, respectively; (b) Relationship between the aspect ratio and the stress ratio, k, with the horizontal maximum principal stress varying from -2 to -10 MPa. Extensional stress is negative.
References
- Smith RL, Bailey RA (1968) Resurgent calderas. Geol Soc Am Mem 116: 613-662.
- Druitt TH, Sparks RS (1984) On the formation of calderas during ignimbrite eruptions. Nature 310: 679-681.
- Lipman PW (1997) Subsidence of ash-flow calderas: relation to caldera size and magma-chamber geometry. Bull Volcanol 59: 198-218.
- Fiske R, Naka J, Iizasa K, Yuasa M (1995) Caldera-forming submarine pyroclastic eruption at Myojin knoll, Izu-Bonin arc. JAMSTEC Jour Deep Sea Res 11: 315-322.
- Wright IC, Gamble JA (1999) Southern Kermdec submarine caldera are volcanoes (SW Pacific): caldera formation by effusive and pyroclastic eruption. Mar Geol 161: 207-227.
- Wright IC, Gamble JA, Shane PAR (2003) Submarine silicic volcanism of the Healy caldera, southern Kermadec arc (SW Pacific): I - volcanology and eruption mechanisms. Bull Volcanol 65: 15-29.
- Komuro H (1987) Experiments on caldron formation: A polygonal cauldron and ring fractures. Jour Volcanol Geotherm Res 31: 139-149.
- Marti J, Ablay GJ, Redshaw LT, Sparks RSJ (1994) Experimental studies of collapse calderas. Jour Geol Soc London 151: 919-929.
- Gudmundsson A, Marti J, Turon E (1997) Stress field generating ring faults in volcanoes. Geophys Res Lett 24: 1559-1562.
- Acocella V, Cifelli F, Funiciello R (2000) Analogue models of collapse calderas and resurgent domes. Jour Volcanol Geotherm Res 104: 81-96.
- Roche O, Druitt TH, Merle O (2000) Experimental study of caldera formation. Jour Geo phys Res 105: 395-416.
- Walter TR, Troll VR (2001) Formation of caldera periphery faults: An experimental study. Bull Volcanol 63: 191-203.
- Troll VR, Walter TR, Schmincke HU (2002) Cycle caldera collapse: Piston or piecemeal subsidence? Field and experimental evidence. Geology 30: 135-138.
- Geyer A, Folch A, Marti J (2006) Relationship between caldera collapse and magma chamber withdrawal: an experimental approach. Jour Volcanol Geotherm Res 157: 375-386.
- Kusumoto S, Gudmundsson A (2009) Magma-chamber volume changes associated with ring-fault initiation using a finite-sphere model: Application to the Aira caldera, Japan. Tectonophysics 471: 58-66.
- Holohan EP, Walter TR, Schopfer MPJ, Walsh JJ, van Wyk de Vries B, et al. (2013) Origins of oblique-slip faulting during caldera subsidence. Jour Geophys Res 118: 1778-1794.
- Acocella V, Korme, T, Salvini F, Funiciello R (2002) Elliptic calderas in the Ethiopian Rift: control of pre-existing structures. Jour Volcanol Geotherm Res 119: 189-203.
- Lavallee Y, Stix J, Kennedy B, Richer M, Longpre M (2004) Caldera subsidence in areas of variable topographic relief: results from analogue modeling. Jour Volcanol Geotherm Res 129: 219-236.
- Belousov A, Walter TR, Troll VR (2005) Large-scale failures on domes and stratocones situated on caldera ring faults: sand-box modeling of natural examples from Kamchatka, Russia. Bull Volcanol 67: 457-468.
- Bosworth W, Burke K, Strecker M (2003) Effect of stress fields on magma chamber stability and the formation of collapse calderas. Tectonics 22.
- Bonini M, Mazzarini F (2010) Mud volcanoes as potential indicators of regional stress and pressurized layer depth. Tectonophysics 494: 32-47.
- Bonini M (2012) Mud volcanoes: indicators of stress orientation and tectonic controls. Earth-Sci Rev 115:121-152.
- Holohan EP, Troll VR, Walter TR, Munn S, McDonnell S, et al. (2005) Elliptical calderas in active tectonic settings: an experimental approach. Jour Volcanol Geotherm Res 144: 119-136.
- Mogi K (1958) Relations between eruptions of various volcanoes and the deformations of the ground surfaces around them. Bull Earthq Res Inst Univ Tokyo 36: 99-134.
- Kusumoto S, Takemura K (2005) Caldera geometry determined by the depth of the magma chamber. Earth Plan Space 57: e17-e20.
- Jaeger JC, Cook NG, Zimmerman RW (2007) Fundamentals of Rock Mechanics, 4th ed. Methuen, London.
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical Recipes in C: The Art of Scientific Computing, 2nd ed. Cambridge University Press, Cambridge, 994p.
- Forsyth D, Uyeda S (1975) On the relative importance of the driving forces of plate motion. Geophys J R Astro Soc 43: 163-200.
- Jarrard RD (1986) Relations among subduction parameters. Rev Geophys 24: 217-284.
- Golke M, Coblentz D (1996) Origins of the European regional stress field. Tectonophysics 266: 11-24.
- Lithgow-Bertelloni C, Guynn JH (2004) Origin of the lithospheric stress field. Jour Geophys Res 109.
- Heidbach O, Hohe J (2008) CASMI-A visualization tool for the world stress map database. Comp Geosci 34: 783-791.
- Gudmundsson A (1983) Stress estimates from the length/width ratios of fractures. Jour Struct Geol 5: 623-626.
- Andrew REB, Gudmundsson A (2008) Volcanoes as elastic inclusions: their effects on the propagation of dikes, volcanic fissures, and volcanic zones in Iceland. Jour Volcanol Geotherm Res 177: 1045-1054.
- Lama RD, Vutukuri VS (1978) Handbook on mechanical properties of rocks: testing tech-niques and results - Vol. 2, Trans Tech Publications, Clausthal, 481p.
- Du Y, Aydin A (1995) Shear fracture patterns and connectivity at geometric complexities along strike-slip faults. Jour Geophys Res 100: 18093-18102.
- Aldrich MJ, Chapin CE, Laughlin AW (1986) Stress history and tectonic development of the Rio Grande Rift, New Mexico. Jour Geophys Res 91: 6199-6211.
- Bosworth W, Burke K, Strecker M (2000) Magma chamber elongation as an indicator of intraplate stress field orientation: "borehole breakout mechanism" and examples from the Late Pleistocene to Recent Kenya Rift Valley. In: (Ed.) Mark Jessell, Janos Urai, Stress, Structure and Strain: a volume in honour of Win D. Means, Jour Virt Expl 2.
- Gudmundsson A (1995) Infrastructure and mechanics of volcanic systems in Iceland. Jour Volcanol. Geotherm Res 64: 1-22.
- Wallmann PC, Pollard DD, Hildreth W, Eichelberger JC (1990) New structural limits on magma chamber locations at the Valley of Ten Thousand Smokes, Katmai National Park, Alaska. Geology 18: 1240-1243.
Author Details
Shigekazu Kusumoto1* and Toshiyasu Nagao2
1Graduate School of Science and Engineering for research (Science), University of Toyama, Japan
2Earthquake Prediction Research Center, Institute of Oceanic Research and Development, Tokai University, Japan
Corresponding author
Shigekazu Kusumoto, Graduate School of Science and Engineering for research (Science), University of Toyama, 3910 Gofuku, Toyama 930-8555, Japan, E-mail: [email protected]
Accepted: February 17, 2016 | Published Online: February 20, 2016
Citation: Kusumoto S, Nagao T (2016) Relationship between the Aspect Ratio of a Collapsed Caldera and the Regional Stress Field - Their Evaluations Using a Single Small Spherical Magma Chamber Model in an Anisotropic Stress Field. Int J Earth Sci Geophys 2:006.
Copyright: © 2016 Kusumoto S, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We show a fundamental equation that yields a caldera morphology caused by a single magma chamber in an anisotropic homogeneous regional stress field, where the ratio between the maximum and minimum horizontal principal stresses is constant. The equation was obtained by evaluating the surface stress field due to the magma chamber's change in volume and the regional stress field using the Coulomb failure criteria. The fundamental equation included information on the crust, magma chamber and regional stress field. The caldera morphology given by the equation was consistent with caldera morphology observed in the field and previous analogue experiments, and it was found that changes in the stress ratio and the maximum principal stress of the regional stress field greatly affected the aspect ratio of the caldera. In addition, the derived equation gave information on several constraining conditions on the formation mechanism of elliptical calderas in the field, since the formation mechanism of an elliptical caldera is limited by the tensile strength of mother rock.
Keywords
Aspect ratio of collapsed caldera, Regional stress field, Collapsed caldera, Elliptical caldera
Introduction
Collapsed calderas are well known as volcanic depressions on the kilometer scale caused by the collapse of the roofs of magma chambers under the Earth's surface [1-3]. They are distributed not only on continents but also on ocean floors [4-6]. Understanding the mechanism that forms collapsed calderas is very important, not only for scientific knowledge but also for social purposes, such as the construction of hazard maps. Thus, many geological and geophysical surveys, analogue experiments, numerical simulations and theoretical studies have been conducted for better understanding the processes and other important factors in caldera formation. They have yielded that the depth, shape and scale of the magma chamber, as well as the magma transfer process, are important factors in determining the morphology and structure of calderas [7-16].
As it is well known, many calderas are elliptical like those in Taupo (New Zealand), Long Valley (USA), Campi Flegrei (Italy) and Taal (Philippines). Many studies have cited that elliptical magma chambers are caused by the overlapping of several calderas, and asymmetric subsidence due to differences in volcanic edifice loading [17-19]. It has also been considered that the regional stress field affects the elliptical caldera morphology since there are calderas elongated to the minimum compressional stress axis of the regional stress field. In field data, the caldera morphology is used as an indicator of the regional stress field [20-22]. Holohan et al. [23] conducted analogue experiments on the effect of the regional stress field, and found that ring faults and/or peripheral faults of the caldera will be elongated in the minimum compressional stress direction even if the shape of the magma chamber is not elliptical. They also found that changing the regional stress field would affect the aspect ratio of the caldera.
In this study, we showed a fundamental equation that quantifies how the regional stress field affects the caldera morphology. In order to show the equation, we assumed the magma chamber forming a caldera as a single small sphere and the regional stress field as a homogeneous isotropic or anisotropic field, where the ratio between the maximum and minimum horizontal stresses is constant (Figure 1). To simulate the small sphere, we employed a point source Mogi model [24], and approximated the collapse of the magma chamber as it contracts [15,25]. To facilitate the derivation of the equation, we evaluated the surface stress field due to contraction of the sphere together with the regional stress field, using the Coulomb failure criteria.
Superposition of Local and Regional Stress Fields
We superimposed the surface stress field caused by the magma chamber's change in volume with the regional stress field by the principle of superposition. As previously mentioned, we assumed a homogeneous regional stress field and a point source magma chamber. Then we solved the problem as a 2D problem (plane stress condition) in order to facilitate the mathematical treatment.
Actually, this problem should be solved as a 3D problem. However, in 3 D analysis, we have to evaluate stress components of the regional stress field and the stress field caused by volume change of the magma chamber not only in the x and y direction but in the z direction, and it is very difficult to analyze them. It is difficult to observe the calculated results in the field. Thus, in this study, we treated observable caldera morphology at the surface. In addition, since we discuss caldera morphology caused by the anisotropic regional stress and the area through which the regional stress field is distributed is much wider than the size of calderas that would be expected to form, we assumed the plane stress condition.
The total stress components (σxtotal, σytotal, τxytotal) of a homogeneous regional stress field with a magma chamber changing in volume, can be expressed as a sum of the regional stress field (σx∞, σy∞, τxy∞) and the surface stress field (σx, σy, τxy) caused by the magma chamber's change in volume.
In this case, the principal stress components, σ1 and σ3 are given by
And the angle, θ, defined between σ1 and x-axis is given as follows [26]:
The surface stress field (σx, σy, τxy) caused by the magma chamber's change in volume, ΔV, is given as follows,
Where d is depth of the magma chamber and λ and μ are Lame's constants for the medium. R2 = x2 + y2 + d2 (Figure 1). Equations (4) were derived by applying Hooke's law under plane stress conditions to the surface strain due to the volume change of the magma chamber, which was approximated as a point source [25].
Although the regional stress field is given by σx∞, σy∞ and τxy∞ in equation (1), a more general form can be written for the principal stress. We identify the principal stress components of the homogeneous regional stress field as σ∞Hmax and σ∞Hmin, with the orientation of σ∞Hmax being given by θ∞Hmax, which is measured counterclockwise from the x axis (Figure 2). In this case, by replacing σ1, σ3, σx, σY, τxY and θ in equations (2) and (3) with σ∞Hmax,σ∞Hmin, σx∞, σY∞, τxY∞ and θ∞Hmax, we obtain σx∞, σY∞, τxY∞ as follows.
If we introduce the following stress ratio k,
Then we can rewrite equation (5) as,
The maximum and minimum horizontal principal components of the regional stress field are then separate x-y components in the x-y coordinate plane as in equation (7) and can be used in equation (1).
Evaluation of Stress Field
Here, we evaluate the stress field made by superposition of a regional stress field and a surface stress field caused by a volume reduction, using the Coulomb failure criteria, and show the relationship between the regional stress field and the morphology of an elliptical caldera.
The Coulomb failure criteria is given as [26]
Where c0 is the compressional strength and φ is the angle of interior friction. By substituting the principal stresses given by equation (2) into equation (8), we obtain
Here, w is w = tan2 (45°+φ/2).
We substitute equations (4) and (7) into equation (9), and assume θ∞Hmax = 0 to simplify the mathematical treatment of the equations. This assumption of θ∞Hmax = 0 means the condition that the maximum principal stress axis of the regional stress field corresponds to the x-axis (Figure 3). In this case, equation (9) is described as follows.
Where r2 = x2 + y2, x = r cos ψ and y = r sin ψ (Figure 3). The r that satisfies equation (10) gives locations of ring faults and the track of r will be the morphology of caldera. Since it is difficult to solve algebraically for an r that satisfies equation (10), r is determined by numerical methods, such as the bisection method, secant method, and Laguerre's method [27]. In this study, we employed the bisection method for simplicity. In the calculation, we obtained the r satisfying the equation (10) at the interval of π/180 radian in the range of ψ = 0 - 2π, by the bisection method.
Numerical Examples and Discussion
There are many studies on stress fields at and around plate boundaries [28-30], and a world stress map database has been compiled [31,32]. In addition, because it is well known that in Iceland, which has been subjected to an extensional stress field of several MPa [33,34], and the general tensile strength of the rock is around -10 MPa (in a compressional stress system), we set -10 MPa as the upper limit of the regional extensional stress field.
It was assumed that Young's modulus, Poisson's ratio, the angle of internal friction, and compressional strength of the crust (basaltic crust) are 40 GPa, 0.25, 30° and 150 MPa respectively [25,35]. We employed the equation giving the necessary minimum volume change to form a caldera shown by Kusumoto and Gudmundsson [15] to set our volume change, ΔV. Since we assumed a point source model in this paper to simulate the magma chamber, the magma chamber radius is set to zero in their equation and the depth of the chamber is 10 km (d = 10 km).
In figure 4, we show caldera morphology estimated under the following conditions: (a) no regional stress field, (b) a regional stress field that is isotropic and homogeneous, with a magnitude of 25 MPa, (c) a regional stress field where σ∞Hmax = 25 MPa, σ∞Hmin = 5 MPa (stress ratio k = 0.2, as per [36]) and (d) a regional stress field where σ∞Hmax =-10 MPa, σ∞Hmin =-2 MPa (stress ratio k = 0.2).
As shown in figure 4a, the caldera is circular when there is no regional stress. This supports the results of previous analogue experiments [10,11]. When the regional stress field is isotropic and homogeneous, the caldera morphology is circular as shown in figure 4b, but its radius is smaller. The gray circle shown in figure 4b shows the caldera morphology when there is no regional stress (Figure 4a). From this result, in a regional stress field with isotropic compression, circular calderas form with radii smaller than those without regional stress fields.
In an anisotropic compressional stress field, a caldera will shrink towards the maximum compressional principal stress axis and will elongate towards the minimum compressional principal stress axis (Figure 4c). While in an anisotropic extensional stress field, a caldera will elongate towards the maximum extensional principal stress axis and will shrink towards the minimum extensional principal stress axis (Figure 4d). The gray circles shown in figures 4c and 4d are caldera morphology when there is no regional stress (Figure 4a). These results support the relationship between the regional stress field and caldera morphology as shown in analogue experiments given by Holohan et al. [23] and also support the relationship between the caldera morphology and the regional stress field in the field, such as Valles caldera (New Mexico), Suswa caldera (Kenya), Krafla (Iceland), Katmai (Alaska), and mud calderas located in Azerbaijan [21,37-40].
In this study, as shown in figure 5, we defined the aspect ratio of an elliptical caldera as the semi-major axis b/semi-minor axis a, and we estimated the relationship between the magnitude of the maximum horizontal stress and the aspect ratio of the caldera being formed when the stress ratio, k, defined in equation (6) is a constant value of 0.2.
From figure 6a, it can be seen that even if the magnitude of k was constant, if the magnitude of the maximum horizontal compressional stress increased, the caldera was elongated more in the direction of the minimum horizontal compressional stress and has a high aspect ratio. In the case of an extensional stress field, if the magnitude of the maximum horizontal extensional stress increased, the caldera elongated more in the direction of the maximum horizontal extensional stress and has a high aspect ratio (Figure 6b). These are the same results given in analogue experiments by Holohan et al. [23].
Up to this point, we have discussed caldera morphology under the assumption of a constant stress ratio. Next, we discuss the case when the stress ratio, k, varies.
Figure 7a shows the relationship between the stress ratio of the regional stress field and the aspect ratio of the elliptical caldera when the magnitude of the maximum horizontal compressional stress varies from 5 to 50 MPa. Figure 7b shows the relationship between the stress ratio of the regional stress field and the aspect ratio of the elliptical caldera when the magnitude of the maximum horizontal extensional stress varies from 2 to 10 MPa. These figures show that a small stress ratio, indicating a large difference in stress, is necessary for an elliptical caldera with a large aspect ratio to form. A negative stress ratio here means that the sign of the maximum horizontal stress has been reversed from a compressional stress to an extensional stress. Considering the tensile strength of rock, an extension of 10 MPa (-10 MPa in a compressional stress system) would be suitable as the upper limit for the regional extensional stress field. The grey line in figure 7a shows the relationship between the aspect ratio and the stress ratio for σ∞Hmin = -10 MPa given a range of σ∞Hmax values. For reference, we also include a dotted grey line showing the same curve when σ∞Hmin is -20 MPa. An elliptical-shaped caldera can form only on the left side of the σ∞Hmin = -10 MPa (or σ∞Hmin = -20 MPa) line. This suggests that elliptical calderas can only form under limited conditions, and that a certain magnitude for the compressional regional stress field is necessary to form an elliptical caldera, when the small spherical magma chamber model is employed. Although, it would be necessary to consider the effects of elastic and strength constants of the crust.
In the field, there are many elliptical calderas with a large aspect ratio, such as Long Valley, Yellowstone-Snake River Plain, and mud calderas in Azerbaijan [20,21]. In these calderas, there are elliptic calderas that were formed not by the regional stress field but by an elliptical magma chamber or an assembly of several calderas. In order to specify whether a caldera morphology is controlled by structural factors or the regional stress field, it is necessary to carry out careful geological and geophysical surveys and examine the obtained data from a mechanical viewpoint. These conditions should be considered with the modeling and interpretation of other elliptical calderas with a large aspect ratio. Since the equation obtained in this study gives us some constraints on which elliptical calderas would be formed by the regional stress field, the equations contribute quantitative discussions on the formation mechanism of elliptical calderas.
Conclusion
The morphology of a caldera is controlled by many important physical factors. In this study, we focused on how the regional stress field affects the morphology of a caldera, and derived a fundamental equation that yields the morphology of a caldera being formed under an arbitrary homogeneous regional stress field. We derived the equation by evaluating the surface stress field due to the change in volume of the magma chamber in combination with the regional stress field using the Coulomb failure criteria. The fundamental equation included elastic and strength constants of the crust, depth and volume changes of the magma chamber, and information on the regional stress field (stress ratios and the magnitude of the maximum horizontal principal stresses).
The caldera morphology given by the equation was consistent with analogue experiments and field data. In addition, it was found that the magnitude of the stress ratio and the maximum principal stress of the regional stress field had a great effect on the aspect ratio of the elliptical caldera, and that the conditions required to form an elliptical caldera would be quite limited. There are many causes for determining the caldera morphology, such as the magma chamber shape (including activity of multiple magma chambers), and existing structures. It is difficult to specify the cause of a caldera morphology only by surveys. However, since the equation shown in this study give us several constraining conditions on the caldera morphology due to the regional stress field, the equation would contribute to discussions on the main causes that dominate caldera morphology in the field from a mechanical viewpoint.
Acknowledgments
We are most grateful to three anonymous reviewers for their constructive reviews and comments on the manuscript. The manuscript was improved. This study was supported partially by JSPS (Japan Society for the Promotion of Science) KAKENHI Grant Number 15K14274. We are grateful to JSPS.

