
International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 6, Issue 1
Research Article
DOI: 10.35840/2631-5068/6526
Angular Momentum Emission by a Rotating Dipole
Radi I Khrapko*
Table of Content
Figures
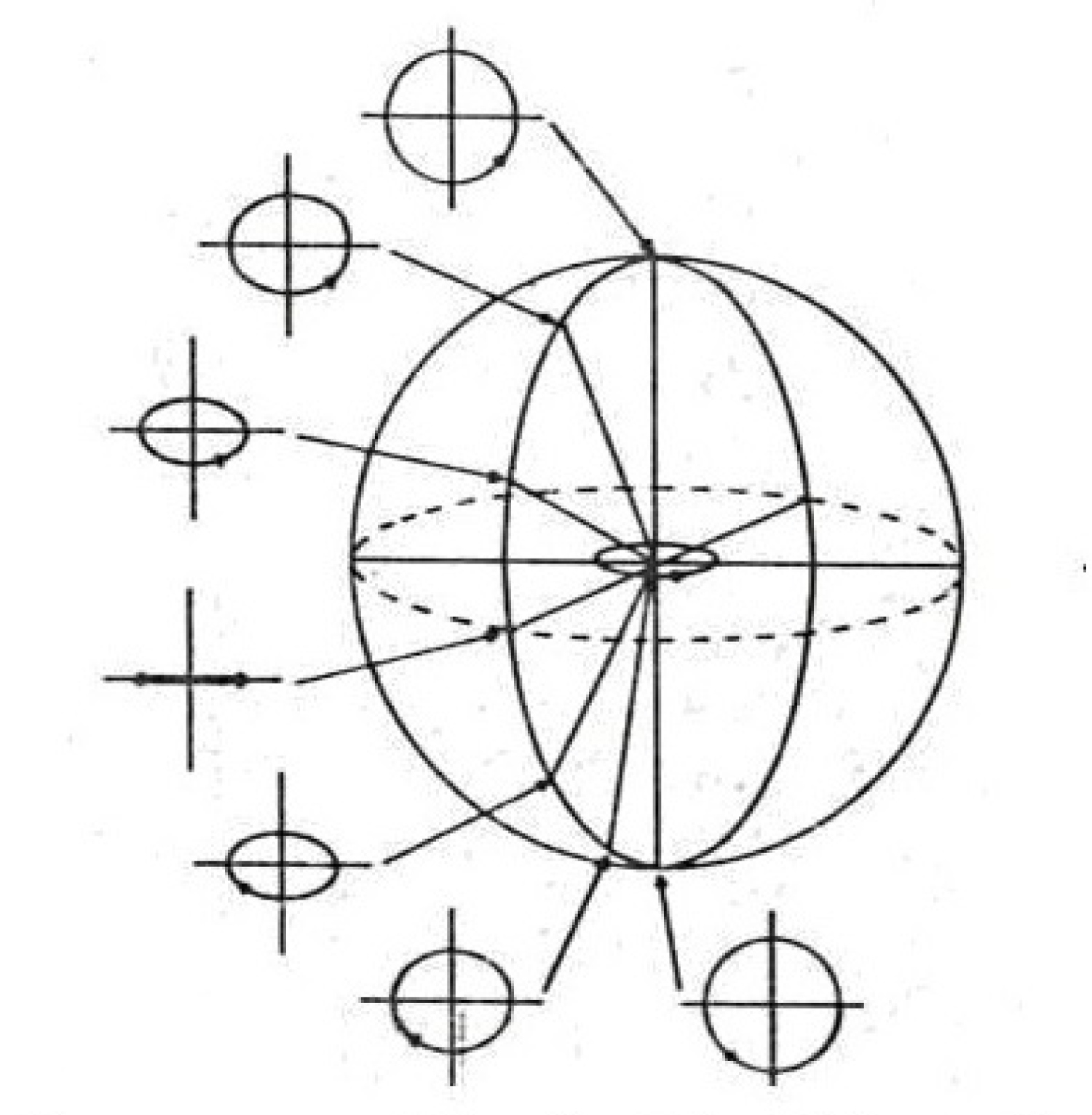
Figure 1: Polarization of the electric field seen....
Polarization of the electric field seen by looking form different directions at a circular oscillator.
References
- Sadowsky A (1899) Acta et Comm. Imp. Universitatis Jurievensis, Russia, 7: 1-3.
- ???nting J? (1909) The wave motion of a revolving shaft, and a suggestion as to the angular momentum in a beam of circularly polarised light. Proc R Soc Lond A 82: 560-567.
- Weyssenhoff J, Raabe A (1947) Relativistic dynamics of spin-fluids and spin-particles. Acta Phys Polon 9: 7-19.
- Crawford FS (1968) Waves: Berkley physics course. Berkeley, California, USA, 3.
- Feynman RP, Leighton RB, Sands M (1965) The Feynman lectures on physics. Addison-Wesley, London, 3: 17.
- Corson EM (1953) Introduction to tensors, spinors, and reativistic wave-equation. Hafner, USA, 71.
- Soper DE (2008) Classical field theory. Dover, USA, 114.
- Barut AO (1964) Electrodynamics and classical theory of particles and fields. Macmillan, USA, 102.
- Khrapko RI (2018) Absorption of spin by a conducting medium. AASCIT Journal of Physics 4: 59-63.
- Khrapko RI (2018) Absorption of angular momentum of a plane wave. Optik 154: 806-810.
- Khrapko R (2019) Unknown spin radiation. J Phys: Conf Ser 1172: 012055.
- Khrapko RI (2006) Origin of spin: Paradox of the classical Beth experiment. In: Smarandache F, Christianto V, Yuhua Fu, Khrapko R, Hutchison J, Unfolding the Labyrinth: Open Problems in Mathematics, Physics, Astrophysics, and other areas of science. Hexis - Phoenix, 57-71.
- Khrapko RI (2008) Mechanical stresses produced by a light beam. J Modern Optics 55: 1487-1500.
- Khrapko RI (2017) Reflection of light from a moving mirror. Optik 136: 503-506.
- Khrapko RI (2019) Spin radiation from a rotating dipole. Optik 181: 1080-1084.
- Khrapko RI (2020) Radiation damping of a rotating dipole. Optik 203: 164021.
- Khrapko RI (2020) Absorption of spin of a plane circularly polarized wave. Optik 210: 164527.
- Khrapko RI (2002) True energy-momentum tensors are unique. Electrodynamics spin tensor is not zero. Moscow Aviation Institute, Russia.
- Khrapko RI (2001) Violation of the gauge equivalence. Moscow Aviation Institute, Russia.
- Khrapko RI (2005) Spin transmitted to the mirror when light is reflected. Moscow Aviation Institute, Russia.
- Andrews DL, Babiker M (2013) The angular momentum of light. Cambridge University Press, UK.
- Heitler W (1954) The quantum theory of radiation. Oxford University Press, Clarendon, UK, 401.
- Allen L, Padgett MJ (2002) Response to question #79. Does a plane wave carry spin angular momentum? Am J Phys 70: 567.
- Simmonds JW, Guttmann MJ (1970) States, waves and photons. Addison-Wesley, Reading, USA.
- Ohanian HC (1986) What is spin? Amer J Phys 54: 500-505.
- Landau LD, Lifshitz EM (1975) The classical theory of fields. Pergamon, NY, USA.
- Jackson JD (1999) Classical electrodynamics. John Wiley, USA, 350.
- Hehl FW (1976) On the energy tensor of spinning massive matter in classical field theory and general relativity. Reports on Mathematical Physics 9: 55-82.
- Becker R (1982) Electromagnetic fields and interactions. Dover, NY, USA,1: 284.
- Corney A (1977) Atomic and laser spectroscopy. Oxford University Press, Clarendon, UK, 36.
- Meyers RA (1987) Encyclopedie of physics science and technology. Academic Press, NY, USA, 2: 266.
- Sommerfeld A (1951) Atombau und Spektrallinien. Vieweg F, Braunschweio S, UK.
- Vul'fson KS (1987) Angular momentum of electromagnetic waves. Sov Phys Usp 30: 724-728.
- Barabanov AL(1993) Angular momentum in classical electrodynamics. Phys Usp 36: 1068-1074.
- Khrapko RI (2001) Spin of dipole radiation. Moscow Aviation Institute, Russia, 34635.
- Khrapko RI (2003) Radiation of spin by a rotator. Mathematical Physics Preprint Archive, 03-315.
- Khrapko RI (2012) Spin is not a moment of momentum. Moscow Aviation Institute, Russia, 28834.
- Khrapko RI (2001) Does plane wave not carry a spin? Amer J Phys 69: 405.
Author Details
Radi I Khrapko*
Moscow Aviation Institute, Volokolamskoe Shosse 4, Russia
Corresponding author
Radi I Khrapko, Moscow Aviation Institute, Volokolamskoe Shosse 4, 125993, Moscow, Russia.
Accepted: December 09, 2020 | Published Online: December 11, 2020
Citation: Khrapko RI (2020) Angular Momentum Emission by a Rotating Dipole. Int J Magnetics Electromagnetism 6:026.
Copyright: © 2020 Khrapko RI. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
A new calculation confirms the presence of spin radiation along the axis of rotation of a dipole. This is further proof of the need to introduce the spin tensor into classical electrodynamics, along with the energy-momentum tensor.
Keywords
Classical spin, Electrodynamics, Spin radiation
PACS
75.10.Hk, 03.50.De
Introduction
Circularly polarized electromagnetic radiation contains angular momentum in the form of the angular momentum density [1,2].
JH Poynting [2]: "If we put E for the energy in unit volume and G for the torque per unit area, we have ".
This means that such radiation is Weyssenhoff's spin-fluid [3].
J Weyssenhoff: "By spin-fluid we mean a fluid each element of which possesses besides energy and linear momentum also a certain amount of angular momentum, proportional - just as energy and the linear momentum - to the volume of the element".
This is recorded in textbooks [4,5]. Since Emma Noether, this angular momentum has been described by the spin tensor density [6-8].
Where is the free electromagnetic field Lagrangian, is the vector potential, and is the field-strength tensor. The local sense of a spin tensor is as follows. [J*s/m3] is spin volume density, [J*s/m2] is spin flux density, i.e. torque per unit area (cf. J. H. Poynting). The spin tensor is used in the publications [9-20]. However, the spin tensor is ignored in works expressing the common point of view, e.g. [21-25].
Besides spin, any electromagnetic field contains mass-energy and momentum, which are described by the energy-momentum tensor [26,27].
The local sense of the energy-momentum tensor is as follows. [N*s/m3] is momentum volume density, [kg/m2*s] is mass-energy flux density. It means, e.g., is the momentum in the volume .
Moment of momentum, e.g., is the orbital angular momentum of the momentum contained in the volume . So, the total angular momentum possessed by the volume is
The total torque per the area , i.e. angular momentum flux, is
It is important that spin is not associated with a moment of a linear momentum, or even with a motion of matter. Hehl writes about spin of an electron [28]:
"The current density in Dirac's theory can be split into a convective part and a polarization part. The polarization part is determined by the spin distribution of the electron field. It should lead to no energy flux in the rest system of the electron because the genuine spin 'motion' take place only within a region of the order of the Compton wavelength of the electron".
Electromagnetic Field of a Rotating Dipole
Electromagnetic field of a rotating dipole p is well known [27,29,30].
The first terms of (5), (6) are proportional to and so represent radiation. This radiation is of circular polarization in the direction of the rotational axis, z-axis (see Figure 1 from [31]). Therefore this field contains the spin flux . We calculate this spin flux per sphere in Section 3.
At the same time this radiation contains no orbital angular momentum flux per elements of the sphere . . Really, the first terms fields E & H are orthogonal to each other and to the vector r. So, in any point, we can enter local Cartesian coordinates such that , , i.e. are not equal to zero only. Using this coordinates we find according to (2): . So the orbital angular momentum is not radiated.
The second terms field of (5), (6) contains the orbital angular momentum flux, or torque, per the sphere . In Refs [32-37], spherical coordinates were used, and the angular distribution of the torque was obtained (see Figure 2):
Where, . This torque is located in the neighborhood of the plane of rotation where the polarization is near linear. This torque is not radiated. This torque is like a static torque that someone can apply (Figure 2).
Spin Radiation by a Rotating Dipole
Spin radiated by the first terms field was calculated in [15] using the spin volume density on the assumption that this density is moving at the speed of light. Here the spin flux density is used. This is more naturally.
Using
yields
Using yields
Accordingly to , we have
Because of , we need the Cartesian coordinates of elements of the sphere , which spherical coordinates are . The transformation coefficients are;
, and . So we have
This result, , is coincided with Ref. [15]. The angular distribution of the spin radiation is represent in Figure 3.
Conclusion
A rotating electric dipole emits angular momentum flux of two types: (i) Spin flux, which is directed mainly along the axis of rotation and determined by the spin tensor, and (ii) Orbital angular momentum flux determined by the energy-momentum tensor. The spin flux is not recognized by nowadays electrodynamics.
I am eternally grateful to Professor Robert Romer for the courageous publication of my question: "Does a plane wave really not carry spin?" [38] (was submitted on 07 October, 1999).



