International Journal of Metallurgy and Metal Physics
(ISSN: 2631-5076)
Volume 2, Issue 2
Research Article
DOI: 10.35840/2631-5076/9209
Simulation on Dendrite Growth during Solidification of Ti-45%Al Alloy in the Weld Pool
Min Zhang*, Yulan Zhou, Qin Xue, Jihong Li and Yuanyuan Xi
Table of Content
Figures
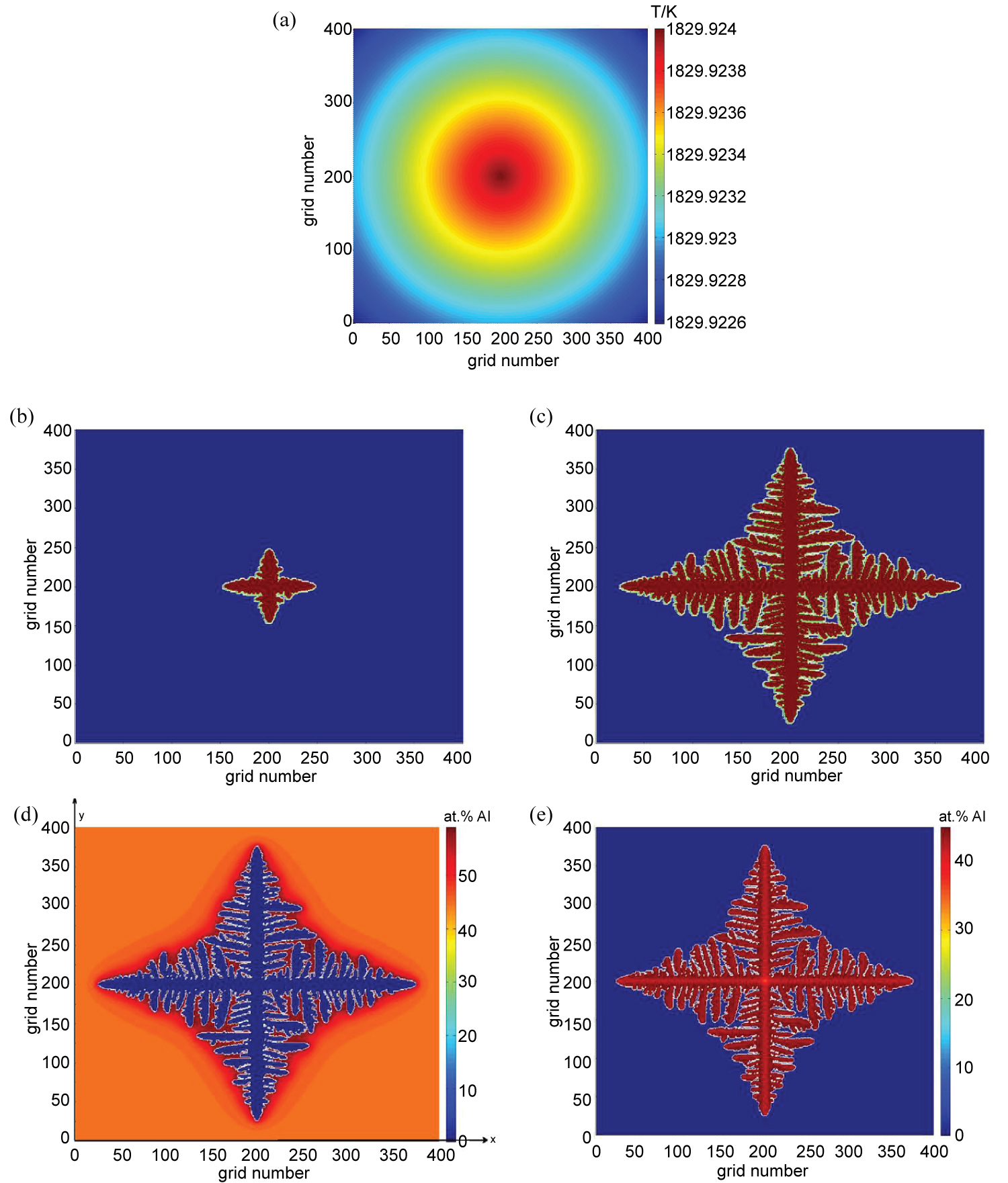
Figure 1: Growth morphology of single equiaxed dendrite...
Growth morphology of single equiaxed dendrite, a) Ideal temperature field for simulating isometric crystal; b,c) Single equiaxed crystal morphology at different time; d) Liquid solute distribution; e) Solid solute distribution.
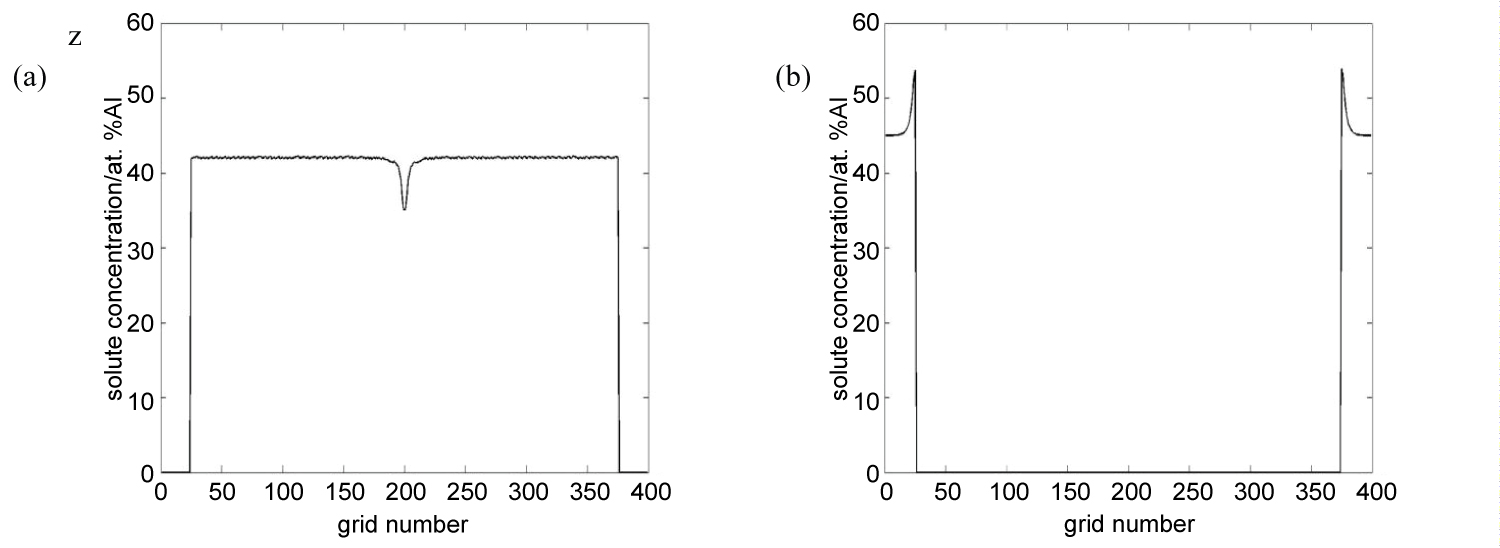
Figure 2: Solute distribution of single...
Solute distribution of single equiaxed dendrite at line y = 200, a) Solid solute distribution; b) Liquid solute distribution.
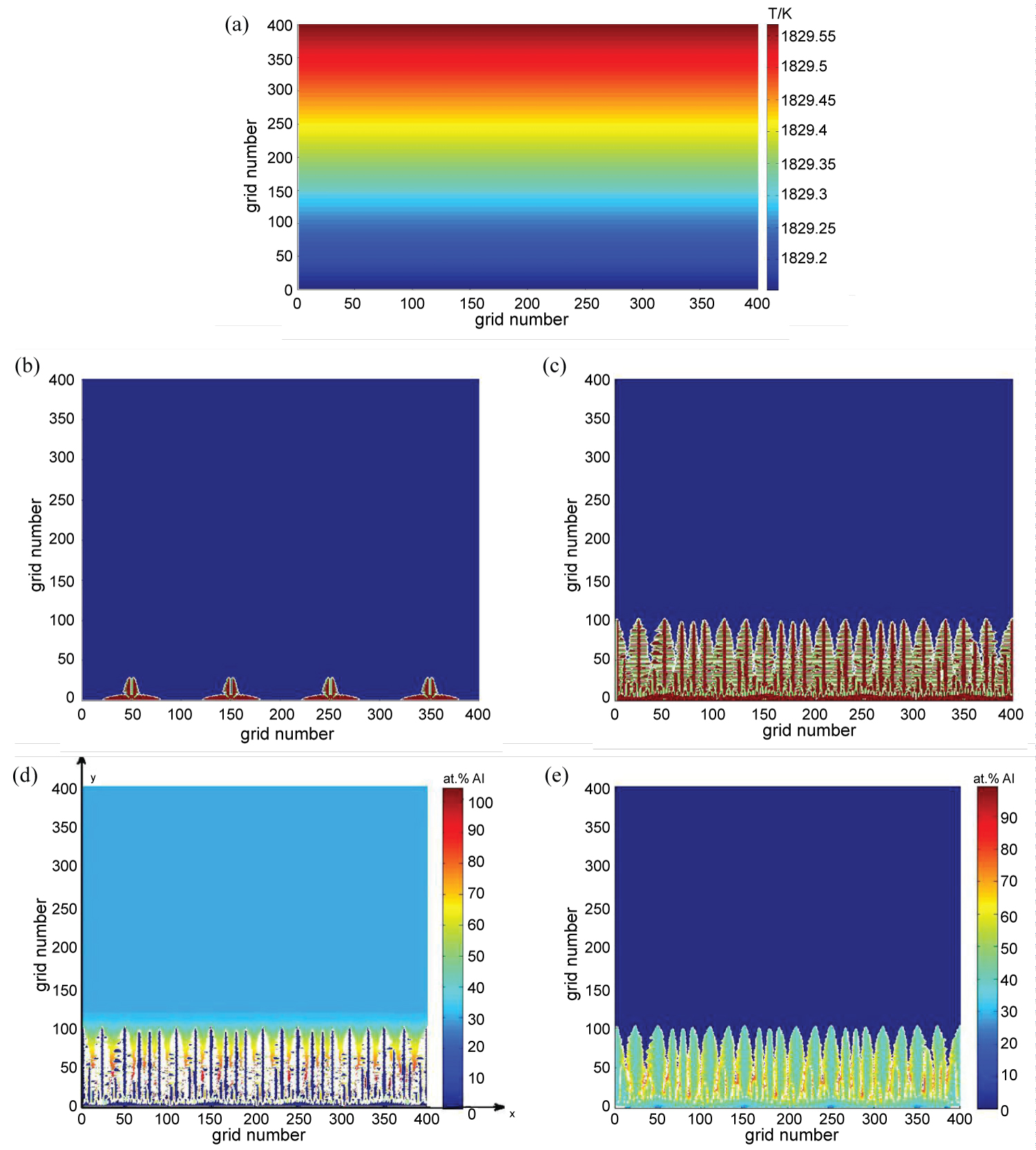
Figure 3: The cylindrical crystal growth morphology...
The cylindrical crystal growth morphology, a) Ideal temperature field for simulating columnar crystal; b,c) Cylindrical crystal morphology at different time; d) Liquid solute distribution; e) Solid solute distribution.
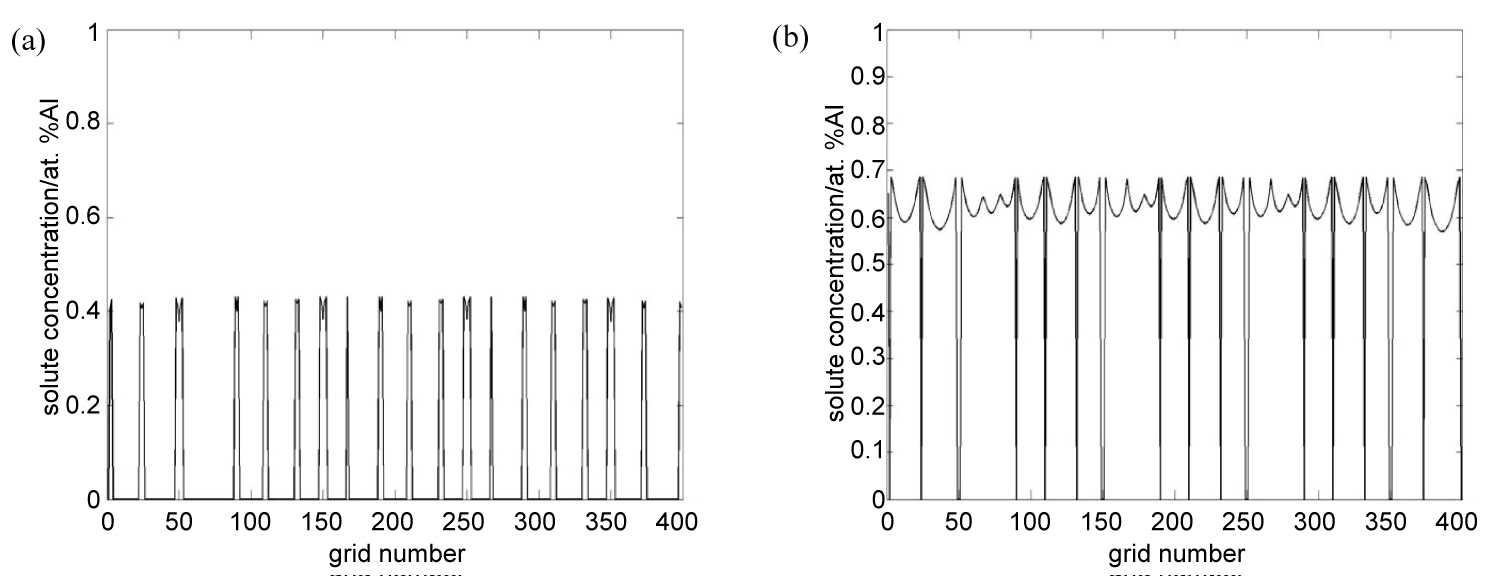
Figure 4: Solute distribution of cylindrical...
Solute distribution of cylindrical crystal at line y = 100, a) Solid solute distribution; b) Liquid solute distribution.
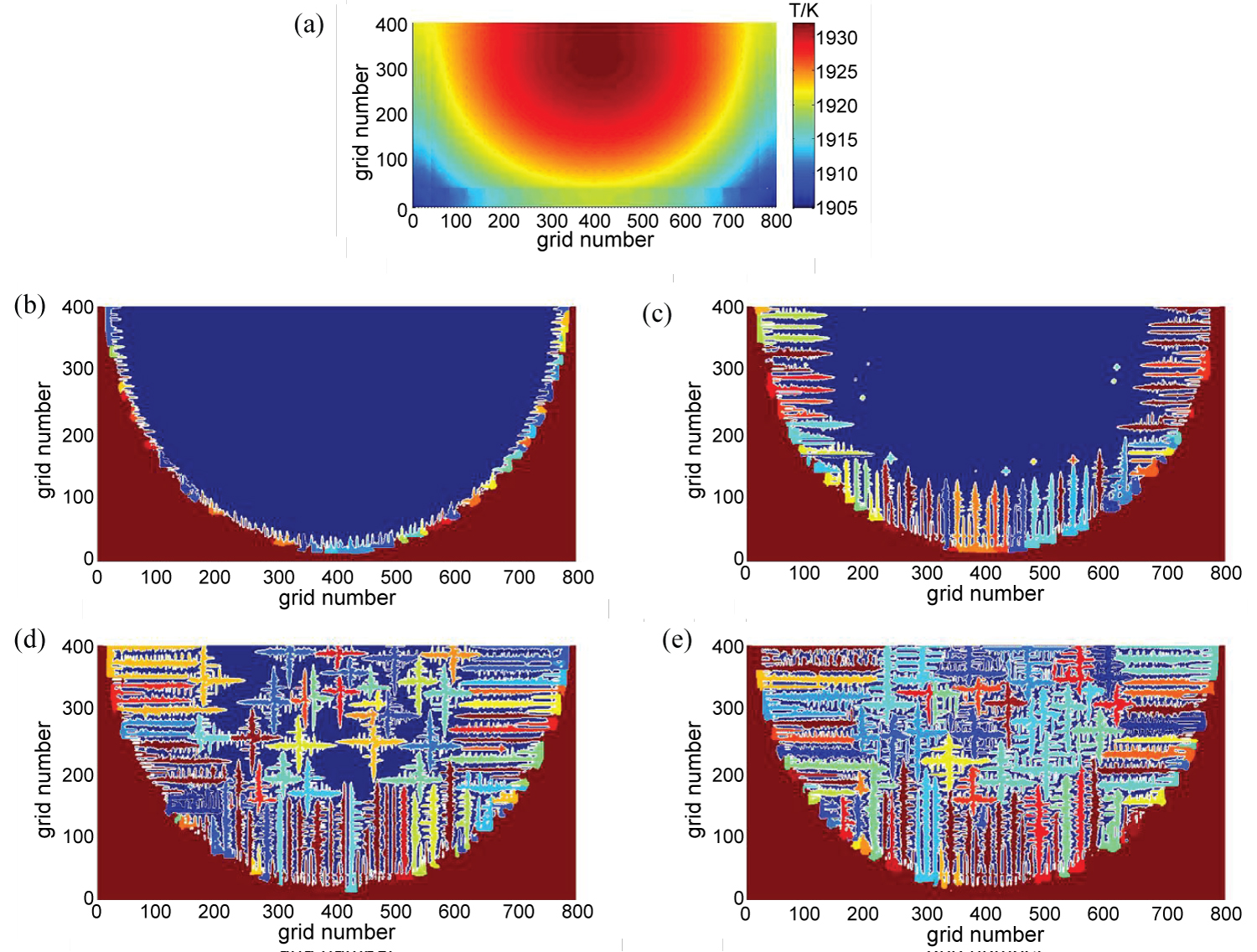
Figure 5: The morphology of grains in the...
The morphology of grains in the weld pool at different time, a) Temperature filed of welding; b) t = 0.25 s; c) t = 0.7 s; d) t = 1 s.
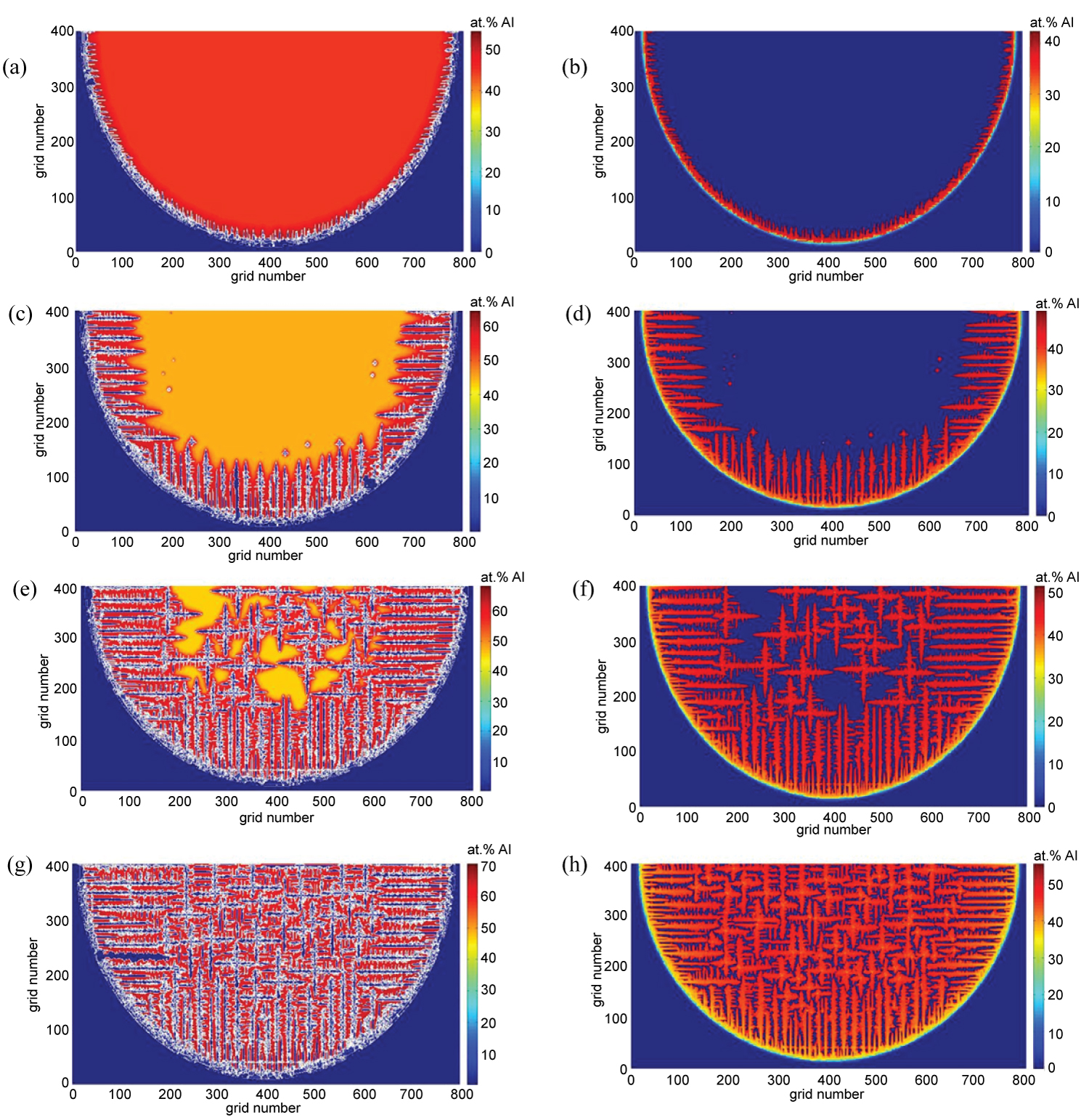
Figure 7: The distribution of solute in the...
The distribution of solute in the weld pool at different time, a,b) t = 0.25 s; c,d) t = 0.65 s; e,f) t = 0.8 s; g,h) t = 1 s.

Figure 8: Micrographs of Ti-45%Al alloy in...
Micrographs of Ti-45%Al alloy in the welding pool, a) Experimental result; b) Simulated result.
References
- Joaquim Barbosa, Silva Ribeiro C, Caetano Monteiro A (2007) Influence of superheating on casting of γ-TiAl. Intermetallics 15: 945-955.
- W Tan, N Bailey, YC Shin (2012) Numerical modeling of transport phenomena and dendritic growth in laser spot conduction welding of 304 stainless steel. J Manuf Sci Eng 134.
- R Han, S Lu, W Dong, D Li, Y Li (2015) The morphological evolution of the axial structure and the curved columnar grain in the weld. J Cryst Growth 431: 49-59.
- YL Lu, Z Chen, YX Wang (2008) Microscopic phase-field simulation of the early precipitation mechanism of Ni3Al phase in Ni-Al alloys. Materials Letters 62: 1385-1388.
- RS Qin, ER Wallach, RC Thomason (2005) A phase-field model for the solidification of multicomponent and multiphase alloys. Journal of Crystal Growth 279: 163-169.
- Heather Betel, Paola Flocchini (2009) On the Relationship Between Boolean and Fuzzy Cellular Automata. Electronic Notes in Theoretical Computer Science 252: 5-21.
- P Flocchini, F Geurts, A Mingarelli, N Santoro (2000) Convergence and aperiodicity in fuzzy cellular automata: revisiting rule 90. Physica D 42: 20-28.
- Javier F Botía, Ana M Cárdenas, Carlos M Sierra (2017) Fuzzy cellular automata and intuitionistic fuzzy sets applied to an optical frequency comb spectral shape. Engineering Applications of Artificial Intelligence 62: 181-194.
- H Betel, P Flocchini (2011) On the asymptotic behavior of circular fuzzy cellular automata. J Cellular Automata 6: 25-53.
- ZM Zhou, BZ Sun (2013) Computer material science mathematical model and computer simulation. Science Press, Beijing, 2013: 37-40.
- M Zhang, Q Xue, LL Li, J Li (2016) Dendrite growth in solidification process of Ti-Al alloy. Ordnance Material Science & Engineering 39: 1-5.
- SP Wu, DR Liu, JJ Guo (2015) Modeling of solidification grain structure for Ti-45% Al alloy ingot by cellular automaton. Trans Nonferrous Met Soc China 15: 291-295.
- KF Wang, JJ Guo, GF Mi, HZ Fu, BS Li (2008) Numerical simulation of microstructure evolution during directional solidification of Ti-45at% Al alloy. Acta Physica Sinica 57: 3048-3058.
- J Cheng, QY Xu, H Zhang, LJ Zheng, BC Liu (2010) Numerical simulation of directional solidification microstructure of Ti-45%Al alloy based on CA method. Foundry 59: 903-907.
- JQ Chen, SH Xiao, XY Yang, Wu G (2005) The development of heart source models for numerical simulation of welding processes. Equipment Manufacturing Technology 3: 10-13.
- YH Xiao, HF Zhang, XC Ping (2014) Treatment of Two Kinds of Thermal Boundary Conditions in Meshless Symmetric Particle Method. Journal of East China Jiaotong University 32: 65-70.
- DC Tsai, WS Wang (2010) Numerical simulation of solidification morphologies of Cu-0.6Cr casting alloy using modified cellular automaton model. Transaction of Nonferrous Metal Society of China 20: 1072-1077.
- Y Minoru, N Yukinobu, H Hiroshi, O Kenichi (2006) Numerical simulation of solidification structure formation during continuous casting in Fe-0.7mass%C alloy using cellular automaton method. ISIJ International 46: 903-908.
- MF Zhu, DM Stefanescu (2007) Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys. Acta Materialia 55: 1741-1755.
- Nastac (1999) Numerical modeling of solidification morphology and segregation patterns in cast dendritic alloys. Acta Metallurgica 47: 4253-4262.
- R Sasikumar, M Kumar (1995) The strength of the coupling between macroscopic heat flow and equiaxed grain formation in castings. Acta Metall Mater et Materialia 43: 4387-4392.
Author Details
Min Zhang*, Yulan Zhou, Qin Xue, Jihong Li and Yuanyuan Xi
School of Materials Science and Engineering, Xi'an University of Technology, China
Corresponding author
Min Zhang, School of Materials Science and Engineering, Xi'an University of Technology, Xi'an 710048, PR China, E-mail: [email protected]
Accepted: November 08, 2017 | Published Online: November 10, 2017
Citation: Zhang M, Zhou Y, Xue Q, Li J, Xi Y (2017) Simulation on Dendrite Growth during Solidification of Ti-45%Al Alloy in the Weld Pool. Int J Metall Met Phys 2:009.
Copyright: © 2017 Zhang M et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
A dendritic growth model was established by a combination of the characteristics of Cellular Automata (CA) and the physical properties of dendritic growth, the growth morphology of equiaxial and cylindrical crystal of Ti-45%Al alloy was simulated in the isothermal field, and the distribution of solute concentration was analyzed. Based on the CA model of dendritic growth, the welding heat process and the arc-shaped pool model in the process of welding solidification were coupled by the interpolation method, followed by the simulation of the micro structural growth during the solidification of the molten pool. The results show that the single equiaxed crystal and cylindrical crystal present symmetrical morphology under the uniform temperature field. With the progress of solidification, the growth becomes more severe among the dendrites with the emergence of tertiary dendrite. The solute atoms are enriched in between dendrite arms with the segregation of solute. However, the temperature at the center of the molten pool presents the gradual distribution in the non-uniform temperature field. The microstructure grows competitively at the center of the molten pool. With the change of temperature field, the dendrites have asymmetry morphology. The simulation is in a good accordance with that of the experimental results.
Keywords
Cellular automaton, Dendritic growth, Solute concentration, Welding heat process
Introduction
As a kind of important metal structure material, Ti-Al alloy has the advantages of high strength, corrosion resistance, and heat resistance, which has been widely used in aerospace and automotive field [1]. However, due to its high melting point and poor thermal conductivity, it will produce a larger molten pool under the condition of the incorrect parameters. Under this circumstance above, the solidification time after welding is longer and solidification microstructure is in a high temperature state for a long time. However, the grain is relatively large with resulting in crack, which seriously affects the practicability of titanium alloy. Therefore, it is greatly significant to study the evolution of microstructure of Ti-Al alloy after welding. Numerical simulation is a kind of technology to overcome time-consuming and costly consumable in the experimental process, and it is reasonable to develop the experimental process on the computer, so far it has become the research hotspot of the scholars [2,3].
The existing simulation methods of titanium aluminium alloy mainly concentrate in the temperature field, stress field and other macro simulations, but the microstructure simulation also needs to be improved. So far, the Phase-Field method (PF) [4,5] and the Cellular Automaton method (CA) [6-9] has been widely used. Compared with the phase-field method, the binary cellular automaton method [10,11] is relatively simple. It belongs to a stochastic simulation method, and makes many discrete cells interact with each other under pre-defined rules to realize the evolution of the organization. Liu [12] and Wang, et al. [13] established the macro and microscopic model for the binary alloys during solidification microstructure change by using cellular automaton method and finite difference method. In addition, it has been successfully applied in the simulation of the Ti-(45-48 at %) Al alloy. Cheng, et al. [14] simulated the Ti-45%Al alloy microstructure simulation in solidification process of liquid metal by using the CA method. However, the above research focuses on the thick grain simulation of Ti-Al alloy in the process of casting. Compared with casting, the volume of molten pool is in small size, the solidification speed of the liquid metal is very quickly, the metal of molten pool is in the overheated state with large temperature gradient. These characteristics make the simulation in the molten pool solidification process with certain particularity and cause the increased difficulty of the simulation. Hence, the studies on this subject are relatively few.
In this paper, the CA model of isothermal solidification is coupled with the welding heat process and the arc-shaped pool model during the solidification process. The growth of equiaxial crystal and cylindrical crystal in the isothermal field, as well as competitive growth of dendrite crystal after applying non-uniform temperature field inside the pool are simulated. Besides, the distribution of the solute field in the process of dendritic growth is quantitatively studied. At the same time, for the simulation results, the relevant metallographic experiments are designed to simulate.
Mathematical Formulation
This paper establishes the mathematical model of dendritic growth in binary alloy of weld pool by using CA method. The whole calculation area is defined as the internal of welding pool, which is divided into evenly distributed and interacting with the orthogonal cells. Each cell evolves with certain rules, and the evolution rules of the cells are determined by physical processes which are the temperature field, the solute field, the nucleation and the growth of the grains during the solidification process. Then, the physical model is transformed into a mathematical model by using finite difference method. The mathematical model is implemented by means of MATLAB platform and the detailed description of algorithm is illustrated as follows.
Temperature field model
The establishment of the heat source model and the simulation of the welding temperature field play an important role on the numerical simulation of welding. From the previous experience, the calculated results of Gaussian heat source distribution are in good agreement with the actual welding process. During the welding process, the heat transfer from the arc heat source to the weldment through a certain area of action, this area is called heating spots. The heating spots have uneven heat distribution; the edge is few while the center is more. The Gaussian function is used to approximately describe the heat flux distribution on the heated spot. The heat flux at the distance from the center of the heated spot is [15]:
Where, qm is the maximum heat flux at the center of the heated spot in , r is the direct distance from the arc heating spot in mm, rh is effective radius of arc in mm. The effective radius of arc rh is related to thermal concentration factor K, i.e. , its value is used to represent the degree of concentration of heat flow. In the simulation calculation, the moving gauss heat source model is expressed as:
Where, h is the thickness of the weldment in mm, v is the moving speed of welding heat source in m/s, Δt is the time step in S.
In order to accurately simulate the solidification process of the molten pool, it is necessary to consider the convective heat transfer behaviour of the liquid metal in the molten pool and the thermal process of the external solid region of the molten pool. However, the fluid flow process is more complex, in order to simplify the calculation and facilitate the practical application, while the heat conduction problem of arc welding is considered without considering the convective heat transfer in welding process. The two-dimensional transient thermal equation can be expressed as [16]:
Where, ρ is density in , Cp is volume specific heat capacity in , λ is thermal conductivity in .
The difference equation is displayed on the differential equation, the super cooled melt temperature is:
Where, α is the thermal diffusivity in m2/s, Δt is the time step in s, Δx is the grid size in mm.
Dendrite growth model
In the CA model, the under cooling [17] of the liquid-solid interface mainly includes three parts: temperature, concentration and curvature. The anisotropy of the interface energy has a great influence on the curvature under cooling, so the model must consider the interface anisotropy. At time tn, the degree of super cooling in the solid-liquid interface prerequisite is calculated as [18-20].
Where, T' is the temperature at the interface, Ti,j is the temperature of the super cooled melt. C0 is the initial solute concentration, is the solute concentration of the liquid at the interface, mL is the slope of the liquidus. is the Gibbs-Thompson coefficient, K(tn) is the interface curvature, which calculated from Eq. (6), Gx is anisotropy intensity of the liquid-solid interface, θ0 is the angle between the growth direction of the dendrites and the positive direction of the coordinate axes, θ is the angle between the normal of the solid/liquid interface and the positive direction of the coordinate axis, which calculated from Eq. (7).
Coupling of dendritic growth and welding thermal processes
In the actual molten pool, the temperature in the same time is unequal at different positions. In order to simulate the process of dendrites growth in the molten pool, we will couple the welding temperature field and the CA model of dendritic growth during the solidification process, and discuss the relationship of temperature changes in the weld interface and the dendritic growth process. Due to the temperature field is macroscopic while dendritic growth is microscopic, we first convert the obtained macroscopic unit temperature into the microscopic unit temperature. The temperature of the microscopic unit is generally obtained by using the interpolation formula. The interpolation formula is expressed as [21]:
Where T is the temperature of microscopic grid in ℃, Ti is the macroscopic unit temperature around the microscopic grid in ℃, Li is the distance from the microscopic grid to the surrounding macro element in mm.
During the simulation process, it is also necessary to firstly determine the location of the fusion line in the molten pool which determines the calculated area for the simulated dendritic growth. The actual shape of the molten pool is an irregular circular boundary, which is controlled by various factors such as the welding line energy, the work piece thickness and the thermal conductivity of the work piece etc. In order to approximate the simplified actual model, we use an ideal model by setting the radius of molten pool and assuming that the shape of molten pool remains the same during solidification. The distance from any cell to the nucleation core can be obtained by the following equation:
Where, R is the distance from the welding arc to the heat source center as (i0,j0); i,j is used to represent the horizontal and vertical coordinates in the simulation area, respectively. The physical properties of Ti Al alloy in the process of simulation are shown in the Table 1.
Experimental procedure
In order to compare the simulated results, the 5 mm thick Ti-45%Al alloy is prepared for welding test. The experimental conditions are illustrated as follows:
• The welding method is manual argon arc welding,
• The welding current is 90 A,
• The welding voltage is 13.8 V,
• The welding temperature is 26 ℃.
In addition, the microstructure of Ti-Al alloy plate is kept by natural cooling. The welded samples are cut into metallographic specimen, and then the interface which is vertical to the direction of the heat source is investigated. For the purpose of obtaining the metallographic microstructure, the inverted metallographic microscope GX671 (OLYMPUS Corporation) is used.
Results and Discussion
Growth morphology of single equiaxed dendrite in the isothermal field
The whole two-dimensional calculation area is divided into 400*400 square grids. In addition, the grid size is 3 μm and the time step is 1 μs, the number of iterations is 500, 2000, respectively. The Figure 1 illustrates the equiaxed crystal growth in ideal temperature field. The Figure 1a shows the distribution of the ideal equidistant temperature field and Figure 1b and Figure 1c is the growth morphology of the equiaxed crystal. According to the Figure 1a, Figure 1b and Figure 1c, it can be seen that at the beginning of the solidification, the primary dendrites of the initial grains grow rapidly along the direction of the axis, and their growth direction coincides with the coordinate axis, which is the preferred growth direction of the crystal. As time goes by, the primary dendrite arm is quickly elongated. When the primary dendrite grows to a certain extent, the primary dendritic arm gradually appears secondary dendrites with the competing growth in the direction of 45 degrees.
It should be noted that the secondary dendrites near the roots of the dendrites rapidly grow, so the morphology of the secondary dendrites is ladder-like. In the secondary dendritic arm grown well, it can be found that the three dendrites appear on secondary dendritic arm by carefully observating. This is because in the growth process of dendrites, another side of the solute concentration is higher with inhibiting the growth of three dendrites. A single equiaxed crystal exhibits good symmetry in morphology. The Figure 1d and Figure 1e describes the distributions of solid solute and liquid solute concentration. The color gradient on the right represents different concentration gradients. The similar graphs appearing in this paper represent the same meaning. It can be shown that with the growth of two or three dendrites, many local regions gradually form closed or semi-enclosed areas. Then, the solute atoms continuously diffuse with the solutes not being discharged, resulting in gathering high concentrations of solute in these closed areas. When the solidification is completed, it forms a micro segregation in the liquid phase with high solute concentration.
In order to further analyze the distribution of solutes in the local region, the coordinate system shown in Figure 1c is defined. Then the liquid and solid solute concentration of a single equiaxed on this line of y = 200 is tracked, as shown in Figure 2. As shown in Figure 2a, the grid from 25 to 375 is solid solute concentration region where the concentration of solid solute at the core is the lowest at 35.1%. Then along the growth direction of a dendritic arm in turn gradually increased until the equilibrium state, the solute concentration keeps at around 42%. The Figure 2b shows the distribution curve of liquid solute concentration. It can be found that the solute concentration in the solid-liquid interface is up to 50%. The closer the solid-liquid interface, the higher the solute concentration.
The state of the alloy away from the solid-liquid interface is liquid, and the solute concentration is 45% of the initial solute concentration of the alloy. The distribution mentioned above is mainly due to the interface advancing forward with the solidification progress, the excess solute continuously discharged, so that the concentration of the liquid phase solute at the front of the interface is increased, and the concentration of the solid phase solute gradually is increased. The solute is redistributed in the solidification process. In addition, it can be seen that the concentration of solute in the solid phase is lower than the initial value. The solute diffusion rate in the liquid phase is smaller than that in the dendritic growth rate and the solute accumulated in the solidification is enriched at the frontier. When the liquid phase solute concentration reaches the balance liquid phase component and remains stable, the solid phase component tends to be stable, and the dendrites enter steady state growth.
Growth morphology of cylindrical crystal in the isothermal field
The whole two-dimensional calculation area is divided into 400*400 square grids. In addition, the grid size is 3 μm and the time step is 8 ms, the number of iterations is 1000, 2000, respectively. The Figure 3 shows the growth of columnar crystals when four initial nuclei are implanted under the ideal temperature field.
The Figure 3a shows the distribution of the columnar ideal temperature field. The Figure 3b and Figure 3c indicates the growth morphology of the columnar crystals. On the basis of the Figure 3a, Figure 3b and Figure 3c, it can be seen that at the beginning of growth, cell-like dendrites began to appear in the bottom, its longitudinal growth and lateral growth difference is not large. On the first dendritic arm perpendicular to the bottom, smaller secondary dendrites are sprouted but not obvious. With the time increasing, the dendritic arms in the transverse direction of the four cells meet each other, so that a large amount of dendrites are grown in the vertical direction and the number of columnar crystals reach to 22. At the same time, due to the temperature drop, the temperature gradient is larger, the protruding cell will quickly deep into the liquid inside to growth, i.e. the dendrite can rapidly grow along the increased direction of temperature gradient, namely longitudinal growth dominating. Simultaneously, the dendritic morphology tends to be stable; the three dendrites grown on the secondary dendrite arm are obvious. The Figure 3d and Figure 3e illustrate the concentration distribution of liquid solute and solid solute. It can be found that with the extension of the solidification time, the concentration of solute gradually is increased. At the beginning, the solute concentration is mainly concentrated in the dendritic tip region. With the appearance of high-order dendrites, the solute atoms discharged during the growth of dendrites cannot be diffused, resulting in the formation the solute enrichment area between adjacent dendritic arms.
In order to well study the distribution of solute concentration during the process of columnar crystal growth, we define the coordinate system as shown in Figure 3d. The liquid and solid solute concentration in the y = 100 straight line are tracked as shown in Figure 4. It can be seen that the distribution of solid and liquid solute concentration in the process of columnar crystals growth is similar. The solute concentration distribution of each dendritic tip is u-shaped, and the inter granular solute distribution is close to exponential distribution. The higher the solute concentration at the tip of the dendrites and the lowest solute concentration in the dendrites. Similar to the equiaxed crystal, the concentration of solid phase solute at the core of the dendrites is the lowest with increasing along the growth direction of the secondary dendrites, and solute enrichment occurs at the solid-liquid interface of the tip of the dendrites. At the same time, according to the u-shaped span size, the radius of the dendritic tip is obtained. Similarly, the dendritic spacing is derived from the length between two adjacent u-shaped centers.
The competitive growth of molten pool during solidification
The calculation area is divided into 20*40 rectangular macroscopic grids composed of 20*20 uniform microscopic grids. In addition, the grid size is 5 μm and the time step is 0.5 ms, the number of iterations is 500, 1300, 1600, 2000, respectively. The Figure 5a illustrates the micro-temperature field distribution of the weld. The Figure 5b, Figure 5c, Figure 5d and Figure 5e shows the growth morphology of the dendrites during the solidification process of the weld pool at different times.
It can be seen that at the initial stage of solidification, such as Figure 5b, columnar crystals are formed on the edge of the weld pool while the pool center is not basically nucleated. This is because, in the initial solidification of the molten pool, the internal temperature of the molten pool is higher and the component is too low. But welding edge away from heat faster, the temperature is decreased rapidly, the temperature gradient is large and the difference between the components of the liquid-solid metal is large. In addition, a lot of small crystal nucleus is preferentially formed on the edge of the molten pool. This crystal nucleus continues to grow around in the role of super cooling degree, because the initial longitudinal growth rate is greater than the lateral growth rate. Therefore, the tip of the grain crystal goes quickly deep into the molten liquid and grow up toward the molten pool center with forming the columnar crystal.
With the solidification carried out, such as Figure 5c, columnar crystals continue to grow, and a lot of fine equiaxed crystals appear in its tip and pool center. With the solidification layer inward, solid-phase cooling capacity is gradually weakened and the inside temperature gradient tends to flatten, and solute atoms in the liquid phase are more and more enriched, which make the composition under cooling of interface edge gradually increase. When the composition is super cooling enough to cause the non-uniform nucleation, it starts to generate equiaxed crystals at the center of the molten pool. The formed equiaxed crystals grow along different directions, and the growth speed is similar. It can be seen that the number of equiaxed crystals nucleation near the columnar tip position is larger. The reason is the solute atoms of the columnar crystals grown at the edge of the molten pool during the growth are diffused to the dendritic tip liquid phase. The regional liquid phase composition is changed, resulting in components under cooling. Hence, it is the first to meet the equiaxed crystal nucleation conditions. In the subsequent solidification process, the number of equiaxed grains increases abruptly and grows simultaneously with the columnar crystals, as shown in Figure 5d. When the equiaxed grains meet the columnar crystals, such as Figure 5e, the growth of the columnar crystals will be hindered by the growth of the central equiaxed grains. It leads to stop the longitudinal growth of the part of columnar crystal while the radial growth is intensified and the secondary dendrite arm also is intensified, which finally achieves the transformation from the columnar crystals to the equiaxed crystals.
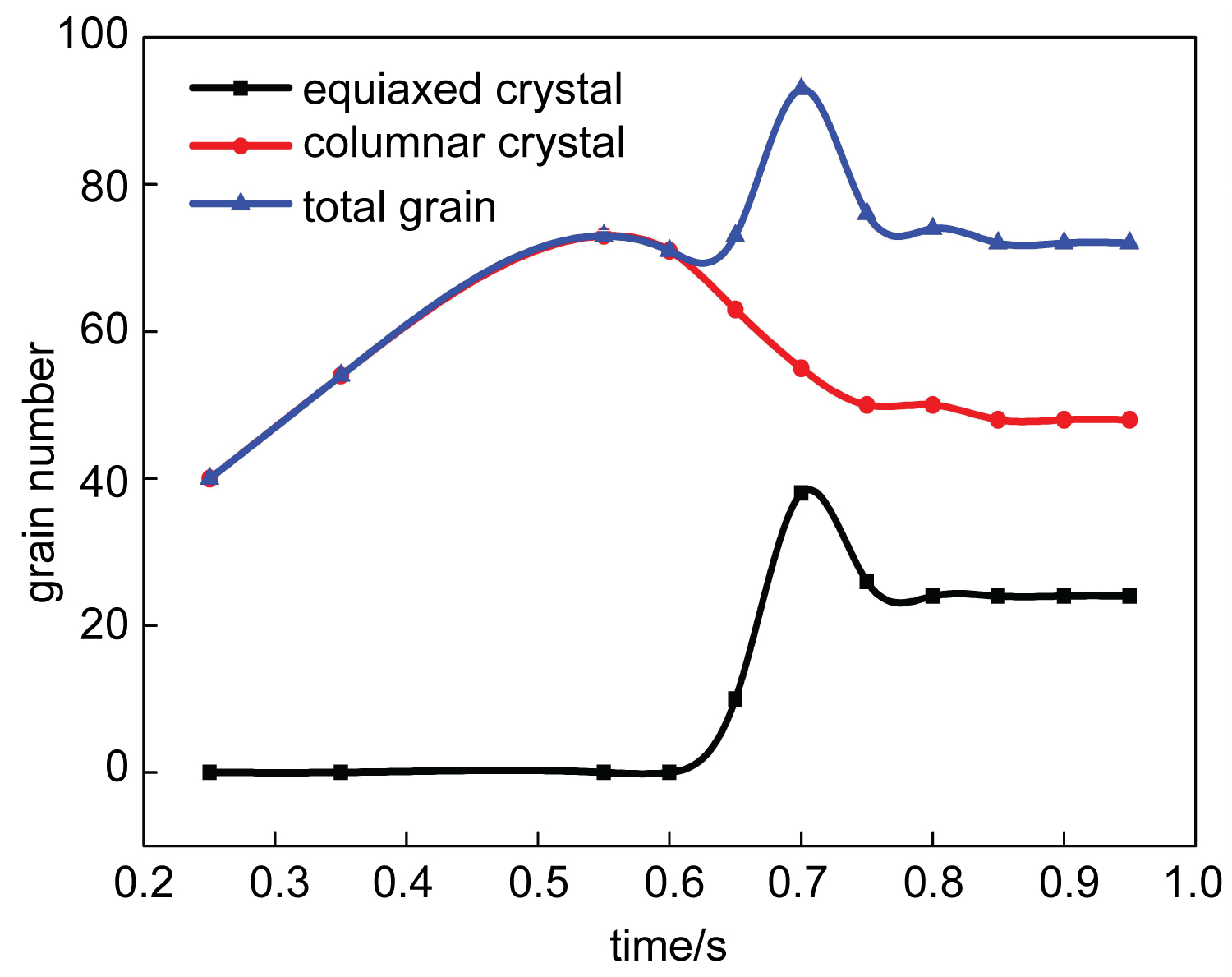
Compared with the growth morphology of equiaxed and columnar crystals under the ideal temperature field, the morphology of the dendrites in the molten pool after the coupled welding temperature field also follows the respective growth rules, but exhibits randomness and symmetry under the effect of the changing temperature field. In order to further study the nucleation rules of the weld pool under the non uniform temperature field, this paper presents the change of the number of grains in the molten pool under different solidification time, as shown in Figure 6.
It can be seen that when the initial solidification, the growth of columnar crystal is dominant. The number of nucleation is dramatically increased while the pool center is almost no nucleation and the number of equiaxed grains is zero. With the solidification, the degree of under cooling reaches the internal nucleation conditions and the number of equiaxed crystal nucleation begin to increase rapidly, while the growth of columnar crystals begin to slow down and the number is slightly decreased. This is due to the existing of the competitive growth among the columnar crystals, the re-melting phenomenon occurred between some grains, which makes the columnar crystals morphology sturdy but the number is reduced.
In the middle of the solidification, the competitive growth between the columnar grains and the equiaxed grains and the equiaxed grains is very intense, and the nucleation area is limited. Therefore, the morphology of the equiaxed and columnar crystals with the growth advantage is developed while the number of nucleation shows a decreased trend. In the late of the solidification, the dendritic growth in the molten pool reaches a steady state and the number of equiaxed and columnar grains tends to be stable. Finally, the total number of nucleation in the molten pool tends to be fixed. In light of the Figure 6, it can be seen that the size of the CET transition and the size of the grains can be basically determined when the whole dendrites enter the roughen growth stage at about 0.78 s.
The distribution of solute in the weld pool at different time
The solute concentration is the key factor of liquid-solid state change during the dendritic nucleation and growth process. When the solute field changed, the grain growth direction and morphology will be changed. Hence, the corresponding liquid solute concentration and solid solute concentration as shown in Figure 7 are discussed. The Figure 7a, Figure 7c, Figure 7e and Figure 7g show the liquid solute concentration at different moments, while the Figure 7b, Figure 7d, Figure 7f and Figure 7h are the solid solute concentration distribution.
It can be seen that the release of solute in the solid phase makes the solute concentration in liquid phase located at the front of solid-liquid interface increase from the Figure 7a which is due to the competitive growth of dendrites with resulting in the solute diffusion time and space shortage. Simultaneously, the solute diffusion rate in the liquid phase of the dendritic tip is much smaller than the growth speed at the solid-liquid interface. Besides, the high concentration solute is also enriched in the vicinity of the tip of the dendritic arm. As shown in Figure 7c and Figure 7e, when the competitive growth of columnar and equiaxed crystals occurred, the solute fields formed by the growth of equiaxed grains and columnar crystals will affect each other.
The columnar crystals around the equiaxed crystals is owing to absorbing the discharged solutes during the growth process of equiaxed crystals with the rapidly rising of liquid solute concentration and the decreasing of the grow speed at the dendritic tip. The columnar crystals to be far from the equiaxed crystals are less affected by its solutes and the growth rate is not changed much. In the Figure 7g, with the dendrites continue to grow, the growth of the columnar crystals is completely impaired by equiaxed crystals. The competitive growth is more and more intense; the higher dendrite arm is gradually increased and roughened with solute diffusion space getting smaller and smaller and the solute concentration increasing continuously.
According to the Figure 7b, Figure 7d, Figure 7h and Figure 7f, it can be seen that the growth of dendrite is always accompanied by the segregation phenomenon by observing the distribution of solute concentration in solid phase during the process of CET transformation. The solid phase solute concentration of the columnar crystals is the lowest and the distribution is about 40%, which is lower than the initial solute concentration. At the beginning of the CET transition, the columnar crystal gradually increases along the main axis direction, and the highest solute concentration region is the columnar crystal tip. The fine equiaxed crystal formed at the center of the molten pool is similar to the solute concentration in the columnar tip, which is the initial solute concentration of alloy. Then the central component of the molten pool, the equiaxed crystals begin to grow dramatically, while the growth rate of the columnar crystals is slowed down. The increase of the dendrites solute concentration is not obvious. When the CET transformation is carried out in the final stage, the equiaxed crystals grow well and the solid solute concentration reaches to 52%. It can be found that the concentration of solid solute in the equiaxed crystal and columnar crystal tip is the highest, and it is easy to form regional segregation after solidification, at the same time the columnar region is always accompanied by microscopic segregation. Therefore, the evolution of columnar-equiaxed crystals is not only due to the columnar crystals being hindered by the equiaxed grains, but also the interaction between the solid and liquid solute concentrations.
Experimental verification
The rationality and accuracy of the model used in the simulation can be judged by comparing the simulated results with the experimental results.
The metallographic photograph of the weld specimen is as shown in Figure 8. From the Figure 8, the columnar and dendritic morphology in the molten pool are clearly shown. The columnar crystals grow from the vicinity of the fusion line and extend to the center of the weld. At the same time, in the weld center also formed the isometric organization. The many phases are produced during the solidification process. It can be found that the above simulated results are in good agreement with the experimental results for the directional study of dendritic morphology.
Conclusions
(1) The single equiaxed crystal and cylindrical crystal present symmetrical morphology under the uniform temperature field. With the progress of solidification, the growth becomes more severe among the dendrites with the emergence of tertiary dendrite. The solute atoms are enriched in between dendrite arms with the segregation of solute.
(2) The temperature at the center of the molten pool presents the gradual distribution in the non-uniform temperature field. The microstructure grows competitively at the center of the molten pool that the transformation of the columnar crystal-equiaxed crystal occurs. With the change of temperature field, the dendrites have asymmetry morphology.
(3) In the oriented research of dendritic morphology, the simulation is in a good accordance with that of the experimental results.
Acknowledgements
The authors gratefully acknowledge the financial support from Natural Science Foundation of China (Grant No.51274162), Department of Shaanxi Provincial Government scientific research projects of key laboratory (Grant No.15JS082), Education Department of Shaanxi Provincial Government service local special projects (Grant No.16JF021).