
International Journal of Metallurgy and Metal Physics
(ISSN: 2631-5076)
Volume 3, Issue 2
Original Article
DOI: 10.35840/2631-5076/9216
A Modified Johnson-Cook Model for Cp-Ti to Incorporate the Effects of Dynamic Strain Aging and Phase Transformation
Sindhura Gangireddy*
Table of Content
Figures
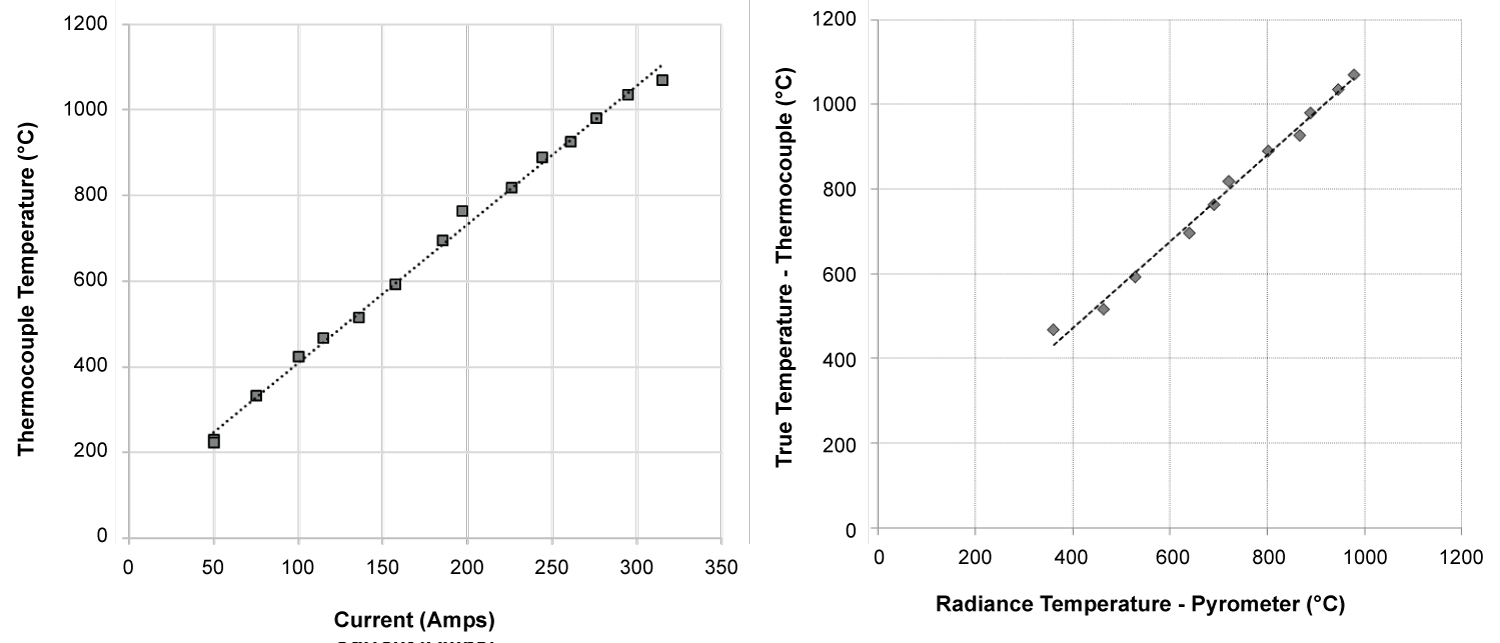
Figure 1: Linear variation of thermodynamic temperature...
Linear variation of thermodynamic temperature, measured from thermocouple, with a) The heating current; b) The radiance temperature from pyrometer.
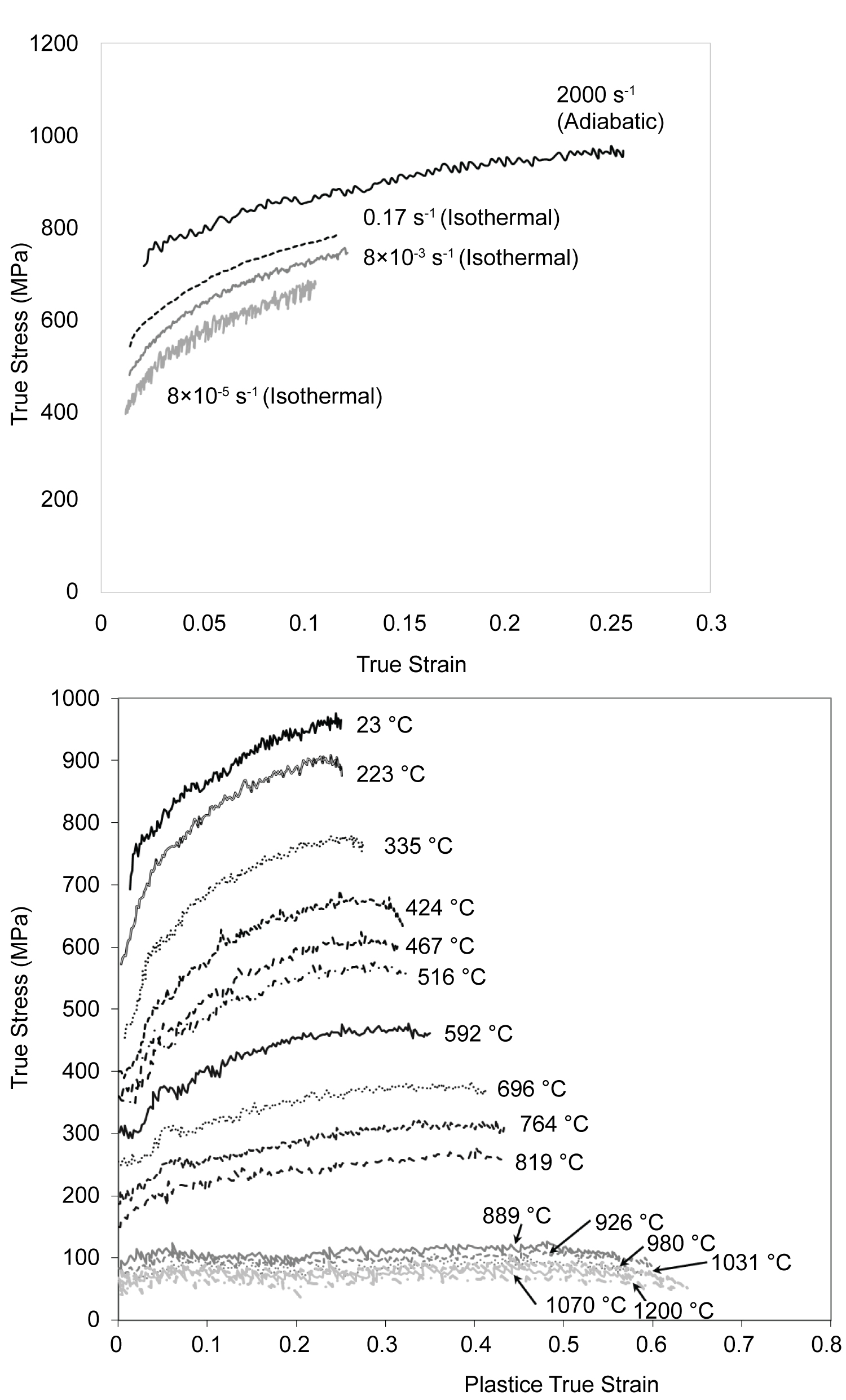
Figure 2: a) High temperature dynamic stress-strain curves;...
a) High temperature dynamic stress-strain curves; b) Room temperature quasi-static stress-strain curves.
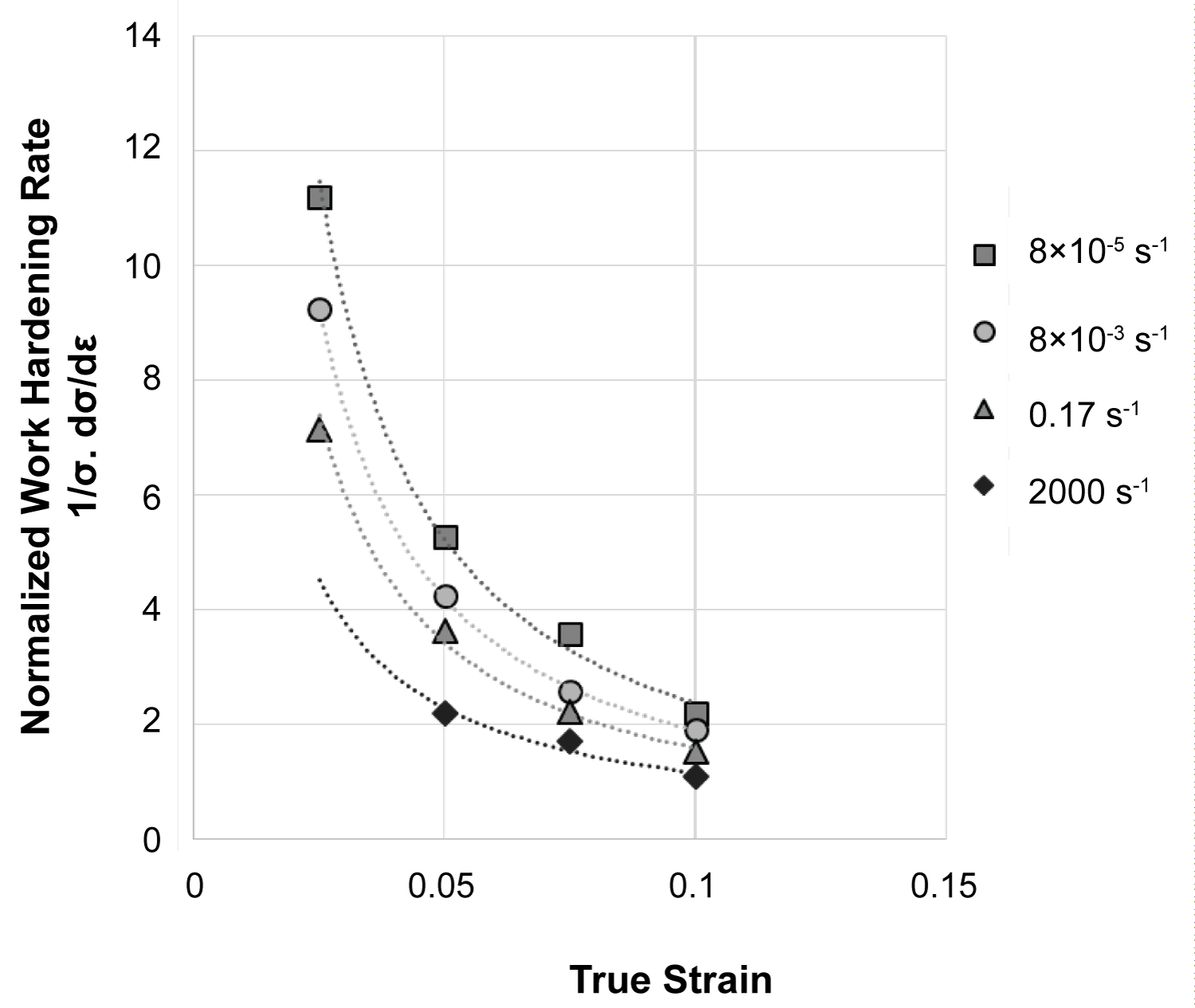
Figure 3: Reduction in the work hardening with...
Reduction in the work hardening with plastic strain, typical of Ludwik's equation, , with a small work hardening exponent "n".
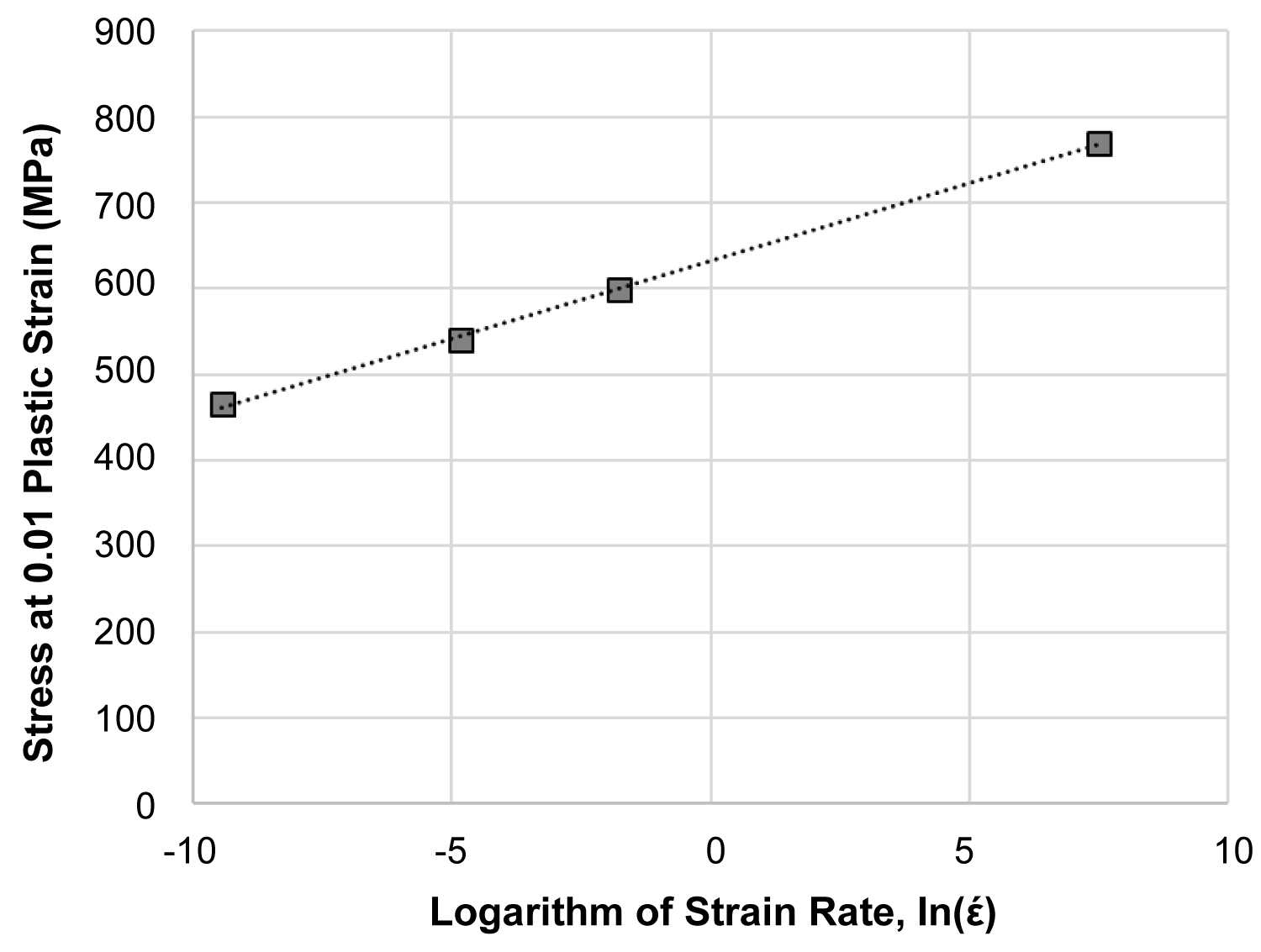
Figure 4: Correlation between the flow stresses and the...
Correlation between the flow stresses and the logarithm of strain rate.
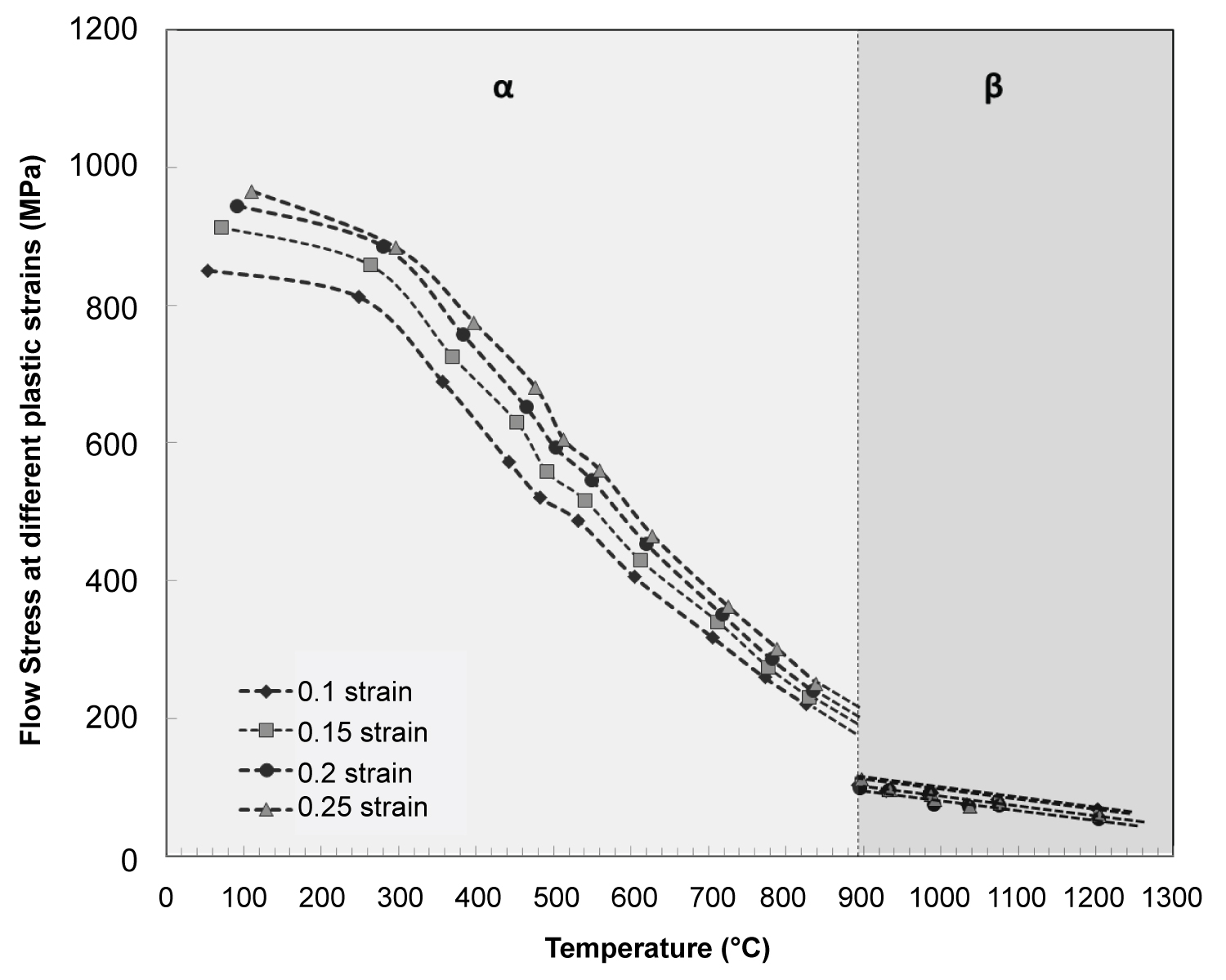
Figure 5: Thermal softening of the dynamic flow stresses at 0.1, 0.15, 0.2,...
Thermal softening of the dynamic flow stresses at 0.1, 0.15, 0.2, and 0.25 strain as a function of temperature in the two phase fields, hcp (α) and bcc (β).
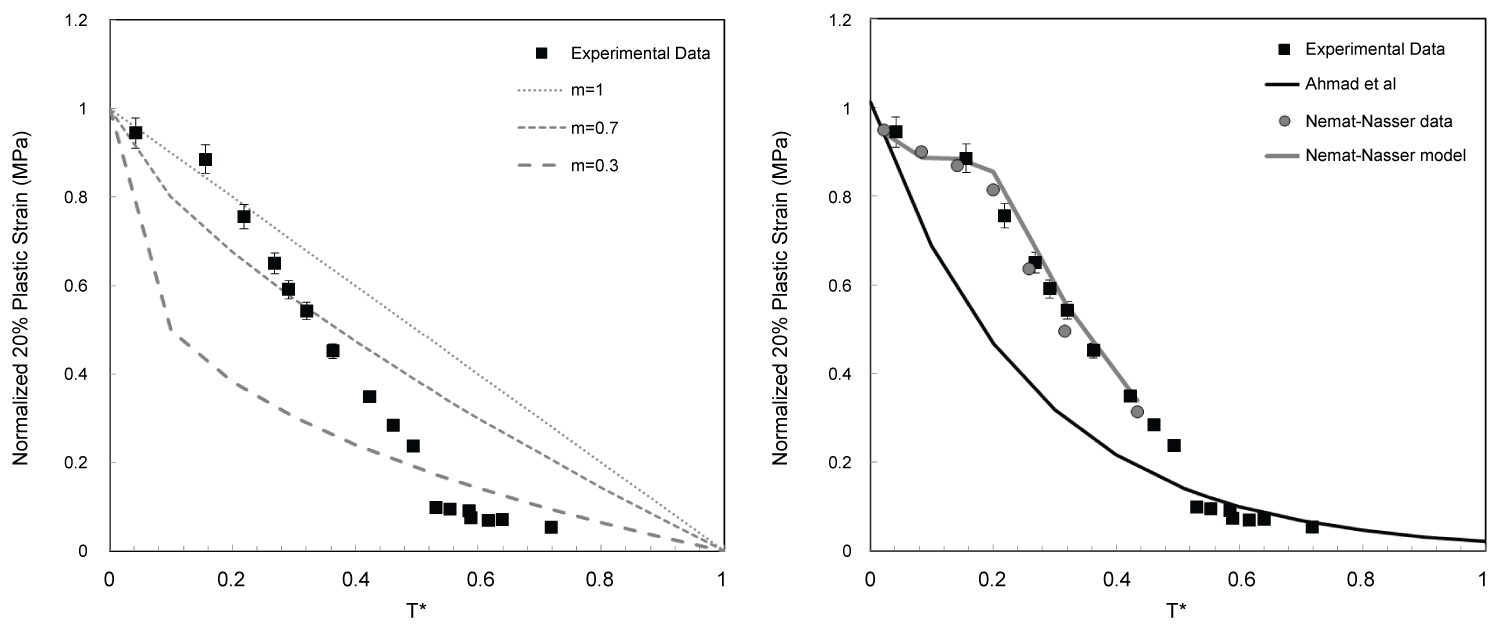
Figure 6: Comparison of experimental data...
Comparison of experimental data (normalized flow stresses at 0.2 plastic strain) with a) Johnson-Cook original model setting the softening coefficient m = 0.3, 0.7, and 1.0; b) Sheikh-Ahmad's modification [12], Cheng and Nemat-Nasser's data [9] and their physical model's prediction [10].
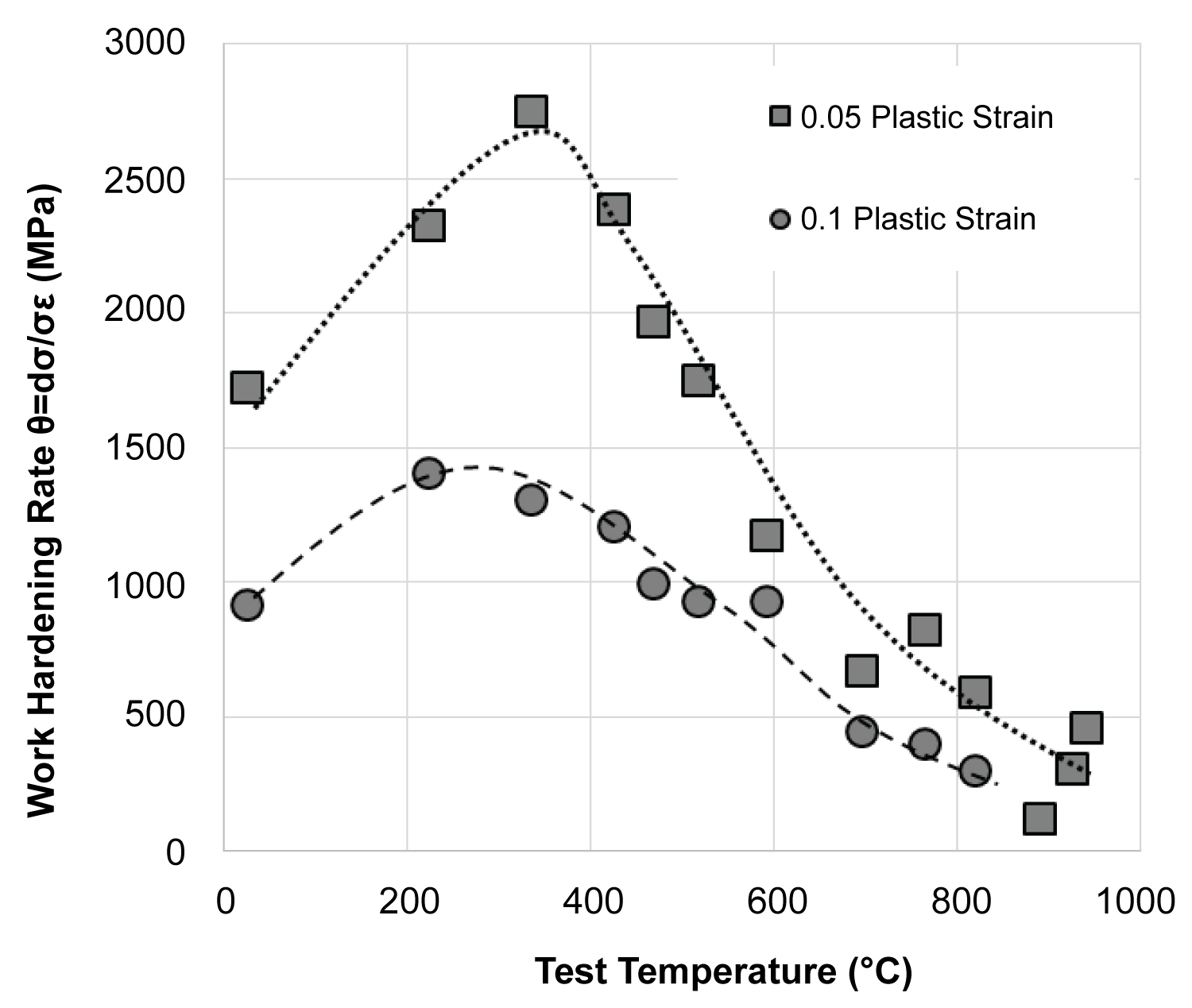
Figure 7: Work hardening another manifestation of...
Work hardening another manifestation of dynamic strain aging behavior: A spike in the temperature range of 23 ℃-500 ℃, in the exact temperature range where thermal softening rate also slowed down.
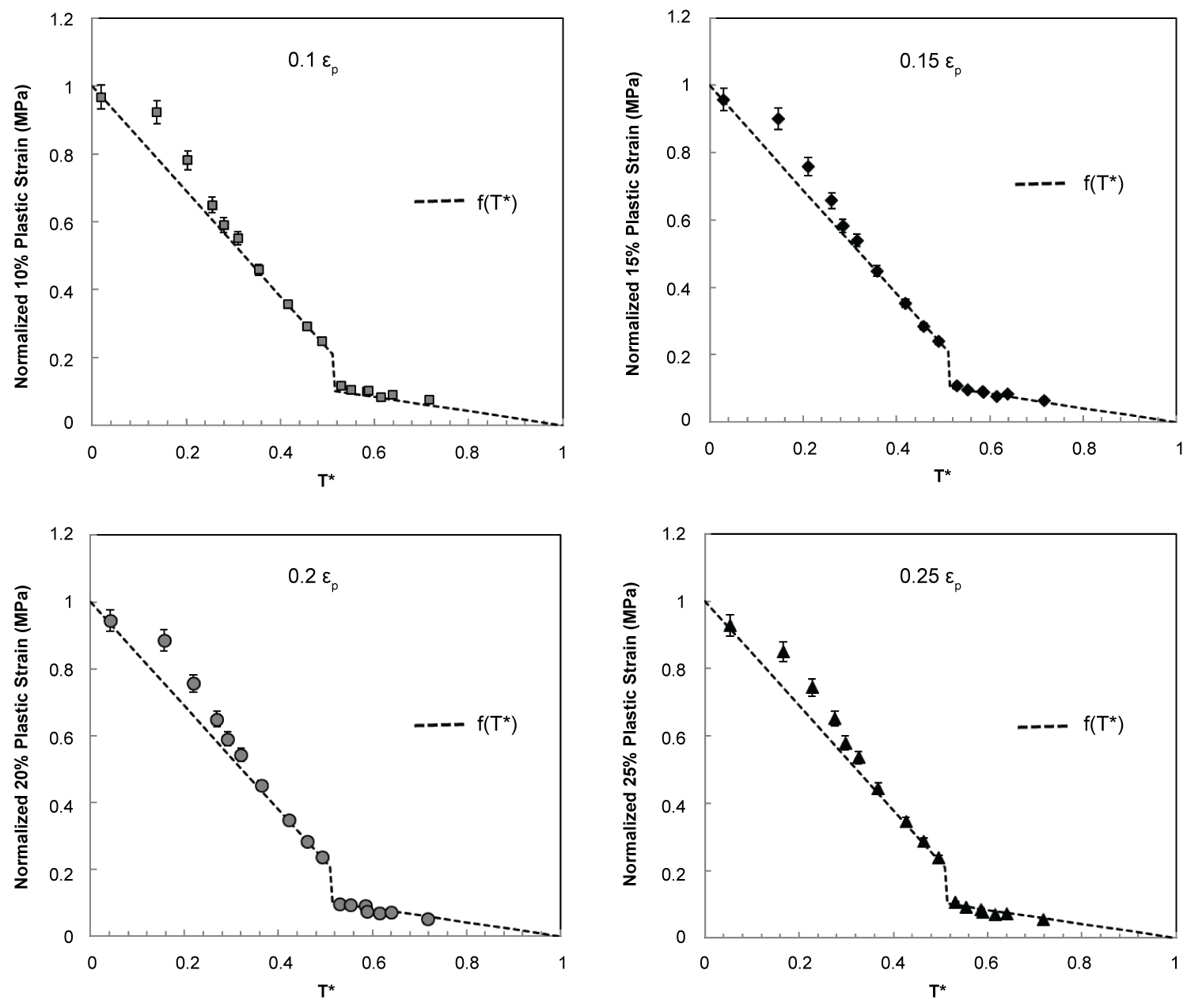
Figure 8: Comparison of experimental data, normalized...
Comparison of experimental data, normalized flow stresses at plastic strains of - 0.1, 0.15, 0.2, 0.25 with thermal softening trend predicted by modification term f(T*) in Equation 4.
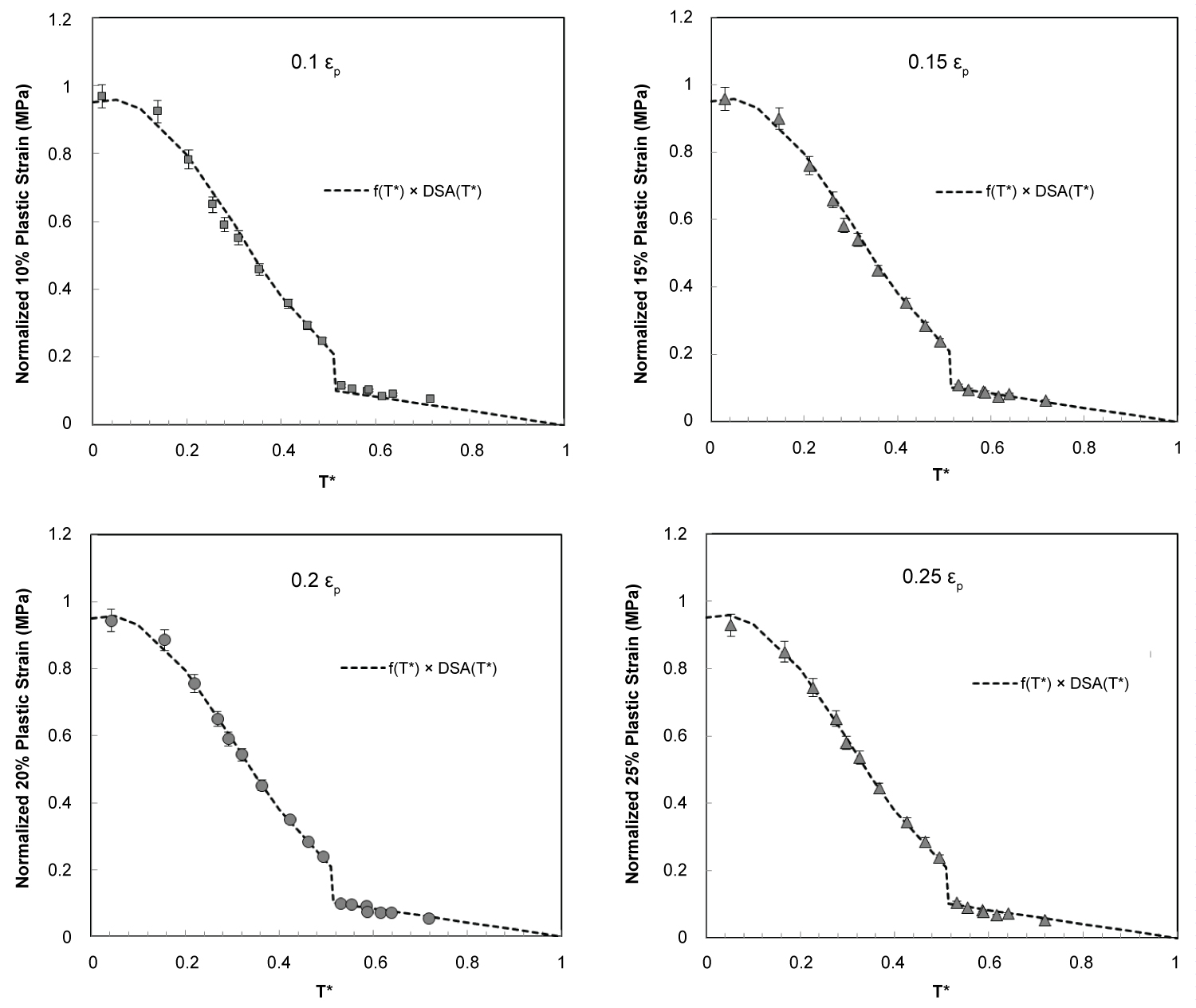
Figure 9: Comparison of experimental data, normalized....
Comparison of experimental data, normalized flow stresses at plastic strains of - 0.1, 0.15, 0.2, 0.25 with thermal softening trend predicted by a combination of modification terms f(T*) and DSA(T*) in Equation 4 and Equation 5.
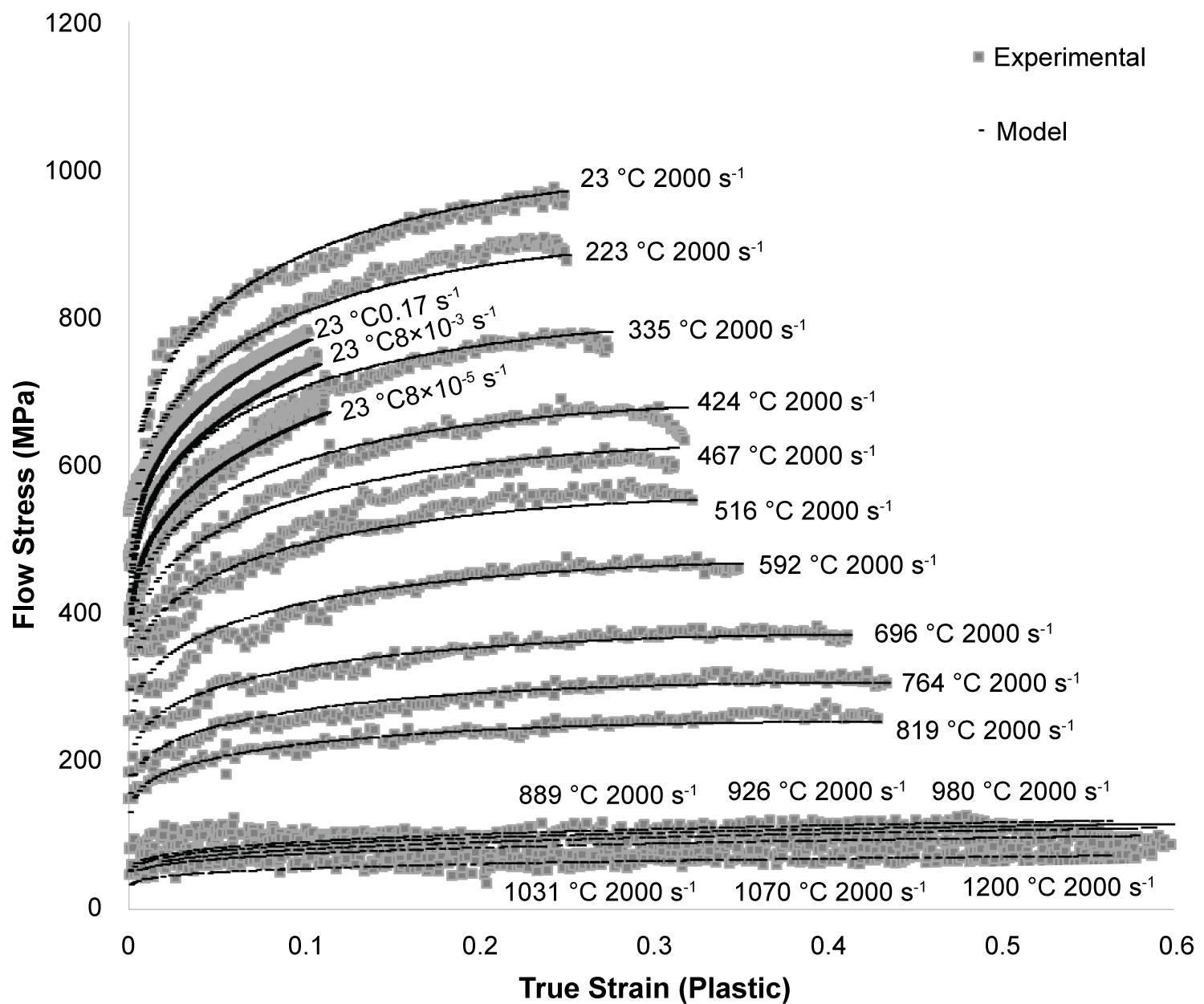
Figure 10: Comparison of the experimental flow stress data...
Comparison of the experimental flow stress data and the predictions of the modified Johnson-Cook model showing a good fit.
Tables
Table 1: Comparison of the ASTM standard and the chemical composition of the commercial material from spectrographic analysis.
Table 2: Room temperature dynamic flow stress comparison.
Table 3: Modified Johnson-Cook model's parameters.
References
- Donachie MJ (2000) Titanium: A technical guide. ASM International.
- Rahman M, Zhi-Gang Wang, Yoke-San Wong (2006) A review on high-speed machining of Titanium alloys. JSME International Journal Series C Mechanical Systems, Machine Elements and Manufacturing 49: 11-20.
- Yang X, C Richard Liu (1999) Machining Titanium and its alloys. Machining Science and Technology 3: 107-139.
- Umbrello D (2008) Finite element simulation of conventional and high speed machining of Ti6Al4V alloy. Journal of Materials Processing Technology 196: 79-87.
- Sun S, M Brandt, MS Dargusch (2009) Characteristics of cutting forces and chip formation in machining of Titanium alloys. International Journal of Machine Tools and Manufacture 49: 561-568.
- Calamaz M, Dominique Coupard, Franck Girot (2008) A new material model for 2D numerical simulation of serrated chip formation when machining Titanium alloy Ti-6Al-4V. International Journal of Machine Tools and Manufacture 48: 275-288.
- Arisoy YM (2015) Machine learning based predictive modeling of machining induced microhardness and grain size in Ti-6Al-4V alloy. Materials and Manufacturing Processes 30: 425-433.
- Mates SP, R Rhorer, E Whitenton, T Burns, D Basak (2008) A pulse-heated Kolsky bar technique for measuring the flow stress of metals at high loading and heating rates. Experimental Mechanics 48: 799-807.
- Cheng J, Sia Nemat-Nasser (2000) A model for experimentally-observed high-strain-rate dynamic strain aging in Titanium. Acta Materialia 48: 3131-3144.
- Nemat-Nasser S, WG Guo, JY Cheng (1999) Mechanical properties and deformation mechanisms of a commercially pure Titanium. Acta Materialia 47: 3705-3720.
- Johnson GR (1983) A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. Proceedings of the 7th International Symposium on Ballistics.
- Sheikh-Ahmad JY, JA Bailey (1995) A constitutive model for commercially pure Titanium. Balance 117: 139-144.
- (2011) Standard Specification for Titanium and Titanium Alloy Strip, Sheet, and Plate. ASTM.
- Gangireddy S, SP Mates (2017) High temperature dynamic response of a Ti-6Al-4V alloy: A modified constitutive model for gradual phase transformation. Journal of Dynamic Behavior of Materials 3: 557-574.
- Ravichandran G (2002) On the conversion of plastic work into heat during high‐strain‐rate deformation. AIP Conference Proceedings 620: 557.
- Gurao NP, Rajeev Kapoor, Satyam Suwas (2011) Deformation behaviour of commercially pure Titanium at extreme strain rates. Acta Materialia 59: 3431-3446.
- Li Q, YB Xu, MN Bassim (2004) Dynamic mechanical behavior of pure Titanium. Journal of Materials Processing Technology 155: 1889-1892.
- Wang L, Yingchun Wang, Alexander P Zhilyaev, Alexander V Korznikov, Shukui Li, et al. (2014) Dynamic compressive behavior of ultrafine-grained pure Ti at elevated temperatures after processing by ECAP. Journal of Materials Science 49: 6640-6647.
- Huang W, Xiang Zan, Xu Nie, Ming Gong, Yang Wang, et al. (2007) Experimental study on the dynamic tensile behavior of a poly-crystal pure Titanium at elevated temperatures. Materials Science and Engineering: A 443: 33-41.
- Yuan JM, VPW Shim (2002) Tensile response of ductile α-titanium at moderately high strain rates. International Journal of Solids and Structures 39: 213-224.
- Welsch G (1993) Materials properties handbook: Titanium alloys. ASM International, 134.
- Lütjering G, JC Williams, A Gysler (2000) Microstructure and mechanical properties of Titanium alloys. Microstructure and Properties of Materials 2: 1-77.
- Magargee J (2013) Analysis and observations of current density sensitivity and thermally activated mechanical behavior in electrically-assisted deformation. Journal of Manufacturing Science and Engineering 135: 061022.
Author Details
Sindhura Gangireddy*
University of North Texas, Denton, USA
Corresponding author
Sindhura Gangireddy, University of North Texas, Denton, TX 76207, USA.
Accepted: August 11, 2018 | Published Online: August 13, 2018
Citation: Gangireddy S (2018) A Modified Johnson-Cook Model for Cp-Ti to Incorporate the Effects of Dynamic Strain Aging and Phase Transformation. Int J Metall Met Phys 3:016.
Copyright: © 2018 Gangireddy S. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The high temperature mechanical behavior of the commercial CP-Ti can be strongly affected by phase transformation above 880 ℃. But literature documents the flow stresses of CP-Ti only upto 750 ℃. We investigated the mechanical response at a wide range of temperatures, starting from room temperature to a very high temperature of 1200 ℃ while under dynamic loading conditions of strain rates ~2000 s-1. The thermal softening pattern of the flow stresses is studied for effects of both dynamic strain aging (low temperature data showing good agreement with previous studies), and hitherto unreported sharp drop at the allotropic transition point (high temperature data). Another unique discovery of this study is the transition of thermal softening "rate", distinctly different prior and after the transition. The high strain rate data is combined with quasi-static mechanical response, to obtain strain rate sensitivity. The work hardening behavior at different strain rate regimes is shown to be similar. The three characteristics (thermal softening, strain rate dependence, work hardening) are coupled to generate a modified Johnson-Cook model that can cover high temperature constitutive response including dynamic strain aging at low temperatures and allotropic phase transformation at high temperatures.
Keywords
High-temperature, Kolsky-Bar, CP-Ti, Dynamic strain aging, Phase transformation, Modified Johnson-Cook model
Introduction
Titanium alloys have a great combination of properties, high specific strength which can be retained at even elevated temperatures, and exceptional corrosion resistance [1]. However, their poor thermal properties and reactivity with tool materials makes manufacturing Titanium alloys highly problematic [2]. This difficulty in machining limits these materials' use in commercial markets where rapid manufacturing processes are desired for cost reductions [3]. Rapid high temperature forming, high speed machining etc. processes create extreme conditions of high temperatures, rapid heating rates, and rapid loading rates which are hard to study. In the past decade, numerous modeling efforts have been undertaken to optimize cutting forces and improve productivity, frequently focusing on the role of chip segmentation on tool chatter and tool life [4,5] and the effect of machining parameters on surface integrity and surface hardening [6,7]. Such studies use advanced finite element models now reaching the capability of predicting such phenomena, but their reliability still relies on the accuracy of the constitutive models used. Understanding the material behavior under the conditions imposed by these processes is therefore highly critical for cost-effective production. At NIST, a new configuration of Split-Hopkinson Pressure Bar/Kolsky Bar has been developed, capable of reaching heating rates upto 10,000 ℃/s, loading rates 10,000 s-1 with testing temperatures reaching over 1200 ℃ [8]. Using this equipment, we investigated the dynamic response even beyond the allotropic transition point of 882 ℃, upto 1200 ℃, at a strain rate of 2000 s-1. Previous literature on high temperature dynamic deformation has been limited to below 750 ℃. Studies such as Nemat-Nasser, et al. [9] have revealed important phenomena occurring in this temperature range, particularly the presence of dynamic strain aging (DSA) in the temperature range between 23 ℃ and 500 ℃. In a subsequent publication, Cheng and Nemat-Nasser [10] have well described the associated strengthening of DSA through a physics based model considering a thermal long range, and thermally activated short range barriers for dislocation motion and coupling them with evolution of the core atmosphere. It was a very complex model requiring 14 material constants and an iterative processing step. Such models indeed enhance the physical understanding of phenomena, but are preventive in use of machining simulations. Numerical studies find it highly practical to use simple models with only a few factors, Johnson-Cook's being the usual choice [11]. Sheikh-Ahmad, et al. [12] have previously published a modified Johnson-Cook model for CP-Ti where they replaced the thermal softening term with an exponential decay term. However, this study used only 5 temperatures and the predictions of their model had no physical basis, did not match other well-recognized studies such as Cheng and Nemat-Nasser [9,10]. It is possible their data resolution was not sufficient to resolve the thermal softening behavior properly. So this study, we used data from 16 different temperatures covering 23-1200 ℃. At low temperatures, our data is found to agree with the well-established results of Nemat-Nasser, et al. [9,10] study, including the DSA peak at ~250 ℃ for the strain rates used. However, we also explore the constitutive behavior beyond the allotropic transition point at 882 ℃ and discover how this transformation causes a distinct shift in both the material's strength and the softening rate. In this paper, we attempt to incorporate this phenomenon, as well as the DSA, into a simple, modified Johnson-Cook model that can be readily used in machining studies.
Experimental Procedure
Material and specimen preparation
Commercial Grade-2 Titanium material was purchased as a 2 mm thick plate and was cut using electrical discharge machining (EDM) to make cylindrical compression samples measuring 4 mm in diameter. The chemical composition of the material is compared to the ASTM standard in Table 1 [13].
Mechanical testing
Dynamic deformation was conducted using the Kolsky Bar at strain rates of ~2000 s-1 and at temperatures of 23-1200 ℃ in a vacuum chamber. Samples were resistively heated with a high-amperage, low-voltage electric current conducted directly through the sample while it sat fixed between the incident and transmission bars. Due to the small sample cross-section (4 mm diameter) compared to the bars (15 mm diameter), the bars do not undergo significant heating and wave propagation would not be affected [14]. Using an infrared spot pyrometer as a feedback sensor, the heating power is modulated through a PID controller to obtain the set radiance temperature. Temperature uniformity during heating is monitored through a second pyrometer focused on the other side of the specimen. A thermocouple is also spot welded to obtain the thermodynamic temperature of the specimen before impact as well as the subsequent cooling rate. Arrival of the loading wave is Timed to occur approximately 30 ms after heating is turned off. At the impact Time, the thermodynamic temperature measured by the thermocouple was linearly correlated to the radiance temperature measured by the pyrometer, as well as the heating current used (Figure 1). This correlation makes it possible both to adjust amperage as well as set temperature values to obtain the desired thermodynamic temperature of a test. Further details of this heating method, its performance capabilities and assessment of its uncertainties have been described elsewhere [8,14].
All the specimens were impacted at 20 psi gas gun pressure to compress at a true strain rate of about 2000 s-1. The strain gauge measurements of incident, reflected and transmitted pulses were analyzed to obtain the true stress-strain curves, which are presented in the results section below. These flow stresses at a fixed strain value are studied to understand the thermal softening behavior. The other factors of the constitutive model, work hardening and strain rate dependence, are derived from quasi-static deformation response. Compression tests were performed at room temperature using a servo hydraulic test machine using fixed displacement rates to achieve strain rates of 0.00008 s1, 0.008 s-1, and 0.17 s-1.
Results and Discussion
Dynamic and quasi-static stress-strain curves
The dynamic true stress-strain curves obtained from Kolsky-Bar testing conducted between 23 ℃ and 1200 ℃ are depicted in Figure 2a. At the beginning of a Kolsky-Bar test, strain rate changes very rapidly and these portion of initial rise of the stress-strain curve is to be ignored. Only the portion of the stress strain curves where the strain rate was stable is plotted. The temperatures quoted are the initial thermodynamic temperatures measured by the thermocouple just before impact. As dynamic testing at such high strain rates becomes adiabatic [15], the temperature of the sample would rise due to the conversion of plastic work to heat.
Figure 2b shows the room temperature quasi-static test results (the dynamic flow stress curve is also included for comparison) at 8 × 10-5 s-1, 8 × 10-3 s-1, and 0.17 s-1 strain rates. These three isothermal curves show comparable work hardening which is substantially higher than that of the adiabatic curve at 2000 s-1 strain rate. Hence this drop in work hardening at high strain rates is attributed to an effective softening caused by the progressive rise of temperature with deformation.
During room temperature compression in the Kolsky Bar at 2000 s-1, Figure 2a shows the dynamic flow stress increasing from about 750 MPa at 0.025 strain to 950 MPa at 0.25 strain. These results are quite comparable to those reported in literature. Gurao, et al. [16] at a strain rate of 1500 s-1 during dynamic compression in Kolsky Bar at room temperature reported the flow stresses of 650 MPa at 0.025 strain increasing to 900 MPa at 0.25 strain. Li, et al. [17] reported higher flow stresses of 700 MPa at 0.025 strain increasing to almost 1200 MPa at 0.25 strain, but at a higher strain rate of 3000 s-1. Similarly, Wang, et al. [18] also have reported even higher flow stresses at a larger strain rate of 4000 s-1, 800 MPa at 0.025 strain. But this ultra-fine grained ECAP processed material had a weaker work hardening and the flow stress at 0.25 strain was only 1000 MPa. W. Huang, et al. [19] and Yuan and Shim [20] used a tensile SHPB at 1400 s-1 and 1100 s-1 strain rates respectively yielding flow stresses of around 500 MPa at 0.025 strain, much smaller than the above mentioned studies. S. Nemat-Nasser, et al. [9,10] reported results from compression SHPB at a strain rate of 2200 s-1. Their flow stresses were smaller than even Huang and Yuan at low strains, 300 MPa at 0.025 strain, but due to stronger work hardening the flow stresses at larger strains increased beyond Huang and Yuan's data, to 800 MPa at 0.25 strain. Table 2 summarizes data from these literature sources and compares with flow stresses from our experiments [6,16-20].
But when it comes to high temperature dynamic response, the literature is extremely limited. The few existing studies were restricted to below 750 ℃ [9]. In this study, we will explore thermal softening trends at much higher temperatures, such as those occurring in rapid machining conditions, and incorporate them into a simple constitutive model, Johnson-Cook's.
Johnson cook model
The Johnson-Cook (J-C) equation [11] is an empirical model commonly used for describing mechanical response of metals subjected to large plastic strains, high strain rates and high temperatures. The flow stress is given by a combination of three terms which delineate the work hardening, the strain rate sensitivity, and the thermal softening behavior of the material respectively.
Where and are the plastic strain and plastic strain rate respectively, and T*, the homologous temperature is given by T* = and we use Tref = 23 ℃ and Tmelt = 1668 ℃. The first term on the right hand side of Equation 1 describes the yield stress and strain hardening. A defines the yield stress, and strain hardening behavior is described by the strength coefficient, B, and the work hardening exponent, n. The strain rate dependence is incorporated in the second term by C, the strain rate sensitivity parameter. Typically, the reference plastic strain rate, , is set at 1 s-1 and we follow the same. The temperature dependence is given by the term [1 - (T*)m where m is a material constant that signifies the thermal softening effect. Each of the three constituents of the Johnson-Cook model, will be comprehensively explored in the following sections.
Plastic strain and adiabatic temperature rise
The Johnson-Cook model requires an estimation of both plastic strain as well as the temperature rise from the plastic work due to the adiabatic heating. Plastic Strain is obtained from subtraction of elastic strain from the true strain data using a temperature dependent elastic modulus: E [GPa] = 129.3 - 0.0633 T[℃] [21]:
where Ti is the initial test temperature and σ (0, Ti) is the corresponding flow stress from the stress-strain curve at yield, or zero plastic strain. The experimental stress value observed immediately after strain rate stabilization is as close an approximation to the yield stress as possible with this dataset. The resulting plastic strain is used to estimate the adiabatic temperature rise due to the conversion of plastic work to heat. The net temperature at a given strain is calculated from:
where Ti is the initial test temperature, ρ is the density, cp is the temperature-dependent heat capacity and n is the efficiency of the conversion of mechanical energy of plastic deformation to thermal energy. For metals, the value assigned to is usually 0.8-0.9, but values as high as 1.0 have been reported for CP-Ti [9]. In this study, we used a conversion efficiency of 1. A constant density of 4.51 × 103 kg/m3 and a temperature-dependent heat capacity given by cp(T) = 669 - (3.7188 × 10-2 T[℃]) - (1.08 × 107T[℃]-2) [21] were used in Equation 2 to estimate temperature as a function of plastic strain.
Work hardening
The Johnson-Cook model's first term describes the work hardening in the material through a Ludwik type of equation, . All the stress-strain curves, quasi-static and dynamic, appear to suit this equation. The work hardening rate, dσ/dε, was strong initially at small strains but decreased exponentially with increasing strain. Figure 3 is a plot of normalized work hardening rate, 1/σ (dσ/dε), in the room temperature stress-strain curves all of which demonstrate this exponential decline with increasing strain indicative of a small work hardening exponent, "n", value. With increasing strain rate, work hardening at a given strain decreases. This is especially pronounced in the dynamic stress-strain curve at 2000 s-1 strain rate due to the adiabatic softening described in the previous section.
Strain rate sensitivity
The second term of the Johnson-Cook model describes the effect of strain rate on the flow stresses. In this study, the strain rate sensitivity is investigated through room temperature tests conducted at strain rates ranging from 8 × 10-5 s-1 to 1800 s-1. Figure 4 plots the flow stresses at a fixed strain value (0.01 plastic strain) as a function of the logarithm of strain rate. Even as adiabatic heating occurs during compression at 1800 s-1, the temperature increment by the small strain of 0.01 would be insignificant. The increase in flow stress with logarithm of strain rate is highly linear, complying with the equation in the J-C model. The slope of this line is proportional to the strain rate sensitivity, C.
Thermal softening
Johnson-Cook model attempts to describe the effect of temperature in its last term. However the deterioration in the flow stresses with temperature is very often not monotonic, as is also the case here (Figure 2a). Further, CP-Ti undergoes allotropic transformation from hcp (α) to bcc (β) crystal structure at 882 ℃. In this series of experiments, the range of test temperatures (23-1200 ℃) was designed to cover both α and β phase fields, while most of the previous studies were limited to low temperatures below this transition temperature. Figure 5 demonstrates the variation in the dynamic flow stresses as a function of temperature. Here the flow stresses at different plastic strains are plotted against with their corresponding net temperatures, the sum of initial test temperature and the strain dependent temperature rise from adiabatic heating as calculated by Equation 3. This thermal softening trend reveals that:
• The flow stresses decreased significantly with temperature in α phase field. The trend is almost linear, except for a reduced softening rate between room temperature and 500 ℃. Similar phenomenon has been reported previously by Nemat-Nasser, et al. [9] and attributed to dynamic strain aging (DSA). This phenomenon occurs at a particular combination of temperature and strain rate, when dislocation motion defined by the strain rate matches the solute mobility activated by the temperature. Therefore the peak temperature of DSA would vary with the deformation rate. During deformation at a strain rate of 2200 s-1, Nemat-Nasser, et al. [9] observed the DSA to peak ~250 ℃, exactly matching the temperature where we observe the deviation in the softening rate at similar strain rates of 2000 s-1.
• Between the tests conducted at 819 ℃ (α phase) and 889 ℃ (β phase), there is a sudden drop in the flow stress. This could be due to the allotropic transformation at 882 ℃ from the stronger hcp α phase to the weaker bcc β phase, which has more number of the available slip systems to accommodate plastic flow [22].
• The thermal softening rate in the β phase field, tests between 889 ℃ and 1200 ℃, also appears monotonically linear. But the slope is significantly milder than that of the α phase field.
Obviously this complex thermal softening behavior cannot be described using the Johnson-Cook model's last term (1-T*m). Figure 6a shows the prediction lines with different values of the coefficient m = 0.3, 0.7, and 1.0, demonstrating that none of these can capture the data pattern. Some previous investigations on CP-Ti have also used modified thermal softening terms, Sheikh-Ahmad, et al. [12] used an exponential term f(T*) = α exp(β(1-T*)) to modify the Johnson-Cook equation. Magargee, et al. [23] studied electrically assisted tension testing and used the above Sheikh-Ahmad's modification to the Johnson-Cook model. However, this modification had no physical basis and was purely derived from their data of 5 temperatures. It's predicted softening pattern did not agree with either Nemat-Nasser's [9,10] or our data, as shown in Figure 6b. This discrepancy could be arising due to the small number of data points used to derive the softening trend in these two studies. Sheikh-Ahmad, et al.'s results composed of only 5 temperatures, 150 ℃, 300 ℃, 450 ℃, 600 ℃, and 750 ℃ [12], while Magargee, et al.'s data was based on 4 temperatures of 25 ℃, 74 ℃, 249 ℃, and 435 ℃ [23]. So it is highly probable that the data resolution in these studies was not sufficient to accurately reveal the softening trend.
In this study, we conducted tests at 16 different temperatures over a temperature range of 23-1200 ℃. Cheng and Nemat-Nasser [10] reported flow stresses from 8 temperatures between -196 ℃ and 725 ℃, and described a physics based model which considered the athermal long range, and thermally activated short range barriers for dislocation motion together with evolution of the core atmosphere, and interaction of dislocation and point defects. As demonstrated in Figure 6b, our thermal softening observations were in good agreement with Cheng and Nemat-Nasser's data [9] as well as the physical model [10], even as their flow stresses were slightly smaller than most literature sources (Table 2). Further, this model is exceedingly complicated with about 14 material constants and requires an iterative processing step for dynamic strain aging. Also, this model can predict flow stresses only over low temperatures below the transformation temperature. Use of such models is extremely difficult in machining simulations which for practical purposes require models with only a few factors. Dynamic strain aging is clearly manifested in our data, both in the lowered thermal softening rate described above, as well as a sharp rise in the work hardening behavior in this temperature range. Figure 7 displays the spike in work hardening in the temperature range of 23-500 ℃. The behavior became more distinct at higher strains. We attempt to capture this complex behavior while retaining the simplicity of the Johnson-Cook empirical model.
The (1-T*m) term in the original model is replaced with two terms: The first of which incorporates the different softening rates in the two phase fields as well as the drop at the transition temperature; and the second one accounting for the dynamic strain aging effect. In the first term, thermal softening is described by two linear lines, one with a larger slope for the α phase field below 882 ℃, and one with smaller slope for the β phase field above 882 ℃. The flow stress-temperature data from the tests outside the dynamic strain aging range was used to fit this linear function. Figure 8 compares the experimental data at different plastic strains (0.1, 0.15, 0.2, 0.25) with the thermal softening trend predicted by thus fitted first term, f(T*):
f(T*) = 1 - 1.55T* (T < 882 ℃) = 0.21 - 0.21T* (T > 882 ℃) (4)
It can be observed that the dynamic strain aging effect causes the experimental flow stresses to be stronger in the temperature range of 23-500 ℃ (T* ~ 0-0.35). In Figure 8, this effect is revealed as a 'bump' above the linear prediction line. Further, it can be observed that the DSA 'bump' is unaffected by strain, i.e. the extent of the deviation appears similar in all the four graphs. Hence a simple polynomial correction factor can be applied to the flow stresses in the temperature range of 23 ℃ to 500 ℃:
DSA(T*) = 1 + 1.65T* - 5.1T*2 (5)
Figure 9 shows the softening trend at the same 4 different strains can be described with the prediction from the combination of the two factors, f(T*) and DSA(T*). So, the modified Johnson-Cook equation we propose is:
Model parameters
In the determination of the parameters of this modified Johnson-Cook model, the least square method was employed over the entire range of quasi-static and the dynamic experimental data with same number of data points utilized in each stress-strain curve. Through multiple parameter optimization, the following parameters were found to give a good fit with R2 = 0.991, applicable over these conditions: (a) Temperatures between 23 ℃ and 1200 ℃; (b) Strain rates of 8 × 10-5 s-1 to 3500 s-1; and (c) Plastic strains of 0.05 to 0.6. The reference strain rate for the J-C model was taken to be 1 s-1. These Johnson-Cook model parameters are listed in Table 3.
Figure 10 demonstrates that the flow stresses from the 16 high temperature dynamic, and the 3 room temperature quasi-static tests, could be well described by this modified model in Table 3.
Conclusion
This paper explores the dynamic mechanical response of commercially pure Titanium (Grade-2) material at very high temperatures much beyond existing literature. The focus is particularly on thermal softening behavior, i.e. the variation of flow stresses with temperature. The room temperature flow stress and low temperature softening was similar to existing literature, including the presence of dynamic strain aging in the temperature range of 23-500 ℃. High temperature data indicated that allotropic transformation also causes a sharp deviation from a monotonic softening trend. The transformation from hcp to bcc crystal structure at 882 ℃ had a twofold effect, a sharp drop in the flow stress and a shift in the softening rates. A combination of two modification factors are proposed to replace the usual term in the Johnson-Cook model and this modified model was shown to effectively capture this flow stress trend.
Acknowledgements
The author gratefully acknowledges the support of Dr. Steven Mates and NIST Mechanical Performance Group as well as James Warren, NIST Technical Program Director for Materials Genomics. We also acknowledge the valuable assistance of Mr. Eran Vax and Mr. Eli Marcus of the Nuclear Research Center, Negev, Israel, for many improvements to the electrical heating control system.

