International Journal of Robotic Engineering
(ISSN: 2631-5106)
Volume 3, Issue 1
Research Article
DOI: 10.35840/2631-5106/4105
Computed-Torque Control of a Wheeled Mobile Manipulator
Mohamed Boukattaya*, Neila Mezghani and Tarak Damak
Table of Content
Figures
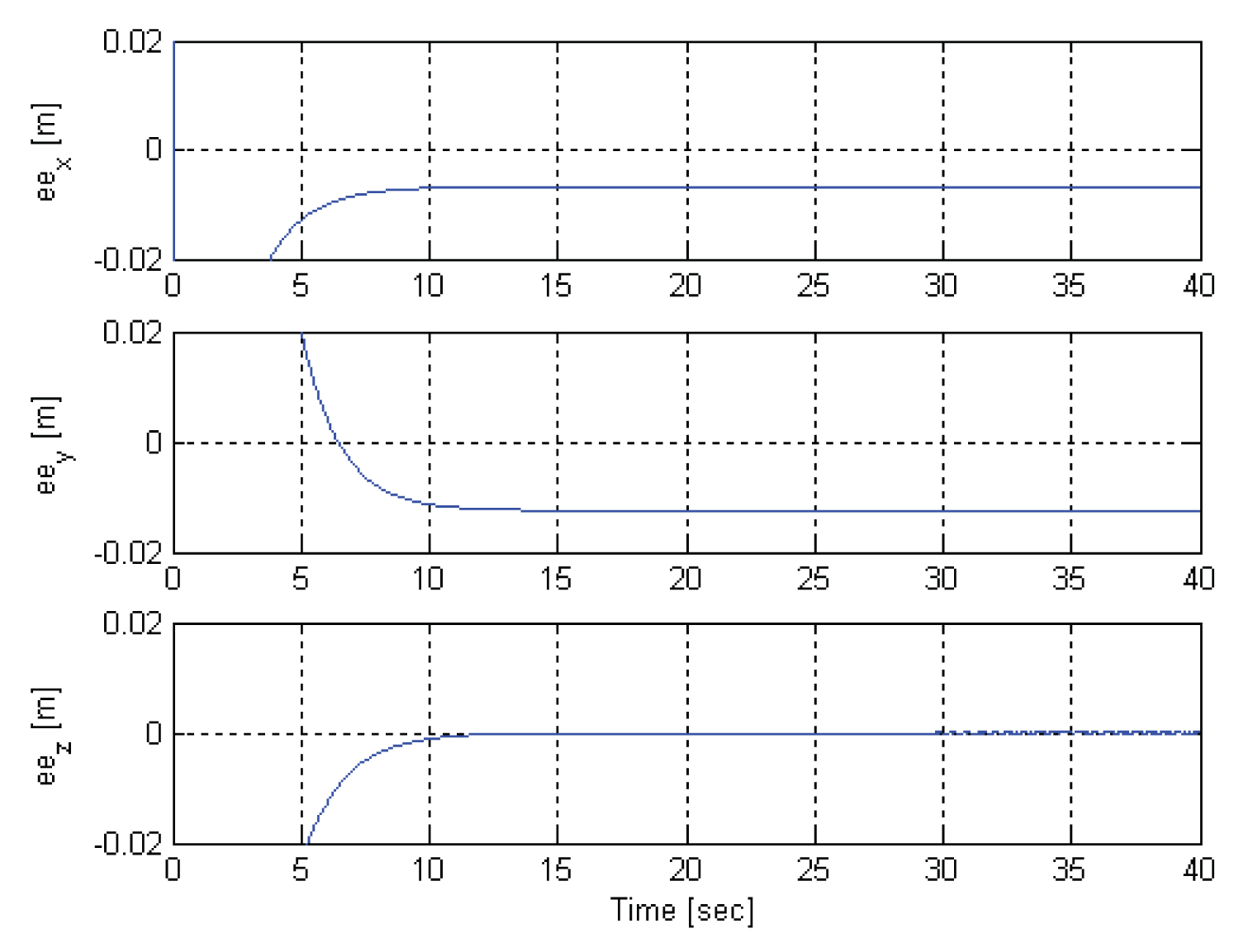
Figure 3: The position tracking...
The position tracking errors for the end effector in x, y and z coordinates.
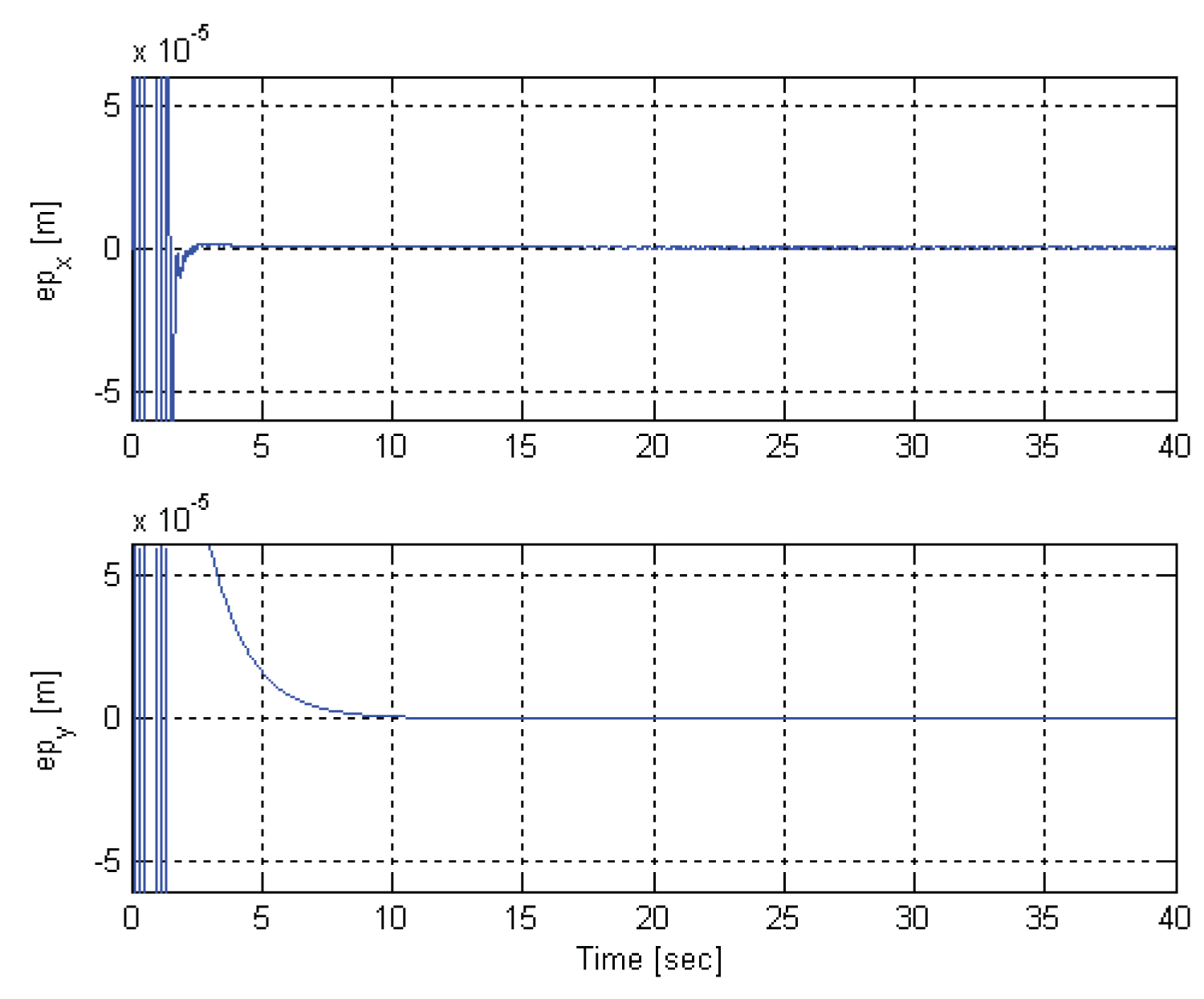
Figure 4: The position tracking...
The position tracking errors for the platform in x and y coordinates.
References
- V Pavlov, A Timolev (1976) Construction and stabilization of programmed movements of a mobile robot-manipulator. Eng Cybern 14: 70-79.
- J Chung, S Velinsky (1998) Modeling and control of a mobile manipulator. Robotica 16: 607-613.
- K Watanabe, K Sato, K Izumi, Y Kunitake (2000) Analysis and control for an omnidirectional mobile manipulator. J Intell Robot Syst 27: 3-20.
- B Bayle, J Fourquet, F Lamiraux, M Renaud (2002) Kinematic Control of Wheeled Mobile Manipulators. Proceedings on the 2002 IEEE/RSJ. Int Conference on Intelligent Robots and Systems. EPFL, Lausanne, Switzerland.
- B Bayle, M Renaud (2003) Nonholonomic Mobile Manipulators, Kinematics, Velocities and Redundancies. Journal of Intelligent and Robotic Systems 36: 45-63.
- N Chaabane, P Delarue, P Hoppenot, E Colle (2008) Strategy of Approach for seizure of an Assistive Mobile Manipulator. Journal for Robotics and Autonomous Systems.
- L Xiao, Y Zhang (2014) A new performance index for the repetitive motion of mobile manipulators. IEEE Transactions on Cybernetics 44: 280-292.
- Y Yamamoto, Y Xiaoping (1996) Effect of the dynamic interaction on coordinated control of mobile manipulators. IEEE Trans on Robotics and Automation 12: 816-824.
- N Hootsmanns, S Dubowsky (1991) The motion control of manipulators on mobile vehicles. Proc IEEE Int Conf Robot Automat 2336-2341.
- L Yangmin, L Yugang (2003) Hybrid kinematics and dynamics analysis for a mobile manipulator. CCECE 2003-CCGEI 20031767-1770.
- E Papadopoulos, J Poulakakis (2000) Planning and Model-Based Control for Mobile Manipulators. Proceedings of the IEEE/RSJ Internatzonal Conference on Intellegent Robots and Systems 1810-1815.
- J Peng, J Yu, J Wang (2014) Robust adaptive tracking control for nonholonomic mobile manipulator with uncertainties. ISA Transactions 53: 1035-1043.
- G Dai, Y Liu (2016) Distributed coordination and cooperation control for networked mobile manipulators. IEEE Transactions on Industrial Electronics 64: 5065-5074.
- S Mishra, P Londhe, S Mohan, S Vishvakarma, M Patre (2017) Robust task-space motion control of a mobile manipulator using a nonlinear control with an uncertaity estimator. Computers and Electrical Engineering 1-12.
- N Chen, F Song, G Li, X Sun, C Ai (2013) An daptive sliding mode backstepping control for mobile manipulator with nonholonomic constraints. Commun Nonlinear Sci Numer Simulat 18: 2885-2899.
- J Wen, D Bayard (1998) New class of control laws for robotics manipulators. part 1. non-adaptive case. Int J Control 47: 1361-1385.
- J Vazquez, M Valasco (2007) Computed torque control of an omnidirectional mobile robot. 4th International Conference on Electrical and Electronics Engineering. Mexico, 5-7.
Author Details
Mohamed Boukattaya*, Neila Mezghani and Tarak Damak
Laboratory of Sciences and Techniques of Automatic control & computer engineering (Lab-STA), National School of Engineering of Sfax, University of Sfax, Tunisia
Corresponding author
Mohamed Boukattaya, Laboratory of Sciences and Techniques of Automatic Control & Computer Engineering (Lab-STA), National School of Engineering of Sfax, University of Sfax, Postal Box 1173, 3038 Sfax, Tunisia.
Accepted: March 24, 2018 | Published Online: March 26, 2018
Citation: Boukattaya M, Mezghani N, Damak T (2018) Computed-Torque Control of a Wheeled Mobile Manipulator. Int J Robot Eng 3:005.
Copyright: © 2018 Boukattaya M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
The path-tracking problem of a wheeled mobile manipulator is addressed in this work. Instead of the classical kinematics model-based control commonly considered, the analysis of the problem is based on the dynamic model of the system. Borrowed from the rigid robot manipulator literature, the well-known computed torque control strategy is applied to control a wheeled mobile manipulator in the task space. It is shown that the considered strategy solves the problem assuring the closed loop stability of the system, allowing in this way the convergence of the tracking errors. The performance of the tracking strategy is evaluated by simulation, showing an acceptable performance.
Keywords
Wheeled mobile manipulator, Dynamic model, Computed torque
Introduction
Mobile manipulators refer to robotic manipulator mounted on a mobile platform. Such systems combine the advantages of mobile platform and robotic manipulator and reduce their drawbacks. The mobile platform extends the arm's workspace, whereas the manipulator offers much operational functionality. Applications for such systems could be found in mining, construction, forestry, planetary exploration, and military [1-3]. The path tracking problem of a mobile manipulator associated with its kinematics model has been widely treated in the literature in the last years. In [4], a generic scheme to solve the kinematic control problem of mobile manipulator is proposed when the operational motion is based on the additional task. In [5], a reduced velocity kinematics and velocity redundancy schemes are presented in order to realize an operational task while optimizing criteria such as manipulability. In [6], a manipulability criterion is defined to deal with the kinematic redundancy of the system. In [7], a quadratic performance index is proposed to achieve the repetitive motion control of mobile manipulators.
Most of the related work has concentrated on the kinematic models excluding the dynamic effects. However, control of mobile manipulators considering the dynamics of systems, is essential in many practical applications. For these reasons, much research has been carried out. In [8], nonlinear feedback control for the mobile manipulator was developed to compensate for the dynamic interaction between the mobile platform and the arm to achieve tracking performance. In [9], a control method based on an extended Jacobian transpose to compensate for dynamic interactions between the manipulator and base was developed. In [10], a Hybrid kinematics and dynamics analysis for a mobile manipulator was treated. In [11], we developed a model-based PD-like controller based on the dynamics of the mobile manipulator in order to eliminate tracking errors. In [12], a robust control scheme is proposed for the joint space control of a nonholonomic mobile manipulator under uncertainties and external disturbances. Most of the above-mentioned controllers were designed in joint space. However, in practical applications, the end-effector of a robot is usually specified to fulfil some operations such as grinding, painting, object grasping, etc. Consequently, it seems natural to develop task space control schemes. The works in [13-15] consider the end-effector tracking problem where the reference signals are given in the task space, but they consider a simple structure of mobile manipulators. It is well-known that the computed torque control strategy has been considered to tackle the regulation and path tracking problems of many nonlinear systems such as flexible manipulators [16], omnidirectional mobile robot [17], etc. A computed torque control strategy to solve the path-tracking control of a complex structure of a mobile manipulator with three-link rigid manipulator in task space was not treated yet and will be proposed in this work.
The main contributions of this paper are as follows: 1) The considered mobile manipulator has a complex structure and operates in the three-dimensional task space. 2) The entire mobile manipulator is modeled as an integrated structure. 3) A simple computed torque control method in the task space is suggested for the tracking control of a kinematically redundant mobile manipulator. 4) The problem of redundancy is resolved using an extended approach where the velocity of the mobile base and the motion of the end-effector are simultaneously controlled.
This paper is organized as follows. We derive the kinematics and dynamics modeling for the three-link wheeled mobile manipulator in section 2. Section 3 presents the design of the proposed computed torque controller with stability analysis. Section 4 presents computer simulation results to illustrate the effectiveness of the proposed algorithm. Conclusions are formulated in section 5.
Modeling of a Wheeled Mobile Manipulator
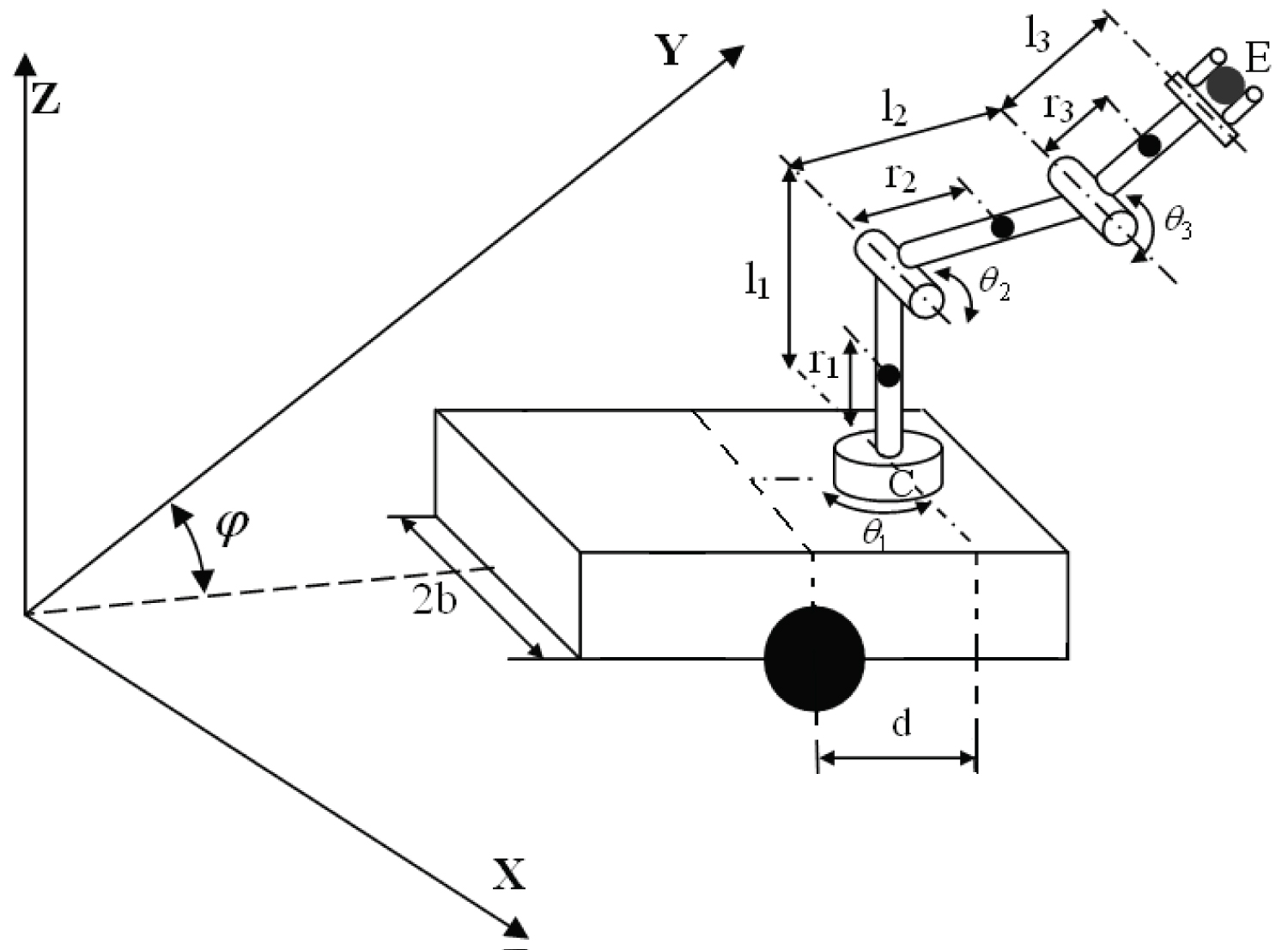
Considering the mobile manipulator as shown in Figure 1. The platform is actuated by two independently driving wheels with radius . The two wheels are separated by a distance of . The manipulator is located at a distance from the driving wheels axis and constructed as a three-link spatial arm with servo motors attached at the joints. The link 1 can rotate around Z, and the links 2 and 3 can rotate up and down. Let , and denote the link lengths. , and denote the distance between joint and the center mass of links. , , , and , , , represent the masses and inertias of platform, link1, link2 and link3 respectively.
Kinematic modeling
Since the platform is driven by two independent wheels. The velocity constraint is nonholonomic, the kinematics equation can be written as follows:
Where is the heading angle of the platform, and are the coordinate of point .
Select , the above equation can express as follow:
Where , and according to the known matrix theory, there exists a full rank matrix formed by a set of smooth and linearly independent vector fields spanning the null space of , i.e., , as:
Where are the independent velocity of the system.
The coordinate of the end-effector and the platform can be expressed in world frame as follows:
The linear velocity of the end-effector and the platform, can be found by differentiating the above equation (4) and can be expressed as:
Where is the jacobian matrix.
Finally, by substituting the relationship (4) into equation (5) we get the reduced matrix relating the task space to the independent joint rates as:
Dynamic modeling
The dynamics of a mobile manipulator subject to nonholonomic constraints can be obtained using the Lagrangian approach in the following form [15]:
is a symmetric and positive definite inertia matrix, represents the matrix of centripetal and Coriolis forces term. represents the vector of gravity term. is the constraint matrix. is the Lagrange multiplier which denotes the vector of constraint force. is the input transformation matrix and is the vector of input torques.
Substitute equation (3) into (7), and eliminate , then we can obtain:
Where , , ,
Eq. (8) can be transformed further in the operational space using Eq. (6). The result is:
Where , , ,
Path Tracking Problem
Suppose that the desired trajectory is described by , and . In order to track the desired trajectory, we have to design a computed-torque controller such that for the closed loop system it is possible to assure the convergence of the tracking error to zero.
Consider now the following controller originally proposed in the robot manipulator field [11], expressed as:
Where is the trajectory that is desired to follow and represents the tracking error of the system. and are respectively the proportional and derivatives gain matrices, which is also considered to be diagonal positive definite matrices.
Substituting the dynamic model in the operational space of the mobile manipulator (9), in the control law (10), the closed loop of the system is obtained as:
After simple calculation, we have
Since matrix is invertible, the stability of the error equation (12) can be analyzed in terms of the equivalent equation,
Closed loop stability
The dynamics of the system (11) in closed-loop with the feedback (10) can be studied from the tracking error equation (13). For doing this, note that the origin is an equilibrium point for system (13) and consider the candidate Lyapunov function of the quadratic type of the form,
It is a simple task to verify that the function is positive definite for a sufficiently small constant .
In order to state the stability of the closed loop system (13) consider now the time derivative of the function (14), yielding,
From where the asymptotic closed loop stability is stated for a sufficiently small .
Simulations Results
The experiments were developed under the MATLAB simulation environment. The aim is to verify the effectiveness of the proposed algorithm on a three-link wheeled mobile manipulator (Figure1). In the simulation, we assume that the parameters of the system are:
, , , , , , , , , , , , , , , ,
The desired trajectory for the mobile manipulator has been chosen as follows:
It consists of a straight line in (x-z) plane for the end-effector and a straight line in (x-y) plane for the platform. The time of the motion is 40 seconds and the initial position of the platform was equal to: and the initial position of the manipulator was equal to
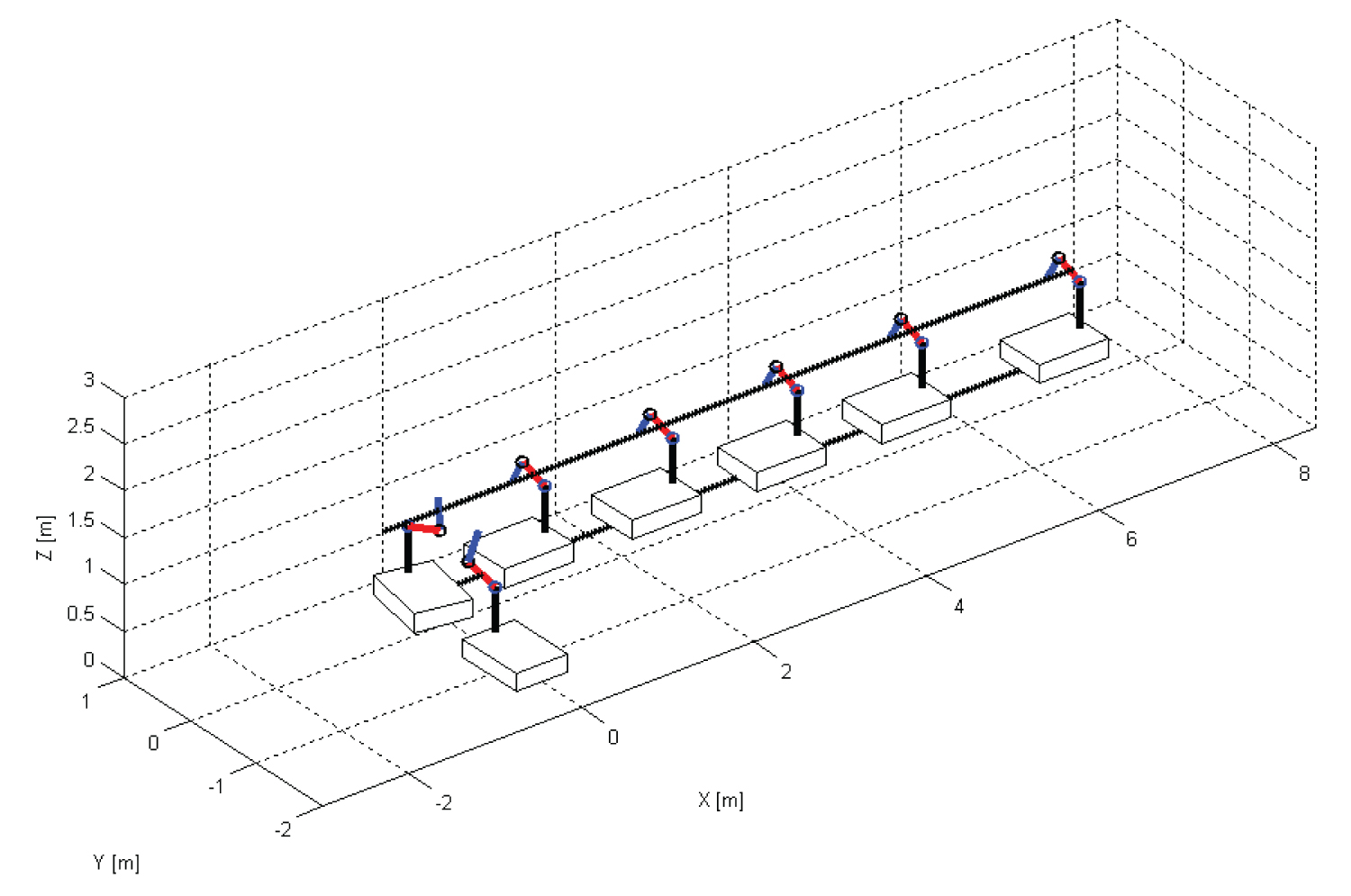
Figure 2 illustrates motion trajectories of the mobile manipulator when its end-effector is moving along a straight line in (x-z) plane and the platform is moving along a straight line in (x-y) plane. We can see that the mobile manipulator track the desired trajectories in 3-D space with a perfect coordination between the arm and the platform which demonstrate the effectiveness of the proposed dynamic algorithm.
The position tracking errors for the end-effector and the mobile platform are shown in Figure 3 and Figure 4, respectively. It is also important to notice that all the trajectories tracking errors asymptotically tend to zero. It is less than 2 cm for the end-effector and less than 1 mm for the mobile platform, which demonstrate that the goal control performance was reached.
Conclusion
In this work it is considered the dynamic model-based control of a wheeled mobile manipulator in order to solve the path-tracking problem of the system subject to nonholonomic constraints. To solve the problem in task space, the well-known computer torque control strategy that it is commonly used in the field of robot manipulators was considered. The stability of the overall closed loop system was proved. The simulation results show that the mobile manipulator can tracks end-effector path in (x-z) plane and platform path in (x-y) plane with a perfect coordination between the subsystems which demonstrate the effectiveness of the proposed computed torque controller.
Acknowledgements
We thank the ministry of higher education and scientific research of Tunisia for funding this work.