International Journal of Robotic Engineering
(ISSN: 2631-5106)
Volume 3, Issue 2
Original Article
DOI: 10.35840/2631-5106/4113
Genetic Algorithm-Based Structure Optimization and Load-Carrying Analysis for the Body Frame of Heavy-Duty AGVs
Xing Wu1*, Jingyang Wu2, Peng Jin1, Hua Chen1, Chao Sun1 and Peihuang Lou1
Table of Content
Figures

Figure 1: The planar dimensions of the...
The planar dimensions of the body frame of the heavy-duty AGV.
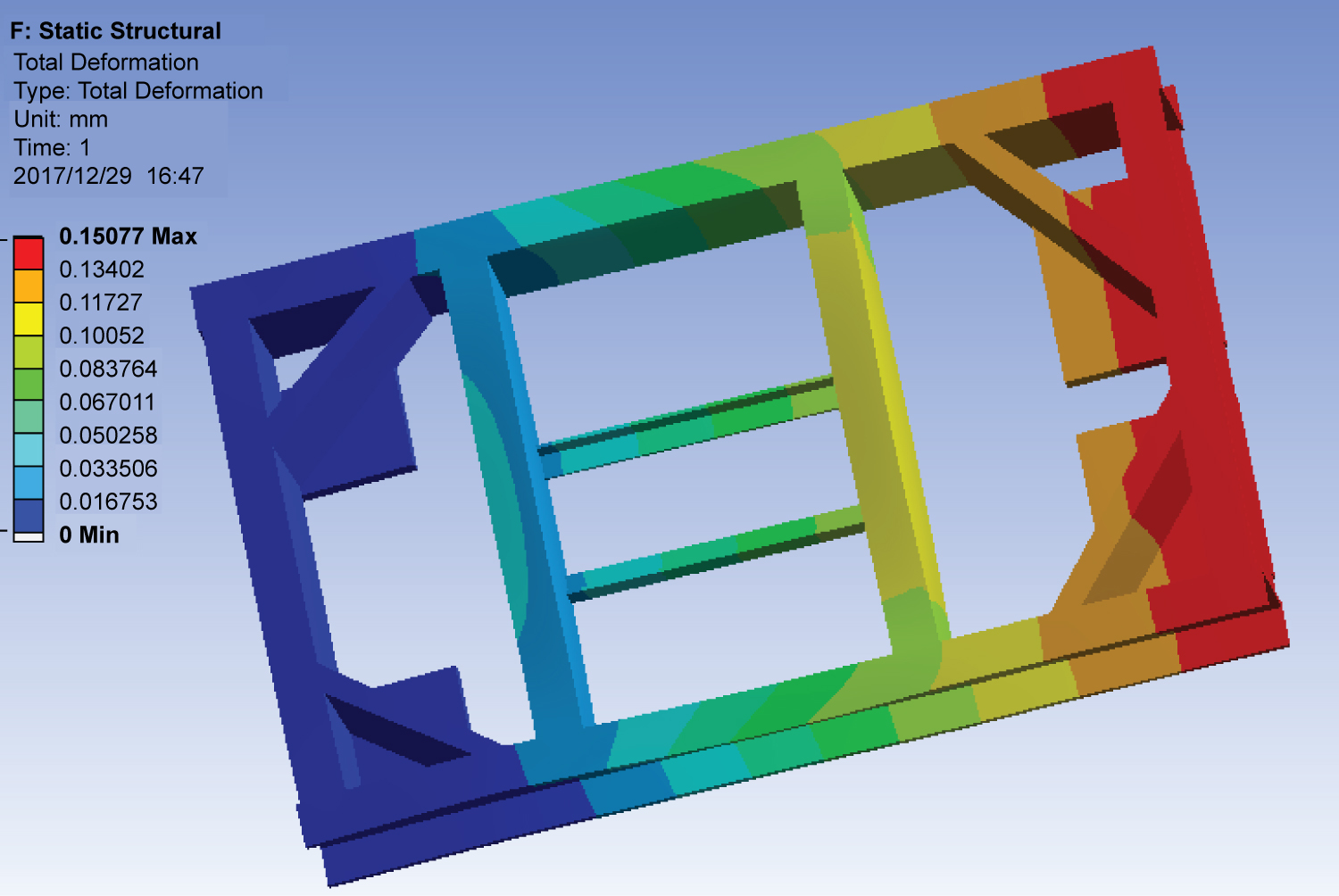
Figure 9: The cloud map of the maximum...
The cloud map of the maximum deformation and displacement.
Tables
Table 1: The dimensional and mechanical parameters of the wheels.
Table 2: The parameters of the genetic algorithm.
Table 3: The binary encoding of individual chromosome for each parameter.
Table 4: Parameters of the preliminary model and the improved model.
References
- Vis Iris FA (2006) Survey of research in the design and control of automated guided vehicle systems. Eur J Oper Res 170: 677-709.
- Do KD (2013) Bounded controllers for global path tracking control of unicycle-type mobile robots. Robot Auton Syst 61: 775-784.
- Hwang CL (2016) Comparison of path tracking control of a car-like mobile robot with and without motor dynamics. IEEE/ASME Trans on Mechatronics 21: 1801-1811.
- Wu X, Shen WL, Lou PH, Wu B, Wang L, et al. (2016) An automated guided mechatronic tractor for path tracking of heavy-duty robotic vehicles. Mechatronics 35: 23-31.
- Wu X, Zhang Y, Zou T, Zhao L, Lou P, et al. (2018) Coordinated path tracking of two vision-guided tractors for heavy -duty robotic vehicles. Robot Comput Integr Manuf 53: 93-107.
- Guo X, Cheng GD (2010) Recent development in structural design and optimization. Acta Mesh Sin 26: 807-823.
- Liu ST, Su WZ (2010) Topology optimization of couple-stress material structures. Struct Multidiscip O 42: 243-254.
- Diego AC de Souza, Sérgio LMRF, André Luís Cerávolo de Carvalho, Neimar SS, Samuel MB, et al. (2013) Topological optimization and genetic algorithms used in a wheel project for a drone. Int J Stat Appl 3: 155-161.
- Wu B, Qian XM, Wu X, Shen K (2014) Optimization design on AGV frame structure. China Mechanical Engineering 25: 2653-2657.
- Sekulski Z (2009) Structural weight minimization of high speed vehicle-passenger catamaran by genetic algorithm. Pol Marit Res 16: 11-23.
- Ahmad MN, Muhamad WMW (2013) Application of size optimization on steel wheel rim. Appl Mech Mat 315: 309-314.
- Vahid M, Morteza MGH, Mehdi MK (2016) Optimization of the component sizing for a plug-in hybrid electric vehicle using a genetic algorithm. P I Mech Eng D-J Aut 230: 692-708.
- Nan Li, Minghui Wang, Shugen Ma, Bin Li, Yuechao Wang (2012) Mechanism-parameters design method of an amphibious transformable robot based on multi-objective genetic algorithm. Chinese Journal of Mechanical Engineering 48: 10-20.
- G Zhao, H Chen, C Zhang, Guan Y (2013) Multiobjective optimization design of porthole extrusion die using Pareto-based genetic algorithm. Int J Adv Manuf Technol 69: 1547-1556.
- Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95: 51-67.
- Kirkpatrick S, Gelatt CD, Vecchi MP (1983) Optimization by simulated annealing. Science 220: 671-680.
- Gupta S, Deep K (2018) Random walk grey wolf optimizer for constrained engineering optimization problems. Comput Intel 34: 1025-1045.
- Gupta S, Deep K (2018) Cauchy grey wolf optimiser for continuous optimisation problems. J Exp Theor Artif In 30: 1051-1075.
- Xu SL, Cheng GD (2010) Optimum material design of minimum structural compliance under seepage constraint. Struct Multidiscip O 41: 575-587.
- Ganzerli S, Pantelides CP, Reaveley LD (2015) Performance-based design using structural optimization. Earthq Eng Struct D 29: 1677-1690.
Author Details
Xing Wu1*, Jingyang Wu2, Peng Jin1, Hua Chen1, Chao Sun1 and Peihuang Lou1
1College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, China
2College of Mechanical and Electrical Engineering, Hohai University, China
Corresponding author
Xing Wu, Associate Professor, College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, 29 Yudao Street, Nanjing 210016, Postbox 347, China, Tel: 086+025-84893155.
Accepted: December 27, 2018 | Published Online: December 29, 2018
Citation: Wu X, Wu J, Jin P, Chen H, Sun C, et al. (2018) Genetic Algorithm-Based Structure Optimization and Load-Carrying Analysis for the Body Frame of Heavy-Duty AGVs. Int J Robot Eng 3:013.
Copyright: © 2018 Wu X, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
For a 2-ton heavy-duty automated guided vehicle (AGV), structure optimization and load-carrying analysis are investigated in order to improve the dynamics response performance and the energy utilization efficiency of the AGV frame. The mechanical and geometric constraints are firstly defined for the structure optimization of the AGV frame. Secondly, a multi-objective optimization function is formulated for the structure size, and then the optimal solution is solved by means of the genetic algorithm. Thirdly, the design scheme of the AGV frame is refined according to the optimized structure-size parameters. Moreover, the ANSYS software is used to verify the stiffness and strength of the frame. The results show that the mass and the moment of inertia of the frame is reduced by 33.7% and 19.3% respectively, and the frictional forces of AGV wheels decrease by 16.8%. A light-weight mechanical base is provided for motion control of the heavy-duty AGV.
Keywords
Automated guided vehicle, Structure optimization, Size optimization, Multi-objective optimization, Genetic algorithm
Introduction
Automated Guided Vehicle (AGV) is a mobile robot that can travel automatically along a predetermined path. Nowadays a large number of AGVs are needed to carry out repeating transport tasks in manufacturing and warehouse industries [1]. Many motion control methods have been developed based on kinematics model or dynamic model for AGVs [2-5]. In fact, the dynamic performance of an AGV is greatly influenced by the structure of its body frame. The mass and the moment of inertia of the frame determine the inertial matrix of the AGV dynamics model, which fundamentally limits the dynamic response performance of an AGV. On the other hand, the energy utilization efficiency is also related to the frame structure, especially to the friction resistance of a body frame, for a heavy-duty AGV. Improving the energy utilization efficiency of AGV is helpful for reducing the capacity and quality of the onboard battery pack, which further reduces the mass and the moment of inertia of an entire AGV in return. Hence, structural optimization of an AGV frame is regarded as the basic work to improve the control performance of a heavy-duty AGV.
Structural optimization contains three different types of problems, i.e., size, shape and topology optimization [6]. Among them, topology optimization aims at finding the optimal way of material distribution in the structure by means of objective functions under constraint conditions, which is often used for the initial design area on the stage of conceptual design [7-9]. After the structure topology and shape are determined, size optimization is used to work out the optimum design size of structural components and the best usage of material properties [10-14]. Genetic algorithm is used to optimize the plate thickness, section size and spacing parameters by Sekulski [10], in order to reduce the hull weight of the high-speed catamaran. The area of circular hole of hub steel ring is also optimized by means of genetic algorithm [11]. The mechanism parameter design of an amphibious transformable robot is formulated as a multi-objective optimization problem, based on the mapping relationships between the performance indexes and the mechanism parameters. The non-dominated sorting genetic algorithm II (NSGA-II) is then adopted to solve this optimization problem and to get the Pareto optimization [13].
After the structural optimization problems are formulated, how to search the optimum solutions then needs to be taken into account. Nature-inspired meta-heuristic algorithms can be used to solve these problems by mimicking biological or physical phenomena [15]. They can be grouped into three main categories: Evolution-based, physics-based, and swarm-based methods. The most popular evolution-inspired technique is Genetic Algorithms [8,10,12-14]. Physics-based methods imitate the physical rules in the universe. The most popular algorithms are Simulated Annealing [16]. The third group of nature-inspired methods includes swarm-based techniques that mimic the social behavior of groups of animals, such as mimicking the hunting behavior of humpback whales [15], or inspired by the leadership and social behavior of grey wolves [17,18].
The size optimization of an AGV body frame pertains to a kind of nonlinear optimization problem under constraints. The optimization model contains the objectives or constraint parameters that have a nonlinear relation with design variables [9]. A direct search method is adopted in this paper, instead of handling the constraint conditions of the optimization problem in advance [19]. Genetic algorithm is employed to make a quick search for the optimum solution of the multi-objective optimization problems.
The rest of this paper is organized as follows. The optimization objective of a heavy-duty AGV is described in Section 2. In Section 3, the multi-objective optimization model under constraints is formulated for the size design of the AGV frame. A genetic algorithm is used to search the optimum size parameters in Section 4. In Section 5, the stiffness and strength of the AGV frame, which has been refined according to the optimization results, are analyzed by means of the ANSYS software. Finally, conclusions are drawn in Section 6.
Problem Descriptions
The optimization results of the AGV frame can be evaluated in the perspective of the dynamic response characteristics and the energy utilization efficiency. Since driving wheels and caster wheels are chosen from commercial off-the-shelf products, their dimensions have already been known before the optimization of the AGV frame. For example, the bearing plates for driving wheels have the dimensions of 200 mm × 200 mm × 20 mm in length, width and thickness, while the three dimensions of that for casters are 200 mm × 240 mm × 20 mm.
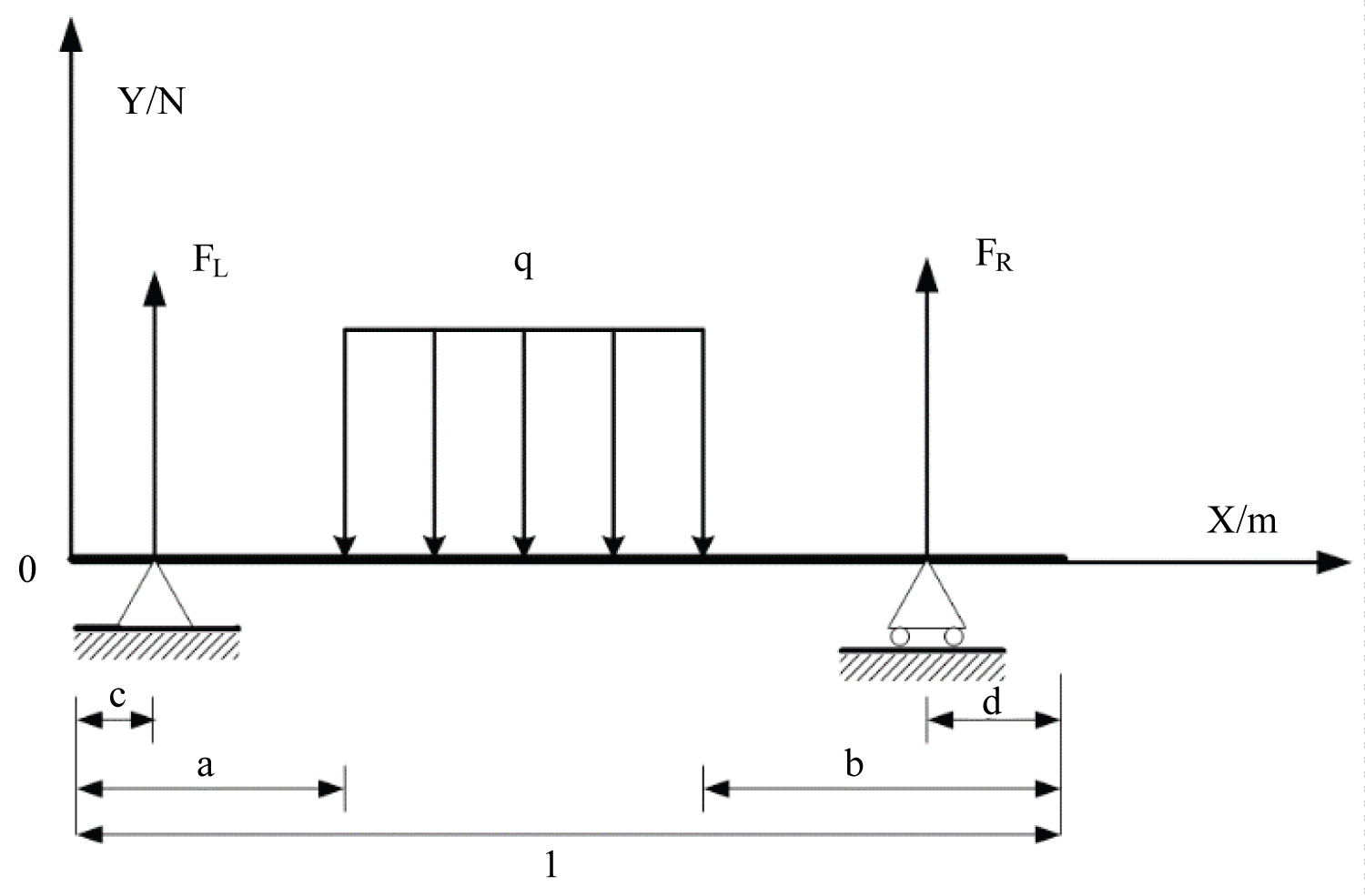
The dimensions of the AGV frame needed to be optimized are shown in Figure 1. The length and the width of the body frame are l and l1. BB1 denotes the axis of two driving wheels. The distance between BB1 and AA1 is c. The distance between the bearing plate of driving wheels and the middle line of the AGV is t1. EE1 represents the axis of two caster wheels, and its distance from FF1 is d. The distance between the bearing plate of caster wheels and the middle line of AGV is t2. Suppose the payload to be distributed on the CD segment uniformly. The lengths of AC, CD and DF are a, e and b respectively.
The total load of the AGV is composed of the payload m1, the body frame m2, driving wheels m3 and caster wheels m4. The payload capacity is usually determined by the requirements, while the driving wheels and caster wheels are chosen from the off-the-shelf products. Hence, the objective is only to consider the optimization of the mass of the body frame m2 in this paper. The moment of inertia of the AGV also comprises the payload J1, the body frame J2, driving wheels J3 and caster wheels J4, shown as follows:
Where I1 and I2 are the moment of inertia of the bearing plate of driving wheels and caster wheels with respect to (w. r. t.) their centers, respectively.
The friction resistance of an AGV in motion is related to the payload carried by the driving wheels and caster wheels, while the distribution of the payload between the driving wheels and caster wheels is affected by the structure of the AGV frame. Size optimization can be used to reduce the friction resistance of the heavy-duty AGV significantly, and to improve the energy utilization efficiency of the AGV consequently.
Optimization Modeling
General mathematical model
The general mathematical model of optimization problems can be expressed as [20]:
Where x is the design variable vector, and n is the number of design variables in x. is the objective function for optimization design, and and are the constraint conditions of the system.
Constraint conditions
Constraints include mechanical and geometric constraints. When the heavy-duty AGV carries its payload, the main mechanical effect caused by the payload is bending deformation. Thus, the normal bending stress is considered as the major strength constraint when the load-carrying structure of the AGV frame is designed.
Where and Mmax are the maximum bending stress and the maximum moment of the bearing beam, respectively. W is the bending resistance of the cross-section of the bearing beam, and is the allowable design stress. According to Eq.(3), one can effectively enhance the load-carrying capacity of the structure by increasing the bending resistance of the cross-section W, or by reducing the maximum bending moment Mmax , i.e., designing a reasonable shape and size of cross sections or a reasonable load distribution of bearing beams. In this paper, channel steels are used to construct the frame structure of the heavy-duty AGV. The safety factor ns is selected as 1.5, and the allowable stress is prescribed as 156.7 MPa, according to the reference [11].
Generally, heavy-duty AGVs have load-carrying mechanisms, through which the pressures of payloads are imposed and distributed uniformly on the bearing beams. The load-bearing beam is supported by the driving wheels and the caster wheels. On the static analysis stage, the structure can be regarded as a simply-supported beam, the force analysis of which is shown in Figure 2.
After defining the coordinate system shown in Figure 2, we can formulate the shearing force and the bending moment of cross section of the bearing beam as
Where Fs and Ms are the shearing force and the bending moment of the bearing beam.
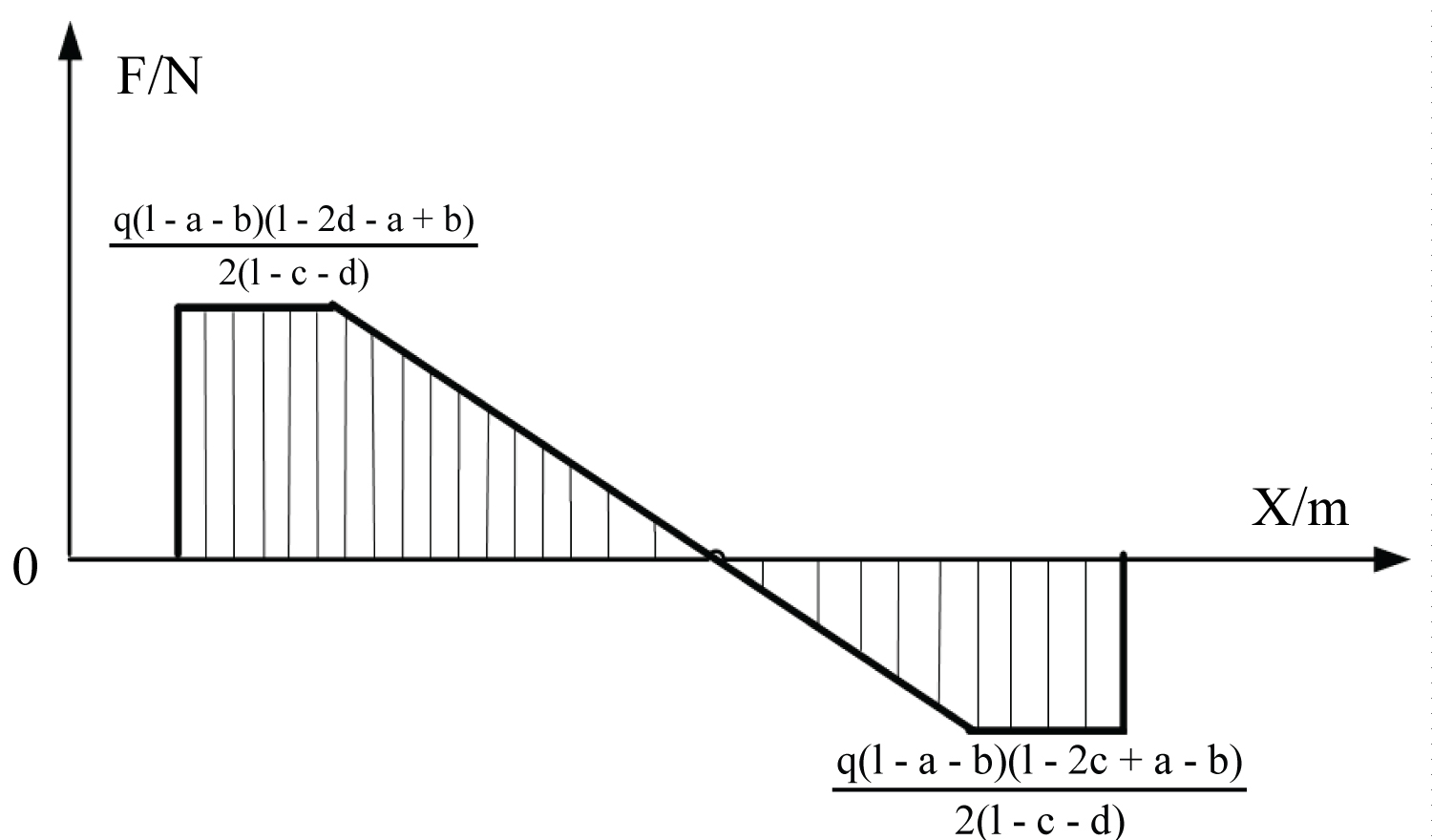
The distribution of the shearing force and the bending moment are shown in Figure 3 and Figure 4, respectively. According to Eq.(4), the support force FL and FR of the load-bearing beam on the left and right brackets, and the maximum bending moment Mmax of the bearing beam can be obtained.
Where q is the concentration of uniformly distributed load on the bearing beam.
The heavy-duty AGV designed in this paper has a rated load of two tons. In the simply-support beam model of Figure 2, the left and right brackets represent the driving wheels and the caster wheels of the heavy-duty AGV, respectively. The dimensional and mechanical parameters of these wheels are shown in Table 1. It is seen that the load-carrying capacities of these wheels have a large safe margin, compared to the rated load.
In order to improve the energy efficiency of the heavy-duty AGV, it is reasonable to reduce the sum of frictional resistances of multiple wheels if possible. Since the friction coefficient of caster wheels is obviously greater than that of driving wheels, the bearing capacity FR of caster wheels should be decreased and the bearing capacity FL of driving wheels should be increased, when Mmax complies with the condition Eq.(3).
Objective function
The objective of size optimization lies in reducing the moment of inertia of the heavy-duty AGV and the frictional resistance of the wheels. This problem can be described as a multi-objective optimization problem, expressed as follows:
Where G is the set of feasible points that satisfy the constraint conditions. In order to facilitate the problem-solving process, the multi-objective optimization problem is equivalently converted into a single-objective one by means of a weighted sum, as
Where w1 and w2 are weight coefficients, which are predefined as w1 = 0.6 and w2 = 0.4 by means of the trail and error procedure. Because of different dimensions of J and FR, normalization process is used here to construct the objective function containing dimensionless variables.
Where and are the estimated values of the moment of inertia and the bearing capacity, i.e., = 150 kg•m2, = 4000 N.
Size optimization model of the AGV frame
The optimization model can be formulated under the constraint conditions of the AGV frame.
Where J is defined in Eq.(1), the allowable stress is prescribed as 156.7 MPa, and the bending section coefficient W is 10.4 cm3.
Optimization Solving
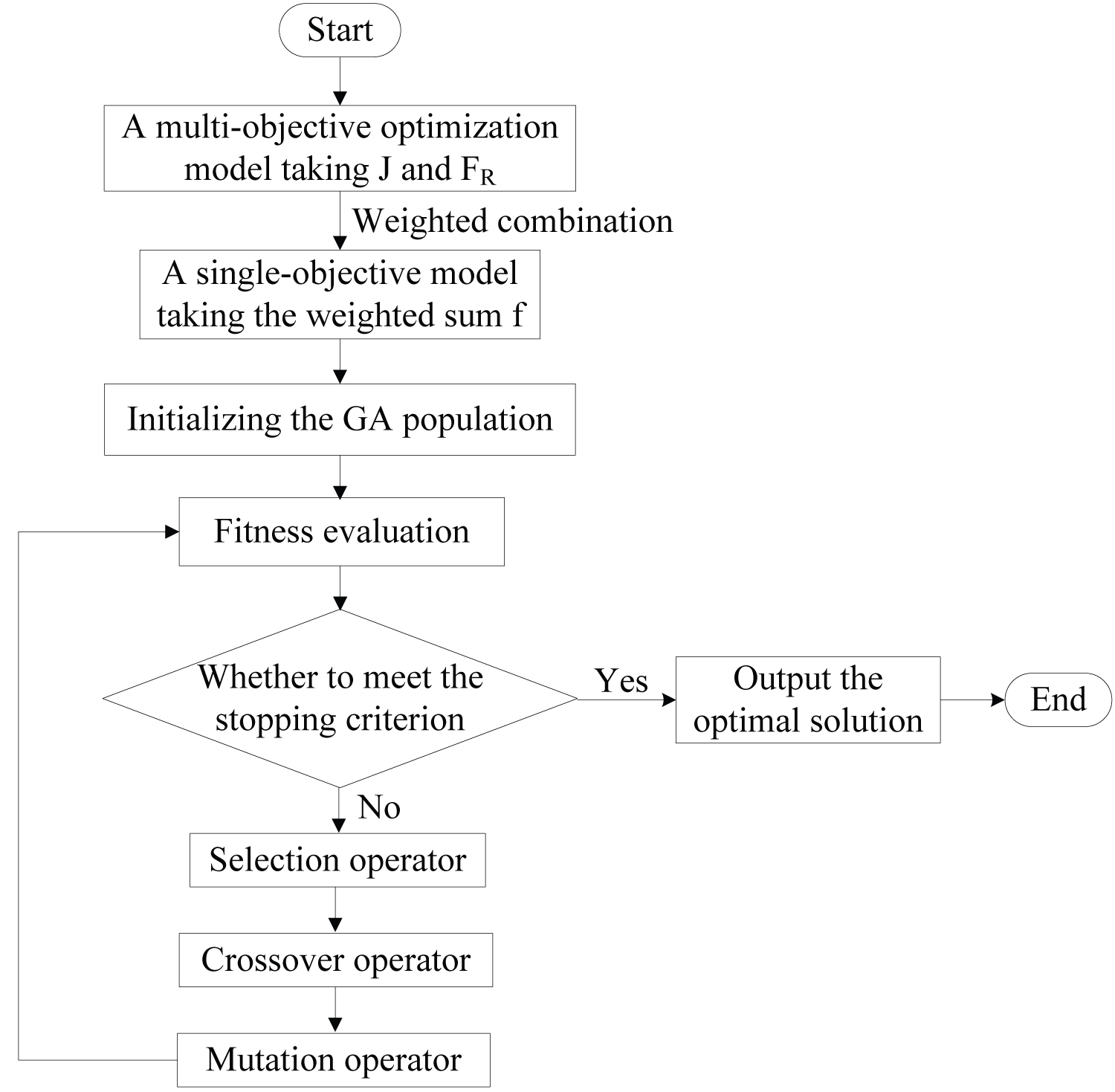
The genetic algorithm (GA) is utilized here to find the optimal size of the AGV frame according to the optimization model Eq.(9). This algorithm mimics the evolutionary process in nature. Like creatures in nature evolve to adapt to the environment, solutions in the GA evolve to adapt to the optimization problem. It can be directly applied to the structure object without the limitation of the derivation and the function continuity. GA, which has the inherently implicit parallelism and the better global optimization ability, can automatically acquire and guide the searching space for optimization, and can adaptively adjust the search direction without the need of explicit rules [10-13]. The flowchart of the genetic algorithm in this paper is shown in Figure 5. The parameters of the algorithm are listed in Table 2. The detailed steps are described as follows:
Initialize the population
Solutions in GAs are defined as a chromosome of an individual, and a group of individuals is referred to as a population. The initial population is randomly generated. The population number N and the evolution step G are set as 200 and 100, respectively. Each chromosome is divided into 8 gene segments and encoded into a binary form. Each gene segment corresponds to one dimensional parameter, as shown in Figure 1. They join together sequentially to constitute one chromosome for this size optimization problem. The length of gene segment, i.e., the number of binary bits, is designed in the consideration of the range and accuracy of each parameter, as shown in Table 3. The total length of one chromosome is 57 bits.
Fitness evaluation
The solution quality of each individual is evaluated by the fitness function. The reciprocal of the objective function f (x) is employed as the fitness function here. The raw individual fitness of each generation of population is calculated according to the fitness function. Then, the rank selection method is used to scale the raw individual fitness to the range of the fitness selection function.
Selection operator
In the selection operation, several preferable individuals are selected from the current generation of population by means of the roulette wheel, in which individual chromosomes with higher fitness value have the higher probability of reproducing new offspring in the next generation. However, due to the randomness of the roulette wheel method, there is also a possibility of losing preferable individuals in the process of selection. Hence, the elitist reservation mechanism is adopted here by transferring directly the best 10 individuals into the next generation.
Crossover operator
Given two parents, the task of crossover is to generate the offspring by inheriting features (gene structures) from the parents. For the binary encoding scheme, since a chromosome only contains binary bits, the single-point crossover is applicable. In the algorithm, a random integer n is selected from the range of the chromosome length. One gene fragment is selected from the first parent by extracting the first n genes, and the other gene fragment is generated by inheriting the rest genes from the second parent. Then the two fragments are combined to reproduce a new offspring. The crossover probability Pc is set as 0.8. Feasibility must be checked after crossover.
Mutation operator
The mutation operator introduces random changes to several genes of a chromosome. It gives the new information to the population and adds the diversity to the mating pool. The single-point mutation operator is used here to decide which genes to be changed. The mutation probability Pm is set as 0.1.
Stopping criterion
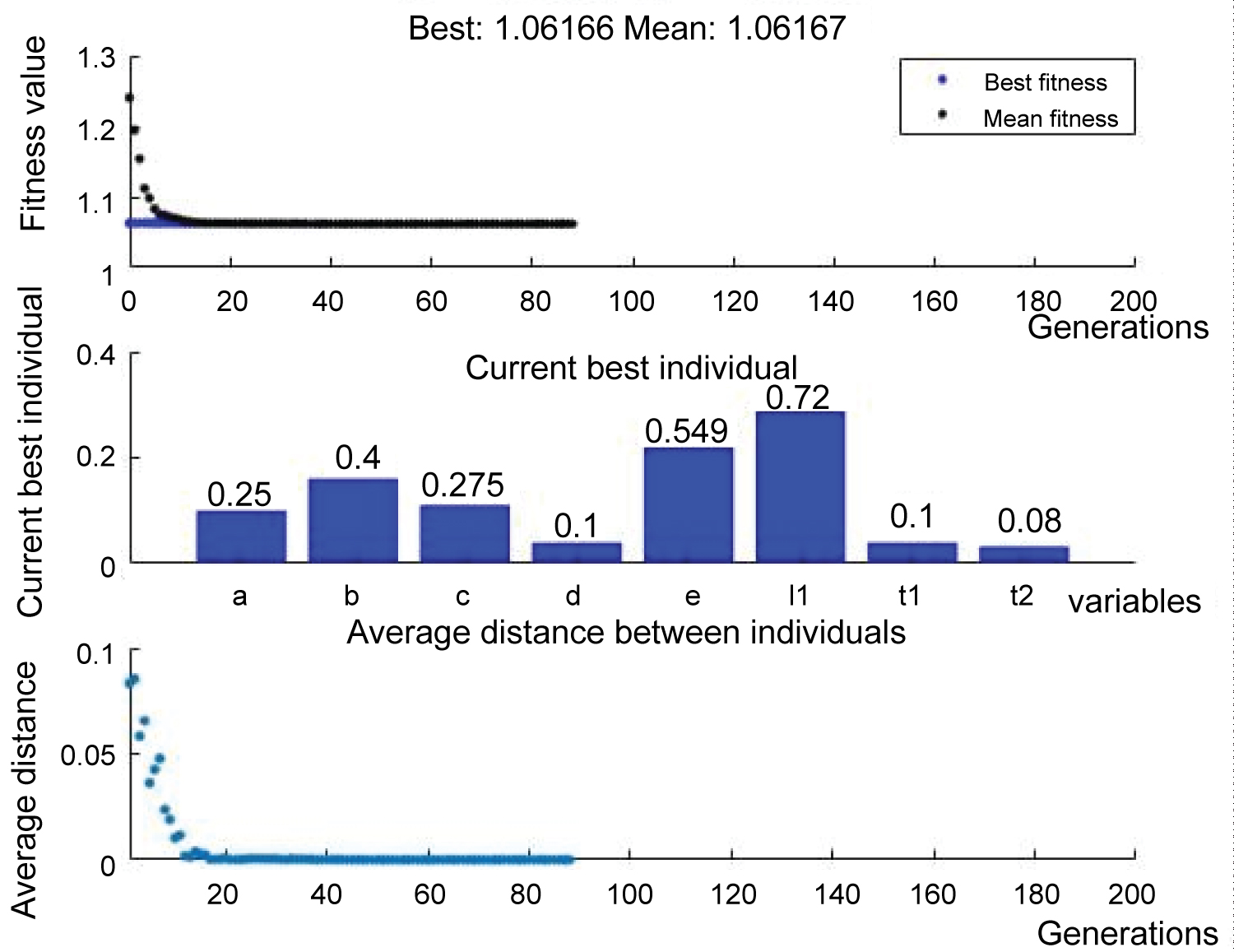
When the number of iterations exceeds 100 times or the average weighted fitness is less than the tolerance value (10-6), the algorithm will stop evolving. The optimization result of the AGV frame is obtained, which is shown in Figure 6.
It is seen from Figure 6 that the optimal dimensions of AGV frame are: a = 0.25 m, b = 0.4 m, c = 0.275 m, d = 0.1 m, e = 0.549 m, l1 = 0.72 m, t1 = 0.1 m, and t2 = 0.08 m. After the 20th generation, the best fitness value has already converged to the average value, and the average distance of individual fitness of each generation has also approached zero. For the group of dimensional parameters, the payload on the AGV frame is FR = 3030 N, FL = 6970 N and Mmax = 1161 N•m. Since the channel steel #14a is used to construct the AGV frame, the maximum bending stress is = 144.5 MPa according to Eq.(3).
Statics Analysis
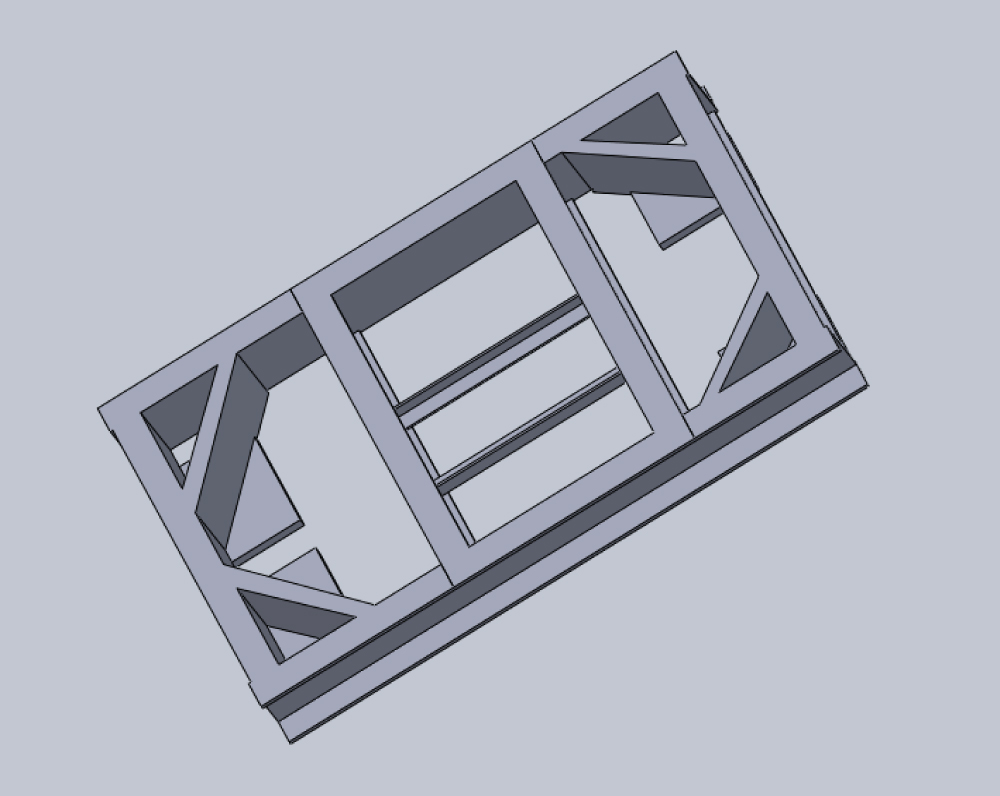
The preliminary model of the AGV frame is designed empirically by using the channel steel 14a, as shown in Figure 7. This model is then improved by the GA-based structure optimization, as shown in Figure 8. The parameter comparison of the two models is listed in Table 4. It is seen that the mass and the moment of inertia of the AGV frame are reduced significantly on the same condition of the frame strength, by means of the GA-based size optimization. It improves the dynamic response performance of the heavy-duty AGV. Furthermore, the size optimization also decreases the friction resistance of the AGV when it moves, consequently raising the efficiency of energy utilization.
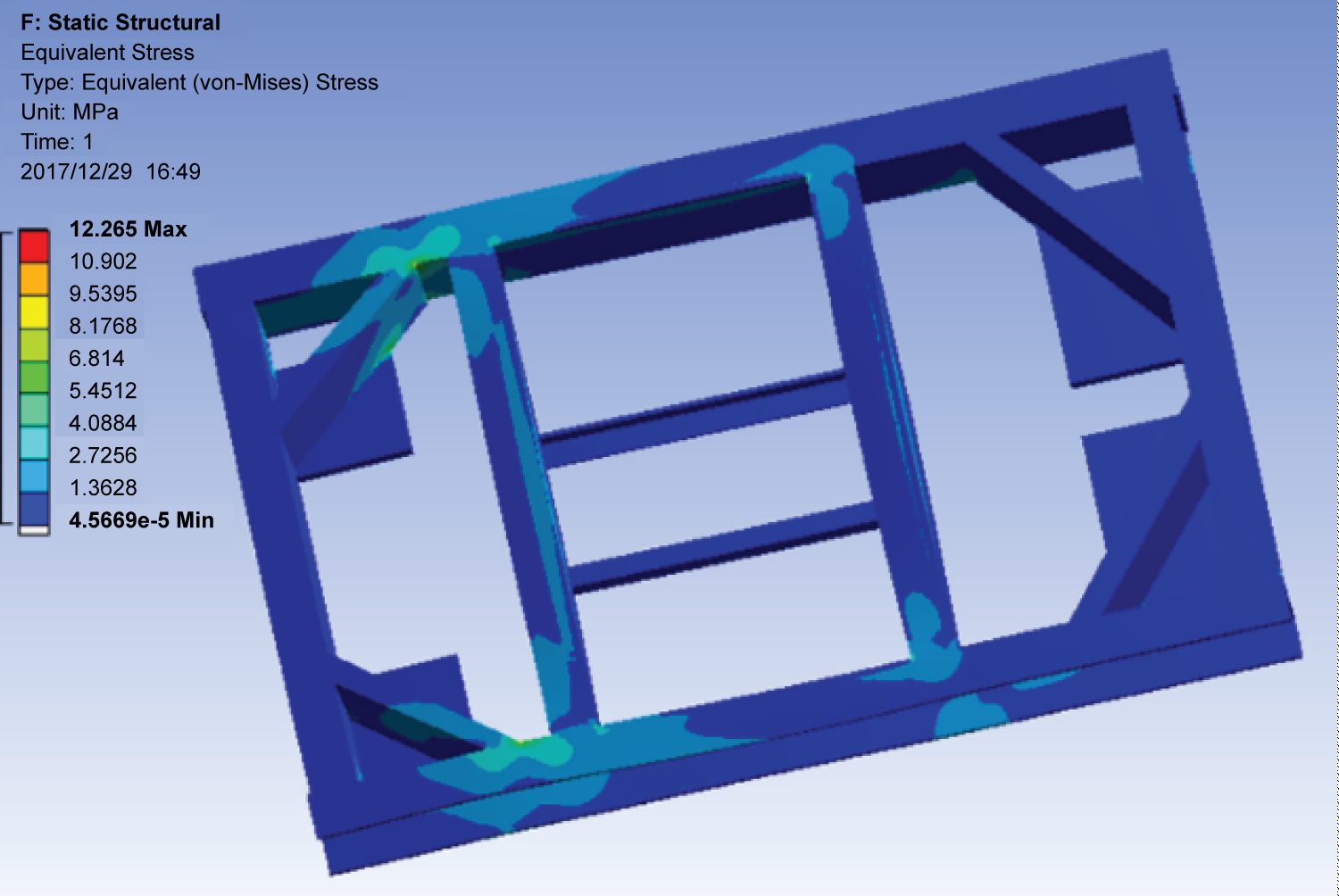
Then, the ANSYS software is used to analyze the static force state of the AGV frame and then to check its strength and stiffness. The analysis process includes selecting the frame material, importing the three-dimension model, constructing the unit and partitioning the grid, defining the loads and constraints, solving the problem and displaying the result. The cloud map of the maximum deformation and displacement of the AGV frame is drawn in Figure 9. It shows that the maximum displacement is 0.15 mm, occurring at the vicinity of the bearing plates of caster wheels. The cloud map of the maximum equivalent stress is shown in Figure 10. The maximum stress of the AGV frame occurs at the junction of the supporting frame and the bearing beam, which is 12.265 MPa, less than the allowable stress. The stress on the area nearby the bearing plates of driving wheels is also relatively high. The simulation results of the maximum deformation, displacement, and equivalent stress conform to the foregoing theoretical analysis.
Conclusions
The mechanical and geometric constraints are firstly defined for the structure optimization of a 2-ton heavy-duty AGV. Secondly, the multi-objective optimization function is formulated for the structure size, and then the optimal solution is solved by means of the genetic algorithm. Thirdly, the design scheme of the AGV frame is refined according to the optimized structure-size parameters, which improves the dynamic response performance and the efficiency of energy utilization of the heavy-duty AGV. Finally, the stiffness and strength of the frame are verified by means of the ANSYS software.
Acknowledgments
This research work is supported by the National Natural Science Foundation of China (61105114), the China Postdoctoral Science Foundation (2015M580421), the Key Technology R&D Program of Jiangsu Province of China (BE2014137), the Fundamental Research Funds for the Central Universities of China (NS2016050) and the Foundation of Graduate Innovation Center in NUAA (KFJJ20180513).