
International Journal of Robotic Engineering
(ISSN: 2631-5106)
Volume 5, Issue 2
Research Article
DOI: 10.35840/2631-5106/4128
A Two-Link Robot Manipulator: Simulation and Control Design
Mahboub Baccouch1* and Stephen Dodds2
Table of Content
Figures

Figure 1: A simplified model of a two-link....
A simplified model of a two-link planar robot manipulator.
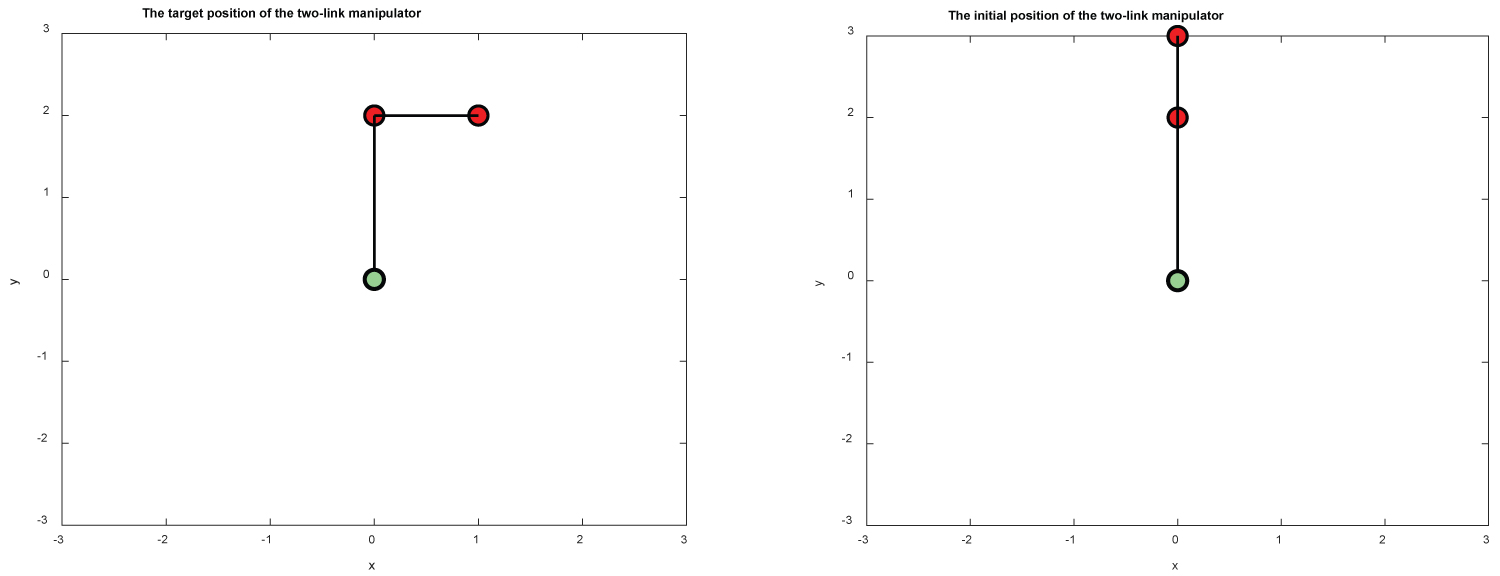
Figure 2: The initial positions (left) and the.....
The initial positions (left) and the final position (right) of M1 and M2 for example 1.
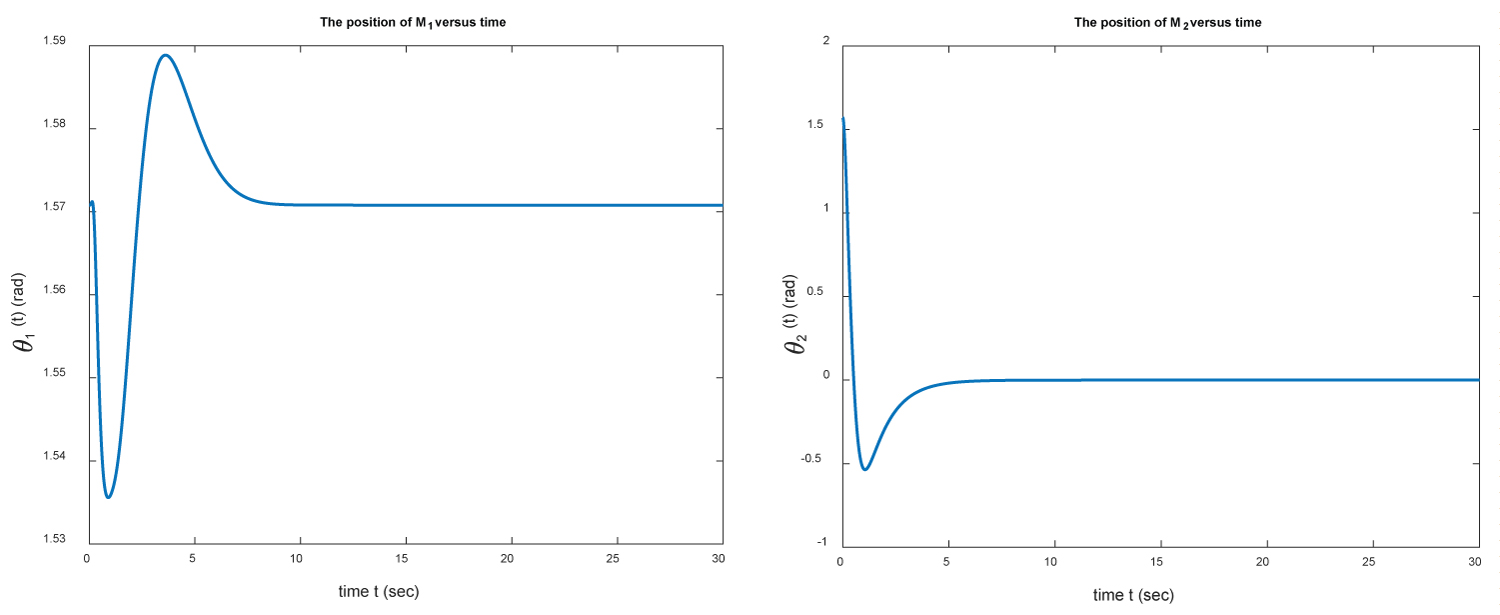
Figure 3: The positions of M1 (left) and M2....
The positions of M1 (left) and M2 (right) versus time for example 1.
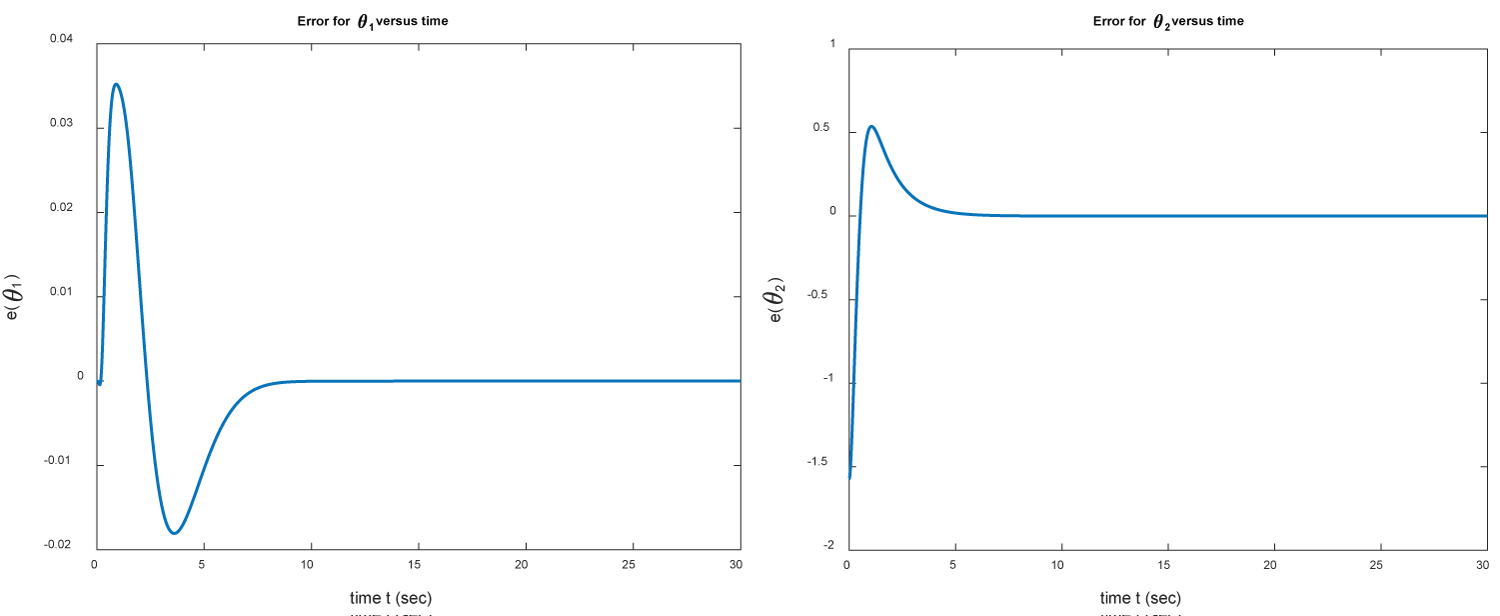
Figure 4: The errors e(θ1) = θ1(t) - θ1f and....
The errors e(θ1) = θ1(t) - θ1f and e(θ2) = θ2(t) - θ2f versus time for example 1.
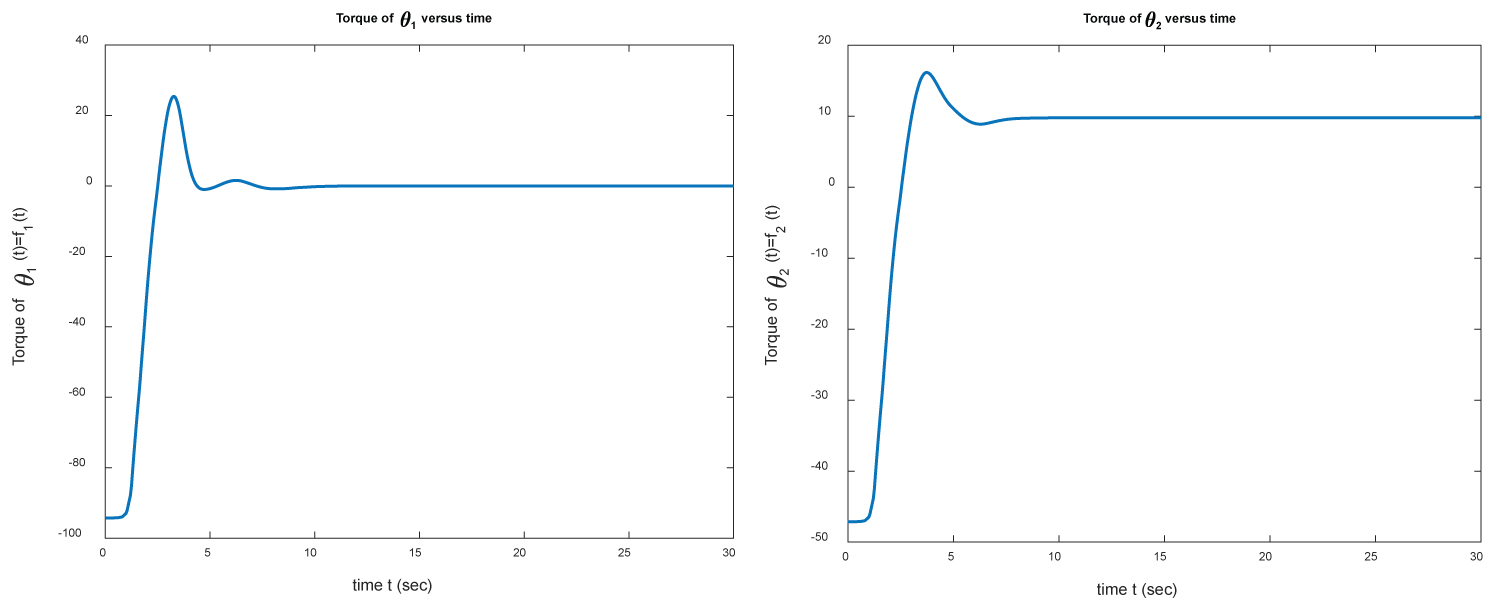
Figure 5: The torques of θ1 (left) and θ2 (right)....
The torques of θ1 (left) and θ2 (right) versus time for example 1.
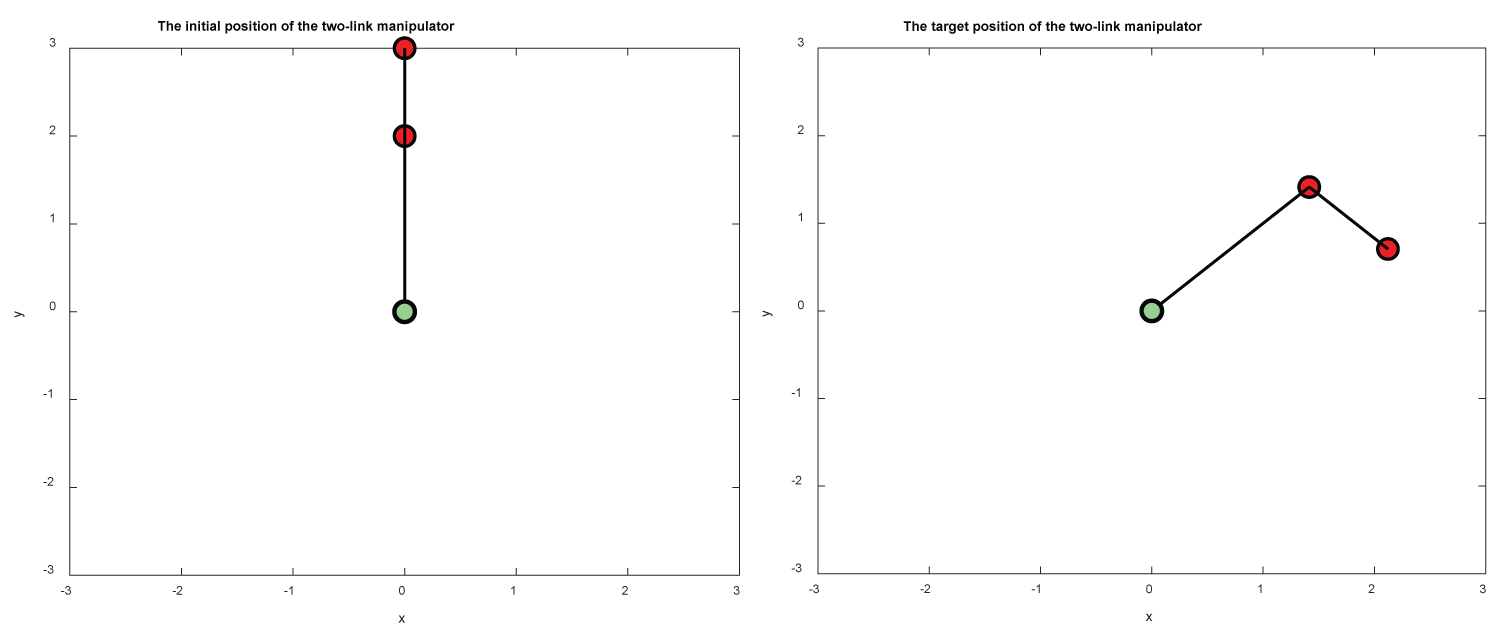
Figure 6: The initial positions (left) and the final....
The initial positions (left) and the final position (right) of M1 and M2 for example 2.
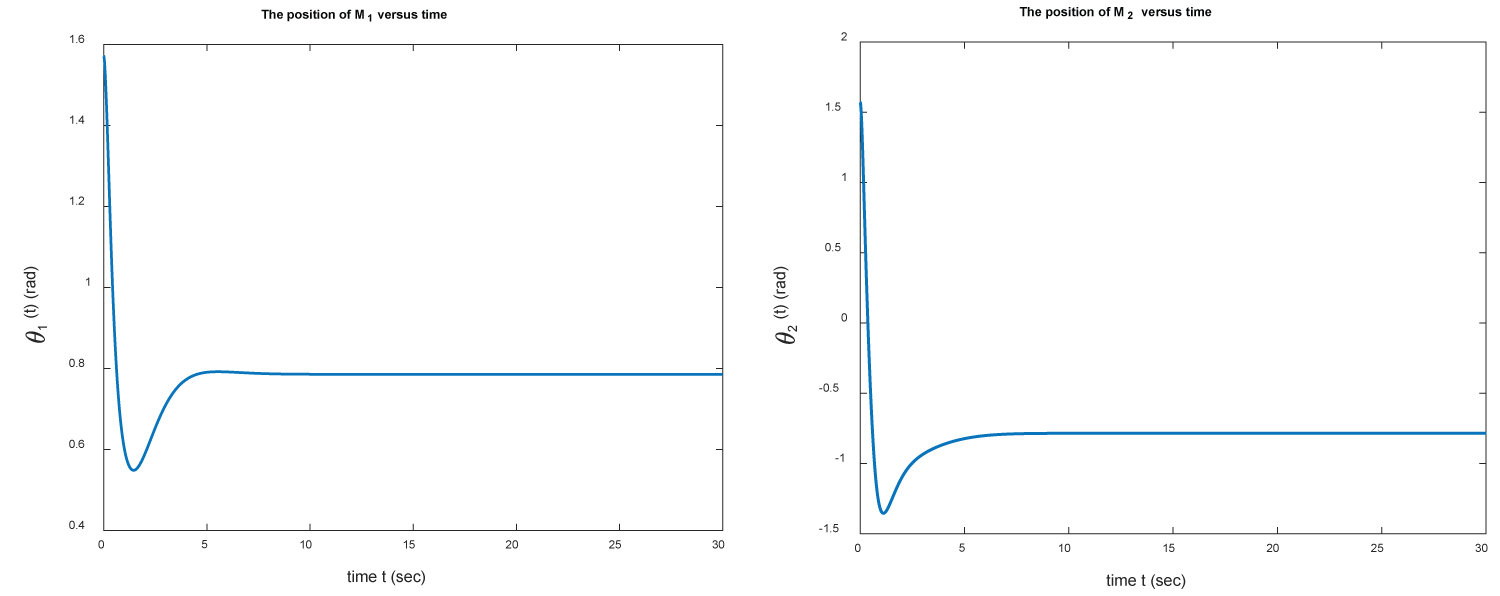
Figure 7: The positions of M1 (left) and M2...
The positions of M1 (left) and M2 (right) versus time for example 2.
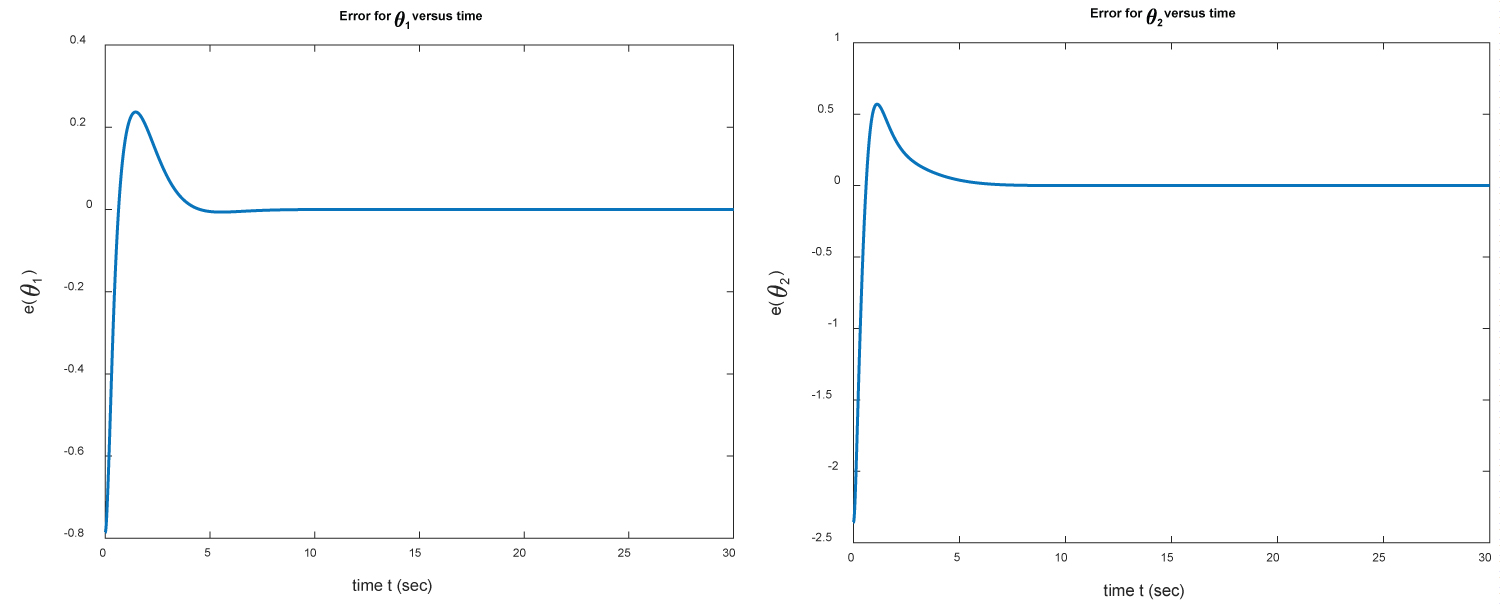
Figure 8: The errors e(θ1) = θ1(t) - θ1f and...
The errors e(θ1) = θ1(t) - θ1f and e(θ2) = θ2(t) - θ2f versus time for example 2.
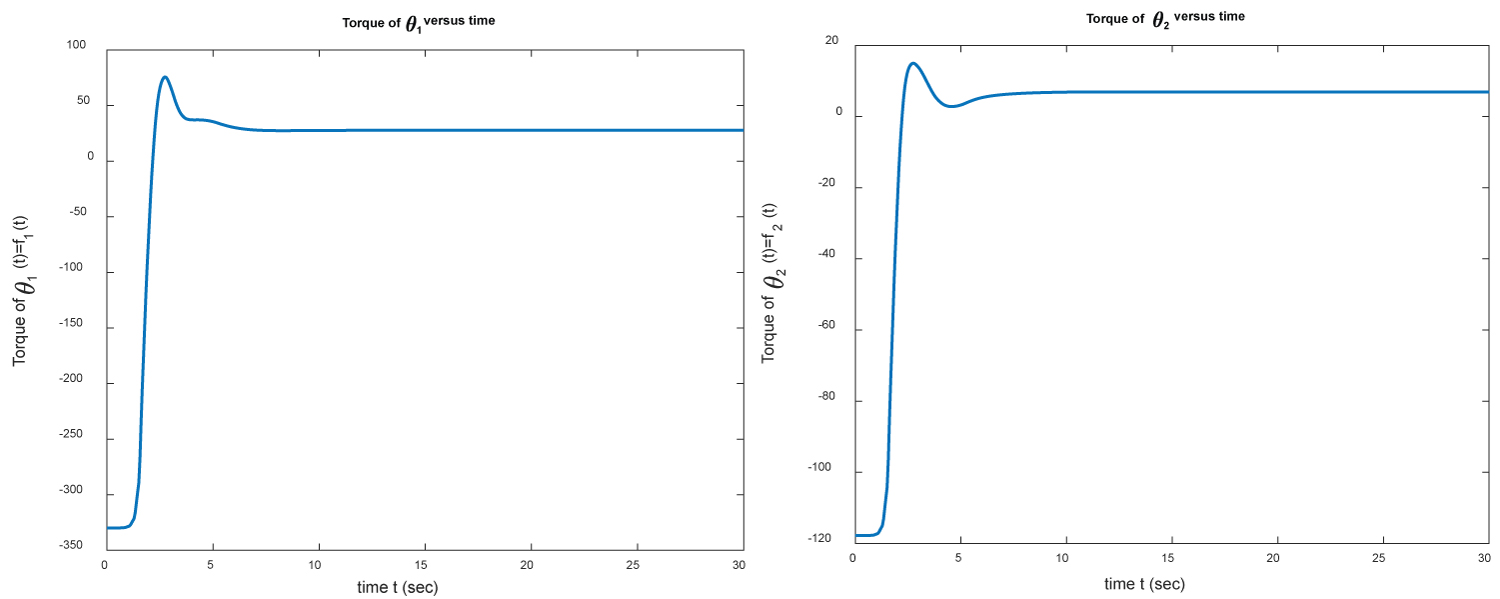
Figure 9: The torques of θ1 (left) and θ2 (right)...
The torques of θ1 (left) and θ2 (right) versus time for example 2.
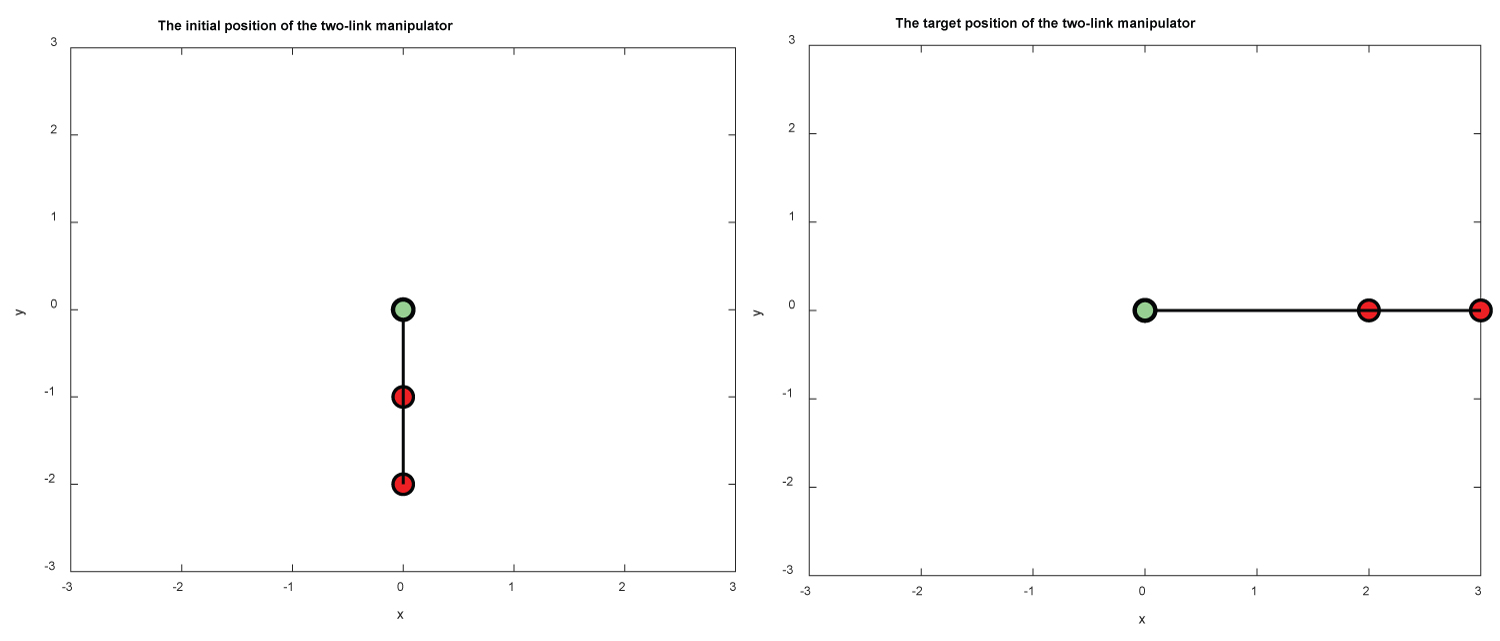
Figure 10: The initial positions (left) and the final position...
The initial positions (left) and the final position (right) of M1 and M2 for example 3.
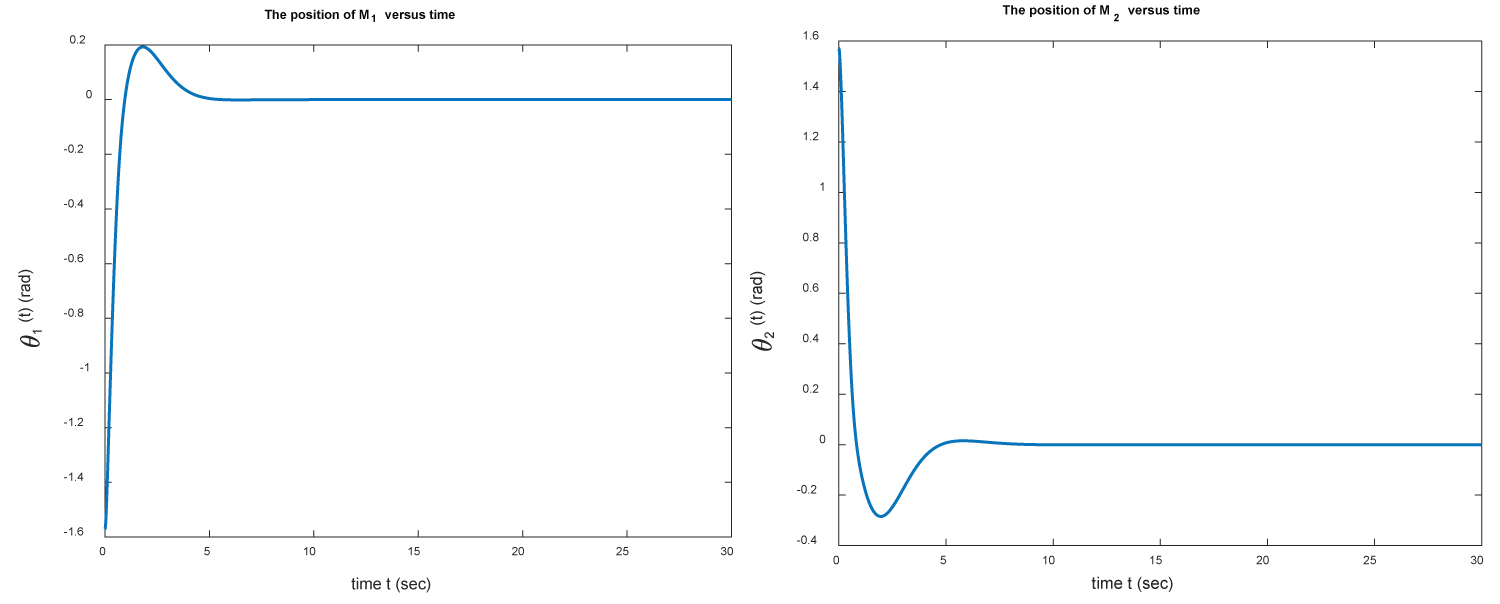
Figure 11: The positions of M1 (left) and M2 (right)...
The positions of M1 (left) and M2 (right) versus time for example 3.
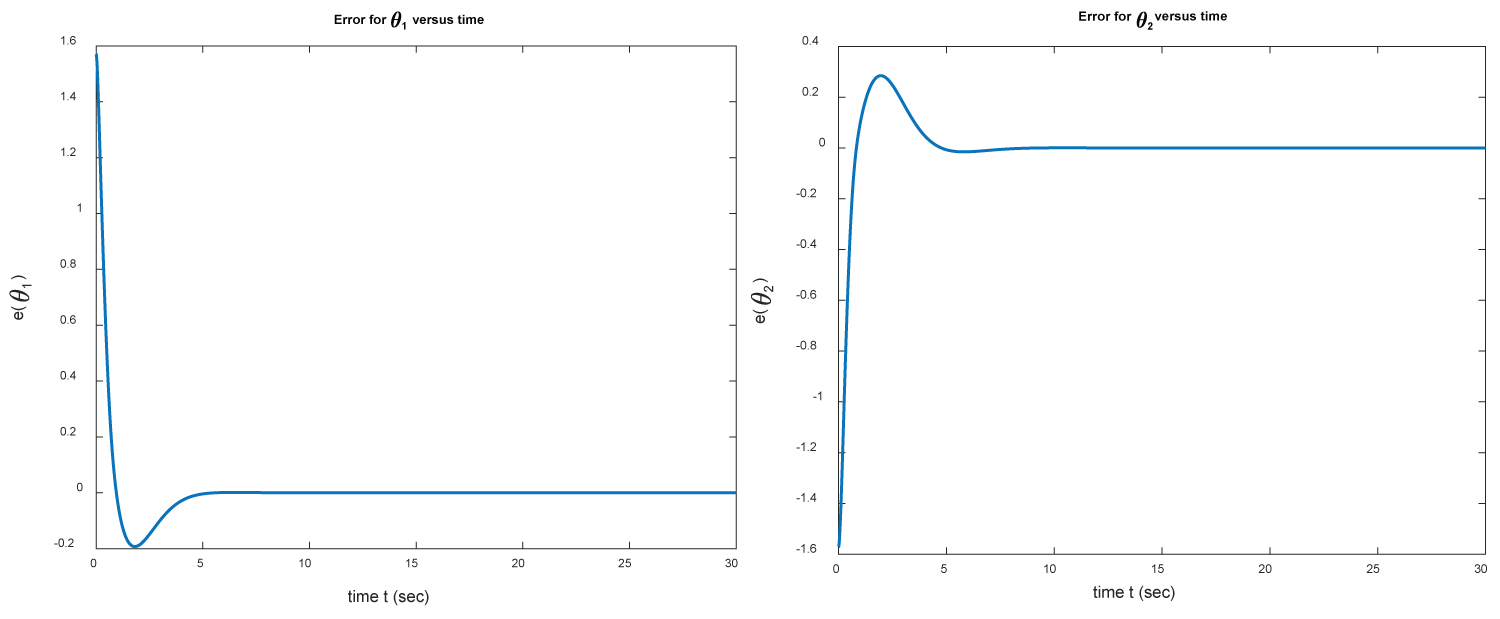
Figure 12: The errors e(θ1) = θ1(t) - θ1f and...
The errors e(θ1) = θ1(t) - θ1f and e(θ2) = θ2(t) - θ2f versus time for example 3.
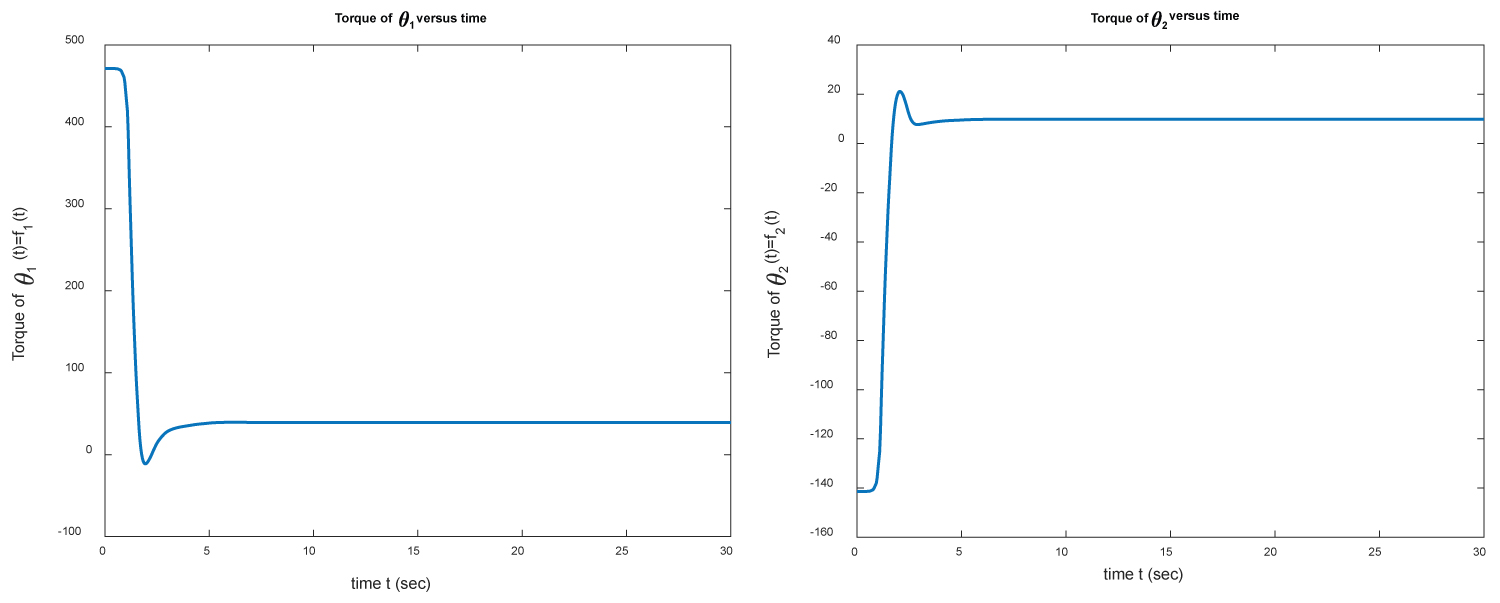
Figure 13: The torques of θ1 (left) and θ2 (right)....
The torques of θ1 (left) and θ2 (right) versus time for example 3.
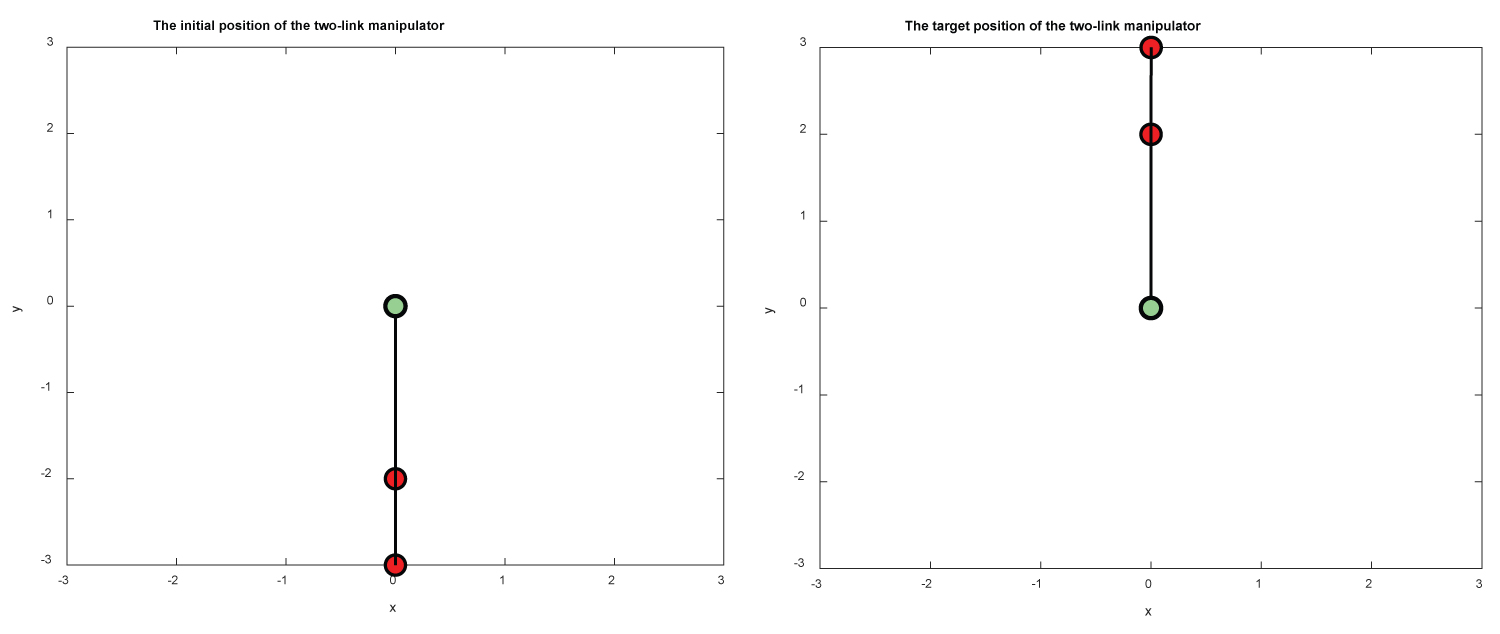
Figure 14: The initial positions (left) and the final...
The initial positions (left) and the final position (right) of M1 and M2 for example 4.

Figure 15: The positions of M1 (left) and M2....
The positions of M1 (left) and M2 (right) versus time for example 4.
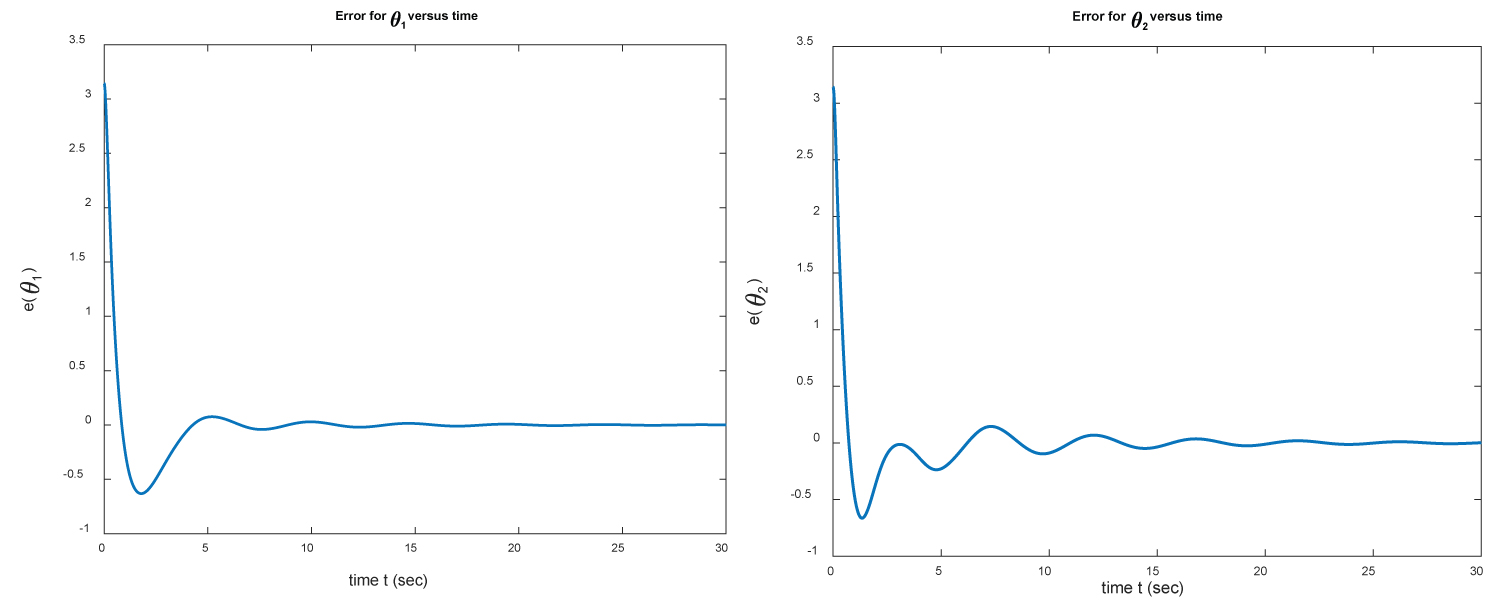
Figure 16: The errors e(θ1) = θ1(t) - θ1f and....
The errors e(θ1) = θ1(t) - θ1f and e(θ2) = θ2(t) - θ2f versus time for example 4.
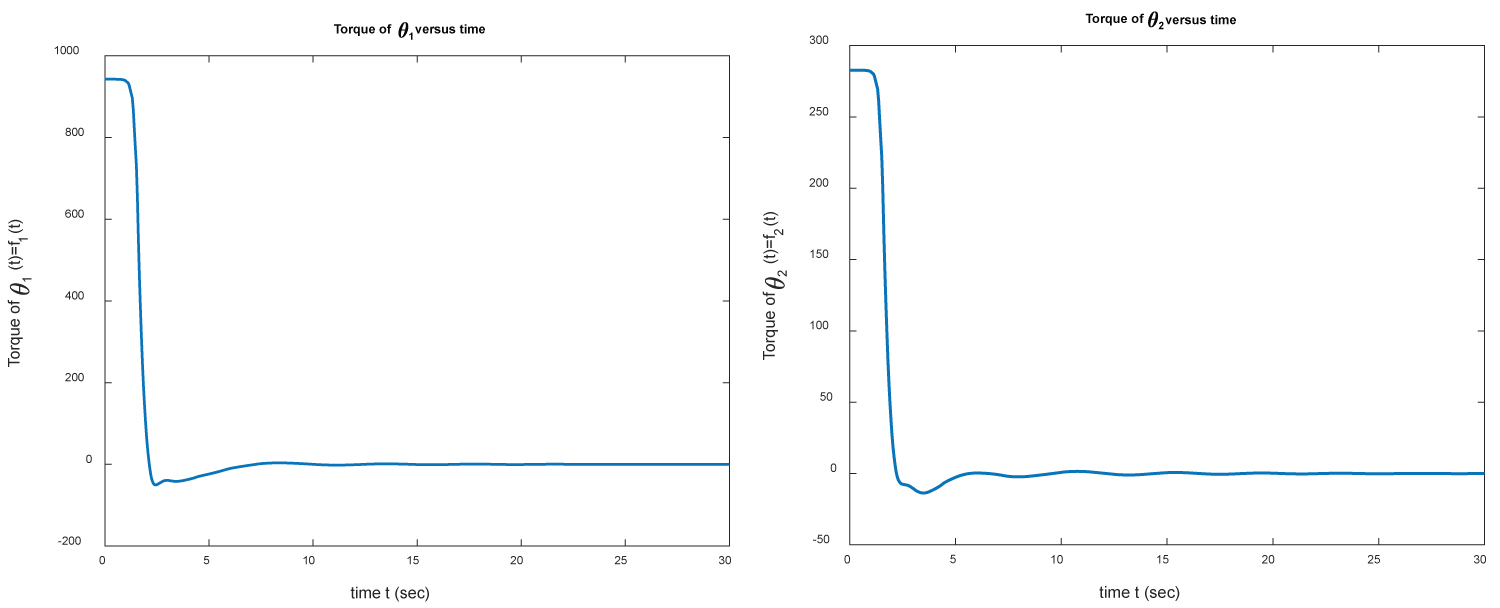
Figure 17: The torques of θ1 (left) and θ2...
The torques of θ1 (left) and θ2 (right) versus time for example 4.
References
- RM Murray, Z Li, SS Sastry (1994) A mathematical introduction to robotic manipulation. CRC press.
- RL Burden, JD Faires, AM Burden (2016) Numerical analysis. Cengage Learning, Boston, MA.
- JYS Luh (1983) Conventional controller design for industrial robots a tutorial. IEEE Transactions on Systems, Man, and Cybernetics SMC-13: 298-316.
- J Shah, S Rattan, B Nakra (2015) Dynamic analysis of two link robot manipulator for control design using computed torque control. International Journal of Research in Computer Applications and Robotics 3: 52-59.
- G Nandy, B Chatterjee, A Mukherjee (2018) Dynamic analysis of two-link robot manipulator for control design. Advances in Communication, Devices and Networking, Springer, 767-775.
- JS Kumar, EK Amutha (2014) Control and tracking of robotic manipulator using PID controller and hardware in loop simulation. International Conference on Communication and Network Technologies, IEEE.
- A Mohammed, A Eltayeb (2018) Dynamics and control of a two-link manipulator using PID and sliding mode control. International Conference on Computer, Control, Electrical, and Electronics Engineering (ICC- CEEE), IEEE.
- NK Chaturvedi, L Prasad (2018) A comparison of computed torque control and sliding mode control for a three link srobot manipulator. International Conference on Computing, Power and Communication Technologies (GUCON), IEEE.
- J Romero, L Diago, J Shinoda, I Hagiwara (2015) Evaluation of brain models to control a robotic origami arm using holographic neural networks. International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 57137.
- DM Wolpert, RC Miall, M Kawato (1998) Internal models in the cerebellum. Trends in cognitive sciences 2: 338-347.
- CH Edwards, DE Penney, DT Calvis (2016) Differential equations and boundary value problems. Pearson Education Limited.
Author Details
Mahboub Baccouch1* and Stephen Dodds2
1Professor, Department of Mathematics, University of Nebraska at Omaha, USA
2CEO, JUUK CO, Austin, USA
Corresponding author
Mahboub Baccouch, Professor, Department of Mathematics, University of Nebraska at Omaha, USA, Tel: 402-554-4016, Fax: 402-554-2975.
Accepted: December 08, 2020 | Published Online: December 10, 2020
Citation: Baccouch M, Dodds S (2020) A Two-Link Robot Manipulator: Simulation and Control Design. Int J Robot Eng 5:028
Copyright: © 2020 Baccouch M, et al. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this paper, we design a robust, fast, and practical proportional-integral-derivative (PID) controller for the classical double pendulum system. We first derive the equations of motion for the two-link robot manipulator using the Lagrangian approach. These equations are described by nonlinear system of ordinary differential equations. Because closed form solutions of the equations of motion are not available, we use the classical fourth-order Runge-Kutta method to approximate the solution of the initial-value problem. Because of the nonlinear behavior, it is a challenging task to control the motion of the two-link robot manipulator at accurate position defined by the user. For this, we focus mainly on control of the robot manipulator to get the desired position using the computed torque control method. After deriving the equation of motion, control simulation is represented using MATLAB. Several computer simulations are used to verify the performance of the controller. In particular, we present a PID controller to simulate how we would balance the two-links on a moving robot to any specific angle including upside-down.
Keywords
Two-link robot manipulator, Robotics, PID controller, Dynamic control, Simulation
Introduction
Robotic manipulators are a major component in the manufacturing industry. They are used for many reasons including speed, accuracy, and repeatability. Increasingly, robotic manipulators are finding their way into our everyday life. In fact in almost every product we encounter, a robotic manipulator has played a part in its production. In robotics, one of the most difficult tasks is to perform a precise and fast movement of a robotic arm. In this paper, one control model is proposed to solve this problem.
The double pendulum system is a common and typical model to investigate nonlinear dynamics due to its various and complex dynamical phenomenon. The double pendulum is an example of a simple dynamical system that exhibits complex behavior, including chaos. It consists of two point masses at the end of light rods. Each mass plus rod is a regular simple pendulum. The two pendula are joined together and the system is free to oscillate in a plane. Two-link manipulators are two-degree-of-freedom robots. They are useful because they function like human arms. We can begin to understand the complex movement of human arms after defining the movement of the two-link manipulator [1]. The total potential and kinetic energies of the two-link system are defined and used to form the Lagrangian. The Euler-Lagrangian equation was used to define the torques applied to each link [2]. A proportional-integral-derivative (PID) controller is implemented to simulate the behavior of the system when torques are applied [3]. The PID controllers are the most common used controllers, due to their easy implementation and versatility. PID controllers remain the standard for industry and research given their flexibility and ease of use in both simulation and hardware systems [4-6].
Due to the nonlinear nature of the two-link manipulator, specialized control systems are often required to maintain a position or perform a task [7]. Researchers have found success using Sliding Mode Control compared to PID [8]. Others have used Artificial Neural Networks and Holographic Neural Networks as part of their PID feedback loop to perform the task of folding paper [9,10]. The proposed solution uses the command ode45 in MATLAB to solve for the angle of each link relative to the positive X-axis. PID control is developed and considered to show how you can force the system to specific angles. We also show graphical results of the system after the PID control is applied.
In this paper, we propose a PID controller for a double pendulum system. We derive the equations of motion for a two-link robot manipulator based on Lagrangian Formulation. The equation of motion for two link robot is a nonlinear differential equation. As the closed form solutions are not available we have to use numerical solution. After deriving the equation of motion, control simulation is represented using MATLAB. We expand upon the standard two-link manipulator problem, to that of an upside-down pendulum with multiple links on top of a moving object. In this case we look to implement the control system into a mobile robot called the Computer and Electronics Engineering Robot (CEEnBot).
The structure of this paper is as follows. In section 4, we derive the equations of motion for a two-link robotic manipulator using the Lagrangian method. We also describe how to obtain the numerical solution using the ode45 command defined in MATLAB to solve the system of ordinary differential equations numerically. We explain the design of the PID controller for the double pendulum system in section 5. In section 6, we present several numerical examples to test the PID controller. Finally, we provide some concluding remarks in section 7.
Dynamics of Two-Link Manipulators
Double pendula are an example of a simple physical system which can exhibit chaotic behavior. Understanding the two-link manipulator is key to learning robotic manipulators as a whole. We consider the two-link robotic manipulator which is a classic example studied in introductory robotics courses. The physical system is shown in Figure 1.
The system consists of two masses connected by weightless bars. The bars have lengths L1 and L2. The masses are denoted by M1 and M2, respectively. Let θ1 and θ2 denote the angles in which the first bar rotates about the origin and the second bar rotates about the endpoint of the first bar, respectively. This system has two degrees of freedom θ1 and θ2.
The first step in deriving the equations of motion using the Lagrangian approach is to find the kinetic energy KE and the potential energy PE of the system.
The equations for the x-position and the y-position of M1 are given by
Similarly, the equations for the x-position and the y-position of M2 are given by
Next, we calculate the velocities of M1 and M2 using the following formulas
where,
Here and below the dot ˙ is a derivative with respect to t, i.e., for k = 1, 2.
The kinematic energy can be calculated as follows
The equation for the kinetic energy can be written as
Substituting (4.1) - (4.2) into (4.5), we get
which can be simplified as
In order to calculate the Lagrangian, the potential energy PE has to be calculated. By definition the potential energy of the system due to gravity of the ith pendulum is
which hi is the height of the center of mass of the ith pendulum, g is the acceleration due to gravity constant, and Mi is the mass of the ith pendulum. Therefore, the total potential energy for both pendulums can be given by
Next, by Lagrange Dynamics, we form the Lagrangian which is defined as
Substituting the expressions for the kinetic energy (4.6) and potential energy (4.8) in for KE and
PE we get
The Euler-Lagrange equation is given by the equation
where is the torque applied to the ith link.
The derivations for the Lagrangian equation and Euler-Lagrange equation can be found in [1]. We were more concerned with using the formulas in this problem rather than going into too much in detail for these derivations.
From (4.10), we have
and
Similarly, we compute
and
Therefore, (4.11) gives the following two nonlinear equations of motion which are second-order system of ordinary differential equations
or equivalently,
where, .
Solving for and , we get the normal form of the dynamics equations
where,
In order to solve for the angles and , we need to solve the above second-order system of ordinary differential equations. To do this, we first reduce the system into an equivalent system of first-order ordinary differential equations.
Let us introduce four new variables
After differentiating, we have
Thus, we obtain a system of first-order nonlinear differential equations of the form
Where and with
The initial conditions are given by
Where,
The system (4.16a) subject to the initial condition (4.16b) can be solved for the unknown vector U, using, for example, the ode45 command defined in MATLAB to solve the system of ordinary differential equations numerically. This command is based on the fourth-order Runge-Kutta method. For more details consult [2,11].
PID Controller Design
Robotic manipulators are generally difficult to control. In particular, it is a challenging task to stabilize a robot manipulator at a fixed, accurate position. In this section, we focus mainly on control of the robot manipulator to get the desired position using computed torque control method. After deriving the equation of motion, control simulation is represented using MATLAB.
We define control as the ability to hold the system of two links in a particular position on the xy-plane. Having control gives us the ability to hold each link at a particular angle with respect to the positive x-axis. The proportional-integral-derivative (PID) controller is a common control algorithm. The "P" in PID stands for Proportional control, the "I" stands for Integral control, and the "D" stands for Derivative control. This algorithm works by defining an error variable Verror = Vset - Vsensor that takes the position we want to go (Vset) minus the position we are actually at (Vsensor). We get the proportional part of the PID control by taking a constant defined as KP and multiplying it by the error. The I comes from taking a constant KI and multiplying it by the integral of the error with respect to time. Derivative control is defined as a constant KD multiplied by the derivative of the error with respect to time. Many industrial processes are controlled using PID controllers. Below is a table describing PID control Table 1.
The equations of motion (4.12) can be written compactly as
where,
We can solve for some theoretical values of forces given certain initial inputs. Solving for we get
Where
Thus, we decoupled the system to have the new input
However, the physical torque inputs to the system arė
Let us denote the error signals by
Where the target positions of M1 and M2 are given by the angles and , respectively.
We assume that the system has initial positions
A common technique for controlling a system with input is to use the following general structure of PID controller
In our situation, the technique for controlling the double pendulum system with inputs f1 and f2
is to employ two independent controllers, one for each link, as follows
Where and are given constants.
The complete system of equations with control is then
Where
We would like to emphasize that the actual physical torques are
To implement the PID controller, we introduce the following new states
Differentiating with respect to t gives
The complete equations are
To discretize the above system of differential equations in time, we transform them into a system of first-order ordinary differential equations. To do this, we define six new variables as follows
After differentiating, we have
,
were and are expressed in terms of uk, k = 1-6, as
and .
A simple calculation shows that
Thus, we obtain a system of first-order nonlinear differential equations of the form
Where and with
The initial conditions are given by
Where,
The system (3.10) can be solved for the unknown vector U, using, for example, the ode45 command defined in MATLAB to solve the system of ordinary differential equations numerically. This command is based on the fourth-order Runge-Kutta method. For more details consult [2,11].
Once we solve for, we obtain to torques using
or equivalently,
Simulations Results
The PID controller helps get the outputs, which are the final positions of M1 and M2 determined by the angles and , where we want it, in a short time, with minimal overshoot, and with little error. This will be demonstrated using the following examples.
Example 1. We consider the simplified model of a two-link manipulator shown in Figure 1. In this experiment, we take the following parameters
The target positions (final positions) are .
The initial positions, initial angle velocities, and initial states are, respectively, taken as
The PID parameters for and , are taken as
KP1 = 30, KD1 = 15, KI1 = 20,
KP2 = 30, KD2 = 10, KI2 = 20.
In Figure 2, we show the initial and target positions of the two-link manipulator. Next, we plot the positions and of M1 and M2 versus time over the interval [0,30] in Figure 3.
In Figure 4 we present the difference between where we want to go and where we are actually at i.e.,
Where θ1f and θ2f are the target positions and θ1(t) and θ2(t) are the numerical approximations obtained by solving the system of ODEs. These results indicate that the PID controller gets the final positions of M1 and M2 determined by the angles θ1 and θ2, in a short time (almost 7 seconds) with very small error.
Finally, in Figure 5, we show the torques f1 and f2 versus time
Note that the actual joints torques are
Example 2. We repeat the previous example with all parameters kept unchanged except for the final positions where we use
The initial and target positions of M1 and M2 are shown in Figure 6. We present the positions θ1 and θ2 of M1 and M2 versus time in Figure 7. In Figure 8 we present the errors between the estimate positions and target positions. Finally, in Figure 9, we show the torques versus time. Once again, these results demonstrate that the PID controller gets the final positions of M1 and M2 in a short time (approximately 5 seconds).
Example 3. In this example, we consider the two-link manipulator shown in Figure 1 with the following parameters
The initial positions, initial angle velocities, and initial states are, respectively, taken as
The target positions (final positions) are .
The PID parameters for θ1 and θ2, are taken as
KP1 = 30, KD1 = 15, KI1 = 20,
KP2 = 30, KD2 = 20, KI2 = 20.
The initial and target positions of the two-link manipulator are shown in Figure 10. In Figure 11 we present the positions θ1 and θ2 of M1 and M2 versus time over the interval [0,30]. In Figure 12 we present the errors e(θ1) and e(θ2) between the target position and the estimate position found numerically. Again it takes only few seconds to get the target position. We would like to mention that the PID controller gets the final positions of M1 and M2 in a short time (approximately in seconds) with very small error. Finally, we show the torques f1 and f2 versus time in Figure 13.
Example 4. Finally, we consider the two-link manipulator shown in Figure 1 with the following parameters
The initial positions, initial angle velocities, and initial states are, respectively, taken as
The target positions (final positions) are .
The PID parameters for θ1 and θ2, are taken as
KP1 = 30, KD1 = 15, KI1 = 20,
KP2 = 30, KD2 = 20, KI2 = 20.
The initial and target positions of the two-link manipulator are shown in Figure 14. The positions θ1 and θ2 of M1 and M2 versus time over the interval [0, 30] are shown in Figure 15. In Figure 16 we plot the errors e(θ1) and e(θ2) between the target position and the approximate position found numerically. As in the previous examples, it takes only few seconds to get the target position. Finally, we present the torques f1 and f2 versus time in Figure 17.
Conclusion
In this paper, a two-link robotic manipulator was studied and its dynamics were modeled using Lagrange mechanics. First, we derived the dynamical equation of the two-link robot manipulators using Euler-Lagrange method and then a simple and efficient control scheme was developed. More specifically, a robust Proportional-Integral-Derivative (PID) controller was introduced to control the motion of the robot at a specific position. In particular, we described how a PID controller can be used to keep the links in a desired position. The efficiency of the PID controller is verified by the simulation results. The proposed research can be used to design and code control algorithms for a mobile robot. These algorithms allow us to balance upside-down pendulums on a mobile robot. There could be many solutions for coding this PID control depending on what sensors are used to find the angles of the links. In this study, we considered a planar robot having rotational joints. However, the PID controller presented in this paper can be extended for robots having prismatic joints. In the future, we are planning to consider complex joints such as a ball and socket joint.
Acknowledgement
This project was funded by the Kerrigan Research Minigrant Program. The authors would like to thank the anonymous reviewer for the valuable comments and suggestions which improved the quality of the paper.
Conflict of Interest
The Authors declare that there is no conflict of interest.

