International Journal of Robotic Engineering
(ISSN: 2631-5106)
Volume 5, Issue 2
Research Article
DOI: 10.35840/2631-5106/4129
Finite-Time Consensus of Nonlinear Multi-Agent Systems in the Presence of Unknown Communication Time Delays and Partial Access to Neighboring Agents Signals
Maryam Sharifi*
Table of Content
Figures
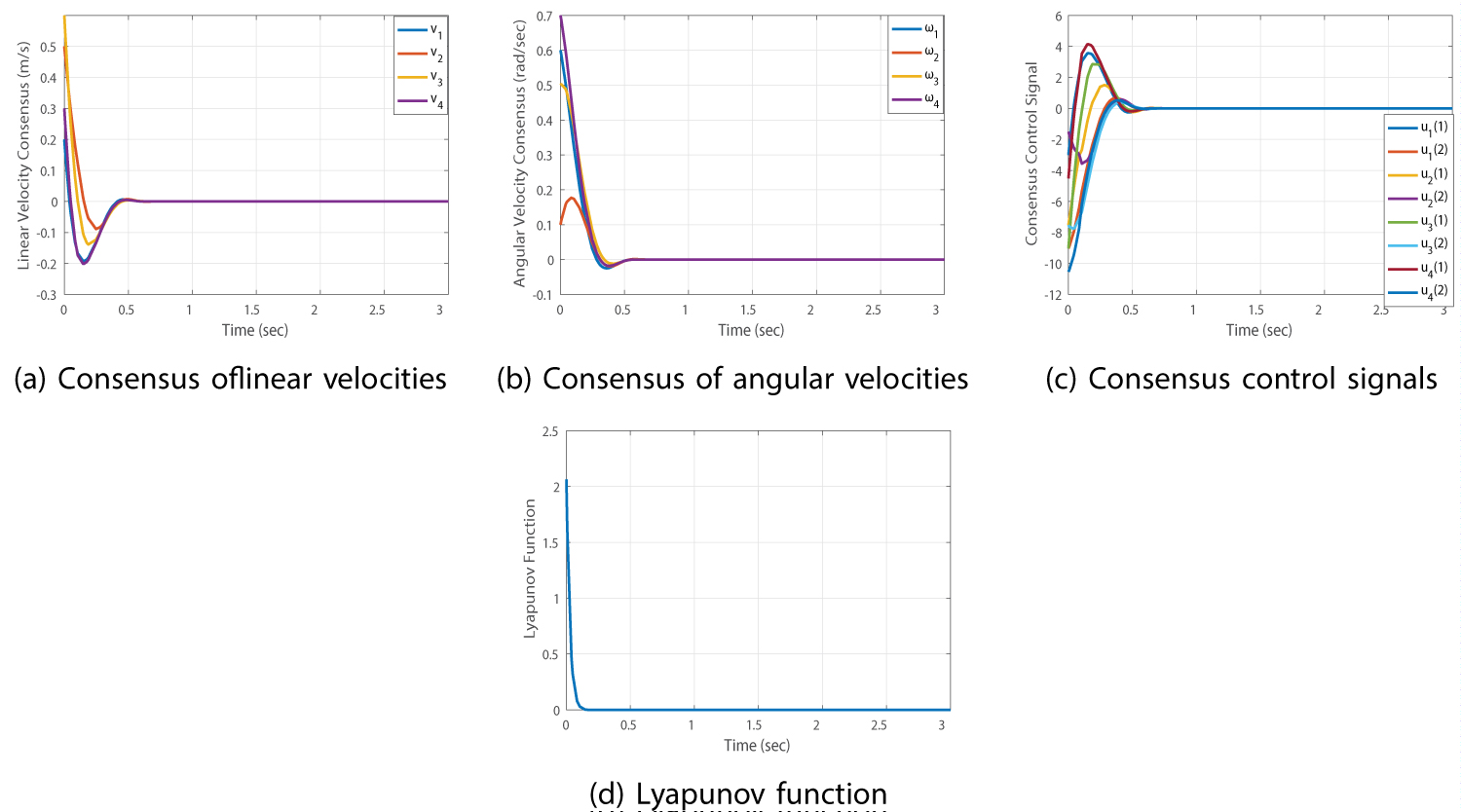
Figure 3: Finite-time consensus with full access....
Finite-time consensus with full access to neighbor signals: a) Consensus of linear velocities; b) Consensus of angular velocities; c) Consensus control signals; d) Lyapunov function.
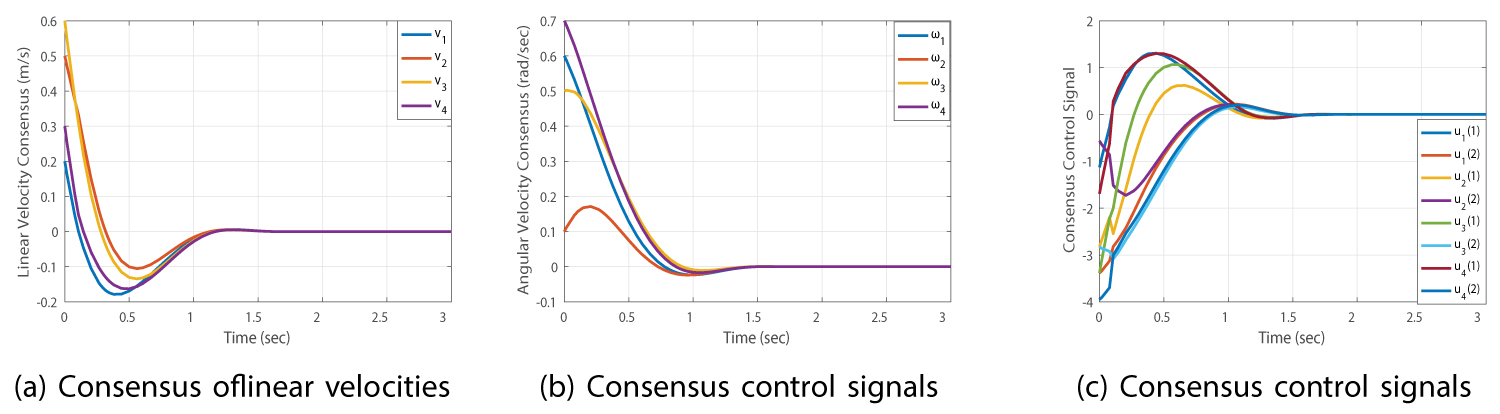
Figure 4: Finite-time consensus with partial....
Finite-time consensus with partial access to neighbor signals: a) Consensus of linear velocities; b) Consensus control signals; c) Consensus control signals.
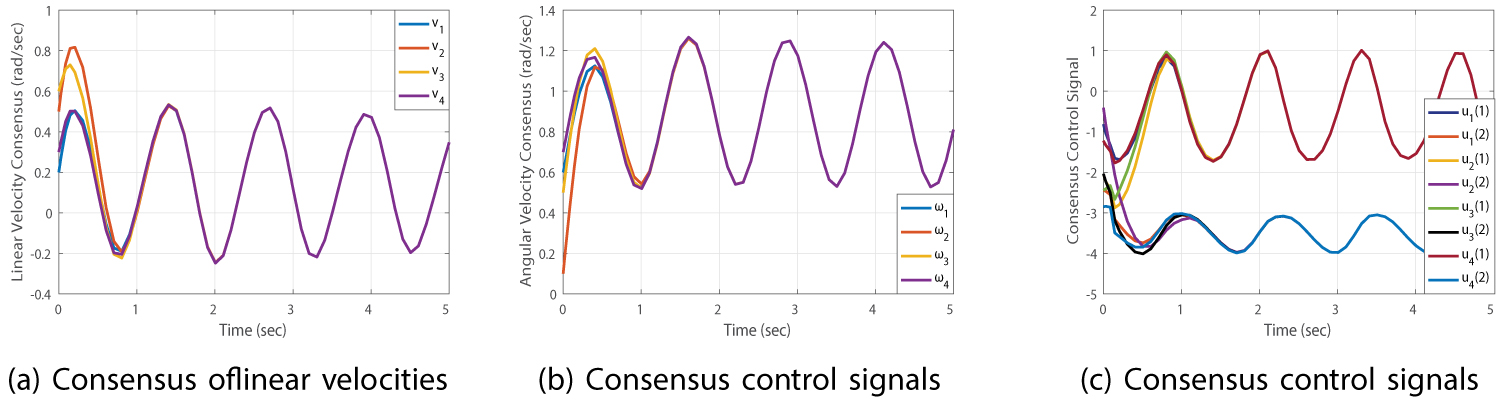
Figure 5: Finite-time dynamic consensus....
Finite-time dynamic consensus: a) Consensus of linear velocities; b) Consensus control signals; c) Consensus control signals.
References
- H Chehardoli (2020) Decentralized second-order adaptive protocol of multi-agent systems with nonlinear disturbance based on only onboard partial measurement. ISA transactions 104: 329-335.
- SP Bhat, DS Bernstein (2000) Finite-time stability of continuous autonomous systems. SIAM J Control Optim 38: 751-766.
- J Wu, W Chen, J Li (2016) Global finite-time adaptive stabilization for nonlinear systems with multiple unknown control directions. Automatica 69: 298-307.
- M Golestani, I Mohammadzaman, MJ Yazdanpanah (2016) Robust finite-time stabilization of uncertain nonlinear systems based on partial stability. Nonlinear Dynamics 85: 87-96.
- H Wang, B Chen, C Lin, Y Sun, F Wang (2017) Adaptive finite-time control for a class of uncertain high-order non-linear systems based on fuzzy approximation. IET Control Theory & Applications 11: 677-684.
- G Oliva, R Setola, CN Hadjicostis (2017) Distributed finite-time average-consensus with limited computational and storage capability. IEEE Transactions on Control of Network Systems 4: 380-391.
- Y Cao, W Ren (2014) Finite-time consensus for multi-agent networks with unknown inherent nonlinear dynamics. Automatica 50: 2648-2656.
- Y Yang, C Hua, X Guan (2014) Adaptive fuzzy finite-time coordination control for networked nonlinear bilateral teleoperation system. IEEE Transactions on Fuzzy Systems 22: 631-641.
- J Huang, C Wen, W Wang, YD Song (2015) Adaptive finite-time consensus control of a group of uncertain nonlinear mechanical systems. Automatica 51: 292-301.
- J Mei, M Jiang, Z Wu, X Wang (2015) Periodically intermittent controlling for finite-time synchronization of complex dynamical networks. Nonlinear Dynamics 79: 295-305.
- M Cai, Z Xiang (2017) Adaptive finite-time consensus tracking for multiple uncertain mechanical systems with input saturation. International Journal of Robust and Nonlinear Control 27: 1653-1676.
- Z Meng, T Yang, G Shi, DV Dimarogonas, Y Hong, et al. (2017) Targeted agreement of multiple lagrangian systems. Automatica 84: 109-116.
- A Shariati, M Tavakoli (2017) A descriptor approach to robust leader-following output consensus of uncertain multi-agent systems with delay. IEEE Transactions on Automatic Control 62: 5310-5317.
- M Lu, L Liu (2017) Consensus of linear multi-agent systems subject to communication delays and switching networks. International Journal of Robust and Nonlinear Control 27: 1379-1396.
- Z Wang, J Xu, H Zhang (2014) Consensusability of multi-agent systems with time-varying communication delay. Systems & Control Letters 65: 37-42.
- M Sharifi, HA Talebi (2017) Adaptive control strategy for a bilateral tele-surgery system interacting with active soft tissues. AUT Journal of Modeling and Simulation 49: 209-216.
- KD Nguyen, H Dankowicz (2017) Cooperative control of networked robots on a dynamic platform in the presence of communication delays. International Journal of Robust and Nonlinear Control 27: 1433-1461.
- G Zheng, H Wang (2017) Finite-time estimation for linear time-delay systems via homogeneous method. International Journal of Control 92: 1252-1263.
- M Sharifi, MJ Yazdanpanah (2020) Finite time consensus of nonlinear multi-agent systems in the presence of communication time delays. European Journal of Control 53: 10-19.
- Y Cheng, V Ugrinovskii (2016) Event-triggered leader-following tracking control for multivariable multi-agent systems. Automatica 70: 204-210.
- R Yang, Y Wang (2013) Finite-time stability analysis and H8 control for a class of nonlinear time-delay hamiltonian systems. Automatica 49: 390-401.
- X Liao, G Chen, EN Sanchez (2002) Delay-dependent exponential stability analysis of delayed neural networks: An lmi approach. Neural Networks 15: 855-866.
- C Qian, W Lin (2001) Non-lipschitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization. Systems & Control Letters 42: 185-200.
- MZ Sarikaya, E Set, H Yaldiz, N Basak (2013) Hermite-hadamard inequalities for fractional integrals and related fractional inequalities. Mathematical and Computer Modelling 57: 2403-2407.
- K Gu, J Chen, VL Kharitonov (2003) Stability of time-delay systems. Springer Science & Business Media.
- R Fierro, FL Lewis (1998) Control of a nonholonomic mobile robot using neural networks. IEEE Transactions on Neural Networks 9: 589-600.
Author Details
Maryam Sharifi*
School of Electrical and Computer Engineering, University of Tehran, Iran
Corresponding author
Maryam Sharifi, School of Electrical and Computer Engineering, University of Tehran, Tehran, Iran.
Accepted: December 09, 2020 | Published Online: December 11, 2020
Citation: Sharifi M (2020) Finite-Time Consensus of Nonlinear Multi-Agent Systems in the Presence of Unknown Communication Time Delays and Partial Access to Neighboring Agents Signals. Int J Robot Eng 5:029
Copyright: © 2020 Sharifi M. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
In this paper, finite-time consensus of a group of nonlinear multi-agent systems in the presence of communication time delays is considered. The required criteria to guarantee the delay- independent/dependent consensus are derived. The communication delays are not assumed time invariant, uniform, symmetric or even known. The only requirement is that all delays satisfy a known upper bound. The proposed strategy is appropriate for cases where an agent has a partial access to its neighbor agents signals with no need to estimate the unknown states. In the line of showing the consensus, the finite-time version of Lyapunov-Razumikhin theorem is utilized. The strategy applies to a large class of nonlinear systems. For verification of the proposed approach, simulation results on a group of mobile robot manipulators as the agents of the system are presented.
Keywords
Multi-agent systems, Finite-time consensus, Communication delay, Lyapunov-Razumikhin theorem, Delay-dependent consensus
Introduction
In the past few decades, distributed cooperative control of multi-agent systems has been extensively studied [1]. In these systems, the main objective is designing local controllers for each agent to achieve an appropriate group behavior. Among different types of group coordination such as formation, flocking, coverage, rendezvous, etc, consensus over multi-agent systems has a wide variety of applications. Moreover, a consensus scheme is often applied to other types of multi-agent system coordination. Consensus control aims to achieve an agreement among agents' states, by designing controllers using the states or outputs of their neighbors.
There are two significant challenges associated with the performance of multi-agent systems that are mainly inevitable; The presence of time-delay in the communication between agents, and the rate of consensus achievement.
Classical stability analysis approaches consider the steady-state performance of the systems and study their stability during an infinite time interval; In which convergence of the system trajectories to the equilibrium is guaranteed. However, in many practical systems such as communication networks, robotic control systems, etc, the transient performance of the system is of great importance. We seek control objectives in a finite-time interval, which is faster and more precise compared to stability in the traditional sense of Lyapunov. Consider a cooperative robotic system that fulfills several tasks ranging from approaching and grasping a given object to some more complicated and precise tasks like minimally invasive robotic surgeries. In these applications, reaching the goal in a finite-time is indispensable. Important criteria in such task performance are the convergence rate and ultimate bound of the consensus error. The strategy which brings up finite settling, error vanishing time can be beneficial; since it guarantees that the task is performed exactly as commanded. The finite-time stabilization concept originates from optimal control problems that pertain to the dynamical systems whose operation time is limited to a fixed finite-time interval [2]. Some more recent work in this field include [3-6].
The work of [7] analyzed the finite-time convergence of a nonlinear consensus algorithm for multi-agent networks with unknown inherent nonlinear dynamics. For this aim, the authors proposed a stability tool based on a generalized comparison lemma and showed that the proposed nonlinear consensus algorithm can guarantee finite-time convergence if the directed switching interaction graph forms a spanning tree at each time interval. The master-slave finite-time synchronization control problem using an adaptive-fuzzy approach was considered in [8] for the networked teleoperation systems. They developed a new nonsingular fast terminal sliding mode (NFTSM) to provide faster convergence and higher precision compared with the linear hyperplane and classic terminal-sliding mode (TSM).
In [9], distributed adaptive finite-time continuous control algorithms for leaderless consensus of nonlinear mechanical multi-agent systems under an undirected graph are suggested and transient performance in terms of convergence rates is analyzed. Authors of [10] considered finite-time synchronization between two complex dynamical networks by using periodically intermittent control. The work reported in [11] investigates the problem of finite-time consensus tracking for a class of multiple uncertain mechanical systems under switching topologies, uncertainties and input saturations. In [12], the authors studied the targeted agreement problem of a group of Lagrangian systems for fixed and switching graphs. Each system targets a convex set and the objective is to reach a coordinate agreement towards the sets.
In none of the above references, the problem of the presence of time-delays in the communication between the agents has been considered. However, in the real world, many practical systems experience time delays because of the finite speed of information processing/transmission between agents and limited channels bandwidth. It is well known that a time delay may cause undesirable dynamic behaviors such as oscillation, performance degradation, and instability in the system. Consider a networked multi-agent system in which agents communicate with each other through links that suffer from inevitable communication delays. Besides, in teleoperation systems that use communication networks for interaction among master and slave robots, time-delays are unavoidable. Since the whole stability of the system is influenced by time delays, one of the main tasks in such systems is reducing their adverse effects. Thus, it is necessary to study multi-agent systems in the presence of time delays. There are few results in the context of multi-agent systems that consider time delay in the communication links between agents (see e.g., [13-16]).
None of the mentioned works studied finite-time control, and in all of them, linear dynamic networks are considered. In [17], the synchronization analysis of the networked manipulators operating on an under- actuated dynamic platform in the presence of communication delays was performed. There are also some few works considering the finite-time stability of time-delayed linear systems (see [18]) but none of them are applied for control of nonlinear multi-agent systems. In our recent work, [19], the finite-time consensus in the presence of time-delays was considered. However, the nature of delayed consensus is apparent in this work, and consensus between all agents does not happen synchronously, i.e., the consensus error is defined as xi (t) - xj (t - τ ), where τ is the communication delay and i, j are agent indices. Moreover, the delays are assumed to be known.
Our strategy to compensate the time-delay effect is providing a scheme. in which each agent has a local consensus control algorithm that uses its own signals and delayed signals of its neighbors. An agent does not have to possess all the neighbor signals and only part of them is sufficient. Furthermore, the communication time-delays can be time-varying, non-uniform, non-symmetric and even unknown. Besides, the proposed algorithm works for a large class of nonlinear systems. These characteristics extend the generalization of the proposed consensus control algorithm. It is conspicuous that establishing the multi-agent consensus is much more difficult in the finite-time sense, especially when there is a delay in the transmissions. The reason is that the dynamics of the cooperative system in the presence of delays are more complicated and much more restrictive conditions should be confirmed in the case of finite-time consensus.
The contributions of this paper are threefold: 1) Design of a control law to guarantee the finite-time consensus in the presence of communication time-delays. In this regard, the sufficient conditions to establish the delay-independent/dependent consensus are presented. The difference between these two approaches is that in the delay-dependent one, the consensus criteria depend on the upper-bound of delays and therefore is less conservative. The suggestion of these new control strategies is possible by defining a novel consensus error vector, which does not read a direct difference of agent's signals, unlike the common consensus approaches. 2) Providing conditions by which the algorithms work in the presence of partial access to the neighboring agent signals, which is a prevalent condition in many practical multi-agent systems, where the finite-time consensus is considered. 3) There are no strong restrictions about the communication time-delays between agents. They do not need to be constant, uniform, symmetric or even known. Instead, knowing an upper- bound on all of them is required. To the best of author' knowledge, it is the first time to extend the solution of finite-time consensus problem, which applies to a large class of nonlinear systems in the presence of communication delays.
The paper is organized as follows: In Section 4, some preliminaries including a short description of graph theory and required finite-time algorithm lemmas, the problem statement, system description, and its properties are presented. The delay-independent and delay-dependent consensus strategies are provided in Section 5. Simulation results and conclusive points are given in Sections 6 and 7, respectively.
Preliminaries
Communication graph [20]
A communication graph G is denoted by G = (V, E, A), where V = {1, ..., N} is a finite nonempty node set, is the edge set of pairs of nodes and A is the adjacency matrix.
The edge set E, represents the communication links between the nodes. The ordered pair shows that node i obtains information from node j. In other words, j is the neighbor of i. The neighbor set of node i is defined as . We assume that G does not contain any self loops. The adjacency matrix of G is defined as aij = 1 if and aij = 0 otherwise.
The in-degree of a node is the number of edges that this node is the ending point for them. Similarly, the out-degree is the number of edges that this node is the beginning point for them. If the in-degree and out-degree are equal for all the nodes, the graph is said to be balanced. Assume as the in-degree of node and . Hence, L = D - A is the Laplacian matrix of the graph G. When the graph G is undirected, i.e., will be symmetric.
In this paper, we consider both undirected and directed communication graph topologies. We assume the undirected graph is connected and the directed one is balanced and strongly-connected. Besides, since there are packet losses and asynchronous clocks in the communications, there unavoidably exist delays in the transmission of agent signals. Therefore, the graph in this paper is considered along with communication time delays between the agents.
Lemmas
Lemma 1. [21] (Finite-time version of Lyapunov-Razumikhin theorem ). Consider the system below:
Where is the state vector, Ω is a bounded neighborhood of the origin. The function f(x(t), x(t-h)) is a continuous vector field which satisfies f(0, 0) = 0, h > 0 is a constant time-delay and φ(θ) is a vector value initial condition function. If there exist real numbers β > 1, k > 0, a class-K function σ and a C1 Lyapunov function V(x) for system (1), such that the following conditions hold whenever V (x(t + θ)) ≤ V(x(t)) for θ ∈ [-h, 0], then system (1) is finite-time stable.
Furthermore, if and σ is a K∞ function, then the origin would be globally finite-time stable. In addition, the settling time of the system (1) with respect to the initial condition φ satisfies the following equation for all t ≥ 0:
Lemma 2. [22] Consider real matrices A, B and symmetric positive-definite matrix C and a scalar ε. The following inequality holds:
ATB + BTA ≤ εATCA + ε-1BTC-1B. (4)
Lemma 3. [23] For i = 1, ..., n, 0 < p ≤ 1, the following inequalities hold:
Lemma 4. Hermite-Hadamard inequality [24]: If a function is convex, then the following chain of inequalities hold:
Model description
In this paper, the following class of nonlinear systems is considered for N agents of the multi-agent system:
Where i, j = 1, ..., N . The indices i and j represent each agent and its neighbors, respectively. Moreover, is the state vector, is the vector of control input signals which is a function of current agent's signals and the delayed signals of the neighbors. The communication delay from agent j to i is τi,j. Besides, and are nonlinear functions.
The following assumptions hold for the system (7):
Assumption 1. The agents have the same dynamic structure as (7). However, the nonlinear functions (i.e., fi(xi(t)), φi(xi(t))) can be different.
Assumption 2. The functions φi(xi(t)) are invertible.
Assumption 3. Communication delays between agents i and j can be time-varying, non-uniform and asymmetric, providing that they satisfy the following requirement:
Where d is a constant.
Remark 1. Considering Assumption 3, Lemma 1 can be used with d as the delay of the system.
As conclusion, the complete dynamics of the multi-agent system consisting of N agents can be described as follows:
Where
and is the Kronecker product notation.
Consensus Control Strategy
In this section, a consensus algorithm based on a novel consensus error is suggested. The criteria for the finite-time consensus of the coupled multi-agent system in two senses of delay-independent and delay-dependent will be presented. In this paper, by delay independent case, we mean that the conditions for establishing the finite-time consensus are independent of the upper bound of delays. In the delay- dependent case, however, the conditions depend on the mentioned upper bound. In [25], it has been affirmed that delay-independent criteria often provide more conservative evaluations especially in cases of small and known delays. This fact led us to express delay-dependent consensus conditions, too. Furthermore, the communications between agents can be through a connected, undirected graph or a balanced, strongly-connected digraph.
First, consider the following consensus error vector:
For the undirected graph topology, matrix M is a vector consisting of the left eigenvectors of the Laplacian matrix of the multi-agent system corresponding to N - 1 nonzero eigenvalues of the laplacian matrix. In other words, if the Laplacian matrix eigenvalues are arranged from the smallest value to the largest one, i.e., λ0 = 0 to λN-1, the matrix M , in this case, is defined as follows:
Note that the eigenvectors of the Laplacian matrix of an undirected graph; which is also symmetric, are perpendicular to each other. It is also known that the corresponding eigenvector of the eigenvalue λ0 = 0 is Thus, it will be concluded that each row of the matrix M is perpendicular to . Therefore, e(t) = 0, i.e., (M In) X(t) = 0, if and only if
Where, k is a real number. Thus, the consensus is achieved.
For the directed graph topology, consider l = [l1, ..., lN ]T as the left eigenvector of a Laplacian matrix of a strongly-connected directed graph associated with the zero eigenvalue. It is easy to show that 0 is a simple eigenvalue of the matrix (IN - 1lT) with 1 as a right eigenvector and 1 is the other eigenvalue with multiplicity N - 1. Provided that the digraph is balanced, (IN - 1lT) is symmetric. Therefore, in this case, matrix M is constructed from the matrix (IN - 1lT) the same manner as it was constructed from the Laplacian matrix of the undirected graph.
Delay-Independent algorithm
In this section, the objective is to design a control protocol for the agents of the system to achieve consensus in a finite time. Consider the following consensus control algorithm for each agent of the system (7):
Where are appropriate gain matrices which should satisfy some conditions given later. In addition, α is a real number greater than 1. Therefore, the complete control signal of the multi-agent sytem (8) is obtained as
in which, is the Laplacian matrix of the system. Furthermore, consider the following definitions:
Where, N and n are the number of agents and agents' states, respectively. Moreover, (.)+ indicates the right pseudo-inverse of a non square matrix, (i.e., A+ = AT (AAT)-1). As the matrix M is constructed from the (strongly-) connected graphs, P is a positive-definite matrix.
Theorem 1: Consider the multi-agent system defined in (8) satisfying the Assumptions (1)-(3) and the consensus error definition of (9). Utilizing the control signal of (13), the delay-independent finite-time consensus in the presence of communication time-delays is achieved if there exists a positive scalar a such that the following inequality holds.
Furthermore, the finite consensus time, tci, is bounded by
Proof. Consider the following Lyapunov function for the error dynamics:
By getting the derivative of (17) one can reach to the following:
In addition, getting the derivative of e(t), we obtain:
After substitution of (13) in (19), the following relation is obtained:
In addition, by replacing and with and , respectively, using (9) and some manipulations, it is concluded that:
Substituting (21) in (18) leads to the following equation:
Using the consensus error vector equation and utilizing the mentioned definitions in (14), (22) can be written as follows:
Rewriting the last two terms of (23) in the quadratic form, the following inequality will be acquired:
Finally, can be expressed as below:
In addition, the last term of (25) can be written as below by utilizing Lemma 3 and meeting the required condition of Lemma 1:
Therefore, after substitution of (26) in (25), the following relation for the Lyapunov function dynamics will be achieved:
In conclusion, if q defined in (15) establishes the mentioned inequality, the proof is complete and the finite- time consensus in the presence of communication time-delay will be proved.
Remark 2. Whenever the accessibility to all states of the neighbor agents is not possible, the control signal can be changed to the following form:
in which a new control gain with l as the number of accessible neighbor outputs is utilized. Besides, C = diag is the augmented output matrix of the multi-agent system. Consider the following new definitions:
By choosing appropriate matrices K1 and K3 and provided that there exists a positive scalar a to satisfy the following inequality, the finite-time consensus for this case is established.
Delay-Dependent algorithm
Theorem 2. Consider the multi-agent system defined in (8) satisfying the Assumptions (1)-(3) and the consensus error definition of (9). Utilizing the control signal of (13), the delay-dependent finite-time consensus in the presence of communication time-delays is achieved if there exist positive scalars a and b such that the following inequalities hold.
In addition, the finite-time of consensus tcd for this case is as follows:
Proof. The relation (20) can be written as follows:
Using Lemma 2 and what was obtained from the proof of Theorem 1, the following inequality is formed:
By adding (33) (which has been multiplied by ) to the right side of (34) and after some simple manipulations we have the following:
(35)
On the other hand, using Lemma 4 we obtain
Where b is a positive real number.
Besides, utilizing (26) and meeting the required condition of Lemma 1 the following is acquired:
By adding the left side of (37) to the right side of (35) and rewriting the integral terms in a quadratic form, the following inequality is established:
Where
By considering Schur complement Lemma we have
Therefore, provided that the inequalities of (31), (32) and conditions of Lemma 1 are satisfied, the delay- dependent finite-time consensus is guaranteed.
Remark 3. Note that the structure of consensus control signal for both delay-independent and delay- dependent algorithms are the same, as stated in (13). The main difference between the two cases lies in the sufficient conditions for achieving finite-time consensus (see (15) and (31)).
Remark 4. Suggested algorithms could be extended for the leader-follower scenario. For this aim, an error is defined for the leader agent, which is the deviation between its state trajectories and the reference signal. Then, we augment this error with the followers error, which is defined the same as (9). Appropriate stability criteria could be extracted for the new augmented system similar to what was proposed according to Theorems 1 and 2.
Simulation Results
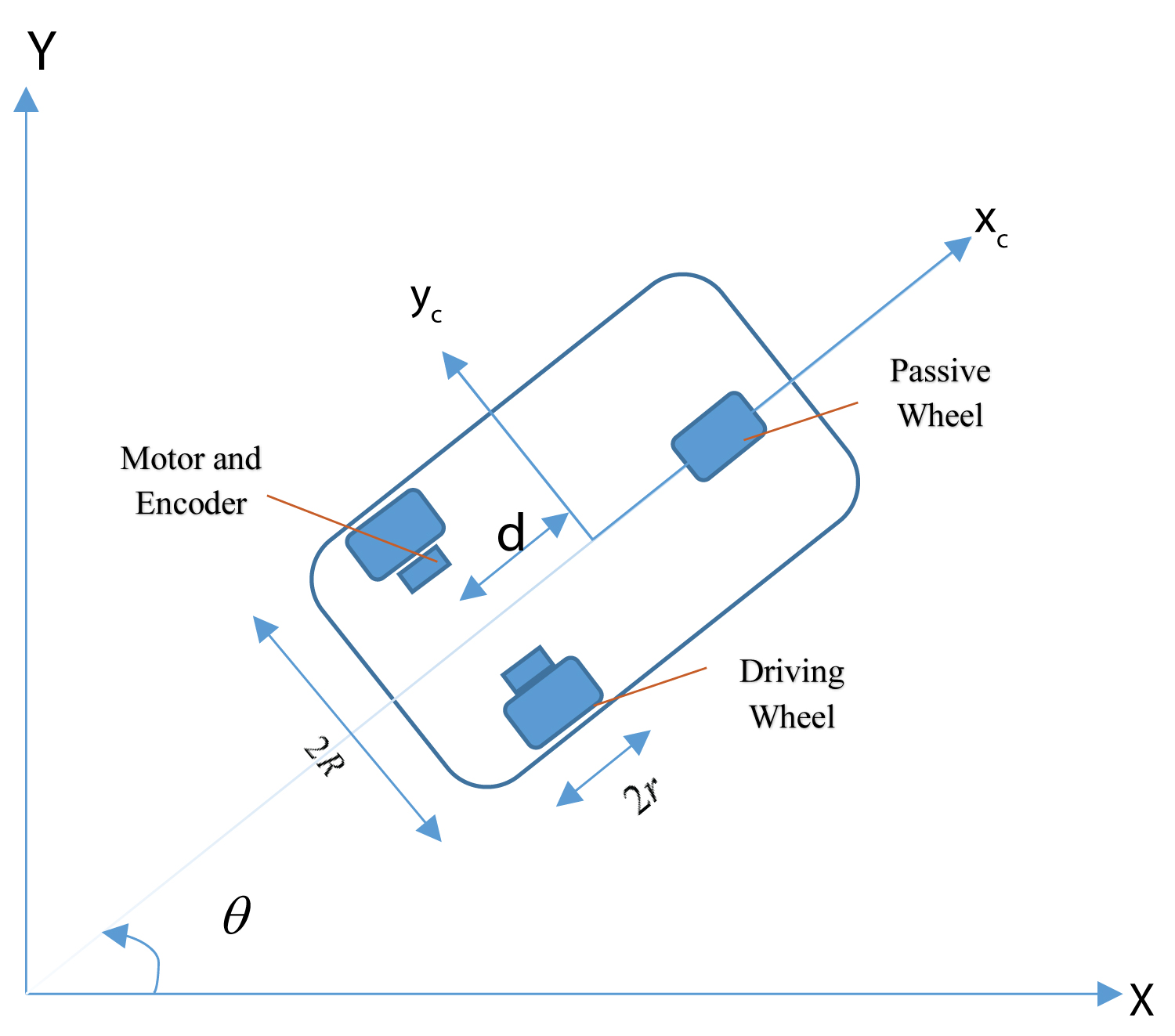
In this section, to evaluate the effectiveness of the proposed approach, simulations are performed on a group of four identical nonholonomic mobile robots as the agents shown in Figure 1. The mobile robots consist of a vehicle with two driving wheels mounted on the same axis and a front freewheel. The motion and orientation are achieved by independent actuators, e.g., dc motors which provide the necessary torques to the rear wheels. The nonlinear dynamics of each robot in a n dimensional configuration space with coordinates (q1, ..., qn) and subject to m constraints are as below described in [26].
Where
The inertia matrix is symmetric positive definite , is the coriolis and centripetal matrix, stands for the surface friction, denotes the gravitational forces, is the bounded unknown disturbance including unmodeled dynamics, indicates the input transformation matrix, is the input vector and are the constraint associated matrix and vector force, respectively.
Furthermore, kinematic equality constraints can be expressed as follows:
There would be a full rank matrix constituting a set of smooth linearly independent vector fields which span the null space of , i.e.
According to (42) and (43), a vector time function could be found such that for all t
The nonholonomic constraint forces the robot to move only in the direction normal to the axis of the driving wheels. If r = n - m, after transformation from q coordinates to ν configuration, the new input matrix would be a constant nonsingular one which depends on the distance between the driving wheels and the wheel radius, which brings up an appropriate form to the proposed strategy. In this case, the mentioned matrices can be described as follows:
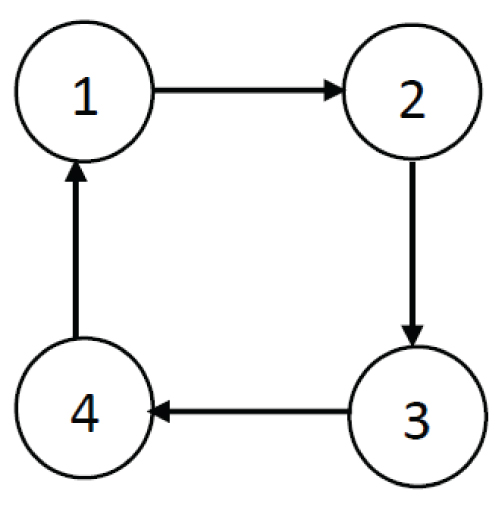
Where v and w are the linear and angular velocities of the mobile robot. Besides, xc and yc are indicators of its position and θ is the corresponding orientation. For the simulations, the agents communicate with each other via the specified directed graph in Figure 2. According to the graph topology, the Laplacian matrix is as follows:
The eigenvalues of the Laplacian matrix and the resulting matrix M to build the consensus error vector are as
Therefore, it is concluded that P = 4 × I6. The nominal parameters of the model are taken as mi = 10 kg as the mass of vehicle, Ri = 0.5 m for the distance between driving wheels, ri = 0.05 m for the radius of wheels and di = 0.04 m as the distance between the center of mass of the vehicle and wheels (i = 1, ..., 4). The initial conditions of agents are set as v(1) = [0.2, 0.6]T, v(2) = [0.5, 0.1]T, v(3) = [0.6, 0.5]T, v(4) = [0.3, 0.7]T. In addition, the delays between all connected agents are chosen as (0.1 + 0.25e-t)s.
The control signal parameters are set as K1 = 5 × I2 for the case of Figure 3 and K1 = 12 × I2 for the cases of Figure 4 and Figure 5. K2 = 2 × I2 for the cases of Figure 3 and K3 = [3.2 2.4] for the cases of Figure 4 and Figure 5. These cases will be introduced later. By choosing such values for the control signal, all the required conditions mentioned in (15), (31) and (32) are satisfied with α = 1.3, a = 6 and b = 0.1. Besides, we obtain tcd ≤ 4.8 s for the first scenario and tcd ≤ 7.2 s for the others.
The simulation results are shown in Figure 3, Figure 4 and Figure 5. In Figure 3, full access of the agents to their neighbor agent signals is considered and linear and angular velocities consensus, control signals and evolution of the Lyapunov function are shown in Figure 3a, Figure 3b, Figure 3c and Figure 3d, respectively. In Figure 4, it is assumed that each agent only has accessibility to the delayed linear velocity signals of its neighbors and angular velocities of the neighbors are not available for them. Consensus of linear and angular velocities of agents and control signals in this case are presented in Figure 4a, Figure 4b and Figure 4c, respectively. Besides, in Figure 5, the dynamic finite-time consensus condition in which the agents reach to the same velocities, with respect to a time-varying reference signal, and keep on moving with them are provided. Results show a good convergence rate to the desired values. It is worth mentioning that all scenarios are simulated with the delay-dependent finite-time consensus criterion. As mentioned before, the delay-independent one brings conservative results especially in the presence of small and known delays.
Conclusions
In this paper, the problem of finite-time consensus of a class of nonlinear systems in the presence of communication delays was considered. To compensate for the adverse effects of time-delay in communication between agents in a finite time interval, a novel consensus algorithm with two approaches, i.e., delay- independent/dependent was proposed. The algorithms may be used for cases with partial access of agents to their neighbor signals. Besides, there are no strong restrictions on the communication time-delays. Furthermore, the results of simulations on a group of mobile robot agents confirmed the theoretical findings. Future works include designing robust approaches with respect to the agents dynamics and considering Leader-follower scenarios and time-varying graph topologies.