International Journal of Signal Processing and Analysis
(ISSN: 2631-5025)
Volume 1, Issue 1
Research Article
DOI: 10.35840/2631-5114/3501
Design of Accurate α-β Tracker based on Steady-State Performance Index
Kenshi Saho*
Table of Content
Figures
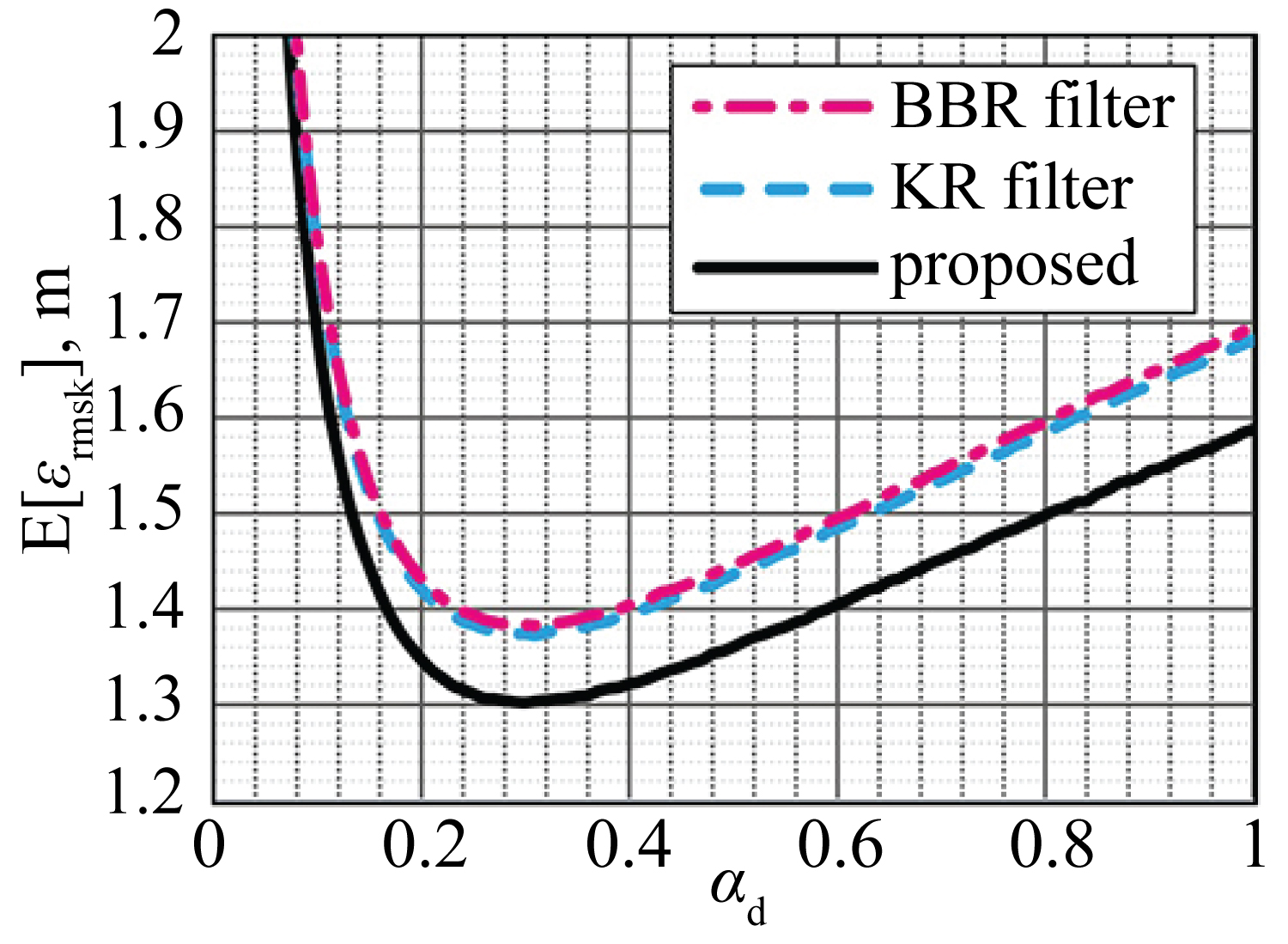
Figure 3: E[εrmsk] for the...
E[εrmsk] for the constant-acceleration target (0.3 m/s2) of the tracker designed with the proposed method and the BBR and KR filters whose β(efin)is same as the proposed method.
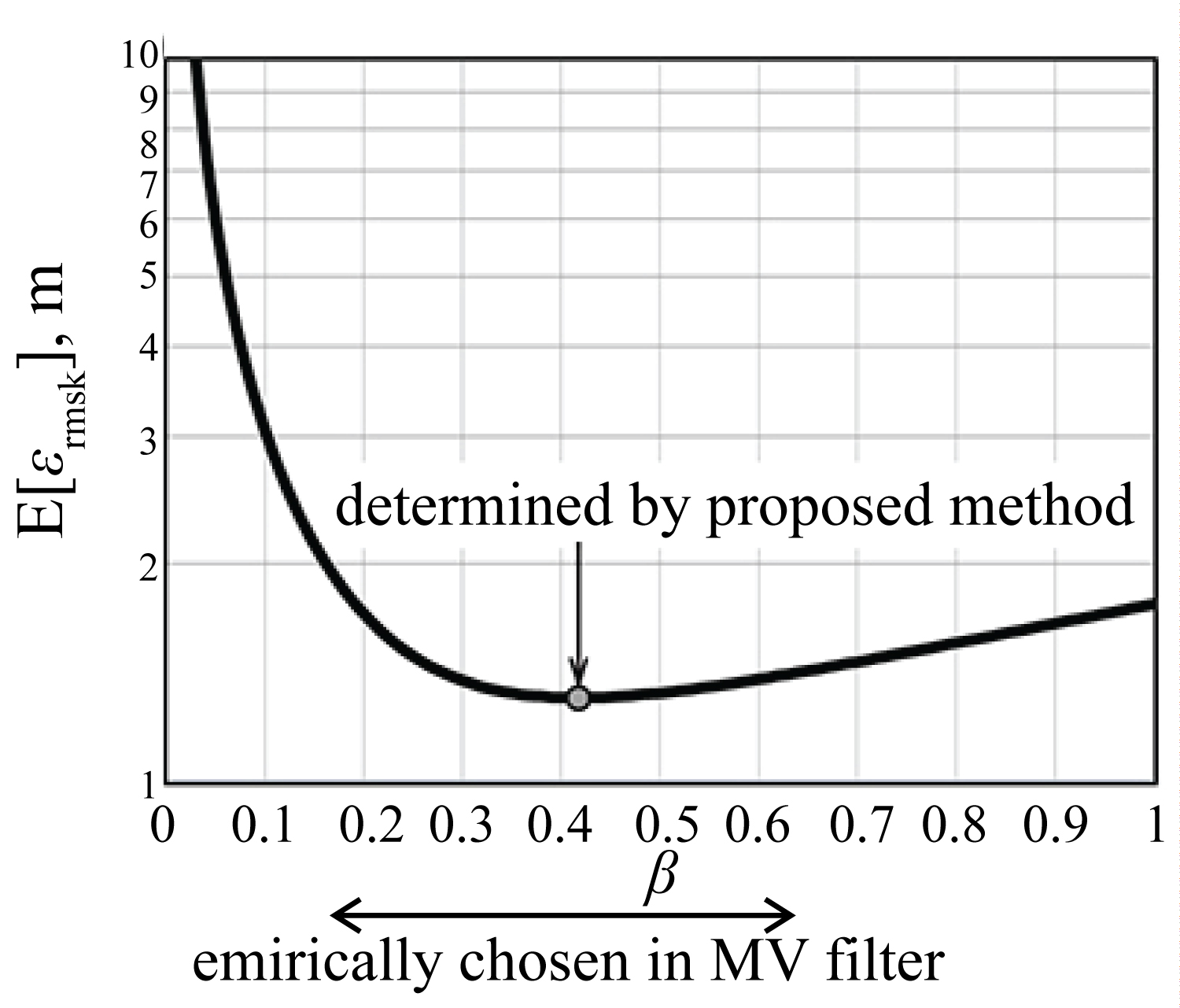
Figure 4: Relationship between β...
Relationship between β and E[εrmsk] for the proposed method and MV filter.
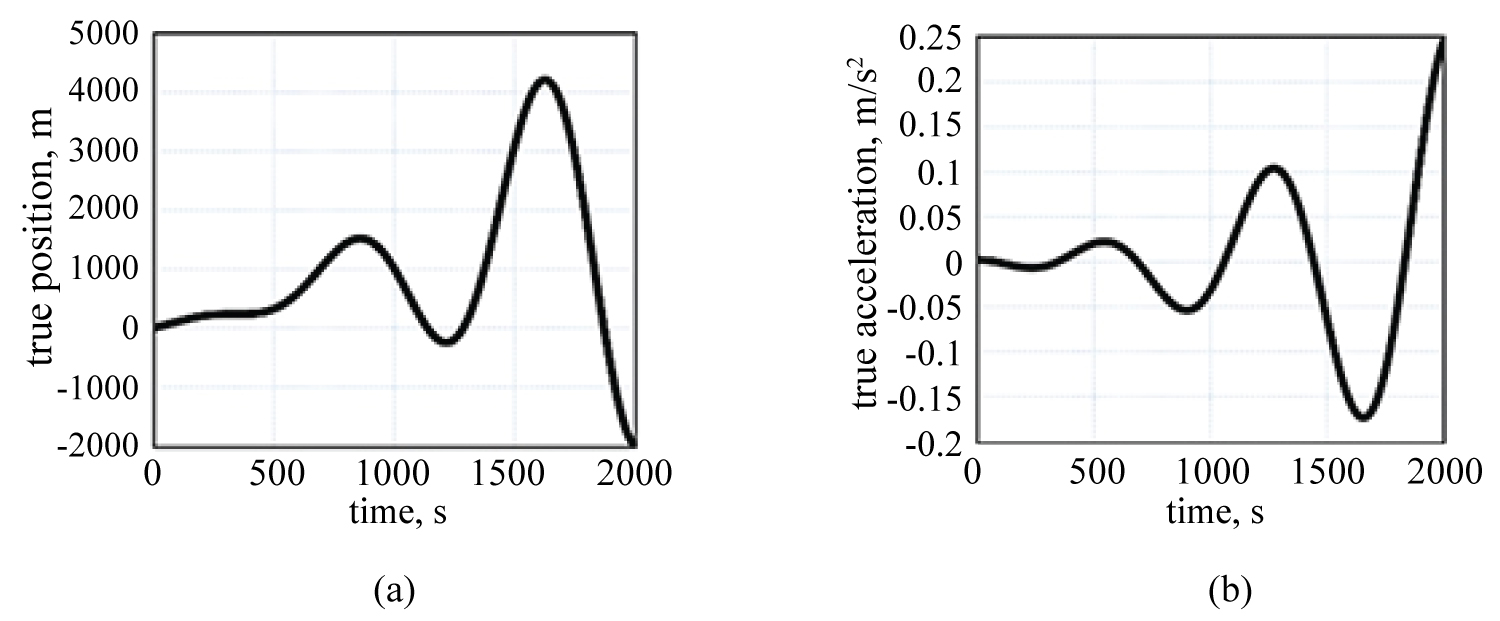
Figure 5: True position (a) and...
True position (a) and acceleration (b) of assumed maneuvering target in numerical simulation.
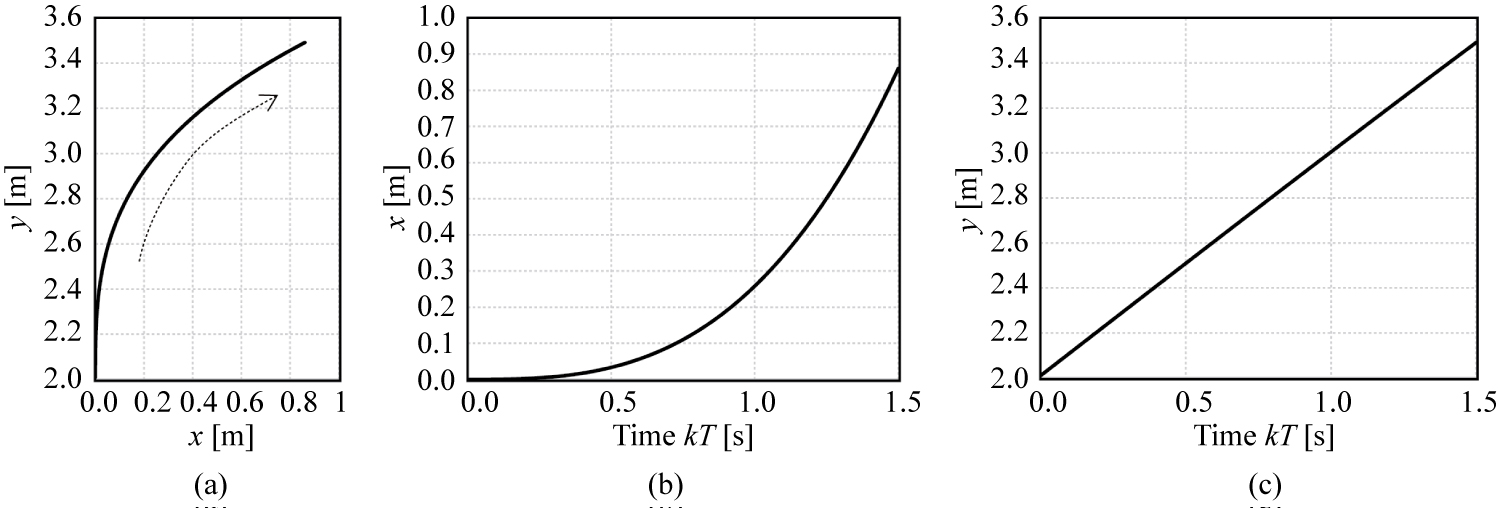
Figure 8: True target position...
True target position in 2D simulation. (a) Target trajectory in xy; (b) Time variation of x; (c) Time variation of y.
References
- Ekstrand B (2012) Some Aspects on Filter Design for Target Tracking. Journal of Control Science and Engineering 870890: 15.
- Ng KH, Yeong CF, Su ELM, Wong LX (2012) Alpha Beta Gamma Filter for Cascaded PID Motor Position Control. Procedia Engineering 41: 244-250.
- Lee YS, Lee HJ (2009) Multiple object tracking for fall detection in real-time surveillance system. Advanced Communication Technology: 2308-2312.
- Sharma S, Deshpande S, Silvalingam KM (2011) α-β filter based target tracking in clustered wireless sensor networks. Third International Conference on Communication Systems and Networks 1-4.
- Tenne D, Singh T (2000) Optimal design of α-β- γ(γ) filters. Proceedings of American Control Conference: 4348-4352.
- Benedict T, Bordner G (1962) Synthesis of optimal set of radar track-while-scan smoothing equations. IRE Transactions on Automatic Control: 27-32.
- Kalata PR, (1784) The Tracking Index: A Generalized Parameter for α-β and α-β-γ Target Trackers. IEEE Transactions on Aerospace and Electronic Systems AES-20: 174-182.
- Crouse DF (2014) A general solution to optimal fixed-gain (α-β -γ etc.) filters. IEEE Signal Processing Letters 22: 901-904.
- Kosuge Y, Ito M (2003) Evaluating an α-β filter in terms of increasing a track update-sampling rate and improving measurement accuracy. Electronics and Communications in Japan (Part I: Communications) 86: 10-20.
- K. Saho and M. Masugi (2015) Performance analysis of alpha-beta-gamma tracking filters using position and velocity measurements," EURASIP J Adv Signal Process 15: 1-15.
- Bar-Shalom Y, Li X (1998) Estimation and tracking: principles, techniques, and software. Artech House Publishers, Boston, MA, USA.
- Painter JH, Kerstetter D, Jowers S (1990) Reconciling steady-state Kalman and alpha-beta filter design. IEEE Transactions on Aerospace and Electronic Systems 26: 986-991.
- Yujing L, Huadong M, Desheng W (2008) Steady-state analysis of target tracker with constant input/bias constraint. Tshinghua Science and Technology 13: 35-42.
- Saho K, Masugi M (2015) Automatic Parameter Setting Method for an Accurate Kalman Filter Tracker Using an Analytical Steady-State Performance Index. IEEE Access 3: 1919-1930.
Author Details
Kenshi Saho*
Department of Electronic and Computer Engineering, Ritsumeikan University, Japan
Corresponding author
Kenshi Saho, Assistant Professor, Department of Electronic and Computer Engineering, Ritsumeikan University, 1-1-1 Noji-Higashi, Kusatsu, Shiga, 525-8577, Japan, E-mail: saho@fc.ritsumei.ac.jp
Accepted: February 04, 2016 | Published Online: February 06, 2016
Citation: Saho K (2016) Design of Accurate α-β Tracker based on Steady-State Performance Index. Int J Signal Process Anal 1:001.
Copyright: © 2016 Saho K. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
This letter describes a design method for an α-β tracker based on a steady-state performance index. An efficient steady-state index that expresses the comprehensive performance of the smoothing of noise and the tracking of an accelerating target is presented. Using the defined performance index, the automatic determination of the filter gains is presented as a novel design method for an α-β tracker. The proposed method exhibits better accuracy than the well-known Kalman filter-based α-β trackers. Moreover, its design parameter is easily determined based on the assumed target motion. Numerical simulations verify the effectiveness of the proposed design method for targets with realistic motion.
Keywords
α-β tracker, Tracking filter, Gain design, Steady-state performance index
Introduction
Various remote monitoring systems for robots and intelligent vehicles require accurate tracking of moving objects. One effective technique is a α-β tracker, which is a low-cost tracking filter [1]. Because of their small computational load compared with methods such as Kalman and particle filters, α-β trackers have been widely used in various applications [2-4].
To design an α-β tracker, we must determine appropriate gains for α and β. The most common approach is a Kalman filter-based gain calculation, because the α-β tracker can be acquired as the steady-state Kalman filter tracker [1,5-8]. To apply this method, an efficient gain design parameter (the so-called tracking index) [7] and an automatic optimal gain calculation method for an arbitrary target model [8] must be known. However, the performance of α-β trackers derived from the Kalman filter is not optimal when evaluated using the general tracking/smoothing performance indices for the α-β tracker [1,9]. As a solution to this problem, a gain design method that does not use the Kalman filter equations has been proposed. This is called the minimum variance (MV) filter criterion [9,10]. This criterion minimizes the steady-state variance of random errors caused by measurement noise. However, although this criterion determines the optimal α from β with respect to the general performance index, an appropriate design criterion for β has not been discussed. Moreover, only the smoothing performance of random errors is optimized, and the reduction of errors associated with an accelerating target, which is another important function of the tracking filter, has not been considered.
This letter proposes a gain design method for α-β trackers that optimizes a comprehensive performance index in terms of both the smoothing of noise and the tracking of an accelerating target. With the proposed method, we can avoid the difficulties of the conventional MV filter criterion in selecting β. Moreover, the tracking performance of an accelerating target is also considered together with the smoothing performance of measurement noises in the optimization process. Further, the proposed method determines gains from a single design parameter that is easily determined based on target acceleration information. Numerical simulations verify that the tracking accuracy with the proposed method is better than that with the conventional Kalman filter-based approach, and clarify that the criteria for setting the design parameter are simpler than those for the MV filter.
α-β Trackers and their General Performance Indices
An α-β tracker predicts the position of the target by assuming a constant velocity during the sampling interval. Such trackers are essentially characterized by the following equations [1,5-8]:
where xsk is the smoothed target position at time kT, T is the sampling interval, xok is the measured target position, xpk is the predicted target position, vsk is the smoothed target velocity, and α and β are the filter gains.
The design of the α-β tracker requires the filter gains of α and β to be set. This in turn requires an objective performance index. Some researchers have determined appropriate gains based on a steady-state performance index [1,5,11]. The most popular index is the covariance matrix in the Kalman filter equation, because the α-β tracker can be obtained as the steady-state Kalman filter [11-13]. However, this overrates the variance in the measurement errors, as verified in [1]. To evaluate α-β trackers more effectively, the following two steady-state errors are used as general steady-state performance indices [1,10].
Bias error for constant acceleration target (Tracking performance index)
The tracking filter is required to track complicated motion that may include acceleration. When we use an α-β tracker, steady-state bias error occurs when tracking a target moving with constant acceleration because of the difference between the motion and model. This error is an index of the tracking performance. When xok = 1/2 ac(kT)2 (where ac is the constant acceleration), the bias error is expressed as [5,8].
Where efin is the tracking performance index [10].
Measurement error for constant velocity target (Smoothing performance index)
The tracking filter is also required to reduce the random errors caused by measurement noise. One index of this performance is the variance of predicted errors assuming a constant-velocity target in the presence of noise. This variance is expressed as [5,6,8].
Where E[(xpk-xtk)2 ] indicates the mean in terms of time, B is the variance of the measurement noise of xok, and xtk is the true position of the constant-velocity target. σp2 is the smoothing performance index [10]. The smaller the indices σp2 and efin, the better the tracking filter. However, there is a trade-off between these indices, and this is a very important consideration in the design of α-β trackers.
Conventional Gain Design Methods and their Problems
Based on the filter performance indices described in the previous section, various gain design methods have been proposed [5,7-10]. These can be classified as Kalman filter-based approaches and MV filter criterion methods. In the following, the features and problems of each design type are reviewed.
The Kalman filter-based approach is commonly used to design the gains of α-β trackers. This approach calculates the steady-state gains of the Kalman filter equations. Two gain relations derived from this approach are known: the Benedict-Bordner relation (BBR) β = α2/(2-α) [6] and the Kalata relation (KR) β = 2(2-α)-4(1-α)1/2 [7]. We refer to α-β trackers with BBR and KR as BBR filters and KR filters, respectively. In a KR filter, an effective design parameter (known as the tracking index) is used to determine α and/or β. The determination criterion for such filters has been frequently discussed [1,7]. Moreover, we can calculate the gains for arbitrary models other than BBR and KR from the Kalman filter equations [8]. However, in these conventional Kalman filter-based design methods, only the performance using the assumed motion models is optimized, and the general steady-state performance indices of (4) and (5) are not optimized.
Another effective design approach that does not suffer from the above problem is the MV filter criterion. This criterion determines gains by minimizing the smoothing performance index σp2 under the condition that the tracking performance index efin remains constant [9,10]. The optimal gain relation derived from the MV filter criterion is α = β1/2−β/2. We refer to α-β trackers that satisfy this relation as MV filters. The smoothing performance of the MV filter is theoretically better than that of the KR and BBR filters [9]. However, as shown in (4), we must design efin and ac to determine β. However, no methodology to design these indices has been discussed. In addition, the comprehensive performance with respect to both σp2 and efin has not been considered. Thus, there is a lack of knowledge concerning the selection of the design parameter for the MV filter criterion. Table 1 describes the features of these conventional design methods, with bold font signifying the problems with each method. To resolve these problems, we present a novel gain design method in the next section.
Proposed Gain Design Method
We propose a design method for α-β trackers based on the general tracking/smoothing performance indices. In the proposed design method, a comprehensive performance index with respect to both smoothing and tracking is considered. Based on the indices in (4) and (5), an evaluation function for the comprehensive tracking performance can be defined as
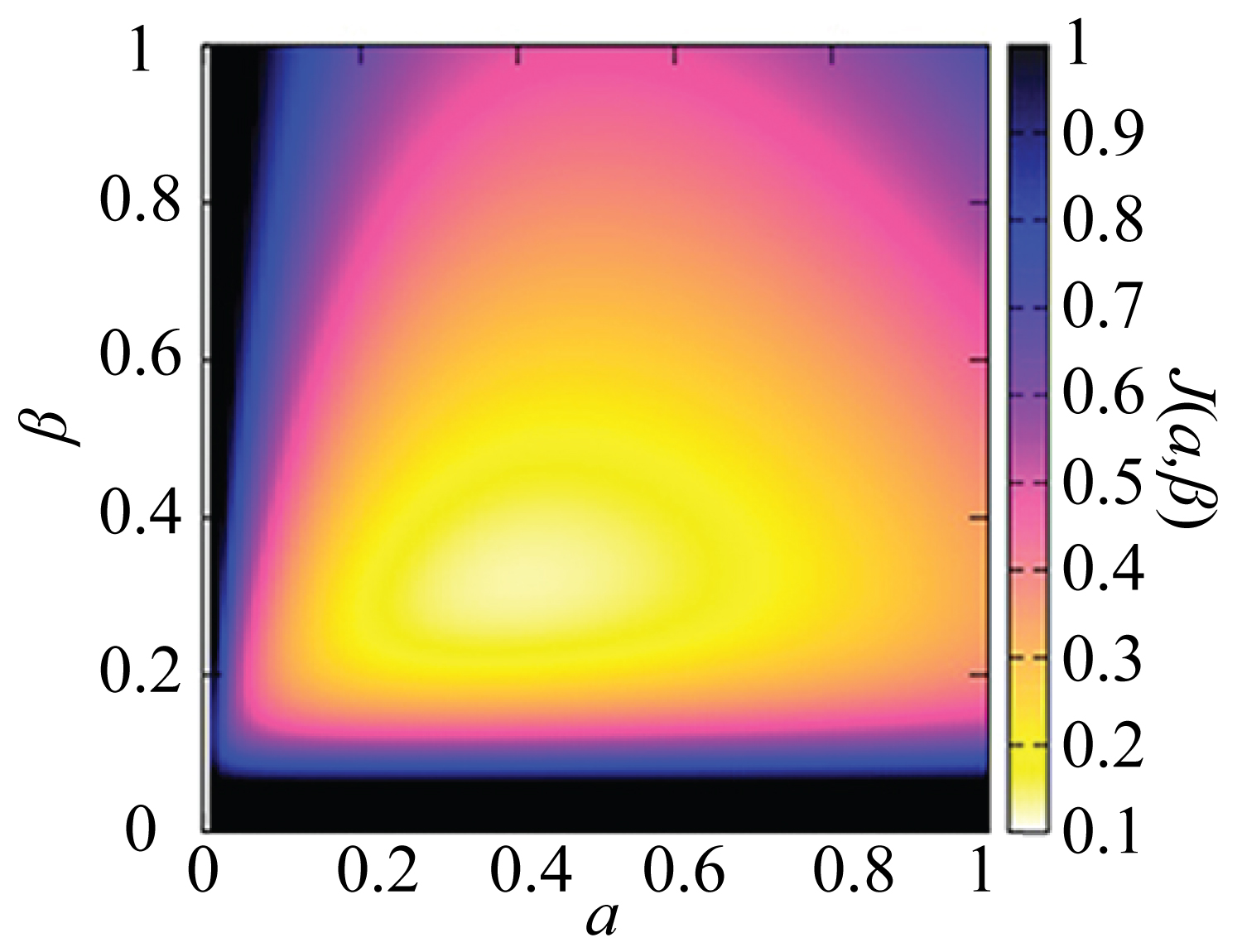
Where ad is a dimensionless constant. The proposed method determines the gains as the arguments that minimize J(α, β). Using (4) and (5), J(α, β) is (σp2+efin2)/B and ad = acT2/B1/2. In addition, ad controls the balance between the smoothing performance (first term) and the tracking performance (second term). Thus, J(α, β) expresses the comprehensive performance of smoothing and tracking. Figure 1 shows an example of J(α, β) for ad = 0.2. This indicates that J(α, β) is downward-convex. Thus, we can easily determine optimal gains for the designed ad by seeking the minimum of the evaluating function, i.e.,
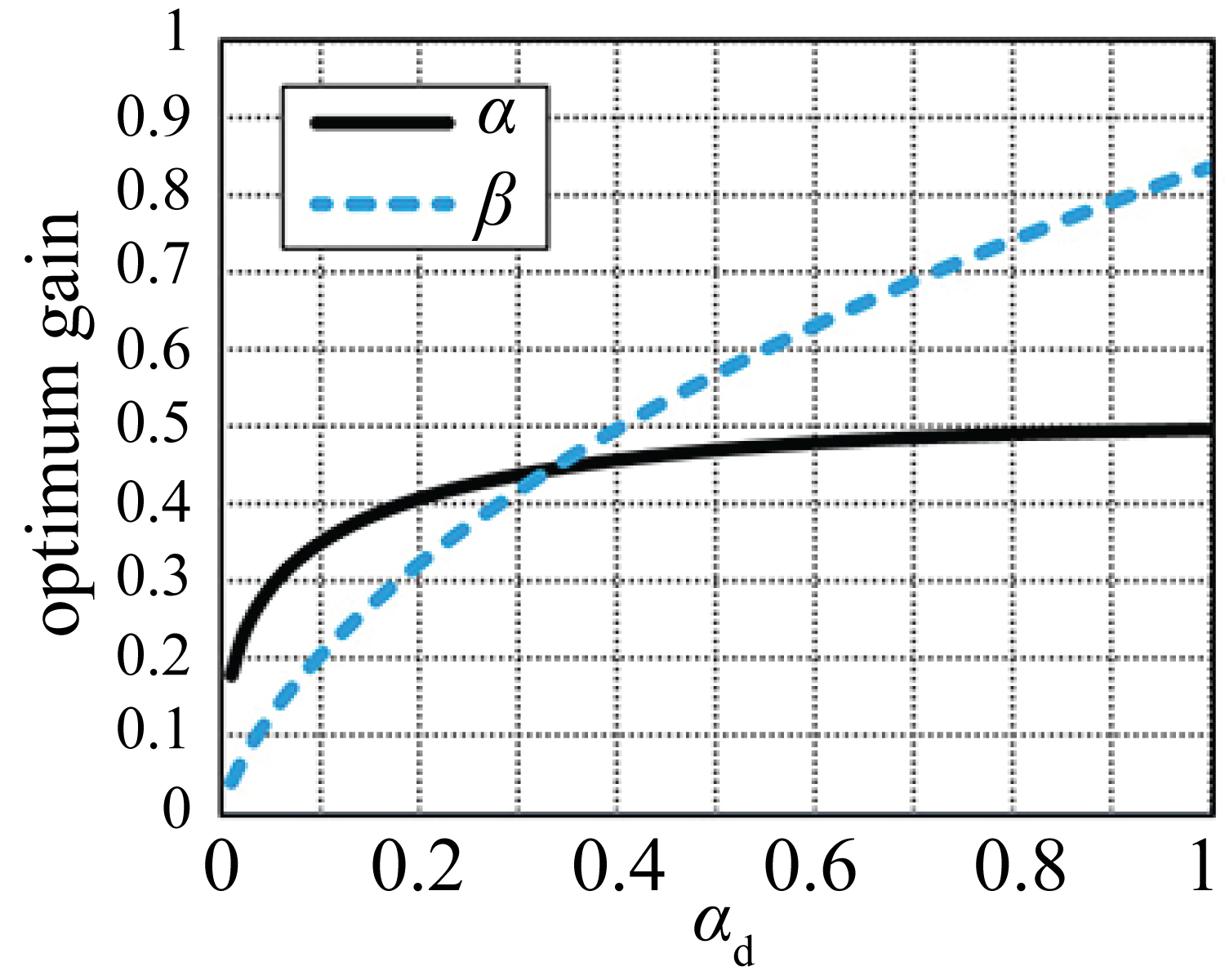
Where the constraint is the stability condition of the α-β tracker [5]. The procedure for the proposed gain design method is as follows: 1) Design ad based on the approximated target acceleration; 2) Calculate optimal α and β as the solutions of (7). The proposed method determines both gains from the single design parameter ad, which is easily determined because its physical meaning is clear (the parameter ad corresponds to the target acceleration).
Figure 2 illustrates the gains for various ad using (7). Note that the relationship between α and β calculated with (7) is the same as for the MV filter. However, the only design parameter is ad, and the determination of this quantity is easy compared with setting β(ac and efin) in the MV filter criterion. Table 1 summarizes the features and problems of the conventional and proposed design methods. In the next section, the design criterion of ad is discussed based on simulation results.
Evaluation and Discussion using Numerical Simulations
The performance of the proposed method is now clarified and compared using numerical simulations. For simplicity, one-dimensional tracking is considered. The measured position xok is generated by adding white Gaussian noise to xtk. The root mean square (RMS) prediction error is calculated from 1000 Monte Carlo simulations for each value of kT to evaluate the comprehensive performance of the tracker. The RMS prediction error at time kT is defined as
Where xipk is the predicted position estimated by the i-th Monte Carlo simulation. The mean and variance of εrmsk correspond to efin and σp2.
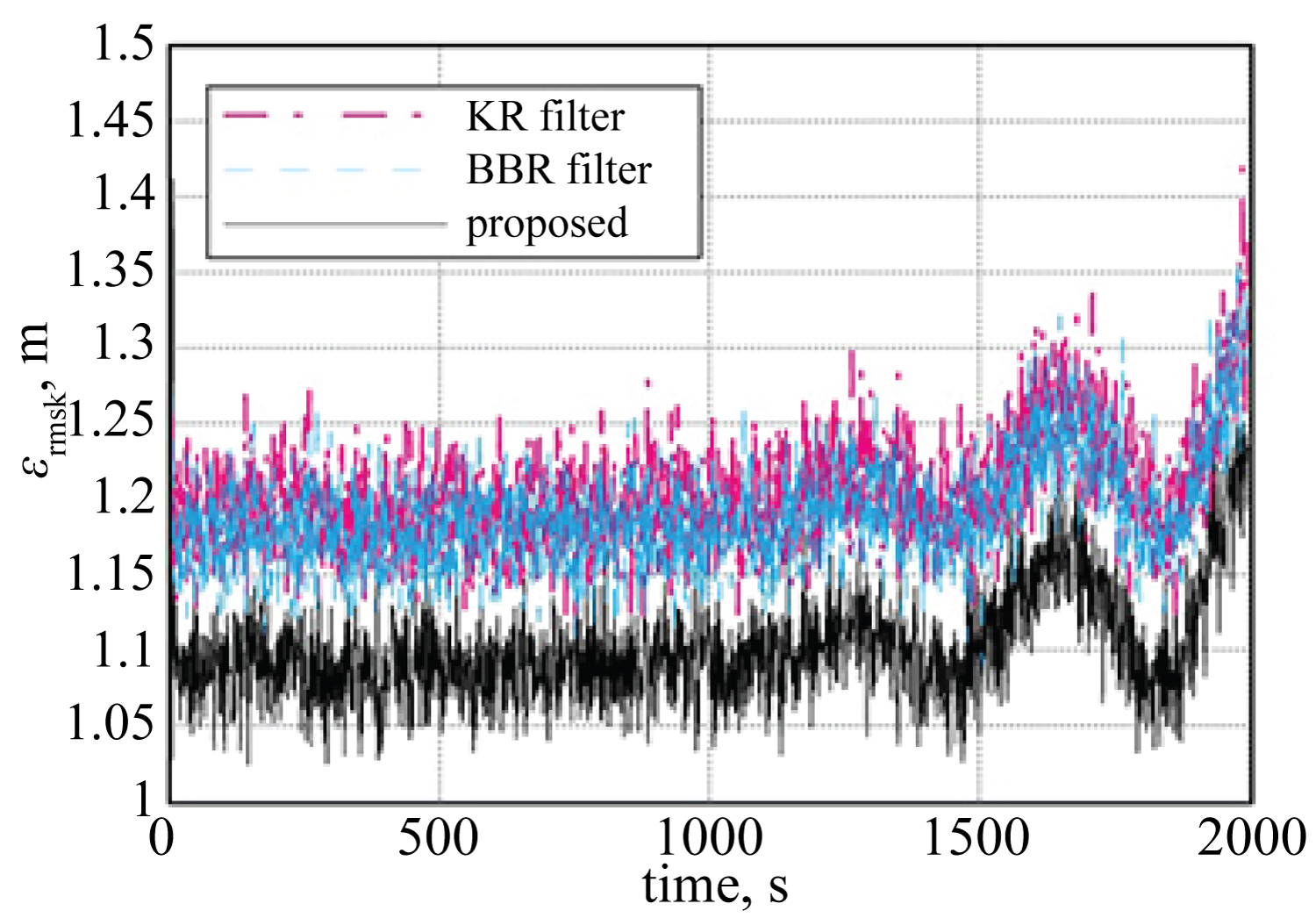
First, we considered a target accelerating at a constant 0.3 m/s2. B and T were set to 1 m2 and 1 s. Figure 3 shows E[εrmsk] given by the proposed method for each ad and the results from the conventional BBR and KR filters, where β in the conventional filters was the same as in the proposed method (i.e., efin of all filters was the same). The error was minimized when ad was equal to the target’s acceleration. Additionally, for all ad, the proposed method achieved the best performance. The proposed method was then compared with the MV filter. Figure 4 shows E[εrmsk] given by the proposed method for each value of β. This is equal to the value in the MV filter, because the gain relation in the proposed method is the same as in the MV filter. However, the MV filter does not include the determination process of β. In contrast, the proposed method determines the optimal β that minimizes the error when ad is designed appropriately. In this case, β = 0.417 was calculated with ad = 0.3.
Next, the performance of the proposed method for tracking a maneuvering target was evaluated. Figure 5 shows the true position and acceleration of the assumed maneuvering target. B and T were again set to 1 m2 and 1 s. Figure 6 shows the results given by the proposed method for ad = 0.3 and the BBR and KR filters with the same value of β as in the proposed method. This figure verifies that the proposed method realizes more accurate tracking than the conventional BBR and KR trackers derived from the Kalman filter.
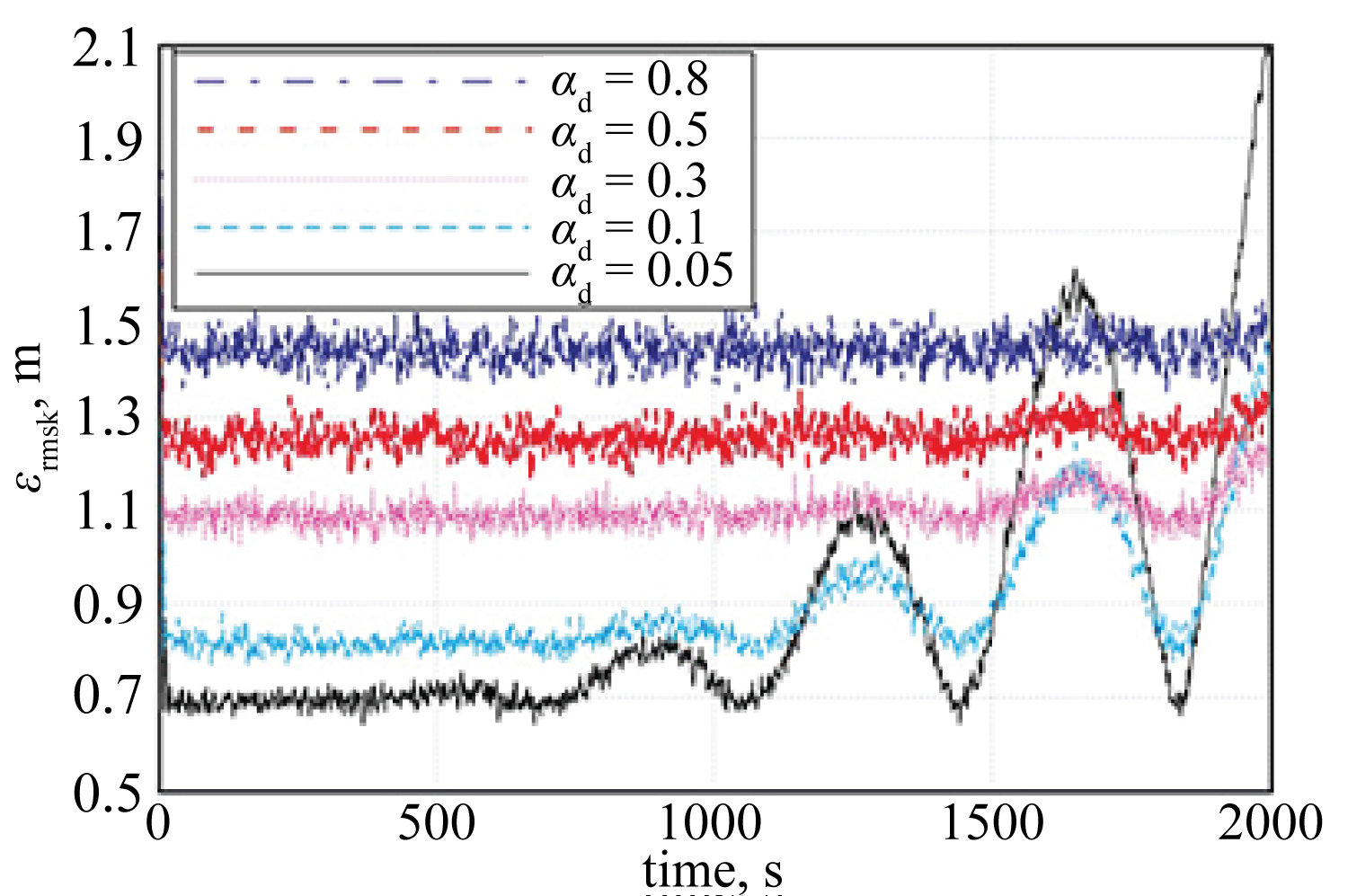
Additionally, the design of an appropriate value of ad was examined for the case of a maneuvering target. Figure 7 shows the RMS prediction errors of the proposed method for the target in Figure 5 for various ad. As shown in this figure, with relatively small values of ad, errors associated with motion under relatively low acceleration can be suppressed, but these errors become large when the acceleration of the target increases. In contrast, relatively large values of ad suppress errors in motion associated with high acceleration. In addition, when ad is large compared with the true acceleration of the target (i.e., ad = 0.5 and 0.8), the errors become large in all time bins. Consequently, the important points in the design of ad can be summarized as follows. ad must be set to a large value when the tracking performance is important. However, ad should not exceed amaxT2/B1/2, where amax is the estimated (or assumed) maximum acceleration of the target. In contrast, when it is more important that the tracking system smooths the measurement noise, relatively small values of ad can be used under consideration of the permissible error for an accelerating target. Additionally, when the target is moving with (nearly) constant acceleration, ad must be set to the corresponding value of the target acceleration to achieve the best comprehensive performance.
Finally, a numerical simulation was conducted to evaluate the tracking performance in a realistic two-dimensional (2D) scenario. Figure 8a shows the true trajectory of the target in the xy-plane, and Figure 8b and Figure 8c show the true x and y at each time point. B and T were set to 10-4 m2 and 10 ms. The α-β tracker was implemented for each axis, with the same gains for both axes. We compared the RMS prediction error in 2D space, which is expressed as
where yipk is the predicted value of y estimated by the i-th Monte Carlo simulation and ytk is the true y. Figure 9 shows the simulation results for ad = 0.5. As shown in this figure, the proposed method achieves better steady-state accuracy than the conventional BBR and KR filters. These results verify the effectiveness of the proposed method for a realistic 2D maneuvering target.
Conclusion
A novel gain design method for α-β trackers has been proposed. This approach is based on a comprehensive index with respect to both the smoothing of measurement noise and tracking of an accelerating target. The proposed method designs a more accurate tracker than the conventional BBR and KR filters. Optimal gains are calculated from the single simple parameter ad, which is determined based on the target acceleration. The determination process is somewhat easier than the MV filter criterion. Numerical simulations indicated that we can easily design the parameter ad so as to achieve accurate tracking of a maneuvering target based on the assumed target motion and the requirements of the tracking system. In addition, the extension of the concept of the proposed method to Kalman filter trackers has also been investigated in [14].