
International Journal of Magnetics and Electromagnetism
(ISSN: 2631-5068)
Volume 8, Issue 1
Research Article
DOI: 10.35840/2631-5068/6540
Extending Weber's Electrodynamics to High Velocity Particles
Qingsong Li*
Table of Content
Figures
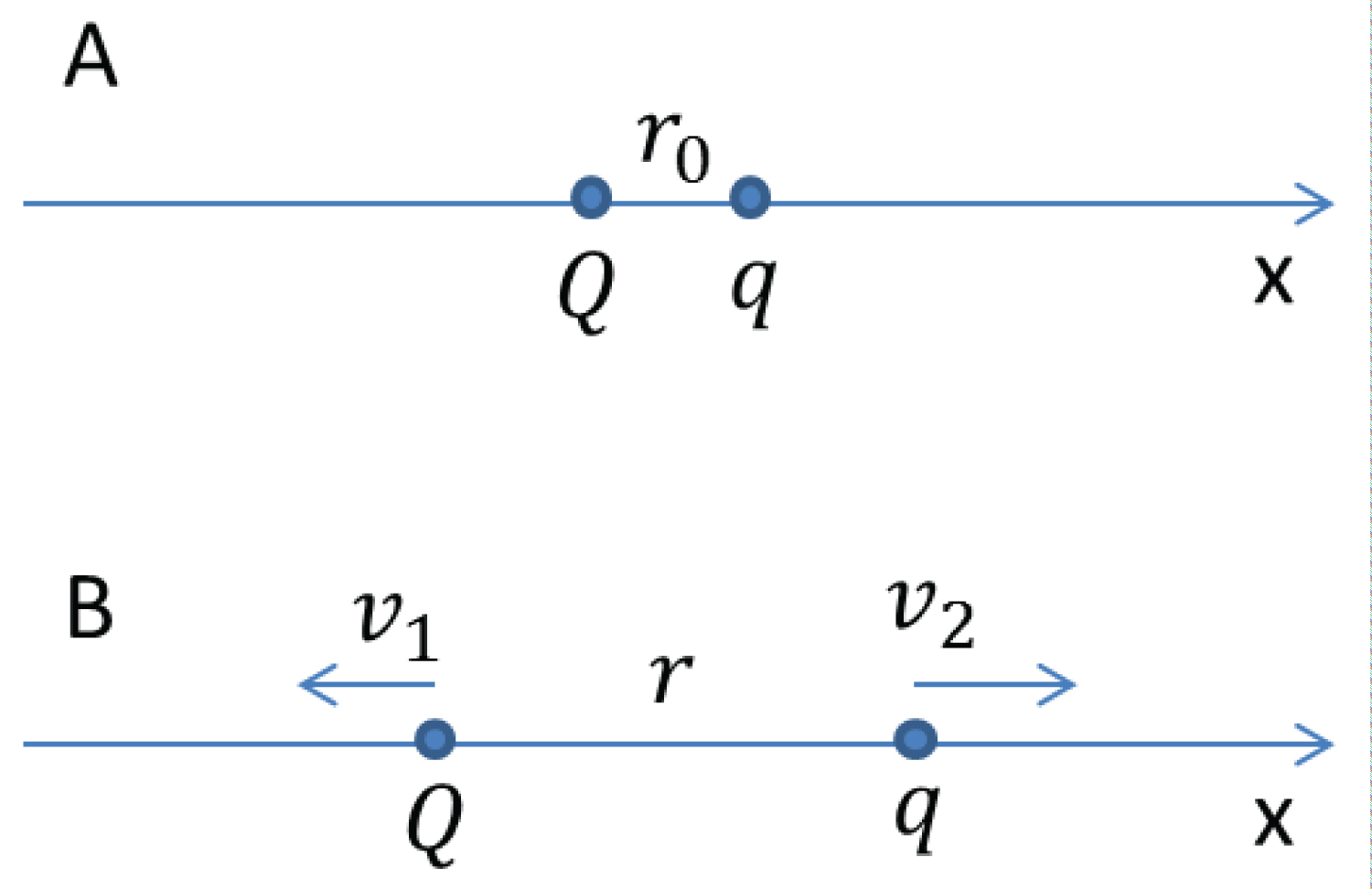
Figure 1: Both charge Q and charge...
A) Both charge Q and charge q are at rest and in a distance of r0 from each other; B) Two charges are in a distance of r from each other, with velocity and respectively.
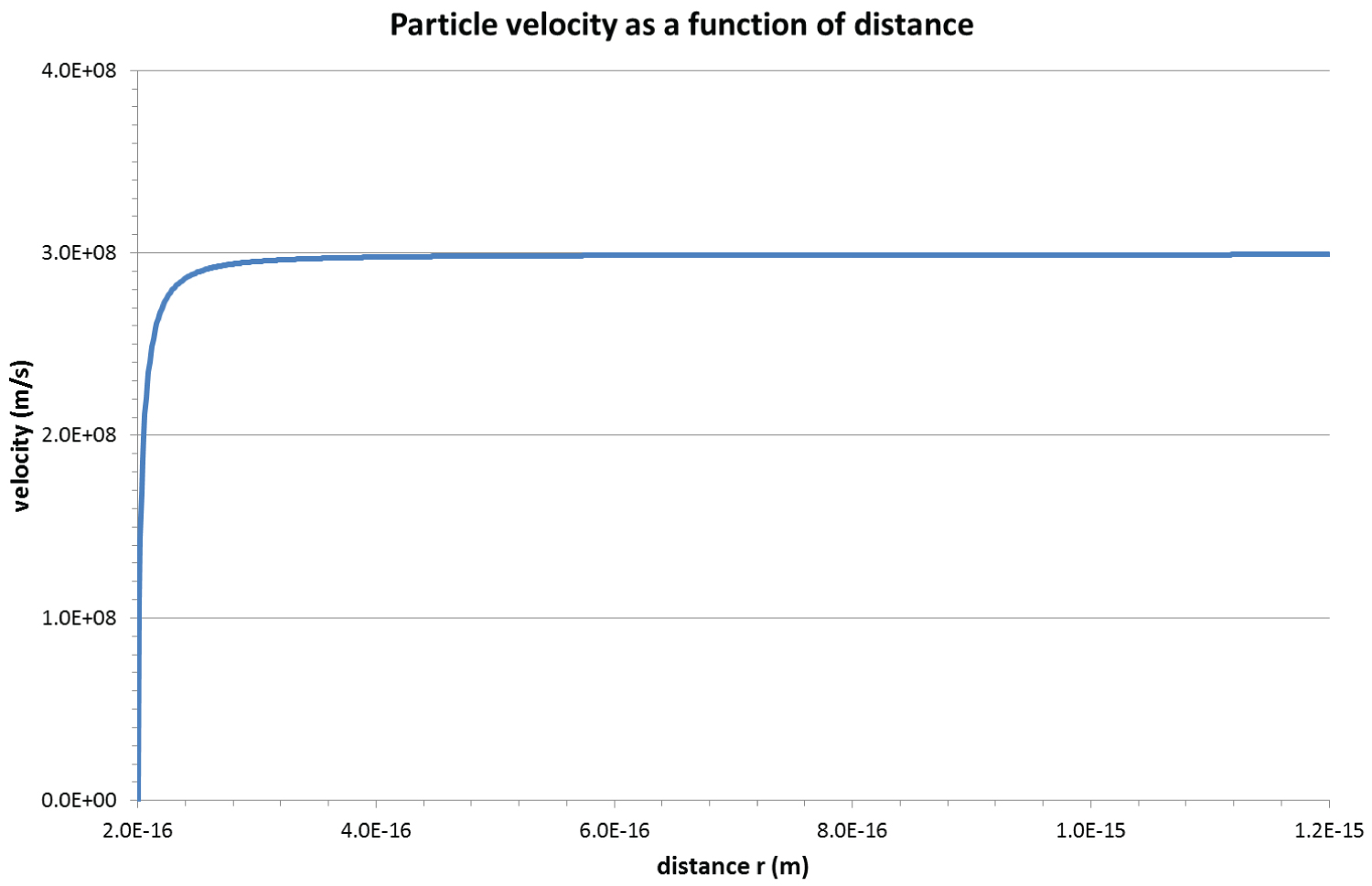
Figure 2: Illustration of particle velocity....
Illustration of particle velocity with equation (14) by assuming particle q is a positron, and particle Q has the same amount of charge as a positron.
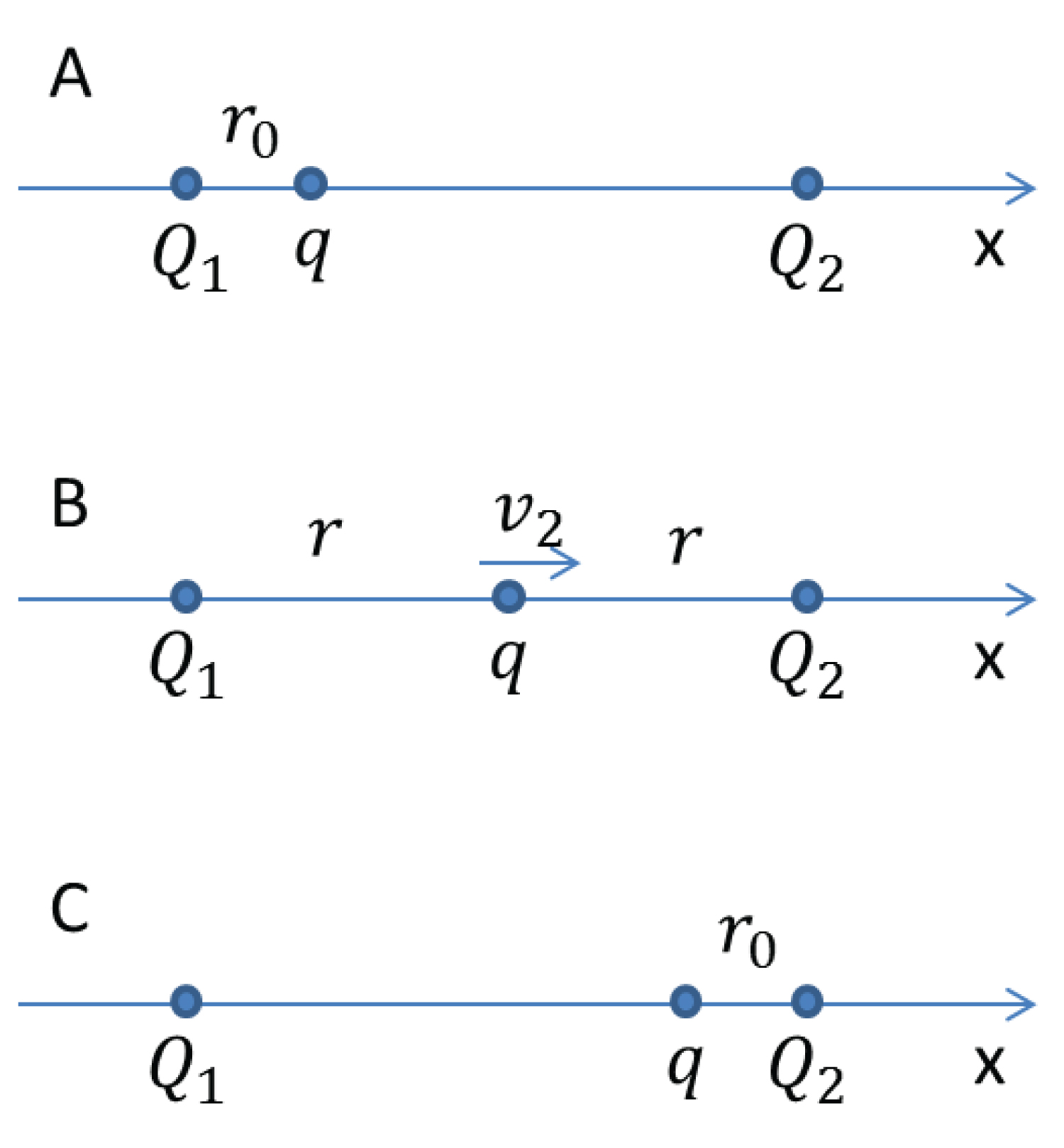
Figure 3: Both charges....
Both charges and are always at rest: A) The charge q is at rest; B) The charge q is accelerated to velocity ; C) The charge q is deaccelerated to rest again.

Figure 4: Illustration of particle energy by....
Illustration of particle energy by assuming particle q is a positron, and particle and have the same amount of charge as a positron. The new Weber-like potential energy and kinetic energy (equation 14) are compared with those from Special Relativity theory (equation 15).
References
- Wesley JP (1990) Weber electrodynamics, part I. general theory, steady current effects. Foundations of Physics Letters 3: 443-469.
- Assis AKT, Bueno M (1995) Longitudinal forces in Weber's electrodynamics. International Journal of Modern Physics B 9: 3689-3696.
- Assis AKT (1991) Can a steady current generate an electric field? Physics Essays 4: 109-114.
- Assis AKT (1992) Deriving gravitation from electromagnetism. Can J Phys 70: 330-340.
- Hernades JA, Assis AKT (2003) The potential, electric field and surface charges for a resistive long straight strip carrying a steady current. American Journal of Physics 71: 938-942.
- Hernandes JA, Assis AKT (2005) The electric field outside and inside a resistive spherical shell carrying a steady azimuthal current. Physica Scripta 72: 212-217.
- Assis AKT, Tajmar M (2017) Superconductivity with Weber's electrodynamics: The London moment and the Meissner effect. Annales de la Fondation Louis de Broglie 42: 307-350.
- Assis AKT, Tajmar M (2019) Rotation of a superconductor due to electromagnetic induction using Weber's electrodynamics. Annales de la Fondation Louis de Broglie 44: 111-123.
- Assis AKT, Fukai J, Carvalho HB (2000) Weberian induction. Physics Letters A 268: 274-278.
- Assis AKT, Torres Silva H (2000) Comparison between Weber's electrodynamics and classical electrodynamics. Pramana Journal of Physics 55: 393-404.
- Baumgärtel C, Smith RT, Maher S (2020) Accurately predicting electron beam deflections in fringing fields of a solenoid. Sci Rep 10: 10903.
- Steffen K (2021) Experimental investigation of an unusual induction effect and its interpretation as a necessary consequence of Weber electrodynamics. Journal of Electrical Engineering 72: 366-373.
- Li Q (2021) Electric field theory based on Weber's electrodynamics. Int J Magnetics Electromagnetism 7: 039.
- Caluzi JJ, Assis AKT (1997) A critical analysis of Helmholtz's argument against Weber's electrodynamics. Foundations of Physics 27: 1445-1452.
- Phipps Jr TE (1990) Toward modernization of Weber's force law. Physics Essays 3: 414-420.
- Assis AKT, Caluzi JJ (1991) A limitation of Weber's law. Physics Letters A 160: 25-30.
- William B (1964) Speed and kinetic energy of relativistic electrons. American Journal of Physics 32: 551-555.
- Caluzi JJ, Assis AKT (1995) An analysis of Phipps's potential energy. J Franklin Inst 332: 747-753.
- Assis AKT, Caluzi JJ (1999) Charged particle oscillating near a capacitor. Galilean Electrodynamics 10: 103-106.
- Roche J (2005) What is mass? European Journal of Physics 26: 225.
- Taylor EF, Wheeler JA (1992) Spacetime physics: Introduction to special relativity. WH Freeman and Company, New York, USA.
- Mach E (1960) The science of mechanics. Open Court, La Salle.
- Assis AKT (1989) On Mach's principle. Foundations of Physics Letters 2: 301-318.
- Assis AKT (1993) Changing the inertial mass of a charged particle. Journal of the Physical Society of Japan 62: 1418-1422.
Author Details
Qingsong Li*
Independent Researcher, Sugar Land, USA
Corresponding author
Qingsong Li, Independent Researcher, Sugar Land, Texas, USA.
Accepted: May 04, 2022 | Published Online: May 06, 2022
Citation: Li Q (2022) Extending Weber's Electrodynamics to High Velocity Particles. Int J Magnetics Electromagnetism 8:040
Copyright: © 2022 Li Q. This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
Weber's electrodynamics has been shown to explain electromagnetic phenomena by a number of researchers. It has a much simpler form for particle-particle interaction than the popularly used Maxwell equations. However, it has also been shown that Weber's electrodynamics got its limitations. It is not suitable for high velocity particles. And it had negative mass issue, causing non-physical explanation in some circumstances. In this article, we introduce a new theory of weber-like electrodynamics, trying to address the shortcomings of Weber's electrodynamics, and extending Weber's electrodynamics to high velocity particles.
Introduction
Weber's electrodynamics has been shown to explain electromagnetic phenomena, such as longitudinal force inside electric wire [1,2], anomalous diffusion in plasmas [3], deriving gravitation from electromagnetism [4], electric and magnetic fields surrounding current [5,6], the London moment and Meissner effect of superconductivity [7], and electromagnetic induction [8,9], etc. Weber's electrodynamics has a much simpler form for particle-particle interaction than the popularly used Maxwell equations and Lorentz force [10]. Moreover, Weber's electrodynamics explains the outcome of two recent electron beam experiments better than Maxwell-Lorentz electrodynamics [11,12]. For applications involving large quantity of particles, a new field theory based on Weber's electrodynamics has been introduced [13].
However, Weber's electrodynamics had been criticized for the negative mass issue by Helmholtz shortly after its introduction [14]. Inside a non-conducting charged spherical shell, a moving particle may gain a negative mass and its velocity may go without limit according to Weber's electrodynamics. Phipps tried to address this issue by introducing a modified form of Weber's electrodynamics [15]. Nevertheless, it was shown that Weber's electrodynamics does not apply to high velocity particles [16]. Particles may be accelerated to a velocity higher than light speed, contradicting the outcome of linear accelerator experiments [17]. Phipps's modified form of Weber's electrodynamics also suffers from this problem [18]. Later, the issue of unlimited velocity seems to have been solved by utilizing Schrodinger's kinetic energy instead of Newtonian kinetic energy [14,19]. Weber's electrodynamics plus Schrodinger's kinetic energy predict a particle oscillation pattern beside a capacitor that is different from the relativistic mechanics [19].
In this article, we introduce a new Weber-like theory of velocity-dependent potential energy and kinetic energy, which can be applied to particles of velocity close to light speed. Using this velocity-dependent potential energy, we can get a weber-like electrodynamic force. This new Weber-like theory may be seen as an extension of Weber's electrodynamics.
Weber-Like Potential Energy
Let's consider a two-body system along x-axis in a laboratory rest frame (Figure 1). Two charged particles (one with mass , charge Q, and the other with mass , charge q) are at rest and in a distance from each other (Figure 1a). The potential energy of the two-body system is:
Where is the permittivity. Because of the electric expelling force, the particles move away from each other. At one time point, they are in a distance from each other, and their velocities become and respectively (Figure 1b). We postulate that the potential energy of the two-body system becomes:
Where c is light speed. In this expression, the potential energy is velocity dependent. If , the potential energy is simplified to Coulomb potential:
If , then . The equation (2) still holds, and can be simplified to:
If is much less than , the equation (2) can be simplified to:
Except being one-dimensional, this expression is the same as the potential proposed by Phipps [15].
If is much less than , we can simplify equation (5) further by only keeping the first and second order terms:
Except being one-dimensional, this expression is exactly the same as the Weber's potential [10]. Thus the potential energy in this article can be seen as an extension of Weber's potential.
New Kinetic Energy and Momentum
We postulate new kinetic energy and momentum expressions by assuming a velocity dependent force-acceleration relationship:
Where m, v, F, and are a particle's mass, velocity, external force and acceleration respectively. The velocity dependency in equation (7) looks similar to relativistic mass [20]. However, here it is a coefficient of acceleration for force, instead of coefficient of velocity for momentum as in Special Relativity theory [21]. The new expressions of kinetic energy and moment can be derived:
When both particles are at rest in a laboratory rest frame (Figure 1a), the kinetic energy and momentum of the two-body system equal zero. When the two particles' velocities become and respectively (Figure 1b), we postulate that the kinetic energy and momentum of the two-body system become:
Where and are the mass additional to the original mass and . The original mass is the particle's mass when the particle is at rest and has no interacting nearby particles.
When two particles are far away from each other, the potential energy is fully converted to kinetic energy. The two particles achieved velocity and respectively. To calculate and in equation (9), we postulate these equations below:
To calculate and , we use equations of conservation of energy and conservation of momentum. The kinetic energy of two particles equal the initial potential energy, and the momentum of two particles equal zero.
From equations (10,11), we can see that additional mass are independent to particle's velocity and . Instead, they are determined with particles final velocity and when potential energy is fully converted to kinetic energy. After rearranging equations (10,11), we can get:
Thus the additional mass is also related to the initial potential energy , and can be seen as a constant, which does not change with particle's velocity. The initial potential energy and the sum of additional mass satisfy the energy-mass relationship, which was first introduced by Special Relativity theory [21].
Velocity and Energy of an Accelerated Particle
Let's consider the two-body system along x-axis in a laboratory rest frame (Figure 1). The two particles are at rest at the beginning, then their velocities become and respectively. According to energy conservation, the decrease of potential energy equals the increase of kinetic energy. From the equations (1), (2), and (9), we get:
The momentum of the two-body system (Equation 9) always equals zero, according to momentum conservation. Thus, if we assume that is way larger than , particle Q will stay at rest, i.e. and approximately equal zero. Using Equations (10, 12), we can get that and . Thus, Equation (13) can be simplified to:
The above equation shows that the particle velocity can be predicted given the initial Coulomb potential and the current Coulomb potential . The particle velocity can approach, but not exceed light speed (Figure 2).
This two-body system may be seen as a greatly simplified representation of the linear accelerator experiment [17]. The stationary particle Q represents the stationary accelerator instrument that creates electric potential, while the moving particle q represents an accelerated electron.
Equation (14) can be re-arranged as:
The above equation is the same as that would be given by Special Relativity theory [21]. The left side of the equation is the Coulomb potential energy change and the right side is the relativistic kinetic energy. Thus the velocity prediction of the new Weber-like theory would match to the linear accelerator experiment [17] the same as Special Relativity theory does.
Even though the predicted particle velocity is the same as that of Special Relativity theory, the potential and kinetic energy of the two theories are very different. To fully illustrate this difference, let's consider a charge q moving along x-axis, which is accelerated by one stationary charge . It is then approaching another stationary charge and being de-accelerated (Figure 3).
In the Special Relativity theory, the particle gains kinetic energy during acceleration. And kinetic energy is converted back to potential energy during de-acceleration. The Special Relativity theory states that the conversion amount is independent to particle velocity, instead only dependent on initial position and current position r (Figure 4).
However, the new Weber-like theory in this article indicates that the conversion is also dependent on velocity. The conversion amount between initial position and current position r is larger than that of Special Relativity theory (Figure 4).
Electrodynamic Force and Effective Mass
The electrodynamic force is the negative gradient of the potential energy. Let's again assume that particle Q is always at rest () (Figure 1). Then the electrodynamic force can be derived with equation (5):
The force in the above equation is the same as that derived by Phipps [15]. Its low velocity approximation can become the Weber's electrodynamic force [10].
Let's use the force-acceleration relationship (equation 7) together with the above equation (16). Note that particle has both original mass and additional mass . We can get:
Since Q is always at rest, we can get that and . After rearranging the above equation and using equation (15), we can get:
Thus, the effective mass (coefficient of acceleration in the right side of the above equation) is always positive in this specific case (one particle is moving and the other particle is always at rest).
Let's consider another scenario that particles Q and q are identical and particle velocities are much less than light speed (Figure 1). We can get , and . The electrodynamic force can be derived with equation (5):
Let's use the force-acceleration relationship (equation 7). We can get:
After rearranging above equation, we can get:
When the two particles are at rest, the effective mass (coefficient of acceleration in the right side of the above equation) can be simplified to:
If the two identical particles are very close to each other , the effective mass becomes negative according to the above equation. Otherwise, the effective mass stays positive.
Discussions
In the new Weber-like potential energy (equation 2), we introduce a term with respective to a laboratory rest frame. This potential energy expression works for cases when the relative velocity of two particles exceeds light speed, while the velocity of each particle stays below light speed. Because of this choice, we have to stick to the laboratory rest frame. If we switch to other reference frames, the new potential energy expression may not be valid. However, if the velocities are much less than light speed, the approximation of the new potential energy (equation 5) gains more flexibility, allowing coordinate systems other than the laboratory rest frame. It regains the relational properties the same way as Weber's electrodynamics does.
This article used a velocity dependent relationship between force and acceleration. It was proposed that mass (or inertia) is from the interactions with the bodies in the universe [22]. Using the Weber-like gravitational forces, Assis [23] derived a mass, which has a form independent to velocity. However, if a gravitational force similar to Phipps's electrodynamic force (or the force in this article) is used, the derived force-acceleration relationship could be velocity dependent and in a form as we postulated in this article.
To calculate the new Weber-like electrodynamic force, we need to know r, and , i.e. the current state of the two body system. However, to calculate particle acceleration, we also need to know the particle's mass, which include particle's original mass and the additional mass. The additional mass is related to the particle's energy, including potential energy (equation 12) and kinetic energy (equation 10). The mass-energy relation is the same as that introduced by Special Relativity theory [21]. To calculate the distribution of additional mass among particles, we need to use the laws of conservation of energy and momentum (equations 11). In the new theory, the total mass (original mass plus additional mass) has a conservation property, similar to energy conservation.
For the case of a charged particle inside a charged non-conducting shell, the new theory will not predict a negative mass (equation 18). Here, the shell is equivalent to the stationary particle, while the charged particle is equivalent to the moving particle. Since the potential energy between the particle and the shell gives an additional mass to the particle, the particle's mass will always be positive. This is different from the previous view using the Weber's electrodynamics and Newtonian kinetic energy [24]. However, when two particles are identical and both are free to move, we can still get negative mass (equation 22).
When one particle is far away from other particles, its kinetic energy in the new theory is in the same expression as that in Schodinger's kinetic energy [14] or the kinetic energy of Special Relativity theory [21]. However, the kinetic energy in the new theory is higher than the kinetic energy of Special Relativity theory if there is potential energy between this particle and a nearby particle (Figure 3).
In this article, the equations are given in a one-dimensional sense. However, it can be extended to 3-dimentional by replacing velocity/acceleration in the equations with some products among velocity/acceleration vectors and unit distance vector between two particles. Similar conversion from radial velocity/acceleration to 3D velocity/acceleration vectors can be found in applications of Weber's electrodynamics [8].
Conclusions
We introduce a new theory of Weber-like potential energy, kinetic energy, and electrodynamic force, which are an extension of Weber's electrodynamics. At low velocity, this new theory can be simplified to Weber's electrodynamics. Thus it shall be able to explain electromagnetic phenomena as Weber's electrodynamics does. On the other hand, the new theory overcomes the shortcoming of Weber's electrodynamics, such as negative mass of a charge inside a charged non-conducting shell. In the new theory, the particle velocity will not exceed light speed. At high velocity, the new theory is compatible with linear accelerator experiment result, which had only been explained by Special Relativity theory before.
Acknowledgment
The author thanks professor Andre Koch Torres Assis and the anonymous viewer for their constructive comments.

