Challenge from O2O model: How can Takeaway Merchants Pricing with Advantages?

International Journal of Industrial and Operations Research
(ISSN: 2633-8947 )
Volume 7, Issue 1
Research Article
DOI: 10.35840/2633-8947/6519
Challenge from O2O model: How can Takeaway Merchants Pricing with Advantages?
TAN Xin-yue, PAN Zhen-dong and TANG Jia-fu
Table of Content
Figures
Tables
Table 1: Symbols and meanings.
Table 2: Platforms' commission to merchants in the three scenarios and the dominant merchant in each specific area.
Table 3: The conditions of equilibrium-points’ positions in the SC2 scenario.
Table 4: The conditions of equilibrium-points’ positions in the SC3 scenario.
Table 5: Advices for pricing strategies based on trust advantage.
Table 6: The spread between merchants A and B.
Table 7: The impact of add-on ratio of commission on merchant optimal pricing.
References
- Rampell A (2010) Why online-2-offline commerce is a trillion dollar opportunity. Tech-Crunch 8.7.
- Beijing Smart Research Consulting (2017) China takeaway O2O industry 2017-2022 Deep market research report Deep Research Report. China Industry Information Network.
- Deqing MA, Jinsong HU, Wang W (2021) Differential game of product-service supply chain considering consumers' reference effect and members' reciprocity altruism under O2O mode. Journal of Industrial Engineering and Engineering Management 35: 151-167.
- He H, Jing D, Yi C (2023) Optimal Pricing and CSR Investment Strategy of the online retailer in O2O mode. Chinese Journal of Management Science 31: 162-172.
- Yong-wu Z, Xin-xin G, Bin C, Xiao-Gang L, Qiang L (2023) Research on price strategy selection of instant freight service sharing platform. Chinese Journal of Management Science 31: 111-121.
- Cong W, Deli Y (2017) Research into O20 sales strategy of uniform price online and offline based on chain-to-chain competition. Operations Research and Management Science 26: 74-80.
- Chunqiao T, Xin W, Li Z (2021) Game analysis for pricing strategies in 020 logistic service supply chain with fairness concern. Operations Research and Management Science 30: 80-85.
- Liwen J, Shoufeng J, Qi S, Yu H (2016) Pricing and ordering strategies of online to offline brand manufacturer based on competitive and cooperative games. Systems Engineering-Theory & Practice 36: 1951-1961.
- Xue Y, Xiaofeng L (2021) Research on pricing and cooperation strategy of dual-channel after-sales service for compound e-commerce platform. Price: Theory & Practice 45: 1-4.
- Li Z, Xingzheng A, Xue-feng D (2021) The pricing and incentive contract design with the product performance improvement of "hardware/software" platform. Chinese Journal of Management Science 26: 1-12.
- Xuemei Z, Haoran C, Zhi L, Guo-Hu Q (2021) Strategies of pricing and channel mode in a supply chain considering showrooms effect. Control and Decision 32: 1-10.
- Li Y, Yu X, Mariuzzo F, Xia S (2021) The underexplored impacts of online consumer reviews: Pricing and new product design strategies in the O2O supply chain. International Journal of Production Economics 237: 108148.
- He Z, Cheng T, Dong J, Wang S (2016) Evolutionary location and pricing strategies for service merchants in competitive O2O markets. European Journal of Operational Research 254: 595-609.
- Pei Z, Wooldridge BR, Swimberghe KR (2020) Manufacturer rebate and channel coordination in O2O retailing. Journal of Retailing and Consumer Services 56: 58-78.
- Liang J (2019) Optimal pricing and offline to online channel strategies undermoney-back guarantees. Journal of Systems Engineering 34: 226-237.
- Ruozhen Q, Xuge L (2021) Online retailer's inventory information disclosure and joint pricing and inventory decision model with strategic consumers. Chinese Journal of Management Science 29: 59-71.
- Fuchang L, Fengrui L (2021) Joint optimization of dual-channel pricing and inventory based on revenue sharing under differential pricing. Soft Science 35: 131-136.
- He P, He Y, Xu H, Zhou L (2019) Online selling mode choice and pricing in an O2O tourism supply chain considering corporate social responsibility. Electronic Commerce Research and Applications 38: 100894.
- Liang J, Benrong Z, Lianke S (2020) Pricing policies and offline to online channel strategies with asymmetric information. Chinese Journal of Management Science 28: 89-103.
- Han Z (2021) Research on sharing economy in the context of O2O. Systems Engineering-Theory & Practice 41: 411-420.
- Weihao W, Jinsong H (2021) Study of dynamic pricing and service decision in supply chain integrating online and offline channel. Operations Research and Management Science 30: 84-91.
- Wenju N, Jing X (2021) Product innovation and pricing strategies in the presence of strategic consumers. Operations Research and Management Science 30: 154-160.
- Na Z, Zhen-zhong G (2020) Optimal pricing strategy of price-quality competition under the salience theory. Operations Research and Management Science 29: 186-195.
- Tong T, Dai H, Xiao Q, Yan N (2020) Will dynamic pricing outperform? Theoretical analysis and empirical evidence from O2O on-demand food service market. International Journal of Production Economics 219: 375-385.
- Peng X, Tian-run H (2020) Optimal quality effort strategy in O20 food delivery service supply chain based on three operation models. Chinese Journal of Management Science 28: 115-126.
- Hou H, Zhao C (2021) Service-enhancement Investments and price competition in a hotelling model. Journal of Innovation and Social Science Research 8: 45-62.
- Economides N (1986) Minimal and maximal product differentiation in Hotelling's duopoly. Economics Letters 21: 67-71.
- Gabszewicz J, Thisse JF (1986) On the nature of competition with differentiated products. Economic Journal 96: 160-172.
- Marcotte P, Zhu DL (1997) Equilibrium with infinitely many differentiated classes of customers in complementarities and variational problems. In: Pang JS, Ferris M, Proceedings of the 13 th International Conference on Complementarities Problems: Engineering and Economics and Applications and Computational Methods. SIAM, Philadelphia, 28: 234-258.
- Reisinger M (2012) Platform competition for advertisers and users in media markets. International Journal of Industrial Organization 30: 243-252.
- Jian-bin L, Pengcheng W, Xiaomeng L (2021) The omnichannel competitive optimization strategy under duopoly. Operations Research and Management Science 30: 1-8.
- Wenjun J (2021) Will data advantages increase platform companies' pricing? - model derivation and theoretical analysis. Chinese Journal of Management Science 29: 227-237.
- Tang CS (2010) A review of marketing-operations interface models: From co-existence to coordination and collaboration. International Journal of Production Economics 125: 22-40.
Author Details
TAN Xin-yue*, PAN Zhen-dong and TANG Jia-fu
School of Management Science and Engineering, Dongbei University of Finance and Economics, Dalian 116025, China
Corresponding author
TAN Xin-yue, School of Management Science and Engineering, Dongbei University of Finance and Economics, Dalian 116025, China.
Accepted: March 05, 2024 | Published Online: March 07, 2024
Citation: Xin-yue T, Zhen-dong P, Jia-fu T (2024) Challenge from O2O model: How can Takeaway Merchants Pricing with Advantages?. Int J Ind Operations Res 7:019.
Copyright: © 2024 Xin-yue T, et al. This This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
O2O (Online to Offline) as a new business model is widely used in the takeaway industry. With Hotelling model, the study found the market equilibrium conditions. Further, location advantage, trust advantage, price difference with rivals and platform pricing all affect their optimal pricing strategy. The study found that (1) The optimal pricing strategy of the decision merchant is the highest, when the equilibrium points fall in a region where the location advantage of the two merchants is equal; (2) The optimal pricing of the merchant increases with the trust advantage, and it enhances with market competitive level; (3) The price difference between two merchants also increases with the trust advantage. The merchant's optimal pricing strategy various in different scenarios in response to changes in platform add-on commission ratio. These results provide a management reference to decision making of O2O takeaway merchants in different competitive scenarios.
Keywords
Hotelling model, Location advantage, Trust advantage, Pricing strategy, O2O takeaway
Introduction
As a new business model, the O2O model [1], featuring the integration of online and offline consumer services, can often be found in life today. The application of O2O model in the catering takeaway industry is a typical example. Resent years the consumers who prefer to order food online and deliver it offline has increased. Facing this demand, the number of O2O catering merchants surging [2]. Hence, pricing strategies can be seen as an effective instrument to enhance competitiveness. How to pricing with advantages is a critical issue for catering merchants to fitting for O2O model.
In light of consumer predilection, operating cost and marketplace rivalry, prevailing pricing methodologies of merchants encompass consumer-centric, cost-sensitive [3], and market-driven [4] strategic approaches. The swift transmission of goods from merchant to consumer, called delivery Instant, is a crucial element which separates O2O catering takeaway from other products' conventional logistics. Obviously, the proximity between merchants and patrons has both a pivotal role in ensuring prompt deliveries, while simultaneously influencing the merchant's payment towards the platform, thereby directly impacting merchant's operational expenditure. As consumers trade off with price and delivery time whilst placing their food orders, the slighter the distance between the distance connecting the merchants with consumers, the more pronounced the rivalry by pricing amongst both businesses operating within that vicinity. Consequently, our research delineates a three classification of competitive scenarios according to merchant's distance, scrutinizing the market equilibrium conditions and the superior pricing strategies of merchants.
Currently, broad cross-industry collaborative studies on O2O pricing strategies encompass several decisive elements. Primarily, the entities involved in pricing decision making such as platforms [5], retailers [6], and suppliers [7]. Subsequently, various items subject to pricing - from tangible goods [8], services [9] to digital content [10]. Moreover, the information situation [11], customer attributes and purchasing tendencies [12], market competitiveness [13], commerce channels [14], and returns mechanism [15] are all key factors to pricing strategy within the O2O model. The decision-making contents include product (service) pricing decision [16], joint inventory and pricing decision [17], joint quality and pricing decision [18], joint information disclosure and pricing decision [19]; and from the perspective of market information updating include: static pricing [20] and dynamic pricing [21]. Pricing strategies cover a wide range of methods and techniques, among which some major pricing strategies include: "cost plus pricing strategy" which based cost to keep profit margins, "target profit pricing strategies" to achieve higher expected profit margins, and "low price pricing strategies" to attract consumers with lower prices, "flexible pricing strategies" that adjust prices according to market conditions, "penetration pricing strategies" which aimed at increasing new product awareness and quickly opening up the market, as well as" discount promotion strategies" that can effectively promote product sales [22-25].
The basic Hotelling model and its extension demonstrate significant superiority for exploring market pricing reflection involving spatial variation. These spatial differences are not only limited to physical space, but also cover a wider range of product characteristics, which are used to analyzing the impact of transaction costs on consumers' purchasing decisions in terms of the distance between the physical location of a merchant and its distance, and to provide strong basis to guide firms' location and pricing strategies [26]. Since then, Economides N, Gabszewicz and Marcotte have made some innovative improvements and extensions to the above basic theoretical models from different perspectives [27-29], including converting the form of the cost function, adjusting the assumption of a uniform distribution of consumers to a non-uniform distribution, and even expanding the model from a single-stage model to a multi-stage model. It is worth mentioning that under the emerging O2O (Online to Offline) model, related studies using this theoretical framework for in-depth analysis have mainly focused on the issues of differentiated platform competition [30], the choice of sales channel model [31], and price strategy [32]. Among the issues we focus on, the geographic distance between merchants and between with consumers and merchants are undoubtedly one of the key factors. The time cost that O2O takeaway consumers pay to wait for the ordered meal can also be regarded as travelling cost.
Therefore, this paper explores the market equilibrium conditions under three types of competitive environments, namely, fierce, medium and light, using the Hotelling model; and quantitatively analyses the impact of the trust effect on merchants' pricing decisions and the interdependence of merchants' pricing strategies under various equilibrium conditions. In addition, the article explores how merchants should adjust their pricing strategies to maintain their competitive advantages when the platforms increase the percentage of commission they extract from merchants. Finally, the study applies the Hotelling model to the pricing problem of merchants in the O2O catering industry and proposes corresponding strategies so that merchants can seize the first opportunity through accurate pricing.
Model Description and Research Case
Problem description
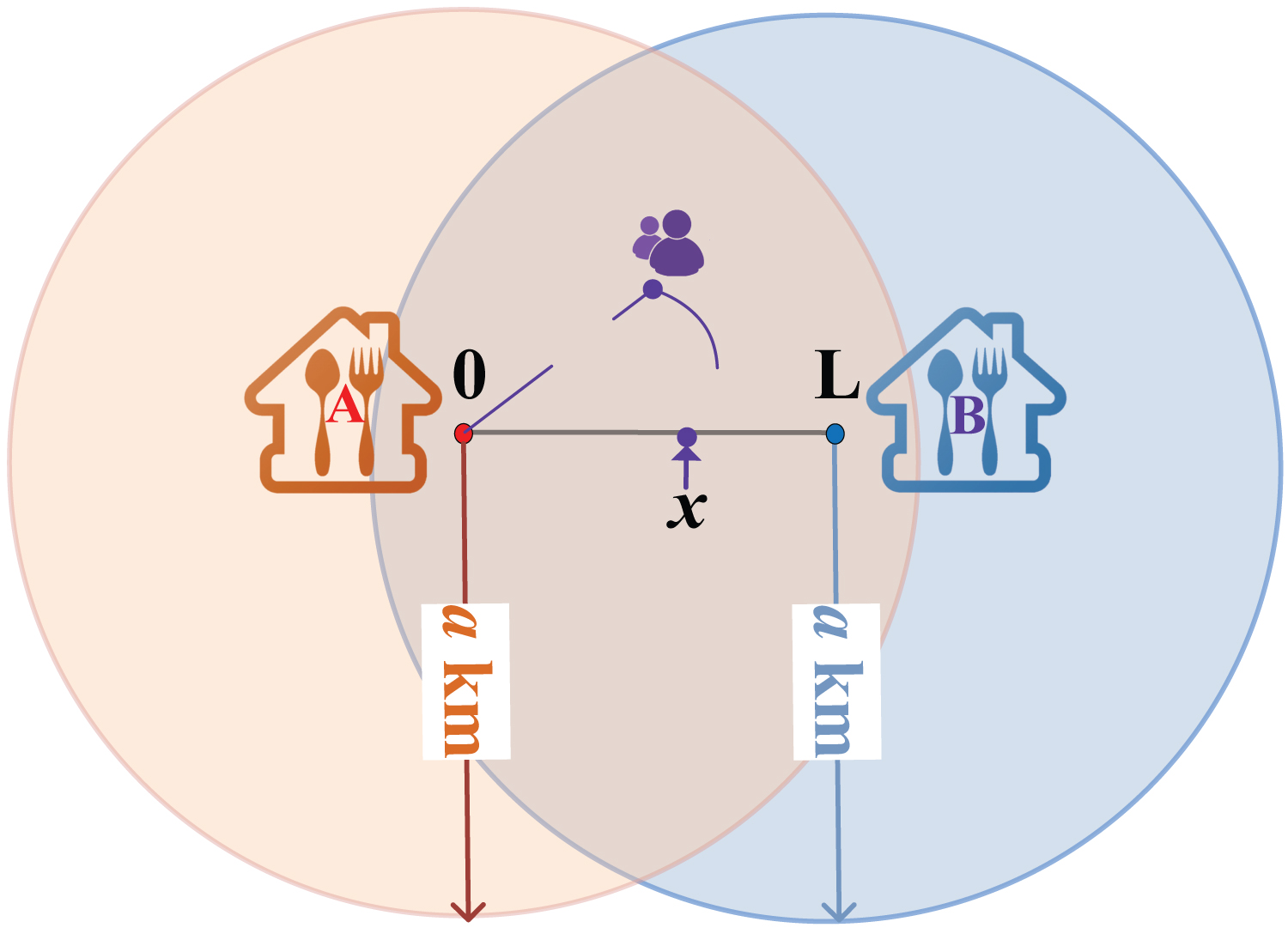
First, assume that the distance between decision merchant A and its competitor B is , which both sell takeout on the O2O platform at the same time. To simplify the model, we reduce the production cost () of both parties to zero . The platform uniformly delivers the meals and fully covers the costs incurred in the process, while the merchants must pay a certain percentage of commission to the platform. The platform adopts a uniform commission extraction method for both merchants: for orders with a delivery distance less than a kilometer, only a fixed commission is charged; for orders exceeding a kilometer, an additional commission of τ yuan per kilometer is extracted. For the sake of analysis, we define the location of the consumer on the straight-line connecting merchants A and B, assume that the consumer is uniformly distributed on this straight line (Figure 1).
Using the Hotelling model in three different scenarios, determine the conditions required for merchants A and B to obtain the highest profit equilibrium point. Through comparative analysis, explore the optimal pricing strategy of merchant A in various scenarios. To meet the demand of O2O consumers for fast pace, the model links consumer utility to waiting time for service, meaning that the shorter the customer's waiting time, the higher their utility will be.
Assuming that merchant A is the origin of the coordinates and the geographical location of the consumer is denoted as x, the value of x is the actual distance between the two. According to previous research, the waiting time cost is set as a quadratic function of the distance between the consumer and the merchant [33], and the parameter reflects the time cost that increases with the distance. Assuming that a consumer can only choose between merchant A and merchant B to order takeaway, the decision process can be summarized as a utility maximization problem. For example, when a consumer places an order with merchant A, the utility obtained by the consumer depends on the residual of the quality value of the meal minus the actual payment and the waiting time cost, which can be represented by . Similarly, when a consumer places an order with merchant B, the utility is expressed as . When is true, consumers will tend to choose merchant A. On the other hand, they will be more likely to choose merchant B. The symbols and their meanings in this paper, see Table 1 for details.
Scenarios description and cases identification
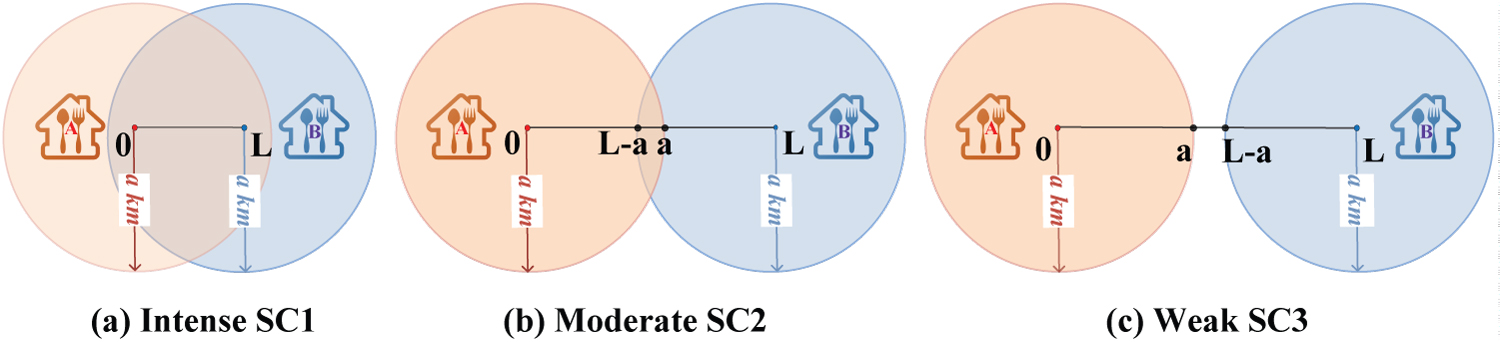
The closer merchants A and B are, the more intense their competition becomes. There are three scenarios based on the distance of the two merchants, as shown in Figure 2. Specifically, when the distance between merchants A and B is less than a kilometer ( ), the two merchants are most competitive. When the distance between merchants A and B is between a and 2a kilometers ( ), the two merchants have an intermediate level of competition. When the distance between merchants A and B is greater than 2a kilometers (), the competition between the two merchants is mild. Figure 2a, Figure 2b and Figure 2c depict each of these three scenarios and gives more details.
Merchants usually have two types of advantages over their competitors: Location advantage and Trust Advantage . Firstly, Location advantages , it is called that a merchant is considered to be in advantageous geographic location when the platform commission from the merchant is lower than that of his competitors. Moreover, consumers are more inclined towards businesses nearer to them. Hence, the location advantage of a business attracts a wider consumer base. In other words, it results in higher demand and lower commission cost for merchants. In the three scenarios mentioned above, the merchants with geographic location advantages and their corresponding commissions to be paid are shown in Table 2.
Secondly, Trust Advantage , if a merchant offers a meal that gains higher utility from consumers than its competitors, then this is known as the merchant's trust advantage. Consumers' trust in merchants comes from expectations of meal quality and delivery service. Consumer trust in businesses stems from considerations such as food quality and delivery efficiency. Obviously, the closer a customer is to a merchant's location, the more likely they are to experience good delivery service and shorter wait times, resulting in higher utility. Denote the Trust advantage by and , when holds, consumers' trust lies with merchant A over B; otherwise, their inclination is for B.
Conditions for Equilibrium in Three Scenarios
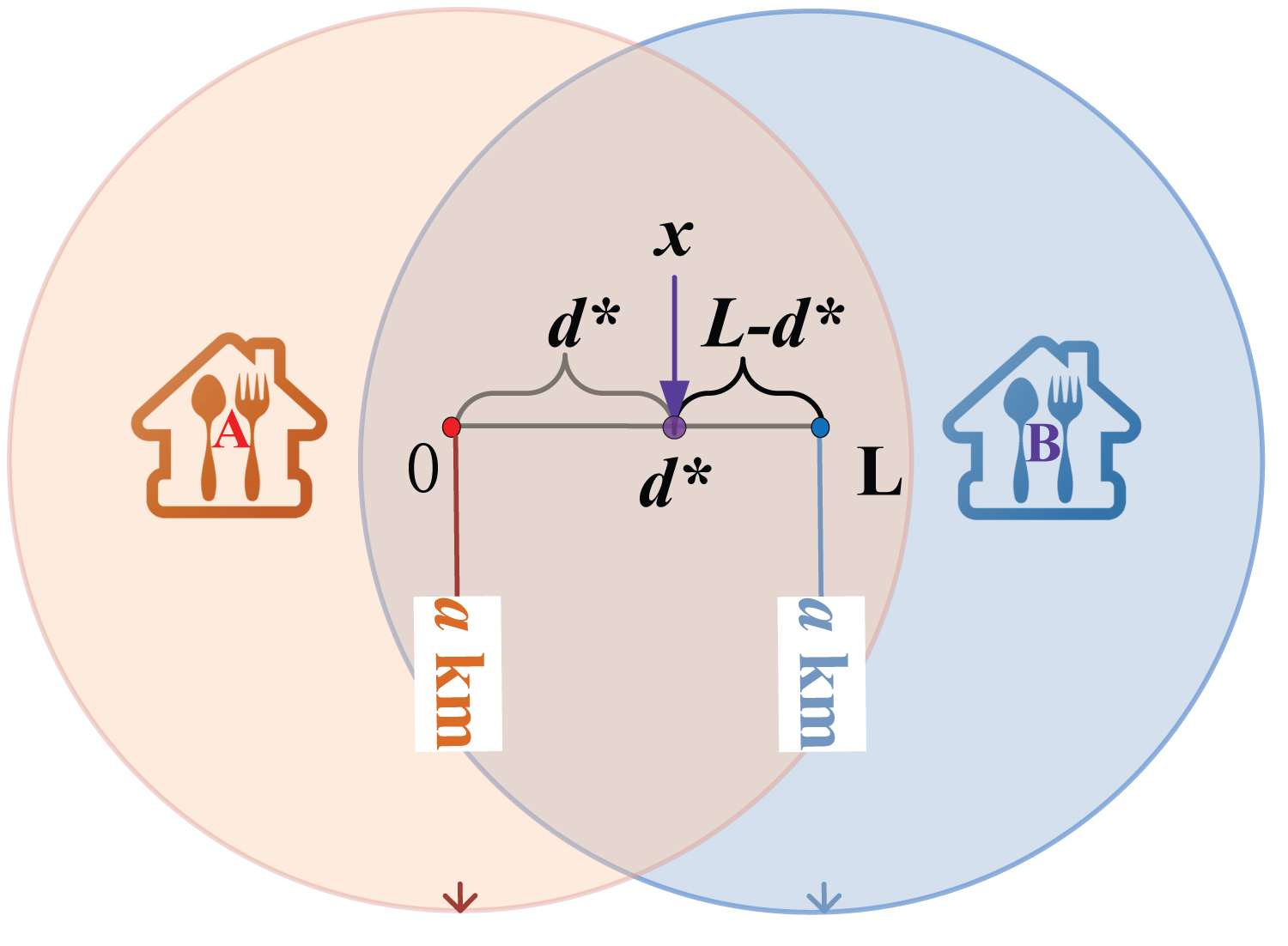
The market reaches equilibrium on Hotelling's model with condition satisfied. In the classic Hotelling model, customers pay travel costs for items. However, in an online-to-offline (O2O) retail situation, waiting time equates to travel cost post-order. Positioned at point denotes the equilibrium.
Lemma 1: The equilibrium point, identified as , is based on merchant A's demand formula at and merchant B's demand formula at .
Proof: Upon meeting condition , equilibrium is attained., the condition equals to and thus the equilibrium point's location can be identified as . Proof completed.
Since consumers strive for maximum utility, those at area are likely to buy from Merchant A, while those at area will opt for Merchant B's offerings. Should a consumer sit exactly at point , its probability of buying food from either party is equal. Thus, the equilibrium point determines A's and B's sales territory size.
SC1: Scenario of intense competition
Figure 3 lists the scenario SC1, the platform charges a basic commission of against both merchants within their competitive zone. Each merchant reaps as revenue from each order, thereby yielding a total profit reported as and for merchants A and B respectively.
Proposition 1: When , there is an equilibrium in the market under SC1 scenario , and the equilibrium point A is located in the interval .
To express clearly, use notation to denote optimal pricing for each merchant in different case. Subscript i signified the pricing of merchant i, with superscript denoting cases where the equilibrium point is placed at a merchant's location advantage (when located in both merchants without geographical superiority are labeled N) in different case. For example, indicates optimal pricing for merchant A under SC2 scenario when located in A's location advantage position.
Proof: Equilibrium prices and can be obtained by taking the first order partial derivatives of formulae and . Substituting and into , reveals that equilibrium existence hinges only on fulfilling condition . Due to , always hold, therefore, in scenario SC1, the equilibrium point must exist. Proof completed.
SC2: Scenario of moderate competition
Figure 4 lists the cases in (a), (b), and (c) where the equilibrium point is located at different positions in the SC2 scenario.
Proposition 2: The conditions required for different equilibrium-points’ positions in the SC2 scenario are shown in Table 3.
Proof: When located between , haven . The profits of merchants A and B are , respectively. Equilibrium prices and can be obtained by taking the first order partial derivatives of formulae. Substituting into the expression for , to yields condition .
When located between , haven . The profits of merchants A and B are , respectively. Equilibrium prices and can be obtained by taking the first order partial derivatives of formulae. Substituting into the expression for , to yields condition .
When located between , haven . The profits of merchants A and B are , respectively. Equilibrium prices and can be obtained by taking the first order partial derivatives of formulae. Substituting into the expression for , to yields condition .
Due to , always hold, means . Therefore, in scenario SC2, the equilibrium point must exist. Proof completed.
SC3: Scenario of Weak Competition
Figure 5 lists the cases in (a), (b), and (c) where the equilibrium point is located at different positions in the SC3 scenario.
Proposition 3: The conditions required for different equilibrium-points’ positions in the SC3 scenario are shown in Table 4 .
Similarly, the conditions for the existence of the equilibrium point position in scenario SC3 can be obtained, such as Proposition 3. Due to , always hold, means . Therefore, in scenario SC3, the equilibrium point must exist. Proof completed.
Analysis of the Impact of Different Factors on Merchants' Optimal Pricing
The impact of trust advantage on pricing strategy
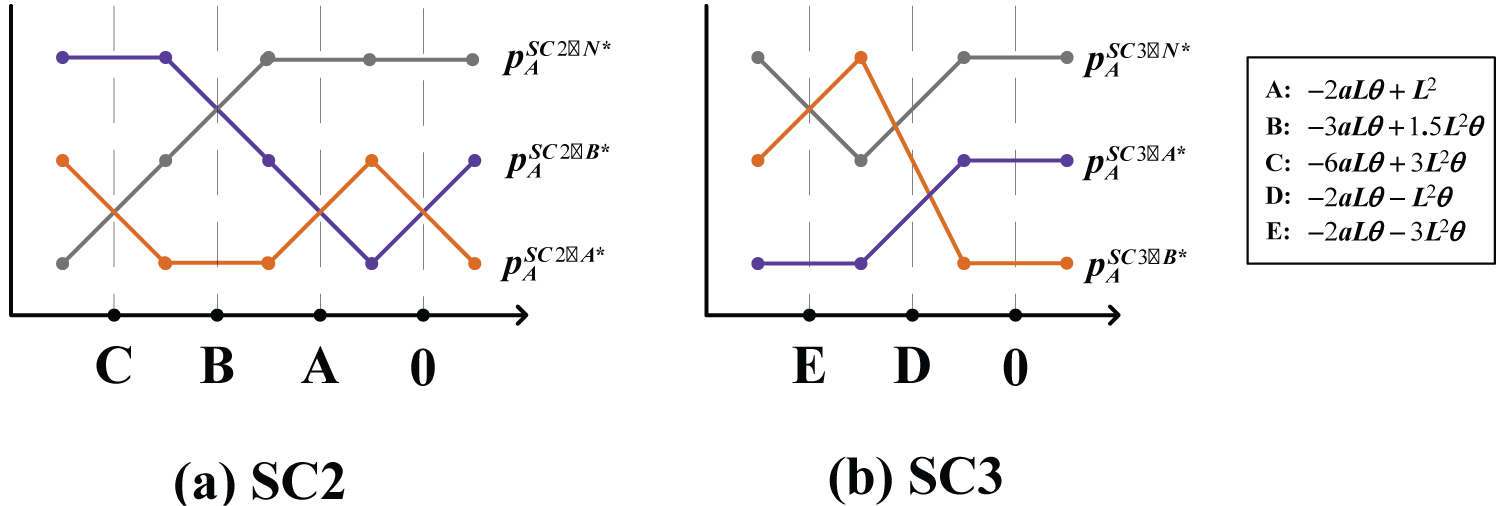
Prior studies have elucidated that the equilibrium point will fall in locations with differently location advantage, thereby yielding multiple cases. ,the results are presented specifically in Appendix - Table 1. Can any relationship be discerned between merchants' optimal pricing across these cases? For instance, under moderate competition, which case results in highest optimal pricing for Merchant A and which factors dictate this result? What are the specific conditions?
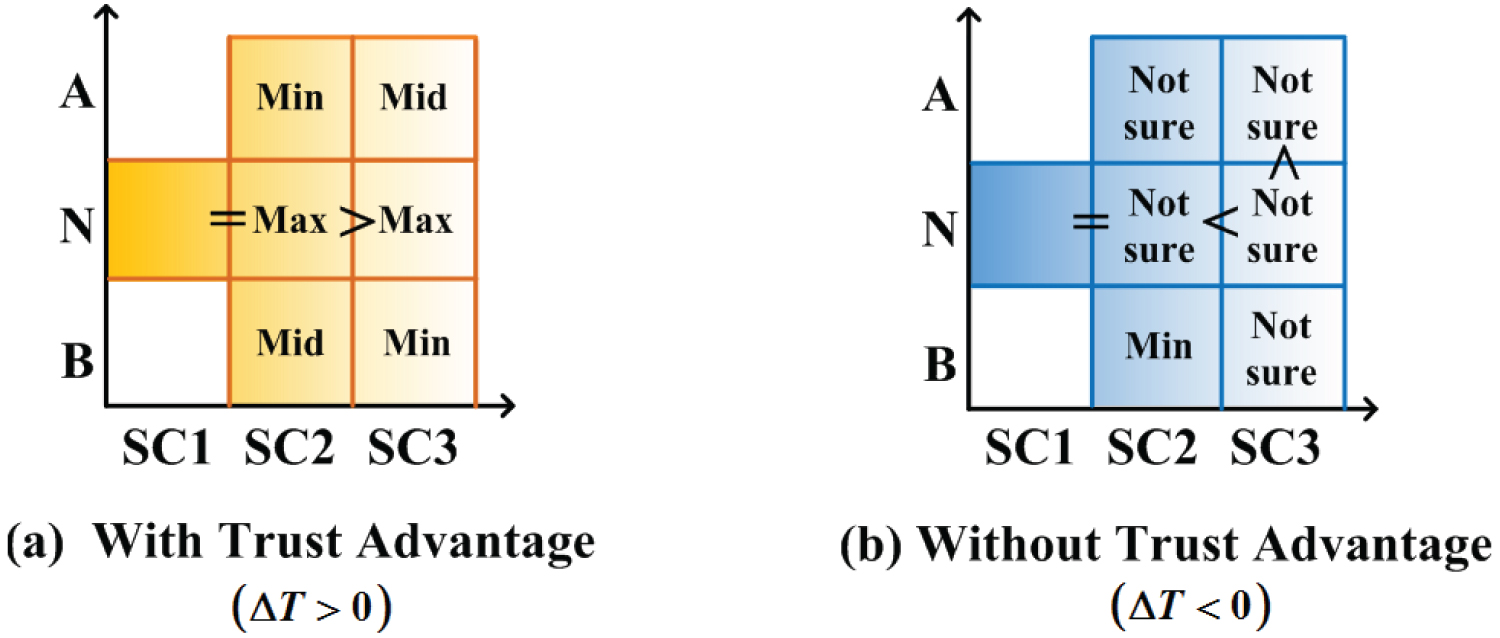
The study unearthed a correlation between the order of optimal pricings and merchant's trust advantage across different cases, illustrated by Figure 6. By the way, in SC1 only one case hence ignored. The optimal pricing relation in scenario SC2 and scenario SC3 are graphically represented in Figures 6a and Figures 6b, respectively.
Corollary 1: When Decision Merchant A has trust advantage ( ), both SC2 and SC3 scenarios have .
According to Corollary 1, if Merchant A has trust advantage, it can set the optimal price higher than other situations in an equilibrium state where both parties have no location advantage. Another interesting phenomenon can be found: when the equilibrium point is located in the geographically advantageous location of the decision-making merchant A, the demand of merchant A is smaller than that of its rival merchant B, and the optimal pricing of the merchant A is the lowest compared to the scenarios where the equilibrium point is located in the other regions. When the equilibrium point is located in an area where the two merchants neither have none geographic advantages, the demand of the decision merchant is similar to that of its rival merchant, and the optimal pricing of merchant A is the highest compared to the case of other equilibrium point location. When the equilibrium-point falls in the region where merchant A has a disadvantageous location, the demand of merchant A is greater than that of its rival, and the optimal pricing of merchant A is in the middle of the all cases.
This suggests that when the equilibrium point is located in the geographically advantageous position of merchant A, the decision-making merchant needs to reduce its price to pass on the reduced cost of the geographic advantage to the consumers; when the equilibrium point is located in the none geographically advantageous position of neither merchant A nor B, the decision-making merchant A, on the contrary, can set the highest optimal price in comparison with the other cases. When the equilibrium point is located in the geographically disadvantaged position of merchant A, the decision maker needs to reduce the price to maintain the demand.
Corollary 2 : When Opponent Merchant B has trust advantage (), in scenario SC3, exist .
From Corollary 2, when decision merchant A does not have trust advantage,if market with weak competition, it can be found that the optimal price for A in neither none geographically advantaged position case always higher than the optimal price in case of geographically disadvantaged position.
How does trust superiority influence pricing in varying competitive markets? The answer is presented by Corollary 3.
Corollary 3 : When , exist , When , exist .
Examining optimal A pricing under three competition scenarios with both A and B location advantages missing, it can be observed the prices of high and moderate competitions always keep the same pace. Conversely, when A lacking this advantage, the weakest competition scenario witnesses maximum pricing for A. However, when A holds a trust advantage, their minimal optimum pricing occurs within this market segment. That is, when decision maker A has a trust advantage, the more competitive the market is the higher its optimal pricing, otherwise, the less competitive the market is the higher its optimal pricing.
Based on the above analysis two perspectives can be suggested for the pricing approach adopted by decision making merchant A:
(1) When decision merchant A have trust advantage ( ):
In a moderately competitive environment (SC2), a merchant may implement a Discounted Promotional Strategy if it is faced with a situation in which it can only offer a limited number of meals due to seasonal constraints on ingredients, such as seasonal or production cycles and other factors. This may seem counterintuitive, but when a merchant has gained the trust of consumers, lowering prices can attract more people to order. By increasing sales, the merchant is still able to grow profits and stabilize its competitive position, thereby further expanding its market share. In a market environment where market share is high and production costs are low, companies may choose to control prices by using strategies such as Cost-plus Pricing Strategy or Target Profit Pricing Strategy to maintain and increase their market share.
In a weakly competitive environment (SC3), when a business operation encounters a situation where the customer's reputation is highly recognized but the demand for food and beverage products is low, the business owner should proactively take measures to reduce production costs and implement a Low-price Strategy in order to increase sales. Examples of this are when a long-established brand has just launched a new product that they have developed, or when a merchant which offers food with a shorter shelf life. If the merchant has successfully developed a quality brand image and dominant position in the market, it can try to adopt a Precise Segmentation Pricing Strategy and differentiate pricing based on consumers' perception of the value of the product in order to obtain a larger consumer surplus.
In light of the scenarios of SC1 and SC2, should there be no unique attributes associated with the merchant's catering products offering, it is feasible for them to endorse a pricing strategy of 'Going-rate Pricing Strategy' . This allows for coexistence amongst industry competitors amid an atmosphere of equilibrium, thereby circumventing potential market instability emanating risk from intense competition.
(2) When decision merchant A does not have trust advantage ( ):
In a moderately competitive environment (SC2), Penetration Pricing Strategy is a prior-choose strategy for merchants that lack market recognition and have only average quality meals. This approach aims to attracting consumers with a relatively moderate price with a view to stimulating market demand and consolidating merchants' position.
Faced with the occasion to launch highly anticipated and well-known new products, businesses can use Discount Promotion Strategy to attract a large number of consumers. For example, when specialty food from other regions moves into new markets, or when online celebrity stores expand their business scale, such pricing strategies are suitable.
The specific advices cope with different market competition level, such as pricing strategies, pricing purposes, and applicable contexts, are summarized in Table 5.
Spreads between the merchant and its rival
The spread between the optimal prices of merchants A and B when the equilibrium point is at different locations in the three scenarios is shown in Table 6. Express as
At what level of market competition is the magnitude of price differences between merchants most significant? What impact will location advantage and trust advantage have on the price Spreads? The relevant answer can be found in the following corollary.
Corollary 4 : Exist .
Corollary 4 shows that, when neither merchant A nor B has a location advantage, the spread between the optimal pricing of merchants in the intensely and moderately competitive scenarios is equal and greater than the spread in the weak competitive market scenario. This suggests that the degree of competition is not only determined by the distance between merchants, but also by price differentials with its rival. In other words, when the distance between two merchants is relatively far, their price spreads will decrease accordingly. In fact, from a certain point of view, the SC1 scenario can be regarded as a special case of the SC2 scenario. Therefore, the optimal selling spread is equal in both scenarios.
Corollary5 : When , exist , ; When , exist , .
Combining the trust advantage with the location advantage, the corresponding price relationship becomes clearer. Specifically, from Corollary 5, when the decision maker has a trust advantage, the spread will be much larger in the absence of a location advantage in both SC2 and SC3 scenarios, while the opposite result is shown in the absence of a trust advantage for the decision maker. It can be said that the correlation between price differences is closely related to trust advantage and location advantage. In order to reveal more clearly the spread relationships between the various scenarios of cases, Figure 7 provides a visual representation. The vertical axis represents the position of the equilibrium point, e.g., A means equilibrium point locates in location advantage area of merchant A, N indicates that the equilibrium is located in an area where neither merchant has a positional advantage and B denotes equilibrium point locates in location advantage area of merchant B. The horizontal axis scales are SC1, SC2, and SC3, representing the intense, moderate, and weak competition scenarios. Each square represents the spread between two merchants in different cases ( ). Figures 7a and Figures 7b show the spread with and without trust advantage for merchants, respectively.
By analyzing the information in each column of the figure, we can intuitively understand the correlation between spread in a given competitive situation. Specifically, as shown in Figure 8a, it can be seen from the second column that in the moderate competition scenario, the price spread is highest when the equilibrium point is located at position N, followed by positions A and B, respectively. The third column reflects the spread relationship in the weak competitive environment. Compared to the moderate competitive environment, spreads are still at their highest level when the equilibrium is in position N, but at this time spreads are higher in position B than in position A. The second row of the figure shows more visually the result of Corollary 5, that the price spread in the intense competition scenario is equal to the price spread in the moderate competition scenario and greater than the price spread in the weak competition scenario.
There are more factors affecting the spread relationship when the merchant does not have a trust advantage than when the merchant has a trust advantage, and the conclusions obtained are limited. However, it can still be found that the price spread is lowest when the equilibrium point is at position A in the medium competition scenario. In the weak competition scenario, although it is not possible to tell at what position the equilibrium point is located the spread is the largest or the smallest, the spread when the equilibrium point is located at position N is always larger than the spread when it is located at position B.
How will the spread change when the trust advantage expands? Will the spread be similarly affected when the demand of merchants A and B fluctuates? Propositions 4 and 5 give clear answers.
Proposition 4: In intense, moderate, weak scenarios, all exist .
Proposition 4 illustrates that merchant A's competitive edge is directly proportional to its trust advantage at all three competitive levels; therefore, consumer trust in a merchant's decisions elevates their optimal pricing spread relative to competitors.
Proposition 5: When , exist ; When , exist .
Proposition 5 reveals a direct correlation between the value gap and the trust advantage of merchants as the demand relationship between the two companies’ changes. Specifically, when merchant A has a trust advantage, if the demand for merchant A is large, the price difference between it and merchant B will increase accordingly; On the contrary, when lacking this advantage, the more demand from merchant A exceeds that of merchant B, the smaller the pricing difference between the two parties.
The decision-merchants are capable of ascertaining whether it possess a trust advantage and the magnitude of this advantage by scrutinizing the credibility of their offerings among consumers. Especially in oligopolistic markets, it is easier to obtain information on the prices of competitors' products. Hence, meticulous research and evaluation on the price discrepancy between two businesses can unequivocally provide effective strategic direction for operators - that is, adjusting their pricing tactics promptly based on the pricing modifications of competitors, to secure more substantial profit returns in enduring market competition.
Effects of platform pricing on merchant pricing strategies
According to the commission policy of the platform, the platform will charge merchants a commission of for orders with a delivery distance of less than kilometers. When the delivery distance is more than kilometers, the platform will charge an add-on ratio of commission per kilometer on top of the amount. How should merchants adjust their pricing in different scenarios in order to adapt to the adjustment of the commission rate by the platform? The answer is given in Proposition 6.
Proposition 6: (1) The optimal price and of merchant donot change with .
(2) The correlation between and in SC2 and SC3 scenarios is shown in Table 7.
Proposition 6 states that in the cases of SC1 and SC2, when the equilibrium point is at N, merchants A and B do not need to bear the additional commission ratio. Therefore, even if changes, it does not affect the prices and set by merchants. The optimal prices displayed in the third column of Table 7 rise with , and the optimal prices in the fourth column decline with . Obviously, price increases are not always the best strategy for merchants in response to platforms increasing their add-on commission rates.
To cope with this change, businesses can consider four pricing strategies,respectively:
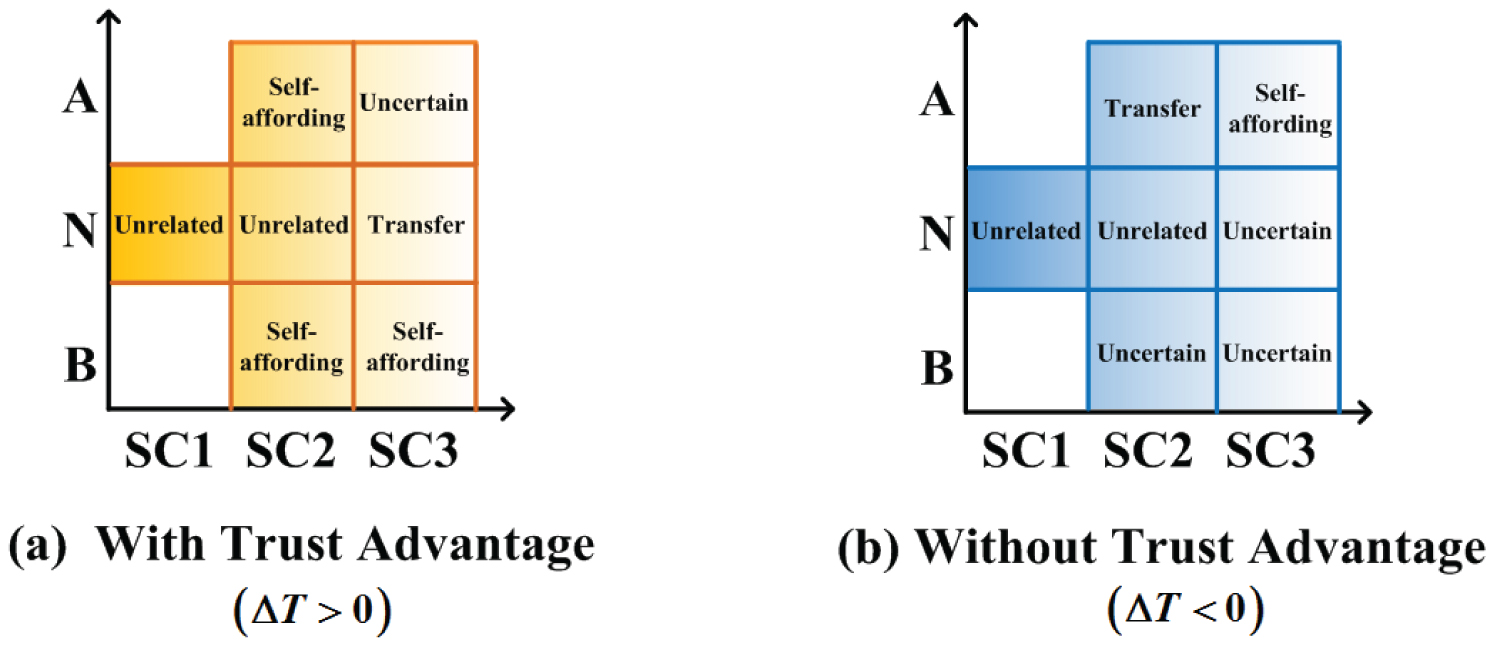
(1) Transfer: It means that when the platform increases add-on commission ratio, merchants also raise prices and transfer the commission costs to consumers. As shown in Figure 8, when merchants have and do not have trust advantages, there is one case where it is recommended that merchants use the transfer strategy. (For example: when , e.g. ; when , e.g. )
(2) Self-affording: It means that when the platform increases the add-on commission ratio, merchants should lower the pricing of their meals and afford the commission cost themselves. As shown in Figure 8, merchants should choose the self-affording strategy in four cases. (For example: when ; ; ; when , )
(3) Uncertain: When the platform increases the add-on commission ratio, the merchant will also need to assess whether they need to adjust their meal pricing upwards or downwards based on other factors, so the merchant's strategy is uncertain. (For example: when , e.g. ; when , e.g. ; ; )
(4) Unrelated: Merchant's optimal pricing remains unaffected by the platform's increased commission ratio. Thus, the merchant doesn't factor this change in pricing. This means that in these cases, merchant pricing is unrelated to the platform's add-on commission ratio. (e.g. ; )
Figure 8 provides a more intuitive display of the most suitable pricing strategies for businesses under various cases. Based on whether the merchant has a trust advantage, it is classified into two categories which are shown in Figure 8a and Figure 8b, respectively.
Conclusion
In the O2O takeaway market, the immediacy of fast delivery services has undoubtedly become one of its most distinctive and indispensable features. This means that compared with other industries, the delivery of O2O catering takeaways has more stringent requirements for logistics efficiency. Obviously, the difference between the geographic locations of merchants and consumers has a direct impact on whether orders can be delivered in the shortest possible time. Delivery in a short period of time is equivalent to saving consumers waiting time cost, and thus naturally becomes one of the key factors that consumers pay attention to when ordering food. Therefore, a merchant has a location advantage when it is closer to the consumer than its competitors. In addition, consumers' trust in the merchant is another important advantage of the merchant. Therefore, the study examines these two key advantages by setting up three levels of market competition: Intense, moderate, and weak. Utilizing the Hotelling model, the equilibrium conditions of the market under the three scenarios are deduced, and a sequence of precise results and conclusions are tabulated.
First, the equilibrium point location may change under different levels of trust advantage. On this basis, the study proves that: In all three scenarios, the optimal pricing of the merchant when the equilibrium point is located in the area where neither merchant has a location advantage is higher than the case where the equilibrium point is located in the other areas; and the trust advantage has a positive effect on raising the price, and the intensity of the competition in the market exacerbates this effect. The study also provides detailed recommendations on pricing strategies based on the level of merchants' trust advantage in different scenarios, which are presented in Table 5.
In addition, by analyzing the optimal pricing in each case, the price gap between merchants is also shown in Figure 6, which reveals that the higher the consumer trust in the decision-making merchant, the greater the price gap between its pricing and that of its competitor. This study on spread helps merchants to understand their pricing relationship with their competitors more accurately and provides an important reference for them to adjust their pricing in order to make more profit.
Finally, the impact of platform commission add-on commission ratio on merchants' pricing strategies is also taken into account. Based on different trust advantages, merchants can adopt four solutions when facing the increase of add-on commission rate by platforms: Transfer, Self-affording, Uncertain, Unrelated, and they are shown in Figure 8 based on specific cases.
In summary, the study of O2O takeaway merchants' pricing strategies considering regional competition based on location and trust advantages provides catering merchants with novel perspectives and solutions for developing pricing strategies. They are provided with targeted and detailed strategy suggestions based on different contexts, which provide decision-making references and management insights for business practices. It is believed that these strategies will enable them to be more flexible and successful in facing challenges in the future market competition. Future research can further expand the study to cover the pricing strategies of merchants under different platform commission modes and uncover more useful management insights.